麦克斯韦速度分布律
合集下载
2.4麦克斯韦速度分布
????242麦克斯韦速度分布maxwellvelocitydistribution麦克斯韦最早用概率统计的方法导出了理想气体分子的速度分布这一分布可表示为?fvxvyvzdvxdvydvzmmexp2????因为fvxvyvzdvxdvydvz?fvxdvxfvydvyfvzdvz?麦克斯韦速度分布有zyxzyxvvvktvvvktddd222223??????????????iiiivktmv2ktmvvfdexp2d221?????????????????其中i可分别代表xyz
•因为f（vx ，vy，vz)= • f(vx)dvxdvx· f(vy)dvy· f(vz)dvz •麦克斯韦速度分布有
m f (vi )dv i 2kT
1/ 2
mv i2 exp 2kT dv i
其中Hale Waihona Puke 可分别代表x、y、z。0
x
误差函数erf(x)有表可查
• [例2.2] 试求在标准状态下氮气分子速 度的x分量小于800m· s-1的分子数占全部 分子数的百分比.
• [解] 首先求出273 K时氮气分子（摩尔 质量Mm=0.028 kg）的最概然速率 .
2 RT vp 402m s 1 Mm
vx 800 ux ~2 vp 402
• ●欲求分子速度的x分量在vx 到vx+dvx内而vy、、 vz任意的分子数dN(vx), • 这就是速度空间中垂直于x 轴的无穷大薄平板中 的代表点数，显然可对vy、vz积分后求出：
dN(v x ) Nf (v x )dvx
f (v y )dvy
f (v z )dvz
dN（vy）/N = f(vy)dvy • dN（vz）/N = f(vz)dvz 分别表示y及z方向速度分量的概率分布函 数。 ●根据处于平衡态的气体的分子混沌性 假设，分子速度没有择优取向，故 f（vx）、f（vy）、f（vz）应具有相同形 式。
•因为f（vx ，vy，vz)= • f(vx)dvxdvx· f(vy)dvy· f(vz)dvz •麦克斯韦速度分布有
m f (vi )dv i 2kT
1/ 2
mv i2 exp 2kT dv i
其中Hale Waihona Puke 可分别代表x、y、z。0
x
误差函数erf(x)有表可查
• [例2.2] 试求在标准状态下氮气分子速 度的x分量小于800m· s-1的分子数占全部 分子数的百分比.
• [解] 首先求出273 K时氮气分子（摩尔 质量Mm=0.028 kg）的最概然速率 .
2 RT vp 402m s 1 Mm
vx 800 ux ~2 vp 402
• ●欲求分子速度的x分量在vx 到vx+dvx内而vy、、 vz任意的分子数dN(vx), • 这就是速度空间中垂直于x 轴的无穷大薄平板中 的代表点数，显然可对vy、vz积分后求出：
dN(v x ) Nf (v x )dvx
f (v y )dvy
f (v z )dvz
dN（vy）/N = f(vy)dvy • dN（vz）/N = f(vz)dvz 分别表示y及z方向速度分量的概率分布函 数。 ●根据处于平衡态的气体的分子混沌性 假设，分子速度没有择优取向，故 f（vx）、f（vy）、f（vz）应具有相同形 式。
04麦克斯韦速率分布律
速率分布函数
速率分布函数的物理意义： 附近， 速率分布函数的物理意义：表示在速率 v 附近，单位 速率区间内分子出现的概率， 速率区间内分子出现的概率，或单位速率区间内分子 数占总分子数的百分比。 数占总分子数的百分比。
由于全部分子百分之百地分布在由0到 由于全部分子百分之百地分布在由 到∞的整个速率范 围内， 取v = 0, v → ∞, 则有 : 围内， 1 2 ∞ N dN 归一化条件
dNv m 2 −mv2 2kT 2 π =4 v dv e N π 2 kT
3 2
麦克斯韦速率分布函数
m π f (v) = 4 e π 2 kT
−m 2 v
2kT 2
v
6
讨论： 讨论： 1. f(v)~v曲线 曲线
v = 0时 f (v) = 0 v → ∞时 f (v) → 0
M
∆N1v1 + ∆N 2 v2 + L + ∆N N v N n ∆N ivi 平均速率： 平均速率：v = =∑ i =1 N N N vdN ∞ dN Q = f (v) dv ∴ v = ∫ vf (v)dv v = ∫1 0 N N 11
v = ∫ vf (v)dv = ∫0
利用积分公式 ∫
麦克斯韦速率分布率
1
气体中个别分子的速度具有怎样的数值和方向完 全是偶然的，但就大量分子的整体来看， 全是偶然的，但就大量分子的整体来看，在一定的条 件下，气体分子的速度分布也遵从一定的统计规律。 件下，气体分子的速度分布也遵从一定的统计规律。 这个规律也叫麦克斯韦速率分布律 麦克斯韦速率分布律。 这个规律也叫麦克斯韦速率分布律。
∆N N∆v
4. ∆v → dv 速率间隔很小， 速率间隔很小， 该区间内分子数为dN， 该区间内分子数为 ， 在该速率区间内分子的概率
大学物理05_5麦克斯韦速率分布律
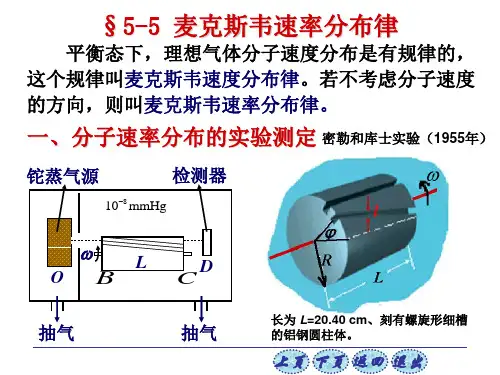
气体分子速率可以取从0到∞之间
的一切数值。速率很大和速率很
小的分子数所占的比率都很小，
f(0)=f(∞)=0 ， 而 具 有 中 等 速 率 的
分子数所占的比率却很大。
上页 下页 返回 退出
例题5-5 从速率分布函数推算分子的三个统计速率
(1)算术平均速率
v
vf (v)dv
v4π(
m
)
3
2
O
v exp
mv2 2kT
共同作用的结果。
上页 下页 返回 退出
麦克斯韦（James Clerk Maxwell 1831—1879）
•他提出了有旋电场和位移电流概念，建 立了经典电磁理论（麦克斯韦方程组）， 预言了以光速传播的电磁波的存在。
•1873年，他的《电磁学通论》问世，这 是一本划时代巨著，它与牛顿的《自然哲 学的数学原理》并驾齐驱，它是人类探索 19世纪伟大的英国 电磁规律的一个里程碑。 物理学家、数学家。 经典电磁理论的奠 •在气体动理论方面，他还提出气体分子 基人，气体动理论 按速率（速度）分布的统计规律。 的创始人之一。
当 v 0时，v dv ；N dN； 2. 速率分布函数 f(v) 的定义 f(v)
f (v) lim N dN v0 vN Ndv
注意：
在平衡态下，f(v)仅是v的函数。 O
v v+Δv
v
上页 下页 返回 退出
3. 速率分布函数 f(v) 的意义：概率密度函数
※分布在速率 v 附近单位速率间隔内的分子数占总 分子数的百分比(比率)；
m不变，T vp
2kT m
曲线的峰值右移，由于曲线下 面积为1不变，所以峰值降低。O
T2 T1
7-(4-5)麦克斯韦速率分布
(1) 不同温度下的同种气体
f (v)
T 1
T2 > T 1
T2
v
T > T2 , orT < T2 ? 1 1
vp1 = 2RT 1
vp1 vp2
2RT2
µ
vp2 =
µ
vp1 < vp2
T < T2 1
第六章 气体动理学理论 (2) 同温度下的不同种气体
f (v)
O2 , H2 ?
1
2RT
2
v
vp1 vp2
对于一定量的气体，在温度为T的平衡态下 的平衡态下， 对于一定量的气体，在温度为 的平衡态下，气体分子速率 出现在v附近 单位速率区间内的分子数dN 附近、 出现在 附近、单位速率区间内的分子数
说出下列各式的物理意义
第六章 气体动理学理论
(4)∫ f (v)dv= ∫
v1
v2
v2
v1
∆Nv1 →v2 dN dv = Ndv N
对于一定量的气体，在温度为 的平衡态下 的平衡态下， 对于一定量的气体，在温度为T的平衡态下，气体分子速率 占总分子数N的百分比 概率 概率)。 v1～v2区间内的分子数△N占总分子数 的百分比 (概率 。 占总分子数
(5)∫ Nf (v)dv = ∫
v1
v2
dN N = ∆Nv1→v2 N
对于一定量的气体，在温度为T的平衡态下 的平衡态下， 对于一定量的气体，在温度为 的平衡态下，气体分子速率 v1～v2区间内的分子数△N。 。
一、分子速率分布函数
速率分布： 速率分布：各种不同速率范围内的分子数占总分子数的 百分比为多大。 百分比为多大。
伽 耳 顿 板
第六章 气体动理学理论
f (v)
T 1
T2 > T 1
T2
v
T > T2 , orT < T2 ? 1 1
vp1 = 2RT 1
vp1 vp2
2RT2
µ
vp2 =
µ
vp1 < vp2
T < T2 1
第六章 气体动理学理论 (2) 同温度下的不同种气体
f (v)
O2 , H2 ?
1
2RT
2
v
vp1 vp2
对于一定量的气体，在温度为T的平衡态下 的平衡态下， 对于一定量的气体，在温度为 的平衡态下，气体分子速率 出现在v附近 单位速率区间内的分子数dN 附近、 出现在 附近、单位速率区间内的分子数
说出下列各式的物理意义
第六章 气体动理学理论
(4)∫ f (v)dv= ∫
v1
v2
v2
v1
∆Nv1 →v2 dN dv = Ndv N
对于一定量的气体，在温度为 的平衡态下 的平衡态下， 对于一定量的气体，在温度为T的平衡态下，气体分子速率 占总分子数N的百分比 概率 概率)。 v1～v2区间内的分子数△N占总分子数 的百分比 (概率 。 占总分子数
(5)∫ Nf (v)dv = ∫
v1
v2
dN N = ∆Nv1→v2 N
对于一定量的气体，在温度为T的平衡态下 的平衡态下， 对于一定量的气体，在温度为 的平衡态下，气体分子速率 v1～v2区间内的分子数△N。 。
一、分子速率分布函数
速率分布： 速率分布：各种不同速率范围内的分子数占总分子数的 百分比为多大。 百分比为多大。
伽 耳 顿 板
第六章 气体动理学理论
麦克斯韦分子速率分布定律的推导
麦克斯韦分子速率分布定律的推导麦克斯韦分子速率分布定律是分子运动理论中一个重要的概念，它用来描述分子或微粒在一定条件下的速率分布情况。
它表明，当以相同速率出射分子时，在不同瞬间可以得到不同的分子速度，而这些分子速度是具有特定分布函数的随机变化，这个分布函数就是麦克斯韦分子速率分布函数。
一般来说，微粒的运动属于无序性运动。
在实验中，出射的分子速度的分布状况不容易分析，只能藉助于实验结果推断出微粒速度的分布规律。
而麦克斯韦分子速率分布定律是1859年俄国物理学家麦克斯韦（Maxwell）推导出来的一个概念，他结合热力学原理和拉格朗日机械统计原理，以蒙特卡洛方法推导出了质点和分子在不同温度下的速率分布情况，结果发现分子速度都符合高斯分布，即可以用一个正态分布概率密度函数来对分子速度进行分析，而这就是麦克斯韦分子速率分布定律。
f(v) = 4πa^3v^2exp(-a^2v^2)其中f(v)是速度为v的粒子数，a是系统的温度模式，用a^3来表示。
其定义概括地表示出温室质点和分子在温度T下的速度分布情况。
而推导时最重要的一个步骤就是综合考虑热力学和机械统计原理，通过这两个原理，可以使得统计模型的概率守恒，即有能量的分配都是满足守恒定律的，从而可得到正态分布，即f(v)为高斯分布函数，最后积分得到麦克斯韦分子速率分布定律。
总的来说，麦克斯韦分子速率分布定律可以较为完整地描述出温室质点或分子在某一温度下的运动规律，统计是一种相对稳定的状态。
它在应用到能量或物质传输等实际场合中有重要作用，比如应用到气体流体动力学中。
历史上，麦克斯韦分子速率分布定律有很多改进版本，比如上面函数中的指数可以做出改变，也可以对新的分子进行同样的推导，从而求出其对应的概率分布函数。
因此，麦克斯韦分子速率分布定律仍然是理解物理世界中的质点运动、热力学和机械统计的重要工具，是实验物理学的理论基础。
麦克斯韦速度分布律
m
vP v v2，与 T 成正比，与 m 成反比。
v 用于碰撞和输运过程的统计规律，v2 用于
温度和压强的统计规律。
【例8.8】计算温度为 300K 时，空气分子的最 概然速率、平均速率和方均根速率。
解 空气分子的平均质量 m = 47.98×1027 kg
vP
2kT m
21.381023 300 47.98 10 27
1859年，麦克斯韦首先用碰撞概率方法导出。
8.5.2 麦克斯韦速率分布律
1. 速率分布函数
f (v) dN (v) Ndv
物理意义：速 率 出 现 在v附近的单位速率区间 的分子数，占系统分子 总数的百分比。
或，一个分子的速率出现在v附近的单位速 率区间的概率 速率分布的概率密度
归一化条件： f (v)dv 1
0
2. 麦克斯韦速率分布律
分子在速度空间分布 概率密度为 FM (vx ,vy ,vz )， 分子速率处于球壳内的概 率：
dN (v) N
4πv2dv FM(vx ,vy ,vz )
速率分布函数可写成
fM (v)
dN (v) Ndv
4π v2FM
(vx
,vy
,vz
)
平衡态系统中分子的速率分布函数：
415
m s1
v 8kT 469 m s1 πm
v2 3kT 509 m s1 m
相当于子弹从枪口射出的速度！
8
π a5
8.5.1 麦克斯韦速度分布律 1. 速度分布函数
F (vx
,vy
,vz
)
dN (vx ,vy ,vz ) Ndv xdv y dv z
物理意义：速度出
麦克斯韦速率分布
一般气体、液体、固体及在恒定外场中的经典系统，
只要系统的能量可写成：
分子的动量分量
E
3N
i 1
Pi2 2m
U
(q1 , q2 ,
qi
,
)
广义坐标
分子间相互作用的能量及在外场中的势能之和
气体分子按速率分布的统计规律最早是由麦克斯韦于1859年 在概率论的基础上导出的，1877年玻耳兹曼由经典统计力学中导 出，1920年斯特恩从实验中证实了麦克斯韦速率分布律。
但由前面 u2 u2 知，vrms v 总成立
例1．速率分布函数 f 的v物理意义为：
（Ａ）具有速率v 的分子占总分子数的百分比． （Ｂ）速率分布在v 附近的单位速率间隔中的
分子数占总分子数的百分比．
（Ｃ）具有速率v 的分子数． （Ｄ）速率分布在 v 附近的单位速率间隔中
的分子数．
3
)2
exp(
m1v12 2kT
)
v12dv1
注意
dN 2 N2
f (v2 )dv2
4
(
m2
2 kT
3
)2
exp(
m2v22 2kT
)
v22dv2
混合气中各组分的麦氏分布率不一样，但有一点一定相同：
混合气达到平衡后，各组分的温度T必然相同。
7. 统计物理证明，麦氏分布率不仅适用于理气，也适用于
速率分布函数为：
麦克斯韦速率分布概率密度
f (v) 4 (
m
)
3 2
exp(
mv
2
)
v
2
2 kT
2kT
ቤተ መጻሕፍቲ ባይዱ
麦克斯韦速率分布定律
(4) 平均速率和方均根速率.
f ( )
解：（1）求 C :
C (0 ) (0 0 ) 0 ( 0 )
0
f ( )d 1 C
6
3 0
（2） N 0 ~ 0 / 4 N
0 / 4
0
5 f ( ) d N 32
0 df ( ) （3）最可几速率 0 p d p 2
6.5 麦克斯韦速率分布定律
气体中个别分子的速度大小和方向完全是偶然的 , 但 平衡态下，气体分子的速度分布遵从一定的统计规律 — — 麦克斯韦速度分布定律. 若不考虑分子速度的方向， 这个规律就成为麦克斯韦速率分布定律.
1859年, 麦克斯韦用概率论导出了气体分子速率分布 定律，后由玻尔兹曼使用经典统计力学理论导出. 1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
f (v )
av ， (0 v v 0 ) 0 ， (v v 0 )
2
f (v )
v0 v 求： （1）常量 a 和υ0 的关系 0 （2）平均速率 v v0 （3）速率在 0 之间分子的平均速率 v 2
解： （1）由归一化条件
0
2 0
0
f ( )d 1
3 得 a 3 v0
f ( v)
T1 300K T2 1200K
f ( v)
麦克斯韦速度分布律公式
麦克斯韦速度分布律公式麦克斯韦速度分布律麦克斯韦速度分布律是统计物理学中描述理想气体速度分布的重要定律之一。
它描述了在给定温度下，气体分子速度的分布情况。
以下是与麦克斯韦速度分布律相关的公式和解释说明：麦克斯韦速度分布律公式1.麦克斯韦速度分布函数：f(v) = (m / (2 * π * k * T) )^(3/2) * 4 * π * v^2 * exp(-m*v^2 / (2 * k * T))其中，f(v)是速度的概率密度函数，m是分子的质量，k是玻尔兹曼常数，T是气体的温度，v是速度。
2.平均速度：<v> = ∫(v * f(v)) dv计算麦克斯韦速度分布函数与速度的乘积的积分，求得平均速度。
3.均方根速度：vrms = √(3 * k * T / m)均方根速度描述了气体中分子速度的大小，它是所有分子速度平方的平均值的平方根。
麦克斯韦速度分布律解释以下是对麦克斯韦速度分布律公式的解释说明和例子：1.麦克斯韦速度分布函数公式解释：麦克斯韦速度分布函数表示了在给定温度下，速度在不同取值上的概率密度。
函数中的指数项含有一个负号，指数的绝对值大小与速度的平方成正比，即速度越大，对应的指数项越小，概率越小。
这符合物质中分子速度的分布趋势，常见的速度大都集中在某个范围内。
2.平均速度解释：平均速度表示在给定温度下，所有可能速度的加权平均值。
将速度与麦克斯韦速度分布函数相乘后积分，可以得到平均速度。
这意味着在一个气体体系中，速度的概率分布决定了平均速度的大小。
3.均方根速度解释：均方根速度是速度分布的一种描述方式，它描述了速度的大小和分散程度。
均方根速度是气体中所有分子速度平方的平均值的平方根。
根据麦克斯韦速度分布律，均方根速度与温度呈正比，与分子质量的平方根成反比。
总结麦克斯韦速度分布律是描述气体速度分布的重要定律，通过麦克斯韦速度分布函数、平均速度和均方根速度等公式，我们可以计算在给定温度下，气体分子速度的分布情况。
麦克斯韦速率分布律.pptx
第3页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(1)nf (v)dv
f (v) dN , n N
Ndv
V
nf (v)dv
dN V
表示单位体积内分布在速率区间 v 内v的 dv
分子数。
第4页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度， 说明下式的物理意义：
(2)Nf (v)dv
f (v) dN Ndv
Nf (v)dv dN
表示分布在速率区间 v v 内的dv分子数。
第5页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(3)n v2 f (v)dv
v1
f (v)
dN
,n
N
Ndv
V
n v2 f (v)dv N N N
把这些量值代入，即得
W v＝ 1 v p 50
N＝
N
4
99 100
2
e
99 100
2
1 50
1.66%
第19页/共20页
f (v ) p3
T1
T2
T1 T2 T3
温度越高，速率 大的分子数越多
T3
v v v O
p1 p 2 p3
v
第15页/共20页
气体的三种统计速率
同一温度下不同种气体速率分布比较
f (v)
m1
m1 m2 m3
m2
分子质量越小，速
率大的分子数越多
。
m3
O
v
第16页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(1)nf (v)dv
f (v) dN , n N
Ndv
V
nf (v)dv
dN V
表示单位体积内分布在速率区间 v 内v的 dv
分子数。
第4页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度， 说明下式的物理意义：
(2)Nf (v)dv
f (v) dN Ndv
Nf (v)dv dN
表示分布在速率区间 v v 内的dv分子数。
第5页/共20页
麦克斯韦速率分布律
f (v)为速率分布函数，n为分子数密度，
说明下式的物理意义：
(3)n v2 f (v)dv
v1
f (v)
dN
,n
N
Ndv
V
n v2 f (v)dv N N N
把这些量值代入，即得
W v＝ 1 v p 50
N＝
N
4
99 100
2
e
99 100
2
1 50
1.66%
第19页/共20页
f (v ) p3
T1
T2
T1 T2 T3
温度越高，速率 大的分子数越多
T3
v v v O
p1 p 2 p3
v
第15页/共20页
气体的三种统计速率
同一温度下不同种气体速率分布比较
f (v)
m1
m1 m2 m3
m2
分子质量越小，速
率大的分子数越多
。
m3
O
v
第16页/共20页
麦克斯韦速率分布律
理气
d(m )F (器 dt壁）
真实气体 d (m ) (F 器 壁 f 内 部 )d t 分 子
pi
β
a
修正为
RT
Pb Pi
由于分子之间存在引力 而造成对器壁压强减少 内压强 P i
基本完成了第二 步的修正
内压强 1) 与碰壁的分子数成正比 2) 与对碰壁分子有吸引力作用的分子数成正比
解： 已知 T27 K,3 p1.0at m 1.01 1350 P,a d3.51 0 1m 0
kT 2d 2 p
1 .4 1 3 .1 1 . 3 4 (3 .5 8 1 1 2 0 3 1 0 2 )0 1 7 .0 3 150 6 .9 1 8 0 m
空气摩尔质量为2910-3kg/mol
讨论
麦克斯韦速率分布中最概然速率 v p 的概念
下面哪种表述正确？
v （A） p 是气体分子中大部分分子所具有的速率. v （B） p 是速率最大的速度值. v （C） p 是麦克斯韦速率分布函数的最大值.
（D） 速率大小与最概然速率相近的气体分子的比
率最大.
例 计算在 27C时，氢气和氧气分子的方均
§7-5 麦克斯韦分子速率分布定律
平衡态下，理想气体分子速度分布是有规律的， 这个规律叫麦克斯韦速度分布律。若不考虑分子速 度的方向，则叫麦克斯韦速率分布律。
麦克斯韦速率分布律: 1、速率分布率的实验测量 2、 分布函数及其意义 3、 麦克斯韦速率分布函数 4、 速率分布函数的应用
1.测定气体分子速率分布的实验
m ( H 2 ) m ( O 2 )
o
2000 v/ms1 vp(H 2)vp(O 2)
vp(H2) vp(O2)
麦克斯韦速度分布定律
麦克斯韦速度分布定律麦克斯韦速度分布定律是描述气体分子速度分布的统计规律之一，由19世纪末的苏格兰物理学家詹姆斯·麦克斯韦提出。
该定律在热力学和统计物理学中有着广泛的应用，能够揭示气体分子运动特征，对于理解气体动力学和热传导等现象具有重要意义。
根据麦克斯韦速度分布定律，理想气体分子的速度服从麦克斯韦-玻尔兹曼速度分布。
其概率密度函数为：f(v) = (m / (2πkT))^(3/2) * 4πv^2 * e^(-mv^2 / (2kT))其中，f(v)表示速度为v的分子的概率密度，m为分子质量，k为玻尔兹曼常数，T为气体温度。
该概率密度函数描述了气体分子速度的分布情况。
根据这一函数，可以得到气体分子不同速度下的概率密度，以及平均速度、平均速度的平方等相关参数。
麦克斯韦速度分布定律具体刻画了速度分布的趋势，从而为研究气体热力学性质提供了重要依据。
根据麦克斯韦速度分布定律可以得到以下几个重要结论：1. 峰值速度：麦克斯韦速度分布定律的概率密度函数在具体速度处取得最大值，即存在一个峰值速度。
这个峰值速度与气体的温度和质量有关，温度越高或质量越小，峰值速度越大。
2. 平均速度：根据麦克斯韦速度分布定律，可以计算出气体分子的平均速度。
平均速度与系统的温度有关，随着温度的升高，平均速度也增加。
3. 速度分散度：麦克斯韦速度分布定律还可以用来计算气体分子速度的分散度。
速度分散度可以通过计算速率最大值附近的速度范围来确定。
由于速度分散度对于描述气体的输运性质至关重要，因此，该定律在研究气体动力学和热学性质时经常被应用。
麦克斯韦速度分布定律是热力学和统计物理学中的重要模型，它将分子速度的概率分布与系统的热力学性质联系在一起。
通过该定律，我们可以更好地理解气体分子的运动规律，研究气体的输运性质和热传导现象。
同时，在工程和科学领域的应用中，麦克斯韦速度分布定律也为材料设计、能源开发和天文物理学等提供了重要指导。
(24) 麦克斯韦气体分子速率分布定律 2
vv1 ~ v2 vf (v )dv
v2 v1
对于v的某个函数g(v)，一般地，其平均值可以表示为
g(v )
0
g(v ) f (v )dv
0
f (v )dv
（24）麦克斯韦速率分布律、三大速率 思考题：解释下列表达式的含义 ① f (v )dv 表示分布在速率v 附近
气体动理论
v0 3 0 v0 3 0
vdN dN
v0 3 0
6 2 N 3 v (v 0 v )dv v0 3v 0 7 N 27 14
（24）麦克斯韦速率分布律、三大速率
气体动理论
讨 速率介于v1~v2之间的气体分子的平均速率的计算 论
vv1 ~ v2
v2
v1 v2 v1
vf (v )dv f (v )dv
气体动理论
实验装置
接抽气泵
2
l v
Hg
金属蒸汽 狭 缝
v l
显 示 屏
l
2
（24）麦克斯韦速率分布律、三大速率 (3)速率介于0~v0/3之间的分子数
气体动理论
N dN Nf (v )dv
v0 3 0
v0 3 0
6 7N N 3 v (v 0 v )dv 27 v0
(4)速率介于0~v0/3之间的气体分子平均速率为
v 0 ~ v0
3
N /( Nv)
N ：分子总数
S
o
v v v
v
（24）麦克斯韦速率分布律、三大速率
气体动理论
N 1 N 1 dN 分布函数 f ( v) lim lim v0 Nv N v0 v N dv
p8_3麦克斯韦速度分布律
{范例8.3} 麦克斯韦速度分布律
麦克斯韦认为：在任何方向，在单位速度间隔v~v + dv 内的分子数dN与总分子数N0的比值的分布规律为
2 d N m1 m v F () v ( )/2 e x p ( ) Nv d 2 π k T 2 k T 0
其中，k是玻尔兹曼常数k = 1.38×10-23J/K，T是热力学温度，m 是分子的质量，v是某方向的速度。F(v)就称为麦克斯韦速度分 布律。(1)氧气分子的分子量为32，氧气分子在300K到600K时 (温度间隔为100K)，速度分布曲线有什么异同？(2)氢气、氦气、 氖气、氮气、氧气和氟气分子的分子量分别为2、4、20、28、 32和38，这些气体分子在300K时的速度分布曲线有什么异同？
温度取300K，不论 分子质量如何，各种 气体分子的速度分布 曲线都是对称的。 当气体温度一定 时，分子的质量 越大则峰值越高， 说明：在相同的 速度间隔内，速 度小的分子数目 越多，速度大的 分子数目越少。
也就是说：在 相同温度下， 质量较大的分 子运动的剧烈 程度较小。
11 /2 2 1 ( ) e x p ( x ) d x 因而得 设 x π m 1 / 2 是归一 1 2 可知： ( ) e x p ( x) d x π 可以证明 化常数。 0 2 πkT 2
m v 2kT
F(v)的单位是速度单位的倒数，即s/m。 质量一定的分子，温度是参数，麦克斯韦速 度分布函数的曲线形状由温度这个参数决定。
{范例8.3} 麦克斯韦速度分布律
麦克斯韦认为：在任何方向，在单位速度间隔v~v + dv 内的分子数dN与总分子数N0的比值的分布规律为
2 d N m1 m v F () v ( )/2 e x p ( ) Nv d 2 π k T 2 k T 0
麦克斯韦认为：在任何方向，在单位速度间隔v~v + dv 内的分子数dN与总分子数N0的比值的分布规律为
2 d N m1 m v F () v ( )/2 e x p ( ) Nv d 2 π k T 2 k T 0
其中，k是玻尔兹曼常数k = 1.38×10-23J/K，T是热力学温度，m 是分子的质量，v是某方向的速度。F(v)就称为麦克斯韦速度分 布律。(1)氧气分子的分子量为32，氧气分子在300K到600K时 (温度间隔为100K)，速度分布曲线有什么异同？(2)氢气、氦气、 氖气、氮气、氧气和氟气分子的分子量分别为2、4、20、28、 32和38，这些气体分子在300K时的速度分布曲线有什么异同？
温度取300K，不论 分子质量如何，各种 气体分子的速度分布 曲线都是对称的。 当气体温度一定 时，分子的质量 越大则峰值越高， 说明：在相同的 速度间隔内，速 度小的分子数目 越多，速度大的 分子数目越少。
也就是说：在 相同温度下， 质量较大的分 子运动的剧烈 程度较小。
11 /2 2 1 ( ) e x p ( x ) d x 因而得 设 x π m 1 / 2 是归一 1 2 可知： ( ) e x p ( x) d x π 可以证明 化常数。 0 2 πkT 2
m v 2kT
F(v)的单位是速度单位的倒数，即s/m。 质量一定的分子，温度是参数，麦克斯韦速 度分布函数的曲线形状由温度这个参数决定。
{范例8.3} 麦克斯韦速度分布律
麦克斯韦认为：在任何方向，在单位速度间隔v~v + dv 内的分子数dN与总分子数N0的比值的分布规律为
2 d N m1 m v F () v ( )/2 e x p ( ) Nv d 2 π k T 2 k T 0
麦克斯韦速率分布律
dN m 3 / 2 mv 2 / 2 kT 2 f ( v) 4 ( ) e v Ndv 2 π kT
23 ´ 当m 2 10 g , T 273k , V 800m / s
f (800) 10 什么含义
6
在800-800+dv速率区间，单位速 率区间分子数占总分子数之比
f (v ) d v
0 v0 2 av d v 0
0
1 3 av 0 3
3 a 3 v0
（2）设总分子数为N， 则
v
v 0
Nf (v ) d v N
2
v 0
f (v ) d v
v0 v 0
a 4 1 3 4 3 av d v v 0 ( 3 )v 0 v 0 4 v0 4 4
m 1.45 1.50 1.55 1.60 1.65 1.70 1.75 1.80 1.85 1.90 1.95
总人数1380 1.50-1.55m的人数130
30 25 20 15 10 5 0 25 26 26 26 27
1.51
1.52
1.53
1.54
1.55
1.56
50 40 30 20 10 0
N v d N v 0 N d Nv 0
i
N v 0
d Nv N
v 0
f (v ) d v
8kT 8RT 对麦氏速率分布经计算得： v πm π
v (v ) f (v ) d v
0
规律：任意v 的函数(v)对 全体分子的平均值都可以用 速率分布函数由上式求得：
麦克斯韦速率分布定律
υ 附近单位速率区
间的分子数
(5) nf ()d N dN dN
VN V
单位体积中速率在υ ~ υ+dυ区间的分子数
(6) 2 f ()d 1
dN N
N1 2 N
速率在υ1 ~ υ2区间的分
子数占总分子数的百分比
(7) 2 Nf ()d 1
1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
p (O2 ) 500 m/s
例4. 设某气体的速率分布函数为
f (v )
av 2，(0 v v0 )
0 ， (v v 0 )
f (v )
求：（1）常量 a 和υ0 的关系 0 v0
v
（2）平均速率 v
（3）速率在 0 v 0 之间分子的平均速率v
2
解：（1）由归一化条件
(1) f () dN Nd
(2) f ( )d dN
N
υ附近单位速率区间的分子
数占总分子数的百分比
速率在υ ~ υ+dυ区间的分
子数占总分子数的百分比
(3) N f ()d N dN dN
N
速率在υ ~ υ+dυ
区间的分子数
(4) N f () N dN dN Nd d
f ()
T1
T2 T1
T2
p
2kT m
麦克斯韦速率分布定律
1859年, 麦克斯韦用概率论导出了气体分子速率分布 定律，后由玻尔兹曼使用经典统计力学理论导出.
1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
氧气分子在 0ºC 时的分子速率分布
(m / s)
100以下
N / N (%)
1.4
100－200
8.1
200－300
16.5
300－400
21.4
400－500
20.6
500－600
15.1
600－700
9.2
700－800
4.8
800－900
2.0
二．气体分子速率分布 N /(Nv)
p (O2 ) 500 m/s
例4. 设某气体的速率分布函数为
f (v )
av 2，(0 v v0 )
0 ， (v v 0 )
f (v )
求：（1）常量 a 和υ0 的关系 0 v0
v
（2）平均速率 v
（3）速率在 0 v 0 之间分子的平均速率v
2
解：（1）由归一化条件
N
0 / 4 0
f ()d
5N 32
（3）最可几速率
df () d p
0p
0
2
（4）
f
( )d
0
0
2
rms
2
[
1920年史特恩用分子束实验, 获得分子有着确定的速 度分布的信息, 但未能给出定量的结果. 1934年我国留学 生葛正权在伯克利首次获得此定律的精确实验验证. 此 成功经报界报道, 当时闻名欧美, 在很大程度上改变了外 国人眼中“中国留学生只会读书不能动手, 我们不欢迎” 的形象, 对当时欧美中国留学生有极大的影响和鼓舞.
氧气分子在 0ºC 时的分子速率分布
(m / s)
100以下
N / N (%)
1.4
100－200
8.1
200－300
16.5
300－400
21.4
400－500
20.6
500－600
15.1
600－700
9.2
700－800
4.8
800－900
2.0
二．气体分子速率分布 N /(Nv)
p (O2 ) 500 m/s
例4. 设某气体的速率分布函数为
f (v )
av 2，(0 v v0 )
0 ， (v v 0 )
f (v )
求：（1）常量 a 和υ0 的关系 0 v0
v
（2）平均速率 v
（3）速率在 0 v 0 之间分子的平均速率v
2
解：（1）由归一化条件
N
0 / 4 0
f ()d
5N 32
（3）最可几速率
df () d p
0p
0
2
（4）
f
( )d
0
0
2
rms
2
[
麦克斯韦气体分子速率分布律
速率区间 （m/s）
100以下 100～200 200～300 300～400 400～500 500～600 600～700 700～800 800～900
900以上
分子数出现的概率 ΔN/N
0.014 0.081 0.165 0.214 0.206 0.151 0.092 0.048 0.020 0.009
25
7-6 麦克斯韦气体分子速率分布律
第七章 气体动理论
1865年春辞去教职回到家乡系统地总结他的关于 电磁学的研究成果，完成了电磁场理论的经典巨著 《论电和磁》，并于1873年出版。1871年受聘为剑桥 大学新设立的卡文迪什实验物理学教授，负责筹建著 名的卡文迪什实验室，1874年建成后担任这个实验室 的第一任主任，直到1879年11月5日在剑桥逝世。
(v)dv
N
v1
N
表示在速率v1～v2速率区间内， 分子出现的概率。
(4)
v2
Nf (v)dv N
表示在速率v1 ～ v2速率区间内， 分子出现的个数。
v1
20
7-6 麦克斯韦气体分子速率分布律
麦克斯韦速率分布律的实验 验证
麦克斯韦在 1860 年 从理论上预言了理想气 体的速率分布律。60 年 后，也就是 1920 年斯特 恩通过实验验证了这一 规律，后来密勒和库将 实验进一步完善。
ΔN→0
v
N vdN
vf (v)dv
0N
0
14
7-6 麦克斯韦气体分子速率分布律
第七章 气体动理论
2.平均速率 v
v 0 vf (v)dv
代入麦克斯韦理想气体的速率分布函数：
v 4
m
3
/
2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 2
m(v
2 x
v
2 y
vz2 )
动能，分子速度的函数。
k
dN (vx ,vy ,vz ) e kT dvxdvydvz
速度分布函数：F (v x
,vy
,vz
)
dN (vx ,vy ,vz ) Ndvxdv ydvz
C
k
e kT
常数 C 由归一化条件确定：
v3e
mv2 2kT
dv
0
4π
m 2π kT
3
2
2(m
1 2kT )2
8kT πm
8RT
π
速度平方的平均值 ：
v2
0
v2
fM (v)dv
4π
m 2π kT
3
2
v
4e
mv 2 2kT
dv
0
4π
m 2π kT
3
积内的概率 分子在速度空间分布的概率密度
归一化条件 ：
F (vx ,vy ,vz )dvxdvydvz 1
分子速度 vx、vy、vz 一定出现在 之间
证明：
F(vx ,vy ,vz )dvxdvydvz
dN (vx ,vy ,vz ) N 1
,vy
,vz
)
平衡态系统中分子的速率分布函数：
fM
(v)
4π
m 2π kT
3
2
v2e
mv2 2kT
麦克斯韦速率分布律 实验验证
fM
(v)dv
dN (v) N
fM (v)dv 1
0
分子的最概然速率：
vP
2kT m
2RT
8.5.3 平均速率 方均根速率
415 m s1
v 8kT 469 m s1 πm
v2 3kT 509 m s1 m
相当于子弹从枪口射出的速度！
vP v v2，与 T 成正比，与 m 成反比。
v 用于碰撞和输运过程的统计规律，v2 用于
温度和压强的统计规律。
【例8.8】计算温度为 300K 时，空气分子的最 概然速率、平均速率和方均根速率。
解 空气分子的平均质量 m = 47.98×1027 kg
vP
2kT m
21.381023 300 47.98 10 27
k
1
F (vx ,vy ,vz )dvxdvydvz C
e kT dvxdvydvz
C
e dv dv dv
m
(v
2 x
v
2 y
v
2 z
)
2kT
x yz
C
3
e
m v2x 2kT
dv x
归一化条件： f (v)dv 1
0
2. 麦克斯韦速率分布律
分子在速度空间分布 概率密度为 FM (vx ,vy ,vz )， 分子速率处于球壳内的概 率：
dN (v) N
4πv2dv FM(vx ,vy ,vz )
速率分布函数可写成
fM (v)
dN (v) Ndv
4π v2FM
(vx
x4eax2dx 3
0
8
π a5
8.5.1 麦克斯韦速度分布律 1. 速度分布函数
F (vx
,vy
, vz
)
dN (vx ,vy ,vz ) Ndv xdv y dv z
物理意义： 速度出
现在P(vx,vy,vz)点附近， 单位速度空间体积内
的分子数占系统分子
总数的百分比。
或，一个分子的速度出现在单位速度空间体
m：一个分子的质量
k：玻耳兹曼常量 T：系统的温度 麦克斯韦速度分布律
1859年，麦克斯韦首先用碰撞概率方法导出。
8.5.2 麦克斯韦速率分布律
1. 速率分布函数
f (v) dN (v) Ndv
物理意义：速 率 出 现 在v附近的单位速率区间 的分子数，占系统分子 总数的百分比。
或，一个分子的速率出现在v附近的单位速 率区间的概率 速率分布的概率密度
在温度为T 的平衡态下，fM (v)dv 代表：速率处 于v到v+dv区间的分子数占分子总数的百分比。 在该状态下，物理量W(v)的统计平均值：
W W (v) fM (v)dv
分布函 数的用途
0
分子的平均速率：
v
vfM (v)dv
0
4π
m 2π kT
3
2
3
C
2
e
mv
2 x
2kT
dv
x
,
0
mv
2 x
e 2kT dvx
0
1 2
32
2πkT m
,
C
m 2π kT
平衡态系统中分子的速度分布函数：
FM
(vx
,vy
,vz
)
m 2π kT
3
2
e
mv2 2kT
8.5 麦克斯韦分布律 8.5.1 麦克斯韦速度分布律 8.5.2 麦克斯韦速率分布律 8.5.3 平均速率 方均根速率
高斯积分公式（π
0
2a
xeax2 dx
1
0
2a
x2eax2dx 1
0
4
π a3
0
x 3eax2 dx
1 2a 2
N
N
2. 麦克斯韦速度分布律
•已经导出分子按势能的分布：
p
dN( x, y, z) e kT dxdydz
p p ( x, y, z)：势能，分子空间位置的函数。
•推广到分子按动能的分布：
k
dN (vx ,vy ,vz ) e kT dvxdvydvz
k
2
3 8
3kT
(m 2kT )5 m
分子的方均根速率：
v2 3kT 3RT
m
也可由 t
mv2 2
3 kT 2
导出。
•分子的最概然速率：vP
2kT m
2RT
•分子的平均速率： v 8kT 8RT
πm π
•分子的方均根速率： v2 3kT 3RT
m