数字模拟电路第三章 触发器
触发器在模数转换中的应用案例

触发器在模数转换中的应用案例模数转换是电子电路中的重要组成部分,它可以将模拟信号转换成数字信号,以便在数字系统中进行处理和分析。
在实际应用中,为了确保模数转换器的准确性和可靠性,触发器是一种常见且关键的元件。
本文将介绍触发器在模数转换中的应用案例,以展示该技术的重要性和实际效果。
第一种应用案例:模拟信号采样与保持(Sample and Hold)模数转换的首要任务是将连续的模拟信号离散化,常用的方法是进行采样与保持。
触发器在该过程中起到了重要的作用,它可以在特定时刻捕获并保持模拟信号的幅值,以供后续的数字化处理。
以下是一个典型的触发器在模拟信号采样与保持中的应用案例:在一个温度传感器电路中,需要将持续变化的模拟温度信号转换为数字形式,以便进一步的处理和控制。
为了实现这一目标,可以使用一个触发器作为样本保持电路,用于定期采集并保留温度传感器的输出。
触发器的触发信号可以由系统的时钟控制,以确保采样频率的稳定性和一致性。
通过这种方式,模拟温度信号就可以以离散的方式被数字系统所接受和分析。
第二种应用案例:数据同步与校准(Data Synchronization and Alignment)在某些应用场景中,模数转换器可能需要与其他模块或设备进行数据同步和校准,以确保系统的正常运行和数据的准确性。
触发器常常被用来实现数据的同步和对齐,以满足系统的时序要求。
以下是一个触发器在数据同步与校准中的应用案例:在一个高速通信系统中,不同的数据信号来源与模数转换器的输入需要保持同步和一致。
触发器可以在数据输入端与输出端之间起到缓冲和同步的作用。
通过合理地配置触发器的时序和触发条件,可以实现数据的精确同步和时序对齐。
这样,模数转换器就能够准确且稳定地将模拟信号转换为数字信号,以供系统进一步处理和分析。
总结:触发器在模数转换中的应用案例体现了其重要性和实际效果。
通过在模拟信号采样与保持、数据同步与校准等场景中的应用,触发器可以帮助实现高精度和高可靠性的模数转换。
施密特触发器的功能

施密特触发器的功能施密特触发器(Schmitt Trigger)是一种具有正反馈的电路,可以在数字电路和模拟电路中使用。
它的主要作用是将输入信号转换为固定幅值的输出信号,并消除输入信号中的噪声等干扰,增强信号的稳定性和可靠性。
在本文中,我们将深入探究施密特触发器的功能和应用。
首先,施密特触发器的最基本功能是将输入信号转换为固定的输出信号幅值。
这种转换可以通过正反馈电路来实现,该正反馈电路具有双阈值特性。
当输入信号超过某个阈值时,输出信号会从低电平切换到高电平;当输入信号低于另一个阈值时,输出信号会从高电平切换到低电平。
这两个阈值通常称为上升沿和下降沿阈值。
施密特触发器的输出信号是具有固定幅值和干净的状态转换的数字脉冲信号。
此外,施密特触发器还可以用于信号重整,即在信号电平失真或干扰的情况下,重建信号,使其恢复原始状态,保证信号质量。
其次,施密特触发器还可以用于信号滤波。
在实际电路应用中,信号干扰和噪声是常见的问题。
这些噪声信号对正常信号的传输和处理产生不利影响。
为了消除这种噪声信号,可以采用滤波器进行滤波处理。
施密特触发器是一种简单而有效的数字滤波器。
通过调整阈值电平和电路的反馈系数,可以调整滤波器的灵敏度,使其滤除干扰信号并保留所需信号。
施密特触发器还可以通过使用 RC 等滤波器元件来实现模拟滤波器。
此外,施密特触发器还可以用于波形整形。
在各种信号处理应用中,波形整形是一种常见的技术,它可以将信号转换为所需的波形形式。
例如,将正弦波转换为方波信号。
施密特触发器可以用作波形整形器,输出一个固定幅值和固定周期的方波信号。
在实际应用中,波形整形可以将信号转换为数字信号进行数字处理和分析。
最后,施密特触发器还可以用于电路开关和数字比较器。
施密特触发器中的两个阈值可以被看作是电路中的两个状态。
在电路开关应用中,当输入信号超过某一阈值时,施密特触发器将导致电路切换状态。
当用于数字比较器时,施密特触发器可以比较两个输入信号的幅值,并输出一个数字比较信号。
数字电路基础知识

第三章 数字电路基础知识1、逻辑门电路(何为门)2、真值表3、卡诺图4、3线-8线译码器的应用5、555集成芯片的应用一. 逻辑门电路(何为门)在逻辑代数中,最基本的逻辑运算有与、或、非三种。
每种逻辑运算代表一种函数关系,这种函数关系可用逻辑符号写成逻辑表达式来描述,也可用文字来描述,还可用表格或图形的方式来描述。
最基本的逻辑关系有三种:与逻辑关系、或逻辑关系、非逻辑关系。
实现基本逻辑运算和常用复合逻辑运算的单元电路称为逻辑门电路。
例如:实现“与”运算的电路称为与逻辑门,简称与门;实现“与非”运算的电路称为与非门。
逻辑门电路是设计数字系统的最小单元。
1.1.1 与门“与”运算是一种二元运算,它定义了两个变量A 和B 的一种函数关系。
用语句来描述它,这就是:当且仅当变量A 和B 都为1时,函数F 为1;或者可用另一种方式来描述它,这就是:只要变量A 或B 中有一个为0,则函数F 为0。
“与”运算又称为逻辑乘运算,也叫逻辑积运算。
“与”运算的逻辑表达式为: F A B =⋅ 式中,乘号“.”表示与运算,在不至于引起混淆的前提下,乘号“.”经常被省略。
该式可读作:F 等于A 乘B ,也可读作:F 等于A 与B 。
由“与”运算关系的真值表可知“与”逻辑的运算规律为:00001100111⋅=⋅=⋅=⋅= 表2-1b “与”运算真值表简单地记为:有0出0,全1出1。
由此可推出其一般形式为:001A A A A A A⋅=⋅=⋅=实现“与”逻辑运算功能的的电路称为“与门”。
每个与门有两个或两个以上的输入端和一个输出端,图2-2是两输入端与门的逻辑符号。
在实际应用中,制造工艺限制了与门电路的输入变量数目,所以实际与门电路的输入个数是有限的。
其它门电路中同样如此。
1.1.2 或门“或”运算是另一种二元运算,它定义了变量A 、B 与函数F 的另一种关系。
用语句来描述它,这就是:只要变量A 和B 中任何一个为1,则函数F 为1;或者说:当且仅当变量A 和B 均为0时,函数F 才为0。
万里学院-数字电子技术基础-第三章习题及参考答案

第三章锁存器与触发器一、选择题1.N个触发器可以构成能寄存位二进制数码的寄存器。
A.N-1B.NC.N+1D.2N2.一个触发器可记录一位二进制代码,它有个稳态。
A.0B.1C.2D.33.对于D触发器,欲使Q n+1=Q n,应使输入D= 。
A.0B.1C.QD.Q4.存储8位二进制信息要个触发器。
A.2B.3C.4D.85.对于T触发器,若原态Q n=0,欲使新态Q n+1=1,应使输入T= 。
A.0B.1C.QD.Q6.对于T触发器,若原态Q n=1,欲使新态Q n+1=1,应使输入T= 。
A.0B.1C.QD.Q7.在下列触发器中,有约束条件的是。
A.主从JK F/FB.主从D F/FC.同步RS F/FD.边沿D F/F8.对于JK触发器,若J=K,则可完成触发器的逻辑功能。
A.RSB.DC.TD.Tˊ9.欲使JK触发器按Q n+1=Q n工作,可使JK触发器的输入端。
A.J=K=0B.J=Q,K=QC.J=Q,K=QD.J=Q,K=0E.J=0,K=Q10.欲使JK触发器按Q n+1=Q n工作,可使JK触发器的输入端。
A.J=K=1B.J=Q,K=QC.J=Q,K=QD.J=Q,K=1E.J=1,K=Q11.欲使JK触发器按Q n+1=0工作,可使JK触发器的输入端。
A.J=K=1B.J=Q,K=QC.J=Q,K=1D.J=0,K=1E.J=K=112.欲使JK触发器按Q n+1=1工作,可使JK触发器的输入端。
A.J=K=1B.J=1,K=0C.J=K=QD.J=K=0E.J=Q,K=0 13.欲使D触发器按Q n+1=Q n工作,应使输入D= 。
A.0B.1C.QD.Q14.下列触发器中,克服了空翻现象的有。
A.边沿D触发器B.主从RS触发器C.同步RS触发器D.主从JK触发器15.下列触发器中,没有约束条件的是。
A.基本RS触发器B.主从RS触发器C.同步RS触发器D.边沿D触发器16.为实现将JK触发器转换为D触发器,应使。
数电触发器PPT演示课件PPT113页
Qn
Q n1
J
0
0
0
0
1
1
1
0
1
1
1
0
第29页,共113页。
5.2.5 电位触发方式的工作特性
电位触发方式——当钟控信号CP为低(高)电平时,触 发器不接受输入激励信号,触发器状态保持不变;当钟控信号CP 为高(低)电平时,触发器接受输入激励信号,状态发生转 移。
电位触发方式的特点: 在约定钟控信号电平(CP=1或CP=0)期间,输入激励信号
/RD=×
/ SD=1
/RD=1 /SD=0
/RD=1 /SD=×
/RD /SD 00
Qn+1 ×
功能 不定
0
1
01
0
置0
/RD=0 /SD=1
10 1
置1
1 1 Qn 保持
①当触发器处在0状态,即Qn=0时,若输入信号 RDSD=01 或11,触发器仍为0状态;
若 RDSD=10,触发器就会翻转成为1状态。
化,输出马上跟着改变。
在时序电路中,常常希望输入信号只作为输出变化的条件, 何时开始翻转要由节拍器(时钟)来决定。显然基本触发器不具 有这样的功能。
给触发器加一个时钟控制端CP,只有在CP端上出现时钟脉 冲时,触发器的状态才能改变。这种触发器称为钟控触发器。
钟控触发器具有按时钟拍节工作的特点,下面我们
②当触发器处在1状态,即Qn=1时,若输入信号 RDSD=10 或11,触发器仍为1状态;
若 RDSD=01,触发器就会翻转成为0状态。
11
第12页,共113页。
B、激励表是用表格的方式表示触发器从一个状态变化到另一个状态或保持原状态不变
数字逻辑课后答案 第三章

第三章 时序逻辑1.写出触发器的次态方程,并根据已给波形画出输出 Q 的波形。
解:2. 说明由RS 触发器组成的防抖动电路的工作原理,画出对应输入输出波形解:3. 已知JK 信号如图,请画出负边沿JK 触发器的输出波形(设触发器的初态为0)1)(1=+++=+c b a Qa cb Q nn4. 写出下图所示个触发器次态方程,指出CP 脉冲到来时,触发器置“1”的条件。
解:(1),若使触发器置“1”,则A 、B 取值相异。
(2),若使触发器置“1”,则A 、B 、C 、D 取值为奇数个1。
5.写出各触发器的次态方程,并按所给的CP 信号,画出各触发器的输出波形(设初态为0)解:6. 设计实现8位数据的串行→并行转换器。
B A B A D +=DC B A K J ⊕⊕⊕==Q AQ B Q D Q C Q E Q F Q7. 分析下图所示同步计数电路解:先写出激励方程,然后求得状态方程状态图如下:该计数器是五进制计数器,可以自启动。
8. 作出状态转移表和状态图,确定其输出序列。
解:求得状态方程如下故输出序列为:000119. 用D 触发器构成按循环码(000→001→011→111→101→100→000)规律工作的六进制同步计数器解:先列出真值表,然后求得激励方程PS NS 输出N0 0 0 0 0 1 00 0 1 0 1 1 0 0 1 1 1 1 1 0 1 1 1 1 0 1 0 1 0 1 1 0 0 0 1 0 0 0 0 0 1化简得:逻辑电路图如下:n Q 2n Q 1n Q 012+n Q 11+n Q 10+n Q n n n nn n n n n n nnQ Q Q Q Q Q Q Q Q Q Q Q Z 121002*********+==+==+++nnn nnn nnnn QQ Q D QQ Q D QQ Q Q D 121211121122+====+==+++10. 用D 触发器设计3位二进制加法计数器,并画出波形图。
模拟电路与数字电路教程

1 - 8 支路电流法
• 利用KCL对 n 个节点列 出n-1个电流方程; • 利用KVL 对 m个网孔列 出m个电压方程, 联立解之.
R1 20 I1 R2
例: 如图求各支路电流 解:
I1 + I2 - I3 = 0 U1= I1R1 + I3R3 U2 = I2R2 + I3R3
联立解得:
一、串联 两个以上电阻串行 连接称为串联。 Rab = R1 + R2 a b a b R1 R2 R1 R2
二、并联
两上以上电阻并行联 接称 并 联。 Rab = R1 // R2 1 = 1 + 1 Rab R1 R2 即
Rab =
R1R2 R1 + R2
12
例:求下图等效电阻Rab。已知各电阻均为10
5
绪论 电子技术的应用领域
计算机、自动控制
雷达技术
航空航天
电视技术
通信技术
6
计算机控制系统
采样 0 采样 1 采样 n ••• ••• 多 路 模 拟 开 关 显示器 放 大 器
ADC
计 算 机
DAC
功 率 放 大
传 感 器
随 动 系 统
执行机构
7
上
篇
模拟电子技术
第一章
1- 5 基尔霍夫定律
例 : 求I =?
解:选择参考点;
将 a b 断开。
1. Uab = (-150 + 20 ) - (-120) = - 10V 2. R0 = Rab = 0 Uab 3. I = = - 1A R4
•
R3
I • •
R1 R2
b •
• a •
施密特触发器的门限电压

施密特触发器的门限电压1.引言1.1 概述概述部分的内容如下:施密特触发器是一种电子电路元件,它在数字电路和模拟电路中广泛应用。
该触发器是由德国物理学家奥托·施密特于1934年发明的,他的名字也因此得以命名。
施密特触发器具有自锁和去抖动的特性,使得它在许多跳变电压信号处理的应用中非常重要。
在施密特触发器中,门限电压是一个关键参数。
它是触发器切换状态的临界电压值,即当输入电压超过门限电压时,触发器会从一个稳定状态切换到另一个稳定状态。
因此,门限电压直接决定了触发器的灵敏度和可靠性。
本文的目的是探索施密特触发器的门限电压,分析其重要性以及影响因素。
通过深入研究施密特触发器的定义和工作原理,我们将探讨门限电压在触发器性能中的关键作用,并讨论影响门限电压的因素。
这将有助于我们更好地理解和应用施密特触发器,同时推动数字电路和模拟电路领域的发展。
在接下来的章节中,我们将首先介绍施密特触发器的定义和工作原理。
然后,我们将着重讨论门限电压的重要性,包括其在信号处理中的应用和作用机制。
接着,我们将详细讨论门限电压的影响因素,并探究如何调节和优化门限电压的方法。
最后,我们将总结本文的结论,强调门限电压在施密特触发器中的重要性及其未来发展的潜力。
通过本文的研究和分析,我们将更加深入地了解施密特触发器的门限电压,并为进一步探索其应用和改进提供有益的指导。
1.2 文章结构文章结构部分的内容可以按照以下内容进行编写:文章结构部分主要介绍了整篇文章的组织框架和各个部分的内容安排。
本文的结构设计如下:1. 引言:通过对施密特触发器的门限电压进行引言,介绍其概述、文章结构和目的。
2. 正文:详细介绍施密特触发器的定义和工作原理,以便读者对该触发器有一个全面的了解。
具体内容包括:2.1 施密特触发器的定义:介绍施密特触发器的基本概念和定义,包括其在逻辑电路设计中的重要性。
2.2 施密特触发器的工作原理:详细解释施密特触发器的工作原理,包括正反馈回路的作用和门限电压的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
触
Qn+1 D
01
Qn
0
1
发
11
器
4.2 钟控触发器(同步,电平,电位)
4.2.4 钟控T触发器
第 四 章
3、次态卡诺图与次态方程 • 次态方程 ① 当cp=0时,
Qn+1 = Qn
② 当cp=1时,有:
触
发
Qn+1 = T Q + T Q
器
4.2 钟控触发器(同步,电平,电位)
4.2.4 钟控T触发器 4、激励表
第
四 • 在基本R-S触发器基础上增加一个时钟
章
控制端,即CP端。
• 优势:
触 ① 提高触发器的抗干扰能力
发 ② 多个触发器能够在同一个控制信号的作用下同
器
步工作
4.2 钟控触发器(同步,电平,电位)
4.2.1 钟控R-S触发器
第 1、逻辑电路图和符号
四
Q
Q
章
&1
&2
触
发 器
&3
R
&4
CP
S
4.2 钟控触发器(同步,电
次态,用Qn+1、Qn+1表示。
触 • 显然,次态是现态和输入的函数,即:
发
Qn+1=f(Qn,X)
器 此函数表达式叫触发器的次态方程,也叫特
征方程,状态方程。
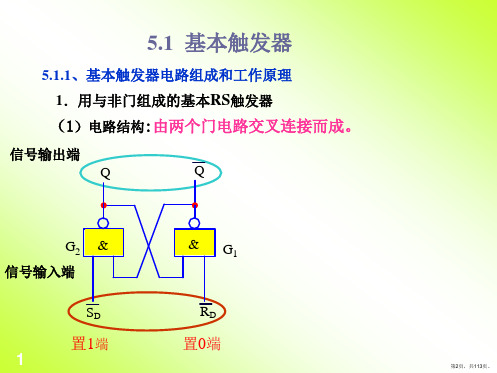
4.1 基本触发器
4.1.3 基本R-S触发器
第 • 基本RS触发器由两个与非门输出交叉反 四 馈而组成。 章 1、逻辑电路图和符号
Q
Q
触 发
CP
1
2
3
4
0
触
D
t
发
0
器
Q
t
0 t
4.4 边沿触发器
4.4.2 边沿J-K触发器
第 四
• 主从JK触发器存在“一次变化现象”, 抗干扰能力较差。
章
• 为了提高触发器的可靠性,增强抗干 扰能力,希望触发器的次态仅仅取决
于CP信号下降沿(或上升沿)到达时
刻输入信号的状态。而在此之前和之
触
后输入状态的变化对触发器的次态没
5、状态图和状态表
第
RS=01
四
0
章
RS=X0
01
10
11 1
RS=0X
01 10 0×
RS=10
触
现态
次态Qn+1
发
Q RS=00 RS=01 RS=11 RS=10
器
00
1×
0
11
1×
0
4.2 钟控触发器(同步,电平,电位)
4.2.1 钟控R-S触发器
第 四
6、小结
• 电路加了一级门电路,用CP统一控制,有效 提高了可靠性,但未能有效地解决空翻现象;
章 • 其次仍存在不定状态,即使用时,需要约束条
件,为了解决不定状态,采用让两路数据成为
互补的数据。 R S Qn+1 功 能
触
0 0 Qn 动态保持
发
0 1 1 置1
器
1 0 0 置0
1 1 × 不确定
4.2 钟控触发器(同步,电平,电位)
4.2.2 钟控D触发器
第 1、逻辑电路图和符号
四
Q
Q
章
00
0
1
1
触
发
11
0
0
1
器
4.2 钟控触发器(同步,电平,电位)
4.2.3 J-K触发器
第 7、小结
四 章
• 消除了“不确定状态”
• 仍存在“空翻”现象
触 发 器
4.2 钟控触发器(同步,电平,电位)
4.2.4 钟控T触发器(计数触发器)
第 1。逻辑图 Q
Q
四
章
&1
&2
触
&3
&4
发
器
R
S
K
CP
J
触
Qn+1 D 01
Qn
00 1
发
10 1
器
4.2 钟控触发器(同步,电平,电位)
4.2.2 钟控D触发器
第 四 章
3、次态卡诺图与次态方程 • 次态方程 ① 当cp=0时,
Qn+1 = Qn
② 当cp=1时,有:
触
发
Qn+1 = D
器
4.2 钟控触发器(同步,电平,电位)
4.2.2 钟控D触发器
R
1 0 1 1 1 0 011 00
触
S
1 1 1 0 1 1 010 01
发
Q
器
Q
4.1 基本触发器
4.1.3 基本R-S触
第
发器
Q
四
章 5、总结
&
• 优点:结构简单
1
• 缺点:
触 发
存在不确定状态,
抗干扰能力不强
R
器
Q
&
2 S
4.2 钟控触发器(同步,电平,电位)
4.2.1 钟控R-S触发器
第
① 当cp=0时,静态保持; Q
四
② 当cp=1时,有:
章 J K Qn+1 功 能
&1
Q
&2
0 0 Qn 动态保持
0 1 0 置0
触 1 0 1 置1
&3
发 1 1 Qn 变反
器
R
K
&4
S
CP
J
4.2 钟控触发器(同步,电平,电位)
4.2.3 J-K触发器
第 3、次态卡诺图与次态方程
四 • 次态卡诺图
第
四 章
• 小结:
① 有两个互补的输出端,两个输入端;
② 输入端的小圆圈表示低电平有效
触 发
③ R称为清零端,复位端,置“0”端 (Reset)
器 ④ S称为置位端,置“1”端(Set)
4.1 基本触发器
4.1.3 基本R-S触发器
注: 两层含义
第 2、功能表
四 • 完整真值表
章
R S Qn Qn+1
• 解:将T端恒接高电平
触 发 器
4.4 边沿触发器
4.4.1 维持阻塞边沿D触发器
第 1。逻辑电路图和符号
四
&
G5
章
&
G3
CP
触
&发G4源自& Q G1& Q G2
D1 D2
&1D Q
SD S
CP RD
C1 R
Q
器
&
D
G6
4.4 边沿触发器
4.4.1 维持阻塞边沿D触发器
第 2。真值表和特性方程
四
CP D Qn Qn+1
章
× × × Qn
00 0
0 1 0 特性方程 Qn+1=D
触
10 1
发
11 1
器
3.CAI演示
4.4 边沿触发器
4.4.1 维持阻塞边沿D触发器
第 四
4。波形图
已知边沿D触发器(正边沿翻转)的时钟信号和输 入信号如图所示,试画出 Q 端的波形,设触发器
章 的初态为Q=0。
T
4.2 钟控触发器(同步,电平,电位)
4.2.4 钟控T触发器
第 2、功能表 四 ① 当cp=0时,静态保持; 章 ② 当cp=1时,有:
T Qn+1 功 能
触
发
0 Qn
保持
器
1 Qn
变反
4.2 钟控触发器(同步,电平,电位)
4.2.4 钟控T触发器
第 3、次态卡诺图与次态方程 四 • 次态卡诺图 章
3、次态卡诺图与次态方程 • 次态方程 ① 当cp=0时,
Qn+1 = Qn
② 当cp=1时,有:
触
发
Qn+1 = S + R ⋅Qn
器
S⋅R = 0
4.2 钟控触发器(同步,电平,电位)
4.2.1 钟控R-S触发器
第 四
4、激励表
• 由已知的Qn+1和Qn的值确定输入端取值的 关系表,叫触发器的激励表。
4.2.3 J-K触发器
第 4、激励表
Qn Qn+1 J K
四
0 0 0×
章
0 1 1×
1 0 ×1
1 1 ×0
触 5、状态图 发
JK=1X
器
0
1
JK=0X
JK=X1
JK=X0
4.2 钟控触发器(同步,电平,电位)
4.2.3 J-K触发器
第 6、状态表
四
章
现态
次态Qn+1
Q JK=00 JK=01 JK=11 JK=10
&1
器
R
&2
S
第
四 4.1 基本触发器
章 4.1.3 基本R-S触发器
2、功能表
Q
• CAI演示 • 功能分析
触
R S Qn Qn+1 00 0 × 00 1 ×
不确定
&
1
发 器
01 0 0
置0
01 1 0
R
10 0 1
10 1
1
置1
11 0 0
11 1
1
保持
Q
&
2 S
4.1 基本触发器
4.1.3 基本R-S触发器
章
J
Qn+1 JK 00
