博赞思维导图二期认证课程02
博赞思维导图 小学第2课 思维导图四大能力

四、分析思维能分析归纳思维能力训练
玫瑰 篱笆 礁石 轮船 章鱼
太阳 月亮 贝壳 海洋 花园
桌子 水池 房子 窗口 椅子
天空 流星 大树 白云 床
注视图形中央的四个黑点30秒,然后闭眼仰头朝上看 天花板,如果你够虔诚,神奇的图像就会慢慢的显现, 你看到了什么?
思维导图制作
“苹果”
作业
“一块砖头的用途”
思维导图的基本特点 ——四大思维能力
一、放射性思维能力
导图特点——发散性
发
1+1=1 2+1=1 3+4=1
散 思 维
1(里)+1(里)=1(公里) 2(月)+1(月)=1(季度) 3(天)+4(天)=1(周)
训
练
4+9=1 5+7=1 6+18=1
发散思维能力训练
1.一天,你在一个陌生的城市中钱包被偷了,证件和钱都 没有了,这时你该怎么办?
自信宣言
我是最棒的! 我是最优秀的! 我有超强的记忆力! 我有超级的想象力! 我有完美的图像思维能力! 我有超人的能力! 我充满自信! 我相信自己就是一座宝藏! 我是最棒的!
“自我介绍”
你是谁? 你爱玩什么? 你喜欢什么? ......
课程学习重点:
1、专注力训练; 2、思维导图的基本特点; 3、思维导图绘制规则 4、思维导图制作练习。
2.用四条直线把所有九个点连接起来,不能移动任何点、
连线必须一笔完成,连线画完成前不能离开纸面。
OOO OOO OOO
수업
二、创造思维能力 导 图 特 点
联 想 性
——
创造思维能力训练 树叶——动物
三、归纳思维能力
获取精神力量的10种方法 东尼·博赞《思维导图》精选导读

也会有最糟糕 的品行 ,如 贪婪、 自私、
剥 削 与残 忍 。这 就 是 人 类 的奇 迹 所 在 。
当然 能 f你 说 的每 一句 话 ,每 一 个
因为生于泥土 ,所以谦卑, 因为星辰锻造 ,所以高贵。
—
举 动 或 创 造 都 会 影 响 到 周 围 的 环 境 和 人 。而 他 们 又 将 影 响 到 别 的 环 境 和 其 他 更 多 的人 ,直 到 无 穷 。 这 种 因果 关系 得 到 混 沌理 论 的 证 明 。 根 据 混 沌 理 论 ,在
迷 ,并 对 此 深 为 敬 畏 。 他 制 作 的 有 关动
么 ,现 在 你 应 该 采 用 以下 方式 进 行精 神
维普资讯
智 能 训练 , 以捕获 “ 景 ” : 全 ★1 提 醒 自己你 是 多 么神 奇 请 提 醒 自 己 ,你 是 一 个 奇 迹 。要 尽
单 、便捷的思雏工具,以大脑 先生 ( . r n)闻名世 MrB a i 界。 曾因帮助 英国查 尔斯王子提高记忆 力而被誉 为英 国
的 “ 忆 力之 父 ” 。 记
生 活 中有许 多愿 望和 目标 。却 找 不 到 实现 它 的指 南
针 。 本 书 引 导 你 领 略 精 神 巨人 的 风 采 。帮 助 你 了解 自 己 ,理 解他 人 ,懂 得 同情 和给 予 ,寻 求 内・ 宁 ,做 一 安 个 精神 富人 . .
既 然 你 已 经 知 道 你 自 己 是 那 么 伟 大 、神 奇 ,你 居 住 的宇 宙 是 那 么浩 淼 无 穷 、 美 丽壮 观 , 自然 造 化 是 那 么令 人 惊 叹 , 你 自 己 的 灵 魂 是 永 恒 的 存 在 , 那
的例 子 。他对 自然 的 美丽和 复 杂 性着
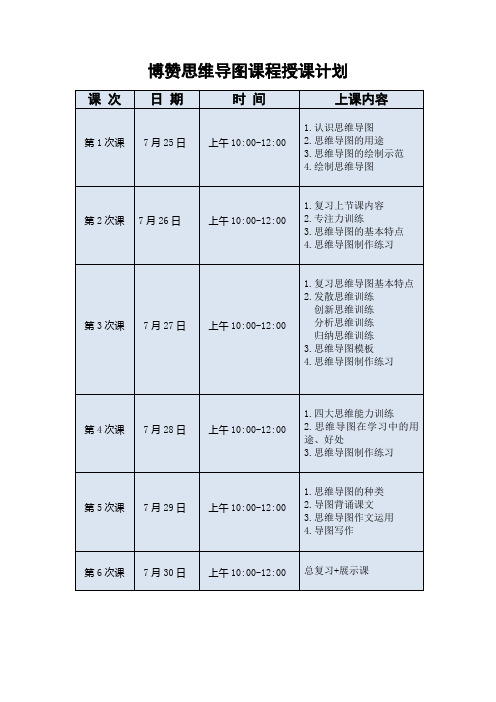
思维导图课程表
课 次
日 期
时 间
上课内容
第1次课
7月25日
上午10:00-12:00
1.认识思维导图
2.思维导图的用途
3.思维导图的绘制示范
4.绘制思维导图
第2次课
7月26日
上午10:00-12:00
1.复习上节课内容
2.专注力训练
3.思维导图的基本特点
4.思维导图制作练习
第3次课
7月27日
上午10:00-12:00
1.复习思维导图基本特点
2.发散思维训练
创新思维训练
分析思维训练
归纳思维训练
3.思维导图模板4.思维来自图制作练习第4次课7月28日
上午10:00-12:00
1.四大思维能力训练
2.思维导图在学习中的用途、好处
3.思维导图制作练习
第5次课
7月29日
上午10:00-12:00
1.思维导图的种类
2.导图背诵课文
3.思维导图作文运用
4.导图写作
第6次课
7月30日
上午10:00-12:00
总复习+展示课
东尼博赞为您讲思维导图

东尼.博赞亲自为您阐释思维导图(mind map)原题为:《全脑经营的革命——思维导图铸就财富人生》【嘉宾介绍】东尼·博赞先生思维研究领域的权威,脑力运动界的鼻祖,思维导图 (MindMap) 思维工具的创始人和推广者,具有着广泛的国际影响力,以下是有关于他的简单介绍:著名大脑潜能和学习方法研究专家。
世界脑力运动发起人和推广者。
思维导图学习工具的创建者、研究权威和推广者。
思维导图在各领域应用的实践者、专家和推广者。
巨大国际影响力的知名人士。
【精彩看点】什么叫思维导图思维导图(mind map)包含三方面思维导图的特点脑图是怎么画思维导图(mind map)怎么运用思维导图的具体作用思维导图和财富的关系思维导图是否适合任何人(14:05:08) 主持人说:各位网友大家下午好,今天下午的直播现在开始,我们今天直播的主题“全脑经营的革命——思维导图(mind map)铸就财富人生”,今天是有关于思维工具的一个主题,就是如何充分利用人的大脑机能发掘自身潜在天赋,成为全社会科学家们共同的课题,东尼.博赞是著名的大脑潜能研究专家、脑力开发权威,他所创的思维导图(mind map)这一行之有效的思维工具。
(14:05:14) 主持人说:今天请东尼.博赞先生跟我们做这方面的分享,前四十分钟时间,在两点到两点四十东尼.博赞先生给我们做一个演讲,两点四十到四点跟我们网友做一个互动。
(14:05:23) 主持人说:请东尼.博赞先生跟各位网友打个招呼?(14:06:02) 东尼·博赞说:各位亲爱的中国朋友们、你们下午好,我非常高兴能够再一次跟我们中国的、东方的学习者,对智力开发有无限兴趣的爱好者,跟大家一起分享人类大脑开发的奥妙。
(14:06:53) 东尼·博赞说:首先我知道各位朋友,可能在在网上了解到思维导图(mind map)这样一个思维工具,也了解到我个人,世界各地很多的朋友了解我当时是为什么能够产生这样一个兴趣来发展思维导图,我想跟大家简单分享一下。
东尼博赞的思维导图

东尼博赞的思维导图“世界大脑先生”东尼·博赞的“思维导图”系列,是一套在全世界销量高达千万册的畅销图书。
系列包括:《思维导图》《启动大脑》《超级记忆》《快速阅读》《博赞学习技巧》共5本。
思维导图系列介绍方法包括“思维导图”方法、“照相式记忆”阅读,博赞有机学习技巧(BOST)专题等。
是东尼·博赞在学习技巧、脑力、学习后回忆、发散性思维、专注力、多维记忆工具和思维导图等领域40多年经验的总结。
包括记忆人名、数字、日期、表格,以及演讲、文章、诗歌,甚至一整本书的方法。
结合了心理学、大脑神经生理学、语义学、神经语言学、信息理论、记忆和助记法、感知理论、创造性思维等科学,将发散性思维与开拓性笔记技巧结合在一起,被人们称为“大脑瑞士军刀”。
思维导图一经出现,即在全球教育界和商界刮起了一场风暴。
目前全世界已有超过3亿人在使用它,并从中受益。
提供了大量实用练习、颇具启发性的图片,以及演示这种技巧的原创性思维导图。
作为精装全彩典藏版,特别由东尼·博赞本人更新了为国际培训课程最新研发和改进的一系列实用训练实例以及很多从未披露的思维导图。
物理学家尼尔斯·玻尔曾经批评学生,“你不是在思考,而只是有逻辑而已”。
因此,我想逻辑并非评估我们思维潜能的标准。
大脑实际上有别于一台有逻辑的电脑。
在21世纪,对大脑的正确认识比以往更显重要。
我们比以往活得时间更长也更健康,但有时候会忘记,如果不能使头脑健全,活得更长更健康是没有意义的。
健全头脑意味着我们的大脑能够活跃运转——有记忆力,高效思考和富于创意——最终实现个人潜能,而这在不久之前曾受制于出身和身体健康的不同;这样我们就可以摆脱某种宿命,从而开创新的人生。
想大脑思维研究的兴起,不仅是因为对如何使人们有更好表现或者甚至拥有更好的记忆力提供解决方案——虽然这些都极受欢迎——而是一些更值得探究的问题。
“什么使得我成为与众不同的那一个?”和“如何伸展我未被开发的潜能?”。
力学知识结构思维导图建构的研究方法和主要目的

力学知识结构思维导图建构的研究方法和主要目的结构力学是土木工程专业非常重要的一门专业基础课,内蒙古农业大学除土木工程专业外,其他开设结构力学的专业有道路桥梁与渡河工程、农业水利工程、水利水电工程、给排水科学与工程、木材科学与工程等。
与其他工科学校相类似,结构力学是继理论力学、材料力学后非常重要的一门力学课程,它为后续钢筋混凝土结构、钢结构、高层建筑结构、桥梁工程等相关专业课程的学习提供必要的力学基础,同时课程中的基本概念、基本原理和方法对以后指导工程设计非常重要,要求同学们重点掌握。
但是,由于结构力学知识点多,部分内容理解上比较抽象,再加上学时有限,教师不能将每个知识点讲得非常透彻,所以大部分同学反映该课程比较难学,因此,如何让同学们准确把握知识点的内涵与相互关系,学会力学分析问题的方法和提高其学习的能力,是所有结构力学授课教师必须面对与思考的问题。
思维导图是表达发散性思维的有效图形思维工具,改变了传统的线性思维模式,将形象思维与抽象思维进行了很好地结合,帮助人们用联想思维进行思考问题,改善记忆和想象力,充分地开发左右脑的无限潜能。
思维导图是发散性的,有助于培养一个人的全面性思维与逻辑性;思维导图是记忆性的,有助于人们学习和记忆各类知识,更高效地完成工作。
笔者尝试将思维导图作为一种工具引入到结构力学教学中,给同学们提供一种学习方法,打通知识点掌握到能力提高的壁垒,调动同学们学习结构力学的兴趣,推动结构力学的教学改革,更好地适应新时代工程教育认证对工科学生提出的具备解决复杂工程问题的能力要求。
一、结构力学课程教学的特点结构力学是研究结构的合理形式以及结构在受力状态下内力、变形、动力反应和稳定性等方面的规律性学科。
传统的结构力学课程具有以下特点:1.知识点多,前后内容环环相扣。
既有平面几何组成规律的内容,也有静力荷载作用下五种基本类型结构(梁、拱、桁架、刚架和组合结构)的内力与位移计算问题,还有影响线问题,结构的动力计算、弹性稳定、塑性分析与极限荷载等内容。
思维导图里有什么——东尼博赞的“思维导图系列”读后
思维导图⾥有什么——东尼博赞的“思维导图系列”读后思维导图⾃上世纪⼋⼗年代传⼊中国以来,受到了越来越多⼈们的重视。
随着越来越多的⼈对思维导图的运⽤,⼤家都深切地感受到它作为⼀种促进思维扩展的⼯具在⾃⼰⼯作学习中起到了不可替代的作⽤,其中有不少⼈结合⾃⼰多年的实践,围绕思维导图著书⽴说,肯定了思维导图能让⾃⼰的⽣活变得更好,也表达了对创始⼈东尼•博赞的⽆⽐敬意,如吴帝德、孙易新等。
⽽我——每天都要处理⼤量⽂字信息的⼀名阅读推⼴馆员,也是思维导图的受益者。
那么,思维导图是什么? 就是运⽤线条、图像、符号,制定⼀套易被⼤脑接受的规则,提升⼈们记忆能⼒的思维⼯具。
它在全世界已经成功改变超过3亿⼈的思维习惯,正⼴泛应⽤于⼈们学习、⼯作、⽣活的各个⽅⾯。
⽽思维导图⾥究竟有什么? 英国著名的⼼理学家、教育学家东尼•博赞的“思维导图系列”中的观点、⽅法,让我有如下感悟和⼼得。
思维导图⾥有醒⼈的世界观我⾃认为是⼀个智⼒平平的⼈,记忆能⼒、思维能⼒⾮常有限。
在关键时刻⾯临选择的时候,总觉得⾃⼰⽆法完成,不能胜任。
这种情绪恶性循环,让我⼀度⾮常⾃卑,以致在学习⼯作中错过了不少机会。
随着年龄的增长,“笨”的阴影始终像毒蛇⼀样缠绕在⼼中。
我、包括⾝边的许多⼈都这么认为:⼈的智⼒⽔平在30岁之前达到巅峰,以后逐年衰退,所以⼈越来越“笨”是⼀个⾃然规律。
然⽽事实上不是这样的,这也是我提笔写书评的原因所在。
作者告诉我们:“纵观⼈的⼀⽣,智能最⾼点和最低点之间的差距不过5%——10%,这⼀衰退幅度与⼤脑巨⼤的潜能相⽐,⼏乎可以忽略不计。
如果⼤脑得到持续的应⽤且能⼒不断拓展,⼈们的智能不会随着年龄的增长⽽降低,记忆能⼒、理解和学习新知识的能⼒也远远超出那些同样勤奋、年轻⽽缺乏经验的⼈”。
也就是说,脑⼒训练是不受年龄限制的。
通过训练,⼤脑可以变得极端敏锐,就像⾝体可以通过饮⾷和锻炼获得健康⼀样。
这是作者在学习了⼤量的⼼理学、⼤脑神经⽣理学、创造性思维等各类学科之后,通过实验后得出的结论。
梦想学习课程思维导图
《思维导图》课程纲要【开发人员】鲍贤清:上海师范大学教育技术系讲师徐夏云:上海师范大学教育技术系硕士研究生,研究方向为绩效技术郭新燕: 上海师范大学教育技术系硕士研究生,研究方向为网络技术与管理杨艳艳: 上海师范大学教育技术系硕士研究生,研究方向为信息化教学设计吴玉莲:上海师范大学教育技术系硕士研究生,研究方向为信息化教学设计吴宙旭:上海师范大学教育技术系硕士研究生,研究方向为网络技术与管理【所需课时】16课时/每课时40分钟【适应年级】1-3年级【课程简介】思维导图是英国学者东尼• 博赞(Tony Buzan )在70 年代所创,它是表达发散性思维有效的图形思维工具。
思维导图符合人类大脑的思考方式和思维方式,它就像大脑中的地图,能够完整地将大脑的思维、想法呈现出来。
手绘是掌握思维导图的基础,通过不断的手绘可以培养学生放射性全面思考问题的习惯,促使学生进行创新性的思考,培养学生的创新能力,而且还是提高学生记忆能力和学习效率的有效工具。
本课程通过初识篇、基础篇让学生在轻松愉快的学习氛围中逐步掌握思维导图这一学习工具,通过实用篇让学生掌握思维导图在学习、生活中的应用。
【课程目标】通过本课程的学习,学生将能够:1.了解思维导图的基本要素;2.学会思维导图的简单绘制;3.学会运用思维导图表达信息;4.培养学生的发散思维、创新思维能力,增强学生的自信心。
【课程框架】第1课时:令人惊奇的大脑第2课时:牵线活动第3课时:水果大荟萃背景分析教学目标学习自己绘制思维导图,掌握颜色的基本使用教学资源水果歌、大白纸(画好中心图像“水果篮子”)、彩色笔、水果思维导图示范图课前准备了解水果和水果制品及用途,黑板中央贴上中心图像“水果篮子”教学活动活动一: 儿歌问答(10分钟)1.素材:水果歌什么水果红通通?(苹果苹果红通通。
)什么水果黄橙橙?(桔子桔子黄橙橙。
)什么水果绿油油?(西瓜西瓜绿油油。
)2.游戏规则:这首儿歌是问答式的,老师提出问题,学生举手,老师抽答,注意问答的韵律,尽量不要有间断,也可是是接龙式的,可以让小朋友来回答或问,回答时可以用其他的水果名称来替换苹果、桔子和西瓜。
东尼博赞思维导图经典普及系列博赞学习技巧
“思维导图是一种强大的图形工具,它利用色彩、形状和图像来帮助我们理解 和记忆信息。”东尼·博赞这样写道。通过思维导图的绘制,我们可以将复杂 的信息进行层次化、结构化的整理,使信息变得更加直观、易于理解。同时, 思维导图还能激发我们的创造力,帮助我们从不同的角度思考问题,从而产生 新的创意和想法。
在书中,东尼·博赞还强调了学习技巧的重要性。他认为,学习技巧是影响学 习效果的关键因素之一。通过学习技巧的不断提升,我们可以更加高效地掌握 知识,提高自己的学习效率。例如,他提到了“主动学习”的理念,即在学习 过程中不仅要听讲、阅读,还要积极参与讨论、提问和实践,以加深对知识的 理解和记忆。
阅读过程中,我不禁想到了自己的学习经历。曾几何时,我也曾为如何提高学 习效率、如何更好地记忆知识而苦恼。而这本书,就像一盏明灯,照亮了我前 进的道路。书中的思维导图方法,让我重新认识了学习的本质。思维导图,不 仅仅是一种笔记方法,更是一种思维方式,它能够帮助我们将复杂的知识体系 化、将琐碎的信息整合起来,从而更好地理解和记忆。
东尼·博赞还分享了许多实用的学习技巧,如如何制定学习计划、如何高效记 笔记、如何复习等。这些技巧不仅适用于学校学习,同样也适用于职场培训、 自我提升等各个领域。通过掌握这些技巧,我们能够更好地管理自己的学习过 程,提高学习效果。
《东尼博赞思维导图经典普及系列博赞学习技巧》是一本非常值得一读的书。 它不仅为我们提供了一种全新的思维方式和学习方法,还帮助我们更好地理解 和应用思维导图。这本书对于渴望提升自己的学习和工作效率的人来说是一本 必备的指南。通过认真阅读并实践书中的理念和技巧,我们能够不断提高自己 的学习能力,成为一个更好的学习者。
更为难得的是,这本书不仅仅提供了理论知识,还提供了大量的实用训练实例。 这些实例能够帮助我们将理论知识转化为实际操作,真正地提高我们的学习效 率。通过这些训练,我逐渐学会了如何绘制思维导图,如何利用思维导图进行 学习和思考。在这个过程中,我的记忆力、理解力和学习效率都得到了显著的 提升。
博赞思维导图 小学第1课 认识和绘制思维导图
第4次课 第5次课 第6次课
日期
7月25日 7月26日
7月27日
7月28日 7月29日 7月30日
时间
上午10:00-12:00 上午10:00-12:00
上午10:00-12:00
上午10:00-12:00 上午10:00-12:000 上午10:00-12:00
上课内容
1.认识思维导图 2.思维导图的用途 3.思维导图的绘制示范 4.绘制思维导图
导图背诵课文
®
快乐记忆+快乐思考=快乐学习
记忆我的语文书、英语单词、英语句子… 我的笔记能帮我高效学习 老师上课讲的内容我都能够轻松听懂和掌握 轻松复习功课,每次考试都能拿到好成绩 自信演讲 轻松写作文 学习时注意力很集中 很快乐地学习,又有很多时间可以玩,做自己喜欢做的事 ……
22
使用者:北近京3汉0立0,英0教00育,000人
7
一 类 一 色 。 布 局 、 线 条 灵 活 。 使 用 箭 头 或 连 线 。
8
수업
测测你的眼力
思维导图归类练习
狗
白菜
老师 小草
松鼠 土豆
运动员 桂花
教练 狮子 明星 猴子
柳丝 冬瓜 松树 豆角
猫 青瓜 作者 玫瑰花 长颈鹿 茄子 学者 枫叶
➢0—4张:弱智; ➢5—8张:一般人; ➢9—11张:特别感性; ➢11—13张:精神分裂。
一 类
一
色
。
布
局
、
线
条
灵
活
。
使
用
箭
头
或
连
线
。
4
一 类 一 色 。 布 局 、 线 条 灵 活 。 使 用 箭 头 或 连 线 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江西省南昌市2015-2016学年度第一学期期末试卷(江西师大附中使用)高三理科数学分析一、整体解读试卷紧扣教材和考试说明,从考生熟悉的基础知识入手,多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力,立足基础,先易后难,难易适中,强调应用,不偏不怪,达到了“考基础、考能力、考素质”的目标。
试卷所涉及的知识内容都在考试大纲的范围内,几乎覆盖了高中所学知识的全部重要内容,体现了“重点知识重点考查”的原则。
1.回归教材,注重基础试卷遵循了考查基础知识为主体的原则,尤其是考试说明中的大部分知识点均有涉及,其中应用题与抗战胜利70周年为背景,把爱国主义教育渗透到试题当中,使学生感受到了数学的育才价值,所有这些题目的设计都回归教材和中学教学实际,操作性强。
2.适当设置题目难度与区分度选择题第12题和填空题第16题以及解答题的第21题,都是综合性问题,难度较大,学生不仅要有较强的分析问题和解决问题的能力,以及扎实深厚的数学基本功,而且还要掌握必须的数学思想与方法,否则在有限的时间内,很难完成。
3.布局合理,考查全面,着重数学方法和数学思想的考察在选择题,填空题,解答题和三选一问题中,试卷均对高中数学中的重点内容进行了反复考查。
包括函数,三角函数,数列、立体几何、概率统计、解析几何、导数等几大版块问题。
这些问题都是以知识为载体,立意于能力,让数学思想方法和数学思维方式贯穿于整个试题的解答过程之中。
二、亮点试题分析1.【试卷原题】11.已知,,A B C 是单位圆上互不相同的三点,且满足AB AC →→=,则AB AC →→⋅的最小值为( )A .14-B .12-C .34-D .1-【考查方向】本题主要考查了平面向量的线性运算及向量的数量积等知识,是向量与三角的典型综合题。
解法较多,属于较难题,得分率较低。
【易错点】1.不能正确用OA ,OB ,OC 表示其它向量。
2.找不出OB 与OA 的夹角和OB 与OC 的夹角的倍数关系。
【解题思路】1.把向量用OA ,OB ,OC 表示出来。
2.把求最值问题转化为三角函数的最值求解。
【解析】设单位圆的圆心为O ,由AB AC →→=得,22()()OB OA OC OA -=-,因为1OA OB OC ===,所以有,OB OA OC OA ⋅=⋅则()()AB AC OB OA OC OA ⋅=-⋅-2OB OC OB OA OA OC OA =⋅-⋅-⋅+ 21OB OC OB OA =⋅-⋅+设OB 与OA 的夹角为α,则OB 与OC 的夹角为2α所以,cos 22cos 1AB AC αα⋅=-+2112(cos )22α=--即,AB AC ⋅的最小值为12-,故选B 。
【举一反三】【相似较难试题】【2015高考天津,理14】在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠= ,动点E 和F 分别在线段BC 和DC 上,且,1,,9BE BC DF DC λλ==则AE AF ⋅的最小值为 .【试题分析】本题主要考查向量的几何运算、向量的数量积与基本不等式.运用向量的几何运算求,AE AF ,体现了数形结合的基本思想,再运用向量数量积的定义计算AE AF ⋅,体现了数学定义的运用,再利用基本不等式求最小值,体现了数学知识的综合应用能力.是思维能力与计算能力的综合体现. 【答案】2918【解析】因为1,9DF DC λ=12DC AB =,119199918CF DF DC DC DC DC AB λλλλλ--=-=-==, AE AB BE AB BC λ=+=+,19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+,()221919191181818AE AF AB BC AB BC AB BC AB BCλλλλλλλλλ+++⎛⎫⎛⎫⋅=+⋅+=+++⋅⋅ ⎪ ⎪⎝⎭⎝⎭19199421cos1201818λλλλ++=⨯++⨯⨯⨯︒2117172992181818λλ=++≥+= 当且仅当2192λλ=即23λ=时AE AF ⋅的最小值为2918. 2.【试卷原题】20. (本小题满分12分)已知抛物线C 的焦点()1,0F ,其准线与x 轴的交点为K ,过点K 的直线l 与C 交于,A B 两点,点A 关于x 轴的对称点为D . (Ⅰ)证明:点F 在直线BD 上; (Ⅱ)设89FA FB →→⋅=,求BDK ∆内切圆M 的方程. 【考查方向】本题主要考查抛物线的标准方程和性质,直线与抛物线的位置关系,圆的标准方程,韦达定理,点到直线距离公式等知识,考查了解析几何设而不求和化归与转化的数学思想方法,是直线与圆锥曲线的综合问题,属于较难题。
【易错点】1.设直线l 的方程为(1)y m x =+,致使解法不严密。
2.不能正确运用韦达定理,设而不求,使得运算繁琐,最后得不到正确答案。
【解题思路】1.设出点的坐标,列出方程。
2.利用韦达定理,设而不求,简化运算过程。
3.根据圆的性质,巧用点到直线的距离公式求解。
【解析】(Ⅰ)由题可知()1,0K -,抛物线的方程为24y x =则可设直线l 的方程为1x my =-,()()()112211,,,,,A x y B x y D x y -,故214x my y x =-⎧⎨=⎩整理得2440y my -+=,故121244y y m y y +=⎧⎨=⎩则直线BD 的方程为()212221y y y y x x x x +-=--即2222144y y y x y y ⎛⎫-=- ⎪-⎝⎭令0y =,得1214y yx ==,所以()1,0F 在直线BD 上.(Ⅱ)由(Ⅰ)可知121244y y m y y +=⎧⎨=⎩,所以()()212121142x x my my m +=-+-=-,()()1211111x x my my =--= 又()111,FA x y →=-,()221,FB x y →=-故()()()21212121211584FA FB x x y y x x x x m →→⋅=--+=-++=-,则28484,93m m -=∴=±,故直线l 的方程为3430x y ++=或3430x y -+=213y y -===±,故直线BD 的方程330x -=或330x -=,又KF 为BKD ∠的平分线,故可设圆心()(),011M t t -<<,(),0M t 到直线l 及BD 的距离分别为3131,54t t +--------------10分 由313154t t +-=得19t =或9t =(舍去).故圆M 的半径为31253t r +== 所以圆M 的方程为221499x y ⎛⎫-+= ⎪⎝⎭【举一反三】【相似较难试题】【2014高考全国,22】 已知抛物线C :y 2=2px(p>0)的焦点为F ,直线y =4与y 轴的交点为P ,与C 的交点为Q ,且|QF|=54|PQ|.(1)求C 的方程;(2)过F 的直线l 与C 相交于A ,B 两点,若AB 的垂直平分线l′与C 相交于M ,N 两点,且A ,M ,B ,N 四点在同一圆上,求l 的方程.【试题分析】本题主要考查求抛物线的标准方程,直线和圆锥曲线的位置关系的应用,韦达定理,弦长公式的应用,解法及所涉及的知识和上题基本相同. 【答案】(1)y 2=4x. (2)x -y -1=0或x +y -1=0. 【解析】(1)设Q(x 0,4),代入y 2=2px ,得x 0=8p,所以|PQ|=8p ,|QF|=p 2+x 0=p 2+8p.由题设得p 2+8p =54×8p ,解得p =-2(舍去)或p =2,所以C 的方程为y 2=4x.(2)依题意知l 与坐标轴不垂直,故可设l 的方程为x =my +1(m≠0). 代入y 2=4x ,得y 2-4my -4=0. 设A(x 1,y 1),B(x 2,y 2), 则y 1+y 2=4m ,y 1y 2=-4.故线段的AB 的中点为D(2m 2+1,2m), |AB|=m 2+1|y 1-y 2|=4(m 2+1).又直线l ′的斜率为-m ,所以l ′的方程为x =-1m y +2m 2+3.将上式代入y 2=4x ,并整理得y 2+4m y -4(2m 2+3)=0.设M(x 3,y 3),N(x 4,y 4),则y 3+y 4=-4m,y 3y 4=-4(2m 2+3).故线段MN 的中点为E ⎝ ⎛⎭⎪⎫2m2+2m 2+3,-2m ,|MN|=1+1m 2|y 3-y 4|=4(m 2+1)2m 2+1m 2.由于线段MN 垂直平分线段AB ,故A ,M ,B ,N 四点在同一圆上等价于|AE|=|BE|=12|MN|,从而14|AB|2+|DE|2=14|MN|2,即 4(m 2+1)2+⎝ ⎛⎭⎪⎫2m +2m 2+⎝ ⎛⎭⎪⎫2m 2+22=4(m 2+1)2(2m 2+1)m 4,化简得m 2-1=0,解得m =1或m =-1, 故所求直线l 的方程为x -y -1=0或x +y -1=0.三、考卷比较本试卷新课标全国卷Ⅰ相比较,基本相似,具体表现在以下方面: 1. 对学生的考查要求上完全一致。
即在考查基础知识的同时,注重考查能力的原则,确立以能力立意命题的指导思想,将知识、能力和素质融为一体,全面检测考生的数学素养,既考查了考生对中学数学的基础知识、基本技能的掌握程度,又考查了对数学思想方法和数学本质的理解水平,符合考试大纲所提倡的“高考应有较高的信度、效度、必要的区分度和适当的难度”的原则. 2. 试题结构形式大体相同,即选择题12个,每题5分,填空题4 个,每题5分,解答题8个(必做题5个),其中第22,23,24题是三选一题。
题型分值完全一样。
选择题、填空题考查了复数、三角函数、简易逻辑、概率、解析几何、向量、框图、二项式定理、线性规划等知识点,大部分属于常规题型,是学生在平时训练中常见的类型.解答题中仍涵盖了数列,三角函数,立体何,解析几何,导数等重点内容。
3. 在考查范围上略有不同,如本试卷第3题,是一个积分题,尽管简单,但全国卷已经不考查了。
四、本考试卷考点分析表(考点/知识点,难易程度、分值、解题方式、易错点、是否区分度题)。
