西南交通大学材料力
西南交通大学钢结构设计原理复习题(含答案)

.cc
D.容许应力法
A.钢材强度高
B.钢材塑性好
C.钢材韧性好
D.钢材材质均匀
5.钢材具有可焊接性 6.密封性好 7.耐热性较好、耐火性差 8. 耐锈蚀性差
第二章 钢结构的材料
内。 ) 1.钢结构对钢材要求( C ) A.塑性愈大愈好
一、单项选择题(从每小题的四个备选答案中,选出一个正确的答案,并将其号码填在题干的括号
答:用作钢结构的钢材必须具有下列性能: 1.较高的强度 2.足够的变形能力 3.良好的加工性能
磷含量的合格保证;焊接结构尚应具有冷弯试验的合格保证;对某些承受动力荷载的结构以及重要 的受拉或受弯的焊接结构尚应具有常温或负温冲击韧性的合格保证。 2.影响结构钢材力学性能的因素有哪些?
答:化学成分、冶金缺陷、钢材的硬化、温度影响、应力集中、热处理、重复荷载。 3.选用钢材时应考虑哪些主要因素? 答: (1)结构或构件的重要性;
19.普通螺栓抗拉强度设计值 ftb 与其钢材抗拉强度设计值 f 相比( C ) D.不同钢材有不同关系
20.在弯矩和轴力共同作用下的摩擦型高强度螺栓,计算内力时的中和轴位于( A )
8.钢板按厚度分组的原因是:不同的厚度的钢板,其( D )
ww
A.承载力大小不同,厚钢板承载力大 C.强度大小不同,厚钢板强度大
9.冷作硬化可以提高钢材的( A) A.屈服强度 B.抗拉强度 C.屈服强度和抗拉强度 D.塑性和韧性
10.设计中应尽量避免截面突变目的是为了减少( B) A.偏析 D.非金属杂质
一、单项选择题(从每小题的四个备选答案中,选出一个正确的答案,并将其号码填在题干的括号
.cc
A.三级抗压
B.三级抗拉
C.三级抗剪
水性阻尼涂料的力学性能研究

: 二
图 1 附着 力 随丙烯 酸质 量分 数 变化 图
甩 电子天 平称 量一 定 的云母 粉 及碳 酸钙 粉 , 然
后将 其倒 人分 散砂 磨 机 中均匀 分散 , 待 分 散均 匀 后
图 1为 阻 尼 浆 体 系 中纯 丙 乳 液 质 量 分 数 从 3 5 %逐渐 增 加 至 5 0 %的过 程 中 , 阻尼 浆 涂层 附着 力
原料: 纯 丙 乳液 , 云母 粉 , 碳 酸钙 粉 , 玻璃 纤 维 ,
硅 溶胶
\ L / 、
.一 ,
设备: S D F 一 4 0 0分 散 砂 磨 机 , Q C j型漆 膜 冲击
器, P o s i T e s t A T — M 型漆膜 附着力 测试 仪, 电子 天平 。
取出. 放人 干 燥烧 杯 中待用 。称取 一定 量 的纯 丙 乳 液, 加 入分 散 砂 磨 机搅 拌 桶 , 后 称 取一 定 量 的玻 璃 纤 维加 入 搅 拌 桶 中 , 开始 搅 拌 , 待 纤维 在乳 液 中均 匀分散 后 , 逐 量加 入先 分散好 的云母碳 酸钙 混合 粉
的变 化趋 势 。 由图可 以看 出 , 随着 纯 丙乳 液 质量 分
低 振动 和 噪声 的 目的 , 而 阻尼 涂 料能 否 对 车体减 振
降噪有 持久 良好 的贡献 , 取决 于 涂料 能 否 与车壁 紧
密 持久 结合 。 以及涂 料 自身耐 外 力破 坏 的能 力 。 因
此, 研究 水性 阻尼 涂料 的力学 性能 显得 尤为必 要 。
1试 验
1 . 1试 验原 料设 备
冲 击 强度 测 试 的镀 锌 板 上,控 制漆 膜 厚度 在 2 m m
(材料力学)能量法

l l1
Dl
Dl
Dl
或
1 Vε W F Dl 2 EA(Dl ) 2 2l
Fl (Dl ) EA
F
F
l l1 Dl Dl
F Dl
应变能密度
vε
——杆件单位体积内的应变能
两端受轴向荷载的等直杆,由于其各横截面上 所有点处的应力均相等,故全杆内的应变能是均匀 分布的。 F l l1 F
1 2 M x1 qx1 2
a 1 2 M x2 qax2 qa x2 qa 2 2
因为:
Vε
a
0
2 a M x M 2 x1 2 dx1 dx2 0 2 EI 2 EI
则有
1 2 1 2 qx1 qa a 2 a 2 dx Vε dx1 2 0 0 2 EI 2 EI
1
m
2m2'
m
1m'1
=
3 m
+
' 3m 3
(a)
(b)
(c)
在m作用下,图b无形状改变,且其体积应变同图a, 而对图c,因为:
2 3 0 1
则体积不变,仅发生形状改变(图c) 。
与此对应,图a的体积改变能密度等于图b的应变能密度,
其转向与Me 相同。
三 弯曲应变能
图示纯弯曲梁,弹性范围内的变形有:
M el EI l
或
EI Me l
Me
Me
l
O
(b)
(a)
可见,满足线性关系。
外力功:
1 W M e 2
基于能量等效原理的金属材料硬度预测方法

文章编号:1000-4750(2021)03-0017-10基于能量等效原理的金属材料硬度预测方法张志杰1,2,郑鹏飞1,陈 辉3,蔡力勋2(1. 核工业西南物理研究院,成都 610041;2. 西南交通大学力学与工程学院,成都 610031;3. 长沙理工大学土木工程学院,长沙 410114)摘 要:硬度是一种广泛应用于材料科学与工程实际中的力学性能参数。
基于能量等效原理,对于均匀连续、各向同性、应力-应变关系符合Hollomon 律的金属材料,提出了一种获取布氏、洛氏硬度的半解析预测模型,已知材料的Hollomon 律参数即可预测其布氏、洛氏硬度。
使用少量有限元计算确定出预测模型的待定参数,再进行更广泛的有限元计算验证预测模型,结果表明,模型预测效果良好。
选取6种延性金属材料完成了布氏、洛氏硬度试验,采用该文方法预测的硬度值与试验结果吻合良好。
关键词:硬度;能量等效原理;Hollomon 律;预测模型;硬度试验中图分类号:O341 文献标志码:A doi: 10.6052/j.issn.1000-4750.2020.04.0249THE METHOD FOR HARDNESS PREDICTION OF METAL MATERIALSBASED ON ENERGY EQUIVALENCE PRINCIPLEZHANG Zhi-jie 1,2, ZHENG Peng-fei 1, CHEN Hui 3, CAI Li-xun2(1. Center for Fusion Science of Southwestern Institute of Physics, Chengdu 610041, China;2. School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China;3. School of Civil Engineering, Changsha University of Science and Technology, Changsha 410114, China)Abstract: Hardness of materials is a mechanical property widely used in material science and engineering. Based on energy equivalent principle, a semi-analytical prediction model is proposed to obtain Brinell hardness and Rockwell hardness if materials are uniform, continuous, isotropic and their stress-strain relations conform to Hollomon-law. The hardness can be determined by Hollomon-law parameters of materials. Several parameters in the prediction model are determined through finite element analysis (FEA). For a wide range of assumed materials, a large number of FEA calculations are carried out to verify the prediction model. The results show that the model generates a good prediction. For six kinds of tested ductile metallic materials by hardness test, the Brinell hardness and Rockwell hardness predicted by the model are in good agreement with the hardness test results.Key words: hardness; energy equivalent principle; Hollomon-law; prediction model; hardness test硬度是材料局部抵抗硬物压入其表面的能力,综合反映了材料的基本力学性能、软硬程度,因此常作为工程安全的重要指标,材料力学性能评判的关键参数。
超静定问题——精选推荐

西南交通大学应用力学与工程系材料力学教研室第八章简单的超静定问题§8-1 概述静定结构: 仅靠静力平衡方程就可以求出结构的全部未知的约束反力或内力FAB2A F1BααC平面任意力系:3个平衡方程平面共点力系:2个平衡方程独立平衡方程数:超静定结构(静不定结构): 仅凭静力学平衡方程不能求解全部未知内力或反力的结构。
超静定结构的未知力的数目多于独立的平衡方程的数目;两者的差值称为超静定的次数。
BD C A 132FααF F CF B F A BC ABCADA FααF N1y xF N3F N2BD C A 132FααF F CF B F A BC AA FααF N1y xF N3F N2•习惯上把维持物体平衡并非必需的约束称为多余约束,相应的约束反力称为多余未知力。
•超静定的次数就等于多余约束或多余未知力的数目。
•注意:从提高结构的强度和刚度的角度来说,多余约束往往是必需的,并不是多余的。
超静定的求解:根据静力学平衡条件确定结构的超静定次数,列出独立的平衡方程;然后根据几何、物理关系列出需要的补充方程;则可求解超静定问题。
F F CF B F A BC A•补充方程的数目=多余未知力的数目=多余约束数。
•根据变形几何相容条件,建立变形几何相容方程,结合物理关系(胡克定律),则可列出需要的力的补充方程。
•补充方程的获得,体现了超静定问题的求解技巧与关键。
此处我们将以轴向拉压、扭转、弯曲的超静定问题进行说明。
BD C A 132FααF F CF B F A BC AA FααF N1yxF N3F N2§8.2 拉压超静定问题1拉压超静定问题解法例两端固定的等直杆AB ,在C 处承受轴向力F 如图,杆的拉压刚度为EA ,求杆的支反力.解:一次超静定问题=−+F F F B A F BA F AB ablFC (1) 由节点A 的平衡条件列出杆轴线方向的平衡方程(2)变形:补充方程(变形协调条件)可选取固定端B 为多余约束,予以解除,在该处的施加对应的约束反力F B ,得到一个作用有原荷载和多余未知力的静定结构--称为原超静定结构的基本静定系或相当系统注意原超静定结构的 B 端约束情况,相当系统要保持和原结构相等,则相当系统在B 点的位移为零。
西南交通大学《材料力学B》_在线作业二

西南交《材料力学B》在线作业二
分析任意实心截面形状杆件的斜弯曲时,荷载分解的方向应当是一对()
A:任意正交坐标轴
B:过形心的正交坐标轴
C:过形心的水平与垂直正交坐标轴
D:形心主惯性轴
参考选项:D
在单元体的主平面上,()
A:正应力一定最大
B:正应力一定为零
C:剪应力一定最小
D:剪应力一定为零
参考选项:D
构件做匀速直线运动时,其内的动应力和相应的静应力之比,即动荷载系数Kd ()。
A:等于1
B:不等于1
C:恒大于1
D:恒小于1
参考选项:B
压杆由钢管套在铝棒上组成,作用轴向力P后产生相同的缩短量,若钢管和铝棒的抗拉截面刚度相等,则二者的()。
A:轴力相等,应力不等
B:轴力不等,应力相等
C:轴力和应力都相等
D:轴力和应力不等
参考选项:A
外力包括()。
A:集中荷载和分布荷载
B:静荷载和动荷载
C:所有作用在物体外部的力
D:荷载和支反力
参考选项:D
两端球铰的正方形截面压杆,当失稳时,截面将绕哪个轴转动,有4种答案:
A:绕y轴弯曲
B:绕z1轴弯曲
C:绕z轴弯曲
1。
西南交通大学专业目录
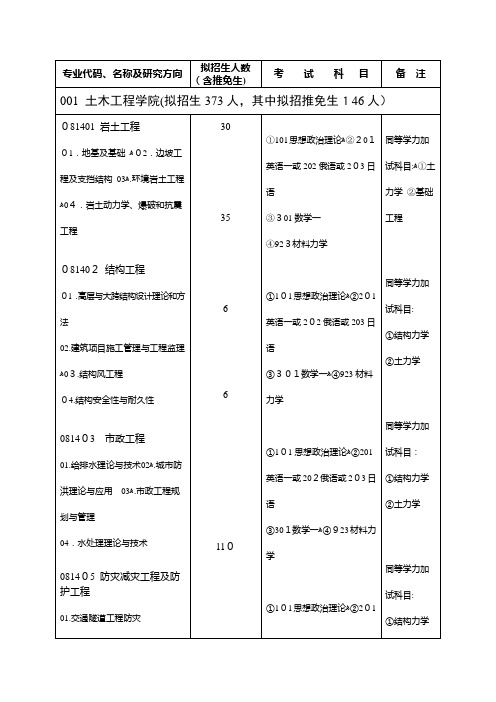
③301数学一ﻫ④922电路分析一
①101思想政治理论
②201英语一
③301数学一ﻫ④922电路分析一
①101思想政治理论
②201英语一
③301数学一
④922电路分析一
①101思想政治理论ﻫ②204英语二
③302数学二
④956电路分析二
①101思想政治理论ﻫ②204英语二ﻫ③302数学二
①101思想政治理论
②201英语一
③301数学一ﻫ④924信号与系统一
①101思想政治理论
②201英语一
③301数学一
④859密码学或924信号与系统一
①101思想政治理论ﻫ②201英语一ﻫ③301数学一
④924信号与系统一
①101思想政治理论
②201英语一
③301数学一
④840数据结构与程序设计
①101思想政治理论ﻫ②201英语一
同等学力加试科目:ﻫ①工程图学②机械设计
同等学力加试科目:
①工程图学②机械设计
同等学力加试科目:
①工程图学②机械设计
同等学力加试科目:
①工程图学②机械设计
同等学力加试科目:
①传感器原理②精密测控与系统
同等学力加试科目:ﻫ①机械设计②工程图学
同等学力加试科目:
①空气调节②工业通风
同等学力加试科目:ﻫ同学术型相关专业
③301数学一ﻫ④824机械原理
①101思想政治理论ﻫ②201英语一或202俄语或203日语或244自命题德语
③301数学一ﻫ④824机械原理
①101思想政治理论
②201英语一或202俄语或203日语或244自命题德语
③301数学一ﻫ④824机械原理
材料力学知识点

第六章弯曲变形知识要点1、弯曲变形的概念1)、挠曲线弯曲变形后梁的轴线变为挠曲线。
平面弯曲时,挠曲线为外力作用平面内的平面曲线。
2)、平面弯曲时的变形在小变形情况下,梁的任意二横截面绕各自的中性轴作相对转动,杆件的轴线变为平面曲线,其变形程度以挠曲线的曲率来度量。
1》纯弯曲时,弯矩—曲率的关系(由上式看出,若弯曲刚度EI为常数则曲率为常数,即挠曲线为圆弧线)2》横力弯曲时,弯矩—曲率的关系3)、平面弯曲时的位移1》挠度——横截面形心在垂直于梁轴线方向上的线位移,以表示。
2》转角——横截面绕其中性轴旋转的角位移,以表示。
挠度和转角的正负号由所选坐标系的正方向来确定。
沿y轴正方向的挠度为正。
转角的正负号判定规则为,将x轴绕原点旋转90°而与y轴重合,若转角与它的转向相同,则为正,反之为负。
4)、挠曲线近似微分方程5)、受弯曲构件的刚度条件,2、积分法求梁的挠度和转角由积分常数C、D由边界条件和连续性条件确定。
对于梁上有突变载荷(集中力、集中力偶、间断性分布力)的情况,梁的弯矩M(x)不是光滑连续函数,应用上式时,应分段积分,每分一段就多出现两个积分常数。
因此除了用边界条件外,还要用连续性条件确定所有的积分常数。
边界条件:支座对梁的位移(挠度和转角)的约束条件。
连续条件:挠曲线的光滑连续条件。
悬臂梁边界条件:固定端挠度为0,转角为0连续条件:在载荷分界处(控制截面处)左右两边挠度相等,转角相等简支梁边界条件:固定绞支座或滑动绞支座处挠度为0连续条件:在载荷分界处(控制截面处)左右两边挠度相等,转角相等连接铰链处,左右两端挠度相等,转角不等3、叠加原理求梁的挠度和转角1)、叠加原理各载荷同时作用下梁任一截面的挠度和转角等于各个载荷单独作用时同一截面挠度和转角的代数和。
2)、叠加原理的限制叠加原理要求梁某个截面的挠度和转角与该截面的弯矩成线性关系,因此要求:1》弯矩M和曲率成线性关系,这就要求材料是线弹性材料2》曲率与挠度成线性关系,这就要求梁变形为小变形4、弯曲时的超静定问题——超静定梁1)、超静定梁约束反力数目多于可应用的独立的静力平衡方程数的梁称为超静定梁,它的未知力不能用静力平衡方程完全确定,必须由变形相容条件和力与变形间的物理关系建立补充方程,然后联立静力平衡方程与补充方程,求解所有的未知数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西南交大材料力学最新教学大纲
一、课程内容与基本要求
01.绪论
材料力学的任务,变形固体的基本假定,杆件变形的基本形式。
02.轴向拉伸和压缩
力的可移动性原理,截面法,轴力和轴力图;横截面上的应力,圣文南原理;纵向变形,线应变,拉压胡克定律,弹性模量、横向变形、泊桑比,变形与位移的计算;材料拉伸和压缩时的力学性能,安全系数,容许应力,强度条件;应力集中的概念。
03.扭转
薄壁圆筒扭转,纯剪切,剪应变,剪应力互等定理,剪切胡克定律,剪切弹性模量;外力偶矩计算,扭矩与扭矩图;圆柱扭转时横截面上的应力;极惯性矩、抗扭截面模量,强度条件;扭转角和单位长度扭转角,刚度条件;矩形截面杆的扭转,自由扭转和约束扭转。
04.弯曲应力
平面弯曲的概念,梁的计算简图;剪力和弯矩的概念,剪力方程和弯矩方程,剪力图和弯矩图;直梁弯矩、剪力与分布荷载集度间的关系及其应用;平面刚架及曲杆的内力图;直梁纯弯曲时的正应力;弯矩与曲率之间的关系,抗弯刚度,抗弯截面模量;横力弯曲时梁的正应力,梁的正应力强度条件;矩形截面梁的弯曲剪应力,工字型及薄壁环形截面梁的腹板及翼缘上的剪应力,梁的剪应力强度条件。
05.梁弯曲时的位移
梁的变形和位移,挠度和转角,梁的挠曲线近似微分方程,位移边界条件和连续条件;挠曲线的描绘;用积分法求梁的挠度和转角;用叠加法求梁的挠度和转角;梁的刚度校核;弯曲应变能。
06.简单超静定问题
拉压超静定问题(一次超静定),装配应力,温度应力;简单的扭转超静定问题;简单超静定梁。
07.应力状态和强度理论
应力状态的概念;平面应力状态的分析(以应力圆为主)主平面(包括求其方位),主应力;三向应力圆、最大剪应力;广义胡克定律;主单元体形式的三向应力状态的应变能密度,体积改变和形状改变应变能密度,体积应变的概念;强度理论的概念,脆性断裂和塑性流动(屈服)破坏形式;最大拉应力理论,最大拉应变理论,最大剪应力理论,形状改变比能理论,相当应力的概念;莫尔强度理论简介;强度理论的应用。
08.组合变形及连接部分的计算
斜弯曲的概念,斜弯曲时的正应力强度计算和位移计算;拉伸(压缩)与弯曲组合时的正应力强度计算和位移计算(含偏心拉伸与偏心压缩);截面核心的概念(土木类);扭转与弯曲的组合;连接件的实用计算(着重普通螺栓连接)。
09.压杆稳定
压杆稳定性的概念;欧拉公式,杆端约束的影响,长度系数、相当长度、柔度、欧拉公式的适用范围;计算临界应力的直线公式(机械类);实际压杆的稳定因数;压杆的稳定计算和合理截面设计。
10.弯曲问题的进一步研究
非对称截面梁的平面弯曲,剪切中心(弯曲中心)的概念。
11.考虑材料塑性的极限分析
拉压杆系的极限荷载;等直圆杆的极限扭矩的计算;梁的极限弯矩。
12.能量方法
应变能;卡氏第二定理,用卡氏定理理解超静定问题。
13.应变分析和电阻应变计法基础
根据一点处三个方向的线应变确定平面应力状态。
14.动应力
构件作匀加速直线运动或匀速转动时的动应力计算;构件受冲击时的近似计
算;交变应力的概念,金属疲劳破坏的概念;材料的持久极限及其测定;影响构件持久极限的主要因素;对称循环下构件的疲劳强度校核。
15.截面的几何性质
面积矩及图形的形心确定;惯性矩、惯性积和惯性半径;平行移轴公式;主轴和主惯性矩的概念,转轴公式。
二、对学生的能力培养要求
通过材料力学课程的学习,学生应掌握杆件的强度、刚度和稳定性问题的基本概念、基础知识和一定的分析能力,具有比较熟练的计算能力和一定的实验能力。
三、说明
1. 本大纲对机械、土木类教学要求的差别已在课程内容中说明。
2. 大纲所列课程内容是教学基本要求,各任课教师可根据实际情况和自己的教学经验适当调整。
四、主要参考书
1.《材料力学》(第四版)孙训方等高等教育出版社
2.《材料力学》(第二版)李庆华主编西南交通大学出版社
3.《材料力学》[美]S·铁摩辛柯、丁盖尔著科学出版社
结构力学的不太了解,材料力学的倒可以帮你一下,材力教材分上下册,是孙训方主编的,高教出版的,上册基本各个章节都要考,最好全看下,下册有个别重点的,我整理的规律:
1.截面几何特征:每年都会考到,不管是独立的题目还是在答题中出现的中间步骤,这个是很关键的,要学会静矩,惯性矩,极惯性矩等课本(1)附录中截面集合特征里面的内容,都要了解并能做出来。
这个是在复试中也是有好处的。
2.应力应变分析和强度理论:每年必有大题,一般以第三第四强度理论校核为主,这方面,就考大家对课本第7章内容的理解上了。
记得,一定要看课后题。
3.组合变形:这个不用说,肯定会考,有时也结合强度理论进行综合考核,一定要看课本和那本胡增强编写的学习指导,里面的题目很好,能帮助你全面理解。
4.压杆稳定:必考的,基本是每年都有,记住重要的欧拉公式,在进行一定的综合题目分析,拿到分不是问题。
5.能量法和动荷载:在复习能量法的时候,建议先对结构力学的位移计算先复习一遍,因为在考试中,实在不会能量法,用叠加法也是可以的。
6.容易被忽略的小知识点:截面核心,弯曲中心,塑性跤,斜弯曲非对称弯曲纵弯曲等概念,还有关于应变片的贴法(重点),都要很明白的了解。
另外,你如果考材力的话,建议你最好买一本西南交大出版的材料力学学习指导书,是西南交大材力教研室编的,很好很系统的一本书,而且每年真题都有这本书的原题。
最后祝你复习顺利!
2012年西南交通大学硕士研究生入学考试考试大纲
考试科目:材料力学
课程编号:923
试题形式:
1.选择题 20%
2.计算题: 80%
考试内容
1.了解材料力学的任务,同相关学科的关系,变形固体的基本假设。
熟悉
截面法和内力、应力、变形、应变。
了解单向应力状态的本构关系. 2.掌握轴力与轴力图,直杆横截面及斜截面的应力,圣维南定理,应力集中的
概念;材料拉伸和压缩时的力学性能, 应力-应变曲线;拉压杆强度条件和刚度条件, 安全因素及许用应力;拉压变形,胡克定律, 弹性模量,泊松比;拉压超静定问题, 温度及装配应力。
3.熟悉剪切及挤压的概念和实用计算。
掌握切应力互等定律, 剪切胡克定
律。
4.掌握扭矩及扭矩图, 圆轴扭转的应力和应变, 扭转强度及刚度条件。
了
解矩形截面及薄壁杆件扭转。
5.掌握静矩与形心的概念, 组合截面的一次矩与形心计算, 截面二次矩,平
行移轴公式。
6.熟悉平面弯曲内力概念,掌握剪力,弯矩方程,剪力图和弯矩图及
q-Q-M的微分关系, 熟悉利用微分关系画梁的剪力和弯矩图。
掌握平面刚架和曲杆的内力图。
7.掌握弯曲正应力公式,矩形截面弯曲切应力计算,弯曲强度条件。
了解薄壁
截面梁的弯曲切应力;提高梁的弯曲刚度的措施。
8.熟悉挠曲轴及其近似微分方程,积分法求梁的位移, 叠加法求梁的位移,
梁的刚度校核。
了解提高梁的弯曲刚度的措施.
9.掌握应力状态的概念,平面应力状态下应力分析的解析法及图解法,广义
胡克定律。
了解体积应变,三向应力状态下应变能、体积改变能、畸变能
的概念.
10.熟悉强度理论的概念,破坏形式的分析,脆性断裂和塑性屈服。
掌握最大拉
应力理论, 最大拉应变理论,最大切应力理论, 畸变能密度理论。
了解莫
尔强度理论。
11.掌握组合变形下杆件的强度计算;斜弯曲,拉弯组合变形,弯扭组合变
形。
12.掌握压杆稳定的概念,细长压杆临界载荷的欧拉公式,临界应力、经验公
式、临界应力总图, 压杆的稳定校核。
了解安全因素法,提高稳定性的
措施的概念。
13.掌握杆件变形位能计算,卡氏定律,莫尔定律,图形互乘法,用力法解
超静定问题。
熟悉功的互等定律。
了解位移互等定律。
14.熟悉变形比较法,力法的正则方程,对称条件的应用。
15.熟悉构件作等加速度运动和匀速转动的应力计算。
掌握冲击应力和变形
计算。
了解冲击韧度,提高构件抗冲击能力措施的概念。
16.了解疲劳破坏的概念,S-N曲线及材料的疲劳极限, 影响构件疲劳极限的
主要因素,提高构件疲劳强度的措施。
二、参考书目
1.孙训芳,《材料力学I 、II》,高等教育出版社,2004。
