材力2-2
【材力】2拉压变形(1)

1 f 30
60kN 2 f 20 40kN 3 f 35 30kN 50kN
FN1 0 FN 2 60 kN FN 3 50 kN
FN1 0 A1
1
2
60
3 50 20
kN
FN图
1
+
FN 2 60 10 3 4 2 191MPa A2 (20 10 3 ) 2 FN 3 50 10 3 4 3 52 MPa 3 2 A3 (35 10 )
x+dx A B' x
d x d d x x lim x 0 x dx
材料力学
河南城建学院土木工程系力学教研室 §2-4 轴向拉伸或压缩时的变形
d1
F
2、横向变形 l l1
d
F
横向绝对变形 横向线应变
d d1 - d
d d
材料力学
河南城建学院土木工程系力学教研室 §2-4 轴向拉伸或压缩时的变形
F FN A A
FN:横截面上的轴力 A:横截面面积
拉应力为正,压 应力为负。
对于等直杆:
当有多段轴力时,最大轴力所对应的 截面-----危险截面。
危险截面上的正应力----最大工作应力
材料力学 max
A
FN,max
河南城建学Leabharlann 土木工程系力学教研室3、拉压杆斜截面上的应力
河南城建学院土木工程系力学教研室 §2-4 轴向拉伸或压缩时的变形
1、纵向变形 当杆件因荷载或截面尺寸变化的原 因而发生不均匀变形时,不能用总长度内的平均线 应变代替各点处的纵向线应变。 y x截面处沿x方向的纵向平 d x 均线应变为 C x O x截面处沿x方向的纵向线应 x z A x B 变为
材力习题册(第六版)参考答案(1-3章)

解①②③④式,得 =xF 当 x=l 时, 当 x=0 时, 当 x=l/2 时, /l, =(1-x/l)F, =(l-x)Fx/l =F =F =Fl/4
达到最大值,即 达到最大值,即 达到最大值,即
-5-
第二章
一、选择题
轴 向 拉 压
1.图 1 所示拉杆的外表面上有一斜线,当拉杆变形时,斜线将 ( A.平动 应是( C ) B.转动 C.不动 D.平动加转动
2
D.
h 3d D 4
(图 9)
(图 10)
(图 11)
二、填空题
1.直径为 d 的圆柱放在直径为 D=3d,厚为 t 的圆基座上,如图 11 所示地基对基座的支 反力为均匀分布,圆柱承受轴向压力 P,则基座剪切面的剪力 Q = 8P/9 。 2. 判断剪切面和挤压面时应注意的是: 剪切面是构件的两部分有发生 相对错动 趋势的 平面;挤压面是构件 受挤压 的表面。 3.试判断图 12 所示各试件的材料是低碳钢还是铸铁? A 为 铸铁 ,B 为 低碳钢 ,C 为 铸铁(45 度螺旋面) ,D 为 低碳钢,E 为 铸铁 , F 为 低碳钢 。
17. 由拉压变形公式 l A C A C
F l FN l 即 E N 可知,弹性模量 ( A )。 A l EA
B 与载荷成正比 D 与横截面面积成正比
与载荷、杆长、横截面面积无关 与杆长成正比 A )是正确的。 内力随外力增大而增大 内力随外力增大而减小 C B D
18. 在下列说法,(
2 3
A
)。
B σ 2>σ 3>σ D σ 2>σ 1>σ A
1 3
C σ 3>σ 1>σ
13. 图 8 所示钢梁AB由长度和横截面面积相等的钢杆1和铝杆2支承,在载荷P作用 下,欲使钢梁平行下移,则载荷P的作用点应 ( A 靠近 A 端 C 在 AB 梁的中点 A 分别是横截面、 45 斜截面 C 分别是 45 斜截面、横截面 A 分别为 σ /2 和 σ C 分别为 σ 和 σ /2 16. 材料的塑性指标有 ( A σ s和δ C )。 B σ s和ψ
材力练习册(简)
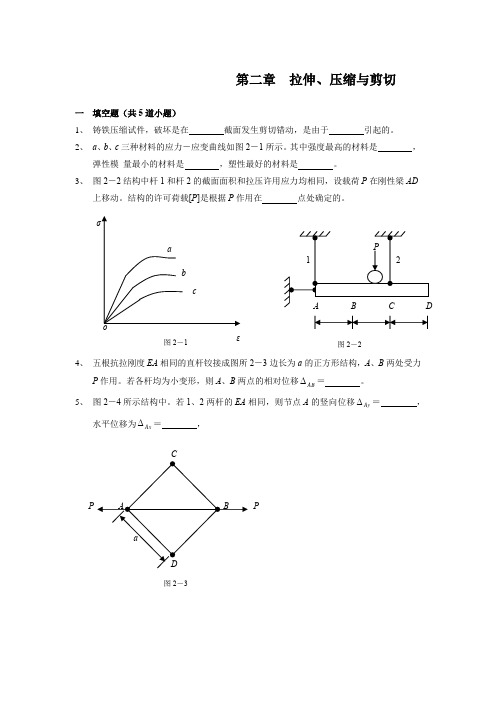
第二章 拉伸、压缩与剪切一 填空题(共5道小题)1、 铸铁压缩试件,破坏是在 截面发生剪切错动,是由于 引起的。
2、 a 、b 、c 三种材料的应力-应变曲线如图2-1所示。
其中强度最高的材料是 ,弹性模 量最小的材料是 ,塑性最好的材料是 。
3、 图2-2结构中杆1和杆2的截面面积和拉压许用应力均相同,设载荷P 在刚性梁AD上移动。
结构的许可荷载[P ]是根据P 作用在 点处确定的。
4、 五根抗拉刚度EA 相同的直杆铰接成图所2-3边长为a 的正方形结构,A 、B 两处受力P 作用。
若各杆均为小变形,则A 、B 两点的相对位移∆AB = 。
5、 图2-4所示结构中。
若1、2两杆的EA 相同,则节点A 的竖向位移∆Ay = ,水平位移为∆Ax = ,CAP图2-3ε图2-1图2-2二 选择题(共9道小题)1、图2-5所示木接头,水平杆与斜杆成α角,其挤压面积为A bs 为:( ) (A )bh ; (B )bh tg α ; (C )bh/cos α ; (D )bh/(cos α sin α)。
2、图2-6所示铆钉联接,铆钉的挤压应力为:( )(A )2P/(πd 2); (B )P/(2dt ); (C )P/(2bt ); (D )4P/(πd 2)。
3、图2-7所示杆(Ⅰ和Ⅱ)连接木头,承受轴向拉力作用,下面说法错误的是:( ) (A )1-1截面偏心受拉; (B )2-2截面为受剪面; (C )3-3截面为挤压面; (D )4-4截面为挤压面。
4、由同一种材料组成的变截面杆的横截面积分别为2A 和A ,受力如图2-8所示,E 为常数,下面结论正确的是:( )(A )D 截面位移为0; (B )D 截面位移为Pl/(2EA ); (C )C 截面位移为Pl/(2EA ); (D )D 截面位移为Pl/(EA )。
tt图2-6图2-5图2-45、图2-9所示直杆,杆长为3a ,材料的抗拉刚度为EA ,受力如图。
材力习题集.
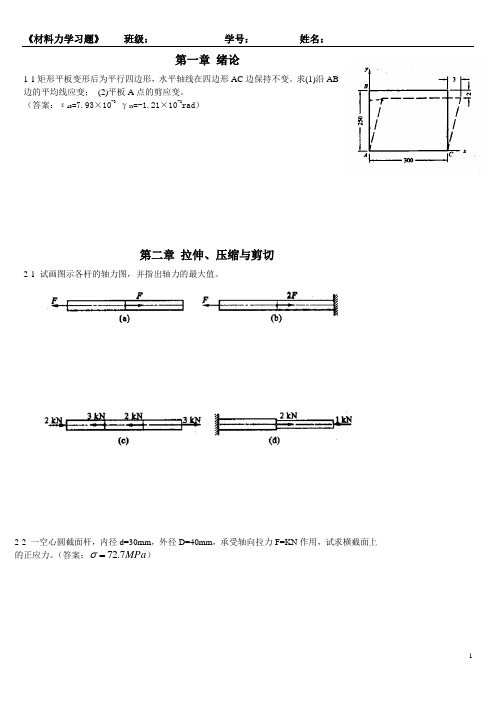
第一章 绪论1-1矩形平板变形后为平行四边形,水平轴线在四边形AC 边保持不变。
求(1)沿AB边的平均线应变; (2)平板A 点的剪应变。
(答案:εAB =7.93×10-3 γXY =-1.21×10-2rad )第二章 拉伸、压缩与剪切2-1 试画图示各杆的轴力图,并指出轴力的最大值。
2-2 一空心圆截面杆,内径d=30mm ,外径D=40mm ,承受轴向拉力F=KN 作用,试求横截面上的正应力。
(答案:MPa 7.72=σ)2-3 题2-1 c 所示杆,若该杆的横截面面积A=502m m ,试计算杆内的最大拉应力与最大压应力(答案:MPa t 60max ,=σ MPa c 40max ,=σ)2.4图示轴向受拉等截面杆,横截面面积A=5002m m ,载荷F=50KN 。
试求图示截面m-m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
(答案:MPa MPa MPa MPa 50 ; 100 ; 24.49 ; 32.41max max ==-==τστσαα)2.5如图所示,杆件受轴向载荷F 作用。
该杆由两根木杆粘接而成,若欲使粘接面上的正应力为其切应力的二倍,则粘接面的方位角θ应为何值(答案: 6.26=θ)2.6 等直杆受力如图所示,试求各杆段中截面上的轴力,并绘出轴力图。
2.7某材料的应力-应变曲线如图所示,图中还同时画出了低应变去区的详图,试确定材料的弹性模量E 、屈服极限s σ、强度极限b σ、与伸长率δ,并判断该材料属于何种类型(塑性或脆性材料)。
2.8某材料的应力-应变曲线如图所示,试根据该曲线确定: (1)材料的弹性模量E 、比例极限P σ与屈服极限2.0σ; (2)当应力增加到MPa 350=σ时,材料的正应变ε, 以及相应的弹性应变e ε与塑性应变p ε2.9图示桁架,杆1与杆2的横截面均为圆形,直径分别为d1=30mm 与d2=20mm ,两杆材料相同,许用应力[]σ=160MPa ,该桁架在节点A 处承受铅垂方向的载荷F=80KN 作用。
材力

一概念(名词解释)1、缺口效应:绝大多数机件的平面不是均匀变化的光滑体,往往存在截面的急剧变化,由于缺口的存在,在静载荷作用下缺口截面上的应力状态将发生变化,产生所谓的“缺口效应”,从而影响金属材料的力学性能。
(简言之,缺口材料在静载荷作用下,缺口截面上的应力状态发生的变化。
)2、韧脆转变温度:中、低强度钢在试验温度低于某一温度t k时,会由韧性状态转变为脆性状态,冲击吸收功明显下降,断裂机理有微孔聚集型变为穿晶解理型,断口特征由纤维状变为结晶状,这就是低温脆性,转变温度t k 称为韧脆转变温度(或者说在试验温度低于某一温度t k时,会由韧性状态转变未脆性状态,冲击吸收功明显下降,断裂机理由微孔聚集型转变微穿晶断裂,断口特征由纤维状转变为结晶状,这就是低温脆性。
tk称为韧脆转变温度)。
3、冲击韧性:指材料在冲击载荷作用下吸收塑性变形功和断裂功的能力,常用标准试样的冲击吸收功A K表示。
4、应力腐蚀:金属在拉应力和特定的化学介质共同作用下,经过一段时间后所产生的低应力脆断现象。
5、接触疲劳:是机件两接触面作滚动或滚动加滑动摩擦时,在交变接触压应力作用下,材料表面应疲劳损伤,导致局部区域产生小片或小块状金属剥落而是材料流失的现象。
6、弹性比功:又称弹性比能,应变比能。
表示材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示,即:Ee e e 221ae 2σεσ==. 7、缺口敏感度:用缺口试样的抗拉强度bn σ 与等截面尺寸光滑试样的抗拉强度b σ的比值表示,即:nbn NSR σσ=。
8、氢致延滞断裂:高强钢或钛合金中,含有适量的处于固溶状态的氢,在低于屈服强度的应力持续作用下,经过一段孕育期后,在金属内部,特别是在三向拉应力状态区形成裂纹,裂纹逐渐扩展,最后突然发生脆性断裂。
这种由于氢的作用而产生的延滞断裂现象称为氢致延滞断裂。
9、磨损:机件表面相接触并作相对运动时,表面逐渐有微小颗粒分离出来形成磨屑,使表面材料逐渐流失,造成表面损伤的现象。
材力2-4

A
A
A
F
F
F
判断:静不定次数 判断:静不定次数
B C D
FN1 FN2 FN3
3个未知力 2个平衡方程
A F
A F
1次静不定
5. 多余未知力
redundant unknown force
多余约束提供的约束力。 静不定次数 = 多余未知力数目
二. 静不定问题的解法: 1. 判断静不定次数: 方法1 方法1: 未知力数目-平衡方程数目 方法2 方法2:多余未知力数目 2. 列平衡方程 3. 列几何方程: 反映各杆变形之间的关系, 需要具体问题具体分析。 4. 列物理方程:变形与力的关系。 列物理方程:变形与力的关系。 5. 列补充方程:物理方程代入几何方程即得 列补充方程:物理方程代入几何方程即得
y
FN3 FN1
B
EA
C
EA
D
3 3 1 3 l 2 EA l α α3 l
α α
A
FN2
∆l2
A
∆l1 ∆l3
x F
A´
研究平衡
F
研究变形
内力假设受拉
变形假设伸长
内力假设与变形假设一致 !
思考:几何方程的求法 思考:几何方程的求法
B C D B C D
1 3
α α
∆l2 A
2
1 3
α α
A
2
∆l1
= 0,
F N 2 sin α − F N 1 sin α = 0
FN 2 = FN 1
y
⑴ ⑵
F N 3 + F N 2 cos α + F N 1 cos α − F = 0
2-2力的合成与分解

2-2 力的合成与分解一、力的合成1.合力与分力:如果几个力共同作用产生的效果与某一个力单独作用时的效果相同,则这一个力为那几个力的合力,那几个力为这一个力的分力.2.共点力:几个力都作用在物体的 同一点,或者它们的作用线相交于一点,这几个力叫做共点力.3.力的合成:求几个力的合力的过程.4.平行四边形定则:求互成角度的两个共点力的合力,可以用表示这两个力的线段为邻边 作平行四边形,这两个相邻边之间的对角线就表示合力的大小和方向.二、力的分解1.力的分解:求一个力的分力的过程,力的分解与力的合成互为逆运算.2.遵从原则:平行四边形定则.3.矢量运算法则(1)平行四边形定则(2)三角形定则:把两个矢量的首尾顺次连结起来,第一个矢量的首到第二个矢量的尾的 有向线段为合矢量.特别提醒:(1)合力不一定大于分力;(2)合力与它的分力是力的效果上的一种等效替代关系,而不是力的本质上的替代.三、共点力合力的大小范围的确定1.两个共点力的合力范围:| F 1-F 2|≤F ≤F 1+F 2即两个力的大小不变时,其合力随夹角的增大而减小.当两力反向时,合力最小,为|F1-F2|;当两力同向时,合力最大,为F 1+F 2. 二个力垂直时,合力F=(F 12+F 22)1/22.三个共面共点力的合力范围(1)三个力共线且方向相同时,其合力最大为F =F 1+F 2+F 3.(2)以这三个力的大小为边,如果能组成封闭的三角形,则其合力最小值为零,若不能组成封闭的三角形,则合力最小值的大小等于最大的一个力减去另外两个力的代数和的绝对值. 两个大小均为F 的力合成,夹角越小(大),合力越大(小),当夹角为120°时,合力大小也为F.三个大小为F 的力夹角互为120°时,合力为零.四、力的正交分解法1.将一个力分解为相互垂直的两个分力的分解方法叫做力的正交分解法,如图4所示.2.多个共点力合成的正交分解法,把各力沿相互垂直的x 轴、y 轴分解,F 1分解为F 1x 和 F 1y , F 2分解为F 2x 和F 2y ,F 3分解为F 3x 和F 3y …则x 轴上的合力F x =F 1x +F 2x +F 3x +…,y 轴上的合力F y =F 1y +F 2y +F 3y +….合力F =F 2x +F 2y ,设合力与x 轴夹角为θ,则tan θ=F y F x. 五、矢量与标量矢量:既有大小又有方向的物理量。
整理材力习题
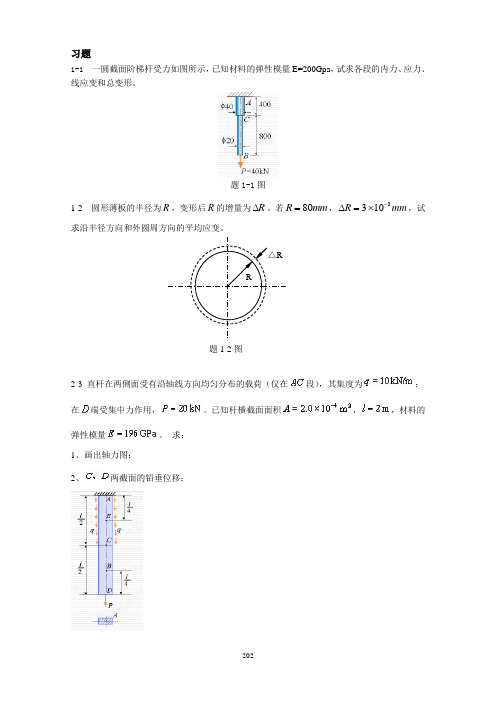
习题1-1 一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa ,试求各段的内力、应力、线应变和总变形。
题1-1图1-2 圆形薄板的半径为R ,变形后R 的增量为R ∆。
若mm R 80=,mm R 3103-⨯=∆,试求沿半径方向和外圆周方向的平均应变。
2-3 直杆在两侧面受有沿轴线方向均匀分布的载荷(仅在段),其集度为;在端受集中力作用,。
已知杆横截面面积,,材料的弹性模量。
求: 1、画出轴力图;2、两截面的铅垂位移;题1-1图 R △R 题1-2图3、分别过两点与轴线夹角斜截面上的应力。
2-4螺旋压紧装置如图所示。
现已知工件所受的压紧力为,旋紧螺栓螺纹内径,固定螺栓内径。
两根螺栓材料相同,其许用应力。
试校核各螺栓之强度是否安全。
3-3 空心钢轴的外径D=100mm,内径d=50mm。
已知间距为=2.7m之两横截面的相对扭转角 1.8°,材料的剪变模量G=80GPa。
求:(1)轴内的最大剪应力;(2)当轴以n=80r/min 的速度旋转时,轴传递的功率(kW)。
3-5 阶梯形圆杆,AE 段为空心,外径D=140mm,内径d=100mm,BC 段为实心,直径d=100mm。
外力偶矩,,。
已知[τ]=80MPa,,G=80GPa。
试校核该轴的强度和刚度。
4-4 设已知图示各梁的载荷P、q、m和尺寸a,(选做b和f)(1)列出梁的剪力方程和弯矩方程;(2)作剪力图和弯矩图;(3)确定及。
4-5 用微分关系作下列各梁的剪力图和弯矩图。
(选做j)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
pe
弹性阶段
特点:变形是完全弹性的
特征应力:
ε 弹性极限e elastic limit
比例极限p proportional limit
比例阶段proportional limit: σ ≤ σp
胡克定律 Hookes Law
σ = Eε
E——弹性模量Young ,modulus of elasticity
求:校核强度 解:(1)计算内力
取结点A
∑Fy= 0, FN1 sin30°-F = 0
FN1 2F 80kN
∑Fx= 0, -FN1cos30°-FN2 = 0
FN2 3F 69.3kN
例2-2
A
1
30°
B
C2
FN1
F
30°
FN2
B
F
FN1 80kN FN2 69.3kN
木材的力学性质
σ
顺纹拉伸
顺纹压缩 横纹压缩
ε
木材抗拉强度高于 抗压强度。
木材顺纹方向的 强度高于横纹方向的 强度;
木材是 各向异性材料
结论与讨论
1.强度、变形计算必须了解材料的力学性能; 2.了解材料的力学性能主要是分析σ-ε曲线;
问题1:如何得到σ-ε曲线? 问题2:如何分析σ-ε曲线? 3.工程材料按其断后伸长率大小分成两大类:
F
拉压杆的
任意截面上
F
30
应力随截面 变化
30
σ60
F
τ60
结论与讨论
1. 拉压杆横截面上的内力只有轴力,
因此,横截面上只存在正应力,没有切应力。
2. 拉压杆横截面上的正应力是均匀分布的,
即
FN
A
3. 拉压杆的斜截面上一般既有正应力,
又有切应力。
正应力最大值位于横截面上,数值为 σ ;
切应力最大值在与轴线成45°角的截面上,
数值为 σ/2.
§2.4 材料在拉压时的力学性能
力学性能mechanical properties—— 又称机械性能,指材料在外力作用下 表现出的破坏和变形等方面的特性。
目的——确定材料破坏和变形方面的 重要性能指标,以作为强度和变形 计算的依据。
方法——试验。
(2)校核强度
AB杆
FN
A
1
FN 1 A1
80 103 600 106
133 MPa
1
BC杆
2
FN 2 A2
69.3 103 10000 106
6.93 MPa
2
满足强度条件
例题 已知:空心柱的外直径D=25cm, F=500kN,
塑性材料和脆性材料; 塑性材料 δ>5﹪ 脆: 塑性材料取σs或σ0.2, 脆性材料取σb.
5.根据卸载定律,一般地一点线应变ε由两部 分组成:弹性应变εe和塑性应变εp ;
ε = εe+εp
σ
εε
εp
εe
6.三种拉伸应力-应变曲线
塑性金属材料
0.2
等于0.2%
时的应力值
0. 2%
ε
拉延(drawn)现象
σ σs
聚合物
颈缩
σb
ε
四、铸铁拉伸
σ(MPa)
100
50
σb
0.45
ε(%)
1.强度极限低;
σb=110~160MPa
2.非线性;
近似用割线代替
3.无屈服,无颈缩; 4. δ<0.5﹪; 5.平断口。
不宜受拉!
五、压缩
低碳钢
σ(MPa)
A 100%
A
Q235钢 ψ = 60﹪
三、其他塑性材料拉伸
16锰钢
σ
ε
退火球墨铸铁
σ
ε
σ
锰钢
ε
σ
玻璃钢
ε
塑性材料的共同
σ
锰钢
特点只有一个,那
玻璃钢
就是断后伸长率大
16锰钢
于5﹪.
退火球墨铸铁
问题:对无明显屈
服阶段的塑性材料
如何确定强度指标? ε
名义屈服极限σ0.2
σ
塑性应变
d D2 4A 252 4 167 20.3cm
D d 25 20.3 2.4cm
2
2
例题
B ① 30°45° ②
y
C
FN1 30°45° FN2
已知: A1 = 706.9 mm2, A2= 314 mm2,
〔σ〕=160 MPa
A
A
x 求:许可载荷〔F〕
cos sin
2
sin 2
k
F
α pα
α
k
可见,斜截面上既有正应力,也有切应力。
讨论
2
cos2
sin 2
ⅰ α = 0 , σαmax= σ , τα = 0 ⅱ α =45° ,σα = σ/2 , ταmax = σ/2
ⅲ α = 90° , σα = 0 , τα = 0
6. 许用应力 o
n
7. 强度条件
max
FN A max
σmax —最大工作应力
等截面杆强度条件
max
FN max A
强度计算的三类问题
max
FN max A
1. 强度校核 2. 截面选择
max
单位: GPa,
1 GPa = 109 Pa
物理意义:材料抵抗弹性变形的能力。
几何意义:σ-ε 图比例阶段斜率。
②屈服阶段
yield stage
σ
σs 屈服阶段
特点:材料失去抵抗变形的能力 ——屈服(流动) yield
特征应力:屈服极限σs yield limit
Q235钢 σs=235MPa
滑移线 slip liens: 方位—与轴线成45°
FN max A
?
A FNmax
3. 确定许用载荷 FNmax A
例2-2
B
1
30°
A
C2
FN1
F
30°
FN2
A
F
已知: AB杆: 横截面积 A1=600mm², []1=160 MPa;
BC杆:横截面积A2=10000mm², []2=7 MPa , F=40kN.
F
F
解:1. 内力计算
取结点 A
∑Fx = 0, FN2sin45°-FN1sin30° = 0 ∑Fy = 0, FN1cos30°+FN2cos45°-F = 0
解出
FN1 = 0.732 F FN2 = 0.518 F
(2)计算[F]
AB杆
FN1 0.732F
A1
A1
F A1 706.9 160 154.5kN
ε
原因—最大切应力
机理—晶格滑移
45°
③强化阶段
strengthing stage σ
σb
强化阶段
ε
特点:
应变硬化 strain
hardening 材料恢复变形抗力,
σ-ε 关系非线性, 滑移线消失, 试件明显变细。
特征应力:强度极限σb ultimate strength
④颈缩阶段(局部变形阶段)
[]=30 MPa 求:筒壁厚度δ
F=500kN
解: FN=F=500kN
250
FN
A
A
FN
500 103 30 106
167 cm2
A D2 d 2 4
例题
F=500kN
250
A 167cm2
A D2 d 2 4
拉伸 压缩 拉伸 压缩
二、低碳钢拉伸时的力学性质
低碳钢:含碳量低于0.3﹪
1. 拉伸图
F
F
l
⊿l
低碳钢拉伸试验——拉伸图
拉伸图
F
ΔL
2.应力-应变图(σ-ε图)
克服拉伸图的尺寸效应 σ
FN
A
l
l
名义应力 名义应变
ε
A——初始横截面面积
l ——原长
σ
①弹性阶段
elastic stage
卸载后重新加载,
σ
σ-ε则沿卸载路径变化,
至卸载点附近后则
回到未经卸载的曲线。
再加载
冷拉时效
卸载后过几天再 重新加载,σ-ε则按 ε 卸载路径变化,高于 卸载点的曲线,获得 更高的强度指标。
冷作硬化 cold hardening
σ 现比例极限
原比例极限
现残余应变
原残余应变
ε
在强化阶段卸载,材料的 比例极限提高,塑性降低。
压缩 400
拉伸
200
0.10
0.20
ε
1.Eσe,,σσsp ,,
与拉伸相同; 2.测不出σb;
3.试件呈鼓状。
压缩试验无意义
铸铁
σ(MPa) 600
压缩 400 300
拉伸
1.σb高于拉伸; ( 接近4倍)
2.δ大于拉伸; (接近5﹪)
3.E与拉伸不同;
4.斜断口.
可制成受压构件
0.05
0.10 ε
课堂练习
