海赛(Hesse)矩阵
02工程优化 第2章基础知识HESSE矩阵凸集凸函数

f x f x0 f x0 ( x x0 ) o x x0
T
(5)
这与一元函数展开到两项的 Taylor 公式是相对应的。
T
x f x0 f 0 f x0 l 0 p f p x 利用方向导数定义并将上式中的fp 换成 te f (3) = x0 l , , , lim 0, 有:
T
T
x1 x2 p xn T f x0 f x0 p f x0 tf x0 e o t T lim lim f x0 e. t 0 t 0 p t t
设 x1 x1 , x2 x2 ,xn xn 是过点 x0 同时又完全在等值面(6)
f x1 , x2 ,xn r0
f x1 , x2 ,xn r0
两边同时在 0 处关于 求导数,根据求导的链式法则有:
则
f x0 t 0 0
T
f x f x f x f x , , x1 x2 xn
f x0
T
即函数f(x) 在 x0 处的梯度 f x0 与过该点在等值面上的任一条曲
线L在此点的切线垂直。
f x0 f x0 f x0 l , , , x1 x2 xn
T
证明:令 l (l1 , l2 ,, ln )T,依次取 p i ei , i 1,2,, n, i R
f 在
x0 处可微,则 (3) 对 p i ei 成立,
黑塞矩阵具体操作算法

论文题目_ 黑塞矩阵简述及其应用学院专业建筑工程学院土木工程专业2014年11月20日黑塞矩阵简述及其应用摘要黑塞矩阵于19世纪由德国数学家Ludwig Otto Hesse首次提出,目前在理论、实际中发挥着重大的作用。
本文简要介绍了黑塞矩阵并主要阐述其应用,重点结合工科学生的专业特点对其在工程实际方面的应用做了简要探讨,对黑塞矩阵的价值以及应用前景做出了较为客观的评价。
关键字:矩阵,黑塞矩阵,工程应用一.研究背景黑塞矩阵19世纪由德国数学家Ludwig Otto Hesse提出后,便在各种理论及实践中起到了极为重要的作用,不仅在高等数学中用于判定多元函数的极值,而且推广到实践中即为优化多元函数模型的各种实际问题,黑塞矩阵在工程实际中的应用不胜枚举,其应用的广泛性以及有效性促使我们不断研究它并将它同理论、实践应用相结合。
二.黑塞矩阵的历史发展黑塞矩阵(Hessian MatriX),又译作海森矩阵、海瑟矩阵、海塞矩阵等,是一个多元函数的二阶偏导数构成的方阵,描述了函数的局部曲率。
黑塞矩阵最早于19世纪由德国数学家Ludwig Otto Hesse提出,并以其名字命名。
黑塞矩阵常用于牛顿法解决优化问题,经过多年的发展,目前在三维重建、中心提取、算法研究等方面都有广泛应用,极大地优化了各项技术,提高了效率。
三.黑塞矩阵的定义及性质1.定义对于一个实值多元函数如果函数的二阶偏导数都存在,则定义的黑塞矩阵为其中表示对第个变量的微分算子,。
那么,的黑塞矩阵即为2.对称性如果函数在区域内二阶连续可导,那么的黑塞矩阵在内为对称矩阵。
原因是:如果函数连续,则二阶偏导数的求导顺序没有区别,即则对于矩阵,有,所以为对称矩阵。
四.黑塞矩阵的应用黑塞矩阵在高等数学中最简单的应用就是判定多元函数的极值,推广到生活中即为优化多元函数模型的各种实际问题。
它在计算机工程、机械设计、电力工程、生物工程乃至土木工程、水利工程以及运筹学中都有广泛的应用。
海赛(Hesse)矩阵与二次型_运筹学_[共2页]
![海赛(Hesse)矩阵与二次型_运筹学_[共2页]](https://img.taocdn.com/s3/m/77ee1902360cba1aa911da72.png)
113第4章 非线性规划 是一部分可行域上的极小值点,称为局部极小点(或相对极小点),对应的目标函数值称为局部极小值(相对极小值)。
而D 点则是整个可行域上的极小值点,称为全局极小值点(最小值点)或绝对极小点,对应的目标函数值称为全局极小值(最小值)或绝对极小值。
此例中,约束条件[式(4.1.8)]自然对最优解是有影响的。
若不考虑约束条件,便是无约束问题。
它的最优解显然是**122,1x x ==,*()0f X =。
下面给出局部极小点和全局极小点的定义。
定义4.1.1 设f (X )为定义在n 维欧式空间E n 某一区域R 上的实函数,对于X *∈R n E ⊂,若存在某个>0ε,使得满足*<X X ε−的所有的X 都有*()()f X f X ≥ (4.1.9)则称*X 为()f X 在R 上的局部极小点,*()f X 为局部极小值。
若*()>()f X f X ,则称*X 为()f X 在R 上的严格局部极小点,*()f X 为严格局部极小值。
定义4.1.2 设f (X )为定义在n 维欧式空间E n 某一区域R 上的实函数,对于X *∈R n E ⊂,若对所有的X R ∈都有*()()f X f X ≥ (4.1.10)则称*X 为()f X 在R 上的全局极小点,*()f X 为全局极小值。
若*()>()f X f X ,则称*X 为()f X 在R 上的严格全局极小点,*()f X 为严格全局极小值。
若将上述定义中的不等号反向,则可得到极大点和极大值的定义。
下面先介绍海赛矩阵与二次型,然后讨论多元函数极值存在的条件。
4.1.3 海赛(Hesse)矩阵与二次型定义 4.1.3 设函数()f X 为定义在n 维欧式空间n E 某一区域R 上的n 元实函数,()T12,,,n X x x x = 。
若()f X 在R 上可微,令T12()()()()grad ,,,n f X f X f X f X f x x x ⎛⎞∂∂∂∇==⎜⎟∂∂∂⎝⎠(4.1.11)则称()f X ∇为()f X 的梯度向量,亦记作grad f 。
黑塞矩阵——精选推荐
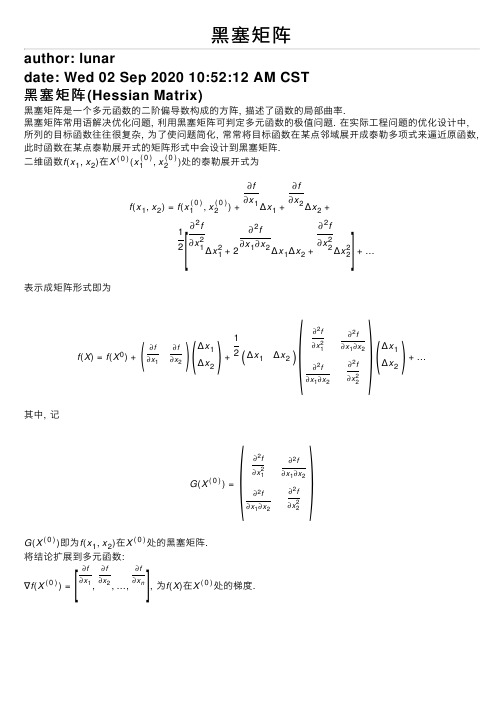
⿊塞矩阵author: lunardate: Wed 02 Sep 2020 10:52:12 AM CST⿊塞矩阵(Hessian Matrix)⿊塞矩阵是⼀个多元函数的⼆阶偏导数构成的⽅阵, 描述了函数的局部曲率.⿊塞矩阵常⽤语解决优化问题, 利⽤⿊塞矩阵可判定多元函数的极值问题. 在实际⼯程问题的优化设计中,所列的⽬标函数往往很复杂, 为了使问题简化, 常常将⽬标函数在某点邻域展开成泰勒多项式来逼近原函数,此时函数在某点泰勒展开式的矩阵形式中会设计到⿊塞矩阵.⼆维函数f(x1,x2)在X(0)(x(0)1,x(0)2)处的泰勒展开式为f(x1,x2)=f(x(0)1,x(0)2)+∂f∂x1Δx1+∂f∂x2Δx2+1 2∂2f∂x21Δx21+2∂2f∂x1∂x2Δx1Δx2+∂2f∂x22Δx22+…表⽰成矩阵形式即为f(X)=f(X0)+∂f∂x1∂f∂x2Δx1Δx2+12Δx1Δx2∂2f∂x21∂2f∂x1∂x2∂2f∂x1∂x2∂2f∂x22Δx1Δx2+…其中, 记G(X(0))=∂2f∂x21∂2f∂x1∂x2∂2f∂x1∂x2∂2f∂x22G(X(0))即为f(x1,x2)在X(0)处的⿊塞矩阵.将结论扩展到多元函数:∇f(X(0))=∂f∂x1,∂f∂x2,…,∂f∂x n, 为f(X)在X(0)处的梯度.[] ()()()()()() []G (X (0))=∂2f ∂x 21∂2f ∂x 1∂x 2…∂2f∂x 1∂x n ∂2f ∂x 2∂x 1∂2f ∂x 22…∂2f∂x 2∂x n⋮⋮⋱⋮∂2f ∂x n ∂x 1∂2f ∂x n ∂x 2…∂2f ∂x 2nX (0)为函数f (X )在X (0)处的⿊塞矩阵.利⽤⿊塞矩阵判断多元函数的极值当多元函数f (x 1,x 2,…,x n )在点M 0(a 1,a 2,…,a n )的邻域内存在连续⼆阶偏导数且满⾜:∂f ∂x j(a 1,a 2,…,a n )=0,j =1,2,…,n且有A =∂2f∂x 21∂2f∂x 1∂x 2…∂2f∂x 1∂x n ∂2f∂x 2∂x 1∂2f∂x 22 (2)∂x 2∂x n⋮⋮⋱⋮∂2f ∂x n ∂x 1∂2f∂x n ∂x 2…∂2f∂x 2nX (0)则有当A 为时, f 在M 0为极⼩值;当A 为负定矩阵时, f 在M 0存在极⼤值;当A 为时, M 0不是极值点.当A 为或半负定矩阵时, M 0是"可疑"极值点.[]|[]Processing math: 100%。
海森矩阵法

海森矩阵法
海森矩阵法(Hessian matrix method)是一种用于求解函数极值点的优化算法。
它是二阶优化方法的一种,可以通过计算函数的海森矩阵(Hessian matrix)来确定函数的极值点。
海森矩阵是函数的二阶偏导数构成的矩阵,是一个正定矩阵。
通过计算海森矩阵,可以确定函数极值点的位置和性质。
海森矩阵法可以用于求解最小化或最大化问题。
对于最小化问题,通过计算海森矩阵的特征值和特征向量,可以确定极小值点的位置和优化方向。
对于最大化问题,可以通过求解海森矩阵的负值来转化为最小化问题。
海森矩阵法的一般步骤如下:
1. 计算函数的一阶偏导数和二阶偏导数,得到海森矩阵。
2. 判断海森矩阵的正定性。
如果海森矩阵是正定矩阵,则存在极小值点;如果是负定矩阵,则存在极大值点;如果是不定矩阵,则不存在极值点。
3. 如果海森矩阵是正定矩阵,可以通过求解海森矩阵的特征值和特征向量,确定极小值点的位置和优化方向。
4. 对于最大化问题,可以求解海森矩阵的负值,转化为最小化问题。
海森矩阵法相对于一阶优化方法(如梯度下降法)具有更快的收敛速度和更高的精度。
然而,由于海森矩阵的计算量较大,对于复杂的函数,计算海森矩阵的成本较高。
因此,在实际应
用中,海森矩阵法往往用于求解简单的优化问题或者作为其他优化算法的一种改进方法。
总结来说,海森矩阵法是一种基于二阶导数的优化算法,通过计算函数的海森矩阵来确定函数的极值点。
它具有较快的收敛速度和更高的精度,但在计算复杂函数时成本较高。
heese矩阵多元函数极值点

heese矩阵多元函数极值点海塞矩阵(Hessian Matrix),又译作海森矩阵,是一个多元函数的二阶偏导数构成的方阵。
虽然它是一个具有悠久历史的数学成果。
可是在机器学习和图像处理(比如SIFT和SURF特征检測)中,我们也经常遇到它。
所以本文就来向读者道一道Hessian Matrix的来龙去脉。
本文的主要内容包括:多元函数极值问题回想一下我们是如何处理求一元函数极值的问题的。
比如。
f(x)=x2,我们会先求一阶导数,即f′(x)=2x,依据费马定理极值点处的一阶导数一定等于 0。
但这仅是一个必要条件。
而非充分条件。
对于f(x)=x2来说,函数的确在一阶导数为零的点取得了极值,可是对于f(x)=x3来说,显然只检查一阶导数是不足以下定论的。
这时我们须要再求一次导,假设二阶导数 f″<0,那么说明函数在该点取得局部极大值;假设二阶导数 f″>0,则说明函数在该点取得局部极小值;假设 f″=0。
则结果仍然是不确定的,我们就不得不再通过其它方式来确定函数的极值性。
假设我们要找一个多元函数中的极值点,方法也差不多。
作为一个演示样例。
最好还是用一个三元函数 f=f(x,y,z) 来作为演示样例。
首先要对函数中的每一个变量分别求偏导数,这会告诉我们该函数的极值点可能出如今哪里。
即∂f∂x=0∂f∂y=0∂f∂x=0下一个。
继续求二阶导数,包括混合偏导数在内有9种情况。
假设用矩阵形式表示,你会得到H=⎡⎡⎡⎡⎡⎡⎡⎡⎡∂2f∂x∂x∂2f∂y∂x∂2f∂z∂x∂2f ∂x∂y∂2f∂y∂y∂2f∂z∂y∂2f∂x∂z∂2f∂y∂z∂2f∂z ∂z⎡⎡⎡⎡⎡⎡⎡⎡⎡这个矩阵就称为Hessian矩阵。
当然上面所给出的不过一个三阶的Hessian矩阵。
稍作扩展。
我们能够对一个在定义域内二阶连续可导的实值多元函数 f(x1,x2,⋯,xn) 定义其Hessian矩阵H例如以下H=⎡⎡⎡⎡⎡⎡⎡⎡⎡⎡⎡∂2f∂x21∂2f∂x2∂x1⋮∂2f∂x n∂x1∂2f∂x1∂x2∂2f∂x22⋮∂2f∂xn∂x2⋯⋯⋱⋯∂2f∂x1∂xn∂2f∂x2∂xn⋮∂2f∂x2n⎡⎡⎡⎡⎡⎡⎡⎡⎡⎡⎡当一元函数的二阶导数等于 0 时,我们并不能确定函数在该点的极值性。
hesse矩阵非正定的牛顿法

hesse矩阵非正定的牛顿法
Hesse矩阵非正定的牛顿法是用于求解非线性规划问题的一种迭代算法。
它是牛顿法的一个扩展,专门用于处理Hesse矩阵非正定(半正定)的情况。
牛顿法是一种二阶收敛的优化算法,其基本思想是利用目标函数的二阶导数(Hesse矩阵)来近似求解最优化问题。
牛顿法的迭代公式为:
x_{k+1} = x_k - [Hessian(x_k)]^{-1} gradient(x_k)
其中,x_k 表示第k 步的迭代解,Hessian(x_k) 表示在x_k 处的Hesse 矩阵,gradient(x_k) 表示在x_k 处的目标函数梯度。
当Hesse 矩阵非正定时,牛顿法可能无法收敛。
为了解决这个问题,可以使用Hesse矩阵非正定的牛顿法。
这种方法的主要思想是在每一步迭代中,使用一个正定的矩阵来近似Hesse 矩阵。
常用的正定矩阵替代方法有:Levenberg-Marquardt 方法、修正牛顿法等。
在实际应用中,Hesse矩阵非正定的牛顿法常常用于求解非线性最小二乘问题、非线性优化问题等。
需要注意的是,尽管这种方法可以处理Hesse 矩阵非正定的情况,但其收敛速度可能受到近似方法的影响。
因此,在实际问题中,需要根据具体问题特性选择合适的近似方法和参数设置。
黑塞矩阵和模型协方差矩阵

黑塞矩阵和模型协方差矩阵1. 黑塞矩阵的概念黑塞矩阵,又称为海森矩阵(Hessian Matrix),是二阶偏导数构成的方阵。
它在优化问题和数值计算中起到了重要的作用。
黑塞矩阵是一个对称矩阵,其中每个元素是二阶偏导数的导数矩阵。
2. 黑塞矩阵的应用黑塞矩阵在许多领域中都有广泛的应用,特别是在优化算法和机器学习中。
它可以提供有关函数局部性质的信息,例如极小值、鞍点和局部二次型特性。
黑塞矩阵的应用可以帮助优化算法更快地收敛,从而在求解问题时提高效率和准确性。
2.1 优化算法中的黑塞矩阵在优化算法中,黑塞矩阵被用来描述目标函数的曲率。
通过分析黑塞矩阵的特征值,可以判断目标函数的最小值、最大值或鞍点的存在。
根据这些信息,可以选择合适的优化算法来优化目标函数。
2.2 机器学习中的黑塞矩阵在机器学习中,黑塞矩阵有助于解决参数估计问题。
通过对参数估计模型的损失函数计算黑塞矩阵,可以得到模型参数的方差估计和相关性。
这对于模型的可靠性评估和参数的置信区间估计非常重要。
3. 模型协方差矩阵的概念模型协方差矩阵是描述模型参数之间相关性的矩阵。
它是一个对称矩阵,其中每个元素表示对应参数之间的协方差。
模型协方差矩阵可以通过训练数据和模型参数的估计得到。
3.1 协方差矩阵的定义协方差矩阵是描述两个随机变量之间关系的矩阵。
在机器学习中,模型参数可以视为随机变量,其协方差矩阵用于表示参数之间的关系。
协方差矩阵的对角线元素表示各个参数的方差,非对角线元素表示参数之间的协方差。
3.2 模型协方差矩阵的应用模型协方差矩阵在机器学习中被广泛应用于参数估计、模型选择和模型优化等方面。
它可以提供关于参数的置信区间、参数选择的准则和模型优化的方向等重要信息。
4. 黑塞矩阵和模型协方差矩阵之间的关系黑塞矩阵和模型协方差矩阵之间存在一定的联系。
在某些情况下,黑塞矩阵的逆和模型参数的方差估计矩阵相等。
4.1 黑塞矩阵和模型协方差矩阵的关系对于具有凸损失函数的模型,黑塞矩阵的逆等于模型参数的方差估计矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海赛(Hesse)矩阵
在数学中,海色矩阵是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,此函数如下:
如果f所有的二阶导数都存在,那么f的海色矩阵即:
H(f)ij(x) =DiDjf(x)
其中,即
(也有人把海色定义为以上矩阵的行列式)海色矩阵被应用于牛顿法解决的大规模优化问题。
混合偏导数和海色矩阵的对称性
海色矩阵的混合偏导数是海色矩阵主对角线上的元素。
假如他们是连续的,那么求导顺序没有区别,即
上式也可写为
在正式写法中,如果f函数在区域D内连续并处处存在二阶导数,那么f的海色矩阵在D区域内为对称矩阵。
在 R^2→R 的函数的应用
给定二阶导数连续的函数,海色矩阵的行列式,可用于分辨f的临界点是属于鞍点还是极值。
对于f的临界点(x0,y0)一点,有,然而凭一阶导数不能判断它是鞍点、局部极大点还是局部极小点。
海色矩阵可能解答这个问题。
∙H > 0 :若,则(x0,y0)是局部极小点;若,则(x0,y0)是局部极大点。
∙H < 0 :(x0,y0)是鞍点。
∙H = 0 :二阶导数无法判断该临界点的性质,得从更高阶的导数以泰勒公式考虑。
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等
等
打造全网一站式需求。
