stata上机实验操作
stata上机实验第一讲

添加标签
1。为整个数据添加标签:例如,将数据命名
为“工资表”。 菜单:Data->Labels->Label dataset 命令:label data “工资表“ 2。为变量增加标签,例如,给变量wage增 加标签“年工资总额” 菜单:Data->Labels->Label variables 命令 label variable wage “年工资总额"
1。所有的系统自带数据可以利用sysuse命令
打开。 2。Use命令只能打开 C:\data 或者 D:\data 中的数据。 3。如果需要打开其他文件夹的数据,必须改 变目录(例如,将自己的数据放入D:\abc) cd "D:\abc” 或者直接 file------open
先学习几条最简单的命令
Stata的菜单介绍
最重要的菜单项:
Data菜单 Graphic菜单
Statistics菜单
每执行一个菜单性会自动产生相应的命令。
(以summarize为例)。 我们的讲述尽量兼顾到命令操作和菜单操作 两种方法,以命令方式为主。
安装指南
解压 setup.rar
运行 setup 安装时选择 Stata SE
装到: C:\Program file\stata10 中。 将所用系统自带的一些系统数据、应用程序、 帮助文件安装到 C:\Program file\stata10\ado\base 中 将所有升级程序安装到: C:\Program file\stata10\ado\update 中
Stata数据的录入
1。直接录入。
stata选择实验法

stata选择实验法
Stata是一种统计分析软件,可以用于分析各种数据,包括实验数据。
在使用Stata进行实验法选择时,以下步骤可以作为参考:
1. 数据准备:将实验数据导入Stata中,并确保数据格式正确。
2. 描述性统计:使用Stata的描述性统计功能,对实验数据进行总体特征的描述,包括均值、标准差等。
3. T检验:如果实验中涉及到两个样本之间的比较,可以使用Stata的T检验功能,比较两个样本的均值是否存在显著差异。
4. 方差分析:如果实验中有多个组别,可以使用Stata的方差分析功能,比较不同组别之间的均值是否存在显著差异。
5. 回归分析:如果实验中有多个自变量和一个因变量,可以使用Stata的回归分析功能,探究自变量对因变量的影响,同时进行显著性检验。
6. 实验设计优化:根据实验结果,可以使用Stata的设计优化功能,对实验方案进行调整,以获得更准确和可靠的结果。
以上是使用Stata进行实验法选择的一般步骤,具体分析方法和步骤可能因实验的具体要求而有所不同。
stata上机实验第五讲 工具变量(IV)

究竟该用OLS 还是IV
即解释变量是否真的存在内生性? 假设能够找到方程外的工具变量。 1。如果所有解释变量都是外生变量,则OLS
比IV 更有效。在这种情况下使用IV,虽然估 计量仍然是一致的,会增大估计量的方差。2。 如果存在内生解释变量,则OLS 是不一致的, 而IV 是一致的。
豪斯曼检验(Hausman specification test)原假设: H0 :所有解释变量均为外生变量。 H1:至少有一个解释变量为内生变量。
检验方法: estat firststage 1。初步判断可以用偏R2(partial R2) (剔除掉模型中原有外生变量的影响)。 2。 Minimum eigenvalue statistic(最小特征 值统计量),经验上此数应该大于10。
ivregress 2sls lw80 expr80 tenure80 (s80 iq=med kww mrt age), first
使用grilic.dta估计教育投资的回报率。
变量说明:lw80(80年工资对数),s80 (80年时受教育年限),expr80(80年时工 龄),tenure80(80年时在现单位工作年 限), iq(智商),med(母亲的教育年 限),kww(在‘knowledge of the World of Work’测试中的成绩),mrt(婚姻虚拟变量, 已婚=1),age(年龄)。
ivregress 2sls lw80 expr80 tenure80 (s80 iq=med kww mrt age), first estat overid ivregress gmm lw80 expr80 tenure80 (s80 iq=med kww mrt age) estat overid
(最新整理)stata上机实验第五讲——面板数据的处理..

• corr(u_i, Xb) 个体效应与解释变量的相关系数,相关 系数为0或者接近于0,可以使用随机效应模型;相 关系数不为0,需要使用固定效应模型。u-i不表示残 差,表示个体效应。
2021/7/26
19
模型选择
• 固定效应还是混合OLS? 可以直接观测F值
• 随机效应还是混合OLS? 先用随机效应回归,然后运行xttest0
• xtgls Panel-data models using GLS
• xtpcse OLS or Prais-Winsten models with panelcorrected standard errors
• xtrchh Hildreth-Houck random coefficients models
计量经济学stata操作指南

计量经济学stata操作指南计量经济学stata操作(实验课)第一章stata基本知识1、stata窗口介绍2、基本操作(1)窗口锁定:Edit-preferences-general preferences-windowing-lock splitter (2)数据导入(3)打开文件:use E:\example.dta,clear(4)日期数据导入:gen newvar=date(varname, “ymd”)format newvar %td 年度数据gen newvar=monthly(varname, “ym”)format newvar %tm 月度数据gen newvar=quarterly(varname, “yq”)format newvar %tq 季度数据(5)变量标签Label variable tc ` “total output” ’(6)审视数据describelist x1 x2list x1 x2 in 1/5list x1 x2 if q>=1000drop if q>=1000keep if q>=1000(6)考察变量的统计特征summarize x1su x1 if q>=10000su q,detailsutabulate x1correlate x1 x2 x3 x4 x5 x6(7)画图histogram x1, width(1000) frequency kdensity x1scatter x1 x2twoway (scatter x1 x2) (lfit x1 x2) twoway (scatter x1 x2) (qfit x1 x2) (8)生成新变量gen lnx1=log(x1)gen q2=q^2gen lnx1lnx2=lnx1*lnx2gen larg=(x1>=10000)rename larg largeg large=(q>=6000)replace large=(q>=6000)drop ln*(8)计算功能display log(2)(9)线性回归分析regress y1 x1 x2 x3 x4vce #显示估计系数的协方差矩阵reg y1 x1 x2 x3 x4,noc #不要常数项reg y1 x1 x2 x3 x4 if q>=6000reg y1 x1 x2 x3 x4 if largereg y1 x1 x2 x3 x4 if large==0reg y1 x1 x2 x3 x4 if ~large predict yhatpredict e1,residualdisplay 1/_b[x1]test x1=1 # F检验,变量x1的系数等于1test (x1=1) (x2+x3+x4=1) # F联合假设检验test x1 x2 #系数显著性的联合检验testnl _b[x1]= _b[x2]^2(10)约束回归constraint def 1 x1+x2+x3=1cnsreg y1 x1 x2 x3 x4,c(1)cons def 2 x4=1cnsreg y1 x1 x2 x3 x4,c(1-2)(11)stata的日志File-log-begin-输入文件名log off 暂时关闭log on 恢复使用log close 彻底退出(12)stata命令库更新Update allhelp command第二章有关大样本ols的stata命令及实例(1)ols估计的稳健标准差reg y x1 x2 x3,robust(2)实例use example.dta,clearreg y1 x1 x2 x3 x4test x1=1reg y1 x1 x2 x3 x4,rtestnl _b[x1]=_b[x2]^2第三章最大似然估计法的stata命令及实例(1)最大似然估计help ml(2)LR检验lrtest #对面板数据中的异方差进行检验(3)正态分布检验sysuse auto #调用系统数据集auto.dtahist mpg,normalkdensity mpg,normalqnorm mpg*手工计算JB统计量sum mpg,detaildi (r(N)/6)*((r(skewness)^2)+[(1/4)*(r(kurtosis)-3)^2]) di chi2tail(自由度,上一步计算值)*下载非官方程序ssc install jb6jb6 mpg*正态分布的三个检验sktest mpgswilk mpgsfrancia mpg*取对数后再检验gen lnmpg=log(mpg)kdensity lnmpg, normaljb6 lnmpgsktest lnmpg第四章处理异方差的stata命令及实例(1)画残差图rvfplotrvfplot varname*例题use example.dta,clearreg y x1 x2 x3 x4rvfplot # 与拟合值的散点图rvfplot x1 # 画残差与解释变量的散点图(2)怀特检验estat imtest,white*下载非官方软件ssc install whitetst(3)BP检验estat hettest #默认设置为使用拟合值estat hettest,rhs #使用方程右边的解释变量estat hettest [varlist] #指定使用某些解释变量estat hettest,iidestat hettest,rhs iidestat hettest [varlist],iid(4)WLSreg y x1 x2 x3 x4 [aw=1/var]*例题quietly reg y x1 x2 x3 x4predict e1,resgen e2=e1^2gen lne2=log(e2)reg lne2 x2,nocpredict lne2fgen e2f=exp(lne2f)reg y x1 x2 x3 x4 [aw=1/e2f](5)stata命令的批处理(写程序)Window-do-file editor-new do-file#WLS for examplelog using E:\wls_example.smcl,replaceset more offuse E:\example.dta,clearreg y x1 x2 x3 x4predict e1,resgen e2=e1^2g lne2=log(e2)reg lne2 x2,nocpredict lne2fg e2f=exp(lne2f)*wls regressionreg y x1 x2 x3 x4 [aw=1/e2f]log closeexit第五章处理自相关的stata命令及实例(1)滞后算子/差分算子tsset yearl.l2.D.D2.LD.(2)画残差图scatter e1 l.e1ac e1pac e1(3)BG检验estat bgodfrey(默认p=1)estat bgodfrey,lags(p)estat bgodfrey,nomiss0(使用不添加0的BG检验)(4)Ljung-Box Q检验reg y x1 x2 x3 x4predict e1,residwntestq e1wntestq e1,lags(p)* wntestq指的是“white noise test Q”,因为白噪声没有自相关(5)DW检验做完OLS回归后,使用estat dwatson(6)HAC稳健标准差newey y x1 x2 x3 x4,lag(p)reg y x1 x2 x3 x4,cluster(varname)(7)处理一阶自相关的FGLSprais y x1 x2 x3 x4 (使用默认的PW估计方法)prais y x1 x2 x3 x4,corc (使用CO估计法)(8)实例use icecream.dta, cleartsset timegraph twoway connect consumption temp100 time, msymbol(circle) msymbol(triangle) reg consumption temp price incomepredict e1, resg e2=l.e1twoway (scatter e1 e2) (lfit e1 e2)ac e1pac e1estat bgodfreywntestq e1estat dwatsonnewey consumption temp price income, lag (3)prais consumption temp price income, corcprais consumption temp price income, nologreg consumption temp l.temp price incomeestat bgodfreyestat dwatson第六章模型设定与数据问题(1)解释变量的选择reg y x1 x2 x3estat ic*例题use icecream.dta, clearreg consumption temp price incomeestat icreg consumption temp l.temp price incomeestat ic(2)对函数形式的检验(reset检验)reg y x1 x2 x3estat ovtest (使用被解释变量的2、3、4次方作为非线性项)estat ovtest, rhs (使用解释变量的幂作为非线性项,ovtest-omitted variable test)*例题use nerlove.dta, clearreg lntc lnq lnpl lnpk lnpfestat ovtestg lnq2=lnq^2reg lntc lnq lnq2 lnpl lnpk lnpfestat ovtest(3)多重共线性estat vif*例题use nerlove.dta, clearreg lntc lnq lnpl lnpk lnpfestat vif(4)极端数据reg y x1 x2 x3predict lev, leverage (列出所有解释变量的lev值)gsort –levsum levlist lev in 1/3*例题use nerlove.dta, clearquietly reg lntc lnq lnpl lnpk lnpfpredict lev, leveragesum levgsort –levlist lev in 1/3(5)虚拟变量gen d=(year>=1978)tabulate province, generate (pr)reg y x1 x2 x3 pr2-pr30(6)经济结构变动的检验方法1:use consumption_china.dta, cleargraph twoway connect c y year, msymbol(circle) msymbol(triangle)reg c yreg c y if year<1992reg c y if year>=1992计算F统计量方法2:gen d=(year>1991)gen yd=y*dreg c y d ydtest d yd第七章工具变量法的stata命令及实例(1)2SLS的stata命令ivregress 2sls depvar [varlist1] (varlist2=instlist)如:ivregress 2sls y x1 (x2=z1 z2)ivregress 2sls y x1 (x2 x3=z1 z2 z3 z4) ,r firstestat firststage,all forcenonrobust (检验弱工具变量的命令)ivregress liml depvar [varlist 1] (varlist2=instlist)estat overid (过度识别检验的命令)*对解释变量内生性的检验(hausman test),缺点:不适合于异方差的情形reg y x1 x2estimates store olsivregress 2sls y x1 (x2=z1 z2)estimates store ivhausman iv ols, constant sigmamore*DWH检验estat endogenous*GMM的过度识别检验ivregress gmm y x1 (x2=z1 z2) (两步GMM)ivregress gmm y x1 (x2=z1 z2),igmm (迭代GMM)estat overid*使用异方差自相关稳健的标准差GMM命令ivregress gmm y x1 (x2=z1 z2), vce (hac nwest[#])(2)实例use grilic.dta,clearsumcorr iq sreg lw s expr tenure rns smsa,rreg lw s iq expr tenure rns smsa,rivregress 2sls lw s expr tenure rns smsa (iq=med kww mrt age),restat overidivregress 2sls lw s expr tenure rns smsa (iq=med kww),r first estat overidestat firststage, all forcenonrobust (检验工具变量与内生变量的相关性)ivregress liml lw s expr tenure rns smsa (iq=med kww),r *内生解释变量检验quietly reg lw s iq expr tenure rns smsaestimates store olsquietly ivregress 2sls lw s expr tenure rns smsa (iq=med kww) estimates store ivhausman iv ols, constant sigmamoreestat endogenous (存在异方差的情形)*存在异方差情形下,GMM比2sls更有效率ivregress gmm lw s expr tenure rns smsa (iq=med kww)estat overidivregress gmm lw s expr tenure rns smsa (iq=med kww),igmm*将各种估计方法的结果存储在一张表中quietly ivregress gmm lw s expr tenure rns smsa (iq=med kww)estimates store gmmquietly ivregress gmm lw s expr tenure rns smsa (iq=med kww),igmmestimates store igmmestimates table gmm igmm第八章短面板的stata命令及实例(1)面板数据的设定xtset panelvar timevarencode country,gen(cntry) (将字符型变量转化为数字型变量)xtdesxtsumxttab varnamextline varname,overlay*实例use traffic.dta,clearxtset state yearxtdesxtsum fatal beertax unrate state yearxtline fatal(2)混合回归reg y x1 x2 x3,vce(cluster id)如:reg fatal beertax unrate perinck,vce(cluster state)estimates store ols对比:reg fatal beertax unrate perinck(3)固定效应xtreg y x1 x2 x3,fe vce(cluster id)xi:reg y x1 x2 x3 i.id,vce(cluster id) (LSDV法)xtserial y x1 x2 x3,output (一阶差分法,同时报告面板一阶自相关)estimates store FD*双向固定效应模型tab year, gen (year)xtreg fatal beertax unrate perinck year2-year7, fe vce (cluster state)estimates store FE_TWtest year2 year3 year4 year5 year6 year7(4)随机效应xtreg y x1 x2 x3,re vce(cluster id) (随机效应FGLS)xtreg y x1 x2 x3,mle (随机效应MLE)xttest0 (在执行命令xtreg, re 后执行,进行LM检验)(5)组间估计量xtreg y x1 x2 x3,be(6)固定效应还是随机效应:hausman testxtreg y x1 x2 x3,feestimates store fextreg y x1 x2 x3,reestimates store rehausman fe re,constant sigmamore (若使用了vce(cluster id),则无法直接使用该命令,解决办法详见P163)estimates table ols fe_robust fe_tw re be, b se (将主要回归结果列表比较)第九章长面板与动态面板(1)仅解决组内自相关的FGLSxtpcse y x1 x2 x3 ,corr(ar1) (具有共同的自相关系数)xtpcse y x1 x2 x3 ,corr(psar1) (允许每个面板个体有自身的相关系数)例题:use mus08cigar.dta,cleartab state,gen(state)gen t=year-62reg lnc lnp lnpmin lny state2-state10 t,vce(cluster state)estimates store OLSxtpcse lnc lnp lnpmin lny state2-state10 t,corr(ar1) (考虑存在组内自相关,且各组回归系数相同)estimates store AR1xtpcse lnc lnp lnpmin lny state2-state10 t,corr(psar1) (考虑存在组内自相关,且各组回归系数不相同)estimates store PSAR1xtpcse lnc lnp lnpmin lny state2-state10 t, hetonly (仅考虑不同个体扰动性存在异方差,忽略自相关)estimates store HETONL Yestimates table OLS AR1 PSAR1 HETONL Y, b se(2)同时处理组内自相关与组间同期相关的FGLSxtgls y x1 x2 x3,panels (option/iid/het/cor) corr(option/ar1/psar1) igls注:执行上述xtpcse、xtgls命令时,如果没有个体虚拟变量,则为随机效应模型;如果加上个体虚拟变量,则为固定效应模型。
stata入门操作

-1-
任务:按学号录入五个学生的经济学成绩
id
economy
1
40
2
80
3
90
4
70
5Hale Waihona Puke 53操作:在 command 窗口中键入(注:前面的点号不必健入,每完成一行按回车键,黑体为命令,
斜体为变量名或文件名):
• clear
• input id name
• 1 40
• 2 80
• 3 90
• use economy,clear • sum economy • sum • sum economy in 1/2 • sum economy in 1/4 if economy>60
补充: Format 用来控制数据输出的格式
任务 2:生成新的数据 x, (x=1,2,…1000); y=x+100. • clear • set obs 1000 • gen x=_n • gen y=x+100
• 4 70
• 5 53
• end
• save economy
• save economy,replace
• exit,clear 其中后两命令先保存数据,文件名为 economy,然后清除内存中的数据并退出 STATA. 如果重复执行 save economy 回出现错误提示”file economy have already exist”,意味着
pwd
显示当前路径
pwd
dir
列示当前路径文件夹中的所有文件 dir
mkdir
在当前路径下创建一个新的文件夹 mkdir d:/mydata
cd
将 cd 后面的路径设定为当前路径 cd “d:/mydata”
stata上机实验第六讲

不同,其参数估计值并不直接可比。雨宫 (Amemiya)提出:同一个模型的logit和 probit模型大概具有如下关系: Blogit 约等于 1.6*BProbit 但利用mfx计算的两者的边际效应应该大致相 同。
一个综合例子
使用美国妇女就业数据集“womenwork.dta”,
估计决定就业的Probit与Logit模型。被解释 变量为work=1,就业;work=0,不就业。解 释变量为age(年龄), married(婚否), children(子女数), education(教育年限)。
排序选择模型
根据GSS的调查数据,不同的家庭母亲与子 女之间的关系也不同。根据调查显示,有的 家庭母子(女)关系比较紧张,有的比较融 洽。变量包括:warm=关系融洽度(0、1、2、 3);educ=子女接受教育的程度;age=子女 年龄;male=儿子;prst=职业威望;white= 白人;y89=89年调查结果。分析不同因素对 母子(女)关系的融洽程度有何影响。
sysuse auto,clear truncreg price weight length gear_ratio, ll(10000) reg price weight length gear_ratio if price>=10000
截取回归
对于线性模型yi =x’B+εi,如果满足yi ≥ c或者
nbreg daysabs langarts male 命令结果中将提供一个LR 检验, 原假设:不存在过度分散,应该使用泊松回 归。此时alpha=0。 备则假设: alpha<>0,不能使用泊松回归。
受限因变量模型
1。断尾回归
2。截取回归
stata上机实验操作
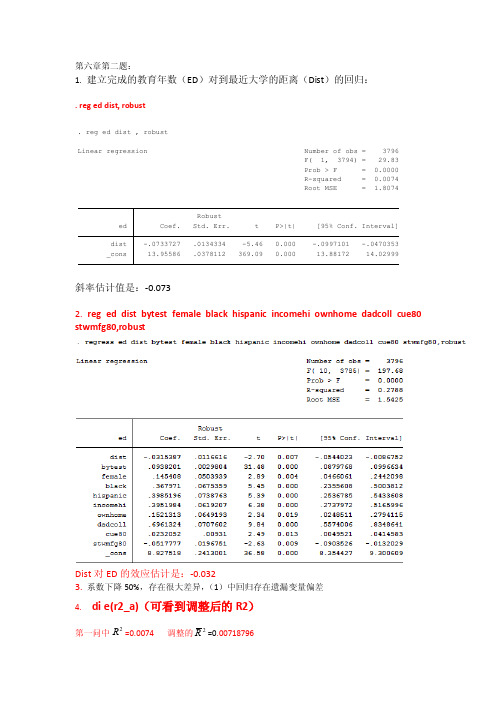
第六章第二题:1. 建立完成的教育年数(ED )对到最近大学的距离(Dist )的回归:. reg ed dist, robust斜率估计值是:-0.0732. reg ed dist bytest female black hispanic incomehi ownhome dadcoll cue80 stwmfg80,robustDist 对ED 的效应估计是:-0.0323. 系数下降50%,存在很大差异,(1)中回归存在遗漏变量偏差4. di e(r2_a)(可看到调整后的R2)第一问中=0.0074 调整的2R =0.00718796_cons 13.95586 .0378112 369.09 0.000 13.88172 14.02999dist -.0733727 .0134334 -5.46 0.000 -.0997101 -.0470353ed Coef. Std. Err. t P>|t| [95% Conf. Interval]RobustRoot MSE = 1.8074R-squared = 0.0074Prob > F = 0.0000F( 1, 3794) = 29.83Linear regression Number of obs = 3796. reg ed dist , robust2R第二问中=0.2788 2R = 0.27693235可以得到第二问中的拟合效果要优于第一问。
第二问中相似的原因:因为n 很大。
5. Dadcoll 父亲有没有念过大学:系数为正(0.6961324)衡量父亲念过大学的学生接受的教育年数平均比其父亲没有年过大学的学生多。
-.0517777 1)原因:这些参数在一定程度上构成了上大学的机会成本。
2)它们的系数估计值的符号应该如此。
当Stwmfg80增加时,放弃的工资增加,所以大学入学率降低了;因而Stwmfg80的系数对应为负。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章第二题:1. 建立完成的教育年数(ED )对到最近大学的距离(Dist )的回归:. reg ed dist, robust斜率估计值是:-0.0732. reg ed dist bytest female black hispanic incomehi ownhome dadcoll cue80 stwmfg80,robustDist 对ED 的效应估计是:-0.0323. 系数下降50%,存在很大差异,(1)中回归存在遗漏变量偏差4. di e(r2_a)(可看到调整后的R2)第一问中=0.0074 调整的2R =0.00718796_cons 13.95586 .0378112 369.09 0.000 13.88172 14.02999dist -.0733727 .0134334 -5.46 0.000 -.0997101 -.0470353ed Coef. Std. Err. t P>|t| [95% Conf. Interval]RobustRoot MSE = 1.8074R-squared = 0.0074Prob > F = 0.0000F( 1, 3794) = 29.83Linear regression Number of obs = 3796. reg ed dist , robust2R第二问中=0.2788 2R = 0.27693235可以得到第二问中的拟合效果要优于第一问。
第二问中相似的原因:因为n 很大。
5. Dadcoll 父亲有没有念过大学:系数为正(0.6961324)衡量父亲念过大学的学生接受的教育年数平均比其父亲没有年过大学的学生多。
.0232052-.0517777 1)原因:这些参数在一定程度上构成了上大学的机会成本。
2)它们的系数估计值的符号应该如此。
当Stwmfg80增加时,放弃的工资增加,所以大学入学率降低了;因而Stwmfg80的系数对应为负。
而当Cue80增加时,人们会发现找工作很困难,这降低上大学的机会成本,所以平均的大学入学率就会增加;因而Cue80的系数对应为正。
7.带入计算即可(14.75)8.同7.(14.69)第七章第二题1. . reg course_eval beauty,robust95%置信区间见上表。
2.2R_cons 3.998272 .0253493 157.73 0.000 3.948458 4.048087beauty .1330014 .0323189 4.12 0.000 .0694908 .1965121course_eval Coef. Std. Err. t P>|t| [95% Conf. Interval]RobustRoot MSE = .54545R-squared = 0.0357Prob > F = 0.0000F( 1, 461) = 16.94Linear regression Number of obs = 463Linear regression Number of obs = 463 F( 7, 455) = 14.43 Prob > F = 0.0000 R-squared = 0.1556 Root MSE = .51377Robustcourse_eval Coef. Std. Err. t P>|t| [95% Conf. Interval]age -.0019545 .0026218 -0.75 0.456 -.0071068 .0031978 beauty .1592092 .0306846 5.19 0.000 .098908 .2195104 minority -.1694282 .067891 -2.50 0.013 -.3028471 -.0360093 female -.1832345 .0521947 -3.51 0.000 -.2858071 -.0806619 onecredit .633 .1077655 5.87 0.000 .4212201 .8447798 intro .0079488 .0565469 0.14 0.888 -.1031766 .1190742 nnenglish -.2438402 .0958959 -2.54 0.011 -.432294 -.0553863 _cons 4.16853 .1390349 29.98 0.000 3.8953 4.44176由P值得出age 及intro 变量均不显著。
所以应该去掉。
Source SS df MS Number of obs = 463F( 5, 457) = 16.71Model 21.9857702 5 4.39715404 Prob > F = 0.0000Residual 120.25285 457 .263135339 R-squared = 0.1546Adj R-squared = 0.1453Total 142.23862 462 .307875801 Root MSE = .51297course_eval Coef. Std. Err. t P>|t| [95% Conf. Interval]minority -.1647853 .0756893 -2.18 0.030 -.3135275 -.0160431female -.1741755 .049113 -3.55 0.000 -.2706909 -.0776601onecredit .6413254 .1063165 6.03 0.000 .4323955 .8502554beauty .1660434 .0306266 5.42 0.000 .1058569 .2262299nnenglish -.2480077 .1052349 -2.36 0.019 -.4548121 -.0412033_cons 4.072006 .032976 123.48 0.000 4.007203 4.13681变量均显著合理的置信区间应为(0 .1058569 0.2262299)第八章第二题:1.reg course_eval beauty intro onecredit female minority nnenglish,r2. gen age2=age*age. reg course_eval age age2,beauty intro onecredit female minority nnenglish ,r由age 与age2 的p值可看出均大于0.05,因此不能拒绝原假设,即没有充分的证据显示age 对course_eval的效应是非线性的,也没有证据显示Age对Course_Eval 有影响。
3.生成交互项:generate a= female* beauty.regress course_eval beauty intro onecredit female minority nnenglish fb,robustfemale与Beauty的交互作用的变量后,其P值为0.000变量是显著的,即有充分证据表明性别不同时,Beauty的效应之差存在。
4.. sum beautyVariable Obs Mean Std. Dev. Min> Max>beauty 463 4.75e-08 .7886477 -1.450494> 1.970023可知:手术前的beauty为-0.7886,术后为0.7886,上升了0.231 * (2 * 0.79) = 0.37.课程提高的95%置信区间为(0.231*1.96*0.048) *(2 *0.79) ,即(0.22 ,0.51)5.计算略第八章第四题:keep if country_name != "Malta"reg growth tradeshare yearsschool //回归1est store m1gen ly=ln( yearsschool )reg growth tradeshare lyest store m2gen lr=ln( rgdp60)reg growth tradeshare ly rev_coups assasinations lrest store m3gen tly= tradeshare* lyreg growth tradeshare ly rev_coups assasinations lr tlyest store m4gen t2= tradeshare* tradesharegen t3= tradeshare* t2reg growth tradeshare t2 t3 ly rev_coups assasinations lrest store m5outreg2 [m1 m2 m3 m4 m5] using myfile , word replace see或者分步:首先drop in 651.. reg growth tradeshare yearsschoolSource SS df MS Number of obs = 64 F( 2, 61) = 5.84 Model 33.3764711 2 16.6882356 Prob > F = 0.0048 Residual 174.431689 61 2.85953588 R-squared = 0.1606 Adj R-squared = 0.1331 Total 207.80816 63 3.29854222 Root MSE = 1.691growth Coef. Std. Err. t P>|t| [95% Conf. Interval]tradeshare 1.897823 .9360473 2.03 0.047 .0260808 3.769565 yearsschool .2429753 .083702 2.90 0.005 .0756027 .4103478 _cons -.1222363 .6626687 -0.18 0.854 -1.447324 1.2028522.. gene ly=ln( yearsschool ). reg growth tradeshare lySource SS df MS Number of obs = 64F( 2, 61) = 12.29Model 59.6761976 2 29.8380988 Prob > F = 0.0000Residual 148.131962 61 2.42839283 R-squared = 0.2872Adj R-squared = 0.2638Total 207.80816 63 3.29854222 Root MSE = 1.5583growth Coef. Std. Err. t P>|t| [95% Conf. Interval]tradeshare 1.748979 .8599768 2.03 0.046 .0293485 3.468608ly 1.016292 .2230901 4.56 0.000 .5701953 1.462388_cons -.185739 .5642853 -0.33 0.743 -1.314097 .94261913. gen lr=ln( rgdp60). reg growth tradeshare ly rev_coups assasinations lrSource SS df MS Number of obs = 64F( 5, 58) = 9.61Model 94.1730235 5 18.8346047 Prob > F = 0.0000Residual 113.635136 58 1.95922649 R-squared = 0.4532Adj R-squared = 0.4060Total 207.80816 63 3.29854222 Root MSE = 1.3997growth Coef. Std. Err. t P>|t| [95% Conf. Interval]tradeshare 1.10353 .8331579 1.32 0.191 -.5642168 2.771277ly 2.161291 .3626545 5.96 0.000 1.435359 2.887223rev_coups -2.299537 1.004465 -2.29 0.026 -4.310193 -.2888816assasinations .2277195 .4336512 0.53 0.602 -.6403278 1.095767lr -1.621135 .3985046 -4.07 0.000 -2.418829 -.8234416_cons 11.74591 2.919804 4.02 0.000 5.901285 17.590534. gen tly= tradeshare* ly. reg growth tradeshare ly rev_coups assasinations lr tlySource SS df MS Number of obs = 64F( 6, 57) = 8.00Model 94.9878003 6 15.8313001 Prob > F = 0.0000Residual 112.82036 57 1.97930455 R-squared = 0.4571Adj R-squared = 0.3999Total 207.80816 63 3.29854222 Root MSE = 1.4069growth Coef. Std. Err. t P>|t| [95% Conf. Interval]tradeshare 1.882807 1.475292 1.28 0.207 -1.071415 4.837029ly 2.524742 .6736203 3.75 0.000 1.175841 3.873644rev_coups -2.35021 1.012683 -2.32 0.024 -4.378073 -.3223463assasinations .2242049 .435902 0.51 0.609 -.6486738 1.097084lr -1.641397 .4017843 -4.09 0.000 -2.445956 -.8368374tly -.6900855 1.075573 -0.64 0.524 -2.843883 1.463712_cons 11.49852 2.959949 3.88 0.000 5.57132 17.425715.gen t2= tradeshare* tradeshare. gen t3= tradeshare* t2. regress growth tradeshare t2 t3 ly rev_coups assasinations lrSource SS df MS Number of obs = 64 F( 7, 56) = 7.13 Model 97.8981719 7 13.9854531 Prob > F = 0.0000 Residual 109.909988 56 1.96267836 R-squared = 0.4711 Adj R-squared = 0.4050 Total 207.80816 63 3.29854222 Root MSE = 1.401growth Coef. Std. Err. t P>|t| [95% Conf. Interval]tradeshare -5.701945 9.755116 -0.58 0.561 -25.24379 13.8399 t2 8.487876 17.43505 0.49 0.628 -26.43872 43.41448 t3 -2.759735 9.249782 -0.30 0.767 -21.28927 15.76981 ly 2.133188 .3669534 5.81 0.000 1.398092 2.868284 rev_coups -2.035454 1.025946 -1.98 0.052 -4.09067 .0197616 assasinations .1021111 .4435059 0.23 0.819 -.7863379 .9905601 lr -1.584348 .4079428 -3.88 0.000 -2.401556 -.7671405 _cons 12.92906 3.098466 4.17 0.000 6.722087 19.136031.散点图----------twoway (scatter growth yearsschool)2.预测growth回归1预测Growth 的增长为0.243×(6-4)=0.486回归2预测Growth 的增长为1.016×(ln6-ln4)=0.412。
