stata上机实验第五讲——面板数据的处理..教学内容
面板数据的常见处理

面板数据的常见处理面板数据(Panel Data)是一种涉及多个个体(cross-section units)和多个时间点(time periods)的数据结构。
它在经济学、社会科学和其他领域中被广泛应用。
处理面板数据需要采取一系列的方法和技巧,以确保数据的准确性和可靠性。
下面将介绍面板数据的常见处理方法和步骤。
一、面板数据的类型面板数据可以分为两种类型:平衡面板数据和非平衡面板数据。
1. 平衡面板数据:每个个体在每个时间点都有观测值,数据完整且连续。
2. 非平衡面板数据:个体在某些时间点上可能没有观测值,数据不完整或不连续。
二、面板数据的处理步骤1. 数据清洗和准备面板数据的处理首先需要进行数据清洗和准备工作,包括以下步骤:- 去除缺失值:对于非平衡面板数据,需要检查并去除缺失值,确保数据的完整性和连续性。
- 数据排序:根据个体和时间变量对数据进行排序,以便后续处理和分析。
- 数据转换:根据需要,对数据进行转换,如对数转换、差分等,以满足模型的要求。
2. 面板数据的描述性统计分析描述性统计分析是对面板数据的基本特征进行总结和分析,包括以下内容:- 平均值和标准差:计算每个变量在不同时间点上的平均值和标准差,了解变量的分布情况。
- 相关性分析:计算不同变量之间的相关系数,了解变量之间的关系。
- 可视化分析:绘制折线图、散点图等可视化图形,展示变量的变化趋势和关系。
3. 面板数据的面板单位根检验面板单位根检验是判断面板数据是否存在单位根(unit root)的一种方法,常用的检验方法有以下几种:- Levin-Lin-Chu (LLC)检验:用于检验面板数据是否存在单位根。
- Fisher ADF检验:用于检验面板数据是否存在单位根。
- Im-Pesaran-Shin (IPS)检验:用于检验面板数据是否存在单位根。
4. 面板数据的固定效应模型固定效应模型是用于分析面板数据的一种方法,它考虑了个体固定效应对数据的影响。
STATA面板数据模型操作命令讲解
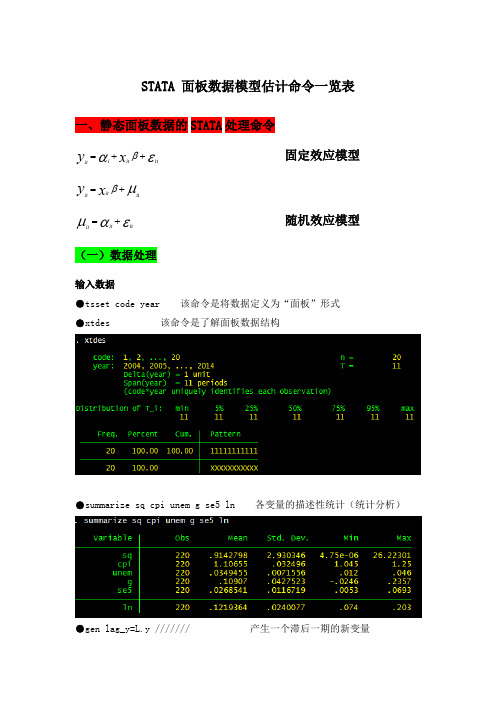
STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令固定效应模型εαβit ++=x y it i it μβit +=x y it it随机效应模型εαμit +=it it (一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例子中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量)(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现)xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应非常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。
(完整word版)STATA面板数据模型操作命令讲解

STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型(一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例子中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量)(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应非常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。
第十三章面板数据的处理

第十三章面板数据的处理第十三章面板数据的处理一、面板数据的定义、意义和种类面板数据是调查经历一段时间的同样的横截面数据,具有空间和时间的两种特性。
它还有其他一些名称,诸如混合数据,纵列数据,平行数据等,这些名字都包含了横截面单元在一段时期的活动。
面板数据的优点在于:1.提供了更有价值的数据,变量之间增加了多变性和减少了共线性,并且提高了自由度和有效性。
2.能够更好地检测和度量单纯使用横截面数据或时间序列数据无法观测到的影响。
3.能够对更复杂的行为模型进行研究。
形如01122it it it it Y X X u βββ=+++其中,i 表示第i 个横截面单元,t 表示第t 年。
一般,我们用i 来表示横截面标识符,用t 表示时间标识符。
假设N 个横截面单元的观测次数相同,我们称之为平衡面板,反之,称为非平衡面板。
一般假设X 是非随机的,误差项遵从经典假设。
二、面板数据回归模型的类型与估计方法(一)面板数据回归模型的类型对于面板数据模型 i t i i t i Y X u αβ=++,可能的情形主要有如下几种。
1.所有系数都不随时间和个体而变化在横截面上无个体影响、无结构变化,即i j αα=,i j ββ=。
则普通最小二乘估计给出了和的一致有效估计。
相当于将多个时期的截面数据放在一起作为样本数据。
it it it Y X u αβ=++。
2.变截距模型在横截面上个体影响不同,个体影响表现为在模型中被忽略的反映个体差异的影响,又分为固定效应和随机效应两种。
it i it it Y X u αβ=++3.变系数模型除了存在个体影响之外,在横截面上还存在变化的经济结构,因而结构参数在不同横截面单位是不同的。
i j αα≠,i j ββ≠。
it i it i it Y X u αβ=++。
看到面板数据之后,如何确定属于哪一种类型呢?用F 检验假设1:斜率在不同的横截面样本点上和时间上都相同,但截距不相同,即情形2。
面板数据的处理

数学: consider fatality rates in 1988 and 1982:
FatalityRatei1988 = 0 + 1BeerTax i1988 + 2Zi + ui1988 FatalityRatei1982 = 0 + 1BeerTax i1982 + 2Zi + ui1982
• 截距对 CA 是独特的, 但是斜率对所有州是相同的: 平行
线.
D
28
For TX:
YTX,t = 0 + 1XTX,t + 2ZTX + uTX,t = (0 + 2ZTX) + 1XTX,t + uTX,t
or
YTX,t = aTX + 1XTX,t + uTX,t, where aTX = 0 + 2ZTX
California (that is, i = CA)的总体回归:
YCA,t = 0 + 1XCA,t + 2ZCA + uCA,t = (0 + 2ZCA) + 1XCA,t + uCA,t
or
YCA,t = aCA + 1XCA,t + uCA,t
• aCA = 0 + 2ZCA 不随时间改变 • aCA 是 CA 的截距, 1 是斜率
二、案例研究: 啤酒税与交通死亡率
观测的单位: a year in a U.S. state
• 48 U.S. states, so n = of entities = 48 • 7 years (1982,…, 1988), so T = # of time periods = 7 • Balanced panel, so total # observations = 748 = 336 变量:
stata之面板数据处理-长面板

在Stata中,可以使用`import delimited`命令导入长面板数据。需 要指定数据文件的位置和格式,以及 时间变量和个体变量的名称。
导出数据
在Stata中,可以使用`export`命令将 长面板数据导出为其他格式,例如 CSV或Excel。需要指定数据文件的位 置、格式和名称。
长面板数据的描述性统计
长面板数据的创建
创建长面板数据
在Stata中,可以使用`xtset`命令 创建长面板数据。需要指定数据 的时间变量和个体变量,以及数
据的时间和个体范围。
时间变量的选择
时间变量通常是每个观测值所属的 时间点标识,例如年份或月份。
个体变量的选择
个体变量是每个观测值所属的个体 标识,例如公司或家庭。
长面板数据的导入与导
可视化功能相对较弱
相比一些其他统计分析软件,Stata的可视化功能相 对较弱。
无法处理实时数据
Stata主要用于处理离线数据,对于实时数据处理能 力有限。
Stata长面板数据处理的发展趋势
云计算与大数据处理
随着云计算技术的发展,未来Stata可能会加强在云计算环境下 的数来自处理能力,以应对大数据的挑战。
描述性统计
在Stata中,可以使用各种描述性统计命令来分析长面板数据,例如 `summarize`、`tabulate`和`codebook`等。这些命令可以帮助了解数据的分 布和特征。
数据清洗
在进行描述性统计之前,可能需要对数据进行清洗,例如处理缺失值、异常值 和重复值等。可以使用Stata中的各种数据清洗命令来进行处理。
根据研究目的和数据特征选择合适的面板数 据分析模型。
模型建立
使用Stata命令构建面板数据分析模型,并 指定相应的参数和选项。
面板数据stata处理步骤介绍

xA6_Panel_Data - Printed on 2011-11-25 10:43:02 149 reg y x dum1 dum2 dum3, nocons 150 est store m_pooldum3 151 152 *-M2:放入两个虚拟变量,三家公司有一个公共的截距项 153 reg y x dum2 dum3 154 est store m_pooldum2 155 156id t 158 xtreg y x, fe 159 est store m_fe 160 est table m_*, b(%6.3f) star(0.1 0.05 0.01) 161 162 163 *-6.1.4.3 stata的估计方法解析 164 165 * 目的:如果截面的个数非常多,那么采用虚拟变量的方式运算量过大 166 * 因此,要寻求合理的方式去除掉个体效应 167 * 因为,我们关注的是 x 的系数,而非每个截面的截距项 168 * 处理方法: 169 * 170 * y_it = u_i + x_it*b + e_it (1) 171 * ym_i = u_i + xm_i*b + em_i (2) 组内平均 172 * ym = um + xm*b + em (3) 样本平均 173 * (1) - (2), 可得: 174 * (y_it - ym_i) = (x_it - xm_i)*b + (e_it - em_i) (4)//within估计 175 * (4)+(3), 可得: 176 * (y_it-ym_i+ym) = um + (x_it-xm_i+xm)*b + (e_it-em_i+em) 177 * 可重新表示为: 178 * Y_it = a_0 + X_it*b + E_it 179 * 对该模型执行 OLS 估计,即可得到 b 的无偏估计量 180 181 egen y_meanw = mean(y), by(id) /*公司内部平均*/ 182 egen y_mean = mean(y) /*样本平均*/ 183 egen x_meanw = mean(x), by(id) 184 egen x_mean = mean(x) 185 gen dy = y - y_meanw + y_mean 186 gen dx = x - x_meanw + x_mean 187 reg dy dx 188 est store m_stata 189 190 est table m_*, b(%6.3f) star(0.1 0.05 0.01) 191 192 193 *-6.1.4.4 解读 xtreg,fe 的估计结果 194 195 use invest2.dta, clear 196 tsset id t 197 edit 198 xtreg market invest stock, fe 199 200 *-- R^2 201 * y_it = a_0 + x_it*b_o + e_it (1) pooled OLS 202 * y_it = u_i + x_it*b_w + e_it (2) within estimator 203 * ym_i = a_0 + xm_i*b_b + em_i (3) between estimator 204 * 205 * -> R-sq: within 模型(2)对应的R2,是一个真正意义上的R2 206 * -> R-sq: between corr{xm_i*b_w,ym_i}^2 207 * -> R-sq: overall corr{x_it*b_w,y_it}^2 208 209 *-- F(2,93) = 33.23 检验除常数项外其他解释变量的联合显著性 210 * 93 = 100-2-5 211 212 *-- corr(u_i, Xb) = 0.5256 213 214 *-- sigma_u, sigma_e, rho 215 * rho = sigma_u^2 / (sigma_u^2 + sigma_e^2) 216 dis e(sigma_u)^2 / (e(sigma_u)^2 + e(sigma_e)^2) 217 dis 1023.5914^2 / (1023.5914^2 + 370.9569^2) 218 219 *-- 个体效应是否显著?(假设检验) 220 * F(4, 93) = 97.68 H0: a1 = a2 = a3 = a4 = 0 221 * Prob > F = 0.0000 表明,固定效应高度显著 222 Page 3
stata上机实验第五讲——面板数据的处理

• xtabond Arellano-Bond linear, dynamic panel data estimator (动态面板估计) • xtabond2 Arellano-Bond system dynamic panel data estimator(需要从网上下载) • xttobit Random-effects tobit models • xtintreg Random-effects interval data regression models • xtreg Fixed-, between- and random-effects, and population-averaged linear models • xtregar Fixed- and random-effects linear models with an AR(1) disturbance • xtgls Panel-data models using GLS
tab company,gen(dum)(批量生成变量) drop dum1 reg invest mvalue kstock dum*( *表示未 知数) 与上述方法比较一下: xi:reg invest mvalue kstock pany 结果完全一样。
• xtpcse OLS or Prais-Winsten models with panelcorrected standard errors • xtrchh Hildreth-Houck random coefficients models • xtivreg Instrumental variables and two-stage least squares for panel-data models • xtabond Arellano-Bond linear, dynamic panel data estimator • xtabond2 Arellano-Bond system dynamic panel data estimator(需要从网上下载) • xttobit Random-effects tobit models • xtintreg Random-effects interval data regression models
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
mvalue
4833 4924.9 6241.7 5593.6 2289.5 2159.4 2031.3 2115.5 1819.4 2079.7 2371.6 2759.9
面板数据模型
• 考虑如下模型:
•
Yit=Xitb+Uit
•
uit=ai+εit
其中, i=1,2,… N ; t=1, 2,…T(既有i又有t的 情况则一般是用面板数据)
• xtgls Panel-data models using GLS
• xtpcse OLS or Prais-Winsten models with panelcorrected standard errors
• xtrchh Hildreth-Houck random coefficients models
• xtgls
Panel-data models using GLS
• xtpcse OLS or Prais-Winsten models with panelcorrected standard errors
面板向量自回归模型(Panel VAR) 面板单位根检验(Panel Unit Root test) 面板协整分析(Panel Cointegeration) 门槛面板数据模型(Panel Threshold) 面板联立方程组 面板空间计量
静态面板数据
• 静态面板数据模型,是指解释变量中不包 含被解释变量的滞后项(通常为一阶滞后项) 的情形。但严格地讲,随机干扰项服从某 种序列相关的模型,如AR(1), AR(2), MA(1) 等,也不是静态模型。静态面板数据主要 有两种模型------固定效应模型和随机效应 模型。
• xtreg
ed-, between- and random-effects, and
population-averaged linear models
• xtregar Fixed- and random-effects linear models with an AR(1) disturbance
xtdes。分组内、组间和样本整体计算各个变量的 基本统计量xtsum。采用列表的方式显示某个变 量的分布xttab,较少使用。 • 3、list、sum、des、tabstat、histogram、 kdensity等命令都可以用。 • 4、对每个个体分别显示该变量的时间序列图: xtline。 • 5、静态面板数据基本回归命令:xtreg,系统默 认GLS估计(广义最小二乘法)。
• xtivreg Instrumental variables and two-stage least squares for panel-data models
• xtabond Arellano-Bond linear, dynamic panel data estimator (动态面板估计)
use grunfeld,clear
xtset company year
xtdes
xtline invest 混合回归:reg invest mvalue kstock(pool回归,
其会扩大样本量,) 固定效应:xtreg invest mvalue kstock ,fe 随机效应:xtreg invest mvalue kstock ,re 用F值或P值进行判断,如果p值较大,则应该用
• xtabond2 Arellano-Bond system dynamic panel data estimator(需要从网上下载)
• xttobit Random-effects tobit models
• xtintreg Random-effects interval data regression models
具有相同的截距项,个体的差异主要反应
在随机干扰项的设定上。
• 怎样选择固定效应和随机效应?
• 随机效严格要求个体效应与解释变量不相 关,即
• Cov(ai,XitB)=0 • 而固定效应模型并不需要这个假设条件。 • 这是两种模型选择的关键。
面板数据基本命令
• 1、指定个体截面变量和时间变量:xtset( • 2、对数据截面个数、时间跨度的整体描述:
固定效应模型
• 固定效应模型的公式变为:
•
Yit=ai+Xitb+εit
• 回归结果是每个个体都有一个特定的截距
项。(ai在这里就独立出来了)
随机效应模型
• 随机效应模型将个体效应ai视为随机因素, 即把个体效应设定为干扰项的一部分。公
式将变为:
•
Yit=Xitb+(ai+εit)
• 回归的结果是随机效应模型的所有的个体
company
1 1 1 1 2 2 2 2 3 3 3 3
面板数据的格式
year
1951 1952 1953 1954 1951 1952 1953 1954 1951 1952 1953 1954
invest
755.9 891.2 1304.4 1486.7 588.2 645.5 641 459.3 135.2 157.3 179.5 189.6
面板数据
一些面板数据教材
• 面板数据分析 (美)萧政 著 • 横截面与面板数据的经济计量分析 伍德里
奇 著,王忠玉 译 • Baltagi. Econometric Analysis of Panel
Data
• 最新动态可关注期刊: Journal of Econometrics
面板数据一些前沿问题
pool回归)
• xtreg Fixed-, between- and random-effects, and population-averaged linear models
• xtregar Fixed- and random-effects linear models with an AR(1) disturbance
uit称为复合扰动项。
固定效应模型
• 对于特定的个体i而言,ai 表示那些不随时 间改变的影响因素,如个人的消费习惯、 国家的社会制度、地区的特征、性别等, 一般称其为“个体效应” (individual effects)。如果把“个体效应”当作不随时 间改变的固定性因素, 相应的模型称为 “固定效应”模型。
