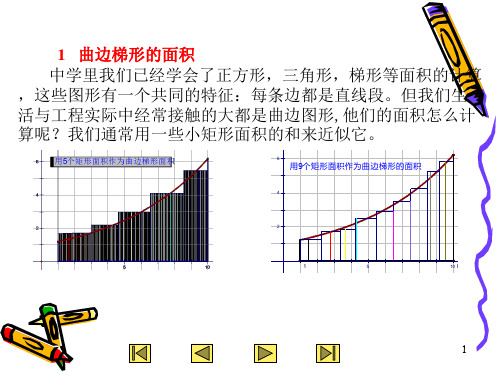
理解定积分定义要注意以下三点47页PPT
合集下载
理解定积分定义要注意以下三点
yy A
C C
时,性质 3的公式的几何意义就是 曲边梯形面积
A
的可加性 . 如右图所示:曲边梯形 AabB 的面积等 于曲边梯形 AacC 的面积与 CcbB 的面积.
o oa
a
c c
a
a
b
2)、若规定: f (x)dx 0, f (x)dx f (x)dx.
a
b
a
推论:若 f在[ A,B]上可积,且 a、b、c [ A,B] ,
(a).
a
证
16
公式使用说明:
b
1、在应用公式求 f (x)dx 时,f (x)的原函数必须是初等函数,否则使用
a b
公式求 f (x)dx失效。即f (x)的原函数F (x)可由 f (x)dx求出。
a
2、 定理的条件还可适当减弱,如: 1)、对F的要求可减弱为:在[a, b]上连续,在(a, b)内可导,且: F (x) f (x). 不影响定理的证明。 2)、对 f 的要求可减弱为:在[a,b]上可积(不一定连续),这时 公式仍成立。 3)、若定理中的F与 f 同时减弱为:f在[a,b]上可积,F在[a,b]上连 续,且除有限个点外有F (x) f (x),则公式仍成立。 4)、在学习连续函数必存在原函数的定理后,定理中对F的假设 便是多余的条件。
b
c
b
则: f (x)dx f (x)dx f (x)dx
a
a
c
BB bx x b
27
于曲边梯形AacC的面积与CcbB的面积.
a
a
b
2)、若规定: f (x)dx 0, f (x)dx f (x)dx.
a
b
a
推论:若f在[ A,B]上可积,且a、b、c [ A,B] ,
《高数》定积分课件

《高数》定积分ppt 课件
目录
• 定积分的概念 • 定积分的计算 • 微积分的应用 • 定积分的物理应用 • 定积分的进一步理解
01
CATALOGUE
定积分的概念
定积分的定义
01
定积分是积分的一种,是函数在区间上积分和的极 限。
02
定积分常用于计算平面图形的面积、体积等。
03
定积分的定义基于极限思想,通过分割、近似、求 和、取极限等步骤来定义。
物体在重力作用下的功与能
总结词
通过定积分计算重力做功和能量变化
详细描述
在重力作用下,物体运动过程中重力所做的功和能量变化可以用定积分表示。 通过定积分计算,可以得出重力做功和能量变化的具体数值。
05
CATALOGUE
定积分的进一步理解
定积分的极限思想
定积分是通过对曲线下的面积进行极限分割,再求和得到的结果,这个过 程体现了极限的思想。
可加性
对于任意分割的两个区间上的定积分,其和等于两区间上定积分的和 。
区间区间上定积分的值 之和。
比较性质
如果函数在不同区间上单调增加或减少,则其定积分的值也相应增加 或减少。
02
CATALOGUE
定积分的计算
微积分基本定理
总结词
微积分基本定理是定积分计算的基础, 它建立了积分与微分的联系,为解决定 积分问题提供了重要的思路和方法。
另一个函数的定积分进行计算。这些方法在实际应用中具有广泛的应用价值。
积分中值定理
总结词
积分中值定理揭示了定积分与被积函数之间 的关系,它是解决定积分问题的一个重要工 具。
详细描述
积分中值定理指出,对于连续函数f(x)在闭 区间[a,b]上的定积分∫baf(x)dx=f(ξ)(b−a) ,其中ξ∈[a,b]。这个定理说明了定积分的 结果等于被积函数在一个子区间上的取值与 该区间长度的乘积。这个定理在解决定积分 问题时非常有用,特别是当我们需要找到被
目录
• 定积分的概念 • 定积分的计算 • 微积分的应用 • 定积分的物理应用 • 定积分的进一步理解
01
CATALOGUE
定积分的概念
定积分的定义
01
定积分是积分的一种,是函数在区间上积分和的极 限。
02
定积分常用于计算平面图形的面积、体积等。
03
定积分的定义基于极限思想,通过分割、近似、求 和、取极限等步骤来定义。
物体在重力作用下的功与能
总结词
通过定积分计算重力做功和能量变化
详细描述
在重力作用下,物体运动过程中重力所做的功和能量变化可以用定积分表示。 通过定积分计算,可以得出重力做功和能量变化的具体数值。
05
CATALOGUE
定积分的进一步理解
定积分的极限思想
定积分是通过对曲线下的面积进行极限分割,再求和得到的结果,这个过 程体现了极限的思想。
可加性
对于任意分割的两个区间上的定积分,其和等于两区间上定积分的和 。
区间区间上定积分的值 之和。
比较性质
如果函数在不同区间上单调增加或减少,则其定积分的值也相应增加 或减少。
02
CATALOGUE
定积分的计算
微积分基本定理
总结词
微积分基本定理是定积分计算的基础, 它建立了积分与微分的联系,为解决定 积分问题提供了重要的思路和方法。
另一个函数的定积分进行计算。这些方法在实际应用中具有广泛的应用价值。
积分中值定理
总结词
积分中值定理揭示了定积分与被积函数之间 的关系,它是解决定积分问题的一个重要工 具。
详细描述
积分中值定理指出,对于连续函数f(x)在闭 区间[a,b]上的定积分∫baf(x)dx=f(ξ)(b−a) ,其中ξ∈[a,b]。这个定理说明了定积分的 结果等于被积函数在一个子区间上的取值与 该区间长度的乘积。这个定理在解决定积分 问题时非常有用,特别是当我们需要找到被
《定积分的概念》ppt课件

f
()(ba)
(ab).
性质7的几何意义:
在[a,b]上至少有 ,一使得 [a,以 b]为底边,以曲
y f (x)为曲边的曲A边a梯 B的 b形 面积等于同一
而高f为 ()的矩形的. 面积
假如函数f〔x〕在闭区间[a,b]上连续,我们
称b1aabf (x)dx
如已知某为地函某数时f自〔0x至〕2在4时[a,天b]上气的温平度均曲值线.为f(t),
曲线 f(x)f((x)0 )、x轴及两条直线x=a,x=b所围 成的曲边梯形面积A等于函数f(x)在区间[a,b]上的定积 分,即
Aabf(x)dx.
质点在变力F(s)作用下作直线运动,由起始位置a 移动到b,变力对质点所做之功等于函数F(s)在[a,b] 上的定积分,即
WabF(s)ds
假如函数f〔x〕在区间[a,b]上的定积分存在, 那么称函数f〔x〕在区间[a,b]上可积.
如果在[a,b]上 f(x)0,此时由曲线y=f(x),直线 x=a,x=b及x轴所围成的曲边梯形位于x轴的下方,则
定积分ab f (x)dx在几何上表示上述曲边梯形的面积A的
相反数.
假如在[a,b]上f〔x〕既可取正值又可取负值,那
么定积ab分f (x)dx 在几何上表示介于曲线y=f〔x〕,
直线x=a,x=b及x轴之间的各部分面积的代数和.
[x0,x1],[x1,x2],,[xi1,xi],,[xn1,xn]
各个小区间的长度为
xi xi xi1
在每一个小[x区 i1,x间 i]上任取一i(点 xi 1ixi),
n
作和 (简式 称积 ) 分 f和 (i)x式 i
i1
记max{xi,x2,...,xn},如果对[a区 ,b]间 任一分法 和小区[x间 i1,xi]上点 i任意取法,只 要0时 当,上
最新定积分的概念ppt

和曲线 y f (x) 所
b
a f (x)dx S
围成的的曲边梯形 的面积
合作探究
如何用定积分表示图中蓝色部分的面积?
yf (x) y
Oa
y gx
b
b
a f(x)dxag(x)dx
bx
用定积分表示下列图中阴影部分的面积
y
y 2x
y
针
y sin x
对
训
01
x
0 1 3
x
4
练
1
0 2 xd x
b f (x)dx =
b
f (t)dt
a
a
如何用定积分表示抛物线 y x 2 、 直线 x 1 和 x 轴所围成的曲边梯形
的面积。
探
y的几何意义( f (x) 0 )
设阴影部分面积为S
b
a f ( x)dx
表示由直线 x a,
x b (a b), y 0
a a 0 i 1
即 abf(x)dxlni m i n1b naf(i)
积分上限
[ a , b ] 叫做积分区间
结
构
分
b
n
f(x)dxlim
baf()
a
n n i1
i
析
积分下限
被 积
被 积
积 分
函
式
变
数
量
合作探究
(1)定积分的结果是一个 数值
(2)定积分的值只与被积函数和积分区 间有关,而与积分变量用什么字母表 示 无关 , 即
定积分的概念ppt
§1.5 定 积 分 --§1.5.3定积分的概念
滨海中学 李鹏
n
i1
定积分的概念 课件

的速度为 v(t)=3t2+2(单位:km/h),那么该汽车在 0≤t≤2(单
位:h)这段时间内行驶的路程 s(单位:km)是多少? [解] (1)分割 在时间区间[0,2]上等间隔地插入 n-1 个分点,将它等
分成 n 个小区间,记第 i 个小区间为2i-n 1,2ni(i=1,2,…, n),其长度为 Δt=2ni-2i-n 1=n2.每个时间段上行驶的路程
y=0 所围成的曲边梯形的面积时,将区间[0,t]等分成 n
个小区间,则第 i-1 个区间为
()
A.i-n 1,ni C.ti-n 1,tni
B.ni ,i+n 1 D.ti-n 2,ti-n 1
[解析]
每个小区间长度为
t n
,故第i-1个区间的左
端点为0+(i-2)×
t n
=
ti-2 n
,右端点为
ti-2 n
+
t n
=
ti-1 n.
[答案] D
[易错防范] 1.解决本题易错误地认为区间左端为ti-n 1,从而误选 C. 2.在将区间[0,1]等分成 n 个小区间时,其第 1 个小区间的 左端点为 0,第 2 个小区间的左端点为n1,…,依次类推,第 i 个小区间的左端点为i-n 1.
小区间长 Δx=n1为其邻边的小矩形面积,近似代替小曲边梯形面
积.第 i 个小曲边梯形面积,可以近似地表示为ΔSi≈ξ3i ·Δx=
n+ni-13·n1(i=1,2,3,…,n).
(3)求和 因为每一个小矩形的面积都可以作为相应的小曲边梯形面
积的近似值,所以 n 个小矩形面积的和就是曲边梯形 ABCD 面积 S 的近似值,
n
n
即 S=ΔSi≈
i=1
位:h)这段时间内行驶的路程 s(单位:km)是多少? [解] (1)分割 在时间区间[0,2]上等间隔地插入 n-1 个分点,将它等
分成 n 个小区间,记第 i 个小区间为2i-n 1,2ni(i=1,2,…, n),其长度为 Δt=2ni-2i-n 1=n2.每个时间段上行驶的路程
y=0 所围成的曲边梯形的面积时,将区间[0,t]等分成 n
个小区间,则第 i-1 个区间为
()
A.i-n 1,ni C.ti-n 1,tni
B.ni ,i+n 1 D.ti-n 2,ti-n 1
[解析]
每个小区间长度为
t n
,故第i-1个区间的左
端点为0+(i-2)×
t n
=
ti-2 n
,右端点为
ti-2 n
+
t n
=
ti-1 n.
[答案] D
[易错防范] 1.解决本题易错误地认为区间左端为ti-n 1,从而误选 C. 2.在将区间[0,1]等分成 n 个小区间时,其第 1 个小区间的 左端点为 0,第 2 个小区间的左端点为n1,…,依次类推,第 i 个小区间的左端点为i-n 1.
小区间长 Δx=n1为其邻边的小矩形面积,近似代替小曲边梯形面
积.第 i 个小曲边梯形面积,可以近似地表示为ΔSi≈ξ3i ·Δx=
n+ni-13·n1(i=1,2,3,…,n).
(3)求和 因为每一个小矩形的面积都可以作为相应的小曲边梯形面
积的近似值,所以 n 个小矩形面积的和就是曲边梯形 ABCD 面积 S 的近似值,
n
n
即 S=ΔSi≈
i=1
定积分的概念201901-PPT精选文档

n n
x
(4)取极限
1 i 1 S lim S lim f n n n i 1n n
n
引入2:汽车行驶的路程
问题:汽车以速度 v 匀速直线运动时, 经过时间 t 所行驶的路程为 S vt .如果 汽车作变速直线运动,在时刻 t 的速度 2 为 v t t 2 (单位: km/h) ,那么它在 0≤ t ≤1(单位:h)这段时间内行驶的路程 S (单位: km)是多少?
b
积 分 f ( x ) d x 在 几 何 上 表 示 yf (x)
a
y
上述曲边梯形面积的负值。
S [f(x)] dx
a
b
S[ f(x )] dx
a
b
ቤተ መጻሕፍቲ ባይዱ
S f f ( x ) d x ( x ) d x f ( x ) d x 。 y f ( x)
练习:
i 1 i 2 , f ( x ) x n 1、当n很大时,函数 在区间 n
上的值,可以用( C )近似代替 1 2 ) ) A. f ( B. f ( n n C. f ( i ) D. f 0
x 2、在“近似代替”中,函数f(x)在区间 i,x i 1 上的 C 近似值等于( ) A.只能是左端点的函数值 f ( xi ) B.只能是右端点的函数值 f ( xi1 ) C.可以是该区间内任一点的函数值 f ( )( x , x ) i i i i 1 D.以上答案均不正确
(2) 设物体运动的速度vv(t),则此物体在时间区间 v v (t ) [a, b]内运动的距离s为 v
b a
s v ( t ) d t 。
定积分的概念及性质PPT

在每个小区间[ xi1, xi ]
上任取
一点
,
i
o a x1
b xi1i xi xn1
x
以 [ xi1, xi ]为底,f (i ) 为高的小矩形面积为
Ai f (i )xi
首页
上页
下页
曲边梯形面积的近似值为
n
A f (i )xi
i 1
当分割无限加细,即小区间的最大长度
max{x1, x2 , xn }
点i 怎样的取法,只要当 0时,和S 总趋于
确定的极限I , 我们称这个极限I 为函数 f ( x)
在区间[a, b]上的定积分,记为
积分上限 b a
f ( x)dx
I
lim 0
n i 1
积分和
f (i )xi
积分下限
被 积 函 数
被
积
[a,b] 积分区间
积
分
表
变
达 式
量
首页
上页
下页
注意:
思路:把整段时间分割成若干小段,每小段上 速度看作不变,求出各小段的路程再相加,便 得到路程的近似值,最后通过对时间的无限细 分过程求得路程的精确值.
首页
上页
下页
(1)分割 T1 t0 t1 t2 tn1 tn T2
ti ti ti1
si v( i )ti
部分路程值
某时刻的速度
i ,(i n
1,2,
,n)
小区间[ xi1 , xi ]的长度xi
1 ,(i n
1,2,
,n)
取i xi ,(i 1,2, , n)
n
n
n
f (i )xi i2xi xi2xi ,
第17讲定积分的概念 46页PPT文档

y yf(x)
h
1 h
1
h
xh
x
f(t)dt f(t)dt
a
a
o
xh
x
f(t)dt f(t)dt
a
a
(x)
a x b x
xh
1
xh
f(t)dt
hx
f ()
(xxh)
因为 f (x) [a , b]连续
(x)
lim (xh)(x)
即得曲边梯 形面积 A .
n
Alim 0 i1
f(i )xi
其中λ=max{Δx1,Δx2,…,Δxn}
(λ→0 表示 [a,b] 被 无限分细 )
2.变速直线运动的路程
2019年10月20日“神州”火箭发射 和回收成功
列车在某时间间隔内行驶的路程
已知:速度 v=v ( t ) , 求在时 间区间 [ t0 ,T ] 内火箭上升的速
A
曲边梯形面积A
注3 : 定积分的几何意义
当 f (x) ≤0 时
b
a f(x)dxA
A
( A为面积 )
当 f (x) 符号不定时 , 例如
y
A1
a
oA2
y f(x) A3
A4
A5 bx
b
a
f (x)dx
=A1-A2+A3-A4+A5
A1
+
A2+A3
+
A4+A5
b a
f (x)dx
F(x) f(x)dxC
a
F(a)C
b
F(b)af(x)dxF(a)
b
a f(x)dx F(b)F(a)
