习题2答案
结构力学课后习题答案(2)
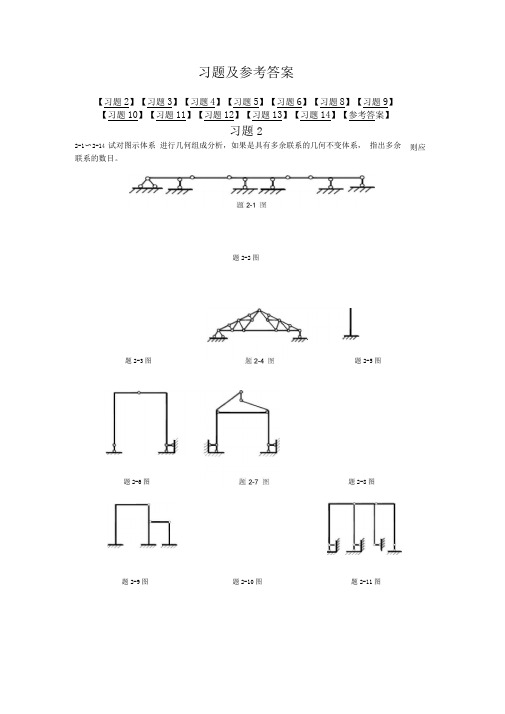
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1〜2-14 试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,指出多余则应联系的数目。
题2-2图题2-3图题2-5图题2-6图题2-8图题2-9图题2-10图题2-11图题4-1图4-2 作图示刚架的M 图。
3-1 试作图示多跨静定梁的M 及Q 图。
习题(a)1.5m 1 2m I2.5m | 1.5m l 4.5m题3-1(b)3-2 试不计算反力而绘出梁的M 图。
4m40kN(a) 5kN/mM(b )4-1 作图示刚架的M 、Q 、N 图。
2kN /m2kN • m (a)2kN 题3-2习题4(b ) (c )4-3 4-4 4-54m(a)(d)作图示三铰刚架的M图。
M=4Pa2a(b)4kN4m 4m(c)珂10kN/m4m(e)题4-2图CE0.5m ]m2J 0.5m7mB7m(a)题4-3作图示刚架的M图。
(a)I 盒lUlUUW已知结构的M图,试绘出荷载。
10kN/m1.5m题4-4图urm*~ G3mC7.35m 7.35m(b)m6Nn m220kN40kN/m4m(b)C_PaPaPaa4-6 检查下列刚架的M图,并予以改正。
5-15-2 题4-5图(b)P(d)(e) (f)(c)题4-6图习题5图示抛物线三铰拱轴线方程4 f1kN/mx)x,(h)试求D截面的内力。
20kN10m题5-1图K15m j 5ml=30m带拉杆拱,拱轴线方程 y ,求截面的弯矩。
题5-3图习题66-1 判定图示桁架中的零杆。
6-2 6-3 6-4 6-5 用结点法计算图示桁架中各杆内力。
(b) (c)m题6-2用截面法计算图示桁架中指定各杆的内力。
3m [ 3m3m I 3m题6-3试求图示组合结构中各链杆的轴力并作受弯杆件的用适宜方法求桁架中指定杆内力。
习题二和上机答案

习题二⒉1描述以下四个概念的区别:头指针变量,头指针,头结点,首结点(第一个结点)。
解:头指针变量和头指针是指向链表中第一个结点(头结点或首结点)的指针;在首结点之前附设一个结点称为头结点;首结点是指链表中存储线性表中第一个数据元素的结点。
若单链表中附设头结点,则不管线性表是否为空,头指针均不为空,否则表示空表的链表的头指针为空。
2.2简述线性表的两种存储结构有哪些主要优缺点及各自使用的场合。
解:顺序存储是按索引直接存储数据元素,方便灵活,效率高,但插入、删除操作将引起元素移动,降低了效率;而链式存储的元素存储采用动态分配,利用率高,但须增设表示结点之间有序关系的指针域,存取数据元素不如顺序存储方便,但结点的插入和删除十分简单。
顺序存储适用于线性表中元素数量基本稳定,且很少进行插入和删除,但要求以最快的速度存取线性表中的元素的情况;而链式存储适用于频繁进行元素动态插入或删除操作的场合。
2.3 在头结点为h的单链表中,把值为b的结点s插入到值为a的结点之前,若不存在a,就把结点s插入到表尾。
Void insert(Lnode *h,int a,int b){Lnode *p,*q,*s;s=(Lnode*)malloc(sizeof(Lnode));s->data=b;p=h->next;while(p->data!=a&&p->next!=NULL){q=p;p=p->next;}if (p->data==a){q->next=s;s->next=p;}else{p->next=s;s->next=NULL;}}2.4 设计一个算法将一个带头结点的单链表A分解成两个带头结点的单链表A和B,使A中含有原链表中序号为奇数的元素,而B中含有原链表中序号为偶数的元素,并且保持元素原有的相对顺序。
Lnode *cf(Lnode *ha){Lnode *p,*q,*s,*hb;int t;p=ha->next;q=ha;t=0;hb=(Lnode*)malloc(sizeof(Lnode));s=hb;while(p->next!=NULL){if (t==0){q=p;p=p->next;t=1;}else{q->next=p->next;p->next=s->next; s->next=p; s=p;p=p->next; t=0;}}s->next=NULL;return (hb);}2.5设线性表中的数据元素是按值非递减有序排列的,试以不同的存储结构,编写一算法,将x插入到线性表的适当位置上,以保持线性表的有序性。
复变函数论第三版课后习题答案 2

第一章习题解答(一)1.设z =z 及Arcz 。
解:由于3i z e π-==所以1z =,2,0,1,3Arcz k k ππ=-+=±。
2.设121z z =,试用指数形式表示12z z 及12z z 。
解:由于6412,2i i z e z i e ππ-==== 所以()64641212222i i iiz z e eee πππππ--===54()146122611222ii i i z e e e z e πππππ+-===。
3.解二项方程440,(0)z a a +=>。
解:12444(),0,1,2,3k ii z a e aek πππ+====。
4.证明2221212122()z z z z z z ++-=+,并说明其几何意义。
证明:由于2221212122Re()z z z z z z +=++2221212122Re()z z z z z z -=+-所以2221212122()z z z z z z ++-=+其几何意义是:平行四边形对角线长平方和等于于两边长的和的平方。
5.设z 1,z 2,z 3三点适合条件:0321=++z z z ,1321===z z z 。
证明z 1,z 2,z 3是内接于单位圆1=z 的一个正三角形的顶点。
证 由于1321===z z z,知321z z z ∆的三个顶点均在单位圆上。
因为33331z z z ==()[]()[]212322112121z z z z z z z z z z z z +++=+-+-=21212z z z z ++=所以, 12121-=+z z z z ,又)())((122122112121221z z z z z z z z z z z z z z +-+=--=-()322121=+-=z z z z故 321=-z z ,同理33231=-=-z z z z ,知321z z z ∆是内接于单位圆1=z 的一个正三角形。
信息检测与信号处理习题2含答案

第二章习题一、选择题2.非线性度是表示定度曲线( )的程度。
A.接近真值B.偏离其拟合直线C.正反行程的不重合3.测试装置的频响函数H (j ω)是装置动态特性在( )中的描述。
A .幅值域 B.时域 C.频率域 D.复数域5.下列微分方程中( )是线性系统的数学模型。
A.225d y dy dx t y x dt dt dt ++=+ B. 22d y dx y dt dt+= C.22105d y dy y x dt dt -=+ 6.线性系统的叠加原理表明( )。
A.加于线性系统的各个输入量所产生的响应过程互不影响B.系统的输出响应频率等于输入激励的频率C.一定倍数的原信号作用于系统所产生的响应,等于原信号的响应乘以该倍数7.测试装置能检测输入信号的最小变化能力,称为( )。
A.精度B.灵敏度C.精密度D.分辨率8.一般来说,测试系统的灵敏度越高,其测量范围( )。
A.越宽B. 越窄C.不变10.线性装置的灵敏度是( )。
A.随机变量B.常数C.时间的线性函数12.输出信号与输入信号的相位差随频率变化的关系就是系统的( )。
A.幅频特性B.相频特性C.传递函数D.频率响应函数13.时间常数为τ的一阶装置,输入频率为 1ωτ=的正弦信号,则其输出与输入间的相位差是( )。
A.-45° B-90° C-180°14.测试装置的脉冲响应函数与它的频率响应函数间的关系是( )。
A.卷积B.傅氏变换对C.拉氏变换对D.微分16.对某二阶系统输入周期信号 000()sin()x t A t ωϕ=+,则其输出信号将保持()。
A.幅值不变,频率、相位改变B.相位不变,幅值、频率改变C.频率不变,幅值、相位可能改变18.二阶系统的阻尼率ξ越大,则其对阶越输入的时的响应曲线超调量()。
A.越大B.越小C.不存在D.无关19.二阶装置引入合适阻尼的目的是()。
A.是系统不发生共振B.使得读数稳定C.获得较好的幅频、相频特性20.不失真测试条件中,要求幅频特性为(),而相频特性为()。
电路基础 (韩春光 著) 电子工业出版社 课后答案 习 题 2-answer

习题22.1在图2.18所示的电路中,求各理想电流源的端电压、功率及各电阻上消耗的功率。
解答:由节点方程得I3=I2-I1=1A,U1=I3R1=1A×20Ω=20V,U2=U1+I2R2=20V+2A×10Ω=40V,P1= U1I1=20V×1A=20W,P2=-U2I2=-80W,电阻上的功率P R1=20V×1A=20W,P R2=20V×2A=40W。
2.2求图2.19所示电路中各支路电流,并计算理想电流源的电压U1。
已知I1=3A,R2=12Ω,R3=8Ω,R4=12Ω,R5=6Ω。
电压和电流的参考方向如图中所示。
解答:节点方程I1+I2+I3=0,I3=I4+I5,网孔方程I2R2=I3R3+I4R4,I4R4=I5R5,联立上述方程得I2=I3=-1.5A,I4=-0.5A,I5=-1A,U1=I2R2=-1.5A×12Ω=-18V。
2.3试用支路电流法求图2.20所示电路中各支路电流,并求三个电源的输出功率和负载电阻RL上的取用功率。
解答:节点方程I1+I2+10=I,网孔方程0.8I1+116=0.4I2+120,0.8I1+4I=120,联立三方程得I1=75/8A,I2=35/4A,I=225/8A,三个电源的输出功率分别为1125W,1015W,1125W;负载电阻上的取用功率为3164.0625W。
2.4用网孔电流法求解习题2.3。
解答:将电流源与负载电阻的位置互换形成三个网孔,网孔参考电流方向均为顺时针方向,网孔电流方程如下1.2I A-0.4I B=120-116,4.4I B-0.4I A-4I C=116,I C=-10A,解得I A=75/8A,I B=145/8A,于是I1=I A=75/8A,I2=I B-I A=35/4A,I=I B-I C=225/8A。
2.5图2.21所示电路,网孔电流如图中所标,试列写可用来求解该电路的网孔方程。
概率论与数理统计(第三版)课后答案习题2

第二章 随机变量2.1 X 2 3 4 5 6 7 8 9 10 11 12 P 1/361/181/121/95/361/65/361/91/121/181/362.2解:根据1)(0==∑∞=k k XP ,得10=∑∞=-k kae,即1111=---eae 。
故 1-=e a2.3解:用X 表示甲在两次投篮中所投中的次数,X~B(2,0.7) 用Y 表示乙在两次投篮中所投中的次数, Y~B(2,0.4) (1) 两人投中的次数相同P{X=Y}= P{X=0,Y=0}+ P{X=1,Y=1} +P{X=2,Y=2}=1122020*********2222220.70.30.40.60.70.30.40.60.70.30.40.60.3124C C C C C C ⨯+⨯+⨯=(2)甲比乙投中的次数多P{X >Y}= P{X=1,Y=0}+ P{X=2,Y=0} +P{X=2,Y=1}=12211102200220112222220.70.30.40.60.70.30.40.60.70.30.40.60.5628C C C C C C ⨯+⨯+⨯=2.4解:(1)P{1≤X ≤3}= P{X=1}+ P{X=2}+ P{X=3}=12321515155++= (2) P {0.5<X<2.5}=P{X=1}+ P{X=2}=12115155+= 2.5解:(1)P{X=2,4,6,…}=246211112222k +++=11[1()]1441314k k lim→∞-=-(2)P{X ≥3}=1―P{X <3}=1―P{X=1}- P{X=2}=1111244--=2.6解:设i A 表示第i 次取出的是次品,X 的所有可能取值为0,1,212341213124123{0}{}()(|)(|)(|)P X P A A A A P A P A A P A A A P A A A A ====18171615122019181719⨯⨯⨯= 1123412342341234{1}{}{}{}{}2181716182171618182161817162322019181720191817201918172019181795P X P A A A A P A A A A P A A A A P A A A A ==+++=⨯⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=12323{2}1{0}{1}1199595P X P X P X ==-=-==--=2.7解:(1)设X 表示4次独立试验中A 发生的次数,则X~B(4,0.4)34314044(3)(3)(4)0.40.60.40.60.1792P X P X P X C C ≥==+==+=(2)设Y 表示5次独立试验中A 发生的次数,则Y~B(5,0.4)345324150555(3)(3)(4)(5)0.40.60.40.60.40.60.31744P X P X P X P X C C C ≥==+=+==++=2.8 (1)X ~P(λ)=P(0.5×3)= P(1.5)0 1.51.5{0}0!P X e -=== 1.5e -(2)X ~P(λ)=P(0.5×4)= P(2)0122222{2}1{0}{1}1130!1!P X P X P X e e e ---≥=-=-==--=-2.9解:设应配备m 名设备维修人员。
《随机过程及其在金融领域中的应用》习题二答案
0
sin
ux
f
xdx
0
sin
ux
f
xdx
0
0
sin
u
x
f
xdx
sin ux 0
f
x dx
0
令其中一式中的 x t
0
sin
ut
f
t
d
t
0
sin
ux
f
xdx
0
sin ut 0
证明:
X u
eiux f xdx
cos ux i sin ux f xdx
cos ux
f
xdx
i
sin
ux
f
xdx
(a)充分性:
当f
x
f
x时,sin ux
f
x
为奇函数
,
则i
c o vY Y, E Y 2 E Y 2 3 80
故(X,Y)的协方差矩阵为
cov X , X cov Y , X
1
cov X ,Y cov Y ,Y
18 0
0
3 80
4、已知二维随机变量(X,Y)服从联合正态分布,且
dFX
x
e tx f xdx
etxexdx etxdx
《现代控制理论》课后习题答案2
( sI − A) −1 =
1 adj( sI − A) det( sI − A)
(1)
式(1)中的 adj( sI − A) 和 det( sI − A) 可分别写成以下形式:
adj( sI − A) = H n −1s n −1 + H n − 2 s n − 2 + " + H 0 det( sI − A) = s + an −1s
故
Φ (t ) = α 0 (t ) I + α1 (t ) A + α 2 (t ) A2
⎡ −2tet + e 2t ⎢ = ⎢ −2(1 + t )et + 2e 2t ⎢ −2(2 + t )et + 4e 2t ⎣
(3t + 2)et − 2e 2t (3t + 5)et − 4e 2t (3t + 8)et − 8e 2t
n n −1
(2) (3) (4)
+ " + a0
,可得 将式(1)两边分别左乘 det( sI − A)( sI − A) ,并利用式(2)和(3)
Is n + an −1 Is n −1 + " + a0 I = H n −1s n + ( H n − 2 − AH n−1 ) s n − 2 + " + ( H 0 − AH1 )s − AH 0
e jt = a0 (t ) + a1 (t ) j , e − jt = a0 (t ) − a1 (t ) j
而
e jt = cos t + j sin t , e− jt = cos t − j sin t 因此, a0 (t ) = cos t , a1 (t ) = sin t 。由此得到状态转移矩阵 ⎡ cos t sin t ⎤ Φ (t ) = e At = a0 (0) I + a1 (t ) A = ⎢ ⎥ ⎣ − sin t cos t ⎦
习题答案 (2)
第三章 消费者行为理论2. 假设某消费者的均衡如图3—1(即教材中第96页的图3—22)所示。
其中,横轴OX 1和纵轴OX 2分别表示商品1和商品2的数量,线段AB 为消费者的预算线,曲线图3—1 某消费者的均衡U 为消费者的无差异曲线,E 点为效用最大化的均衡点。
已知商品1的价格P 1=2元。
(1)求消费者的收入;(2)求商品2的价格P 2;(3)写出预算线方程;(4)求预算线的斜率;(5)求E 点的MRS 12的值。
解答:(1)图中的横截距表示消费者的收入全部购买商品1的数量为30单位,且已知P 1=2元,所以,消费者的收入M =2元×30=60元。
(2)图中的纵截距表示消费者的收入全部购买商品2的数量为20单位,且由(1)已知收入M =60元,所以,商品2的价格P 2=M 20=6020=3元。
(3)由于预算线方程的一般形式为 P 1X 1+P 2X 2=M 所以,由(1)、(2)可将预算线方程具体写为:2X 1+3X 2=60。
(4)将(3)中的预算线方程进一步整理为X 2=-23X 1+20。
很清楚,预算线的斜率为-23。
(5)在消费者效用最大化的均衡点E 上,有MRS 12=P 1P 2,即无差异曲线斜率的绝对值即MRS 等于预算线斜率的绝对值P 1P 2。
因此,MRS 12=P 1P 2=23。
5. 已知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P 1=20元和P 2=30元,该消费者的效用函数为U =3X 1X 22,该消费者每年购买这两种商品的数量应各是多少?每年从中获得的总效用是多少?解答:根据消费者的效用最大化的均衡条件MU 1MU 2=P 1P 2其中,由U =3X 1X 22可得 MU 1=d TU d X 1=3X 22; MU 2=d TU d X 2=6X 1X 2 于是,有 3X 226X 1X 2=2030 整理得 X 2=43X 1 (1) 将式(1)代入预算约束条件20X 1+30X 2=540,得20X 1+30·43X 1=540 解得 X 1=9 将X 1=9代入式(1)得 X 2=12因此,该消费者每年购买这两种商品的数量应该为X 1=9 ;X 2=12。
《误差理论与数据处理》习题2及解答
(mm)
② 重复测量 10 次,计算其算术平均值为: x = 26.2025(mm). 取与①相同的置信度,则测量结果为:26.2025±3σ= 26.2025±0.0015 (mm). ③ 若无该仪器测量的标准差资料,则依 10 次重复测量数据计算标准差和表示测量结 果。选参考值 x0 = 26.202,计算差值 ∆x i = x i − 26.202 、 ∆ x 0 和残差ν i 等列于表中。 序 1 2 3 4 5 6 7 8 9 10 号
∑ν
i =1
i
n( n − 1)
= 1.253
0.0008 5× 4
= 0.000224 (mm)
σx =
σ
n
=
0.000255 5
= 0.000114 ; σ x =
'
σ'
n
=
0.000224 5
= 0.0001
⑤求单次测量的极限误差和算术平均值的极限误差 因假设测量值服从正态分布,并且置信概率 P=2Φ(t)=99%,则Φ(t)=0.495,查附录
∆ x0 = 1 10 ∑ ∆xi = 0.0005 10 i =1
νi
0 +0.0003 +0.0003 0 +0.0001 -0.0003 -0.0002 0 +0.0001 -0.0003
ν i2
0 9×10 9×10 0 1×10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初%
0.75%
41.67%
( )共晶% 1初 % 58.33%
% 0.95 0.50 100% 56.25%
0.95 0.15
% 1 % 43.75%
共晶体中α相和β相的重量%
%
0.95 0.95
0.75 0.15
(
)共晶 %
14.58%
F % 0.77% wc 100% 90% 0.77% 0.0218%
解得,wc 0.097%
5.试说明在正温度梯度下为什么固溶体合金凝固时可以呈树枝状方 式成长,而纯金属则得不到树枝状晶。
解:答:在固溶体合金凝固过程中,虽然实际温度分布一定,但 由于界面前沿液体中溶质分布所发生的变化,必将引起凝固温度 的改变,因此将界面前沿液体中的实际温度低于由溶质分布所决 定的凝固温度时产生的过冷,称为成分过冷。
由β初’中析出的AⅡ的相对量为
AⅡ%
0.90 0.70 0.90 0
初' %
11.11%
所以,室温下β初的相对量为
初% 初' % AⅡ% 50% 11.11% 38.89%
该合金室温下组织组成物的相对量为
(A )共晶% 50% 初 % 38.89%
AⅡ% 11.11%
(4)合金为0.8A-0.2B时 室温下相组成物为A和β相,其相对量为 A% 0.90 0.20 100% 77.78% 0.90 0 % 1 A% 22.22%
(1)试根据相律绘成平衡相图并标注各相区符号及特征 点的温度和成分。
(2)如果希望得到A2B化合物与β共晶组织加上5%的 初的合金,求该合金的成分。
解:(1)设A2B化合物中B的质量百分数为wB,则
wB
50 100% 30 2 50
45%
相图如下图所示:
(2) 设合金的成分为含B wB,则由杠杆定律得
而在纯金属中,在正的温度梯度下,当界面上偶尔有凸起部分而 深入温度较高的液体中时,它的生长速度就会减缓甚至停止,周 围部分的过冷度较凸起部分大而会赶上来,使凸起部分消失,使 液固界面保持稳定的平面状态,而不会形成树枝晶。
6. 组元A和B的熔点分别为700℃和500℃,在液态完全互溶, 在固态部分互溶形成α和β固溶体,其最大溶解度分别为 为5%B和25%A(重量),在零度时溶解度则为2%B和 5%A(重量)。两金属形成熔点为750℃的A2B化合物, A和B的原子量分别为30和50。在450℃和320℃分别发 生液体成分为22%B和60%B(重量)的共晶转变。
% ( )共晶% % 58.33% 14.58% 43.75%
(2) 设该合金中B的重量%为wB,则
初
%
wB 0.75 0.95 0.75
100%
50%
解得 wB 0.85,即该合金成分为含B85%
2. 已知在A-B二元合金中,A (熔点600℃)与B (熔点500℃)在 液态无限互溶,固态时A在B中的最大固溶度(质量分数)为 wA=0.30,室温时为wA=0.10;但B在固态和室温时均不溶 于A。在300℃时,含wB=0.40的液态合金发生共晶反应。 试绘出A-B合金相图;并分析wA=0.20,wA=0.45,wA=0.80 的合金在室温下组织组成物和相组成物的重量%。 。
室温下相组成物为A和β相,其相对量为
% 0.55 0 100% 61.11%
0.9 0
A% 1 % 38.89%
室温下组织组成物为β初+(A+β)共晶+AⅡ 在共晶反应刚完成时,
(A
)共晶 %
0.7 0.55 0.7 0.4
100%
50%
初' % 1(A )共晶% 50%
冷却至室温时,将由β初’和(A+β)共晶的β中析出AⅡ。由 于共晶β中析出的AⅡ与共晶A连接在一起,故略去不计。
1.已知某二元合金的共晶反应为:
L € (75%B)
(15%B) (95%B)
(1) 试求含50%B的合金完全结晶后,初晶α与共 晶(α+β)的重量%,α相与β相的重量%;共 晶体中α相与β相的重量%。
(2) 若测出显微组织中β初晶与(α+β)共晶各占一 半时,试求该合金成分。
解:(1)根据杠杆定律可得
4. 试利用冷却曲线分析含碳量0.3%亚共析钢平衡组织的 形成过程。若已知亚共析组织中先共析铁素体含量为 90%,试确定该钢的大致含碳量。
解:(1) 冷却曲线如图所示。
平衡组织的形成过程为:
1以上,均匀的液相L; 1~2,L→δ,液体中析出 δ相; 2 时,L+δ; 2~2’,L+δ→γ,发生包 晶反应,生成γ相; 2’ 时,L+γ; 2’→3,L→γ,剩余液相 转变为γ;
室温下组织组成物为A+(A+β)共晶,其相对量为
A% 0.40 0.20 100% 50% 0.40 0
( A )共晶% 1 A% 50%
3. 试根据含碳量3.5%亚共晶白口铁的平衡组织, 计算其中各组织组成物的相对含量。
解:含碳量3.5%的亚共晶白口铁的平衡组织为P+Fe3CⅡ+Ld’。 共晶反应刚完成时,
初
%
wB 0.60 0.75 0.60
100%
5%
解得,wB 60.75%
解:(1)A-B合金相图如下图所示
(2)合金为0.2A-0.8B时 室温下相组成物为A和β相,其相对量为
% 0.8 0 100% 88.89%
0.9 0
A% 1 % 11.11%
室温下组织组成物为β+AⅡ,其相对量与相组 成物相同,即
% 88.89%
AⅡ% 11.11%
(3)合金为0.45A-0.55B时
3时,得到单一γ相; 3~4,不发生变化,仍为γ相; 4~5,γ→α,形成铁素体组织(F) 5时, γ+α; 5~5’,γ→(α+Fe3C),发生共析反应,形成珠光体(P)组 织; 5’时,α+P; 5’~6,α→Fe3CⅢ,其量甚少,可以忽略不计; 6时,F+P。
(2) 设钢的大致含碳量wc,则由杠杆定律得
实际合金在通常的凝固中不可避免地会出现成分过冷。当界面前 沿液体处于正温度梯度条件下,如果液固界面前沿存在较大的成 分过冷区,界面某些地方的凸起进入过冷区后,由于过冷度增加, 促使它们进一步凸向液体并不断伸向过冷液相中生长,同时在侧 面产生分枝,形成二次轴,在二次轴上在长出三次轴等,形成树 枝状组织。
Ld % 3.5 2.11100% 63.47% 4.3 2.11
% 1 Ld % 1 63.47% 36.53%
室温下组织组成物的相对量为
Ld '% Ld % 63.47%
Fe3CⅡ%
2.11 6.69
0.77 0.77
%
8.27%
P% % Fe3CⅡ% 36.53% 8.27% 28.26%
