1稳恒磁场
大学物理磁学部分复习资料..

41 磁 学基本内容一、稳恒磁场 磁感应强度1. 稳恒磁场电流、运动电荷、永久磁体在周围空间激发磁场。
稳恒磁场是指不随时间变化的磁场。
稳恒电流激发的磁场是一种稳恒磁场。
2. 物质磁性的电本质无论是永磁体还是导线中的电流,它们的磁效应的根源都是电荷的运动。
因此,磁场是运动电荷的场。
3. 磁感应强度磁感应强度B是描述磁场的基本物理量,它的作用与E 在描述电场时的作用相当。
磁场对处于其中的载流导线、运动电荷、载流线圈、永久磁体有力及力矩的作用。
可以根据这些作用确定一点处磁场的强弱和方向——磁感应强度B。
带电q 的正点电荷在磁场中以速度v运动,若在某点不受磁力,则该点磁感应强度B 的方向必与电荷通过该点的速度v平行。
当该电荷以垂直于磁感应强度B 通过该点时受磁力⊥F ,则该点磁感应强度大小qvF B ⊥=,且⊥F ,v ,B两两互相垂直并构成右手系。
二、毕奥—萨伐尔定律 运动电荷的磁场1. 磁场的叠加原理空间一点的磁感强度等于各电流单独存在时在该点产生磁感应强度的矢量和:∑=ii B B 可推广为 ⎰=B d B42B d是电流强度有限而长度无限小的电流元l d I 或电流强度无限小而空间大小不是无限小的元电流的磁场。
上式中矢量号一般不能略去,只有当各电流产生磁场方向相同时,才能去掉矢量号。
2. 毕奥—萨伐尔定律电流元l d I 在空间一点产生的磁场B d为: 304rr l d I B d πμ⨯= 大小: 02I sin(I ,r)dB 4r dl dl μπ∠=方向:B d 垂直于电流元l d I 与r 所形成的平面,且B d与l d I 、r构成右手螺旋。
3. 电流与运动电荷的关系导体中电荷定向运动形成电流,设导体截面积为S ,单位体积载流子数为n 。
每个载流子带电q ,定向运动速率为v ,则nqvS I =。
电量为q 的带电体作半径为R 、周期为T 的匀速圆周运动相当于半径为R 、电流强度T q I /=的圆电流,具有磁矩TqR I R p m 22ππ==。
大学物理 稳恒磁场的基本性质
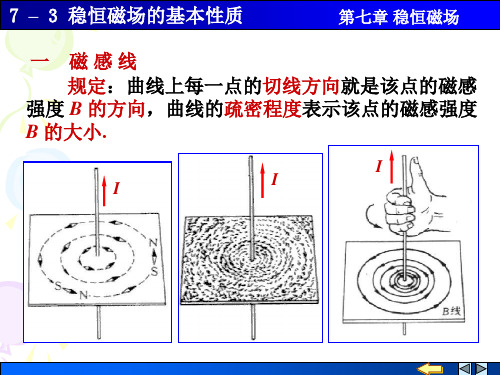
7 – 3 稳恒磁场的基本性质
第七章 稳恒磁场
四 安培环路定理的应用举例
例1 求长直密绕螺线管内磁场
解 1 ) 对称性分析螺旋管内为均匀场 , 方向沿
轴向, 外部磁感强度趋于零 ,即 B 0 .
7 – 3 稳恒磁场的基本性质
第七章 稳恒磁场
2 ) 选回路 L .
磁场 B 的方向与
电流 I 成右螺旋.
s
B dS B dS
S
S
-Br 2
7 – 3 稳恒磁场的基本性质
第七章 稳恒磁场
例 如图载流长直导线的电流为 I ,
形面积的磁通量.
解 先求
试求通过矩 B ,对变磁场
B
给B出dΦ后0I 积分求BΦ// S
I
l
2π x dΦ BdS
0I
ldx
M
NB
++++++++++++
P
LO
B dl B dl B dl BPM
B MN 0nMNI B 0nI
无限长载流螺线管内部磁场处处相等 , 外部磁场 为零.
7 – 3 稳恒磁场的基本性质
第七章 稳恒磁场
例3 无限长载流圆柱体的磁场
I
解 1)对称性分析 2)选取回路
RR
rR
Bdl l
0I
L
2π rB 0I
B 0I
2π r
r B
0 r R
l
B
d
l
0
π π
大学物理 稳恒磁场

第十一章稳恒磁场磁场由运动电荷产生。
磁场与电场性质有对称性,学习中应注意对比.§11-1 基本磁现象磁性,磁力,磁现象;磁极,磁极指向性,N极,S极,同极相斥,异极相吸。
磁极不可分与磁单极。
一、电流的磁效应1819年,丹麦科学家奥斯特发现电流的磁效应;1820年,法国科学家安培发现磁场对电流的作用。
二、物质磁性的电本质磁性来自于运动电荷,磁场是电流的场。
注:1932年,英国物理学家狄拉克预言存在“磁单极”,至今科学家一直在努力寻找其存在的证据。
§11-2 磁场磁感强度一、磁场磁力通过磁场传递,磁场是又一个以场的形式存在的物质。
二、磁感强度磁感强度B 的定义:(1)规定小磁针在磁场中N 极的指向为该点磁感强度B 的方向。
若正电荷沿此方向运动,其所受磁力为零。
(2)正运动电荷沿与磁感强度B 垂直的方向运动时,其所受最大磁力F max 与电荷电量q 和运动速度大小v 的乘积的比值,规定为磁场中某点磁感强度的大小。
即:qvF B max=磁感强度B 是描写磁场性质的基本物理量。
若空间各点B 的大小和方向均相等,则该磁场为均匀磁场....;若空间各点B 的大小和方向均不随时间改变,称该磁场为稳恒磁场....。
磁感强度B 的单位:特斯拉(T)。
§11-3 毕奥-萨伐尔定律 一、毕-萨定律电流元: l Id电流在空间的磁场可看成是组成电流的所有电流元l Id 在空间产生元磁感强度的矢量和。
式中μ0:真空磁导率, μ0=4π×10-7NA 2 dB 的大小: 20sin 4rIdl dB θπμ=d B 的方向: d B 总是垂直于Id l 与r 组成的平面,并服从右手定则.一段有限长电流的磁场: ⎰⎰⨯==l l r r l Id B d B 304πμ二、应用1。
一段载流直导线的磁场 )cos (cos 42100θθπμ-=r IB 说明:(1)导线“无限长":002r I B πμ=(2)半“无限长”: 00004221r I r IB πμπμ==2.圆电流轴线上的磁场 磁偶极矩232220)(2x R R IB +=μ讨论:(1)圆心处的磁场:x = 0 RIB 20μ=;(2)半圆圆心处的磁场: RIR I B 422100μμ==(3)远场:x >>R ,引进新概念 磁偶极矩0n IS m =则: m xB 3012πμ=3.载流螺线管轴线上的磁场)cos (cos 2120ββμ-=nIB讨论:(1)“无限长”螺线管:nI B 0μ=(2)半“无限长”螺线管:nI B 021μ=例:求圆心处的B .§11-4 磁通量 磁场的高斯定理 一、磁感线作法类似电场线。
稳恒磁场的安培环路定理公式

稳恒磁场的安培环路定理公式稳恒磁场的安培环路定理公式揭示了电流在磁场中所受到的力和磁感应强度之间的关系。
这个定理在物理学中扮演着重要的角色。
本文将以通俗易懂的方式介绍这个定理的公式以及其背后的物理原理,希望能够给读者带来指导意义。
安培环路定理的公式是通过一条封闭的路径来描述电流在磁场中所受到的力的总和。
这个路径被称为安培环路,通常采用一个简单的闭合曲线来表示。
具体而言,公式可以表达为:$\sum\overrightarrow{B} \cdot \overrightarrow{dl} = \mu_0 \cdotI_{enc}$,其中$\sum \overrightarrow{B} \cdot\overrightarrow{dl}$表示安培环路上磁感应强度与微小路径元素的内积之和,$\mu_0$是真空中的磁导率,$I_{enc}$表示通过安培环路所围成的面积的电流。
从这个公式可以看出,磁感应强度与路径元素之间的内积是电流所受到的力的量度。
如果磁感应强度和路径元素之间的内积为正值,那么电流将受到一个向内的力;反之,如果内积为负值,电流将受到一个向外的力。
这里需要注意的是,安培环路定理只对稳恒磁场成立,也就是说磁场的强度和方向在空间中不发生变化。
安培环路定理的公式可以通过一个具体的例子来更加生动地说明。
假设有一根直导线通有电流$I$,而周围存在一个磁场$\overrightarrow{B}$。
我们可以通过一个半径为$r$的圆形安培环路来观察这个过程。
根据公式,我们可以计算出磁感应强度在安培环路上的线积分。
在这个例子中,由于磁场的方向与路径元素的方向相同,内积将永远为正值。
因此,电流在环路上将受到一个向内的力。
这个力的大小可以由公式计算得出。
安培环路定理不仅在理论上有重要意义,它还在实际中广泛应用。
例如,当我们需要设计电磁铁时,可以根据安培环路定理来确定所需的电流和磁感应强度,从而使电磁铁能够产生所需要的磁场。
稳恒磁场
安培定律
一、安培力
安培力:电流元在磁场中受到的磁力. 安培力:电流元在磁场中受到的磁力. 一个自由电子受的洛仑兹力为: 一个自由电子受的洛仑兹力为
f 洛 = qv × B = −ev × B
电流元所受磁力: 电流元所受磁力
方向: 方向:×
v
dl
B
I
设截面积为S,单位体积电子数为 设截面积为 单位体积电子数为n 单位体积电子数为
1 2 m = NISn = NI πR n 2
方向:与 B 成600夹角. 夹角. 方向: (2)此时线圈所受力矩的大小为: )此时线圈所受力矩的大小为:
)60
0
B
3 2 πR M = mB sin60 = NIB 4 方向: m× B 方向: ×
0
n
即垂直于 B向上,从上往下俯视,线圈是逆时针转动。 向上,从上往下俯视,线圈是逆时针转动。
1T = 1N ⋅ S ⋅ m−1 ⋅ C−1
磁通量
一、磁力(感)线 磁力( 直线电流的磁力线
磁场的高斯定理
圆电流的磁力线
通电螺线管的磁力线
I
I
I
I
通量(通过一定面积的磁力线数目) 二、磁通量(通过一定面积的磁力线数目)
v v dΦ = B ⋅ dS
v v Φ = ∫s B ⋅ dS
单位
1Wb= 1T ⋅ m
I
该式对任意形状的线圈都适用. 该式对任意形状的线圈都适用.
例1如图,求圆心O点的 B . 如图,求圆心 点的 I O
• × R
B=
µ0 I
4R
I
O• •
R
B=
µ0 I
8R
R
• •O
物理学稳恒磁场课件

B内ab 由安培环路定理
0
N l
abI
n N l
b B内a
c d
B 0nI
均匀场
由安培环路定理可解一些典型的场
无限长载流直导线
密绕螺绕环
匝数
B 0I 2 r
Ir
B 0 NI 2 r
无限大均匀载流平面
B 0 j
2
(面)电流的(线)密度
场点距中心
的距离 r
电流密度
I
Idl
B dF
安培指出 任意电流元受力为
dF Idl B
安培力公式
整个电流受力 F Idl B
l
例1 在均匀磁场中放置一半径为R的半圆形导线, 电流强度为I,导线两端连线与磁感强度方向夹角 =30°,求此段圆弧电流受的磁力。
解:在电流上 任
ab 2R
取电流元 Id l
(b)
洛 仑兹力是相对论不变式 B 磁感强度
(Magnetic Induction)
或称磁通密度 (magnetic flux density) 单位:特斯拉(T)
§3 磁力线 磁通量 磁场的高斯定理
一.磁力线
1. 典型电流的磁力线
2. 磁力线的性质
无头无
与电流
与电流成右
尾 闭 套连
手螺旋关系
合二曲. 线磁通量
IS
(体)电流的(面)密度
如图 电流强度为I的电流通过截面S
若均匀通过 电流密度为 J I S
(面)电流的(线)密度
I
如图 电流强度为I的电流通过截线 l
l
若均匀通过 则
j I l
§6 磁力及其应用
一 1..洛带仑电兹粒力子在磁f场m 中受qv力
稳恒磁场

r oR
R2
1
解:应用磁介质中的安培 环路定理求解 取图示半径为 的圆形 闭合回路,在圆周上 的大小分别为常 数, 方向沿圆周切线方向,则
r
R2
o
R1
rr
o
R1 1
R2
5. 描述稳恒磁场的两条基 本定律 (1)磁场的高斯定理
s
磁场是无源场(涡旋场) B d s 0
(2)安培环路定理 n
L i 1
L
I1
B d l I 0 i
I2
I3
用安培环路定理计算磁场的条件和方法 I i 正负的确定:规定回路环形方向,由 右手螺旋法则定出
2( R x ) I 0 圆形截流导线圆心处的磁场 B 2R
2
2 32
载流长直螺旋管轴线上的磁场 B 0 nI
无限长的载流圆柱体 内 B 0 Ir 2
2R
外
0 I B 2r
i 0 无限大的均匀带电的平板 B 2
4、运动电荷的磁场(注意电荷的正负)
0 qv r0 B 4 r 2
I
p
a
N
(3)半径为R的半圆形载流 线圈,通以电流I,在均匀磁场 B 中,若 以 oo 为轴,线圈受到的磁力矩为多少?
o
I
o
B
1 2 M m B,m IR n 2 M mB sin (
2
)
1 IR 2 B 2 方向:沿oo轴向上
I1
A
I2
dl dF
Idl
o B b x
a
x C
方向: AC
4、+q以速度 沿x轴运动,求使+q不偏 转需加多大的 E
大学物理稳恒磁场理论及习题解读

250 0 方向垂直A面
B
BC
0 N C I C
2 RC
0 20 5
2 0.10
O BA
5000 方向垂直C面
B
2 BA
2 BC
7.02 10 T 方向 : tan
4
1
BC 63.4 BA
NIZQ
第14页
大学物理学
恒定磁场
NIZQ
问题: 磁现象产生的原因是什么?
第 2页
大学物理学
恒定磁场
• 电流的磁效应 1820年奥斯特实验表明: 电流对磁极有 力的作用. 1820年 9月 11日在法国科学院演示的奥 斯特的实验 ,引起了安培的兴趣 .一周之后 安培发现了电流间也存在着相互作用力.
此后安培又提出了著名的安 培定律 : 磁体附近的载流导线 会受到力的作用而发生运动.
NIZQ
第 3页
大学物理学
恒定磁场
结论: 磁现象与电荷的运动有着密切的关系 . 运动电荷既能产 生磁效应,也受到磁力的作用. 安培把磁性归结为电流之间的相互作用 . 1822年安培提 出了分子电流假说:
• 一切磁现象起源于电荷的运动.
• 磁性物质的分子中存在分子电流, 每个分子电流相当于一基元磁体。
写成矢量表示:
0 Idl sin
2 4π r 0 Idl r dB 4π r 3
真空中的磁导率: 0= 410-7亨利· 米-1 (H· m-1)
NIZQ
第 8页
大学物理学
恒定磁场
• 毕奥—萨伐尔定律的应用 恒定磁场的计算: 1.选取电流元或某些典型电流分布为积分元. 2.由毕-萨定律写出积分元的磁场dB .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
稳恒磁场
电与磁
密切联系
11世纪我国——指南针 电场一样,
运动电荷
电场 磁场
14-1 磁场的描述
一、基本磁现象 天然磁石 同极相斥 异极相吸
SN
S
N
电流的磁效应 1820年 奥斯特
I
SN
通电导线周围有磁场
I
F F I
地磁为生命创造条件,也对生命起保护作 用,生命与地磁是紧紧联系在一起的
最近几个世纪科学家经过观测,发现地磁 场在减弱
十年前,美国科学家测出减弱的速度,
如果按此速度减弱,在公元32 世纪,地 磁为零——颠倒
有关地磁的起源一直是科学家们力图探明 的基本课题
根据安培提出的磁性源于分子电流的假设, 地球核心内部存在一个巨大的环形电流, 但此电流怎样形成的呢?又是什么机制促 使如此巨大的环形电流周期性换向呢?
小磁针静止时与水平面的夹角——磁倾角 地磁赤道上,磁倾角为零,磁南极和磁北 极,磁倾角为90度
磁场强度的水平分量,磁偏角,磁倾角— —地磁三要素
北京,地磁场 B 0.5104T 磁偏角 60
磁倾角 5701'
不同地点三要素不同,根据三要素可画地 磁图
人们发现地磁场的方向在过去的4百万年 中已经循环颠倒9次
通电导线之间有力的作用
电子束
S
+
N
磁场能使电子束偏转
产生 电流(运动电荷)
磁场
力 安培指出:
电荷的运动是一切磁现象的根源。
二 、磁 感 强 度 B 的 定 义
1、 磁感强度 B的方向
SN
该点小磁针静止时, N极指向
2、磁感强度大小 运动电荷在磁场中受力
F
qv
B
磁感强度大小 B Fmax qv
单位 特斯拉 1(T) 1N/A m
工程上用高斯 1G 104T
地球周围 B 0.5104T
一般永磁体 102T 大型电磁铁 2T
地球的磁场
地球是一个大磁体,N极在地理南极附近, S极在地理北极附近。
地球的磁场分布近似一个被磁化了的球体 产生的磁场。
不同的地点,磁场的大小方向都不同。
小磁针静止时所在的竖直面 —11—.5地磁子午 面,这个面与地理子午面的夹角磁—偏角—磁偏 角
