第三章 习题解
第三章习题解答

第三章习题解答一、判断下列说法是否正确,凡对的在括号内打“√”,否则打“×”。
(1)现测得两个共射放大电路空载时的电压放大倍数均为-100,将它们连成两级放大电路,其电压放大倍数应为10000。
( )(2)阻容耦合多级放大电路各级的Q点相互独立,( )它只能放大交流信号。
( )(3)直接耦合多级放大电路各级的Q点相互影响,( )它只能放大直流信号。
( )(4)只有直接耦合放大电路中晶休管的参数才随温度而变化。
( )(5)互补输出级应采用共集或共漏接法。
( )二、现有基本放大电路:A.共射电路B.共集电路C.共基电路D.共源电路E.共漏电路根据要求选择合适电路组成两级放大电路。
(1)要求输入电阻为1kΩ至2kΩ,电压放大倍数大于3000,第一级应采用,第二级应采用。
(2)要求输入电阻大于10MΩ,电压放大倍数大于300,第一级应采用,第二级应采用。
(3)要求输入电阻为100kΩ~200kΩ,电压放大倍数数值大于100,第一级应采用,第二级应采用。
(4)要求电压放大倍数的数值大于10,输入电阻大于10MΩ,输出电阻小于100Ω,第一级应采用,第二级应采用。
(5)设信号源为内阻很大的电压源,要求将输入电流转换成输出电压,且,输出电阻R o<100,第一级应采用,第二级应采用。
三、选择合适答案填入空内。
(1)直接耦合放大电路存在零点漂移的原因是。
A.电阻阻值有误差B.晶体管参数的分散性C.晶体管参数受温度影响D.电源电压不稳定(2)集成放大电路采用直接耦合方式的原因是。
A.便于设计B.放大交流信号C.不易制作大容量电容(3)选用差分放大电路的原因是。
A.克服温漂B. 提高输入电阻C.稳定放入倍数(4)差分放大电路的差模信号是两个输入端信号的,共模信号是两个输入端信号的。
A.差B.和C.平均值(5)用恒流源取代长尾式差分放大电路中的发射极电阻R e,将使电路的。
A.差模放大倍数数值增大B.抑制共模信号能力增强C.差模输入电阻增大(6)互补输出级采用共集形式是为了使。
化工原理答案-第三章习题答案-150

第三章习题解答3-1 某圆柱形固定床填充的催化剂直径为p d ,高为h ,试求等体积的当量直径及球形度。
解:h d d e 2p 346ππ=,32p 23h d d e = ()p 312p p 2322218)24(23d h h d h d d h d P P +=⋅⋅+⨯⎪⎭⎫ ⎝⎛=πππφ3-2 求20mm×20mm×25mm 的长方体颗粒的体积当量直径,表面积当量直径,比表面积当量直径及形状系数。
解:体积当量直径:mm V d ev 7.262520206633=⨯⨯⨯==ππ表面积当量直径:mm Sd es 8.282)252020202020(=⨯⨯+⨯+⨯==ππ比表面积当量直径:mm S V a d ea 1.232)252020202020(252020666=⨯⨯+⨯+⨯⨯⨯⨯=== 形状系数:86.08.287.26222222=====es ev es ev P s d d d d S S ππφ 3-3 由边长皆为2mm 的立方体,直径和高度均为2mm 的圆柱体及直径为3mm 的球体各10kg 组成的均匀颗粒床层,床层直径为0.2m ,高度为 1 m 。
已知颗粒的密度皆为1900kg/m 3,求床层的空隙率和颗粒的平均比表面积。
解: 床层体积:3220314.012.044m h d V b =⨯⨯==ππ颗粒体积:30158.01900310m V P =⨯= 床层空隙率:497.00314.00158.00314.0=-=-=bpb V V V ε 颗粒的平均比表面积:3球柱立a a a a ++=-13000002.0002.0002.06002.0002.0-=⨯⨯⨯⨯=m a 立 1223000002.0)002.0(4002.02)002.0(4-=⨯⨯⋅+⨯⨯=m a πππ柱 1322000003.066003.0003.0-==⨯⨯=m a ππ球 11 2.67676232000300030003---==++=++=mm m a a a a 球柱立 3-4 某形状近似球形的微小固体颗粒,其沉降运动处于斯托克斯定理区,试计算(1)该颗粒在20℃与200℃的常压空气中的沉降速度之比为多少?(2)该颗粒在20℃与50℃的水中的沉降速度之比为多少?[(1)1.44,(2)0.55]解:(1)20℃空气的粘度s Pa ⋅⨯=-51081.1μ,200℃空气的粘度s Pa ⋅⨯=-5'106.2μ,因沉降速度处于斯托克斯定律区,ρρ>>p ,故()()()()44.11081.1106.2181855''''22'=⨯⨯=--=--=--μρρμρρμρρμρρs s s s t t g d gd u u (2)20℃水的粘度s Pa ⋅⨯=-3101μ,50℃水的粘度s Pa ⋅⨯=-3'1055.0μ,因沉降速度处于斯托克斯定律区,并考虑到液体的密度随温度变化很小,故()()()()55.01011055.0181833'''''22'=⨯⨯=≈--=--=--μμμρρμρρμρρμρρs s p p p p t t g d g d u u 无论是气体还是液体,温度的改变主要是通过粘度的变化而影响沉降速度。
第03章微分中值定理与导数的应用习题详解

M 12丿」I 2丿第三章 微分中值定理与导数的应用习题3-11.解:(1)虽然 f(x)在[—1,1]上连续,f(—1) = f(1),且 f(x)在(—1,1)内可导。
可见,f(x)在[_1,1]上满足罗尔中值定理的条件,因此,必存在一点 匕€(-1,1),使得f 牡)=0,即:f(X)=cosx, F(X)=1 — sin X 且对任一 x 乏0,—】,F'(X)H 0, ”■. f (x),F (x)满足柯西 I 2丿中值定理条件。
—12©宀2=0,满足、; (2)虽然f(x)在[—1,1]上连续,f(_1)= f (1),但 f (x)在(—1,1)内 x = 0点不可导。
可 见,f (x)在[ —1,1]上不满足罗尔中值定理的条件,因此未必存在一点 £ £ (_1,1),使得 f 徉)=0. 2.因为函数是一初等函数,易验证满足条件 3 3 .解:令 y = 3arccos x - arccos(3x - 4x 3), y ‘ = 一 23 —12x 2厂工®®3)2,化简得 y'=0,「. y =c ( C 为常数),又 y(0.5)=兀,故当-0.5<x<0.5,有 y(x)=兀。
「兀f f 兀、 4 .证明:显然f(x), F(x)都满足在'|0,二I 上连续,在10,二 内可导L 2」 I 2丿 c oxsn ——x、、2丿F Q-F(O)12丿兀--1 2F( x) -1 sixn_c O 弓-x厂(X )_F(x) ZL"2 /兀 X ,,即 tan I - -- U--1,此时l 4 2丿 2f JI「兀X = 2 I — -arctan l — -1L 4l 2显然萨〔0,-〕,即丿」 I 2丿5.解:因为f(0) = f (1)= f (2) = f (3) =0,又因为f(x)在任一区间内都连续而且可导, 所以f (X)在任一区间 0,1 ], 1,2], [2,3]内满足罗尔中值定理的条件, 所以由罗尔定理,得:3" -(0,1), "^(1,2), ©-(2,3),使得:f 徉1 )= 0 r =) &:◎(=), 30 因为6.证明:设f(x) =0的n+1个相异实根为X o V X 1 <X 2 <H( <X n则由罗尔中值定理知:存在J (i =1,2,川n):X0 <:勺1cj ■<X2 vill <-1^Xn ,使得再由罗尔中值定理至少存在So =1,2,川n-1):上11 C 巴21 V ©2 吒 W ©3 V i 11 < J n d W G n ,使得7.解:反证法,倘若 p(X)=0有两个实根,设为X^X 2,由于多项式函数 p(x)在[X 1,X 2]上连续且可导,故由罗尔中值定理存在一点E€(X I ,X 2),使得P 徉)=0,而这与所设p'(x)=0没有实根相矛盾,命题得证。
应用随机过程第三章习题解

g(t) = f (x, tx)|x|dx
3
第三章 更新过程
第三章 更新过程
其中 f (t, tx) 是 Xi 与 TiXi 的联合密度函数, 当 Xi 与 TiXi 独立时,有
∫ g(t) = λ exp{−λtx}f (x)|x|dx
所以这样的 Ti 是存在的.
3.6 如果 p = P (X = ∞) > 0, 则称 X 是广义的随机变量. 设 X 是广
是 3 分钟. 假设每台电话独立工作, 一共有 6 部电话, 估算上午 10:30 时恰
有 5 部电话占线的概率.
解:
由题可知每台电话占线的概率为
p
=
3 23
,
又各电话是否占线独立,
所以 10:30 有 5 部电话占线的概率为:
P = C65p5(1 − p)
3.11 眨眼使泪水均匀地涂在角膜和结膜的表面,以保持眼球润湿而不
∑ ∑k
∑
P ( Xi = j, Xk+1 > t − j) = (kλ)jexp(−kλ)P (X1 > t − j)/j!
0≤j≤t i=1
0≤j≤t
3.9 设更新过程 N (t) 的更新间隔是 Xn, i1, i2, . . . , in 是 1, 2, . . . , n 的一
个全排列. 对于 n ≥ 2, 证明
= 1/p − 1
3.7 对于泊松过程验证定理 1.2(2)成立.
证明: 对于泊松过程 N (t) 有 m(t) = E(N (t)) = λ·t, 而 λ·(t) 是连续的且 在 t≥0 时是严格增加的,当然是单调不减的, 也即定理 1.2(2) 对于泊松过 程是成立的。
3.8 设更新过程N(t)的更新间隔是来自总体 X 的随机变量。
第三章习题解答

第3章 力学基本定律与守恒律 习题及答案1.作用在质量为10 kg 的物体上的力为i t F)210(+=N ,式中t 的单位是s ,(1)求4s 后,这物体的动量和速度的变化.(2)为了使这力的冲量为200 N ·s ,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度j 6-m ·s -1的物体,回答这两个问题.解: (1)若物体原来静止,则i t i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向,ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速,则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理, 12v v ∆=∆,12I I=这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理. (2)同上理,两种情况中的作用时间相同,即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ,(s 20='t 舍去)2.一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入,得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 3.如图所示,一质量为m 的球,在质量为M 半径为R 的1/4圆弧形滑槽中从静止滑下。
第三章部分习题解答
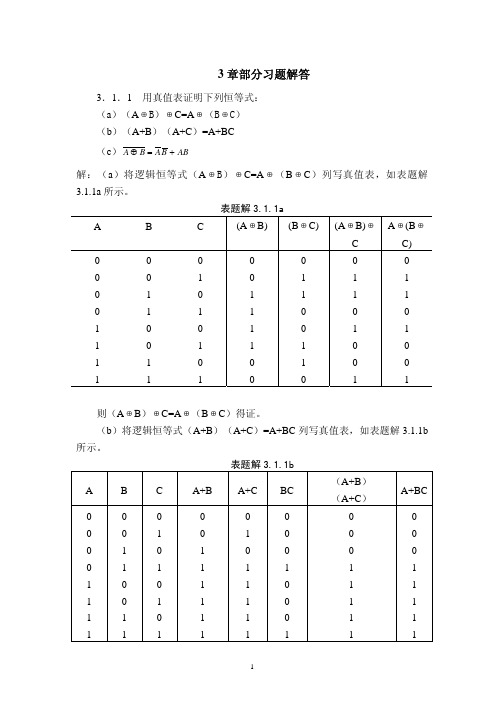
(b) ( A + B)(AB ) = AAB + BAB = AB
(c) ABC(B + C ) = ( A + B + C )(B + C ) = C + B( A + B ) = C + AB
(d) A + ABC + ABC + CB + CB = A(1 + BC + BC) + C(B + B ) = A + C
L3 = A3 ⊕ C
可分别用异或门、三态门设计逻辑电路,如图题解 3.4.4a、b 所示。
图题解 3.4.4
7
3.4.7 某雷达站有 3 部雷达 A、B、C,其中 A 和 B 功率消耗相等,C 的 功率是 A 的两倍。这些雷达由两台发电机 X 和 Y 供电,发电机 X 的最大输出功 率等于雷达 A 的功率消耗,发电机 Y 的最大输出功率是 X 的 3 倍。要求设计一 个逻辑电路,能够根据各雷达的启动和关闭信号,以最节约电能的方式启、停 发电机。
X = ABC + ABC + ABC + ABC = AB ⊕ C + B A ⊕ C
Y =AB+C 由逻辑表达式可设计出最节约电能的发电机启、停方式的逻辑电路,如图 题解 3.4.7b 所示。
表题解 3.4.7
A
B
C
X
Y
0
0
0
0
0
0
0
1
0
1
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
概率统计第三章题解
求(1)X,Y 的边缘分布律; (2)X=3 的条件下,Y 的条件分布律; (3)Y=1 的条件下,X 的条件分布律.
解: (1)X,Y 的边缘分布律见上表. 即
P { X 3, Y k } (2) P{Y k | X 3} , k 0,1,2,3 P { X 3}
K
0
X 和 Y 的联合分布律为
X
0 0 1/8
1 3/8 0
2 3/8 0
3 0 1/8
Y 1
3
3.盒子里装有 3 只黑球,2 只白球,2 只红球,在其中 任取 4 只球,以 X 表示取到黑球的只数,以 Y 表示取到红 球的只数.求 X 和 Y 的联合分布律. 解 X 的可能取值为 0,1,3,Y 的可能取值为 0,1,
由于 X 和 Y 相互独立,因此 X 和 Y 的联合概率密度为
1 1 e 2 , 0 x 1, y 0 f ( x , y ) f X ( x ) fY ( y ) 2 0, 其它
(2)设含有 a 的二次方程为a 2 2 Xa Y 0 ,试求 a 有 实根的概率.
概率统计第三章题解概率统计概率统计简明教程应用概率统计概率统计简明教程pdf概率统计学概率统计pdf理工科概率统计pdf概率统计讲义习题解答概率统计视频
三、习题解答 1.在一箱子中装有 12 只开关,其中 2 只是次品,在其
中取两次,每次任取一只,考虑两种试验: (1)放回抽样, (2)不放回抽样.我们定义随机变量 X、Y 如下:
)dx
1 2 ((1) (0))
=0.1445
14. 设 X 和 Y 是两个相互独立的随机变量,其概率密 度分别为
(1)确定常数k; (2)求P{X<1,Y<3}; (3)求 P{X<1.5};(4)求 P{X+Y 4 }.
热力学与统计物理——第03章单元系的相变习题解ok
第三章 单元系的相变习题3.3试由0>v C 及0)(<∂∂T V p 证明0>p C 及0)(<∂∂S Vp 。
证: 由式(2.2.1) T C C V p =-⇒VT p ⎪⎭⎫⎝⎛∂∂pT V ⎪⎭⎫ ⎝⎛∂∂ =P Cp T H ⎪⎭⎫ ⎝⎛∂∂=pT S T ⎪⎭⎫⎝⎛∂∂;=V C V T U ⎪⎭⎫⎝⎛∂∂V T S T ⎪⎭⎫ ⎝⎛∂∂= =dp dV V p T ⎪⎭⎫ ⎝⎛∂∂dT T p V⎪⎭⎫⎝⎛∂∂+=dp +⎪⎭⎫ ⎝⎛∂∂dV V p S dS S p V⎪⎭⎫ ⎝⎛∂∂=+⎪⎭⎫ ⎝⎛∂∂dV V p S V S p ⎪⎭⎫ ⎝⎛∂∂⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂dT T S dV V S V T⇒=⎪⎭⎫ ⎝⎛∂∂T V p VS p ⎪⎭⎫ ⎝⎛∂∂T V S ⎪⎭⎫ ⎝⎛∂∂+SV p ⎪⎭⎫⎝⎛∂∂ (1) =⎪⎭⎫ ⎝⎛∂∂V T p VS p ⎪⎭⎫ ⎝⎛∂∂TT S ⎪⎭⎫ ⎝⎛∂∂ (2) 由麦氏关系(2.2.3)代入(1)式中 ⇒=⎪⎭⎫ ⎝⎛∂∂S V T -VS p ⎪⎭⎫⎝⎛∂∂⇒=⎪⎭⎫ ⎝⎛∂∂T V p -⎪⎭⎫ ⎝⎛∂∂S V p SV T ⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂T V S -⎪⎭⎫⎝⎛∂∂S V p ()()⋅∂∂S V S T ,,()()T V T S ,,∂∂ =+⎪⎭⎫⎝⎛∂∂S V p ()()⋅∂∂T V S T ,,()()⋅∂∂S V T V ,,()()T V S T ,,∂∂ =+⎪⎭⎫⎝⎛∂∂S V p ()()⋅∂∂S V T V ,,()()2,,⎥⎦⎤⎢⎣⎡∂∂T V S T =+⎪⎭⎫ ⎝⎛∂∂S V p V S T ⎪⎭⎫ ⎝⎛∂∂()()2,,⎥⎦⎤⎢⎣⎡∂∂T V S T 由式(2.2.5) ⇒V C V T S T ⎪⎭⎫ ⎝⎛∂∂=;即0>=⎪⎭⎫⎝⎛∂∂VV C T S T . 于是: 0>=⎪⎭⎫ ⎝⎛∂∂T V p +⎪⎭⎫⎝⎛∂∂S V p 正数于是: SV p ⎪⎭⎫⎝⎛∂∂<0=P C P T S T ⎪⎭⎫ ⎝⎛∂∂()()=∂∂=p T p S T ,,()()⋅∂∂V S p S T ,,()()=∂∂p T V S ,,⋅⎪⎭⎫ ⎝⎛∂∂SV p T ()()p T V S ,,∂∂ ⋅⎪⎭⎫ ⎝⎛∂∂=S V p T ()()⋅∂∂V T V S ,,()()=∂∂p T V T ,,⋅⎪⎭⎫ ⎝⎛∂∂S V p T V T S ⎪⎭⎫ ⎝⎛∂∂Tp V ⎪⎪⎭⎫ ⎝⎛∂∂⋅ ⋅⎪⎭⎫⎝⎛∂∂=SV p V TC p V ⋅⎪⎪⎭⎫⎝⎛∂∂ 0>V C ; 因而0>P C习题3.7试证明在相变中物质摩尔内能的变化为:1p dT U L T dp ⎛⎫∆=-⋅ ⎪⎝⎭如果一相是气相,可看作理想气体,另一相是凝聚相,试将公式化简。
第三章习题解答
第三章 语法分析
对产生式V′→ε |[E] 有:FIRST(ε)∩FIRST(‘[’]= Φ; FIRST(‘[’)∩FOLLOW(V′)={[}∩{#,+,]}=Φ;
对E′→ε | +E 有:FIRST(ε)∩FIRST(‘+’)= Φ; FIRST(‘+’)∩FOLLOW(E′)={+}∩{ ] }=Φ。 故文法G[V′]为LL(1)文法。
第三章 语法分析 表3-12 习题3.24的SLR(1)分析表
状态
ACTION
GOTO
b
d
i
#
T
E
H
0
r3
s3
1
2
1
acc
2
s4
3
r2
4
r6
s6
r6
5
5
s7
r1
6
r4
r4
7
s8
8
r5
r5
第三章 语法分析
序号 状态栈 符号栈 产生式 输入串
10
#
E→ε bibi# 归约 r3
2 02
#E
bibi# 移进
第三章 语法分析
表3-8 优先关系表
a
b
c
a
⋖⋗
⋖≡
⋗
b
⋖
⋖⋗
≡
c
⋗
⋗
由于表中的优先关系不唯一,故文法G[S]不是算符优 先文法。
第三章 语法分析 (4) 消除文法G[S]的左递归: S→aSb | P P→bPc | bQc Q→aQ′ Q′→aQ′| ε 提取公共左因子后得到文法G′[S]: S→aSb | P P→bP′ P′→Pc | Qc Q→aQ′ Q′→aQ′| ε
第三章习题解答及参考答案
(
)
①
2 式中 m 为整数。令 u = αr ,显然上式是 u 的周期函数,周期为 2π ,故可展开成傅里 ∞ 1 1 + sgn (cos u ) = ∑ Cn e inu 2 2 n = −∞
叶级数:
其中,
Cn =
1 2π
∫
π 2
−π 2
e −inu du =
sin (nπ 2) nπ
②
遂有:
∞ 1 1 sin (nπ 2 ) inαr 2 e + sgn cos αr 2 = ∑ 2 2 nπ n= −∞
②
σ ( f x ,0 ) 2λd i =1− f x = 1− f x f0 σ0 l
l l ≤ λd i f x ≤ (见附图3 - 4(b)) 4 2
2 1 l l σ ( f x ,0 ) = (l − λd i f x ) l − = − λd i l f x 2 2 2
λd ;两个一级分量与中央亮斑 L
附图 3-2
习题[3-2]图示
附图 3-3
归一化强度分布
[3-3]
将面积为 10 mm × 10 mm 的透射物体置于一傅里叶变换透镜的前焦面上作频谱分析。
用波长 λ = 0.5 µ m 的单色平面波垂直照明,要求在频谱面上测得的强度在频率 140 线/mm 以下能准确代表物体的功率谱。并要求频率为 140 线/mm 与 20 线/mm 在频谱面上的间隔为 30mm,问该透镜的焦距和口径各为多少? 解:取面积为10mm ×10mm 的透射物体的对角线方向为 x 轴。因要求在 140 线/mm 以下的 空间频率成分不受到有限孔径的渐晕效应的影响,故透镜的口径 D 应满足条件:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P111 9、设二维随机变量(X,Y)的概率密度为 、设二维随机变量 的概率密度为 Cx 2 y x 2 ≤ y ≤ 1 1)试确定常数 ; )试确定常数C; f ( x, y ) = 其它 2)求边缘密度。 求边缘密度。 求边缘密度 0
2 解:1)Q ∫−∞ ∫−∞ f ( x, y ) dxdy = ∫−1 ( ∫x Cx ydy )dx ) 1 1
3 P ( X = 1, Y = 1) = 8 3 P ( X = 2, Y = 1) = 8
P ( X = 3, Y = 1) = 0 P ( X = 0, Y = 3) =
P ( X = 1, Y = 3)
1 8 =0
P ( X = 2, Y = 3) = 0
1 P ( X = 3, Y = 3) = 8
P110 1、一枚银币连掷三次,以X表示在三次中出 、一枚银币连掷三次, 表示在三次中出 现正面的次数, 现正面的次数,以Y表示三次中出现正面次数与反 表示三次中出现正面次数与反 面次数之差的绝对值,试求出(X,Y)的分布律。 的分布律。 面次数之差的绝对值,试求出 的分布律 解: X的可能取值为:0,1,2,3; Y的可能取值为:1,3 的可能取值为: 的可能取值为: 的可能取值为 的可能取值为 则 P ( X = 0, Y = 1) = 0
y 2 1 = ∫ dx[ ∫ x + xy dy + ∫ 0dy ] 0 0 2 3 x x 1 2 2 2 2 2 = ∫ [( x y + xy )0 + 0]dx = ∫ (2 x + x)dx 0 0 6 3 2 3 1 2 1 2 = x + x = x ( 2 x + 1) 3 3 3 当 x > 1, 0 < y ≤ 2 时, x y 1 x y 2 F ( x, y ) = ∫−∞ ∫−∞ f ( x, y ) dxdy = ∫0 dx ∫0 x + 3 xy dy y 1 x 1 2 = ∫ dy[ ∫ x + xy dx + ∫ 0dx] 0 0 1 3
∂x ∂2F − x− y 2 −x −y ln 3 而 = 3 ln 3 ⋅ ( 3 ln 3) = 3 ∂x∂y
3−x− y ln2 3 x ≥ 0, y ≥ 0 ∴ f ( x, y) = 其它 0
P111 7、设二维随机变量(X,Y)可能取的值为 、设二维随机变量 可能取的值为(0,0), 可能取的值为 , (-1,1),(-1,1/3),(2,0)且取这些值的概率依次为 , , 且取这些值的概率依次为
= −e − y
+∞ x
+∞
∫
+∞
x
e − y dy
(0 ≤ x)
(0 ≤ y )
= e− x
y 0
fY ( y ) = ∫
+∞
−∞
−y
f ( x, y ) dx = e − y dx ∫
y 0
=e x
= ye − y
e − x x ≥ 0 ∴ fX ( x) = 0 x < 0
ye − y y > 0 fY ( y ) = 0 y ≤ 0
i = 1,5 = 0.6 2) P (Y = 2 X ) = P ( X = 1, Y = 2 ) + P ( X = 2, Y = 4 )
= 0.1
(
)
P110 4、设随机变量(X,Y)的概率密度为: 、设随机变量 的概率密度为: 的概率密度为
k ( 6 − x − y ) 0 < x < 2, 2 < y < 4 f ( x, y ) = 其它 4) P ( X + Y ≤ 4 ) 0
3 1 0 C3 C2C2 = 2 = 35 C74
P ( X = 3, Y = 2 ) = 0
所以(X,Y)的分布律为: 的分布律为: 所以 的分布律为
X
0 1 2 3
Y
0
0 0 3/35 2/35
1
0 6/35 12/35 2/35
2
2/35 6/35 3/35 0
P110 3、设随机变量(X,Y)的分布律为: 、设随机变量 的分布律为: 的分布律为
2 0 C32C2 C2 3 P ( X = 2, Y = 0 )= = 4 C7 35 1 1 C32C2C2 = 12 P ( X = 2, Y = 1) = 35 C74 3 1 0 C3 C2C2 2 P ( X = 3, Y = 0 ) = = 4 C7 35
P ( X = 3, Y = 1)
则
x ≤ 0, y ≤ 0 0 1 x 3 y + 1 x 2 y 2 0 < x ≤ 1, 0 < y ≤ 2 12 3 1 2 F ( x, y ) = x ( 2 x + 1) 0 < x ≤ 1, y > 2 3 1 x > 1, 0 < y ≤ 2 12 y ( y + 4 ) x > 1, y > 2 1
1 1 3 2 = 6x − 2x + x 8 6 0
2
2 = 3
2 1 x + xy 0 ≤ x ≤ 1, 0 ≤ y ≤ 2 f ( x, y ) = 3 0 其它 3 的分布函数; 求:1)(X,Y)的分布函数; 2) P(0 < x ≤ 1,1 < y ≤ ) ) 的分布函数 2 F ( x, y ) = 0 1) 解:1)当 x ≤ 0 或 y ≤ 0 时,
1 1 1 5 ,, , , 试求(X,Y)的分布律及边缘分布。 的分布律及边缘分布。 试求 的分布律及边缘分布 6 3 12 12
解:
X
-1 0 2
Y
0
0 1/6 5/12 7/12
1/3
1/12 0 0 1/12
1
1/3 0 0 1/3
pi⋅
5/12 1/6 5/12
p⋅ j
P111 8、设二维随机变量(X,Y)的概率密度为 、设二维随机变量 的概率密度为 e − y 0 ≤ x ≤ y 求(X,Y)关于 和关于 的 关于X和关于 关于 和关于Y的 f ( x, y ) = 边缘密度。 边缘密度。 其它 0 解:Q f X ( x ) = ∫−∞ f ( x, y ) dy =
1)确定常数k; )确定常数
+∞ +∞
求: P ( X < 1, Y < 3) 3) P ( X < 1.5 ) 2)
2 4
4
解:1) Q ∫−∞ ∫−∞ f ( x, y ) dxdy = ∫0 dx ∫2 k ( 6 − x − y ) dy )
2 1 2 = k ∫ 2 y − xy − y dx = k ∫0 ( 6 − 2 x ) dx 0 2 2 1 2 2 ⇒k = = k ( 6 x − x ) = 8k = 1 0 8 1 3 1 2) P ( X < 1, Y < 3) = ∫0 dx ∫2 ( 6 − x − y ) dy 8
X
1 2 3
Y
1
0.1 0 0.05
2
0.05 0.1 0.05
3
0.1 0.05 0
4
0 0.05 0.2
5
0.15 0 0.1
求:1)P ( X < 3) )
2) P (Y = 2 X )
解:1)P ( X < 3) = P ( X = 1, Y = i ) + P ( X = 2, Y = i ) )
3
1 27 2 1.5 = (6x − x ) = 0 32 8
4) P ( X + Y ≤ 4 )
4− x 1 2 = ∫ dx ∫ ( 6 − x − y ) dy 2 8 0
4− x
1 2 1 2 1 2 1 2 = ∫ 2 y − xy − y dx = ∫ 6 − 4 x + x dx 8 0 2 8 0 2 2
所以(X,Y)的分布律为: 的分布律为: 所以 的分布律为
X
0 1 2 3
Y
1
0 3/8 3/8 0
3
1/8 0 0 1/8
P110 2、盒子里有 只黑球,2只红球,2只白球, 只黑球, 只红球 只红球, 只白球 只白球, 、盒子里有3只黑球 在其中任取4只球 只球, 表示取到黑球的只数, 在其中任取 只球,以X表示取到黑球的只数,以Y 表示取到黑球的只数 表示取到红球的只数,求出(X,Y)的分布律。 的分布律。 表示取到红球的只数,求出 的分布律 解: X的可能取值为:0,1,2,3; 的可能取值为: 的可能取值为 Y的可能取值为:0,1,2 的可能取值为: 的可能取值为 则 P ( X = 0, Y = 0 ) = 0
1 3 1 2 2 1 2 2 = ∫ x y + xy dx = x y + x y 0 3 12 6
当 0 < x ≤ 1, y > 2 时,
x y
F ( x, y ) = ∫−∞ ∫−∞ f ( x, y ) dxdy = ∫0 dx ∫0
x 2
x
y
2 1 x + xy dy 3
P110 5、设随机变量(X,Y)的概率密度为: 、设随机变量 的概率密度为: 的概率密度为
当 0 < x ≤ 1, 0 < y ≤ 2 时,
x y
F ( x, y ) = ∫−∞ ∫−∞ f ( x, y ) dxdy = ∫0 dx ∫0
x
x
y
2 1 x + xy dy 3
