相图二元系统
第二章 二元体系相图

共晶反应: l(E)
冷却 加热
E
sA(G) + sB(H)
A 水
xB→
盐 B
相图应用
1.盐的精制 ① 理解利用相图原理进 行盐类精制过程; ② 量的关系:
m(B 硫铵) SG m(l 母液) SZ
G
Z
2. 水-盐冷冻液
在化工生产和科学研究中常要用到低温浴,配制合 适的水-盐体系,可以得到不同的低温冷冻液。另外, 冬天里汽车水箱等防冰冻也用这种方法。饱和盐水系统 低共熔温度如下:
编号 1 2 符号 A 温度 0 -5 液相组成 0 7.9 平衡固相 ice ice
3
4 5 6 7 8 9 10 11 Q E
-10
-15 -21.1 -15 -10 -5 0.15 10 20
14.0
18.9 23.3 24.2 24.0 25.6 26.3 26.3 26.4
ice
ice Ice+ NaCl.2H2O NaCl.2H2O NaCl.2H2O NaCl.2H2O NaCl.2H2O+NaCl NaCl NaCl
33.0
40.5 42.3 50.5 54.6 62.3 64.6
ice
Ice+ Mn(NO3)2.6H2O Mn(NO3)2.6H2O Mn(NO3)2.6H2O Mn(NO3)2.6H2O Mn(NO3)2.6H2O Mn(NO3)2.6H2O+ Mn(NO3)2.3H2O Mn(NO3)2.3H2O Mn(NO3)2.3H2O
说明: 水盐体系是凝聚体系,可以不考虑压力的变化,水盐体 系的固液平衡可以在没有水蒸气的情况下实现,所以气 相没有计入相数P中,水盐体系也不研究气相的组成
武汉理工大学相图第六章第3节

包晶转变是指在一定温度下,由一定成分 的液相与一定成分的固相作用,形成另外一个 一定成分的固相的转变过程。
包析转变是指两个成分一定的固相在恒温 下转变为另外一个新固相的过程。
合晶转变是指由两个液相L1、L2相互作用, 生成一个一定成分的固相的恒温转变。
(2)两个组元在固态完全不溶的二元共晶相图
A、B两个组元在固态完全不溶解,则 它们之间不会形成固溶体,而是以纯组元的形 式存在。两个固相的单相区在相图中压缩成两 条垂线,同时没有固态下的脱溶转变。
(3)固溶体的不平衡凝固 ① 不平衡凝固时,固相的成分不是沿固相
线变化,而是要偏离固相线。 而且,冷却速度越大,偏离固相线
的程度越大。
② 凝固后,固相内部的成分不均匀。这种 现象称为偏析。
而偏析的程度,可以用分布系数K0 来描述。分布系数是指溶质在固相中的
浓度与在液相中的浓度的比值 。
k0
CS CL
相平衡 L1↔S1 L2↔S2 L3↔S3
液相成分 固相成分
L1
S1
L2
S2
L3
S3
T2温度 :
WL
S2O S2 L2
100 %
WS
OL 2 S2 L2
100 %
固溶体凝固的特点: ① 异分结晶
异分结晶指的是结晶出的固相与母相化学 成分不同的结晶过程,也称为选择结晶。
通常,固相中含有较多的高熔点组元,而 液相中含有较多的低熔点组元。
① 相图分析 特性点 : a,纯A的熔点 b,纯B的熔点 P,包晶转变液相成分点,也称为转熔点 C,B在A中(或SA(B)固溶体中)的最大溶解度点 D,A在B中(即SB(A)固溶体中)的最大溶解度点
F,室温下B在A中的最大溶解度 G,室温下A在B中的最大溶解度
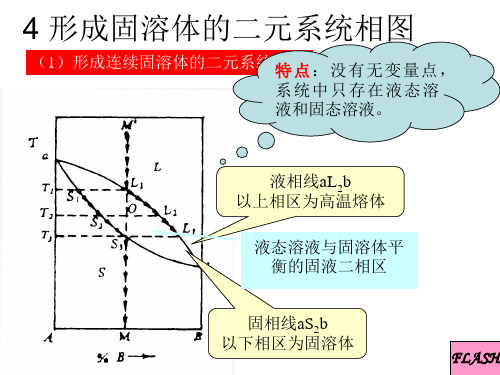
形成固溶体的二元系统相图
界线上任一点的切线与 相应连线的交点实际上 表示了该点液相的瞬时 析晶组成
瞬时析晶组成是指液 相冷却到该点温度, 从该点组成的液相中 所析出的晶相组成
21
(3) 重心规则
判断无变量点的性质
• 如无变量点处于其相应的副三角形的重心位,则该无变 量点为低共熔点;如无变量点处于其相应的副三角形的 交叉位,则为单转熔点;如无变量点处于其相应的副三 角形的共轭位,则为双转熔点。
f=1
E (L C+A+B, f = 0) 固相点 C F M FLASH
16
杠杆规则计算液相量和固相量
液相到达D点时:
固相量 CM 液相量 MD
固相量 CM 固液总量(原始配料量) CD 液相量 MD 固液总量(原始配料量) CD
17பைடு நூலகம்
2 生成一个一致熔融二元化合物
相当于 2 个简 单三元相图 的组合 • 在三元系统 中某二个组分 间生成的化合 物称为二元化 合物 • 二元化合物的 组成点在浓度 三角形的一条 边上 • 一致熔化合物 的组成点在其 初晶区内
2个固溶体
7条线 6个相区 3个无变量点
FLASH
2
析晶路程表示法
液相点
L S B ( A) L M’ L1 E LE S A( B ) S B ( A) , f 0 f=2 f=1
固相点
S1 D H
SB ( A)
SB ( A) S A( B )
着背离C的方向而变化。
9
二、杠杆规则
(1)在三元系统内,由两个相合成一个
新相时,新相的组成点必在原来二相
组成点的连线上;
(2)新相组成点与原来二相组成点的距 离和二相的量成正比。
第六单元2二元相图

重 量%
分析生产硅砖中Al2O3存在降低耐火度的影 响?
因 为此系统中在1595℃低共熔点处生成 含Al2O3 5.5wt%d的液 相,E1点靠近SiO2,当 加入1wt%的,在1595℃就产生 1:5.5=18.2 % 液相,与SiO2平衡的液相线从熔点1723℃ 迅速降为1595℃,因而使耐火度大大降低。
第六单元2二元相图
学习相图的要求:
1、相图中点、线、面含义; 2、析晶路程; 3、杠杆规则; 4、相图的作用。
二元系统相图的表示方法及杠杠规正则
• 相图表示方法
T
T1
M
B content
A content
0
10
20
30
40
50
60
70
80
90 100
A
m %B
B
G=G1+G2
杠杠规则 Gb%=G1b1%+G2b2%
E[D , (SA(B))+SB(A)] SB(A)+ SA(B)[1/ , SA(B)+ SB(A)] p=2 f=1
另一类:生成不连续固溶体且具有回吸点的 二元系统相图
Ta
1
23
SA(B)+L
F SA(B)
G SA(B)+ SB(A)
J L+ SB(A)
SB(A)
b
AO
P
B
1、点G :低共熔点 LSA(B)+ SB(A) f=0
p=2 f=1
[O , A+B]
五、具有多晶转变的二元系统相图
两种类型:A、在低共熔点下发生 B、在低共熔点以上发生
实例应用: 1、CaO.Al2O3.2SiO2-SiO2系统相 图,石
二元相图fec相图

汇报人:
日期:
• 简介 • 二元相图的基本类型 • fec相图的基本构成 • 二元相图和fec相图的绘制方法 • 二元相图和fec相图的分析应用 • 二元相图和fec相图的研究现状及展望
01
简介
定义和概念
要点一
二元相图(Binary Phase Diagram)
又称二元系统相图,是一种描述物质系统中的相平衡状态 的图。它表示了不同成分的物质在温度和压力等条件下的 状态和转变。
利用热力学数据计算
利用热力学数据,计算不同相的稳定性和转变温度。
二元相图和fec相图的绘制软件
1 2
Thermo-Calc
一款常用的热力学计算软件,可用于绘制二元相 图和fec相图。
FactSage
另一款热力学计算软件,可以绘制多种类型的相 图。
3
Visual Phase Diagram
一款可视化相图绘制软件,可用于二元相图和 fec相图的绘制。
THANKS
感谢观看
总结词:合金设计
详细描述:二元相图和fec相图在合金设计方面具有重要应用。通过分析相图,可以了解不同元素之间 的相互作用和合金的相组成,从而设计出具有所需性能的合金。例如,在钢铁工业中,通过调整铁、 碳和其他合金元素的含量,可以制造出具有高强度、高韧性、耐腐蚀等性能的钢材。
工艺优化
总结词:工艺优化
05
二元相图和fec相图的分析应用
材料性能预测
总结词
材料性能预测
详细描述
二元相图和fec相图可以用来预测材料的性能。通过分析相图中的成分和温度,可以了解材料的熔点、密度、热 膨胀系数、热导率等物理性质,以及硬度、抗拉强度、屈服强度、韧性等机械性质。这些信息对于材料的应用和 优化设计至关重要。
材料物理化学二元相图讲解

杠杆规则
如果一个相分解为2个相,则生成的2个相的数量与原
始相的组成点到2个新生相的组成点之间线段成反比。
TD温度下的固相量和液相量
固相量 液相量
OD OF
固相量 固液总量(原始配料量)
OD FD
液相量 固液总量(原始配料量)
OF FD
析晶路程表示法
液相点
L M’
f=2
LA
C
E L A B, f 0
特点: 两个组分在液态时能以任何比例互溶,形成单相溶液;但在
固态时则完全不互溶,二个组分各自从液相中分别结晶。 组分间无化学作用,不生成新的化合物
• 以组成为M的配料加热到高温完全熔融,然后平衡冷却析晶。
M的熔体M’
T=T,L p=1, f = 2
FLASH
t=TC, C点
液相开始对A 饱和,L+A
二元相图
热力学与相平衡第二部分
元相图的基本类型
二元系统:c=2
相律 f c p 1 3 p
pmin 1, fmax 2
温度、浓度
fmin 0, pmax 3
不可能出现4相 或更多相平衡
具有一个低共熔点的简单二元相图
液相线
A的熔点
B的熔点
A和B的二元低共熔点
固相线
4个相区:
L、L+A、 L+B、A+B
平衡冷却过程
FLASH
熔体2 Tk
T,L p=1, f=2
LB p=2, f=1
LP+ B C p=3, f=0
TP
TE 低共熔点 析晶结束
液相点在P点不 变,液相量在减 少,同时固相组 成中B晶体在不 断减少,C晶体 在不断增加,至 D点B晶体被回吸 完毕
二元相图2

The Cu-Zn system
7个单相区:α、β、β`、γ、δ、ε、和η
CaO-SiO2
应用实例
CaO-SiO2系统二元相图
判读依据: 判读依据: 几个化合物 化合物性质 根据一致熔化合 物划分成分系统 3个分二元系统: 个 SiO2-CS CS-C2S C2S-CaO 相区 线 无变量点
t=TC, C点
FLASH
液相同时对晶 体A和B饱和 当最 后一滴低 共 p=3, f=0 熔组 成的液相 析 出A晶体和B晶体 后,液相消失
t=TE, E点
3个概念:系统组成点、固相点、液相点
简称:系统点 取决于系统的总组成,由原始配料组成决定 对于M配料,系统点在MM’线上
系统中的液相组成和固相组成随温度不断变化, 液相点和固相点的位置也随温度不断变化
p=2, f=1
析晶路程表示法
液相点
L L→B 2 K P (LP + B → C , f = 0 ) f=2 f=1
L→C
f=1
固相点
B B +C
E (LE → A + C , f = 0 )
C C+ A
M → F → D → J → H
FLASH
生成一个在固相分解的化合物的二元相图
CaO-SiO2系统中无变量点的性质
符 号 P Q A B C D E F G H M N O R T 相 间 平 衡 CaO 液相 SiO2 液相 α-方石英 + 液相B 液相A α-方石英 + 液相B 液相A α-CS + α-鳞石英 液相A α-CS 液相 α-CS + C3S2 液相 C3S2 α-C2S +液相 α-C2S 液相 α-C2S + C3S 液相 C3S CaO +液相 α‘-C2S + CaO C3S β-CS α-CS α‘-C2S α-C2S γ-C2S α‘-C2S 平衡性质 熔 熔 融 融 赞成(%) CaO 100 0 0.6 28 37 48.2 54.5 55.5 65 67.5 73.6 73.6 51.8 65 65 SiO2 0 100 99.4 72 63 51.8 45.5 44.5 35 32.5 26.4 26.4 48.2 35 35 温度 (°C) 2570 1723 1705 1705 1436 1544 1460 1464 2130 2050 2150 1250 1125 1450 725
形成固溶体的二元系统相图[研究知识]
![形成固溶体的二元系统相图[研究知识]](https://img.taocdn.com/s3/m/69cf515c0242a8956aece48d.png)
不可能出现5相 或更多相平衡
5
一、 三元相图的组成表示方法
通常采用等边三角形表示三元系统的组成
—— 浓度三角形
三个顶点表示三个纯 组分A、B、C的一元 系统;
三条边表示三个二元 系统A-B、B-C、CA的组成;
行业倾力
三角形内任意一点表
示一个含有A、B、C
三个组分的三元系统
的组成。
6
双线法确定三元组成—过M点引另两条边 的平行线
行业倾力
7
浓度三角形的两个性质:
(1) 等含量规则
平行于三角形某
8
(2) 定比例规则 从浓度三角形某角顶
引出之射线上各点,另外
二个组分含量的比例不变。
推论:
从三个组元的混合物中不
断取走C组元,那么这个系统
的组成点将沿CM延长线并沿
着背离C的方向而变化。
判断界线的温度走向
• 将一条界线(或其延长线)与相应的连线(或其延长线) 相交,其交点是该界线上的温度最高点。
行业倾力
20
(2) 切线规则
判断界线的性质
• 将界线上某一点所作的切线与相应的连线相交,如交点 在连线上,则表示界线上该处具有共熔性质;如交点在
连线的延长线上,则表示界线上该处具有转熔性质,其
2个固溶体 7条线 6个相区 3个无变量点
行业倾力
FL2ASH
析晶路程表示法
液相点
M’ L f=2
L
L1
SB(
A)
f=1
E LE S A(B) SB( A) , f 0
固相点
S D H SB( A) 1
SB( A) SA(B)
行业倾力
FL3ASH
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 表示方法1.1 二元系统概述二元系统是含有两个组元(C=2)的系统,如:CaO—SiO2系统,Na2O—SiO2系统等。
根据相律F=C-P+2=4-P,由于所讨论的系统至少应有一个相,所以系统最大自由度数为3,即独立变量除温度、压力外,还要考虑组元的浓度。
对于三个变量的系统,必须用三个坐标的立体模型来表示。
但是,在通常情况下,硅酸盐系统是凝聚系统,可以不考虑压力的改变对系统相平衡的影响,此时相律可以下式表示:F=C-P+1在后面所要讨论的二元、三元、四元系统都是凝聚系统,不再做特别说明。
对于二元凝聚系统:F=C-P+1=3-P当Pmin=1时,Fmax=2;当Pmax=3,Fmin=0可见,在二元凝聚系统中平衡共存的相数最多为三个,最大自由度数为2,这两个自由度就是指温度(T)和两组元中任一组元的浓度(X)。
因此二元凝聚系统相图仍然可以用平面图来表示,即以温度一组成图表示。
1.2 二元系统组成表示法二元系统相图中横坐标表示系统的组成,因此又称为组成轴。
组成轴的两个端点分别表示两个纯组元,中间任意一点都表示由这两个组元组成的一个二元系统。
假设二元系统由AB两组元构成,则两个端点A和B分别表示纯A和纯B。
组成轴分为100等份,从A点到B点,B的含量由0%增加到100%,A的含量由100%减少到0%;从B点到A点则相反。
如图7-24。
AB之间的任意点都是由AB组成的二元系统,如图中的m点是由30%的A和70%的B组成的二元系统。
在相图中组成可以用质量百分数表示,也可以用摩尔百分数或摩尔分数表示,其图形有明显差别,应加以注意,纵坐标表示温度,又称为温度轴。
相图中的任意一点既代表一定的组成又表示系统所处的温度,如M点表示组成为30%的A和70%的B的系统处于T1温度。
由于在二元凝聚系统中温度和组成一定,系统的状态就确定了,所以相图中的每一点都和系统的一个状态相对应,即为状态点。
2 杠杆规则2.1 杠杆规则推导杠杆规则是相图分析中一个重要的规则,它可以计算在一定条件下,系统中平衡各相间的数量关系。
假设由A和B组成的原始混合物(或熔体)的组成为M,在某一温度下,此混合物分成两个新相,两相的组成分别为M1和M2,见图7-25。
若组成为M的原始混合物含B为b%,总质量为G;新相M1含B为b1%,质量为G1;新相M2含B为b2%,质量为G2.因变化前后、后的总量不变,所以:G=G1+G2 (7-5)原始混合物中B的质量为G·b%,新相M1中B的质量为G1·b1%,新相M2中B的质量为C2·b2%。
所以:Gb%=G1b1%+G2b2%将(7-5)式代入,得:(G1+G2)b%=G1b1%+G2b2%G1(b-b1)=G2(b2-b)(7-6)所以: G1·M1M=G2·MM2 (7-7)两个新相M1和M2在系统中的含量则为:G1=(MM2/M1M2)% (7-8)G2=(M1M/M1M2)% (7-9)上式表明:如果一个相分解为二个相,则生成的两个相的数量与原始相的组成点到两个新生相的组成点之间线段成反比。
此关系式与力学上的杠杆很相似,如图7-26所示,M点相当于杠杆的支点,M1和M2则相当于两个力点,因此称为杠杆规则。
2.2 杠杆规则含义可以看出,系统中平衡共存的两相的含量与两相状态点到系统总状态点的距离成反比。
即含量愈多的相,其状态点到系统总状态点的距离愈近。
使用杠杆规则的关键是要分清系统的总状态点,成平衡的两相的状态点,找准在某一温度下,他们各自在相图中的位置。
3 二元系统相图的基本类型3.1 具一个低共熔点的二元系统相图这类系统的特点是:两个组元在液态时能以任意比例互溶,形成单相溶液;固相完全不互溶,两个组元各自从液相分别结晶;组元间不生成化合物。
这种相图是最简单的二元系统相图。
图7-27是最简单的(具有一个低共熔点的)二元系统相图。
(1)相图分析图7-27表示出一个最简单的二元系统相图。
图中的a点是纯组元A的熔点,b点是纯组元B的熔点。
aE线是组成不同的高温熔体在冷却过程中开始析出A晶相的温度的连线,在这条线上液相和A晶相两相平衡共存。
bE线是不同组成的高温熔体冷熔体冷却过程中开始析出B晶相的温度的连线,线上液相和B晶相两相平衡共存。
aE线、bE线都称为液相线,分别表示不同温度下的固相A、B和相应的液相之间的平衡,实际上也可以理解为由于第二组元加入而使熔点(或凝固点)变化的曲线。
根据相律,在液相线上P=2,F=1。
通过E点的水平线GH称为固相线,是不同组成熔体结晶结束温度的连线。
液相线和固相线之间的两个相区aEG和bEH分别为A晶相和液两条液相线和固相线把整个相图分为四个相区:液相线以上的区域是液相的单相区,用L 表示,在单相区内P=1,F=2.相平衡共存(L+A)以及B晶相和液相平衡共存(L+B)的二相区,在该两区域内的液相组成可用结线(等温线)与对应曲线的交点决定。
图7-27中的FD线表示温度在TD时的A晶相与该温度下组成为D的液相平衡。
固相线以下的区域是A晶相和B晶相平衡共存(A+B)的相区,在两相平衡共存的相区内P=2,F=1。
两条液相线与固相线的交点E称为低共熔点。
在这点上组成为E’的液相与A晶相、B晶相三相平衡并存,其平衡关系式为L E↔A+B。
就是说,冷却时相在E点,按E’点的A、B比例同时析出A金相和B金相;加热时按E’点的A、B比例。
这是系统加热时熔融成液相的最低温度,称为低共熔点,在该点析出的固体混合物称为低共熔混合物。
在E点相数P=3自由度数F=0,表示系统的温度和液相的组成都不能变,故E点是二元无变量点。
在此点,当系统被加热或冷却时,只是引起液相对固相的比例量的增加或减少,温度和组成没有变化。
(2)熔体的冷却析晶过程所谓熔体的冷却析晶过程是指将一定组成的二元混合物加热熔化后再将其平衡冷却而析晶的过程。
通过对平衡冷却析晶过程的分析可以看出系统的平衡状态随温度的改变而变化的规律。
以组成为M’的熔体的冷却析晶过程为例。
组成为M’的两元混合物加热成为高温熔体后处于液相区内的M点,将此高温熔体进行平衡冷却。
在温度下降到TC以前,系统为双变量,说明在系统组成已确定的情况下,改变系统的温度不会导致新相的出现。
由于系统组成已定,故系统的状态点只能沿着等组成线(MM’)变化。
当熔体温度下降到TC时,液相开始对组元A饱和,从液相中开始析出A 金相(L→A),系统由单相平衡状态进入二相平衡状态。
由于析出的是纯A,所以固相的状态点应在K点。
同时因A的析出,液相的组成发生变化。
随着温度的下降,液相组成沿着aE线由C点向E点变化,也就是说,向液相中组B含量增加的方向变化。
这时,P=2,F=1。
当温度到达TE时,液相组成到E点,固相的状态点由K点到达G点,此时液相不仅对A金相饱和而且对B晶相也达到饱和,因而将从液相中按E点组成中A和B的比例同时析出A晶相和B晶相(L→A+B)。
由于系统中三相平衡共存,P=3,F=0,因此,系统的温度和液相的组成都不能改变。
但随着析晶过程的进行液相量在不断地减少。
由于有B晶相析出,固相的组成不再停在G点,而由G点向R点变化,当最后一滴液体消失时固相组成达到R点,与系统的状态点重合。
液相消失,析晶过程结束,析晶产物为A和B 两个晶相。
由于系统中只剩下A、B两种晶相,P=2,F=1,温度又可继续下降了。
若是加热,则和上述过程相反。
当系统温度升高到TE时才出现液相,液相组成为E。
因P=3,F=0,系统为无变量,所以系统的温度维持在TE不变,A和B两晶体的量不断减少。
E组成的液相量不断增加。
当B晶相全部熔融后,系统中两相平衡共存,成为单变量,温度才能继续上升,此时A晶相的量继续减少,液相组成沿着aE线向a点变化。
当温度到达TC时,A晶相液完全熔融,系统全部成为熔体。
熔体M的冷却析晶过程具有普遍性,只是如果熔点的组成点在B点和E’点之间时,冷却时首先析出的应是B晶相。
由以上的冷却析晶过程可以看出,在这类最简单的二元系统中:凡事组成在AE’范围的熔体,冷却到析晶温度时首先析出A晶相;凡事组成在BE’范围内的熔体,冷却到析晶温度时首先析出的是B晶相。
所有的二元熔体冷却时都在E点结晶结束,产物都是A晶相和B晶相,只是A,B的比例不同而已。
在整个析晶过程中,尽管组元A和组元B在固相和液相间不断转移,但仍在系统内,不会逸出系统外。
因而系统的总组成是不会改变的,系统总的状态点是沿着原始熔体的等组成线变化,而且成平衡的两相的状态点始终与总状态点在一条水平线上,并分别在其左右两边。
(3)冷却析晶过程中各相含量的计算在图7-27所给的最简单的二元系统相图中,M熔体冷却到TD时,系统中平衡共存两相是A晶相和液相。
这时,系统的总状态点在O点,A晶相的状态点在F点,液相在D点。
根据杠杆规则:固相(A)量:液相量=FO:OD系统中:A%=OD/FD×100% L%=OF/FD×100%冷却过程当液相的状态点刚到E点,固相的状态点为G点时,由于B晶相尚未析出,系统中仍然是A晶相和液相两相平衡共存,此时根据杠杆规则:A%=RE/GE×100% L%=RG/GE×100%当液相在E点消失后,系统中平衡共存的是A晶相和B晶相,这两相的含量则分别是:A%=M’B/AB×100% L%= M’A/AB×100%杠杆规则不但适用于一相分为两相的情况,同样也适用于两相合为一的情况。
甚至多相系统中,都可以利用杠杆规则,根据已知条件计算平衡共存的各相的相对数量及百分含量。
因此,我们可以应用相图确定配料组成一定的制品,在不同的状态下所具有的相组成及其相对含量,以预测和估计产品的性能,这对指导生产和研制新产品具有重要的意义。
3.2 具有一个化合物的二元系统相图(1)具有一个一致熔融化合物的二元系统相图一致熔融化合物是一种稳定的化合物,与正常的纯物质一样具有固定的熔点,加热这样的化合物到熔点时,即熔化为液态,所产生的液相与化合物的晶相组成相同,故称为一致熔融或同成分熔融,其化合物则称为一致熔融化合物或同成分熔融化合物。
由于这种化合物有确定的同成分熔点,并且此熔点在加入其它任一纯组元时会降低直到和两边纯组元的液相线相交得到两个低共熔点E1、E2为止。
这类系统的典型相图如图7-28所示,组元A和组元B生成一个一致熔融化合物AmBn,M点是该化合物的熔点。
曲线aE1是组元A的液相线,bE2是组元B的液相线,E1ME2则是化合物AmBn的液相线。
一致熔融化合物在相图上的特点是化合物组成点位于其液相线的组成范围内,即化合物AmBn的等组成线AmBn-M与液相线相交,交点M(化合物的熔点)是液相线上的温度最高点。
