SAS做的聚类分析
SAS中的聚类分析方法总结
SAS中的聚类分析方法总结（1）——聚类分析概述说起聚类分析，相信很多人并不陌生。
这篇原创博客我想简单说一下我所理解的聚类分析，欢迎各位高手不吝赐教和拍砖。
按照正常的思路，我大概会说如下几个问题：1. 什么是聚类分析？2. 聚类分析有什么用？3. 聚类分析怎么做？下面我将分聚类分析概述、聚类分析算法及sas实现、案例三部分来系统的回答这些问题。
聚类分析概述1. 聚类分析的定义中国有句俗语叫“物以类聚，人以群分”——剔除这句话的贬义色彩。
说白了就是物品根据物品的特征和功用可以分门别类，人和人会根据性格、偏好甚至利益结成不同的群体。
分门别类和结成群体之后，同类（同群）之间的物品（人）的特征尽可能相似，不同类（同群）之间的物品（人）的特征尽可能不同。
这个过程实际上就是聚类分析。
从这个过程我们可以知道如下几点：1) 聚类分析的对象是物（人），说的理论一点就是样本2) 聚类分析是根据物或者人的特征来进行聚集的，这里的特征说的理论一点就是变量。
当然特征选的不一样，聚类的结果也会不一样；3) 聚类分析中评判相似的标准非常关键。
说的理论一点也就是相似性的度量非常关键；4) 聚类分析结果的好坏没有统一的评判标准；2. 聚类分析到底有什么用？1) 说的官腔一点就是为了更好的认识事物和事情，比如我们可以把人按照地域划分为南方人和北方人，你会发现这种分法有时候也蛮有道理。
一般来说南方人习惯吃米饭，北方习惯吃面食；2) 说的实用一点，可以有效对用户进行细分，提供有针对性的产品和服务。
比如银行会将用户分成金卡用户、银卡用户和普通卡用户。
这种分法一方面能很好的节约银行的资源，另外一方面也能很好针对不同的用户实习分级服务，提高彼此的满意度。
再比如移动会开发全球通、神州行和动感地带三个套餐或者品牌，实际就是根据移动用户的行为习惯做了很好的用户细分——聚类分析；3) 上升到理论层面，聚类分析是用户细分里面最为重要的工具，而用户细分则是整个精准营销里面的基础。
sas聚类作业
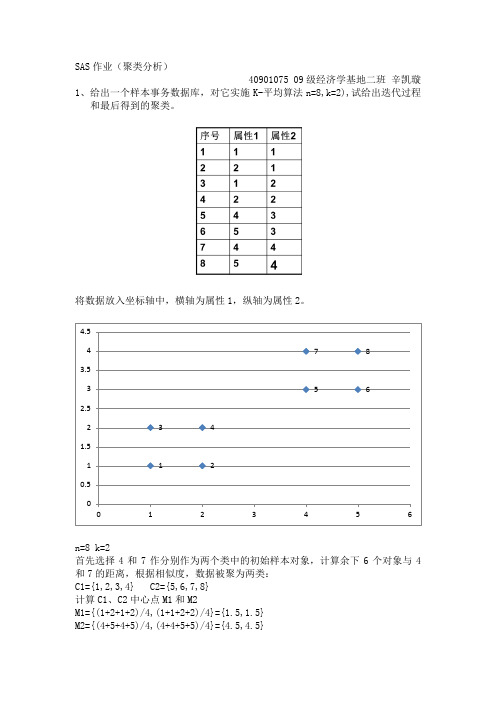
SAS作业（聚类分析）40901075 09级经济学基地二班辛凯璇1、给出一个样本事务数据库，对它实施K-平均算法n=8,k=2),试给出迭代过程和最后得到的聚类。
将数据放入坐标轴中，横轴为属性1，纵轴为属性2。
n=8 k=2首先选择4和7作分别作为两个类中的初始样本对象，计算余下6个对象与4和7的距离，根据相似度，数据被聚为两类：C1={1,2,3,4} C2={5,6,7,8}计算C1、C2中心点M1和M2M1={(1+2+1+2)/4,(1+1+2+2)/4}={1.5,1.5}M2={(4+5+4+5)/4,(4+4+5+5)/4}={4.5,4.5}此时，E2=e12+e22=2+2=4重新计算1-8与M1,M2的距离，数据的聚类仍然保持不变，C1={1,2,3,4} C2={5,6,7,8}此时，算法停止，因为如果继续分析新中心和样本之间的距离，样本会全部分配给同样的类。
因此，数据被分为两类，第一类中心点为{1.5,1.5}，C1=｛1，2，3，4｝，第二类中心点为｛4.5，4.5｝，C2=｛5，6，7，8｝。
2、给出一个样本事务数据库，采用凝聚层次聚类(n=8,k=2)，利用最小距离方法，试给出聚类过程和最后形成的聚类。
将数据放入坐标轴中，横轴为属性1，纵轴为属性2。
n=8 k=2将每个对象看成一个新类。
首先计算两两对象之间的距离，根据最小距离法，分别由1，2和5，6形成一个新类，1，2与3，5，6与7可以分别再形成一个新类，1，2，3与4，5，6，7与8分别可以再形成一个新类。
此时，形成的两个聚类是：C1={1,2,3,4}，C2={5,6,7,8}。
甚至还可以将1，2，3，4，5，6，7，8形成一个聚类。
凝聚层次聚类法需要设定阀值，因此最终的聚类结果和设定的距离阀值有关。
SAS 聚类分析方法
SAS 聚类分析（描述算法）系统聚类法系统聚类法（Hierarchical clustering method ）是目前使用最多的一种方法。
其基本思想是首先将n 个样品看成n 类（即一类包括一个样品），然后规定样品之间的距离和类与类之间的距离。
将距离最近的两类合并为一个新类，在计算新类和其他类之间的距离，再从中找出最近的两类合并，继续下去，最后所有的样品全在一类。
将上述并类过程画成聚类图，便可以决定分多少类，每类各有什么样品。
系统聚类法的步骤为：①首先各样品自成一类，这样对n 组样品就相当于有n 类；②计算各类间的距离，将其中最近的两类进行合并；③计算新类与其余各类的距离，再将距离最近的两类合并；④重复上述的步骤，直到所有的样品都聚为一类时为止。
下面我们以最短距离法为例来说明系统聚类法的过程。
最短距离法的聚类步骤如下：① 规定样品之间的距离，计算样品的两两距离，距离矩阵记为()0S ，开始视每个样品分别为一类，这时显然应有pq d q p D =),(；② 选择距离矩阵()0S 中的最小元素，不失一般性，记其为),(q p D ，则将p G 与q G 合并为一新类，记为m G ，有q p m G G G ⋃=；③ 计算新类m G 与其他各类的距离，得到新的距离矩阵记为()1S ；④ 对()1S 重复开始进行第②步，…，直到所有样本成为一类为止。
值得注意的是在整个聚类的过程中，如果在某一步的距离矩阵中最小元素不止一个时，则可以将其同时合并。
● 系统聚类法是最常用的一种聚类方法，常用的系统聚类方法有最短距离法、最长距离法、中间距离法、类平均法、重心法、Ward 最小方差法、密度估计法、两阶段密度估计法、最大似然估计法、相似分析法和可变类平均法。
● 大多数的研究表明：最好综合特性的聚类方法为类平均法或Ward 最小方差法，而最差的则为最短距离法。
Ward 最小方差法倾向于寻找观察数相同的类。
类平均法偏向寻找等方差的类。
SAS聚类分析程序
SAS聚类分析程序：聚类分析过程命令Data pgm33b;Input x1-x3;cards;9.30 30.55 8.7（样品数据）1.85 20.66 12.75;Proc cluster standard method= single nonormnosquare ccc pseudo out=tree;Proc tree data=tree horizontal spaces=1; run;Data pgm33bInput x1-x4;cards;9.30 30.55 8.7（样品数据）1.85 20.66 12.75;Proc cluster standard method=complete nonormnosquare ccc pseudo out=tree;Proc tree data=tree horizontal spaces=1; run;刷黑该块过程命令程序，提交便计算出相应聚类结果。
语句解释: 聚类指定的方法是在“method=”后面填入一个相应的选择项，它们是：single（最短距离法），complete（最长距离法），average(类平均法), centroid（重心法），median（中位数法），ward（离差平方和法），flexible （可变类平均法），density（非参数概率密度估计法），eml（最大似然法），twostage（两阶段密度法）。
主成分分析程序：1. 主成分分析实验程序例：主成分分析过程命令data socecon;input x1-x6;cards;16369 3504887 66047 2397739 198.46 104395513379 566257 4744 456100 76.96 2026379707 397183 1303 887034 18.88 10594810572 414932 1753 751984 27.67 12826112284 876667 18269 1015669 60.09 3327009738 604935 5822 1307908 30.54 22279916970 778830 2438 630014 76.64 27220310006 617436 13543 866013 58.59 22279410217 636760 9967 996912 34.55 16102520946 1380781 16406 526527 150.15 42693711469 720416 7141 853778 43.41 15727414165 1504005 29413 1025363 149.17 56889912795 966188 11580 723278 45.13 16531912762 584696 13583 343107 65.31 16645412008 501780 4986 278310 15.04 86575 11208 981367 13364 1295189 79.8 337947 12719 716491 4448 408796 15.68 99949 ;proc princomp out=aaa prefix=z;var x1-x6; run;data a2;set aaa;proc print;var z1-z2 ;run;。
SAS 聚类
1、类平均法（METHOD=AVERAGE）测量两类每对观测间的平均距离，2、重心法（METHOD=CENTROID）重心法测量两个类的重心（均值）之间的（平方）欧氏距离。
3、最长距离法（METHOD=COMPLETE）计算两类观测间最远一对的距离，4、最短距离法（METHOD=SINGLE）计算两类观测间最近一对的距离，5、密度估计法（METHOD=DENSITY）密度估计法按非参数密度来定义两点间的距离。
如果两个点和是近邻（两点距离小于某指定常数或在距离最近的若干点内）则距离是两点密度估计的倒数的平均，否则距离为正无穷。
密度估计有最近邻估计（K=）、均匀核估计（R=）和Wong 混合法（HYBRID）。
6、Ward最小方差法（或称Ward离差平方和法，METHOD=WARD）Ward方法并类时总是使得并类导致的类内离差平方和增量最小。
其它的聚类方法还有EML法、可变类平均法（FLEXIBLE）、McQuitty相似分析法（MCQUITTY ）、中间距离法（MEDIAN）、两阶段密度估计法（TWOSTAGE）等。
Data d;Input name$ x;Datalines;li 56jin 58tong 59tie 61xi 62qian 65xin 89gai 95;Proc distance data=d method=euclid out=dist; var interval(x);id name;Run;Proc print data=dist;Id name;Run;proc cluster data=dist method=centroid;id name;var li--gai;run;proc tree h;id name;run;proc tree spaces=2 graphics horizontal h=n ; run;proc tree spaces=2 horizontal n=2 out=result; proc print data=result;run;proc freq data=result;table cluster;run;。
sas聚类分析(SAS)分解
个体与小类、小类与小类间“亲 疏程度”的度量方法
SPSS中提供了多种度量个体与小类、小类 与小类间“亲疏程度”的方法。与个体 间“亲疏程度”的测度方法类似，应首 先定义个体与小类、小类与小类的距离。 距离小的关系亲密，距离大的关系疏远。 这里的距离是在个体间距离的基础上定 义的，常见的距离有：
似程度通常可以用简单相关系数或者等 级相关系数等；一是个体间的差异程度 ，通常通过某种距离来测度。
1、定距型变量个体间距离的计算方式
欧式距离（Euclidean distance）
k
(xi yi )2 (73 66)2 (68 64)2 i1
平方欧式距离（Squared Euclidean distance ） 切比雪夫（Chebychev）距离
各变量间不应有较强的线性相关关系
学校
参加科研 人数
（人）
投入经费 （元）
立项课题 数（项）
样本的欧氏距离
元
万元
1
410
4380000
19
（1，2） 265000
81.623
2
336
1730000
21
（1，2） 218000
193.7
3
490
220000
8
（1，2）
47000
254.897
层次聚类
1 层次聚类的两种类型和两种方式 层次聚类又称系统聚类，简单地讲是指聚类过程
（1）间隔尺度。变量用连续的量来表示，如“ 各种奖金”、“各种津贴”等。
（2）有序尺度。指标用有序的等级来表示，如 文化程度分为文盲、小学、中学、中学以上 等有次序关系，但没有数量表示。
（3）名义尺度。指标用一些类来表示，这些类 之间没有等级关系也没有数量关系，如表中 的性别和职业都是名义尺度。
使用SAS进行数据分析的基础知识
使用SAS进行数据分析的基础知识一、SAS数据分析简介SAS（Statistical Analysis System）是一套全面的数据分析软件工具，它具备强大的数据处理和统计分析能力。
它适用于各种领域的数据分析，包括市场调研、金融分析、医疗研究等。
二、数据准备在进行SAS数据分析之前，首先要进行数据准备。
这包括数据的收集、整理和清洗。
收集数据可以通过调查问卷、实地观察、数据库查询等方式。
整理数据即将数据格式统一，包括去除重复数据、统一变量命名等。
清洗数据则是去除异常值、缺失值处理等。
三、SAS基础语法1. 数据集（Data set）的创建和导入SAS中的数据以数据集的形式存在，可以使用DATA步骤创建数据集，也可以从外部文件导入数据集。
导入数据可使用INFILE 语句指定文件位置，并使用INPUT语句将数据导入到数据集中。
2. 数据操作和处理SAS提供了多种数据操作和处理函数，如排序、合并、拆分等。
常用的函数有SUM、MEAN、COUNT、MAX、MIN等，它们可以对数据集中的变量进行统计和计算。
3. 数据可视化SAS提供了多种可视化方式，用于更直观地展示数据。
可以使用PROC SGPLOT语句进行绘图，如折线图、散点图、柱状图等。
还可以使用PROC TABULATE语句生成数据报表。
四、统计分析SAS强大的统计分析功能是其独特的优势之一。
以下为几种常用的统计分析方法：1. 描述统计分析描述统计分析用于对数据进行概括和描述。
可以使用PROC MEANS进行均值、中位数、标准差等统计指标的计算，使用PROC FREQ进行频数分析。
2. t检验t检验用于比较两组样本均值的差异是否显著。
可以使用PROC TTEST进行t检验分析，根据t值和显著性水平判断差异是否显著。
3. 方差分析方差分析用于比较两个或多个样本均值的差异是否显著。
可以使用PROC ANOVA进行方差分析，根据F值和显著性水平判断差异是否显著。
SPSS聚类分析详解
指标 地区（样品） 1
2
3
456
性能
9 1 10
928
颜色
827
946
式样
728
357
用分类法对6个样品进行分类，以估计哪些地区最有可能经销 这类新产品？
按公式计算两两样品间的相似系数，得相似矩阵
Q (Coij) s(qij)
1
2
3
4
5
6
1 1
2 0.933 1
Q=
3
0.994
2）形成一个由小到大的分析系统。 3）把整个分类系统画成一张分类图
二、聚类统计量
首先定义一些分类统计指标 —— 刻画样或指标之间 的相似程度（这些统计指标称为聚类统计量）
在市场研究中，样品 —— 用作分类的事物
指标 —— 用来作为分类依据的变量。（如： 年龄、收入、销售量）
（一）相似系数（夹角余弦）
0.47
X4
0.93
X2
0.68
X7
X5
-0.94
0.49
X8
主要城市日照时数
注：连续变量
SPSS提供不同类间距 离的测量方法
1、组间连接法 2、组内连接法 3、最近距离法 4、最远距离法 5、重心法 6、中位数法 7、Ward最小偏差平 方和法
观测量概述表
聚类步骤，与图结合看！
4、5
输入格式
55列为城市
15位
输出F及t 统计量
平均法 重心法 最小距离法
输出结果：
新类中的观测值数
观测值之间距离的均方根
类间距离除以 观测值间距离 均方根得来
类数
指出被合并的类
F、t**2峰值(起伏)越大 说明分类显著
spss聚类分析PPT课件
G7
G3
G4
G8
G7
0
G3
3
0
G4
5
2
0
G8
7
4
2
0
30
10/16/2024
（3）在D（1）中最小值是D34＝D48＝2，由于G4与G3合并， 又与G8合并，因此G3、G4、G8合并成一个新类G9，其与其 它类的距离D（2）
G7
G9
G7
0
G9
3
0
31
10/16/2024
（4）最后将G7和G9合并成G10，这时所有的六个样品聚为一 类，其过程终止。 上述聚类的可视化过程如下:
1
2
3
4
5
1
0
8.062 17.804 26.907 30.414
2
8.062 0
25.456 34.655 38.21
3
17.804 25.456 0
9.22 12.806
4
26.907 34.655 9.22 0
3.606
5
30.414 38.21 12.806 3.606 0
26
10/16/2024
系统聚类过程是：假设总共有n个样品（或变量）
第一步:将每个样品（或变量）独自聚成一类，共有 n类；
第二步:根据所确定的样品（或变量）“距离”公式， 把距离较近的两个样品（或变量）聚合为一类，其 它的样品（或变量）仍各自聚为一类，共聚成n 1 类；
第三步:将“距离”最近的两个类进一步聚成一类， 共聚成n 2类；……，以上步骤一直进行下去，最后17 将所有的样品（或变量）全聚成一类。
（1）选择样品距离公式，绝对距离最简单,形成D（0）
sas聚类稳健标准误
SAS聚类稳健标准误技术报告一、引言聚类稳健标准误是一种在统计分析中常用的技术，主要用于处理数据中的聚类问题。
当数据存在聚类效应时，传统的标准误可能会低估模型的异方差性，从而影响模型估计的准确性。
为了解决这个问题，我们可以使用聚类稳健标准误。
本报告将介绍SAS中实现聚类稳健标准误的几种方法。
二、聚类稳健标准误的原理聚类稳健标准误是通过在模型残差中考虑聚类效应来修正标准误的方法。
它假设数据中的每个聚类都有自己的误差项，而这些误差项是相关的。
通过在模型中加入聚类效应，我们可以更好地估计模型的参数和标准误。
三、SAS中实现聚类稳健标准误的方法1.CLUSTER 选项在PROC REG中，可以使用CLUSTER 选项来指定聚类变量。
这个选项告诉SAS在计算标准误时考虑聚类效应。
例如：PROC REG DATA=mydata CLUSTER(id);上述代码中，id 是聚类变量。
2.VIF 选项在PROC REG中，可以使用VIF 选项来计算方差膨胀因子（Variance Inflation Factor），它也可以用于评估聚类效应。
例如：PROC REG DATA=mydata VIF;上述代码中，VIF 选项会计算出方差膨胀因子，这个因子可以用来评估模型是否存在聚类效应。
如果VIF 值大于1，则说明存在聚类效应。
3.使用PROCCLUSTER 过程PROCCLUSTER 过程是专门用于处理聚类数据的过程。
它可以用来计算各种聚类统计量，包括聚类稳健标准误。
例如：PROC CLUSTER DATA=mydata OUTSTAT=stats; VAR var1 var2 var3; CLASS id; RATE; RUN;上述代码中，CLASS 语句指定了聚类变量id，RATE 语句指定了要计算的聚类统计量，包括聚类稳健标准误。
第九章SPSS的聚类分析PPT课件
中心位置变化较小.其中最大的变化率小于2%.
29
K-means快速聚类
(三)基本操作步骤
A.菜单选项:analyze->classify->k means cluster B.选定参加快速聚类分析的变量到variables框 C.确定快速聚类的类数(number of clusters).类数应小
第九章 SPSS的聚类分析
1
聚类分析概述
• 概念：
– 聚类分析是统计学中研究“物以类聚”的一种方法,属多元统计分析方法. – 例如：细分市场、消费行为划分
• 聚类分析是建立一种分类，是将一批样本(或变量)按照在性质上的“亲疏” 程度,在没有先验知识的情况下自动进行分类的方法.其中:类内个体具有 较高的相似性,类间的差异性较大.
•(张三,李四) 2: a=0 b=0 c=1 d=2 J(x,y)=1/1=1 (不相同)
11
聚类分析概述
• 品质型个体间的距离
– Jaccard系数举例:根据临床表现研究病人是否有类似的病
•姓名 性别 发烧 咳嗽 检查1 检查2 检查3 检查4
•张三 男 1 0 1 0 0
0
•李四 女 1 0 1 0 1
•姓名 授课方式 上机时间 选某门课程
•张三
1
1
1
•李四
1
1
0
•王五
0
0
1
•（张三，李四）：a=2 b=1 c=0 d=0 d(x,y)=1/(1+2)=1/3
•（张三，王五）：a=1 b=2 c=0 d=0 d(x,y)=2/(1+2)=2/3
如何用SAS进行统计分析
如何用SAS进行统计分析SAS（统计分析系统）是一种用于数据分析和统计建模的软件工具。
它提供了一系列功能和程序，用于数据处理、统计分析、预测建模、图形展示和报告生成等。
本文将介绍如何使用SAS进行统计分析，涵盖数据导入、数据清洗、描述性统计分析、假设检验、回归分析和聚类分析等内容。
1. 数据导入和数据清洗在使用SAS进行统计分析之前，你需要将待分析的数据导入到SAS软件中。
SAS支持多种数据格式，包括CSV、Excel、Access等。
你可以使用SAS提供的PROC IMPORT过程将数据导入到SAS的数据集中。
导入数据后，你需要对数据进行清洗。
数据清洗的目的是去除数据中的错误、缺失或异常值，以确保数据的质量。
你可以使用SAS的数据步骤（DATA STEP）来处理数据，例如删除缺失值、填补缺失值、去除异常值等。
2. 描述性统计分析描述性统计分析是对数据进行总结和描述的过程。
它包括计算数据的中心趋势（均值、中位数、众数）、数据的离散程度（标准差、方差、极差）、数据的分布形态（偏度、峰度）等。
在SAS中，你可以使用PROC MEANS过程进行描述性统计分析。
该过程可以计算多个变量的均值、标准差、最小值、最大值、中位数等统计指标。
此外，你还可以使用PROC UNIVARIATE过程计算数据的偏度、峰度等统计值，并绘制直方图和箱线图来展示数据的分布情况。
3. 假设检验假设检验是对样本数据进行推断性统计分析的一种方法。
它用于判断观察到的样本差异是否显著，从而对总体参数进行推断。
在SAS中，你可以使用PROC TTEST过程进行双样本t检验、单样本t检验和相关样本t检验等。
此外，PROC ANOVA过程可以用于方差分析，PROC FREQ过程可以用于卡方检验。
4. 回归分析回归分析是研究因变量与自变量之间关系的一种统计分析方法。
它用于预测和解释因变量的变化，并评估自变量对因变量的影响程度。
在SAS中，你可以使用PROC REG过程进行简单线性回归分析和多元线性回归分析。
SAS在生物医学中的应用
SAS在生物医学中的应用引言SAS（Statistical Analysis System）是一种广泛应用于统计分析和数据管理的软件。
在生物医学领域，SAS的使用越来越广泛，因为它具有强大的数据分析和统计建模功能，可以帮助研究人员从大规模数据集中提取有意义的信息。
本文将介绍SAS在生物医学中的应用，包括数据预处理、统计分析和机器学习等方面。
数据预处理在生物医学研究中，数据预处理是非常重要的一步。
SAS提供了一系列强大的数据处理功能，可以帮助研究人员清洗、整合和转换原始数据。
1.数据清洗：SAS可以帮助研究人员检测和处理数据中的异常值、缺失值和重复值。
通过使用SAS的数据处理函数和过滤器，研究人员可以轻松地识别并清除这些不完整的数据。
2.数据整合：在生物医学研究中，研究人员通常需要整合来自不同源头的数据（如基因表达数据、临床数据等）。
SAS提供了强大的数据合并和连接功能，可以帮助研究人员将不同数据源的数据整合在一起，为后续的统计分析和建模提供便利。
3.数据转换：SAS提供了丰富的数据转换函数，可以帮助研究人员对原始数据进行转换和标准化。
例如，研究人员可以使用SAS的函数对基因表达数据进行log转换，以满足统计模型的假设。
统计分析SAS在统计分析方面有着强大的功能和灵活性，可以帮助研究人员进行各种统计假设检验和模型拟合。
1.描述性统计：SAS可以计算各种描述性统计量，如平均值、标准差、中位数等。
这些统计量可以帮助研究人员了解数据的分布特征，为后续的进一步分析提供参考。
2.统计假设检验：SAS提供了一系列假设检验的函数和过程，可以帮助研究人员对不同组别的数据进行比较。
例如，研究人员可以使用SAS的t检验函数来比较两组样本的平均值是否存在显著差异。
3.方差分析：SAS也可以进行方差分析，帮助研究人员比较多个组别之间的差异。
方差分析可以用于不同药物治疗组的比较、基因表达数据的差异分析等。
4.类别数据分析：对于类别数据，SAS提供了一系列的分析方法，如卡方检验、逻辑回归等。
SPSS聚类的分析详解
二、聚类统计量
首先定义一些分类统计指标 —— 刻画样或指标之 间的相似程度（这些统计指标称为聚类统计量） 在市场研究中，样品 —— 用作分类的事物 指标 —— 用来作为分类依据的变量。 （如：年龄、收入、销售量） （一）相似系数（夹角余弦） 一般式：假定每个样品包含有P项指标，若有几个样品 的调查数据
3、步骤：1）首先给出度量“相似”或“关系密切”的 统计指标
指标：（1）统计指标是相似系数。 根据相似性归为一类，否则为另一类。 （2）统计指标是样品（空间的点）之间的距离 将距离近的点归成一类，否则为另一类。 （3）相关系数
（4）关联系数 2）形成一个由小到大的分析系统。
3）把整个分类系统画成一张分类图
CLUSTER过程 开始每个观测值自成一类，然后求两两之间的距离， 将距离最近的两个观测值合成一类。这个过程一直 进行下去，每次减少一类，直到合成一类为止。 聚类方法有11种，可根据问题的性质选用，它们的 区别在于怎样计算两类之间的距离。
METHOD=指定方法
AVERAGE（平均法）、CENTROID（重心法）、 COMPLETE（最大距离法）、DENSITY（密度 法）、MEDIAM（中位数法）等
1
按就近原则将每个观测量选入一个类中，然后计算各个类的中 心位置，即均值，作为新的聚心。 3、使用计算出来的新聚心重新进行分类，分类完毕后继续计 算各类的中心位置，作为新的聚心，如此反复操作，直到两次 迭代计算的聚心之间距离的最大改变量小于初始聚类心间最小 距离的倍数时，或者到达迭代次数的上限时，停止迭代。
观测量概述表
聚类步骤，与图结合看！
4、5
聚类方法有系统聚类和逐步聚类，输入数据集可以是普 通数据集、相关矩阵（CORR过程产生）或协方差矩阵 （FACTOR等过程产生）。SAS提供的聚类过程有：
SAS实验_因子分析_聚类分析
实验过程： 1.搜集数据
通过搜索相关数据库，得到 2008 年我国各地区农村人均生活消费支出的相关数据，共包括 我国 31 个省市自治区，设计 8 个方面的人均消费支出。
2.数据准备和预处理
首先建立数据集，我将数据存在 D:\mydata.txt 中。此处编写 SAS 程序来实现 INPUT 数据。
Step2:加入 cluster 节点，联结，设置相关属性。
Step3：运行 运行结果如下，这个结果本来我看起来十分诡异，31 个地区，分了 31 类，看起来没有起到 任何的聚类效果。 首先，Factor1 和 Factor2 的贡献值都为 0：
其次，画出来的散点图和最终的 stat 结果也如此显示：
注：右上角的制表时间是由于时间跳过程序修改造成的，后同。
3.描述性统计分析
①单变量分析： 首先要对数据的基本情况有一个初步的了解， 因此先进行单变量分析。 再次我们利用 means 过程计算一些描述性统计量，编写程序如下：
解释：proc 语句指定运行 means 过程，并指出分析的数据集为 expend，maxdec=2 表示计算 的描述统计量保留两位小数， 然后指定要计算的统计量为： 均值、 标准差、 最大值、 最小值、 极差、变异系数、偏度。之后指定要分析的变为量 x, x1-x8。运行结果如下：
解决思路：
为了研究上述问题， 我们应当以近年的各地区农村人均生活消费支出相关数据为数据源， 通 过描述性统计分析对整体数据进行初步了解； 并在因子分析的基础上进行聚类分析， 对各地 区依据消费水平的高低进行分类； 还可以参数检验判断不同地区的农民生活水平是否存在差 异；若引入时序数据，则可进一步进行关联分析，预测某些地区未来的消费结构变化。本人 会在数据分析的基础上，结合实际进行分析，解释数据结果的实际意义。由于精力有限，此 次实验本人计划主要进行三项数据分析： 1. 描述性分析 2. 基于主成分法的因子分析 3. 在因子分析的基础上，用 Cluster 和 Tree 过程进行聚类分析 注：部分内容为参考教材自学，理解可能不甚透彻，若有错误恳请老师指出。
sas与聚类分析
1聚类分析介绍1.1基本概念聚类就是一种寻找数据之间一种内在结构的技术。
聚类把全体数据实例组织成一些相似组，而这些相似组被称作聚类。
处于相同聚类中的数据实例彼此相同，处于不同聚类中的实例彼此不同。
聚类技术通常又被称为无监督学习，因为与监督学习不同，在聚类中那些表示数据类别的分类或者分组信息是没有的。
通过上述表述，我们可以把聚类定义为将数据集中在某些方面具有相似性的数据成员进行分类组织的过程。
因此，聚类就是一些数据实例的集合，这个集合中的元素彼此相似，但是它们都与其他聚类中的元素不同。
在聚类的相关文献中，一个数据实例有时又被称为对象，因为现实世界中的一个对象可以用数据实例来描述。
同时，它有时也被称作数据点（Data Point），因为我们可以用维空间的一个点来表示数据实例，其中表示数据的属性个数。
下图显示了一个二维数据集聚类过程，从该图中可以清楚地看到数据聚类过程。
虽然通过目测可以十分清晰地发现隐藏在二维或者三维的数据集中的聚类，但是随着数据集维数的不断增加，就很难通过目测来观察甚至是不可能。
1.2算法概述目前在存在大量的聚类算法，算法的选择取决于数据的类型、聚类的目的和具体应用。
大体上，主要的聚类算法分为几大类。
聚类算法的目的是将数据对象自动的归入到相应的有意义的聚类中。
追求较高的类内相似度和较低的类间相似度是聚类算法的指导原则。
一个聚类算法的优劣可以从以下几个方面来衡量：(1)可伸缩性：好的聚类算法可以处理包含大到几百万个对象的数据集；(2)处理不同类型属性的能力：许多算法是针对基于区间的数值属性而设计的，但是有些应用需要针对其它数据类型（如符号类型、二值类型等）进行处理；(3)发现任意形状的聚类：一个聚类可能是任意形状的，聚类算法不能局限于规则形状的聚类；(4)输入参数的最小化：要求用户输入重要的参数不仅加重了用户的负担，也使聚类的质量难以控制；(5)对输入顺序的不敏感：不能因为有不同的数据提交顺序而使聚类的结果不同；(6)高维性：一个数据集可能包含若干维或属性，一个好的聚类算法不能仅局限于处理二维或三维数据，而需要在高维空间中发现有意义的聚类；(7)基于约束的聚类：在实际应用中要考虑很多约束条件，设计能够满足特定约束条件且具有较好聚类质量的算法也是一项重要的任务；(8)可解释性：聚类的结果应该是可理解的、可解释的，以及可用的。
基于SAS的泻心汤类方模糊聚类分析
用 自编 Ｓ Ｓ Ｖ ｒ ． ３ Ｎ序对泻心汤五个类方的中药组分进行分类 。结果 ： ｌ 味中药分成 ４ 时的结果为 ：半夏 、 Ａ （ ｅ ９ １） 当 Ｏ 类 ｛ 生姜 ） ｛ ； 人参 、 甘草、 大枣 ｝ ｛ ； 附子 、 干姜 ） ｛ ；黄连 、 大黄 、 黄芩 ）与传统中医药理论 吻合 。 ，
ｃｕ ｔｒ ； ｏ ｎｅ＝０ ／＊计 录循环次数 ， 初始值定 义为 ０ ＊／
ｄ ｎ ｉ （ｌｇ １ ； ｏ ｕ ｔｌ ｆａ ＝ ）
ｄ ｏ ｉ＝ １ ｔ ｏ Ｎ：
方法计算模 糊等价矩阵 。具体算 法为 ： 。 Ｒ 一Ｒ＊Ｒ—Ｒ （ｉ Ｖ ｒｋ
＾ ）Ｒ 一Ｒ Ｒ ， ， ＊ 以此 类 推 直 至 出现 Ｒ” ＊ ， 得 一Ｒ Ｒ 。所
１ 资 料 与 方 法
√ 。 荟
Ｒ
（ １ ）
由上述计算法则可 知 ： 理论 上模糊 相似 矩 阵的对 角线 应
为 １ 一１ ， 以对 角线两侧 对称（ —ｒ ） （ ）且 Ｊ。 在此 ， 上 述量 化 处 理 表 中的 数值 以矩 阵 的 形 式 输 入 将
Ｓ ＡＳ软 件 ： 通 迅 作 者 ： 鲲 王
相 对 的 属 于 某 一 类 。很 显 然 ， 种 划 分 是 相 对 的［ 。 目前 这 ６ ］
用 ＸＩ ￣Ｘ１ ０代表 １ 中药 ， 、 为第 ｉ 两种 中药 的 Ｏ味 、
第 尼个量化指标 ， 则可 得到药 物间 的夹 角余 弦 及 模糊等 价
矩阵 Ｒ：
∑ｚ ＊・ ｚ
ｎ 一 — ｋ＝＝ ＝＝ ， ＿＝ ＝ ＝ｌ
ｅ ｄ； ｎ ｐ ｉ ｔＲｎ： ｒ ｎ
该算法 由以下程序实现 ：
Ｒｎ （ Ｎ，） ＊ 定义模糊等价矩阵 Ｒ ＊／ ＝Ｊ Ｎ， Ｏ ；／ ｎ
SAS学习系列35.聚类分析
35.聚类分析（一）概述聚类分析，相当于“物以类聚”，用于对事物的类别面貌尚不清楚，甚至在事前连总共有几类都不能确定的情况下对数据进行分类。
而判别分析，必须事先知道各种判别的类型和数目，并且要有一批来自各判别类型的样本，才能建立判别函数来对未知属性的样本进行判别和归类。
聚类分析是把分类对象按一定规则分成组或类，这些组或类不是事先给定的而是根据数据特征而定的。
在同类的对象在某种意义上倾向于彼此相似，而在不同类里的这些对象倾向于不相似。
根据这种相似性的不同定义，聚类分析也有不同的方法。
聚类分析分为：对样品的聚类，对变量的聚类。
样品聚类：其统计指标是类与类之间距离，把每一个样品看成空间中的一个点，用某种原则规定类与类之间的距离，将距离近的点聚合成一类，距离远的点聚合成另一类。
变量聚类：其统计指标是相似系数，将比较相似的变量归为一类，而把不怎么相似的变量归为另一类，用它可以把变量的亲疏尖系直观地表示出来。
二）原理一、距离和相似系数设有n组样品，每组样品有p个变量的数据如下:例如，Xj到Xj的闵科夫斯基距离定义为：IJ p 9q%=区I Xk- Xjkf ,<k A丿q=2时为欧几里得距离；还有马氏距离：dij=(Xj・XjFS」(Xj-Xj)其中，Xj=(Xii,…,Xjp),S」为n个样品的px p的协方差矩阵的逆矩阵。
注：马氏距离考虑了观测变量之间的相矢性和变异性(不再受各指标量纲的影响)。
距离选择的基本原则：(1) 要考虑所选择的距离公式在实际应用中有明确的意义。
如欧氏距离就有非常明确的空间距离概念。
马氏距离有消除量纲影响的作(2) 要综合考虑对样本观测数据的预处理和将要采用的聚类分析方法。
如在进行聚类分析之前已经对变量作了标准化处理，则通常就可米用欧氏距离。
(3) 应根据研究对象的特点不同做出具体分折。
实际中，聚类分析前不妨试探性地多选择几个距离公式分别进行聚类，然后对聚类分析的结果 进行对比分析，以确定最合适的距离测度方法。
sas聚类分析(SAS)分析
层次聚类
1 层次聚类的两种类型和两种方式 层次聚类又称系统聚类，简单地讲是指聚类过程 是按照一定层次进行的。层次聚类有两种类型，分 别是Q型聚类和R型聚类；层次聚类的聚类方式又 有两种，分别是凝聚方式聚类和分解方式聚类。 Q型聚类：对样本进行聚类，使具有相似特征的样 本聚集在一起，差异性大的样本分离开来。 R型聚类：对变量进行聚类，使具有相似性的变量 聚集在一起，差异性大的变量分离开来，可在相 似变量中选择少数具有代表性的变量参与其他分 析，实现减少变量个数，达到变量降维的目的。
相似性度量
从一组复杂数据产生一个相当简单的类结构，必 然要求进行“相关性”或“相似性“度量。在 相似性度量的选择中，常常包含许多主观上的 考虑，但是最重要的考虑是指标（包括离散的 、连续的和二态的）性质或观测的尺度（名义 的、次序的、间隔的和比率的）以及有关的知 识。 当对样品进行聚类时，“靠近”往往由某种距离 来刻画。另一方面，当对指标聚类时，根据相 关系数或某种关联性度量来聚类。
1、定距型变量个体间距离的计算方式
欧式距离（Euclidean distance）
2 2 2 (x y ) (73 66) (68 64) i i i 1
k
平方欧式距离（Squared Euclidean distance ） 切比雪夫（Chebychev）距离
max xi yi max( 73 66 , 68 64)
k
Phi方（Phi-Square measure）距离
[ xi E ( xi )]2 k [ yi E ( yi )]2 E ( xi ) E ( yi ) i 1 i 1 phisq( x, y) n
k
3、二值（Binary）变量个体间距离的计算方式 简单匹配系数（Simple Matching） 雅科比系数（Jaccard） 简单匹配系数表
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验项目二聚类分析实验目的：通过聚类分析的实验,熟悉聚类分析问题的提出、解决问题的思路、方法和技能，会调用SAS软件聚类分析有关过程命令，根据计算机计算的结果，分析和解决聚类分析问题。
实验原理：解决聚类分析问题的思路、理论和方法。
实验设备：计算机与SAS软件。
实验步骤：调用聚类分析过程命令输入数据得到聚类过程表和聚类图,距离选用欧氏距离,方法选用最短距离法。
实验数据：实验数据：我国西部环境保护的数据一、问题的提出西部大开发是我国在新世纪提出的一项国家发展战略。
基于西部地区特殊的地理位置和生态环境状况，国家在提出西部大开发之初就明确指出，西部开发绝不能以牺牲环境为代价，西部地区生态环境极其脆弱，一经破坏就难以恢复，所以实施西部大开发，环境保护是关键，必须建设一个“山川秀丽的西部”。
近几年国家在保护西部地区的环境上也花了大力气，并取得了良好的效果，但并没有从根本上解决在发展西部过程中环境保护的问题。
西部环境保护现状、特点怎样？本实验就这一问题用聚类分析进行探索并提出一些看法和建议。
指标选取考虑的因素：（1）指标的选择要能尽量反映西部现时的生态环境状况；（2）数据尽量从统计年鉴等规范、权威的刊物中获取。
下面十三个指标和数据符合以上要求。
表1 西部环境保护的原始数据X 1X 2X3X4X5X6X7X8X9X10X11X12X13内蒙古12.14 67.71 78.10 4.23 2.09 1.0446 106 423 3319 7.56 26709 28.5 19.1 广西25.34 4.51 83.20 16.57 1.14 0.553 312 258 3136 6.47 25192.2 46.3 1020.5 重庆7.79 63.23 82.40 43.76 0.60 0.4198 200 245 1793 9.66 26312.6 -38.6 403.5 四川20.37 21.09 70.10 20.71 0.64 0.5223 346 512 5340 13.0 35397.8 0 524.8 贵州14.75 43.05 62.70 5.73 0.96 0.6231 158 263 1930 2.63 16040 -6.1 552 云南24.58 37.52 74.30 9.78 0.78 0.731 225 386 2889 7.06 34661.2 15.3 650 西藏 5.84 9.39 10.00 74.27 0.06 0.0684 28 22 180 33.4 798 7.7 360.2 陕西24.15 67.79 79.90 10.02 0.78 0.6581 341 322 4758 2.89 26589.8 -50.1 103.4 甘肃 4.33 67.01 80.80 7.42 1.08 0.4994 168 248 2444 17.7 20737.1 -28.7 46.7 青海0.35 25.29 46.40 5.18 1.62 0.7036 21 97 683 28.6 3858.2 -7.4 79.7 宁夏 1.54 55.83 62.90 7.96 2.33 0.7655 67 43 629 4.43 29121.8 -2.2 18.3 新疆0.97 64.76 80.30 7.14 1.25 0.4179 85 208 2096 12.8 32008.7 20.4 58.7X1-森林覆盖率（％）；X2-水土流失率(%)；X3-工业废水排放达标率(%)；X4-人均工业废水排放量(万吨/万人)；X5-人均工业废气排放量(亿标立方米/万人)；X6-人均工业固体废物产生量 (万吨/万人)；X7-各地区工业污染治理汇总工业企业数(个)；X8-环保系统机构总数(个)；X9-环保系统人员总数(人)；X10-自然保护区面积占辖区面积比率（%）；X11-污染治理项目本年完成投资（万元）；X12-各地径流深与常年比较（±％）；X13-各地径流深(mm)。
原始数据来自《2002年中国统计年鉴》《2001年中国水资源公报》和《2002中国可持续发展战略报告》。
实验结果、实验分析、结论（有关表图要有序号、中文名、表的上下线为粗线、表的内线为细线、表的左右边不封口、表图不能跨页、表图旁不能留空块；表的序号、中文名在表的上方；图的序号、中文名在图的正下方；引用结论要注明参考文献）：1.给出最短距离法得到的聚类过程表2；表2：最短距离法聚类过程（Cluster History）TMin iNCL --Clusters Joined-- FREQ SPRSQ RSQ ERSQ CCC PSF PST2 Dist e11 OB9 OB12 2 0.0186 .981 . . 5.3 . 2.305210 OB3 CL11 3 0.0358 .946 . . 3.9 1.9 2.52369 OB5 OB6 2 0.0236 .922 . . 4.4 . 2.60038 OB4 CL9 3 0.0465 .875 . . 4.0 2.0 2.61077 OB2 CL8 4 0.0434 .832 . . 4.1 1.2 2.7746 CL7 CL10 7 0.1510 .681 . . 2.6 4.5 2.99255 CL6 OB11 8 0.1041 .577 . . 2.4 2.0 3.05874 CL5 OB8 9 0.0697 .507 . . 2.7 1.2 3.54533 OB1 CL4 10 0.0758 .432 . . 3.4 1.2 3.65592 CL3 OB10 11 0.1319 .300 .431 -1.4 4.3 2.1 3.87911 CL2 OB7 12 0.2996 .000 .000 0.00 . 4.3 5.42312.给出最短距离法聚类图1；图1：最短距离法聚类图3.用有关统计量给出最短距离法分类结果；最短距离法得到的聚类过程表2中，PSF出现峰值4.1所对应的分类数7较合适、PST2出现峰值4.5的前一行所对应的分类数7较合适，故分为7类。
在图1中，取阈值T=2.8，得样品分为七类:第一类：内蒙古；第二类：广西、四川、贵州、云南；第三类：重庆、甘肃、新疆；第四类：宁夏；第五类：陕西；第六类：青海；第七类：西藏。
4.用分类结果和原始数据给出西部最好一类环境保护现状的基本结果。
结合分类结果、原始数据找出西部环境保护的基本情况：表3 七类样品的均值数据1x2x3x4x5x6x7x8x9x10x11x12x13x第一类 第二类 第三类 第四类 第五类 第六类 第七类12.14 21.26 4.3633 1.54 24.15 0.35 5.8467.71 26.5425 65 55.83 67.79 25.29 9.3978.1 72.575 81.167 62.9 79.9 46.4 104.23 13.1975 19.44 7.96 10.025.18 74.272.09 0.88 0.9767 2.33 0.78 1.62 0.061.0446 0.60735 0.4457 0.7655 0.6581 0.7036 0.0684106 260.25 151 67 341 21 28423 354.75 233.666643 322 97 223319 3324 2111 629 4758 683 1807.56 7.29 13.3867 4.43 2.89 28.6 33.426709 27823 26353 29121.8 26589.8 3858.2 79828.5 13.875 -15.633 -2.2 -50.1 -7.4 7.719.1 686.825 169.6333 18.3 103.4 79.7 360.2从表3的数据得出：西部环境保护最好的一类是第七类（即西藏）。
与西部地区的其他省份相比，西藏的水土流失率X 2最小(与其他地区相差2.69-7.2倍)，人均工业废气排放量X 5(与最大废气排放量相差38.8倍）、人均工业固体废物产生量X 6均为最小，自然保护区面积占辖区面积比率X 10最大，各地径流深与常年比较X 12和各地径流深X 13均位于居中位置，说明西藏在控制人为破坏环境的方面做得很好，可是却在工业废水排放达标率X 3做得不够好(只有10%)，人均工业废水排放量X 4却达到最大值74.27万吨/万人。
但由于西藏的地势决定森林覆盖面积不大，本身的环境保护情况基于良好，所以在工业污染治理汇总工业企业数X 7却只有28个(居于倒数第二)，环保系统机构总数X 8和环保系统人员总数X 9均为倒数第一(分别为22个/180人)，故西藏需要增加工业污染治理汇总工业企业、环保系统机构和环保系统人员；在污染治理项目本年完成投资X 11方面是最差的，只有798万元（与其他地区相差4.83-36.49倍），说明西藏在投资污染治理方面还需加强。
实验程序：Data pgm33b; Input x1-x13; cards ;12.14 67.71 78.10 4.23 2.09 1.0446 106 423 3319 7.56 26709 28.5 19.1 25.34 4.51 83.20 16.57 1.14 0.553 312 258 3136 6.47 25192.2 46.3 1020.5 7.79 63.23 82.40 43.76 0.60 0.4198 200 245 1793 9.66 26312.6 -38.6 403.5 20.37 21.09 70.10 20.71 0.64 0.5223 346 512 5340 13.0 35397.8 0 524.8 14.75 43.05 62.70 5.73 0.96 0.6231 158 263 1930 2.63 16040 -6.1 552 24.58 37.52 74.30 9.78 0.78 0.731 225 386 2889 7.06 34661.2 15.3 650 5.84 9.39 10.00 74.27 0.06 0.0684 28 22 180 33.4 7987.7 360.224.15 67.79 79.90 10.02 0.78 0.6581 341 322 4758 2.89 26589.8 -50.1 103.4 4.33 67.01 80.80 7.42 1.08 0.4994 168 248 2444 17.7 20737.1 -28.7 46.7 0.35 25.29 46.40 5.18 1.62 0.7036 21 97 683 28.6 3858.2 -7.4 79.71.54 55.83 62.90 7.96 2.33 0.7655 67 43 629 4.43 29121.8 -2.2 18.3 0.97 64.76 80.30 7.14 1.25 0.4179 85 208 2096 12.8 32008.7 20.4 58.7;Proc cluster standard method=single nonormnosquare ccc pseudo out=tree;Proc tree data=tree horizontal spaces=1; run;Data pgm33b;Input x1-x13;cards;12.14 67.71 78.10 4.23 2.09 1.0446 106 423 3319 7.56 26709 28.5 19.1;Proc corr cov;run;Data pgm33b;Input x1-x13;cards;25.34 4.51 83.20 16.57 1.14 0.553 312 258 3136 6.47 25192.2 46.3 1020.5 20.37 21.09 70.10 20.71 0.64 0.5223 346 512 5340 13.0 35397.8 0 524.8 14.75 43.05 62.70 5.73 0.96 0.6231 158 263 1930 2.63 16040 -6.1 55224.58 37.52 74.30 9.78 0.78 0.731 225 386 2889 7.06 34661.2 15.3 650;Proc corr cov;run;Data pgm33b;Input x1-x13;cards;7.79 63.23 82.40 43.76 0.60 0.4198 200 245 1793 9.66 26312.6 -38.6 403.5 4.33 67.01 80.80 7.42 1.08 0.4994 168 248 2444 17.7 20737.1 -28.7 46.7 0.97 64.76 80.30 7.14 1.25 0.4179 85 208 2096 12.8 32008.7 20.4 58.7 ;Proc corr cov;run;Data pgm33b;Input x1-x13;cards;1.54 55.83 62.90 7.96 2.33 0.7655 67 43 629 4.43 29121.8 -2.2 18.3 ;Proc corr cov;run;Data pgm33b;Input x1-x13;cards;24.15 67.79 79.90 10.02 0.78 0.6581 341 322 4758 2.89 26589.8 -50.1 103.4 ;Proc corr cov;run;Data pgm33b;Input x1-x13;cards;0.35 25.29 46.40 5.18 1.62 0.7036 21 97 683 28.6 3858.2 -7.4 79.7 ;Proc corr cov;run;Data pgm33b;Input x1-x13;cards;5.84 9.39 10.00 74.27 0.06 0.0684 28 22 180 33.4 798 7.7 360.2;Proc corr cov;run;说明:不可改变实验报告项目的具体要求与排版字号，有何不妥之处，欢迎提出意见。