SAS实验_因子分析_聚类分析
SAS 聚类分析方法

SAS 聚类分析(描述算法)系统聚类法系统聚类法(Hierarchical clustering method )是目前使用最多的一种方法。
其基本思想是首先将n 个样品看成n 类(即一类包括一个样品),然后规定样品之间的距离和类与类之间的距离。
将距离最近的两类合并为一个新类,在计算新类和其他类之间的距离,再从中找出最近的两类合并,继续下去,最后所有的样品全在一类。
将上述并类过程画成聚类图,便可以决定分多少类,每类各有什么样品。
系统聚类法的步骤为:①首先各样品自成一类,这样对n 组样品就相当于有n 类;②计算各类间的距离,将其中最近的两类进行合并;③计算新类与其余各类的距离,再将距离最近的两类合并;④重复上述的步骤,直到所有的样品都聚为一类时为止。
下面我们以最短距离法为例来说明系统聚类法的过程。
最短距离法的聚类步骤如下:① 规定样品之间的距离,计算样品的两两距离,距离矩阵记为()0S ,开始视每个样品分别为一类,这时显然应有pq d q p D =),(;② 选择距离矩阵()0S 中的最小元素,不失一般性,记其为),(q p D ,则将p G 与q G 合并为一新类,记为m G ,有q p m G G G ⋃=;③ 计算新类m G 与其他各类的距离,得到新的距离矩阵记为()1S ;④ 对()1S 重复开始进行第②步,…,直到所有样本成为一类为止。
值得注意的是在整个聚类的过程中,如果在某一步的距离矩阵中最小元素不止一个时,则可以将其同时合并。
● 系统聚类法是最常用的一种聚类方法,常用的系统聚类方法有最短距离法、最长距离法、中间距离法、类平均法、重心法、Ward 最小方差法、密度估计法、两阶段密度估计法、最大似然估计法、相似分析法和可变类平均法。
● 大多数的研究表明:最好综合特性的聚类方法为类平均法或Ward 最小方差法,而最差的则为最短距离法。
Ward 最小方差法倾向于寻找观察数相同的类。
类平均法偏向寻找等方差的类。
SAS统计之第十章-因子分析

正交旋转
正交旋转是一种比较简单的方法, 它将因子矩阵进行正交变换,使 得每个因子只与一个原始变量的 相关性较高,与其他变量的相关 性较低。
斜交旋转
斜交旋转是一种更复杂的方法, 它可以使得一个因子与多个原始 变量的相关性较高,但与其他变 量的相关性较低。
因子的解释
因子的解释
因子的解释是根据实际背景和专业知 识,对每个因子的含义进行解释。解 释时需要综合考虑原始变量的含义和 因子的相关性。
03
解释性。
实例分析
01
为了更好地理解PROC Factor过程,我们将通过一个实例来演示其应 用。
02
假设我们有一个包含多个变量的数据集,并且我们想要提取两个公因 子来解释这些变量之间的相关性。
03
我们将使用PROC Factor过程进行因子分析,并选择适当的选项来提 取两个公因子。
04
分析结果将包括因子载荷表、因子图和轮廓图等输出,以帮助我们理 解公因子和变量之间的关系。
04 因子分析的注意事项
因子分析的前提假设
因子分析的前提假设是数据应具有相关 性。在进行因子分析之前,需要检查变 量之间的相关性,以确保分析的有效性。
因子分析的前提假设是变量应具有共同因子。 共同因子是指多个变量之间存在的共同因素, 这些因素反映了变量之间的共同变化趋势。
因子分析的前提假设是变量应具有 可解释性。在进行因子分析之前, 需要对变量进行解释性分析,以确 定变量之间的潜在关系和共同因素。
因子命名
根据解释结果,可以对每个因子进行 命名,使其更加符合实际背景和专业 知识。命名时需要简洁明了,能够准 确地反映因子的含义。
03 因子分析的SAS实现
Байду номын сангаас
使用SPSS软件进行因子分析和聚类分析的方法

使用SPSS软件进行因子分析和聚类分析的方法使用SPSS软件进行因子分析和聚类分析的方法随着统计分析软件的发展,SPSS(Statistical Package for the Social Sciences)软件作为一款功能强大、易于使用的统计分析工具受到广泛欢迎。
它能帮助研究人员进行各种统计分析,其中包括因子分析和聚类分析。
本文将介绍如何使用SPSS软件进行因子分析和聚类分析,并针对每个分析方法提供详细步骤和操作示例。
一、因子分析因子分析是一种常用的统计方法,在数据维度缩减和相关变量结构分析方面具有广泛的应用。
以下是使用SPSS软件进行因子分析的步骤:1. 数据准备首先,需要将原始数据导入SPSS软件中。
可以通过选择“文件”>“打开”>“数据”,然后选择合适的数据文件进行导入。
确保数据是以矩阵的形式存储,每个变量占据一列,每个观察单位占据一行。
2. 因子分析设置在SPSS软件中,选择“分析”>“数据准备”>“特殊分析”>“因子”。
在弹出的对话框中,选择需要进行因子分析的变量,将它们移动到“因子”框中。
然后,选择所需的因子提取方法(如主成分分析或因子分析),并指定所需的因子个数。
可以选择默认值,也可以根据实际需求进行调整。
3. 统计输出完成因子分析设置后,点击“确定”按钮开始分析。
SPSS软件将生成一个因子分析结果报告。
报告中将包含因子载荷矩阵、特征值、解释的方差比例等统计指标。
通过这些指标,可以对变量和因子之间的关系、每个因子的解释能力进行分析。
4. 结果解读对于因子载荷矩阵,可以根据因子载荷的大小来判断变量与因子之间的关系。
一般来说,载荷绝对值大于0.3的变量与因子之间具有显著关联。
解释的方差比例表示每个因子能够解释变量总方差的比例,一般来说,越大越好。
在解读结果时,需要综合考虑因子载荷和解释的方差比例。
二、聚类分析聚类分析是一种用于数据分类的统计方法。
它根据观测值之间的相似性将数据对象分组到不同的类别中。
spss相关、R型聚类、R型因子分析

因子分析激活Statistics菜单选Data Reduction的Factor...命令项,弹出Factor Analysis对话框。
在对话框左侧的变量列表中选变量X1至X7,点击 钮使之进入Variables框。
点击Descriptives...钮,弹出Factor Analysis:Descriptives对话框,在Statistics 中选Univariate descriptives项要求输出各变量的均数与标准差,在Correlation Matrix栏内选Coefficients项要求计算相关系数矩阵,并选KMO and Bartlett’s test ofsphericity项,要求对相关系数矩阵进行统计学检验。
点击Continue钮返回FactorAnalysis对话框。
点击Extraction...钮,弹出Factor Analysis:Extraction对话框(图11.4),系统提供如下因子提取方法:图11.4 因子提取方法选择对话框Principal components:主成分分析法;Unweighted least squares:未加权最小平方法;Generalized least squares:综合最小平方法;Maximum likelihood:极大似然估计法;Principal axis factoring:主轴因子法;Alpha factoring:α因子法;Image factoring:多元回归法。
本例选用Principal components方法,之后点击Continue钮返回Factor Analysis 对话框。
点击Rotation...钮,弹出Factor Analysis:Rotation对话框(图11.5),系统有5种因子旋转方法可选:图11.5 因子旋转方法选择对话框None:不作因子旋转;Varimax:正交旋转;Equamax:全体旋转,对变量和因子均作旋转;Quartimax:四分旋转,对变量作旋转;Direct Oblimin:斜交旋转。
SAS学习系列34.因子分析

34.因子分析(一)基本原理一、概述因子分析,是用少数起根本作用、相互独立、易于解释通常又是不可观察的因子来概括和描述数据,表达一组相互关联的变量。
通常情况下,这些相关因素并不能直观观测。
因子分析是从研究相关系数矩阵内部的依赖关系出发,把一些具有错综复杂关系的变量归结为少数几个综合因子的一种多变量统计分析方法。
简言之,即用少数不可观测的隐变量来解释原始变量之间的相关性或协方差关系。
因子分析的作用是减少变量个数,根据原始变量的信息进行重组,能反映原有变量大部分的信息;原始部分变量之间多存在较显著的相关关系,重组变量(因子变量)之间相互独立;因子变量具有命名解释性,即该变量是对某些原始变量信息的综合和反映。
主成分分析是因子分析的特例。
主成份分析的目标是降维,而因子分析的目标是找出公共因素及特有因素,即公共因子与特殊因子。
因子分析模型在形式上与线性回归模型相似,但两者有着本质的区别:回归模型中的自变量是可观测到的,而因子模型中的各公因子是不可观测的隐变量,而且两个模型的参数意义也不相同。
二、原理假设样品检测p 个指标(变量)X 1, …, X p ,得到观测矩阵X ,这p 个指标变量可能受m (m<p )个共同因素f 1,…f m 的影响,再加上其它影响因素。
表示为:用矩阵表示为111p p m m p X A f e ⨯⨯⨯⨯=+其中,共同影响因素f 1,…f m 是均值为0方差为1的随机变量,称为公共因子;A p×m 称为因子载荷矩阵,a ji 是第j 变量在第i 公共因子上的负荷,即X j 在坐标轴f i 上的投影;e i 是变量X i 所特有的因子,均值为0方差为σi 2,称为特殊因子。
各特殊因子之间及特殊因子与公共因子之间都是相互独立的,即COV(e i , e j )=0, COV(e, f )=0. 因子分析就是用f 1,…f m 代替X 1, …, X p , 达到降维的目的。
SPSS案例-因子分析结果聚类
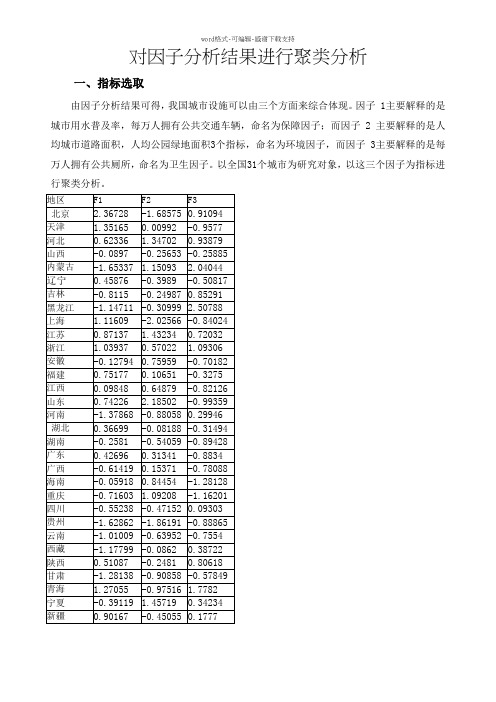
对因子分析结果进行聚类分析
一、指标选取
由因子分析结果可得,我国城市设施可以由三个方面来综合体现。
因子 1主要解释的是城市用水普及率,每万人拥有公共交通车辆,命名为保障因子;而因子 2 主要解释的是人均城市道路面积,人均公园绿地面积3个指标,命名为环境因子,而因子 3主要解释的是每万人拥有公共厕所,命名为卫生因子。
以全国31个城市为研究对象,以这三个因子为指标进行聚类分析。
二、对数据进行系统聚类分析
三、快速聚类结果
四、得出结论
根据系统聚类法的输出结果,可以看出,第一类城市包括北京与上海,第三类包括黑龙江与内蒙古,其他城市为第二类。
显然,第一类城市设施较好,第二类次之,第三类最差。
因子分析与聚类分析
因子分析与聚类分析因子分析和聚类分析是数据分析中常用的统计方法,用于揭示数据中的潜在结构和关系。
本文将介绍因子分析和聚类分析的概念、原理和应用,并比较两者的异同。
一、因子分析因子分析是一种多变量分析方法,旨在通过将一组相关变量转换为较少的无关因子,减少数据的维度。
它基于假设,即这些变量背后存在一些共同的潜在因素,通过这些因素的组合来解释变量之间的关系。
因子分析的步骤如下:1. 收集数据:收集包含多个变量的数据集。
2. 确定因子数目:根据变量之间的相关性和经验判断确定因子的数量。
3. 因子提取:使用主成分分析或常见因子分析方法提取因子。
4. 因子旋转:将提取到的因子进行旋转,以便更好地解释变量之间的关系。
5. 因子解释:解释每个因子的含义和对变量的贡献。
6. 因子得分计算:计算每个观测值在每个因子上的得分。
因子分析的应用广泛,如心理学、市场研究和社会科学等领域。
它可以用于量表的构建、变量筛选和维度简化等。
二、聚类分析聚类分析是一种无监督学习方法,用于将对象分组为具有相似特征的类别或簇。
聚类分析基于样本之间的相似性,旨在发现数据中的结构和关系。
聚类分析的步骤如下:1. 收集数据:收集包含多个样本的数据集。
2. 确定聚类数目:通过观察数据和应用合适的聚类算法,确定聚类的数量。
3. 选择距离度量:选择合适的距离度量方法,如欧氏距离或相关系数。
4. 聚类算法选择:选择适合数据的聚类算法,如层次聚类或 K 均值聚类。
5. 聚类分析:将样本分组到不同的类别或簇中。
6. 结果评估:评估聚类结果的合理性和稳定性。
聚类分析的应用广泛,如市场细分、图像分析和基因表达数据分析等。
它可以帮助理解数据的内在结构和找出相似性较高的样本群体。
三、因子分析与聚类分析的比较尽管因子分析和聚类分析都是常用的数据分析方法,但它们在目标、应用和结果解释方面存在一些差异。
目标:因子分析旨在找到变量之间的潜在结构和因果关系,以减少数据的维度;聚类分析旨在将样本分组为具有相似特征的类别或簇。
使用SPSS软件进行因子分析和聚类分析的方法
使用SPSS软件进行因子分析和聚类分析的方法因子分析和聚类分析是一种常用的数据分析方法,可以用于数据降维和分组。
SPSS是一款常用的统计软件,提供了丰富的分析工具和函数,可以方便地进行因子分析和聚类分析。
一、因子分析:因子分析是一种多变量分析方法,可以将一组相关的变量转化为少数几个互相独立的综合变量,称为因子。
因子分析可以用于降低数据的维度,提取主要的因素,并分析因素之间的关系。
以下是使用SPSS软件进行因子分析的步骤:1.打开SPSS软件,并导入要进行因子分析的数据集。
2.菜单栏选择“分析”-“降维”-“因子”。
3.在弹出的因子分析对话框中,选择要进行因子分析的变量,将其添加到“因子”框中。
4.在“提取”选项中,选择提取的因子个数。
可以根据实际需求和经验进行选择。
5. 在“旋转”选项中,选择旋转方法。
常用的旋转方法有方差最大旋转(Varimax),斜交旋转(Oblique)等。
6.点击“确定”按钮,进行因子分析。
7.SPSS会生成因子载荷矩阵、解释方差表、因子得分等结果。
可以根据因子载荷矩阵和解释方差表来解释因子的含义和解释度。
8.根据具体需求和分析目的,可以进行因子得分的计算和因子分组的分析。
二、聚类分析:聚类分析是一种无监督学习方法,可以将一组样本数据自动分成若干互不相交的群组,称为簇。
聚类分析可以用于数据的分组和群体特征的分析。
以下是使用SPSS软件进行聚类分析的步骤:1.打开SPSS软件,并导入要进行聚类分析的数据集。
2.菜单栏选择“分析”-“分类”-“聚类”。
3.在弹出的聚类分析对话框中,选择要进行聚类分析的变量,将其添加到“变量”框中。
可以选择多个变量进行分析。
4.在“距离”选项中,选择计算样本间距离的方法。
常用的方法有欧几里得距离、曼哈顿距离等。
5. 在“聚类方法”选项中,选择聚类算法的方法。
常用的方法有层次聚类(Hierarchical Clustering)、K均值聚类(K-means)等。
SAS实验_因子分析_聚类分析
实验过程: 1.搜集数据
通过搜索相关数据库,得到 2008 年我国各地区农村人均生活消费支出的相关数据,共包括 我国 31 个省市自治区,设计 8 个方面的人均消费支出。
2.数据准备和预处理
首先建立数据集,我将数据存在 D:\mydata.txt 中。此处编写 SAS 程序来实现 INPUT 数据。
Step2:加入 cluster 节点,联结,设置相关属性。
Step3:运行 运行结果如下,这个结果本来我看起来十分诡异,31 个地区,分了 31 类,看起来没有起到 任何的聚类效果。 首先,Factor1 和 Factor2 的贡献值都为 0:
其次,画出来的散点图和最终的 stat 结果也如此显示:
注:右上角的制表时间是由于时间跳过程序修改造成的,后同。
3.描述性统计分析
①单变量分析: 首先要对数据的基本情况有一个初步的了解, 因此先进行单变量分析。 再次我们利用 means 过程计算一些描述性统计量,编写程序如下:
解释:proc 语句指定运行 means 过程,并指出分析的数据集为 expend,maxdec=2 表示计算 的描述统计量保留两位小数, 然后指定要计算的统计量为: 均值、 标准差、 最大值、 最小值、 极差、变异系数、偏度。之后指定要分析的变为量 x, x1-x8。运行结果如下:
解决思路:
为了研究上述问题, 我们应当以近年的各地区农村人均生活消费支出相关数据为数据源, 通 过描述性统计分析对整体数据进行初步了解; 并在因子分析的基础上进行聚类分析, 对各地 区依据消费水平的高低进行分类; 还可以参数检验判断不同地区的农民生活水平是否存在差 异;若引入时序数据,则可进一步进行关联分析,预测某些地区未来的消费结构变化。本人 会在数据分析的基础上,结合实际进行分析,解释数据结果的实际意义。由于精力有限,此 次实验本人计划主要进行三项数据分析: 1. 描述性分析 2. 基于主成分法的因子分析 3. 在因子分析的基础上,用 Cluster 和 Tree 过程进行聚类分析 注:部分内容为参考教材自学,理解可能不甚透彻,若有错误恳请老师指出。
统计学中的因子分析与聚类分析
统计学中的因子分析与聚类分析统计学是一门重要的学科,它被应用于各种学术和商业领域。
在统计学中,因子分析和聚类分析是两种常见的数据分析方法。
这两种方法可以帮助人们理解和发现数据中的模式和结构,从而做出科学的决策。
一、因子分析因子分析是一种数据分析方法,它可以帮助人们识别数据中的潜在因素。
这些因素通常是无法直接观察到的,但它们对数据分布和相关性有着重要影响。
因子分析的目的是找出这些隐含的因素,并将它们组合成更小的集合,以便更好地解释和理解数据。
因子分析在市场研究中有着广泛的应用。
例如,当消费者对产品或服务进行评价时,他们可能会考虑多个方面,如价格、质量、信誉等。
通过因子分析,可以将这些多个方面归结为几个因素,如品质、价值等。
用这些因素来衡量产品的综合评价。
在因子分析中,最常用的方法是主成分分析。
主成分分析会在数据集中寻找最大的方差,然后将它们组合成不同的因素。
这些因素是适当排序的,第一个因素是方差最大的因素。
通过这种方法,可以将数据压缩成更小的集合,同时保留数据的关键信息。
二、聚类分析聚类分析是一种将数据集合成有意义的组别的方法,它通常用于数据挖掘和市场分析。
聚类分析可以将数据中的相似项归为一类,而将不同项归为不同类。
聚类分析可以应用于很多领域,例如,制造业可以将生产数据集成为相似生产线的组。
在营销领域,聚类分析可以帮助企业发现相似的客户类型和购买模式。
在聚类分析中,最常见的方法是K-Means算法。
该算法会在数据集中寻找到最优的K个簇心,并将数据分配到最近的簇心中。
这个过程会一直重复,直到满足终止条件。
通过使用K-Means算法,可以将数据划分成多个聚类组,并更容易地理解数据集的组织结构。
三、因子分析与聚类分析的联系和区别因子分析和聚类分析都是数据分析领域中常见的方法。
它们的目的都是帮助人们理解和发现数据中的模式和结构。
但二者还是有所不同。
因子分析主要是通过识别数据中的潜在因素,从而帮助人们更好地理解数据的组织结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验过程: 1.搜集数据
通过搜索相关数据库,得到 2008 年我国各地区农村人均生活消费支出的相关数据,共包括 我国 31 个省市自治区,设计 8 个方面的人均消费支出。
2.数据准备和预处理
首先建立数据集,我将数据存在 D:\mydata.txt 中。此处编写 SAS 程序来实现 INPUT 数据。
选中运行结果的第三张表,pearson 相关系数检验表,如图:
分析: x 与其余 8 个变量均高度相关,相关系数都在 0.8 以上,而企鹅他很多变量之间的相关系 数都在 0.7 以上,且显著性检验的 p 值多很小,表明各变量间存在较强的相关性,反应的 信息有所重叠,这启发我们可以做聚类分析、关联分析,而在此之前,我们先利用主成分 法做因子分析,对数据进行降维处理。
4.因子分析
①主成分分析模型与介绍: 用元变量的线性组合提取数据中的信息, 当第一个线性组合不能提取足够多的信息时, 再 用第二个线性组合来继续提取, 如此进行下去, 知道所提取的信息与原变量反应的信息差 不多为止。 判定条件是, 利用变量的来描述, 如果综合指标的方差接近于原来变量的方差, 则认为他们较好地反映了原始数据的信息。 从而这样得到了一系列的线性组合, 将它们作 为综合指标去代替原来的变量,从而达到数据降维的目的,同时保存较多的信息。 具体方法如下: 1) 原始指标数据的标准化采集 p 维随机向量 x = (x1,X2,...,Xp)T)n 个样品 xi = (xi1,xi2,...,xip)T ,i=1,2,…,n, n>p,构造样本阵,对样本阵元进行如下标准化变换:
得到如图所示的而结果:
分析:此步给出了一个载荷矩阵。结合上一步的分析知道,两因子解释的方差占比较高,且 x1-x8 的共同度过都在 0.85 以上,表明该因子模型对原来每个变量的解释能力都较强,可以 较好地代表原变量。 但是自吸查看发现, factor1 在每个变量上的因子载荷基本都在 0.9 附近, factor2 的因子载荷都小于 0.4 且出现较多的负值,这样很难对公公因子作出合理解释,因此 必须进行旋转。 *注:关于公共因子和共同度 求出因子载荷矩阵[A]ij p × m,可以建立因子模型: X = AF + e 其中因子载荷矩阵 A 中第 i 行元素的平方和 h 的平方称为变量 Xi 的共同度过,而由因子模 型知 Xi 的方差包括:1.共同度,描述了公共因子对变量 Xi 的方差贡献,也就是变量 Xi 的方 差中能被公共因子所解释的部分;另一部分是特殊因子对变量 Xi 的方差贡献。因此,变量 的共同度越高,说明因子模型的解释能力越强。
解释: 将原始数据读入到 SAS 数据集中, 并在结果窗格中显示。 我们建立了数据集 expend, 利用 infile 语句读入外部数据文件,假定数据包含在 D 盘根目录下的 mydata.txt 中,选项 delimiter=’09’x 表示分隔符为制表符,firstobs=2,表示从第二行开始读入,input district $, district 表示地区,为字符型变量,x 为总支出,x1-x8 分别表示 8 项消费指标,再利用 label 语句加标签明确其含义。最后用 print 在结果窗口中显示。如图:
解决思路:
为了研究上述问题, 我们应当以近年的各地区农村人均生活消费支出相关数据为数据源, 通 过描述性统计分析对整体数据进行初步了解; 并在因子分析的基础上进行聚类分析, 对各地 区依据消费水平的高低进行分类; 还可以参数检验判断不同地区的农民生活水平是否存在差 异;若引入时序数据,则可进一步进行关联分析,预测某些地区未来的消费结构变化。本人 会在数据分析的基础上,结合实际进行分析,解释数据结果的实际意义。由于精力有限,此 次实验本人计划主要进行三项数据分析: 1. 描述性分析 2. 基于主成分法的因子分析 3. 在因子分析的基础上,用 Cluster 和 Tree 过程进行聚类分析 注:部分内容为参考教材自学,理解可能不甚透彻,若有错误恳请老师指出。
U1 称为第一主成分,U2 称为第二主成分,…,Up 称为第 p 主成分。 5) 对 m 个主成分进行综合评价 对 m 个主成分进行加权求和,即得最终评价值,权数为每个主成分的方差贡献率。 ②分析过程 编写代码如下: 35 36 37 proc factor data=expend; var x1-x8; run;
接下来我们对载荷矩阵进行旋转,进行方差最大的正交旋转,得到旋转后的因子载荷矩阵, 并将因子得分输出到数据集 scoreout 中。代码如下:
结果如图:
分析:从图中可以看出,factor1 在 x1 食品,x3 居住,x4 家庭设备和 x9 其他商品及服务商 有大于 0.7 的正载荷,结合实际该因子可以解释为基本物质生活支出;第二共因子 factor2 在 x3 衣着,x5 交通通信,x6 文教娱乐和 x7 医疗保健上有大于 0.70 的正载荷,可以理解为 文化生活支出。 根据旋转后的载荷矩阵,我们可以建立旋转后的因子模型: x1 = 0.91963 factor1 + 0.33811 factor2 x2 = 0.35111 factor1 + 0.90325 factor2 x3 = 0.75510 factor1 + 0.56795 factor2 x4 = 0.75453 factor1 + 0.57932 factor2 x5 = 0.64002 factor1 + 0.74248 factor2 x6 = 0.55977 factor1 + 0.76499 factor2 x7 = 0.44385 factor1 + 0.84633 factor2 x8 = 0.81261 factor1 + 0.45488 factor2 而当我们获得公共因子和因子载荷矩阵后, 可以计算公共因子在每个样本上对应的数值, 就 是因子得分,然后我们就可以用这些公共因子去代替原来的变量,实现数据降维的目的。计 算因子得分就是用原变量 X 来表示公共因子 F。 下面我们把因子得分排个序,建立新的查询,步骤如下: Step1:
SAS 数据挖掘与应用
实验报告
实验要求:
1. 选择经济领域中的一个问题, 确定相关的分析变量, 描述通过数据挖掘来探究 (或解释、 或解决)问题的逻辑思路,说明预期的结果(结论)等。 2. 查询和搜集相关原始数据 3. 整理、准备数据,建立数据集 4. 采用二种或二种以上的挖掘方法,或进行对比分析,或先后进行多个阶段的分析。 5. 对挖掘结果进行分析和说明。 6. 总结研究结论或结果。
利用 factor 过程实现因子分析, 计算得到相关矩阵的特征值、 方差贡献率及累计方差贡献率:
分析:从图中看出,第一列的特征值从大到小排列,第二列是相邻两行特征值的差异,第三 列是是每个特征值占全部特征值之和的比例,第四列是累计比例。从图中看出,前两个公共 因子的累计方差贡献率已达 9.9171, 表明两个公共因子所代表的信息已经能够很充分地反应 原变量了,因此我们下面制定两个公共因子来进行因子分析(n=2):
实验目的:
1. 2. 3. 4. 熟悉 SAS 软件操作 练习 SAS 编程 学习并练习描述性统计分析、因子分析、聚类分析等方法与实际操作 研究实际问题
问题描述:
“三农”问题是我国现阶段大力需要解决的问题之一,如何拉动农村经济发展,提高农民收 入已成为社会关注的焦点。 为了解决三农问题, 首先应当了解现阶段我国各地农民的生活水 平, 了解农村人均消费支出的情况。 因此, 我们希望通过分析农村人均消费支出的各项指标, 来研究各地农民的整体消费水平和消费结构,以及各地农村人口消费水平和结构的差异。
分析: (1)总支出为 3807.82 元,可以看出农民的生活水平总体来说还是较低的,改善农民生活 仍然任重道远。变量 x 的标准偏差为 1578.54,然而最大值为 9119.67,最小值为 2165.70, 极差达到 6953.97 元, 说明各地区农民生活水平差异很大, 贫富差距明显, 地区发展不平衡。 变量 x 的偏度为 2.08>0,说明为正偏态,均值左边集中右边分散,说明我国大部分地区的农 村消费支出仍然处于中低水平,高消费支出的地区较少,但是消费额很高。 (2)从变异系数来看,x6 文教娱乐的变异系数达到了 61.53,x4 家庭设备、x5 交通通信、 x7 医疗保健的变异系数也都超过了 50,说明各地区在文教、家庭设备、医疗保健等方面存 在较大的相对差异。 ②相关系数分析和 P 值检验 鉴于 x 是 x1-x8 的线性表示,之后我们只分析 x1-x8。此步利用 corr 过程计算变量间的相关 系数,代码如下:
Step2: (F2 类似)
Step3:
结果:
分析: (1)上海、广东、浙江在 Factor1 上的得分居前三位,说明这三个地区的基本物质生活支 出较高,当然生活成本也高,而山西、甘肃、新疆排在最后三位,说明这三个地区基本物质 生活支出很低,这些地区农民的基本生活水平急需改善。 (2)北京、浙江、上海在 Facotr2 上的得分分居前三位,说明这三个地区在文化生活上的 支出较高。而关系、海南和广东排在最后三位,说明这三个地区在文化生活上的支出较低。 (3)北京 Factor1 得分处于中游但是 Facotr2 处于帮手,且得分遥遥领先,说明北京的农 民特别重视文化生活,在文化教育医疗等方面有很大的消费投入。 (4)黑龙江、吉林、内蒙古、山西等再 Factor1 上得分很低,在 Factor2 上得分较高,说 明这几个地区的农民在基本物质生活上的支出不高, 但是文化生活上的投入较多, 可能和生 活习俗有关。 (5)广东在 Factor1 上得分第二,在 Factor2 上排在最后,说明广东农民更重视物质上的 消费,如食品、居住等,却在文化生活上消费不高,这是一种不甚合理的结构,应当积极引 导。
Step2:加入 cluster 节点,联结,设置相关属性。
Step3:运行 运行结果如下,这个结果本来我看起来十分诡异,31 个地区,分了 31 类,看起来没有起到 任何的聚类效果。 首先,Factor1 和 Factor2 的贡献值都为 0:
