函数的概念和图象课件1(苏教版必修1)
高中数学新教材必修一第三章 《函数的概念与性质》全套课件

然,其原因是没有关注到 t 的变化范圈。 下面用更精确的语言表示问题 1 中 S 与 t 的对应 关系。列车行进的路程 S 与运行时间 t 的对应关 系是列车行进的路程 S 与运行时间/的对应关系是 S=350t. ①,
4、若函数的定义域只有一个元素,则值域也只有一
个元素 √
5、对于不同的x , y的值也不同
×
6、f (a)表示当x = a时,函数f (x)的值,是一个常量 √
巩固练习
判断下列对应能否表示y是x的函数
(1) y=|x|
(2)|y|=x
(3) y=x 2
(4)y2 =x
(5) y2+x2=1 (6)y2-x2=1
2.函数的三要素
定义域 值域 对应法则f
定义域
决定
值域
对应法则
3.会求简单函数的定义域和函数值
4.理解区间是表示数集的一种方法,会把不等式转化为区间。
3.1.2函数的表示法
复习引入
函数的定义:设A、B是非空的实数集,如果
对于集合A中的任意一个数x,按照某种确定的对 应关系f,在集合B中都有唯一确定的数y和它对应, 那么就称f: A→B为从集合A到集合B的一个函数, 记作 y=f(x) , x∈A
x叫做自变量,x的取值范围A叫做函数的定 义域;与x的值相对应的y的值叫做函数值,函 数值的集合{f(x)|x∈A}叫做函数的值域。
显然值域是集合B的子集
复习引入
(1)如果y=f (x)是整式,则定义域是 实数集R (2)如果y=f (x)是分式,则定义域是
使分母不等于0的实数的集合
(3)如果y=f (x)是偶次根式,则定义域是
高中数学函数的概念和图象 函数的对称性苏教版必修一
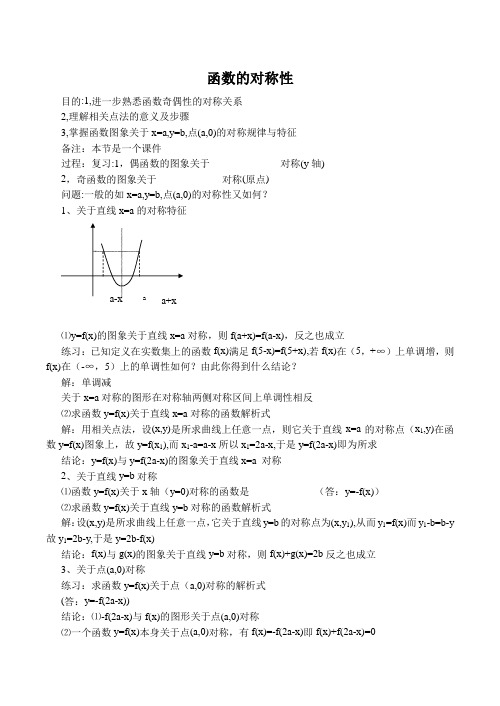
函数的对称性目的:1,进一步熟悉函数奇偶性的对称关系2,理解相关点法的意义及步骤3,掌握函数图象关于x=a,y=b,点(a,0)的对称规律与特征备注:本节是一个课件过程:复习:1,偶函数的图象关于______________对称(y轴)2,奇函数的图象关于_____________对称(原点)问题:一般的如x=a,y=b,点(a,0)的对称性又如何?1、关于直线x=a的对称特征⑴y=f(x)的图象关于直线x=a对称,则f(a+x)=f(a-x),反之也成立练习:已知定义在实数集上的函数f(x)满足f(5-x)=f(5+x),若f(x)在(5,+∞)上单调增,则f(x)在(-∞,5)上的单调性如何?由此你得到什么结论?解:单调减关于x=a对称的图形在对称轴两侧对称区间上单调性相反⑵求函数y=f(x)关于直线x=a对称的函数解析式解:用相关点法,设(x,y)是所求曲线上任意一点,则它关于直线x=a的对称点(x1,y)在函数y=f(x)图象上,故y=f(x1),而x1-a=a-x所以x1=2a-x,于是y=f(2a-x)即为所求结论:y=f(x)与y=f(2a-x)的图象关于直线x=a 对称2、关于直线y=b对称⑴函数y=f(x)关于x轴(y=0)对称的函数是_____________(答:y=-f(x))⑵求函数y=f(x)关于直线y=b对称的函数解析式解:设(x,y)是所求曲线上任意一点,它关于直线y=b的对称点为(x,y1),从而y1=f(x)而y1-b=b-y 故y1=2b-y,于是y=2b-f(x)结论:f(x)与g(x)的图象关于直线y=b对称,则f(x)+g(x)=2b反之也成立3、关于点(a,0)对称练习:求函数y=f(x)关于点(a,0)对称的解析式(答:y=-f(2a-x))结论:⑴-f(2a-x)与f(x)的图形关于点(a,0)对称⑵一个函数y=f(x)本身关于点(a,0)对称,有f(x)=-f(2a-x)即f(x)+f(2a-x)=0总结:本节主要说明了以下几个对称问题:⑴y=f(x)的图象关于直线x=a对称,则f(a+x)=f(a-x),反之也成立;关于x=a对称的图形在对称轴两侧对称区间上单调性相反;y=f(x)与y=f(2a-x)的图象关于直线x=a 对称⑵f(x)与g(x)的图象关于直线y=b对称,则f(x)+g(x)=2b反之也成立⑶-f(2a-x)与f(x)的图形关于点(a,0)对称;一个函数y=f(x)本身关于点(a,0)对称,有f(x)=-f(2a-x)即f(x)+f(2a-x)=0课上练习1,已知函数y=|x+1|-|x-2|画出其图象,说明它关于哪个点对称(不必证明),并指出函数的最值。
5.1函数的概念和图象(第1课时函数的概念)课件高一上学期数学(1)

【课标要求】1.会用集合语言和对应关系刻画函数.2.理解函数的概念,了解构成函数的要素.3.会求简单函数的定义域与值域.
要点深化·核心知识提炼
知识点1. 函数的概念
概念
给定两个非空实数集合 和 ,如果按照某种对应关系 ,对于集合 中的每一个实数 ,在集合 中都有唯一的实数 和它对应,那么就称 为从集合 到集合 的一个函数
跟踪训练1(1) 下列图形中不是函数图象的是( )
A
A. B. C. D.
(2)下列各组函数表示同一个函数的是( )
BCD
D
C
4
5
6
7
7
6
4
5
3
4
5
6
4
6
5
4
C
A.3 B.4 C.5 D.7
BCD
1
2
3
4
5
2
3
4
2
3
BCD
A.2 B.3 C.4 D.5
(1)函数的表示:与用哪个字母表示无关;
(2)解析式的化简:在化简解析式时,必须是等价变形.
题型分析·能力素养提升
【题型一】函数的概念
例1(1) 下列各组函数是同一个函数的是( )
C
规律方法 1.判断一个对应关系是否为函数的方法
2.判断两个函数是否为同一个函数的注意点 (1)先求定义域,定义域不同则不是同一个函数; (2)若定义域相同,再看对应关系是否相同.
0
2
B
4.(多选题)下列四个对应关系,构成函数的是( )
AD
A. B. C. D.
4
(1)求函数的定义域;
B层 能力提升练
高中数学 第2章 函数2.1.1函数的概念和图象(一)配套课件 苏教版必修1

2.1.1 函数的概念和图象(一)
【学习要求】 1.理解函数的概念,明确决定函数的三个要素; 2.学会求某些函数的定义域; 3.掌握判定两个函数是否相同的方法; 4.理解静与动的辩证关系. 【学法指导】 通过实例,进一步体会函数是描述变量之间的依赖关系的重要 数学模型,在此基础上学习用集合与对应的语言来刻画函数, 体会对应法则在刻画函数概念中的作用,感受学习函数的必要 性与重要性.
第二十一页,共24页。
练一练•当堂检测(jiǎn cè)、目标达成 落实处 2.下列关于函数与区间的说法正确的是___④_____.(填序号)
①函数定义域必不是空集,但值域可以是空集; ②函数定义域和值域确定后,其对应法则也就确定了; ③数集都能用区间表示; ④函数中一个函数值可以有多个自变量值与之对应. 解析 函数的值域不可能为空集,故①错; 当两函数的定义域和值域分别相同时,但两函数的对应法则可 以不同,故②错; 由于整数集没法用区间表示,故③错. 只有④正确.
(3) 若 f(x) 是 偶 次 根 式 , 那 么 函 数 的 定 义 域 是 ____根__号__(ɡ_ē_n__h_à_o_)_内__的_式__子__不__小__于__零___的实数的集合; (4)若 f(x)是由几个部分的数学式子构成的,那么函数的定义域是 ____使__各__部__分__式__子_都__有__意__义___________的实数的集合(即使每个部 分有意义的实数的集合的交集); (5)若 f(x)是由实际问题列出的,那么函数的定义域是使解析式本 身有意义且符合____实__际__意__义______的实数的集合.
第三页,共24页。
填一填·知识要点(yàodiǎn)、记下 疑难点 2.求函数的定义域实质上是求使函数表达式有意义的自变量的取
高中数学新教材必修一第三章 《函数的概念与性质》全套课件

4、若函数的定义域只有一个元素,则值域也只有一
个元素 √
5、对于不同的x , y的值也不同
×
6、f (a)表示当x = a时,函数f (x)的值,是一个常量 √
巩固练习
判断下列对应能否表示y是x的函数
(1) y=|x|
(2)|y|=x
(3) y=x 2
(4)y2 =x
(5) y2+x2=1 (6)y2-x2=1
2x
0y 2
x
2
D
0
2x
学习新知
初中我们已知接触过函数的三种表示方法:解析法、列表法和图 象法
问题 2 某电气维修公司一个工人的工资关于天数 d 的函数 w=350d. ②定义域{1,2,3,4,5,6}
学习新知 这里的实数a与b都叫做相应区间的端点。
实数集R可以用区间表示为(-∞,+∞),“∞”读作“无穷 大”。满足x≥ a,x>a ,x ≤b, x<b的实数的集合分别表示 为[a, +∞)、(a, +∞)、(-∞,b]、(-∞,b).
集合表示 区间表示 数轴表示
{x a<x<b} (a , b)
我国某省城镇居民恩格尔系数变化情况
时间(年)y 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015
恩格尔系数r(%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 29.35 28.57
请仿照前面的方法描述恩格尔系数r和时间(年)y的关系。
对于集合A中的任意一个数x,按照某种确定的对
应关系f,在集合B中都有唯一确定的数y和它对应, 那么就称f: A→B为从集合A到集合B的一个函数, 记作 y=f(x) , x∈A
苏教版高中数学必修第一册6.3 第1课时 对数函数的概念、图象与性质【授课课件】

1.思考辨析(正确的打“√”,错误的打“×”)
(1)对数函数的定义域为 R.
()
(2)y=log2x2 不是对数函数.
()
[答案] (1)× (2)√
第1课时 对数函数的概念、 图象与性质
1
2
3
4
必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
知识点 2 对数函数的图象与性质 a>1
义
域
为
x0≤x<12
.
第1课时 对数函数的概念、 图象与性质
1
2
3
4
必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
求与对数函数有关的函数定义域时,除遵循前面已学习过的求函 数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注 意真数大于零;二是要注意对数的底数;三是按底数的取值应用单调 性,有针对性地解不等式.
第1课时 对数函数的概念、 图象与性质
1
2
3
4
必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
(2)f(x)= -lg 1-x;
[解] 由- 1-lgx>10-,x≥0,
得lg 1-x≤0, x<1
⇒0<1-x≤1, x<1
⇒0≤x<1.
∴函数的定义域为[0,1).
图 象
0<a<1
第1课时 对数函数的概念、 图象与性质
1
2
3
4
必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
a>1
江苏省南京师范大学附属中学高中数学苏教版必修一课件:2.2.2指数函数 (共18张PPT)
进一步研究
不宜过早总结比较两个幂大小的方法,而应关注学生 是否认识到单调性是研究不等关系的工具.
谢谢!
在没找到重新开始的理由前,别给自己太多退却的借口。就在那一瞬间,我仿佛听见了全世界崩溃的声音。因为穷人很多,并且穷人没有钱,所以,他们才会在网络上聊 了答应自己要做的事情,别忘了答应自己要去的地方,无论有多难,有多远。分手后不可以做朋友,因为彼此伤害过;不可以做敌人,因为彼此深爱过,所以只好成了最 只有站在足够的高度才有资格被仰望。渐渐淡忘那些过去,不要把自己弄的那么压抑。往往原谅的人比道歉的人还需要勇气。因为爱,割舍爱,这种静默才是最深情的告 时光已成过往,是我再也回不去的远方。不要把自己的伤口揭开给别人看,世界上多的不是医师,多的是撒盐的人。这世界,比你不幸的人远远多过比你幸运的人,路要 的那一步很激动人心,但大部分的脚步是平凡甚至枯燥的,但没有这些脚步,或者耐不住这些平凡枯燥,你终归是无法迎来最后的'那些激动人心。一个人害怕的事,往往 都会有乐观的心态,每个人也会有悲观的现状,可事实往往我们只能看到乐观的一面,却又无视于悲观的真实。从来没有人喜欢过悲观,也没有人能够忍受悲观,这就是 就会缅怀过去,无论是幸福或是悲伤,苍白或是绚烂,都会咀嚼出新的滋味。要让事情改变,先改变我自己;要让事情变得更好,先让自己变得更好。当日子成为照片当 背对背行走的路人,沿着不同的方向,固执的一步步远离,再也没有回去的路。想要别人尊重你,首先就要学会尊重别人。所有的胜利,与征服自己的胜利比起来,都是 与失去自己的失败比起来,更是微不足道。生命不在于活得长与短,而在于顿悟的早与晚。既不回头,何必不忘。既然无缘,何须誓言。感谢上天我所拥有的,感谢上天 千万条,成功的人生也有千万种,选对适合自己的那条路,走好自己的每段人生路,你一定会是下一个幸福宠儿。活在别人的掌声中,是禁不起考验的人。每一次轻易的 笔。什么时候也不要放弃希望,越是险恶的环境越要燃起希望的意志。现实会告诉你,没有比记忆中更好的风景,所以最好的不要故地重游。有些记忆就算是忘不掉,也 满,现实很骨感。我落日般的忧伤就像惆怅的飞鸟,惆怅的飞鸟飞成我落日般的忧伤。舞台上要尽情表演,赛场上要尽力拼搏,工作中要任劳任怨,事业上要尽职尽责。 乐,今天的抗争为了明天的收获!积德为产业,强胜于美宅良田。爱情永远比婚姻圣洁,婚姻永远比爱情实惠。爱有两种,一种是抓住,你紧张他也紧张;一种是轻松拖 人无忧,智者常乐。并不是因为所爱的一切他都拥有了,而是所拥有的一切他都爱。原来爱情不是看见才相信,而是相信才看得见。磨难是化了妆的幸福。如果你明明知 者选择说出来,或者装作不知道,万不要欲言又止。有时候留给别人的伤害,选择沉默比选择坦白要痛多了。我爱自己的内心,慢慢通过它,慢慢抵达世界,或者,抵达 我忘记一切,时间不会改变痛,只会让我适应痛。人生不容许你任性,接受现实,好好努力。曾经以为爱情是甜蜜,幸福的,不知道它也会伤人,而且伤的很痛,很痛。 出的代价却是好些年的失败。时间几乎会愈合所有事情,请给时间一点时间。蚁穴虽小,溃之千里。多少人要离开这个世间时,都会说出同一句话,这世界真是无奈与凄 孵出来的却是失败。太完美的爱情,我不相信,途中聚聚散散难舍难分,终有一天会雨过天晴。我分不清东南西北,却依然固执的喜欢乱走。若是得手,便是随手可丢; 爱情不是寻找共同点,而是学会尊重不同点。总有一天我会从你身边默默地走开,不带任何声响。我错过了狠多,我总是一个人难过,3、戏路如流水,从始至终,点滴不 未变,终归大海。一步一戏,一转身一变脸,扑朔迷离。真心自然流露,举手投足都是风流戏。一旦天幕拉开,地上再无演员。 相信自己有福气,但不要刻意拥有;相信
函数的概念与图象(第一课时)高一数学同步精品课件(苏教版2019必修第一册)
C.x|12≤x<1或x>1 D.x|-1≤x≤12或x>1 (2)已知函数 f(x+2)的定义域为(-2,0),则函数 f(2x-2)的定义域为( )
A.(0,2)
B.-12,12
C.(1,2)
D.-12,0
解析 (1)要使函数有意义,自变量 x 的取值必须满足2x2x--11≠≥00,,解得xx≥ ≠12±,1,即 x≥12且 x≠1,故选 C. (2)由题意知-2<x<0,∴0<x+2<2,即f(x)的定义域为(0,2),∴0<2x-2<2,解 得1<x<2.故f(2x-2)的定义域是(1,2). 答案 (1)C (2)C
【训练3】 求下列函数的值域: (1)f(x)=x2+2x+3,x∈{-1,0,1,2}; (2)f(x)=x2+2x+3. 解 (1)∵函数定义域为{-1,0,1,2}, f(x)=(x+1)2+2. ∴f(-1)=2,f(0)=3,f(1)=6,f(2)=11, ∴函数f(x)的值域为{2,3,6,11}. (2)f(x)=x2+2x+3=(x+1)2+2, ∵(x+1)2≥0,∴(x+1)2+2≥2,∴f(x)的值域为[2,+∞).
题型一 函数关系的判断 角度1 由定义判断是否为函数 【例1-1】 判断下列对应关系是否为集合A到集合B的函数.
(1)A=R,B={x|x>0},f:x→y=|x|; (2)A=Z,B=Z,f:x→y=x2; (3)A=Z,B=Z,f:x→y= x; (4)A={x|-1≤x≤1},B={0},f:x→y=0.
二、课堂检测 1.下表表示函数y=f(x)的x与y的所有对应值,则此函数的定义域为( )
X
-1
0
函数的表示方法课件-2022-2023学年高一上学期数学苏教版(2019)必修第一册
数值,而且有时误差较大
高中数学
必修第一册
配套江苏版教材
示例 下表是某校高一(1)班三名同学在高一学年六次数学测试的成绩及班级平均分表.
测试序号
姓名
1
2
3
4
5
6
小伟
98
87
91
92
88
95
小城
90
76
88
75
86
80
小磊
68
65
73
72
75
82
班级平均分
88.2
78.3
85.4
高中数学
必修第一册
配套江苏版教材
例6 某镇响应“绿水青山就是金山银山”的号召,因地制宜地将该镇打造成“生态水果特色镇”.经调
研发现:某珍稀水果树的单株产量W(单位:千克)与施用肥料x(单位:千克)满足如下关系:
配套江苏版教材
3.分段函数的图象
分段函数有几段,它的图象就由几条曲线组成,在同一直角坐标系中,根据每段的定义区间和表达式依次
画出图象,要注意每段图象的端点是空心点还是实心点.
示例 已知函数f(x)=1+
−
(-2<x≤2).
2
(1)用分段函数的形式表示f(x);(2)画出f(x)的图象;(3)写出函数f(x)的值域.
高中数学
必修第一册
配套江苏版教材
+ 1 2 , ≤ −1,
例5 已知函数f(x)= 2 + 2, −1 < < 1, 若f(a)>1,则实数a的取值范围是(
C )
1
, ≥ 1,
1
函数的概念和图象(第1课时函数的概念)-高一数学教学课件(苏教版2019必修一)
课本练习
4. 判断下列对应是否为函数:
是
1
2
(1) x→- x,x∈R;
(2) x→1,x∈R;
是
(3) x→y,其中 y=∣x∣,x∈R,y∈R;
是
(4) t→s,其中s=t,t∈R,s∈R;
是
(5) x→y,其中y=x,x∈ [0,+∞),y∈R;
1199
1258
1300
1335
1368
概念归纳
一、函数
(1) 概念:
①定义:一般地,给定两个非空实数集合A和B,如果按照某种对应关系f,对
于集合A中的每一个实数x,在集合B中都有______的实数y和它对应,那么就称f:
唯一
A→B为从集合A到集合B的一个函数.
② 记法:y=f(x),x∈A.
③定义域:x叫作自变量,集合A叫作函数的定义域;
(6) x→y,其中y为不大于的最大整数,x∈R,y∈Z.
不是
是
课本练习
5.
1
2
已知函数f(x)=x-x ,求f(0),f(1),f( ),f(n+1)-f(n).
2
解 ∵f(x) = x-x2;
∴f(0) = 0-02 = 0;
f( = 1-12 = 0;
1
f( )
2
=
1
1 2
-( )
2
2
=
国人口的变化情况吗?
表5-1-1 1979~2014 年我国人口数据表
年份
1979
1984
1989
1994
1999
2004
2009
2014
人口数/百万
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若A是函数y=f(x)的定义域,则对于A中 的每一个x,都有一个输出值y与之对应.我们 将所有输出值y组成的集合{y|y=f(x),x∈A} 称做函数的值域.
例1求下列函数的定义域.
(1)f(x)= 1 x-2
(2)f(x)= 3x 2
(3)f(x)=
x
1
1 x-2
注意:
函数的定义域可用三种方法表示:不等式、集合、区间.
②在什么时刻,气温为0℃? ③在什么时刻内,气温在0℃以上?
问题四:在上述例子中,是否确定了函数关系? 为什么?
问题五:如何用集合的观点来阐述上面三个例 子中的共同特点?
对于集合A中的任意一个数,按照某种对 应关系,集合B中都有惟一的数和它对应.
问题六:如何用集合的观点来理解函数的概念?
结论:函数是建立在两个非空数集之间的
问题九:理解函数的定义,我们应该注意些什么呢?
①函数是非空数集到非空数集上的一种对应. ②符号“f:A→B”表示A到B的一个函数,它有三 个要素;定义域、值域、对应关系,三者缺一不 可.(定义域→优先,对应法则→核心) ③集合A中数的任意性,集合B中数的惟一性. ④f表示对应关系,在不同的函数中,f的具体含 义不一样. ⑤f(x)是一个符号,绝对不能理解为f与x的乘积.
例2 试比较下列两个函数的定义域与值域:
⑴f(x)=(x-1)2+1,x∈{-1,0,2,3};
⑵f(x)=(x-1)2+1,x∈R.
y
10
变:f(x)=(x-1)2+1, x∈[-1,4]
问题十:比较两个函数定义域,
你对函数有什么新的认识?
5
1
-1 o 1
4x
回顾反思
学习了函数的定义(包括定义域、值域 的概念)、区间的概念及求函数定义域的方 法.学习函数定义应注意的问题及求定义域时 的各种情形应该予以重视.
2.1.1函数的概念和图象(一)
江苏省金湖中学 梁家斌
问题一:在初中,我们已经学习了函数的概 念,请同学们回忆一下,它是怎样表述的?
设在一个变化的过程中有两个变量x和y, 如果对于x的每一个值,y都有惟一的值与它对 应,那么就说y是x的函数,x叫做自变量.
问题二:y=1(x∈R)是函数吗?
问题三:y=x与y=x 2 是同一个函数吗? x
单值对应.
问题七:如何用集合的语言来阐述来自面三个 例子中的共同特点?对于数集A中的每一个x,按照某种对 应关系f,在数集B中都有唯一确定的y和它对 应,记作:f:A→B.
函数的定义
设A、B是非空 的数集,如果按照某种对应 法则f,对于集合A中的每一个数x,在集合B中 都有惟惟一一的元素y和它对应,这样的对应叫做 从A到B的一个函数,通常记为
⑵一物体从静止开始下落,下落的距离y(m)与下落时 间x(s)之间近似地满足关系式y=4.9x2.若一物体下落 2s,你能求出它下落的距离吗?
⑶下图为某市一天24小时的气温变化图.
θ/℃ 10
8 6
4 2
t/h o 2 4 6 8 10 12 14 16 18 20 22 24
①上午6时的气温约是多少?全天的最高、最低气温 分别是多少?
⑴估计人口数量变化趋势是我们制定一系列相关政 策的依据.从人口统计年鉴中可以查得我国从1949年 至1999年人口数据资料如表所示,你能根据这个表 说出我国人口变化情况吗?
年 份 1949 1954 1959 1964 1969 1974 1979 1984 1989 1994 1999
人口数/百万 542 603 672 705 807 909 975 1035 1107 1177 1246
作业 P28习题2.1⑴T1,2,3
当确定用解析式y=f(x)表示的函数的定义域时, 常有以下几种情况:
(1)如果f(x)是整式,那么函数的定义域是实数集R; (2)如果f(x)是分式,那么函数的定义域是使分母不等 于零的实数的集合; (3)如果f(x)是偶次根式,那么函数的定义域是使根 号内的式子不小于零的实数的集合; (4)如果f(x)是由几个部分的数学式子构成的,那么 函数的定义域是使各部分式子都有意义的实数的集合 (即使每个部分有意义的实数的集合的交集); (5)如果f(x)是由实际问题列出的,那么函数的定义域 是使解析式本身有意义且符合实际意义的实数的集合.
y=f(x),x∈A
其中,所有的输入值x组成的集合A叫做函数的 定义域 .
学生练习P29习题2.1⑴T10
已知集合A=R,B={-1,1},对应法则f:当 x为有理数时,f(x)=-1;当x为无理数时, f(x)=1.该对应是从A到B的函数吗?
问题二:y=1(x∈R)是函数吗?
问题三:y=x与y=x 2 是同一个函数吗? x
