贵阳市2019-2020年度九年级上学期期末数学试题(I)卷
贵州省贵阳市普通中学2022-2023学年高一上学期期末监测考试数学试题(1)

贵阳市普通中学2021-2022学年度第一学期期末监测考试试题高一数学一、选择题(本大题共8小题,每小题4分,共32分.每小题有四个选项,其中只有一个选项正确,请将你认为正确地选项填写在答题卷地相应位置上.)1 已知集合{}3782A x x x =-<-,{}2340B x x x =--<,则A B = ( )A. {}4x x < B. {}34x x << C. {}13x x -<< D. {}43x x -<<【结果】C 【思路】【思路】求出集合A ,B ,再由交集定义求出A B .【详解】∵集合{}{}37823A x x x x x =-<-=<,{}{}234014B x x x x x =--<=-<<,∴{}13A B x x ⋂=-<<.故选:C .2. 已知命题2:,10p n N n n ∀∈++>,则p 地否定为( )A. 2,10n N n n ∀∈++< B. 2,10n N n n ∀∈++≤C. 2,10n N n n ∃∈++< D. 2,10n N n n ∃∈++≤【结果】D 【思路】【思路】全称命题地否定为存在命题,利用相关定义进行判断即可【详解】全称命题地否定为存在命题,命题2:,10p n N n n ∀∈++>,则p ⌝为2,10n N n n ∃∈++≤.故选:D3. 函数12xy =地定义域为( )A. R B. (,0)(0,)-∞+∞ C. (,0)-∞ D. (0,)+∞【结果】B.【思路】【思路】要使函数12xy =有意义,则需要满足0x ≠即可.【详解】要使函数12x y =有意义,则需要满足0x ≠所以12x y =地定义域为(0)(0)∞∞-⋃+,,,故选:B4. 在平面直角坐标系xoy 中,角α与角β项点都在坐标原点,始边都与x 轴地非负半轴重合,它们地终边有关y 轴对称,若1cos 2α=-,则cos β=( )A.12B. 12-C.D. 【结果】A 【思路】【思路】利用终边相同地角和诱导公式求解.【详解】因为 角α与角β地终边有关y 轴对称,所以2,k k Z βπαπ=-+∈,所以 ()1cos cos 2cos 2k βπαπα=-+=-=,故选:A5. 借助信息技术画出函数ln y x =和||y x x a =-(a 为实数)地图象,当 1.5a =时图象如图所示,则函数| 1.5|ln y x x x =--地零点个数为( )A. 3B. 2C. 1D. 0【结果】B 【思路】的【思路】由| 1.5|ln 0y x x x =--=转化为 1.5y x x =-与ln y x =地图象交点个数来确定正确选项.【详解】令| 1.5|ln 0y x x x =--=, 1.5ln x x x -=,所以函数| 1.5|ln y x x x =--地零点个数即 1.5y x x =-与ln y x =地图象交点个数,结合图象可知 1.5y x x =-与ln y x =地图象有2个交点,所以函数| 1.5|ln y x x x =--有2个零点.故选:B6. 设 1.53cos2,0.3,log 2a b c -===,则a ,b ,c 地大小关系是( )A. a b c <<B. c a b<< C. a c b<< D. b c a<<【结果】C 【思路】【思路】比较a ,b ,c 与0和1地大小即可判断它们之间地大小.【详解】cos20a =<,1.500.30.31b -=>=,()333log 1log 2log 3,0,1c c <=<∈,故a c b <<故选:C.7. 已知1(0,),sin cos 5απαα∈+=-,则下面结论正确地是( )A. 4cos 5α= B. 7sin cos 5αα-=C.sin cos 4tan 15ααα+=-D.sin cos 73sin 2cos αααα-=-+【结果】B 【思路】【思路】先求出34sin cos 55αα==-,再对四个选项一一验证即可.【详解】因为1(0,),sin cos 5απαα∈+=-,又22sin cos 1αα+=,.解得:34sin cos 55αα==-.故A 错误。
2019-2020年湖北省武汉市九年级上册期末数学试卷(含详细解析)

湖北省武汉市九年级(上)期末数学试卷一、选择题(共10小题,每小题3分,共30分)1.(3分)方程(﹣5)=0化成一般形式后,它的常数项是()A.﹣5B.5C.0D.12.(3分)二次函数y=2(﹣3)2﹣6()A.最小值为﹣6B.最大值为﹣6C.最小值为3D.最大值为33.(3分)下列交通标志中,是中心对称图形的是()A.B.C.D.4.(3分)事件①:射击运动员射击一次,命中靶心;事件②:购买一张彩票,没中奖,则()A.事件①是必然事件,事件②是随机事件B.事件①是随机事件,事件②是必然事件C.事件①和②都是随机事件D.事件①和②都是必然事件5.(3分)抛掷一枚质地均匀的硬币,正面朝上的概率为0.5,下列说法正确的是()A.连续抛掷2次必有1次正面朝上B.连续抛掷10次不可能都正面朝上C.大量反复抛掷每100次出现正面朝上50次D.通过抛掷硬币确定谁先发球的比赛规则是公平的6.(3分)一元二次方程2+2+m=0有两个不相等的实数根,则()A.m>3B.m=3C.m<3D.m≤37.(3分)圆的直径是13cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是()A.相离B.相切C.相交D.相交或相切8.(3分)如图,等边△ABC的边长为4,D、E、F分别为边AB、BC、AC的中点,分别以A、B、C三点为圆心,以AD长为半径作三条圆弧,则图中三条圆弧的弧长之和是()A.πB.2πC.4πD.6π9.(3分)如图,△ABC的内切圆与三边分别相切于点D、E、F,则下列等式:①∠EDF=∠B;②2∠EDF=∠A+∠C;③2∠A=∠FED+∠EDF;④∠AED+∠BFE+∠CDF=180°,其中成立的个数是()A.1个B.2个C.3个D.4个10.(3分)二次函数y=﹣2﹣2+c在﹣3≤≤2的范围内有最小值﹣5,则c的值是()A.﹣6B.﹣2C.2D.3二、填空题(本大题共6个小题,每小题3分,共18分)11.(3分)一元二次方程2﹣a=0的一个根是2,则a的值是.12.(3分)把抛物线y=22先向下平移1个单位,再向左平移2个单位,得到的抛物线的解析式是.13.(3分)一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是.14.(3分)设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感.按此比例,如果雕像的高为2m,那么上部应设计为多高?设雕像的上部高m,列方程,并化成一般形式是.15.(3分)如图,正六边形ABCDEF中,P是边ED的中点,连接AP,则=.16.(3分)在⊙O中,弧AB所对的圆心角∠AOB=108°,点C为⊙O上的动点,以AO、AC为边构造▱AOD C.当∠A=°时,线段BD最长.三、解答题(共8题,共72分)17.(8分)解方程:2+﹣3=0.18.(8分)如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°(1)若点C在优弧BD上,求∠ACD的大小;(2)若点C在劣弧BD上,直接写出∠ACD的大小.19.(8分)甲、乙、丙三个盒子中分别装有除颜色外都相同的小球,甲盒中装有两个球,分别为一个红球和一个绿球;乙盒中装有三个球,分别为两个绿球和一个红球;丙盒中装有两个球,分别为一个红球和一个绿球,从三个盒子中各随机取出一个小球(1)请画树状图,列举所有可能出现的结果(2)请直接写出事件“取出至少一个红球”的概率.20.(8分)如图,在平面直角坐标系中有点A(﹣4,0)、B(0,3)、P(a,﹣a)三点,线段CD与AB关于点P中心对称,其中A、B的对应点分别为C、D(1)当a=﹣4时①在图中画出线段CD,保留作图痕迹②线段CD向下平移个单位时,四边形ABCD为菱形;(2)当a=时,四边形ABCD为正方形.21.(8分)如图,点D在⊙O的直径AB的延长线上,CD切⊙O于点C,AE⊥CD于点E (1)求证:AC平分∠DAE;(2)若AB=6,BD=2,求CE的长.22.(10分)投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为m(1)设垂直于墙的一边长为y m,直接写出y与之间的函数关系式;(2)若菜园面积为384m2,求的值;(3)求菜园的最大面积.23.(10分)如图,点C为线段AB上一点,分别以AB、AC、CB为底作顶角为120°的等腰三角形,顶角顶点分别为D、E、F(点E、F在AB的同侧,点D在另一侧)(1)如图1,若点C是AB的中点,则∠AED=;(2)如图2,若点C不是AB的中点①求证:△DEF为等边三角形;②连接CD,若∠ADC=90°,AB=3,请直接写出EF的长.24.(12分)已知抛物线y=a2+2+c与轴交于A(﹣1,0)、B(3,0)两点,一次函数y =+b的图象l经过抛物线上的点C(m,n)(1)求抛物线的解析式;(2)若m=3,直线l与抛物线只有一个公共点,求的值;(3)若=﹣2m+2,直线l与抛物线的对称轴相交于点D,点P在对称轴上.当PD=PC时,求点P的坐标.湖北省武汉市九年级(上)期末数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,共30分)1.(3分)方程(﹣5)=0化成一般形式后,它的常数项是()A.﹣5B.5C.0D.1【解答】解:∵(﹣5)=0∴2﹣5=0,∴方程(﹣5)=0化成一般形式后,它的常数项是0,故选:C.2.(3分)二次函数y=2(﹣3)2﹣6()A.最小值为﹣6B.最大值为﹣6C.最小值为3D.最大值为3【解答】解:∵a=2>0,∴二次函数有最小值为﹣6.故选:A.3.(3分)下列交通标志中,是中心对称图形的是()A.B.C.D.【解答】解:A、不是中心对称图形;B、不是中心对称图形;C、不是中心对称图形;D、是中心对称图形.故选:D.4.(3分)事件①:射击运动员射击一次,命中靶心;事件②:购买一张彩票,没中奖,则()A.事件①是必然事件,事件②是随机事件B.事件①是随机事件,事件②是必然事件C.事件①和②都是随机事件D.事件①和②都是必然事件【解答】解:射击运动员射击一次,命中靶心是随机事件;购买一张彩票,没中奖是随机事件,故选:C.5.(3分)抛掷一枚质地均匀的硬币,正面朝上的概率为0.5,下列说法正确的是()A.连续抛掷2次必有1次正面朝上B.连续抛掷10次不可能都正面朝上C.大量反复抛掷每100次出现正面朝上50次D.通过抛掷硬币确定谁先发球的比赛规则是公平的【解答】解:抛掷一枚质地均匀的硬币,正面朝上的概率为0.5,可以用到实际生活,通过抛掷硬币确定谁先发球的比赛规则是公平的.故选:D.6.(3分)一元二次方程2+2+m=0有两个不相等的实数根,则()A.m>3B.m=3C.m<3D.m≤3【解答】解:∵一元二次方程2+2+m=0有两个不相等的实数根,∴△=(2)2﹣4m>0,解得:m<3.故选:C.7.(3分)圆的直径是13cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是()A.相离B.相切C.相交D.相交或相切【解答】解:∵圆的直径为13cm,∴圆的半径为6.5cm,∵圆心与直线上某一点的距离是6.5cm,∴圆的半径≥圆心到直线的距离,∴直线于圆相切或相交,故选:D.8.(3分)如图,等边△ABC的边长为4,D、E、F分别为边AB、BC、AC的中点,分别以A、B、C三点为圆心,以AD长为半径作三条圆弧,则图中三条圆弧的弧长之和是()A.πB.2πC.4πD.6π【解答】解:依题意知:图中三条圆弧的弧长之和=×3=2π.故选:B.9.(3分)如图,△ABC的内切圆与三边分别相切于点D、E、F,则下列等式:①∠EDF=∠B;②2∠EDF=∠A+∠C;③2∠A=∠FED+∠EDF;④∠AED+∠BFE+∠CDF=180°,其中成立的个数是()A.1个B.2个C.3个D.4个【解答】解:不妨设∠B=80°,∠A=40°,∠C=60°.∵△ABC的内切圆与三边分别相切于点D、E、F,∴BE=BF,AE=AD,CF=CD,∴∠BEF=∠BFE=∠EDF=50°,∠CFD=∠CDF=∠FED=60°,∠AED=∠ADE=∠EFD =70°,∴∠EDF≠∠B,2∠A≠∠FED+∠EDF,故①③不正确,∵∠B+∠BEF+∠EFB=180°,∠B+∠A+∠C=180°,∴∠BEF+∠BFE=∠A+∠C,∴2∠EDF=∠A+∠C,故②正确,∵∠AED=∠EFD,∠BFE=∠EDF,∠CDF=∠FED,∴∠AED+∠BFE+∠CDF=∠EFD+∠EDF+∠FED=180°,故④正确.故选:B.10.(3分)二次函数y=﹣2﹣2+c在﹣3≤≤2的范围内有最小值﹣5,则c的值是()A.﹣6B.﹣2C.2D.3【解答】解:把二次函数y=﹣2﹣2+c转化成顶点坐标式为y=﹣(+1)2+c+1,又知二次函数的开口向下,对称轴为=﹣1,故当=2时,二次函数有最小值为﹣5,故﹣9+c+1=﹣5,故c=3.故选:D.二、填空题(本大题共6个小题,每小题3分,共18分)11.(3分)一元二次方程2﹣a=0的一个根是2,则a的值是4.【解答】解:把=2代入方程2﹣a=0得4﹣a=0,解得a=4.故答案为4.12.(3分)把抛物线y=22先向下平移1个单位,再向左平移2个单位,得到的抛物线的解析式是y=2(+2)2﹣1.【解答】解:由“左加右减”的原则可知,二次函数y=22的图象向下平移1个单位得到y=22﹣1,由“上加下减”的原则可知,将二次函数y=22﹣1的图象向左平移2个单位可得到函数y=2(+2)2﹣1,故答案是:y=2(+2)2﹣1.13.(3分)一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是.【解答】解:画树状图如下:随机地摸出一个小球,然后放回,再随机地摸出一个小球,共有16种等可能的结果数,其中两次摸出的小球标号的和等于5的占4种,所有两次摸出的小球标号的和等于5的概率为=,故答案为:.14.(3分)设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感.按此比例,如果雕像的高为2m,那么上部应设计为多高?设雕像的上部高m,列方程,并化成一般形式是2﹣6+4=0.【解答】解:设雕像的上部高m,则题意得:,整理得:2﹣6+4=0,故答案为:2﹣6+4=015.(3分)如图,正六边形ABCDEF中,P是边ED的中点,连接AP,则=.【解答】解:连接AE,过点F作FH⊥AE,∵六边形ABCDEF是正六边形,∴AB=BC=CD=DE=EF=a,∠AFE=∠DEF=120°,∴∠FAE=∠FEA=30°,∴∠AEP=90°,∴FH=,∴AH=,AE=,∵P是ED的中点,∴EP=,∴AP=.∴=16.(3分)在⊙O中,弧AB所对的圆心角∠AOB=108°,点C为⊙O上的动点,以AO、AC为边构造▱AOD C.当∠A=27°时,线段BD最长.【解答】解:如图,连接OC,延长OA交⊙O于F,连接DF.∵四边形ACDO是平行四边形,∴∠DOF=∠A,DO=AC,∵OF=AO,∴△DOF≌△CAO,∴DF=OC,∴点D的运动轨迹是F为圆心OC为半径的圆,∴当点D在BF的延长线上时,BD的值最大,∵∠AOB=108°,∴∠FOB=72°,∵OF=OB,∴∠OFB=54°,∵FD=FO,∴∠FOD=∠FDO=27°,∴∠A=∠FOD=27°,故答案为27°.三、解答题(共8题,共72分)17.(8分)解方程:2+﹣3=0.【解答】解:∵a=1,b=1,c=﹣3,∴b2﹣4ac=1+12=13>0,∴=,∴1=,2=.18.(8分)如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°(1)若点C在优弧BD上,求∠ACD的大小;(2)若点C在劣弧BD上,直接写出∠ACD的大小.【解答】解:(1)∵AO⊥BD,∴=,∴∠AOB=2∠ACD,∵∠AOB=80°,∴∠ACD=40°;(2)①当点C1在上时,∠AC1D=∠ACD=40°;②当点C2在上时,∵∠AC2D+∠ACD=180°,∴∠AC2D=140°综上所述,∠ACD=140°或40°.19.(8分)甲、乙、丙三个盒子中分别装有除颜色外都相同的小球,甲盒中装有两个球,分别为一个红球和一个绿球;乙盒中装有三个球,分别为两个绿球和一个红球;丙盒中装有两个球,分别为一个红球和一个绿球,从三个盒子中各随机取出一个小球(1)请画树状图,列举所有可能出现的结果(2)请直接写出事件“取出至少一个红球”的概率.【解答】解:(1)如图所示:所有等可能结果为(红、绿、红)、(红、绿、绿)、(红、绿、红)、(红、绿、绿)、(红、红、红)、(红、红、绿),(绿、绿、红)、(绿、绿、绿)、(绿、绿、红)、(绿、绿、绿)(绿、红、红)、(绿、红、绿)这12种等可能结果;(2)因为“取出至少一个红球”的结果数为10钟,所以“取出至少一个红球”的概率为=.20.(8分)如图,在平面直角坐标系中有点A(﹣4,0)、B(0,3)、P(a,﹣a)三点,线段CD与AB关于点P中心对称,其中A、B的对应点分别为C、D(1)当a=﹣4时①在图中画出线段CD,保留作图痕迹②线段CD向下平移2个单位时,四边形ABCD为菱形;(2)当a=﹣时,四边形ABCD为正方形.【解答】解:(1)①线段CD如图所示;②当AB=BC时,四边形ABCD是菱形,此时C(﹣4,6),原点C坐标(﹣4,8),∴线段CD向下平移2个单位时,四边形ABCD为菱形;故答案为2.(2)由题意AB=5,当PA=PB=时,四边形ABCD是正方形,∴(a)2+(﹣a﹣3)2=()2,解得a=﹣或(舍弃)∴当a=﹣时,四边形ABCD为正方形.故答案为﹣.21.(8分)如图,点D在⊙O的直径AB的延长线上,CD切⊙O于点C,AE⊥CD于点E (1)求证:AC平分∠DAE;(2)若AB=6,BD=2,求CE的长.【解答】(1)证明:连接O C.∵CD是⊙O的切线,∴∠OCD=90°,∵∠AEC=90°,∴∠OCD=∠AEC,∴AE∥OC,∴∠EAC=∠ACO,∵OA=OC,∴∠OAC=∠OCA,∴∠EAC=∠OAC,∴AC平分∠DAE.(2)作CF⊥AB于F.在Rt△OCD中,∵OC=3,OD=5,∴CD=4,∵•OC•CD=•OD•CF,∴CF=,∵AC平分∠DAE,CE⊥AE,CF⊥AD,∴CE=CF=.22.(10分)投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为m(1)设垂直于墙的一边长为y m,直接写出y与之间的函数关系式;(2)若菜园面积为384m2,求的值;(3)求菜园的最大面积.【解答】解:(1)根据题意知,y==﹣+;(2)根据题意,得:(﹣+)=384,解得:=18或=32,∵墙的长度为24m,∴=18;(3)设菜园的面积是S,则S=(﹣+)=﹣2+=﹣(﹣25)2+∵﹣<0,∴当<25时,S随的增大而增大,∵≤24,∴当=24时,S取得最大值,最大值为416,答:菜园的最大面积为416m2.23.(10分)如图,点C为线段AB上一点,分别以AB、AC、CB为底作顶角为120°的等腰三角形,顶角顶点分别为D、E、F(点E、F在AB的同侧,点D在另一侧)(1)如图1,若点C是AB的中点,则∠AED=90°;(2)如图2,若点C不是AB的中点①求证:△DEF为等边三角形;②连接CD,若∠ADC=90°,AB=3,请直接写出EF的长.【解答】解:(1)如图1,过E作EH⊥AB于H,连接CD,设EH=,则AE=2,AH=,∵AE=EC,∴AC=2AH=2,∵C是AB的中点,AD=BD,∴CD⊥AB,∵∠ADB=120°,∴∠DAC=30°,∴DC=2,∴DC=CE=2,∵EH∥DC,∴∠HED=∠EDC=∠CED,∵∠AEH=60°,∠AEC=120°,∴∠HEC=60°,∴∠HED=30°,∴∠AED=∠AEH+∠HED=90°;故答案为:90°;(2分)(2)①延长FC交AD于H,连接HE,如图2,∵CF=FB,∴∠FCB=∠FBC,∵∠CFB=120°,∴∠FCB=∠FBC=30°,同理:∠DAB=∠DBA=30°,∠EAC=∠ECA=30°,∴∠DAB=∠ECA=∠FBD,∴AD∥EC∥BF,同理AE∥CF∥BD,∴四边形BDHE、四边形AECH是平行四边形,(4分)∴EC=AH,BF=HD,∵AE=EC,∴AE=AH,∵∠HAE=60°,∴△AEH是等边三角形,∴AE=AH=HE=CE,∠AHE=∠AEH=60°,∴∠DHE=120°,∴∠DHE=∠FCE.∵DH=BF=FC,∴△DHE≌△FCE(SAS),∴DE=EF,∠DEH=∠FEC,∴∠DEF=∠CEH=60°,∴△DEF是等边三角形;(7分)②如图3,过E作EM⊥AB于M,∵∠ADC=90°,∠DAC=30°,∴∠ACD=60°,∵∠DBA=30°,∴∠CDB=∠DBC=30°,∴CD=BC=AC,∵AB=3,∵AC=2,BC=CD=1,∵∠ACE=30°,∠ACD=60°,∴∠ECD=30°+60°=90°,∵AE=CE,∴CM=AC=1,∵∠ACE=30°,∴CE=,Rt△DEC中,DE===,由①知:△DEF是等边三角形,∴EF=DE=.(12分)24.(12分)已知抛物线y=a2+2+c与轴交于A(﹣1,0)、B(3,0)两点,一次函数y =+b的图象l经过抛物线上的点C(m,n)(1)求抛物线的解析式;(2)若m=3,直线l与抛物线只有一个公共点,求的值;(3)若=﹣2m+2,直线l与抛物线的对称轴相交于点D,点P在对称轴上.当PD=PC时,求点P的坐标.【解答】解:(1)∵抛物线y=a2+2+c与轴交于A(﹣1,0)、B(3,0)两点,∴,解得.所以,抛物线的解析式为y=﹣2+2+3;(2)∵抛物线上的点C(m,n),∴n=﹣m2+2m+3,当m=3时,n=0,∴C(3,0),∴一次函数y=+b的图象l经过抛物线上的点C(m,n),∴3+b=0,∴b=﹣3,∴一次函数的解析式为y=﹣3,∵直线l与抛物线只有一个公共点,∴方程﹣3=﹣2+2+3有两个相等的实数根,∴(﹣2)2+4(3+3)=0,解得=﹣4;(3)如图,过C点作CH⊥PD于H,C(m,n)在直线y=+b上,∴n=(﹣2m+2)m+b,∵点C在抛物线上,∴n=﹣m2+2m+3,∴b=m2+3,∴直线l为y=(﹣2m+2)+m2+3,∵直线l与抛物线的对称轴相交于点D,∴D的横坐标为1,代入得:y=﹣2m+2+m2+3=8﹣(﹣m2+2m+3)=8﹣n,∴D(1,8﹣n),设P(1,p),则PD=8﹣n﹣p,HC=m﹣1,PH=p﹣n,在Rt△PCH中,PC=PD=8﹣n﹣p,∴(8﹣n﹣p)2=(p﹣n)2+(m﹣1)2∴(8﹣n﹣p)2﹣(p﹣n)2=(m﹣1)2,∴(8﹣2n)(8﹣2p)=m2﹣2m+1,∵n=﹣m2+2m+3,∴2(4﹣n)(8﹣2p)=4﹣n,∵=﹣2m+2≠0,∴m≠1,∴n≠4,∴4﹣n≠0,∴2(8﹣2p)=1,∴p=,∴P(1,).。
2023-2024学年贵州省贵阳市九年级上学期期末考试数学试题
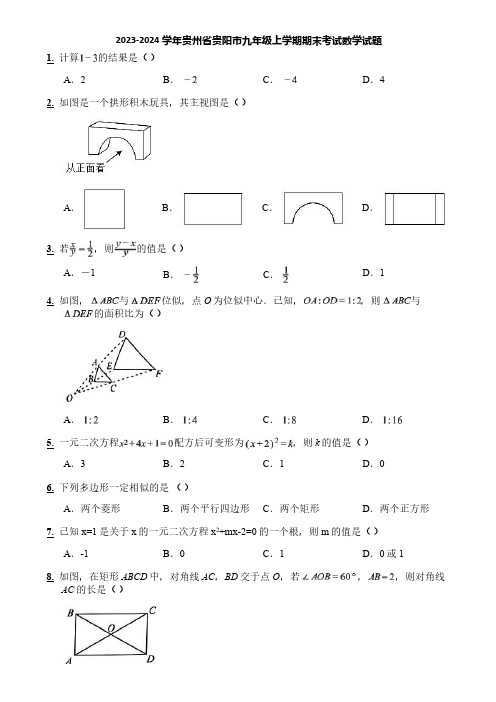
2023-2024学年贵州省贵阳市九年级上学期期末考试数学试题1.计算的结果是()A.2B.C.D.42.如图是一个拱形积木玩具,其主视图是()A.B.C.D.3.若,则的值是()A.-1B.C.D.14.如图,与位似,点O为位似中心.已知,,则与的面积比为()A.B.C.D.5.一元二次方程配方后可变形为,则k的值是()A.3B.2C.1D.06.下列多边形一定相似的是()A.两个菱形B.两个平行四边形C.两个矩形D.两个正方形7.已知x=1是关于x的一元二次方程x2+mx-2=0的一个根,则m的值是()A.-1B.0C.1D.0或18.如图,在矩形ABCD中,对角线AC,BD交于点O,若,,则对角线AC的长是()A .4B .3C .2D .19.已知蓄电池的电压为定值,使用蓄电池时,电流(单位:A )与电阻(单位:)是反比例函数关系.下列反映电流与电阻之间函数关系的图象大致是()A.B.C.D .10.小红拿着一块矩形木框在阳光下做投影实验,这块矩形木框在地面上的投影不可能是()A.B.C .D .11.2023年12月16日,贵阳市轨道交通三号线正式运营.某校共有1000个学生,随机调查了100个学生,其中有16个学生在三号线开通首日乘坐了地铁三号线.在该校随机问一个学生,他在三号线开通首日乘坐该地铁的概率大约是()A .0.016B .0.1C .0.116D .0.1612.国庆期间电影《志愿军:雄兵出击》上映的第一天票房约为2亿元,第二、三天单日票房持续增长,三天累计票房亿元,若第二、三天单日票房增长率相同,设平均每天票房的增长率为x ,则根据题意,下列方程正确的是()A .B .C .D .13.计算(x 3)2的结果是____________.14.方程的解是________.15.如图,在这架小提琴中,点C 是线段AB的黄金分割点().若,则______cm .16.如图,在边长为2的菱形ABCD中,,M是AB的中点,连接DM,EM,且,则CE的长是______.17.如图是一个几何体的三种视图.(1)这个几何体的名称是______;(2)由图中尺寸,计算这个几何体的侧面积.18.“双减”政策下,为了切实提高课后服务质量,某中学开展了丰富多彩的课后服务活动,设置了劳动技能、经典阅读、科普活动三大板块课程(依次记为A、B、C).若该校小红和小星两名同学随机选择一个板块课程.(1)小红选择“科普活动”板块课程的概率是______;(2)利用画树状图或列表的方法,求小红和小星同时选择“劳动技能”板块课程的概率.19.综合实践课上,小星在甲秀楼附近P处放置一面平面镜(平面镜的大小忽略不计),示意图如图所示,他站在C处通过平面镜恰好能看到甲秀楼的顶端A点,此时测得小星的脚到平面镜的距离.已知平面镜到甲秀楼底部中心的距离,小星眼睛到地面的距离,点C,P,B在同一水平直线上,且DC,AB均垂直于水平地面C B.请你用光的反射定理,帮小星计算出甲秀楼AB的高度.20.如图,在中,,,,动点P从点C出发,沿CA方向运动,动点Q同时从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.(1)运动几秒时,点P,Q相距6cm?(2)的面积能等于吗?为什么?21.如图,在中,BE平分,CE平分,,,BC,EF交于点O.(1)判断四边形BFCE的形状,并说明理由;(2)若过点E作交DC于点G,画出线段EG,判断线段EG与EF的数量关系,并说明理由.22.小星根据学习反比例函数的经验,探究函数的图象与性质.(1)下面是画函数图象的步骤:列表:x…-4-2-1124…y…12a b21…其中,______,______,描点、连线:把图象补充完整;(2)观察函数的图象,当时,直接写出自变量x的取值范围.23.如图,小红在学习了正方形相关知识后,对正方形进行了探究,在正方形ABCD的外侧作了直线DP.(1)【动手操作】点C关于直线DP的对称点为E,连接CE,AE,其中AE交直线DP于点F.依题意在图①中补全图形;(2)【问题解决】在(1)的条件下,若,求的度数;(3)【拓展延伸】如图②,若,点C关于直线DP的对称点为E,连接CE,AE,其中AE交直线DP于点F.探究线段AB,AF,EF之间的数量关系,并说明理由.。
四川省眉山市仁寿县2019-2020年九年级(上)期末数学试卷 解析版

2019-2020学年九年级(上)期末数学试卷一.选择题(共12小题)1.二次根式中x的取值范围是()A.x≥﹣2 B.x≥2 C.x≥0 D.x>﹣22.下列计算正确的是()A.B.C.÷D.3.若关于x的一元二次方程kx2+2x﹣1=0有实数根,则k的取值范围是()A.k>﹣1 B.k≥﹣1 C.k>﹣1且k≠0 D.k≥﹣1且k≠0 4.如图,△ABC中,D是AB的中点,DE∥BC,连结BE,若S△DEB=1,则S△BCE的值为()A.1 B.2 C.3 D.45.按如下方法,将△ABC的三边缩小到原来的,如图,任取一点O,连结AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是()A.点O为位似中心且位似比为1:2B.△ABC与△DEF是位似图形C.△ABC与△DEF是相似图形D.△ABC与△DEF的面积之比为4:16.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且AB=BD,则tan D的值为()A.B.C.D.7.下列事件中是随机事件的个数是()①投掷一枚硬币,正面朝上;②五边形的内角和是540°;③20件产品中有5件次品,从中任意抽取6件,至少有一件是次品;④一个图形平移后与原来的图形不全等.A.0 B.1 C.2 D.38.关于二次函数y=x2+4x﹣5,下列说法正确的是()A.图象与y轴的交点坐标为(0,5)B.图象的对称轴在y轴的右侧C.当x<﹣2时,y的值随x值的增大而减小D.图象与x轴的两个交点之间的距离为59.如图,点A、B、C、D均在边长为1的正方形网格的格点上,则sin∠BAC的值为()A.B.1 C.D.10.为解决群众看病贵的问题,有关部门决定降低药价,原价为30元的药品经过连续两次降价,价格变为24.3元,则平均每次降价的百分率为()A.10% B.15% C.20% D.25%11.把抛物线y=(x﹣1)2+2沿x轴向右平移2个单位后,再沿y轴向下平移3个单位,得到的抛物线解析式为()A.y=(x﹣3)2+1 B.y=(x+1)2﹣1 C.y=(x﹣3)2﹣1 D.y=(x+1)2﹣2 12.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE②△DFP∽△BPH③DP2=PH•PC;④FE:BC=,其中正确的个数为()A.1 B.2 C.3 D.4二.填空题(共6小题)13.方程x2=x的解是.14.已知:a,b在数轴上的位置如图所示,化简代数式:=.15.如图,在△ABC中,AB>AC,D、E分别为边AB、AC上的一点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件使△FDB与△ADE相似,则添加的一个条件是.16.如图,已知公路L上A,B两点之间的距离为100米,小明要测量点C与河对岸的公路L的距离,在A处测得点C在北偏东60°方向,在B处测得点C在北偏东30°方向,则点C到公路L的距离CD为米.17.关于x的方程x2﹣3x﹣m=0的两实数根为x1,x2,且,则m的值为.18.已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论:①abc>0;②方程ax2+bx+c=0的两根是x1=﹣1,x2=3;③2a+b=0;④4a2+2b+c<0,其中正确结论的序号为.三.解答题(共8小题)19.计算:20.已知:▱ABCD的两边AB,AD的长是关于x的方程x2﹣mx+﹣=0的两个实数根.(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;(2)若AB的长为2,那么▱ABCD的周长是多少?21.如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF =∠B,且点D、F分别在边AB、AC上.(1)求证:△BDE∽△CEF;(2)当点E移动到BC的中点时,求证:FE平分∠DFC.22.某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:(1)扇形统计图中“优秀”所对应的扇形的圆心角为度,并将条形统计图补充完整.(2)此次比赛有三名同学得满分,分别是甲、乙、丙,现从这三名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丙的概率.23.如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)24.某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高售价减少销售量的办法增加利润,如果这种商品每件的售价每提高0.5元,其销售量就减少10件,问:①应将每件售价定为多少元,才能使每天的利润为640元?②店主想要每天获得最大利润,请你帮助店主确定商品售价并指出每天的最大利润W为多少元?25.在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;(2)如图2,①求证:BP=BF;②当AD=25,且AE<DE时,求cos∠PCB的值;③当BP=9时,求BE•EF的值.26.如图抛物线y=ax2+bx+c的图象过点A(﹣1,0),B(3,0),C(0,3).(1)求抛物线的解析式,并指出抛物线的顶点坐标.(2)在抛物线的对称轴上是否存在一点P,使得△PAC的周长最小,若存在,请求出点P的坐标及△PAC的周长;若不存在,请说明理由.(3)在(2)的条件下,在抛物线上是否存在点M(不与C点重合),使得S△PAM=S△PAC,若存在,请求出点M的坐标;若不存在,请说明理由.参考答案与试题解析一.选择题(共12小题)1.二次根式中x的取值范围是()A.x≥﹣2 B.x≥2 C.x≥0 D.x>﹣2【分析】根据二次根式有意义的条件即可求出x的范围.【解答】解:由题意可知:x+2≥0,∴x≥﹣2,故选:A.2.下列计算正确的是()A.B.C.÷D.【分析】根据二次根式的加减法对A、B进行判断;根据二次根式的除法法则对C进行判断;根据完全平方公式对D进行判断.【解答】解:A、原式=2﹣,所以A选项错误;B、3与不能合并,所以B选项错误;C、原式==2,所以C选项正确;D、原式=3+4+4=7+4,所以D选项错误.故选:C.3.若关于x的一元二次方程kx2+2x﹣1=0有实数根,则k的取值范围是()A.k>﹣1 B.k≥﹣1 C.k>﹣1且k≠0 D.k≥﹣1且k≠0 【分析】方程有实数根,则根的判别式△≥0,且二次项系数不为零.【解答】解:∵△=b2﹣4ac=22﹣4×k×(﹣1)≥0,解上式得,k≥﹣1,∵二次项系数k≠0,∴k≥﹣1且k≠0.故选:D.4.如图,△ABC中,D是AB的中点,DE∥BC,连结BE,若S△DEB=1,则S△BCE的值为()A.1 B.2 C.3 D.4【分析】根据三角形中位线定理和三角形的面积即可得到结论.【解答】解:∵D是AB的中点,DE∥BC,∴CE=AE.∴DE=BC,∵S△DEB=1,∴S△BCE=2,故选:B.5.按如下方法,将△ABC的三边缩小到原来的,如图,任取一点O,连结AO,BO,CO,并取它们的中点D、E、F,得△DEF;则下列说法错误的是()A.点O为位似中心且位似比为1:2B.△ABC与△DEF是位似图形C.△ABC与△DEF是相似图形D.△ABC与△DEF的面积之比为4:1【分析】根据位似图形的性质,得出①△ABC与△DEF是位似图形进而根据位似图形一定是相似图形得出②△ABC与△DEF是相似图形,再根据周长比等于位似比,以及根据面积比等于相似比的平方,即可得出答案.【解答】解:∵如图,任取一点O,连结AO,BO,CO,并取它们的中点D、E、F,得△DEF,∴将△ABC的三边缩小到原来的,此时点O为位似中心且△ABC与△DEF的位似比为2:1,故选项A说法错误,符合题意;△ABC与△DEF是位似图形,故选项B说法正确,不合题意;△ABC与△DEF是相似图形,故选项C说法正确,不合题意;△ABC与△DEF的面积之比为4:1,故选项D说法正确,不合题意;故选:A.6.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且AB=BD,则tan D的值为()A.B.C.D.【分析】设AC=m,解直角三角形求出AB,BC,BD即可解决问题.【解答】解:设AC=m,在Rt△ABC中,∵∠C=90°,∠ABC=30°,∴AB=2AC=2m,BC=AC=m,∴BD=AB=2m,DC=2m+m,∴tan∠ADC===2﹣.故选:D.7.下列事件中是随机事件的个数是()①投掷一枚硬币,正面朝上;②五边形的内角和是540°;③20件产品中有5件次品,从中任意抽取6件,至少有一件是次品;④一个图形平移后与原来的图形不全等.A.0 B.1 C.2 D.3【分析】根据事件发生的可能性大小判断相应事件的类型即可.【解答】解:①掷一枚硬币正面朝上是随机事件;②五边形的内角和是540°是必然事件;③20件产品中有5件次品,从中任意抽取6件,至少有一件是次品是随机事件;④一个图形平移后与原来的图形不全等是不可能事件;则是随机事件的有①③,共2个;故选:C.8.关于二次函数y=x2+4x﹣5,下列说法正确的是()A.图象与y轴的交点坐标为(0,5)B.图象的对称轴在y轴的右侧C.当x<﹣2时,y的值随x值的增大而减小D.图象与x轴的两个交点之间的距离为5【分析】通过计算自变量为0的函数值可对A进行判断;利用对称轴方程可对B进行判断;根据二次函数的性质对C进行判断;通过解x2+4x﹣5=0得抛物线与x轴的交点坐标,则可对D进行判断.【解答】解:A、当x=0时,y=x2+4x﹣5=﹣5,所以抛物线与y轴的交点坐标为(0,﹣5),所以A选项错误;B、抛物线的对称轴为直线x=﹣=﹣2,所以抛物线的对称轴在y轴的左侧,所以B选项错误;C、抛物线开口向上,当x<﹣2时,y的值随x值的增大而减小,所以C选项正确;D、当y=0时,x2+4x﹣5=0,解得x1=﹣5,x2=1,抛物线与x轴的交点坐标为(﹣5,0),(1,0),两交点间的距离为1+5=6,所以D选项错误.故选:C.9.如图,点A、B、C、D均在边长为1的正方形网格的格点上,则sin∠BAC的值为()A.B.1 C.D.【分析】连接BC,由勾股定理得AC2=BC2=12+22=5,AB2=12+32=10,则AC=BC,AC2+BC2=AB2,得出△ABC是等腰直角三角形,则∠BAC=45°,即可得出结果.【解答】解:连接BC,如图3所示;由勾股定理得:AC2=BC2=12+22=5,AB2=12+32=10,∴AC=BC,AC2+BC2=AB2,∴△ABC是等腰直角三角形,∴∠BAC=45°,∴sin∠BAC=,故选:A.10.为解决群众看病贵的问题,有关部门决定降低药价,原价为30元的药品经过连续两次降价,价格变为24.3元,则平均每次降价的百分率为()A.10% B.15% C.20% D.25%【分析】设平均每次降价的百分率为x,根据该药品的原价及经过两次降价后的价格,即可得出关于x的一元二次方程,解之取其较小值即可得出结论.【解答】解:设平均每次降价的百分率为x,依题意,得:30(1﹣x)2=24.3,解得:x1=0.1=10%,x2=1.9(不合题意,舍去).故选:A.11.把抛物线y=(x﹣1)2+2沿x轴向右平移2个单位后,再沿y轴向下平移3个单位,得到的抛物线解析式为()A.y=(x﹣3)2+1 B.y=(x+1)2﹣1 C.y=(x﹣3)2﹣1 D.y=(x+1)2﹣2 【分析】直接根据“上加下减,左加右减”的原则进行解答.【解答】解:把抛物线y=(x﹣1)2+2沿x轴向右平移2个单位后,再沿y轴向下平移3个单位,得到的抛物线解析式为y=(x﹣1﹣2)2+2﹣3,即y=(x﹣3)2﹣1.故选:C.12.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE②△DFP∽△BPH③DP2=PH •PC;④FE:BC=,其中正确的个数为()A.1 B.2 C.3 D.4【分析】由正方形的性质和相似三角形的判定与性质,即可得出结论.【解答】解:∵△BPC是等边三角形,∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,在正方形ABCD中,∵AB=BC=CD,∠A=∠ADC=∠BCD=90°∴∠ABE=∠DCF=30°,∴BE=2AE;故①正确;∵PC=CD,∠PCD=30°,∴∠PDC=75°,∴∠FDP=15°,∵∠DBA=45°,∴∠PBD=15°,∴∠FDP=∠PBD,∵∠DFP=∠BPC=60°,∴△DFP∽△BPH;故②正确;∵∠PDH=∠PCD=30°,∠DPH=∠DPC,∴△DPH∽△CPD,∴,∴DP2=PH•PC,故③正确;∵∠ABE=30°,∠A=90°∴AE=AB=BC,∵∠DCF=30°,∴DF=DC=BC,∴EF=AE+DF﹣BC=﹣BC,∴FE:BC=(2﹣3):3故④正确,故选:D.二.填空题(共6小题)13.方程x2=x的解是x1=0,x2=1 .【分析】将方程化为一般形式,提取公因式分解因式后,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解.【解答】解:x2=x,移项得:x2﹣x=0,分解因式得:x(x﹣1)=0,可得x=0或x﹣1=0,解得:x1=0,x2=1.故答案为:x1=0,x2=114.已知:a,b在数轴上的位置如图所示,化简代数式:=2 .【分析】根据二次根式的性质=|a|开平方,再结合数轴确定a﹣1,a+b,1﹣b的正负性,然后去绝对值,最后合并同类项即可.【解答】解:原式=|a﹣1|﹣|a+b|+|1﹣b|,=1﹣a﹣(﹣a﹣b)+(1﹣b),=1﹣a+a+b+1﹣b,=2,故答案为:2.15.如图,在△ABC中,AB>AC,D、E分别为边AB、AC上的一点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件使△FDB与△ADE相似,则添加的一个条件是DF∥AC,或∠BFD=∠A.【分析】结论:DF∥AC,或∠BFD=∠A.根据相似三角形的判定方法一一证明即可.【解答】解:DF∥AC,或∠BFD=∠A.理由:∵∠A=∠A,==,∴△ADE∽△ACB,∴①当DF∥AC时,△BDF∽△BAC,∴△BDF∽△EAD.②当∠BFD=∠A时,∵∠B=∠AED,∴△FBD∽△AED.故答案为:DF∥AC,或∠BFD=∠A.16.如图,已知公路L上A,B两点之间的距离为100米,小明要测量点C与河对岸的公路L的距离,在A处测得点C在北偏东60°方向,在B处测得点C在北偏东30°方向,则点C到公路L的距离CD为50米.【分析】作CD⊥直线l,由∠ACB=∠CAB=30°,AB=50m知AB=BC=50m,∠CBD=60°,根据CD=BC sin∠CBD计算可得.【解答】解:如图,过点C作CD⊥直线l于点D,∵∠BCD=30°,∠ACD=60°,∴∠ACB=∠CAB=30°,∵AB=100m,∴AB=BC=100m,∠CBD=60°,在Rt△BCD中,∵sin∠CBD=,∴CD=BC sin∠CBD=100×=50(m),故答案是:50.17.关于x的方程x2﹣3x﹣m=0的两实数根为x1,x2,且,则m的值为﹣1 .【分析】根据根与系数的关系即可求出答案.【解答】解:由题意可知:x1+x2=3,x1x2=﹣m,∵,∴﹣3x1+x1+x2=2x1x2,∴m+3=﹣2m,∴m=﹣1,故答案为:﹣118.已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论:①abc>0;②方程ax2+bx+c=0的两根是x1=﹣1,x2=3;③2a+b=0;④4a2+2b+c<0,其中正确结论的序号为②③.【分析】根据二次函数图象的开口方向、对称轴位置、与x轴的交点坐标等知识,逐个判断即可.【解答】解:由图象可知,抛物线开口向下,a<0,对称轴在y轴右侧,a、b异号,b >0,与y轴交于正半轴,c>0,所以abc<0,因此①是错误的;当y=0时,抛物线与x轴交点的横坐标就是ax2+bx+c=0的两根,由图象可得x1=﹣1,x2=3;因此②正确;对称轴为x=1,即﹣=1,也就是2a+b=0;因此③正确,∵a<0,a2>0,b>0,c>0,∴4a2+2b+c>0,因此④是错误的,故答案为:②③.三.解答题(共8小题)19.计算:【分析】利用特殊角的三角函数值、二次根式的性质和二次根式的除法法则运算.【解答】解:原式=4×﹣(﹣)+2﹣+2×=2﹣3++2﹣+2=4﹣1.20.已知:▱ABCD的两边AB,AD的长是关于x的方程x2﹣mx+﹣=0的两个实数根.(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;(2)若AB的长为2,那么▱ABCD的周长是多少?【分析】(1)让根的判别式为0即可求得m,进而求得方程的根即为菱形的边长;(2)求得m的值,进而代入原方程求得另一根,即易求得平行四边形的周长.【解答】解:(1)∵四边形ABCD是菱形,∴AB=AD,∴△=0,即m2﹣4(﹣)=0,整理得:(m﹣1)2=0,解得m=1,当m=1时,原方程为x2﹣x+=0,解得:x1=x2=0.5,故当m=1时,四边形ABCD是菱形,菱形的边长是0.5;(2)把AB=2代入原方程得,m=2.5,把m=2.5代入原方程得x2﹣2.5x+1=0,解得x1=2,x2=0.5,∴C▱ABCD=2×(2+0.5)=5.21.如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF =∠B,且点D、F分别在边AB、AC上.(1)求证:△BDE∽△CEF;(2)当点E移动到BC的中点时,求证:FE平分∠DFC.【分析】(1)根据等腰三角形的性质得到∠B=∠C,根据三角形的内角和和平角的定义得到∠BDE=∠CEF,于是得到结论;(2)根据相似三角形的性质得到,等量代换得到,根据相似三角形的性质即可得到结论.【解答】解:(1)∵AB=AC,∴∠B=∠C,∵∠BDE=180°﹣∠B﹣∠DEB,∠CEF=180°﹣∠DEF﹣∠DEB,∵∠DEF=∠B,∴∠BDE=∠CEF,∴△BDE∽△CEF;(2)∵△BDE∽△CEF,∴,∵点E是BC的中点,∴BE=CE,∴,∵∠DEF=∠B=∠C,∴△DEF∽△ECF,∴∠DFE=∠CFE,∴FE平分∠DFC.22.某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:(1)扇形统计图中“优秀”所对应的扇形的圆心角为72 度,并将条形统计图补充完整.(2)此次比赛有三名同学得满分,分别是甲、乙、丙,现从这三名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丙的概率.【分析】(1)先画出条形统计图,再求出圆心角即可;(2)先画出树状图,再求出概率即可.【解答】解:(1)条形统计图为;;扇形统计图中“优秀”所对应的扇形的圆心角是(1﹣15%﹣25%﹣40%)×360°=72°,故答案为:72;(2)画树状图:由树状图可知:所有等可能的结果有6种,其中符合条件的有2种,所有P(甲、丙)==,即选中的两名同学恰好是甲、丙的概率是.23.如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB(结果保留根号)【分析】作CF⊥AB于点F,设AF=x米,在直角△ACF中利用三角函数用x表示出CF 的长,在直角△ABE中表示出BE的长,然后根据CF﹣BE=DE即可列方程求得x的值,进而求得AB的长.【解答】解:作CF⊥AB于点F,设AF=x米,在Rt△ACF中,tan∠ACF=,则CF====x,在直角△ABE中,AB=x+BF=4+x(米),在直角△ABF中,tan∠AEB=,则BE===(x+4)米.∵CF﹣BE=DE,即x﹣(x+4)=3.解得:x=,则AB=+4=(米).答:树高AB是米.24.某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高售价减少销售量的办法增加利润,如果这种商品每件的售价每提高0.5元,其销售量就减少10件,问:①应将每件售价定为多少元,才能使每天的利润为640元?②店主想要每天获得最大利润,请你帮助店主确定商品售价并指出每天的最大利润W为多少元?【分析】①根据等量关系“利润=(售价﹣进价)×销量”列出函数关系式.②根据①中的函数关系式求得利润最大值.【解答】解:①设每件售价定为x元时,才能使每天利润为640元,(x﹣8)[200﹣20(x﹣10)]=640,解得:x1=12,x2=16.答:应将每件售价定为12元或16元时,能使每天利润为640元.②设利润为y:则y=(x﹣8)[200﹣20(x﹣10)]=﹣20x2+560x﹣3200=﹣20(x﹣14)2+720,∴当售价定为14元时,获得最大利润;最大利润为720元.25.在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E且在AD上,BE交PC于点F.(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;(2)如图2,①求证:BP=BF;②当AD=25,且AE<DE时,求cos∠PCB的值;③当BP=9时,求BE•EF的值.【分析】(1)先判断出∠A=∠D=90°,AB=DC再判断出AE=DE,即可得出结论;(2)①利用折叠的性质,得出∠PGC=∠PBC=90°,∠BPC=∠GPC,进而判断出∠GPF =∠PFB即可得出结论;②判断出△ABE∽△DEC,得出比例式建立方程求解即可得出AE=9,DE=16,再判断出△ECF∽△GCP,进而求出PC,即可得出结论;③判断出△GEF∽△EAB,即可得出结论.【解答】解:(1)在矩形ABCD中,∠A=∠D=90°,AB=DC,∵E是AD中点,∴AE=DE,在△ABE和△DCE中,,∴△ABE≌△DCE(SAS);(2)①在矩形ABCD,∠ABC=90°,∵△BPC沿PC折叠得到△GPC,∴∠PGC=∠PBC=90°,∠BPC=∠GPC,∵BE⊥CG,∴BE∥PG,∴∠GPF=∠PFB,∴∠BPF=∠BFP,∴BP=BF;②当AD=25时,∵∠BEC=90°,∴∠AEB+∠CED=90°,∵∠AEB+∠ABE=90°,∴∠CED=∠ABE,∵∠A=∠D=90°,∴△ABE∽△DEC,∴,设AE=x,∴DE=25﹣x,∴,∴x=9或x=16,∵AE<DE,∴AE=9,DE=16,∴CE=20,BE=15,由折叠得,BP=PG,∴BP=BF=PG,∵BE∥PG,∴△ECF∽△GCP,∴,设BP=BF=PG=y,∴,∴y=,∴BP=,在Rt△PBC中,PC=,cos∠PCB==;③如图,连接FG,∵∠GEF=∠PGC=90°,∴∠GEF+∠PGC=180°,∴BF∥PG∵BF=PG,∴▱BPGF是菱形,∴BP∥GF,∴∠GFE=∠ABE,∴△GEF∽△EAB,∴,∴BE•EF=AB•GF=12×9=108.26.如图抛物线y=ax2+bx+c的图象过点A(﹣1,0),B(3,0),C(0,3).(1)求抛物线的解析式,并指出抛物线的顶点坐标.(2)在抛物线的对称轴上是否存在一点P,使得△PAC的周长最小,若存在,请求出点P的坐标及△PAC的周长;若不存在,请说明理由.(3)在(2)的条件下,在抛物线上是否存在点M(不与C点重合),使得S△PAM=S△PAC,若存在,请求出点M的坐标;若不存在,请说明理由.【分析】(1)根据抛物线y=ax2+bx+c的图象过点A(﹣1,0),B(3,0),C(0,3),可以求得该抛物线的解析式,然后将解析式化为顶点式,即可得到顶点坐标;(2)根据两点之间线段最短,找到点A关于对称轴的对称点是点B,然后连接CB与对称轴的交点,即为所求的点P,然后根据点P在直线BC上,即可求得点P的坐标,进而求得三角形PAC的周长;(3)根据S△PAM=S△PAC,可知以PA为底边时,只要两个三角形等高即可,然后根据题目中的条件,画出相应的图形,利用分类讨论的方法可以求得点M的坐标,本题得以解决.【解答】解:(1)∵抛物线y=ax2+bx+c的图象过点A(﹣1,0),B(3,0),C(0,3),∴,得,∴y=﹣x2+2x+3=﹣(x﹣1)2+4,∴该抛物线的顶点坐标为(1,4),即该抛物线的解析式为y=﹣x2+2x+3,顶点坐标为(1,4);(2)点A关于对称轴的对称点是点B,连接CB与对称轴的交点为P,此时点P即为所求,设过点B(3,0),点C(0,3)的直线解析式为y=kx+m,,得,∴直线BC的解析式为y=﹣x+3,当x=1时,y=﹣1+3=2,∴点P的坐标为(1,2),∵点A(﹣1,0),点C(0,3),点B(3,0),∴AC=,BC=3,∴△PAC的周长是:AC+CP+PA=AC+CB=,即点P的坐标为(1,2),△PAC的周长是;(3)存在点M(不与C点重合),使得S△PAM=S△PAC,∵S△PAM=S△PAC,∴当以PA为底边时,只要两个三角形等高即可,即点M和点C到PA的距离相等,当点M在点C的上方时,则CM∥PA时,点M和点C到PA的距离相等,设过点A(﹣1,0),点P(1,2)的直线l1解析式为:y=kx+m,,得,∴直线AP的解析式为y=x+1,∴直线CM的解析式为y=x+3,由得,,,∴点M的坐标为(1,4);当点M在点C的下方时,则点M所在的直线l2与AP平行,且直线l2与直线AP之间的距离与直线l1与直线AP之间的距离相等,∴直线l2的的解析式为y=x﹣1,由得,,,∴M的坐标为(,)或(,);由上可得,点M的坐标为(1,4),(,)或(,).。
贵州省贵阳市2023-2024学年高一上学期期末考试 数学 含答案

贵阳市普通中学2023—2024学年度第一学期期末监测考试试卷高一数学注意事项:1.本试卷共6页,满分100分,考试时间120分钟.2.答案一律写在答题卡上,写在试卷上的不给分.3.考试过程中不得使用计算器.一、选择题(本大题共8小题,每小题4分,共32分.每小题有四个选项,其中只有一个选项正确,请将你认为正确的选项填写在答题卷的相应位置上.)1.全织U ={0,1,2,3,4,5,6, 7} il s4M = {O, 1,2,3}, N = {3,4,5},U,M, N,找合' 的关系如图所示,则图中阴影部分表示的集合为()u`C.{3}A.{l,2,3,4,5}B.{4,5}D.02命题“3xE R, x2 + x+1 � 0”的否定是()2A.3x e R, x2 + x +l之0B.3x E R, x2 + x+l< 0D.Vx茫R,x·+x+l< 0C.VxER,x2 +x+ l < 0 23对任意角a和fJ."sina = sin/J“是“a=fJ”的()A充分不必要条件B必要不充分条件C.充要条件D既不充分也不必要条件24已知函数f(x)= �+log。
,(2-x),则f(x)的定义域为()4x-3A (扣) B.(扣]C.(-oo,2) D (三)u(扣)5设函数f(x)=2·'+x的零点为X o'则X o所在的区间是()A.(-1,0) C.(1,2)B.(-2,-1) D.(0,1)6设a=(½/,b= 2(c = log2¾,则a,b,c的大小关系为(A. c<a<bB. c < b < aC. a<b<cD.a<c<bII冗7下列选项中,与sin(-飞-)的值不相等的是()A.2sin l5°sin 75°B.cosl8° cos42° -sinl8° sin42°C.2cos2l5°-lD.tan22.5° l-tan2 22.5°8.某池塘野生水葫芦的援盖面积与时间的函数关系图象如图所示.假设其函数关系为指数函数,其中说法错误的是(y/m2l 6t---------------- ,,,81----------t'一气, ,, ,, ,A此指数函数的底数为2B在第5个月时,野生水葫芦的稷盖面积会超过30m2C野生水葫芦从4m2荽延到12m2只需1.5个月D设野生水葫芦蔓延至2m2,3m2,6m2所需的时间分别为x1,x2,x3,则有X1+x2 = X3二、多项选择题(本题共2小题,每小题4分,共8分.在每小题给出的选项中,有多项符合题目要求,全部选对得4分,部分选对得2分,有选错得0分.)9已知a,b,c eR,则下列命题正确的是()I IA若->一,则a<ba bB若ac2> bc2,则(1>bC.若a<b,c <d,则a-c<b-dD若a>b > O,c > 0,则a a+c一>b b+cIO下列说法中,正确的是()IA函数y=-在定义域上是减函数e x -1B.函数y=——一是奇函数e x +lC函数y= f(x+a)-b为奇函数,则函数y=f(x)的图象关于点P(a,b)成中心对称图形D函数f(x)为定义在(-x,,O)U(O冲心)上的奇函数,且f(3) = I.对千任意x,,x2E (0,长't:)),x1:;cx2,汀(x,)-x2f(x2) 3都有1>0成立,则.f(x)三一的解集为(-OCJ,-3] u(0,3]X1 -x2''X三、填空题(本大题共5小题,每小题4分,共20分.请将你认为正确的答案填在答题卷的相应位置上.)11若幕函数f(x)=(11i2-2m-2)义”在(0,+~)上单调递增,则实数m=12函数y= sinx+ cosx的最大值是s13 已知圆和四边形(四个角均为直角)的周长相等,而积分别为S I'鸟,则_]_的最小值为s214已知函数f(x) = 2sin(cv x+(p)(co> O,I例<:)的部分图像如图所示,则f行)=X-2.一一一一-壹15已知函数f(X) = 2kx2 -kx -i (0 ::; X ::;; 2, k E R),若k=I,则该函数的零占为若对沁XE[0,2],不等式f(x) < -2k恒成立,则实数K的取值范围为四、解答题(本大题共4小题,每小题8分,共32分.解答应写出文字说明,证明过程或演算步骤.)16已知角0的终边过点(-3,4),求角0的三个三角函数值.17.(I)已知芦+a令=3,求a+矿的值:(2)已知log2[ l og3 (log4X)] =0'求X的值18 已知函数f(x)=x-�IX(I)判断函数f(x)的奇偶性:1(2)根据定义证明函数f(x)=x--在区间(0,+幻)上单调递增X冗19将函数f(x) =c o s(x+ �)的图象上所有点的横坐标缩短到原来的上,纵坐标不变,得到函数g(x的() 图象(I)求函数g(x)的单调递增区间和对称中心:(2)若关于X的方程2sin2x-m c o s x-4= 0在XE(吟)上有实数解,求实数m的取值范围五、阅读与探究(本大题1个小题,共8分解答应写出文字说明,条理清晰.)20. 《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的瓜要途径,是思想阀门发现新问题、新结论的篮要方法.阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有:(I)整体观察:(2)整体设元;(3)整体代入:(4)整体求和等l l例如,ab=I,求证:一+-=l.I+a I+b证明:原式ab I b I+—=—+—=I. ab+a I+b b+I l+b阅读材料二:解决多元变掀问题时,其中一种思路是运用消元思想将多元问题转化为一元问题,再结合一元问题处理方法进行研究a+b例如,正实数a,b满足ab=L求(l+a)b解:由ab=I,得b=一,的最小值1 a+b a+--;; _ a 2+1_ (a+l }2-2(a+l)+2= = = ..(I+a)b I a+la+I (l+a )� a 2 2 =(a+l)+二-2�2✓(a+l)二-2=2✓2-2,当且仅当a+I =✓2,即a=✓2-1,b = ✓2 +1时,等号成立a+b.. (l+a)b的最小值为2J5-2波利亚在《怎样解题》中指出:“当你找到第一个腮菇或作出第一个发现后,再四处看看,他们总是成群生长”类似问题,我们有更多的式子满足以上特征结合阅读材料解答下列问题:(I)已知ab=I,求+——了的值;l+a 2. l +bI I(2)若正实数a,b 满足ab=I,求M =--=--+ 的最小值I+a I+3b贵阳市普通中学2023—2024学年度第一学期期末监测考试试卷高一数学注意事项:1.本试卷共6页,满分100分,考试时间120分钟.2.答案一律写在答题卡上,写在试卷上的不给分.3.考试过程中不得使用计算器.一、选择题(本大题共8小题,每小题4分,共32分.每小题有四个选项,其中只有一个选项正确,请将你认为正确的选项填写在答题卷的相应位置上.)1.全织U = {0,1,2,3,4,5,6, 7} il s4M = {O, 1,2,3}, N={3,4,5},U,M, N,找合' 的关系如图所示,则图中阴影部分表示的集合为(u`A.{l,2,3,4,5}【答案】B【解析】B.{4,5}【分析】求出M n N,得到阴影部分表示的渠合C.{3}[详解】图中阴影部分表示的渠合为N中元素去掉M n N的元素后的梊合,MnN = {0,1,2,3们{3,4,5}={习,故图中阴影部分表示的集合为{4,5}故选:B2.命题“3xER,x2+x+l2:0”的否定是()A.3x ie R, x2 + x+l ;;:: 0B.3x E R, x2 + x+I <0C.VxER,x2+x+l<0 2D.Vx茫R,X4+x+l< 0【答案】C【解析】【分析】根据命题的否定即可求解D.0【详解】命题“:3x E R, x 2+ x + 1 2:: 0”的否定是“"ix E R,x 2+x+ 1< 0",故选:C3对任意角a 和/3,"sin a = s in/3“是“a=/3”的()A 充分不必要条件B必要不充分条件C.充要条件D 既不充分也不必要条件【答案)B 【解析】【分析】根据三角函数的性质,结合必要不充分的定义即可求解【详解】由sina=s in/3可得a=/J+2朊或者a+/3=冗+2幻,kEZ,故sina=s in/3不能得到a=/3,但a=/3,则sina= s in/3,故“sina=sin/3“是“a=/3”的必要不充分条件,故选:B2 4已知函数f(x) =�+log 。
2019-2020学年福建泉州南安九年级(上)期末数学试卷(含解析)

2019-2020学年福建省泉州市南安市九年级(上)期末数学试卷一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(4分)下列实数中,介于与之间的是()A.B.C.D.π2.(4分)下列计算正确的是()A.B.a+2a=3a C.(2a)3=2a3D.a6÷a3=a23.(4分)为了让市民游客欢度“五一”,泉州市各地推出了许多文化旅游活动和景区优惠,旅游人气持续兴旺.从“五一”假日全市累计接待国内外游客171.18万人次,171.18万这个数用科学记数法应表示为()市文旅局获悉,A.1.7118×102B.0.17118×107C.1.7118×106D.171.18×104.(4分)图①是由五个完全相同的小正方体组成的立方体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是()A.主视图B.俯视图C.左视图D.主视图、俯视图和左视图都改变5.(4分)不透明袋子中装有若干个红球和6个蓝球,这些球除了颜色外,没有其他差别,从袋子中随机摸出一个球,摸出蓝球的概率是0.6,则袋子中有红球()A.4个B.6个C.8个D.10个6.(4分)如图,将直尺与含30°角的三角尺放在一起,若∠1=25°,则∠2的度数是()A.30°B.45°C.55°D.60°7.(4分)如果一个正多边形的内角和等于720°,那么该正多边形的一个外角等于()A.45°B.60°C.72°D.90°8.(4分)如图,在平面直角坐标系中,菱形ABCD的边AB在x轴正半轴上,点A与原点重合,点D的坐标是(3,4),反比例函数y=(k≠0)经过点C,则k的值为()A.12B.15C.20D.329.(4分)完全相同的6个小矩形如图所示放置,形成了一个长、宽分别为n、m的大矩形,则图中阴影部分的周长是()A.6(m﹣n)B.3(m+n)C.4n D.4m10.(4分)如图,矩形ABCD中,E是AB的中点,将△BCE沿CE翻折,点B落在点F处,tan∠DCE=.设AB=x,△ABF的面积为y,则y与x的函数图象大致为()A.B.C.D.二、填空题:本题共6小题,每小题4分,共24分.11.(4分)计算:|﹣3|﹣sin30°=.12.(4分)已知一组数据:12,10,8,15,6,8.则这组数据的中位数是.13.(4分)如图,圆锥侧面展开得到扇形,此扇形半径CA=6,圆心角∠ACB=120°,则此圆锥高OC的长度是.14.(4分)如图,量角器外沿上有A、B两点,它们的读数分别是75°、45°,则∠1的度数为.15.(4分)等腰Rt△ABC中,斜边AB=12,则该三角形的重心与外心之间的距离是.16.(4分)动点A(m+2,3m+4)在直线l上,点B(b,0)在x轴上,如果以B为圆心,半径为1的圆与直线l 有交点,则b的取值范围是.三、解答题:本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤.17.(8分)解不等式组,并把解集在数轴上表示出来:18.(8分)如图:△ABC与△DEF中,边BC,EF在同一条直线上,AB∥DE,AC∥DF,且BF=CE,求证:AC=DF.19.(8分)先化简,再求值:,其中x=1﹣.20.(8分)用列代数式或列方程(组)的方法,解决网络上流行的一个问题:法国新总统比法国第一夫人小24岁,美国新总统比美国第一夫人大24岁,法国新总统比美国新总统小32岁.求:美国第一夫人比法国第一夫人小多少岁?21.(8分)在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:类别家庭藏书m本学生人数A0≤m≤2520B26≤m≤50aC51≤m≤7550D m≥7666根据以上信息,解答下列问题:(1)该调查的样本容量为,a=;(2)随机抽取一位学生进行调查,刚好抽到A类学生的概率是;(3)若该校有2000名学生,请估计全校学生中家庭藏书不少于76本的人数.22.(10分)阅读下列材料,关于x的方程:x+=c+的解是x1=c,x2=;x﹣=c﹣的解是x1=c,x2=﹣;x+=c+的解是x1=c,x2=;x+=c+的解是x1=c,x2=;……(1)请观察上述方程与解的特征,比较关于x的方程x+=c+(a≠0)与它们的关系猜想它的解是什么,并利用“方程的解”的概念进行验证.(2)可以直接利用(1)的结论,解关于x的方程:x+=a+.23.(10分)如图,在Rt△ABC中,∠ACB=90°.(1)利用尺规作图,在BC边上求作一点P,使得点P到边AB的距离等于PC的长;(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)(2)在(1)的条件下,以点P为圆心,PC长为半径的⊙P中,⊙P与边BC相交于点D,若AC=6,PC=3,求BD的长.24.(12分)如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”,这条中线为“匀称中线”.(1)如图①,在Rt△ABC中,∠C=90°,AC>BC,若Rt△ABC是“匀称三角形”.①请判断“匀称中线”是哪条边上的中线,②求BC:AC:AB的值.(2)如图②,△ABC是⊙O的内接三角形,AB>AC,∠BAC=45°,S△ABC=2,将△ABC绕点A逆时针旋转45°得到△ADE,点B的对应点为D,AD与⊙O交于点M,若△ACD是“匀称三角形”,求CD的长,并判断CM是否为△ACD的“匀称中线”.25.(14分)已知:抛物线y=2ax2﹣ax﹣3(a+1)与x轴交于点AB(点A在点B的左侧).(1)不论a取何值,抛物线总经过第三象限内的一个定点C,请直接写出点C的坐标;(2)如图,当AC⊥BC时,求a的值和AB的长;(3)在(2)的条件下,若点P为抛物线在第四象限内的一个动点,点P的横坐标为h,过点P作PH⊥x轴于点H,交BC于点D,作PE∥AC交BC于点E,设△ADE的面积为S,请求出S与h的函数关系式,并求出S 取得最大值时点P的坐标.2019-2020学年福建省泉州市南安市九年级(上)期末数学试卷参考答案与试题解析一、选择题:本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【解答】解:∵<<<<π<,∴介于与之间的是.故选:A.2.【解答】解:A、+,无法计算,故此选项错误;B、a+2a=3a,正确;C、(2a)3=8a3,故此选项错误;D、a6÷a3=a3,故此选项错误;故选:B.3.【解答】解:将171.18万用科学记数法表示为:1.7118×106.故选:C.4.【解答】解:①的主视图是第一层三个小正方形,第二层左边一个小正方形;左视图是第一层两个小正方形,第二层左边一个小正方形;俯视图是第一层中间一个小正方形,第二层三个小正方形;②的主视图是第一层三个小正方形,第二层中间一个小正方形;左视图是第一层两个小正方形,第二层左边一个小正方形;俯视图是第一层中间一个小正方形,第二层三个小正方形;故选:A.5.【解答】解:设袋子中有红球x个,根据题意得=0.6,解得x=4.经检验x=4是原方程的解.答:袋子中有红球有4个.故选:A.6.【解答】解:∵∠BEF是△AEF的外角,∠1=25°,∠F=30°,∴∠BEF=∠1+∠F=55°,∵AB∥CD,∴∠2=∠BEF=55°,故选:C.7.【解答】解:多边形内角和(n﹣2)×180°=720°,∴n=6.则正多边形的一个外角=,故选:B.8.【解答】解:如图,分别过点D,C作x轴的垂线,垂足为M,N,∵点D的坐标是(3,4),∴OM=3,DM=4,在Rt△OMD中,OD==5,∵四边形ABCD为菱形,∴OD=CB=OB=5,DM=CN=4,∴Rt△ODM≌Rt△BCN(HL),∴BN=OM=3,∴ON=OB+BN=5+3=8,又∵CN=4,∴C(8,4),将C(8,4)代入y=,得,k=8×4=32,故选:D.9.【解答】解:设小矩形的长为a,宽为b(a>b),则a+3b=n,阴影部分的周长为2n+2(m﹣a)+2(m﹣3b)=2n+2m﹣2a+2m﹣6b=4m+2n﹣2n=4m,故选:D.10.【解答】解:设AB=x,则AE=EB=由折叠,FE=EB=则∠AFB=90°由tan∠DCE=∴BC=,EC=∵F、B关于EC对称∴∠FBA=∠BCE∴△AFB∽△EBC∴∴y=故选:D.二、填空题:本题共6小题,每小题4分,共24分.11.【解答】解:原式=3﹣=.故答案为:.12.【解答】解:将数据从小到大重新排列为:6、8、8、10、12、15,所以这组数据的中位数为=9,故答案为:9.13.【解答】解:设圆锥底面圆的半径为r,∵AC=6,∠ACB=120°,∴==2πr,∴r=2,即:OA=2,在Rt△AOC中,OA=2,AC=6,根据勾股定理得,OC==4,故答案为:4.14.【解答】解:由图可知,∠AOB=75°﹣45°=30°,根据同弧所对的圆周角等于它所对圆心角的一半可知,∠1=∠AOB=×30°=15°.故答案为15°.15.【解答】解:∵直角三角形的外心是斜边的中点,∴CD=AB=6,∵I是△ABC的重心,∴DI=CD=2,故答案为:2.16.【解答】解:∵动点A(m+2,3m+4)在直线l上,∴直线l解析式为y=3x﹣2如图,直线l与x轴交于点C(,0),交y轴于点A(0,﹣2)∴OA=2,OC=∴AC==若以B为圆心,半径为1的圆与直线l相切于点D,连接BD∴BD⊥AC∴sin∠BCD=sin∠OCA=∴∴BC=∴以B为圆心,半径为1的圆与直线l相切时,B点坐标为(﹣,0)或(+,0)∴以B为圆心,半径为1的圆与直线l有交点,则b的取值范围是故答案为:三、解答题:本题共9小题,共86分.解答应写出文字说明、证明过程或演算步骤.17.【解答】解:由不等式①得:x>4.由不等式②得:x>2.不等式组的解集:x>4.18.【解答】证明:∵AB∥DE,∴∠B=∠E,∵AC∥DF∴∠ACB=∠EFD,∵BF=CE∴BC=EF,且∠B=∠E,∠ACB=∠EFD,∴△ABC≌△DEF(ASA)∴AC=DF19.【解答】解:原式=÷=•=1﹣x,当x=1﹣时,∴原式=1﹣(1﹣)=;20.【解答】解:设法国新总统x岁,则法国第一夫人:(x+24)岁,美国新总统:(x+32)岁,美国第一夫人:(x+32﹣24)=(x+8)岁,故美国第一夫人比法国第一夫人小:(x+24)﹣(x+8)=16(岁).故美国第一夫人比法国第一夫人小16岁.21.【解答】解:(1)调查的样本容量为50÷25%=200(人),a=200﹣20﹣50﹣66=64(人),故答案为200,64;(2)刚好抽到A类学生的概率是20÷200=0.1,故答案为0.1;(3)全校学生中家庭藏书不少于76本的人数:2000×=660(人).答:全校学生中家庭藏书不少于76本的人数为660人.22.【解答】解:(1)方程的解为x1=c,x2=,验证:当x=c时,∵左边=c+,右边=c+,∴左边=右边,∴x=c是x+=c+的解,同理可得:x=是x+=c+的解;(2)方程整理得:(x﹣3)+=(a﹣3)+,解得:x﹣3=a﹣3或x﹣3=,即x=a或x=,经检验x=a与x=都为分式方程的解.23.【解答】解:如图所示:(1)作∠A的平分线交BC于点P,点P即为所求作的点.(2)作PE⊥AB于点E,则PE=PC=3,∴AB与圆相切,∵∠ACB=90°,∵AC与圆相切,∴AC=AE,设BD=x,BE=y,则BC=6+x,BP=3+x,∵∠B=∠B,∠PEB=∠ACB,∴△PEB∽△ACB∴==∴==解得x=2,答:BD的长为2.24.【解答】解:(1)①如图①,作Rt△ABC的三条中线AD、BE、CF,∵∠ACB=90°,∴CF=,即CF不是“匀称中线”.又在Rt△ACD中,AD>AC>BC,即AD不是“匀称中线”.∴“匀称中线”是BE,它是AC边上的中线,②设AC=2a,则CE=a,BE=2a,在Rt△BCE中∠BCE=90°,∴BC=,在Rt△ABC中,AB=,∴BC:AC:AB=.(2)由旋转可知,∠DAE=∠BAC=45°.AD=AB>AC,∴∠DAC=∠DAE+∠BAC=90°,AD>AC,∵Rt△ACD是“匀称三角形”.由②知:AC:AD:CD=:2:,设AC=,则AD=2a,CD=a,如图②,过点C作CH⊥AB,垂足为H,则∠AHC=90°,∵∠BAC=45°,∴,∵=,解得a=2,a=﹣2(舍去),∴,判断:CM不是△ACD的“匀称中线”.理由:假设CM是△ACD的“匀称中线”.则CM=AD=2AM=4,AM=2,∴tan,又在Rt△CBH中,∠CHB=90°,CH=,BH=4﹣,∴tan B=,即∠AMC≠∠B,这与∠AMC=∠B相矛盾,∴假设不成立,∴CM不是△ACD的“匀称中线”.25.【解答】解:(1)y=2ax2﹣ax﹣3(a+1)=a(2x2﹣x﹣3)﹣3,令2x2﹣x﹣3=0,解得:x=或﹣1,故第三象限内的一个定点C为(﹣1,﹣3);(2)函数的对称轴为:x=﹣=,设函数对称轴与x轴交点为M,则其坐标为:(,0),则CM==,则AB=2CM=,则点A、B的坐标分别为:(﹣3,0)、(,0);将点A的坐标代入函数表达式得:18a+3a﹣3a﹣3=0,解得:a=,函数的表达式为:y=(x+3)(x﹣)=x2﹣x﹣;(3)过点E作EF⊥PH,设:∠ACB=α,则∠ACB=∠HPE=∠DEF=α,将点B、C坐标代入一次函数表达式并解得:直线BC的表达式为:y=x﹣,设点P(h,h2﹣h﹣),则点D(h,h﹣),故tan∠ACB=tanα=,则sinα=,y D﹣y E=DE sinα=PD sinα•sinα,S=S△ABE﹣S△ABD=×AB×(y D﹣y E)=××(h﹣﹣h2+h+=﹣h2+h﹣,∵﹣<0,∴S有最大值,当h=时,S的最大值为:,此时点P(,﹣).。
2019-2020学年九年级(华师大版)数学上册期末综合练习卷(含答案) (1)
九年级上册期末综合练习卷一.选择题1.下列各式①;②;③;④;⑤;其中一定是最简二次根式的有()A.4个B.3个C.2个D.1个2.在Rt△ABC中,∠C=90°,AB=5,AC=4,则cos B的值是()A.B.C.D.3.四边形ABCD在平面直角坐标系中的位置如图3所示,若AD⊥CD,AB∥CD,AB=5,A点坐标为(﹣2,7),则点B坐标为()A.(﹣2,2)B.(﹣2,12)C.(3,7)D.(﹣7,7)4.小王抛一枚质地均匀的硬币,连续抛4次,硬币均正面朝上落地,如果他再抛第5次,那么硬币正面朝上的概率为()A.1B.C.D.5.已知方程x2﹣4x+2=0的两根是x1,x2,则代数式的值是()A.2011B.2012C.2013D.20146.如图,在△ABC中,点D在边AB上,则下列条件中不能判断△ABC∽△ACD的是()A.∠ABC=∠ACD B.∠ADC=∠ACB C.D.AC2=AD•AE 7.若分式的值是正整数,则m可取的整数有()A.4个B.5个C.6个D.10个8.一枚均匀的正方体骰子,六个面上分别刻有1,2,3,4,5,6个点.甲乙两人各掷一次,如果朝上一面的两个点数之和为奇数,则甲胜;若为偶数,则乙胜,下列说法正确的是()A.甲获胜的可能性大B.乙获胜的可能性大C.甲乙获胜的可能性一样大D.乙一定获胜9.“凤鸣”文学社在学校举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,某组共互赠了210本图书,如果设该组共有x名同学,那么依题意,可列出的方程是()A.x(x+1)=210B.x(x﹣1)=210C.2x(x﹣1)=210D.x(x﹣1)=210二.填空题10.已知==,且a+b﹣2c=6,则a的值为.11.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是.12.把二次函数y=(x﹣1)2+2的图象向左平移3个单位,再向下平移2个单位,所得函数的表达式是.13.如图,ED为△ABC的中位线,点G是AD和CE的交点,过点G作GF∥BC交AC于点F,如果GF=4,那么线段BC的长是.14.如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE 折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为.三.解答题(共8小题,满分75分)15.计算下列各题(1)(2)(3)(4)16.如图,在△ABC中,∠A=30°,∠B=45°,AC=,求AB的长.17.已知关于x的一元二次方程x2﹣6x+2a+5=0有两个不相等的实数根x1,x2.(1)求a的取值范围;(2)若x12+x22﹣x1x2≤30,且a为整数,求a的值.18.在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是;(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”,求他演唱歌曲“1”和“4”的概率.19.如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C 港口接旅客,停留半小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.(1)求港口A到海岛B的距离;(2)B岛建有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔?20.如图,在△ABC中,∠BAC=90°,AB=AC,点D、E分别在BC、AC上,且∠ADE =45°.(1)求证:△ABD∽△DCE;(2)若AB=2,BD=1,求CE的长.参考答案一.选择题1.C.2.B.3.C.4.B.5.D.6.C.7.A.8.C.9.B.二.填空题10.解:∵==,∴设a=6x,b=5x,c=4x,∵a+b﹣2c=6,∴6x+5x﹣8x=6,解得:x=2,故a=12.故答案为:12.11.解:如图,tanα==故答案为:.12.解:根据“上加下减,左加右减”的原则可知,把二次函数y=(x﹣1)2+2的图象向左平移3个单位,再向下平移2个单位,所得函数的表达式是y=(x﹣1+3)2+2﹣2,即y=(x+2)2,故答案为y=(x+2)2.13.解:∵ED为△ABC的中位线,∴AD、CE为△ABC的中线,∴点G为△ABC的重心,∴AG=2GD,∵GF∥BC,∴△AGF∽△ADC,∴==,∴CD=GF=×4=6,∴BC=2CD=12.故答案为12.14.解:分两种情况:①如图1,过A′作MN∥CD交AD于M,交BC于N,则直线MN是矩形ABCD的对称轴,∴AM=BN=AD=1,∵△ABE沿BE折叠得到△A′BE,∴A′E=AE,A′B=AB=1,∴A′N==0,即A′与N重合,∴A′M=1,∴A′E2=EM2+A′M2,∴A′E2=(1﹣A′E)2+12,解得:A′E=1,∴AE=1;②如图2,过A′作PQ∥AD交AB于P,交CD于Q,则直线PQ是矩形ABCD的对称轴,∴PQ⊥AB,AP=PB,AD∥PQ∥BC,∴A′B=2PB,∴∠P A′B=30°,∴∠A′BC=30°,∴∠EBA′=30°,∴AE=A′E=A′B×tan30°=1×=;综上所述:AE的长为1或;故答案为:1或.三.解答题15.解:(1)原式=﹣1+4﹣2=+1;(2)原式=2﹣3﹣(3﹣2)+3=2﹣;(3)原式=10+3+2=15;(4)原式=3+4+4﹣4+2=9.16.解:过C作CD⊥AB于D,∴∠ADC=∠BDC=90°,∵∠B=45°,∴∠BCD=∠B=45°,∴CD=BD,∵∠A=30°,AC=2,∴CD=,∴BD=CD=,由勾股定理得:AD==3,∴AB=AD+BD=3+,答:AB的长是3+.17.解:(1)∵关于x的一元二次方程x2﹣6x+2a+5=0有两个不相等的实数根x1,x2,∴△>0,即(﹣6)2﹣4(2a+5)>0,解得a<2;(2)由根与系数的关系知:x1+x2=6,x1x2=2a+5,∵x1,x2满足x12+x22﹣x1x2≤30,∴(x1+x2)2﹣3x1x2≤30,∴36﹣3(2a+5)≤30,∴a≥﹣,∵a为整数,∴a的值为﹣1,0,1.18.解:(1)∵转动转盘①一共有3种可能,∴转盘指针指向歌曲“3”的概率是:;故答案为:;(2)分别转动两个转盘一次,列表:(画树状图也可以)45 6BA11,41,51,622,42,52,633,43,53,6共有9种,它们出现的可能性相同.由于指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”,所以所有的结果中,该歌手演唱歌曲“1”和“4”(记为事件A)的结果有2种,所以P(A )=.(说明:通过枚举、画树状图或列表得出全部正确情况得(4分);没有说明等可能性扣(1分).)19.解:(1)过点B作BD⊥AE于D在Rt△BCD中,∠BCD=60°,设CD=x,则BD =,BC=2x在Rt△ABD中,∠BAD=45°则AD=BD=,AB=BD=由AC+CD=AD得20+x=x解得:x=10+10故AB=30+10答:港口A到海岛B的距离为海里.(2)甲船看见灯塔所用时间:小时乙船看见灯塔所用时间:小时所以乙船先看见灯塔.20.解:(1)∵∠BAC=90°,AB=AC,∴∠B=∠C=45°,又因为∠DEC=∠ADE+∠CAD=45°+∠CAD(三角形的外角等于不相邻的两个内角之和),同理∠ADB=∠C+∠CAD=45°+∠CAD,∴∠DEC=∠ADB,又∠ABD=∠DCE=45°,∴△ABD∽△DCE;(2)∵AB=2,∴BC=2,∵△ABD∽△DCE,∴=,即=,=,CE=﹣.。
贵州省贵阳市2024-2025学年高一上学期教学质量监测卷(一)数学试题(含解析)
贵阳2024级高一年级教学质量监测卷(一)数学本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.第I 卷第1页至第3页,第II 卷第3页至第4页.考试结束后,请将答题卡交回.满分150分,考试用时120分钟.第I 卷(选择题,共58分)注意事项:1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚.2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效.一、单项选择题(本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的)1.已知集合,则( )A.B.C. D.2.命题,则的否定是( )A.B.C.D.3.下列四组函数中,是同一个函数的是( )A. B.C.D.4.已知函数,则()A.3B. C. D.95.已知幂函数的图象过点,则下列说法正确的是()A.为偶函数B.为奇函数C.为单调递增函数D.为单调递减函数6.已知集合,则“”是“”的( )A.充分不必要条件B.必要不充分条件{}{15},1,0,1,2A x x B =∈-<<=-N∣A B ⋂={}1,2{}1,0,1,2,3,4-{}0,1,2{}1,0,1,2-[]2:"0,2,11"p x x ∀∈+…p []20,2,11x x ∀∉+<[]20,2,11x x ∀∈+<[]20,2,11x x ∃∉+<[]20,2,11x x ∃∈+<()()21,1x f x x g x x=-=-()()24,f x x g x ==()(),f x x g x ==()()2,f x x g x ==()221461f x x x +=+-()3f -=3-1-()y f x =(()f x ()f x ()f x ()f x {}{}220,2,210A B xx ax a ==++-=∣{}2A B ⋂=1a =-C.充要条件D.既不充分也不必要条件7.已知是定义在上的偶函数,且在区间单调递减,若,则实数的取值范围为( )A.B.C.D.8.已知函数,则的取值范围为( )A.B.C.D.二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得6分,部分选对的得部分分,有选错的得0分)9.下列不等式中取等条件无法满足的是()B.D.10.已知不等式的解集为,函数,则下列说法正确的是()A.函数的图象开口向上B.函数的图象开口朝下C.无论为何值,必有D.不等式的解集为或11.已知定义在上的函数,对任意实数满足,均有.函数在的最大值和最小值分别为,.则下列说法正确的是( )A.必为奇函数B.可能为偶函数C.不一定为定值,且与的单调性有关D.为定值,且定值为6()f x R [)0,∞+()()12f m f m -<m 1,3∞⎛⎫+ ⎪⎝⎭1,3∞⎛⎫- ⎪⎝⎭1,13⎛⎫ ⎪⎝⎭()1,1,3∞∞⎛⎫-⋃+ ⎪⎝⎭()f x =[)0,∞+a []0,1(]0,1{}1[)1,∞+2221222x x +++≧21222x x +++…20ax bx c ++<{23}xx -<<∣()2f x ax bx c =++()f x ()f x ,,a b c a c b +<20cx bx a ++<12x x ⎧<-⎨⎩13x ⎫>⎬⎭R ()y f x =,,a b c 222a b c +=()()()0f a f b f c ++=()()23g x f x x =++[]2,2x ∈-M m ()f x ()f x M m +()f x M m +第II 卷(非选择题,共92分)注意事项:第II 卷用黑色碳素笔在答题卡上各题的答题区域内作答,在试题卷上作答无效.三、填空题(本题共3小题,每小题5分,共15分)12.已知集合,则__________.13.已知函数的定义域为,则的定义域为__________.14.已知函数,若,则__________,的取值范围为__________.四、解答题(共77分.解答应写出文字说明、证明过程或演算步骤)15.(本小题满分13分)已知集合.(1)若,求的取值范围;(2)若,求的取值范围.16.(本小题满分15分)已知定义在上的奇函数满足,当时,.(1)求在上的解析式;(2)若,求的取值范围.17.(本小题满分15分)已知正实数满足:.(1)求的最小值;(2)求的最小值.18.(本小题满分17分)已知函数.(1)若,使得,求的取值范围;(2)若,都有恒成立,求的取值范围;(3)当时,,满足,求的取值范围.19.(本小题满分17分)对于数集,定义点集,若对任意,都{210},{23}A xx B x x =+<=-<<∣∣()A B ⋂=R ð()21f x +[)5,3-()3f x +()(){}()(){}21,0,0f x x ax b x A x f x B x f f x =+++=∈==∈=R R ∣∣A B =≠∅b =a {}{}2{27},21,320A xx B x m x m C x x x =<<=+=-+<∣∣∣……B C C ⋂=m A B A ⋃=m R ()f x [)0,x ∞∈+()22f x x x =+()f x R ()()121f m f m +<-m ,a b ab a b =+2a b +222a b a b++()()()210,2f x mx m g x x x k =+≠=++x ∃∈R ()0g x …k []1,2x ∀∈-()0f x >m 3k =[][]121,2,1,2x x ∀∈∃∈-()()12f x g x …m {}()123,,,,2n A a a a a n = …(){},,B x y x A y A =∈∈∣()11,x y B ∈存在使得,则称数集是“正交数集”.(1)判断以下三个数集是否是“正交数集”(不需要说明判断理由,直接给出判断结果即可);(2)若,且是“正交数集”,求的值;(3)若“正交数集”满足:,,求的值.高一数学参考答案第I 卷(选择题,共58分)()22,x y B ∈12120x x y y ⋅+⋅=A {}{}{}1,11,2,31,1,4---、、4a >{}2,2,4,a -a {}1232024,,,,A a a a a = 12320243,0a a a a =-<<<< 20241012a =2a一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)题号12345678答案CDCACDDA【解析】1.由已知集合,所以,故选C.2.改变量词,否定结论,所以命题的否定为,故选D.3.对于A 选项,的定义域为的定义域为,定义域不同,故不是同一个函数;对于B 选项,的定义域为的定义域为,定义域不同,故不是同一个函数;对于C 选项,的定义域为的定义域为,且,对应关系相同,故是同一个函数;对于D 选项,的定义域为的定义域为,定义域不同,故不是同一个函数,故选C.4.令,解得,故,故选A.5.由幂函数的图象过点,解得,故幂函数为函数,且为增函数,故选C.6.由已知,若,则有或,解得或,当时,满足,当时,不满足,所以是的既不充分也不必要条件,故选D.7.由已知是定义在上的偶函数,且在区间单调递减得函数在上单调递增,若要有则需,即,解得或,故选D.8.若函数,则内函数有定义,故内函数大于或等于0.当时,函数其定义域为,值域为符合题意;当时,内函数开口向上,若要满足题意则需,解得;当时,内函数开口向下,不可能符合题意,综上所述:,故选A.二、多项选择题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项是{}{}0,1,2,3,4,1,0,1,2A B ==-{}0,1,2A B ⋂=[]2:0,2,11p x x ∀∈+…[]20,2,11x x ∃∈+<()f x (),g x R {}0xX ≠∣()f x (),g x R [)0,∞+()f x (),g x R R ()g x x ==()f x (),g x R [)0,∞+213x +=-2x =-()()234(2)6213f -=⨯-+⨯--=y x α=(2α=12α=y =()(){}1,1B a a =-+--{}2A B ⋂=()12a -+=()12a --=3a =-1a =-3a =-{}2,4B ={}2A B ⋂=1a =-{}0,2B ={}2A B ⋂={}2A B ⋂=1a =-()f x R [)0,∞+()f x (),0∞-()()12f m f m -<12m m ->22(12)m m ->13m <1m >()f x =[)0,∞+221ax x ++0a =()f x =1,2∞⎡⎫-+⎪⎢⎣⎭[)0,∞+0a >221ax x ++Δ440a =-…01a <…0a <221ax x ++[]0,1a ∈符合题目要求的.全部选对的得6分,部分选对的得部分分,有选错的得0分)题号91011答案ABDACDABD【解析】9.对于A无实数解;对于B 选项,不等式取等条件为,即,即,无实数解;对于C 选项,不等式取等条件为;对于D 选项,不等式取等条件为,即,即或,无实数解,综上,故选ABD.10.由不等式的解集为,则可知一元二次方程的两根为和3,且二次函数开口向上,,故A 正确,B 错误;当时有,即,故C 正确;由韦达定理得,故,函数的开口向上,对于方程,若是方程的根则有,等式两边同时除以,则有,故是方程的根,故的根为与,则不等式的解集为或,故选ACD.11.令,满足,则有,则;令,满足,则有,即,且定义域为关于原点对称,故函数为奇函数;若,则符合题意且为偶函数;因为与为奇函数,故也为奇函数,设其在的最大值与最小值分别为与,由奇函数的性质,对于函数,其最大值与最小值分别为,故,D 正确,故选ABD.第II 卷(非选择题,共92分)三、填空题(本大题共3小题,每小题5分,共15分)=231x +=22122x x +=+()2221x +=()221x +=±=1x =122x x +=+2(2)1x +=21x +=21x +=-20ax bx c ++<{23}xx -<<∣20ax bx c ++=2-2y ax bx c =++0a >1x =-0a b c -+<a c b +<2360ca=-⨯=-<0c <2y cx bx a =++20ax bx c ++=0x 2000ax bx c ++=20x 200110c b a x x ⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭01x 20cx bx a ++=20cx bx a ++=12-1320cx bx a ++<12x x ⎧<-⎨⎩13x ⎫>⎬⎭0a b c ===222a b c +=()()()0000f f f ++=()00f =,0,a x b c x =-==222a b c +=()()()00f x f f x -++=()()f x f x -=-R ()f x ()0f x =()f x ()f x 2x ()2f x x +[]2,2-0M 0m 000M m +=()()23g x f x x =++003,3M M m m =+=+6M m +=题号121314答案【解析】12.由已知得,则,则.13.已知的定义域为,则的定义域为,故,即,故的定义域为.14.由已知是由函数的所有实数零点构成的集合,,令,是由所有满足且的所有实数构成的集合.若,当满足且因为,则有,即,解得;当时,,此时,符合题意;当时,有,于是,若要使得,只需方程无实数根,故有,解得.综上,的取值范围为.四、解答题(共77分.解答应写出文字说明,证明过程或演算步骤)15.(本小题满分13分)解:(1)易得,,于是有,解得,故当时,.(2),则,①当时,有,解得,符合题意;132x x ⎧⎫-<⎨⎬⎩⎭…[)12,4-[)0,0,41,{23}2A x x B xx ⎧⎫=<-=-<<⎨⎬⎩⎭∣R 12A x x ⎧⎫=-⎨⎬⎩⎭…ð()R 132A B x x ⎧⎫⋂=-<⎨⎬⎩⎭…ð()21f x +[)5,3-()f x [)9,7-937x -+<…124x -<…()3f x +[)12,4-()(){}21,0f x x ax b x A x f x =++-=∈=R∣()f x ()(){}0B x f f x =∈=R ∣()t f x =()0f t =()t f x =A B =1x A ∈()10f x =1x B ∈()()10f f x =()00f =0b =0a =()()()24,f x x f f x x =={}0A B ==0a ≠()()()()()()()22220,f x x ax x x a a f f x x ax a x ax=+=+≠=+++()()()()222x ax x ax a x x a x ax a =+++=+++{}0,A a =-A B =2x ax a ++2Δ40a a =-<04a <<a [)0,4{12}C xx =<<∣,B C C C B ⋂=∴⊆ 1212m m ⎧⎨+⎩ (1)12m ……1,12m ⎡⎤∈⎢⎥⎣⎦B C C ⋂=A B A ⋃= B A ⊆B =∅21m m +<1m <-②当时,有,解得,综上所述,的取值范围为.16.(本小题满分15分)解:(1)令,则,又在上为奇函数,故有故在上的解析式为.(2)与在上单调递增,在上单调递增.又,故当时,.是奇函数,时,且单调递增,故为增函数,若要使得,只需,即,故的取值范围为.17.(本小题满分15分)解:(1)由可得,,当且仅当时等号成立,故的最小值为.(2)由已知得,当且仅当时等号成立,故的最小值为.B ≠∅212217m mm m +⎧⎪>⎨⎪+<⎩…23m <<m ()(),12,3∞--⋃0x <0x ->()f x R ()()()22()22,f x f x x x x x ⎡⎤=--=--+-=-+⎣⎦()f x R ()222,02,0x x x f x x x x ⎧+=⎨-+<⎩…2x 2x [)0,∞+()f x ∴[)0,∞+()00f = [)0,x ∞∈+()0f x …()f x (),0x ∞∴∈-()0f x <()f x ()()121f m f m +<-121m m +<-2m >m ()2,∞+ab a b =+111a b+=()112221233a b a b a b a b b a ⎛⎫∴+=++=++++=+ ⎪⎝⎭…1,a b ==2a b +3+2222222a b a b a b a b ab b a ++==+=+…1a b ==+222a b a b++18.(本小题满分17分)解:(1)若,有成立,只需,解得.(2)若对,都有恒成立,则,解得,综上所述,的取值范围为.(3)当时,,若对,满足,只需,有,当时,,故,有,则有,解得或,综上所述,的取值范围为.19.(本小题满分17分)解:(1)是正交数集,不是正交数集.(2)若,且是正交数集,则对于有序数对能使得其满足条件的有序数对只能为或.若为,则有,解得与矛盾,舍去;故只能是,于是有,解得,经检验符合题意.(3)先证:若集合为正交数集,则至少要有一对相反数,对于,且,有有序数对,故,使得,所以,故集合中至少有一对相反数.因为且是唯一负数,故,x ∃∈R ()0g x …Δ440k =-…1k …[]1,2x ∀∈-()0f x >()()1020f f ⎧->⎪⎨>⎪⎩112m -<<m ()1,00,12⎛⎫-⋃ ⎪⎝⎭3k =()223g x x x =++[][]121,2,1,2x x ∀∈∃∈-()()12f x g x …[]11,2x ∀∈()()12max f x g x <[]21,2x ∈-()max ()211g x g ==[]11,2x ∀∈()111f x <()()111211f f ⎧⎪⎨⎪⎩……0m <05m <…m ()(],00,5∞-⋃13,B B 2B 4a >{}2,2,4,a -()4,a 12120x x y y +=()2,2-()4,2-()2,2-820a -=4a =4a >()4,2-1620a -=8a =8a =A 0a ∀≠a A ∈(),a a B ∈()11,x y B ∃∈110x a y a +=110x y +=A 13a =-3A ∈下证3为最小正数:反证法:若3不为最小正数,则,对于有序数对是最大正数,则与之相匹配的有序数对设为,故有,即,与是最大正数相矛盾,故3为最小正数,综上所述,.23a <()220242024,,a a a ()(),30x x ->2101230a x -⨯=231012a x =⨯23,1012a x <∴> 2024a 23a =。
2019-2020年九年级上学期期末考试物理试题(含答案)(I)
2019-2020年九年级上学期期末考试物理试题(含答案)(I)考生注意:1.本试卷物理部分含五个大题。
2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效。
一、选择题(共16分)下列各题均只有一个正确选项,请将正确选项的代号用2B铅笔填涂在答题纸的相应位置上,更改答案时,用橡皮擦去,重新填涂。
1.家用空调的额定电功率约为A.1500瓦B.150瓦C.15瓦D.1.5瓦2.关于物体所受浮力,下列说法中正确的是A.物体排开水的体积越大,所受浮力越大B.物体没入水中越深,所受浮力越大C.物体的密度越大,所受浮力越大D.漂浮的物体受到浮力,下沉的物体不受浮力3.关于欧姆定律,下列说法中正确的是A.通过导体的电流越大,导体的电阻就越小B.导体两端的电压越大,通过导体的电流就越小C.对于某一导体来说,通过导体的电流与导体两端的电压成正比D.由I=U/R变形可得R=U /I,说明电阻与电压成正比,与电流成反比4.如图1所示,将铅笔的一端削尖,用两个手指作用在铅笔的两端,使铅笔保持静止状态,下列说法中正确的是A.左边手指对铅笔的压力大于右边手指对铅笔的压力B.左边手指对铅笔的压力小于右边手指对铅笔的压力C.左边手指对铅笔的压强大于右边手指对铅笔的压强D.左边手指对铅笔的压强小于右边手指对铅笔的压强5.下列事例中,运用相同科学研究方法的是图1①探究导体中电流大小与导体两端电压的关系②用水流比作电流③用总电阻替代两个串联的电阻④探究物质质量与体积的关系A.①与③ B.①与④ C.②与③ D.②与④6.如图2所示的四个装置中不属于...连通器的是A.玻璃连通管B.托里拆利实验C.茶壶D.液位计图27.在图3所示的电路中,电源电压保持不变,闭合电键S,电路正常工作。
一段时间后,电压表V的示数不变,电流表A的示数变大,若故障只发生在两个电阻R1或R2上,用某完好的电阻R(R<R1<R2)替换R1,替换后电压表的示数不变,电流表的示数变得更大(没有超过电流表量程),则A .R 1可能断路B .R 2一定断路C .R 1可能短路D .R 2一定短路图38.如图4所示,水平面上的圆柱形容器A 、B 中分别盛有甲、乙两种液体,液体等高且甲对容器底部的压强大于乙。
期末模拟预测卷02-九年级数学上学期期中期末考点(人教版)(原卷版)
2022-2023学年九年级数学上学期期末模拟预测卷02(考试时间:100分钟试卷满分:120分)考生注意:1.本试卷26道试题,满分120分,考试时间100分钟.2.本试卷分设试卷和答题纸.试卷包括试题与答题要求.作答必须涂(选择题)或写(非选择题)在答题纸上,在试卷上作答一律不得分.3.答卷前,务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号码等相关信息.一.选择题(共10小题每题3分,满分30分)1.一元二次方程2x2+x﹣1=0的二次项系数为()A.﹣1B.0C.1D.22.如图所示的几何体的主视图是()A.B.C.D.3.小明用一面放大镜观察一个三角形,则这个三角形没有发生变化的是()A.三角形的边长B.三角形的各内角度数C.三角形的面积D.三角形的周长4.2021年的“一圈两场三改”工作标志着贵阳市民生建设迈入新阶段,某区11月开放体育场馆30所,预计到2022年1月开放体育场馆达63所,若设每个月开放体育场馆的平均增长率为x,则所列的方程为()A.30(1+x)=63B.30(1+x)2=63C.30(1﹣x)=63D.30(l﹣x)2=635.如图,在⊙O中,点A,B,C都在⊙O上,∠1+∠2=70°,则∠O=()A.110°B.120°C.130°D.140°6.如果2a=3b,则下列式子正确的是()A.B.C.D.7.如图,点B在反比例函数的图象上,BA⊥y轴于点A,连接OB,则△OAB的面积是()A.B.C.3D.68.如图,将一块含45°角的三角板ABC绕点A按逆时针方向旋转到△AB'C'的位置.若∠CAB'=20°,则旋转角的度数为()A.20°B.25°C.65°D.70°9.在菱形ABCD中,对角线AC,BD相交于点O,若AD=BD=2,则AO的长是()A.1B.C.2D.10.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.则下列结论不正确的是()A.小球在空中经过的路程是40mB.小球运动的时间为6sC.小球抛出3s时,速度为0D.当t=1.5s时,小球的高度h=30m二.填空题(共8小题,每题3分,满分24分)11.中心角为30°的正多边形边数为.12.已知三角形的三边分别为3cm、4cm、5cm,则这个三角形内切圆的半径是.13.已知一斜坡的坡角α=60°,那么该斜坡的坡度为.14.如图是小孔成像原理的示意图,根据图中所标注的尺寸,蜡烛AB在暗盒中所成的像CD的高度是cm.15.发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2+bx+c(a≠0).若此炮弹在第7秒与第15秒时的高度相等,则第秒时炮弹位置达到最高.16.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6.若以AC所在直线为轴,把△ABC旋转一周,得到一个圆锥,则这个圆锥的侧面积等于.17.如图,四边形ABCD内接于⊙O,点M在AD的延长线上,∠AOC=140°,则∠CDM=.18.已知抛物线y=ax2﹣4ax+c(a≠0)与x轴交于A、B两点,若点A的坐标为(﹣2,0),则线段AB的长为.三.解答题(共8小题,满分66分)19.计算:(﹣)﹣1++2cos60°﹣(π﹣1)0.20.如图,在直角坐标平面内,已知点A(8,0),点B(3,0),点C是点A关于点B的对称点.(1)求点C的坐标;(2)若P坐标为(0,2),过点P作直线l∥x轴,点A关于直线l的对称点是D,求△BCD的面积.21.为铸牢中华民族共同体意识,不断巩固民族大团结,红星中学即将举办庆祝建党100周年“中华民族一家亲,同心共筑中国梦”主题活动,学校拟定了演讲比赛、文艺汇演、书画展览、知识竞赛四种活动方案,为了解学生对活动方案的喜爱情况,学校随机抽取了200名学生进行调查(每人只能选择一种方案),将调查结果绘制成如下两幅不完整的统计图,请你根据以下两幅图所给的信息解答下列问题.(1)在抽取的200名学生中,选择“演讲比赛”的人数为,在扇形统计图中,m的值为;(2)根据本次调查结果,估计全校2000名学生中选择“文艺汇演”的学生大约有多少人?(3)现从喜爱“知识竞赛”的四名同学a、b、c、d中,任选两名同学参加学校知识竞赛,请用树状图或列表法求出a同学参加的概率.22.已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.(1)求证:四边形AODE是矩形;(2)若AB=6,∠ABC=60°,求四边形AODE的面积.23.某社区为了更好地开展“垃圾分类,美丽宁波”活动,需购买A,B两种类型垃圾桶,用1600元可购进A型垃圾桶14个和B型垃圾桶8个,且购买3个A型垃圾桶的费用与购买4个B型垃圾桶的费用相同,请解答下列问题:(1)求出A型垃圾桶和B型垃圾桶的单价.(2)若社区欲用不超过3600元购进两种垃圾桶共50个,其中A型垃圾桶至少29个,求有哪几种购买方案?24.如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.(1)求证:AB是⊙O的切线.(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tan∠D=,求的值.(3)在(2)的条件下,设⊙O的半径为3,求AB的长.25.我们规定,对于已知线段AB,若存在动点C(点C不与点A,B重合)始终满足∠ACB的大小为定值,则称△ABC是“立信三角形”,其中AB的长称为它的“立信长”,∠ACB称为它的“立信角”.(1)如图(1),已知立信△ABC中“立信长”AB=2,“立信角”∠ACB=90°,请直接写出立信△ABC面积的最大值;(2)如图(2),在△ABD中,AD=BD=2,,C是立信△ABC所在平面上的一个动点,且立信角∠ACB=60°,求立信△ABC面积的最大值;(3)如图(3),已知立信长AB=a(a是常数且a>0),点C是平面内一动点且满足立信角∠ACB=120°,若∠ABC,∠BAC的平分线交于点D,问:点D的运动轨迹长度是否为定值?如果是,请求出它的轨迹长度;如果不是,请说明理由.26.如图,已知抛物线经过A(﹣1,0),B(3,0),C(0,3)三点.(1)求抛物线的解析式;(2)连接BC,点D是线段BC上方抛物线上一点,过点D作DE∥BC,交x轴于点E,连接AD交BC于点F,当取得最小值时,求点D的横坐标;(3)点G为抛物线的顶点,抛物线对称轴与x轴交于点H,连接GB,点M是抛物线上的动点,设点M 的横坐标为m.①当∠MBA=∠BGH时,求点M的坐标;②过点M作MN∥x轴,与抛物线交于点N,P为x轴上一点,连接PM,PN,将△PMN沿着MN翻折,得△QMN,若四边形MPNQ恰好为正方形,求m的值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
贵阳市2019-2020年度九年级上学期期末数学试题(I)卷
姓名:________ 班级:________ 成绩:________
一、单选题
1 . 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论,其中,正确结论的个数是()
①出发1小时时,甲、乙在途中相遇;
②乙开车速度是80千米/小时;
③出发1.5小时时,乙比甲多行驶了60千米;
④出发3小时时,甲、乙同时到达终点;
A.1B.2C.3D.4
2 . 已知菱形ABCD,对角线交点为O,延长CD至E且CD=DE.下列判断正确个数是()
(1)∠AOB=90°;(2)AE=2OD;(3)∠OAE=90°;(4)∠AEO=∠CEO.
A.1个B.2个C.3个D.4个
3 . 如图,在△ABC中,∠C=90°,D是AC上的一点,DE⊥AB于点E,若AC=8, BC=6,DE=3,则AD的长为()
A.3B.4C.5D.6
4 . 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC 的底部,当他向前再步行20 m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.
5 m,两个路灯的高度都是9 m,则两路灯之间的距离是()
A.24 m B.25 m C.28 m D.30 m
5 . 已知∠A为锐角且tanA=,则∠A = ()
A.30°B.45°C.60°D.不能确定
6 . 以为根的一元二次方程可能是()
A. B. C. D.
7 . 在函数的图象上有三点A1(,),A2(,),A3(,),已知,则下列各式中,正确的是()
A.B.C.D.
8 . 从n张互不相同的普通扑克牌中任意抽取一张,抽到黑桃K的概率为,则n=()
A.54B.52C.10D.5
9 . 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为
()
A.3B.3.5C.4D.4.5
10 . 如图所示图形,下列选项中不是图中几何体的三视图的是()
A.B.C.D.
二、填空题
11 . 已知,则_______________.
12 . 在一个袋子中装入大小、形状完全相同的若干个小球,要使得摸到红球的概率是,请你设计一个实验方案:________.
13 . 已知一次函数的函数图像与轴交于点,且坐标平面内有一点为坐标原点,则_________________.
14 . 抛物线y=﹣x2+x﹣4的顶点坐标为_____.
15 . 在某天的同一时刻,高为的小明的影长为,烟囱的影长为,则这座烟囱的高为________ .
16 . 若分式在实数范围内有意义,则x的取值范围是______.
17 . 把抛物线先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为
________________________________.
三、解答题
18 . 如图,在直角坐标系xOy中,矩形ABCD的DC边在x轴上,D点坐标为(﹣6,0)边AB、AD的长分别为3、8,E是BC的中点,反比例函数y=的图象经过点E,与AD边交于点
A.
(1)求k的值及经过A、E两点的一次函数的表达式;
(2)若x轴上有一点P,使PE+PF的值最小,试求出点P的坐标;
(3)在(2)的条件下,连接EF、PE、PF,在直线AE上找一点Q,使得S△QEF=S△PEF直接写出符合条件的Q点坐标.
19 . (1)计算:
(2)解方程:
20 . 已知反比例函数为常数,)的图象经过两点.
(1)求该反比例函数的解析式和的值;
(2)当时,求的取值范围;
(3)若为直线上的一个动点,当最小时,求点的坐标.
21 . 如图,Rt△APE,∠AEP=90°,以AB为直径的⊙,O交PE于C,且AC平分∠EAP.连接BC,PB:PC=1:2.
(1)求证:PE是⊙O的切线;
(2)已知⊙O的半径为,求AE的长.
22 . 如图,在△ABC中,∠B=45°,∠C=60°,AB=3,AD⊥BC于D,求DC.
23 . 如图,抛物线交轴于两点,与轴交于点,连接.点是第一象限内抛物线上的一个动点,点的横坐标为.
(1)求此抛物线的表达式;
(2)过点作轴,垂足为点,交于点.试探究点P在运动过程中,是否存在这样的点,使得以为顶点的三角形是等腰三角形.若存在,请求出此时点的坐标,若不存在,请说明理由;
(3)过点作,垂足为点.请用含的代数式表示线段的长,并求出当为何值时有最
大值,最大值是多少?
24 . 某校举行“厉害了,我的国”为主题的征文比赛,九年级(1)班从甲、乙、丙、丁 4 名同学中选出 2
名同学参加征文比赛.
(1)已确定甲参加比赛,再从其余 3 名同学中随机选取 1 名,求恰好选中乙的概率;
(2)随机选取 2 名同学,求其中有乙同学的概率.请用列表法或画树状图法分析说明.
25 . 解方程:.。
