河北省邢台市沙河市高考数学总复习 第4讲 直线与圆、圆与圆的位置关系基础巩固题组
高考数学总复习 第8章 第4讲 直线与圆、圆与圆的位置关系课件 理 新人教A版

• (3)两圆x2+y2=r2与(x-3)2+(y+1)2=r2(r>0) 外切,则r=________.
10
1. < = > > = <
填一填:(1)相交 (2)-3 或 1 (3)8
2.填一填:(1)相交
14
(2)解:圆半径 r= 5,圆心 C 到直线 l 的距离为 d= r2-|A2B|2= 23, 由点到直线的距离公式得 m2|-+m-| 12= 23,解得 m= ± 3, 故直线的斜率为± 3,从而直线 l 的倾斜角为π3或23π.
15
判断直线与圆的位置关系常见的有两种方法 (1)代数法:Δ=判―b别―2-→式4ac>= <000⇔ ⇔⇔相 相相交 离切, . , (2)几何法:利用圆心到直线的距离 d 和圆半径 r 的大小 关系:d<r⇔相交,d=r⇔相切,d>r⇔相离.
解之得 m+n≤2-2 2或 m+n≥2+2 2.
[答案] D
20
求圆的切线方程,一般设为点斜式方程.首先判断点是否在 圆上,如果过圆上一点,则有且只有一条切线,如果过圆外 一点,则有且只有两条切线.若利用点斜式方程求得过圆外 一点的切线只有一条,则需结合图形把斜率不存在的那条切 线补上.
21
[变式探究] [2013·银川质检]由直线 y=x+1 上的一点 向圆 x2+y2-6x+8=0 引切线,则切线长的最小值为( )
• (3)直线x=0被x2+y2-6x-2y-15=0,所截 得弦长等于________.
8
• 2.圆与圆的位置关系(⊙O1、⊙O2半径r1、r2,
d=|O相1O离2|) 外切
高考数学一轮复习全程复习构想数学(文)【统考版】第四节 直线与圆、圆与圆的位置关系(课件)

(二)教材改编 2 . [ 必 修 2·P127 例 1 改 编 ] 直 线 y = x + 1 与 圆 x2 + y2 = 1 的 位 置 关 系 为 () A.相切 B.相交但直线不过圆心 C.直线过圆心 D.相离
答案:B
3.[必修2·P129例3改编]两圆x2+y2-2y=0与x2+y2-4=0的位置关 系是( )
切线方程是___x_=__1_或__y=__2__.
5.(忽视两圆相切有两种情况)若半径为r,圆心为(0,1)的圆和定圆 (x-1)2+(y-2)2=1相切,则r的值等于_____________.
5
关键能力—考点突破
考点一 直线与圆的位置关系 [基础性]
1.已知直线l:kx-y+k=0,圆O:x2+y2=2,则直线l与圆O的位 置关系是( )
三、必练4类基础题 (一)判断正误 1.判断下列说法是否正确(请在括号中打“√”或“×”). (1)“k=1”是“直线x-y+k=0与圆x2+y2=1相交”的必要不充分 条件.( × ) (2) 如 果 两 个 圆 的 方 程 组 成 的 方 程 组 只 有 一 组 实 数 解 , 则 两 圆 外 切.( × ) (3)如果两圆的圆心距小于两圆的半径之和,则两圆相交.( × ) (4)圆C1:x2+y2+2x+2y-2=0与圆C2:x2+y2-4x-2y+1=0的公 切线有且仅有2条.( √ )
考点二 圆的切线与弦长问题 [综合性] 角度1 直线与圆的相切问题 [例1] 过点P(2,4)引圆C:(x-1)2+(y-1)2=1的切线,则切线方程 为_x_=__2或__4_x_-__3y_+__4_=_0_.
2.(变问题)在例1中,已知条件不变,设两个切点为A,B,求切点 弦AB所在的直线方程.
高考数学一轮复习 94直线、圆的位置关系课件 理

基础梳理 1.直线与圆的位置关系 位置关系有三种:相离、相切、 相交 . 判断直线与圆的位置关系常见的有两种方法: (1)代数法:Δ=判―b别―2-→式4acΔΔΔ= <>000⇔ ⇔⇔相 相相切 离交, .,
(2)几何法:利用圆心到直线的距离d和圆半径r的大小关系:d <r⇔相交,d=r⇔ 相切 ,d>r⇔相离. 2.圆与圆的位置关系的判定 设⊙C1:(x-a1)2+(y-b1)2=r21(r1>0), ⊙C2:(x-a2)2+(y-b2)2=r22(r2>0),则有: |C1C2|>r1+r2⇔⊙C1与⊙C2 相离 ; |C1C2|=r1+r2⇔⊙C1与⊙C2 外切 ; |r1-r2|<|C1C2|<r1+r2⇔⊙C1与⊙C2相交 ; |C1C2|=|r1-r2|(r1≠r2)⇔⊙C1与⊙C2 内切 ; |C1C2|<|r1-r2|⇔⊙C1与⊙C2 内含 .
|-2k-6+5| k2+-12
=2,得k=
3 4
.
又直线l的斜率不存在时,也满足题意,此时方程为x=0.
难点突破20——高考中与圆交汇问题的求解 从近两年新课标高考试题可以看出高考对圆的要求大大提高 了,因此也就成了高考命题的一个新热点.由于圆的特有性 质,使其具有很强的交汇性,在高考中圆可以直接或间接地综 合出现在许多问题之中,复习备考时值得重视.
单击此处进入 活页限时训练
•11、凡为教者必期于达到不须教。对人以诚信,人不欺我;对事以诚信,事无不成。 •12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 •13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2022/1/182022/1/18January 18, 2022 •14、孩子在快乐的时候,他学习任何东西都比较容易。 •15、纪律是集体的面貌,集体的声音,集体的动作,集体的表情,集体的信念。 •16、一个人所受的教育超过了自己的智力,这样的人才有学问。 •17、好奇是儿童的原始本性,感知会使儿童心灵升华,为其为了探究事物藏下本源。2022年1月2022/1/182022/1/182022/1/181/18/2022 •18、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。 2022/1/182022/1/18
高考数学复习考点知识讲解课件44 直线与圆 圆与圆的位置关系

— 12 —
(新教材) 高三总复习•数学
— 返回 —
5.(教材P98T3改编)已知直线l:y=k(x-2)被圆C:x2+y2-2x-4y=0截得的弦长的范 围是(0, 10),则k的取值范围是____-__13_,__12__∪__12_,__3______.
[解析] 圆C的标准方程为(x-1)2+(y-2)2=5,直线l过定点(2,0),且点(2,0)在圆C
— 6—
(新教材) 高三总复习•数学
— 返回 —
2.直线被圆截得的弦长的求法 (1)几何法:运用弦心距d、半径r和弦长的一半构成的直角三角形,计算弦长|AB|= 2 r2-d2. (2)代数法:设直线y=kx+m与圆x2+y2+Dx+Ey+F=0相交于点M,N,将直线方程 代入圆的方程中,消去y,得关于x的一元二次方程,求出xM+xN和xM·xN,则|MN|= 1+k2· xM+xN2-4xM·xN. 3.两圆相交时,其公共弦所在的直线方程由两圆方程相减得到.
(新教材) 高三总复习•数学
— 返回 —
(2)∵(3-1)2+(1-2)2=5>4,
∴点M在圆C外部.
当过点M的直线斜率不存在时,直线方程为x=3,即x-3=0.
又点C(1,2)到直线x-3=0的距离d=3-1=2=r,
即此时满足题意,所以直线x=3是圆的切线;
当切线的斜率存在时,设切线方程为y-1=k(x-3),即kx-y+1-3k=0,
核心考点突破
02
(新教材) 高三总复习•数学
— 返回 —
考点一 直线与圆的位置关系的判断——自主练透
对点训练
1.(2022·广东茂名一模)过三点A(0,0),B(0,2),C(2,0)的圆M与直线l:kx-y+2-2k
2024年高考数学一轮复习第七章第四讲直线与圆、圆与圆的位置关系课件

B.线段 AB 中垂线方程为 x+y-1=0
C.公共弦
AB
的长为
2 2
D.P 为圆 O1 上一动点,则 P 到直线 AB 距离的最大值为 22+1
外离
d=R+r d>R+r
3
4
【名师点睛】(1)圆的切线方程常用结论
①过圆x2+y2=r2上一点P(x0,y0)的圆的切线方程为x0x+ y0y=r2.
②过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的圆的切线方 程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
③过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两 切点所在直线方程为x0x+y0y=r2.
解析:设圆(x-5)2+(y-5)2=16 的圆心为 M(5,5),由题易 知直线 AB 的方程为4x+2y=1,即 x+2y-4=0,则圆心 M 到直线 AB 的距离 d=|5+2×55-4|= 115>4,所以直线 AB 与圆 M 相离, 所以点 P 到直线 AB 的距离的最大值为 4+d=4+115,4+ 115<10, 故 A 正确;易知点 P 到直线 AB 的距离的最小值为 d-4=115-4,
a2,0,半径 r=a2,
a
圆心 O1 到直线 x-y=0 的距离 d= 22=2 a 2,所以由题意可
得弦长 2 2=2 r2-d2=2
a42-a82,解得 a=4,所以圆 O1 的
方程为 x2+y2-4x=0,即圆心坐标 O1(2,0),半径 r=2,圆 O2 的圆心 O2(4,2),半径 r′=1,
程中,体会用代数方法处理几何 主,难度中等中出现
1.直线与圆的位置关系
判断方法
相交
几何法
d<r
高考数学一轮复习---直线与圆、圆与圆的位置关系知识点与题型复习
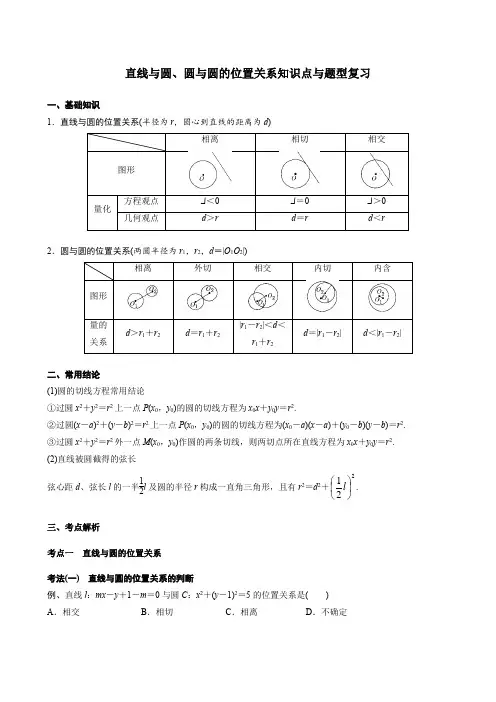
直线与圆、圆与圆的位置关系知识点与题型复习一、基础知识1.直线与圆的位置关系(半径为r ,圆心到直线的距离为d )Δ<0 Δ=0 Δ>02.圆与圆的位置关系(两圆半径为r 1,r 2,d =|O 1O 2|)|r -r |<d <二、常用结论(1)圆的切线方程常用结论①过圆x 2+y 2=r 2上一点P (x 0,y 0)的圆的切线方程为x 0x +y 0y =r 2.②过圆(x -a )2+(y -b )2=r 2上一点P (x 0,y 0)的圆的切线方程为(x 0-a )(x -a )+(y 0-b )(y -b )=r 2. ③过圆x 2+y 2=r 2外一点M (x 0,y 0)作圆的两条切线,则两切点所在直线方程为x 0x +y 0y =r 2. (2)直线被圆截得的弦长弦心距d 、弦长l 的一半12l 及圆的半径r 构成一直角三角形,且有r 2=d 2+221⎪⎭⎫⎝⎛l .三、考点解析考点一 直线与圆的位置关系 考法(一) 直线与圆的位置关系的判断例、直线l :mx -y +1-m =0与圆C :x 2+(y -1)2=5的位置关系是( ) A .相交 B .相切 C .相离 D .不确定[解题技法]判断直线与圆的位置关系的常见方法: (1)几何法:利用d 与r 的关系.(2)代数法:联立方程组,消元得一元二次方程之后利用Δ判断.(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.考法(二) 直线与圆相切的问题例、(1)过点P (2,4)作圆(x -1)2+(y -1)2=1的切线,则切线方程为( )A .3x +4y -4=0B .4x -3y +4=0C .x =2或4x -3y +4=0D .y =4或3x +4y -4=0 (2)已知圆C :x 2+y 2-2x -4y +1=0上存在两点关于直线l :x +my +1=0对称,经过点M (m ,m )作圆C 的切线,切点为P ,则|MP |=________.考法(三) 弦长问题例、(1)若a 2+b 2=2c 2(c ≠0),则直线ax +by +c =0被圆x 2+y 2=1所截得的弦长为( ) A.12 B .1 C.22D.2 (2)设直线y =x +2a 与圆C :x 2+y 2-2ay -2=0相交于A ,B 两点,若|AB |=23,则圆C 的面积为( ) A .4π B .2π C .9π D .22π跟踪练习:1.已知圆的方程是x 2+y 2=1,则经过圆上一点M ⎪⎪⎭⎫⎝⎛2222,的切线方程是________. 2.若直线kx -y +2=0与圆x 2+y 2-2x -3=0没有公共点,则实数k 的取值范围是________.3.设直线y =kx +1与圆x 2+y 2+2x -my =0相交于A ,B 两点,若点A ,B 关于直线l :x +y =0对称,则|AB |=________.考点二 圆与圆的位置关系例、已知圆M :x 2+y 2-2ay =0(a >0)截直线x +y =0所得线段的长度是22,则圆M 与圆N :(x -1)2+(y -1)2=1的位置关系是( )A .内切B .相交C .外切D .相离变式练习:1.若圆C 1:x 2+y 2=1与圆C 2:x 2+y 2-6x -8y +m =0外切,则m =( )A .21B .19C .9D .-112.(变结论)若本例两圆的方程不变,则两圆的公共弦长为________.[解题技法]几何法判断圆与圆的位置关系的3步骤: (1)确定两圆的圆心坐标和半径长;(2)利用平面内两点间的距离公式求出圆心距d ,求r 1+r 2,|r 1-r 2|; (3)比较d ,r 1+r 2,|r 1-r 2|的大小,写出结论.课后作业1.若直线2x +y +a =0与圆x 2+y 2+2x -4y =0相切,则a 的值为( ) A .±5 B .±5 C .3 D .±32.与圆C 1:x 2+y 2-6x +4y +12=0,C 2:x 2+y 2-14x -2y +14=0都相切的直线有( ) A .1条 B .2条 C .3条 D .4条3.直线y =kx +3被圆(x -2)2+(y -3)2=4截得的弦长为23,则直线的倾斜角为( ) A.π6或5π6 B .-π3或π3 C .-π6或π6 D.π64.过点(3,1)作圆(x -1)2+y 2=r 2的切线有且只有一条,则该切线的方程为( ) A .2x +y -5=0 B .2x +y -7=0 C .x -2y -5=0 D .x -2y -7=05.若圆x 2+y 2+2x -6y +6=0上有且仅有三个点到直线x +ay +1=0的距离为1,则实数a 的值为( ) A .±1 B .±24 C .± 2 D .±326.过点P (1,-2)作圆C :(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则AB 所在直线的方程为( ) A .y =-34 B .y =-12 C .y =-32 D .y =-147.在平面直角坐标系xOy 中,直线x +2y -3=0被圆(x -2)2+(y +1)2=4截得的弦长为________. 8.若P (2,1)为圆(x -1)2+y 2=25的弦AB 的中点,则直线AB 的方程为________. 9.过点P (-3,1),Q (a,0)的光线经x 轴反射后与圆x 2+y 2=1相切,则a 的值为________.10.点P 在圆C 1:x 2+y 2-8x -4y +11=0上,点Q 在圆C 2:x 2+y 2+4x +2y +1=0上,则|P Q |的最小值是________.11.已知圆C 1:x 2+y 2-2x -6y -1=0和圆C 2:x 2+y 2-10x -12y +45=0. (1)求证:圆C 1和圆C 2相交;(2)求圆C 1和圆C 2的公共弦所在直线的方程和公共弦长.12.已知圆C 经过点A (2,-1),和直线x +y =1相切,且圆心在直线y =-2x 上. (1)求圆C 的方程;(2)已知直线l 经过原点,并且被圆C 截得的弦长为2,求直线l 的方程.提高练习1.过圆x 2+y 2=1上一点作圆的切线,与x 轴、y 轴的正半轴相交于A ,B 两点,则|AB |的最小值为( ) A. 2 B.3 C .2 D .32.在平面直角坐标系xOy 中,A 为直线l :y =2x 上在第一象限内的点,B (5,0),以AB 为直径的圆C 与直线l 交于另一点D .若AB ―→·CD ―→=0,则点A 的横坐标为________. 3.已知圆C :x 2+(y -a )2=4,点A (1,0).(1)当过点A 的圆C 的切线存在时,求实数a 的取值范围; (2)设AM ,AN 为圆C 的两条切线,M ,N 为切点,当|MN |=455时,求MN 所在直线的方程.。
2025高考数学一轮复习-8.4-直线与圆、圆与圆的位置关系【课件】
6.若圆 x2+y2=1 与圆 x2+y2-6x-8y-m=0 相切,则 m 的值为_-__9__或__1_1.
【解析】 x2+y2-6x-8y-m=0 可化为(x-3)2+(y-4)2=25+m,因为两圆相切, 所以 32+42=1+ 25+m或 32+42=|1- 25+m|,解得 m=-9 或 m=11.
易错易混 5.已知圆 C:x2+y2=9,过点 P(3,1)作圆 C 的切线,则切线方程为 _____x=__3__或__4_x_+__3_y_-__1_5_=__0___.
【解析】 由题意知 P 在圆外.当切线斜率不存在时,切线方程为 x=3,满足题意; 当 切 线 斜 率 存 在 时 , 设 切 线 方 程 为 y - 1 = k(x - 3) , 即 kx - y + 1 - 3k = 0 , 所 以 |k×0k-2+0+-11-23k|=3,得 k=-43,切线方程为 4x+3y-15=0.综上,切线方程为 x=3 或 4x+3y-15=0.
(2)解法一:∵直线 kx-y+1=0 与圆(x+1)2+(y-2)2=4 有公共点,∴直线与圆相切 或相交,又圆心(-1,2)到直线 kx-y+1=0 的距离 d=|-k-k2+2+1 1|= |kk+2+1|1,r=2,∴d≤r, 即 |kk+2+1|1≤2,∴3k2-2k+3≥0,又∵Δ=4-36=-32<0,∴k∈R,∴实数 k 的取值范围 为(-∞,+∞).故选 D.
2.圆与圆的位置关系(两圆半径为 r1,r2,d=|O1O2|)
相离
外切
相交
内切
图形
量的 关系
d>r1+r2
d=r1+r2 |r1-r2|<d<r1+r2
d=|r1-r2|Fra bibliotek内含 d<|r1-r2|
第4节 直线与圆、圆与圆的位置关系--2025高中数学一轮复习课件基础版(新高考新教材)
|O1O2|=2,r2-r1<|O1O2|<r2+r1,所以两圆相交.
7.(人教A版选择性必修第一册第93页2.5.1节练习第3题改编)直线2x-y+2=0
8 5
被圆(x-1)2+(y-2)2=4截得的弦长为__________.
5
解析 圆的圆心坐标为(1,2),半径 r=2.
圆心到直线的距离 d=
)
题组二 回源教材
5.(人教A版选择性必修第一册2.5.1节例1改编)直线y=x+1与圆x2+y2=1的位
置关系为( B )
A.相切
B.相交但直线不过圆心
C.直线过圆心
D.相离
解析 圆心(0,0)到直线 y=x+1,即 x-y+1=0 的距离 d=
而
2
0< <1,但是圆心不在直线
2
1
2
=
2
,
2
y=x+1 上,所以直线与圆相交,但直线不过圆心.
3
=1(m>0)的渐近线与圆x2+y2-4y+3=0
相切,则m=__________.
3
解析 圆的方程可化为 x2+(y-2)2=1,双曲线的一条渐近线方程为 x=my(m>0),
由题意得
|2|
1+
=1,解得
2
3
m= 或
3
3
m=- .又
3
m>0,所以
3
m= .
3
研考点
精准突破
考点一
直线与圆的位置关系
于m,则m的值为__________.
2
解析 由题知,圆心(1,1)到直线
2022年高考数学总复习考点培优——直线与圆、圆与圆的位置关系
第四节直线与圆、圆与圆的位置关系【教材回扣】1.直线与圆的位置关系设圆O的半径为r(r>0),圆心到直线l的距离为d,则直线与圆的位置关系可用下表表示:相离相切相交Δ______0Δ______0Δ______0若P(x0,y0)在圆x2+y2=r2(r>0)上,则以P为切点的切线方程为F7______________.3.圆与圆的位置关系设两圆的半径分别为R,r(R>r),两圆圆心间的距离为d,则两圆的位置关系可用下表表示:相离外切相交内切内含____________________________________【题组练透】题组一判断正误(正确的打“√”,错误的打“×”)1.“k=2”是“直线x+y+k=0与圆x2+y2=2相切”的必要不充分条件.() 2.若直线平分圆的周长,则直线一定过圆心.()3.若两圆相切,则有且只有一条公切线.()4.从两圆的方程中消掉二次项后得到二元一次方程是两圆的公共弦所在的直线方程.()题组二教材改编1.直线l:3x-y-6=0被圆C:x2+y2-2x-4y=0截得的弦AB的长为()A.102B.10C.265D.22652.已知直线4x+3y-35=0与圆心在原点的圆C相切,则圆C的方程为() A.x2+y2=1 B.x2+y2=5C.x2+y2=7 D.x2+y2=493.圆x2+y2-4=0与圆x2+y2-4x+4y-12=0的公共弦的长为________.题组三易错自纠1.若直线l:x-y+m=0与圆C:x2+y2-4x-2y+1=0恒有公共点,则m的取值范围是()A.[-2,2] B.[-22,22]C.[-2-1,2-1] D.[-22-1,22-1]2.(多选题)直线x-y+m=0与圆x2+y2-2x-1=0有两个不同交点的一个充分不必要条件是()A.0<m<1 B.-1<m<0C.m<1 D.-3<m<13.已知圆C:x2+y2=9,过点P(3,1)作圆C的切线,则切线方程为________.题型一直线与圆的位置关系的判断[例1](1)直线l:mx-y+1-m=0与圆C:x2+(y-1)2=5的位置关系是()A.相交B.相切C.相离D.不确定(2)若圆x2+y2=r2(r>0)上恒有4个点到直线x-y-2=0的距离为1,则实数r的取值范围是()A.(2+1,+∞) B.(2-1,2+1)C.(0,2-1) D.(0,2+1)[听课记录]类题通法判断直线与圆的位置关系的一般方法1.几何法:圆心到直线的距离与圆半径比较大小,即可判断直线与圆的位置关系.这种方法的特点是计算量较小.2.代数法:将直线方程与圆方程联立方程组,再将二次方程组转化为一元二次方程,该方程解的情况即对应直线与圆的位置关系.这种方法具有一般性,适合于判断直线与圆锥曲线的位置关系.巩固训练1:(1)已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是()A.相切B.相交C.相离D.不确定(2)若无论实数a取何值时,直线ax+y+a+1=0与圆x2+y2-2x-2y+b=0都相交,则实数b的取值范围为________.题型二圆的切线与弦长问题高频考点角度|圆的切线问题[例2](1)[2020·浙江卷](一题两空)已知直线y=kx+b(k>0)与圆x2+y2=1和圆(x-4)2+y2=1均相切,则k=________,b=________.(2)从直线l:x+y=1上一点P向圆C:x2+y2+4x+4y+7=0引切线,则切线长的最小值为________.[听课记录]类题通法1.求过圆上的一点(x0,y0)的切线方程的方法先求切点与圆心连线的斜率k,若k不存在,则结合图形可直接写出切线方程为y=y0;若k=0,则结合图形可直接写出切线方程为x=x0;若k存在且k≠0,则由垂直关系知切线的斜率为-1k,由点斜式可写出切线方程.2.求过圆外一点(x0,y0)的圆的切线方程的2种方法(1)几何法:当斜率存在时,设为k,则切线方程为y-y0=k(x-x0)即kx-y+y0-kx0=0.由圆心到直线的距离等于半径,即可求出k的值,进而写出切线方程.(2)当斜率存在时,设为k,则切线方程y-y0=k(x-x0),即y=kx-kx0+y0,代入圆的方程,得到一个关于x的一元二次方程,由Δ=0,求得k,切线方程即可求出.[提醒]当点(x0,y0)在圆外时,一定要注意斜率不存在的情况.巩固训练2:(1)(多选题)过点P(2,4)引圆(x-1)2+(y-1)2=1的切线,则切线的方程为()A.x=-2 B.x=2C.4x-3y+4=0 D.4x+3y-4=0(2)直线l是圆x2+y2=4在(-1,3)处的切线,点P是圆x2-4x+y2+3=0上的动点,则点P到直线l的距离的最小值等于________.角度|圆的弦长问题[例3](1)(多选题)[2021·山东德州模拟]直线y=kx-1与圆C:(x+3)2+(y-3)2=36相交于A,B两点,则AB的长度可能为()A.6 B.8C.12 D.16(2)在圆x2+y2-2x-6y=0内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为()A.5 2 B.102C.15 2 D.202(3)[2020·天津卷]已知直线x-3y+8=0和圆x2+y2=r2(r>0)相交于A,B两点,若|AB|=6,则r的值为________.[听课记录]类题通法有关弦长问题的2种求法1.几何法:直线被圆截得的半弦长l2,弦心距d和圆的半径r构成直角三角形,即r2=(l2)2+d2.2.代数法:联立直线方程和圆的方程,消元转化为关于x的一元二次方程,由根与系数的关系即可求得弦长|AB|=1+k2·|x1-x2|=1+k2(x1+x2)2-4x1x2或|AB|=1+1k2·|y1-y2|=1+1k2·(y1+y2)2-4y1y2.巩固训练3:(1)[2020·全国卷Ⅰ]已知圆x2+y2-6x=0,过点(1,2)的直线被该圆所截得的弦的长度的最小值为()A.1 B.2C.3 D.4(2)(多选题)设圆x2+y2-2x-2y-2=0的圆心为C,直线l过(0,3),且与圆C交于A,B两点,若|AB|=23,则直线l的方程为()A.4x-3y+9=0 B.x=0C.3x+4y-12=0 D.3x+4y+12=0(3)已知圆C:(x-1)2+(y-2)2=2截y轴所得线段与截直线y=2x+b所得线段的长度相等,则b=________.题型三圆与圆的位置关系[例4]已知两圆x2+y2-2x-6y-1=0和x2+y2-10x-12y+m=0.求:(1)m取何值时两圆外切?(2)m取何值时两圆内切,此时公切线方程是什么?(3)求m=45时两圆的公共弦所在直线的方程和公共弦的长.[听课记录]类题通法(1)判断两圆位置关系的方法常用几何法,即用两圆圆心距与两圆半径和及差的绝对值的大小关系判断,一般不用代数法.重视两圆内切的情况,作图观察.(2)两圆相交时,公共弦所在直线方程的求法两圆的公共弦所在直线的方程可由两圆的方程作差消去x2,y2项得到.(3)两圆公共弦长的求法求两圆公共弦长,常选其中一圆,由弦心距d,半弦长l2,半径r构成直角三角形,利用勾股定理求解.巩固训练4:(1)已知圆C1:x2+y2+2x+3y+1=0,圆C2:x2+y2+4x-3y-36=0,则圆C1和圆C2的位置关系为()A.相切B.内含C.外离D.相交(2)[2021·山东潍坊模拟]已知圆O:x2+y2=1,圆M:(x-a)2+(y-a+3)2=1.若圆M上存在点P,过点P作圆O的两条切线,切点为A,B,使得∠APB=60°,则实数a的取值范围是________.(3)若圆x2+y2=a2与圆x2+y2+ay-6=0的公共弦长为23,则a=________.[预测1] 核心素养——直观现象 过点P(x 0,y 0)作圆C 1:x 2+y 2=1与圆C 2:(x -2)2+(y -1)2=1的切线,切点分别为A ,B.若|PA|=|PB|,则x 20+y 20的最小值为( )A .52B .54C .54 D .5 [预测2] 新题型——多选题已知圆M 与直线x +y +2=0相切于点A(0,-2),圆M 被x 轴所截得的弦长为2,则下列结论正确的是( )A .圆M 的圆心在定直线x -y -2=0上B .圆M 的面积的最大值为50πC .圆M 的半径的最小值为1D .满足条件的所有圆M 的半径之积为10第四节 直线与圆、圆与圆的位置关系 课前基础巩固[教材回扣]< = > > = <x 0x +y 0y =r 2 d >R +r d =R +r R -r <d <R +r d =R -r 0≤d <R -r [题组练透] 题组一1.× 2.√ 3.× 4.× 题组二1.解析:由已知可知圆C 的圆心为(1,2),半径为5,圆心到直线的距离为d =|3×1-2-6|32+12=102.∴|AB |=2r 2-d 2=252-⎝⎛⎭⎫1022=10. 故选B. 答案:B2.解析:由题意知:圆心到直线4x +3y -35=0的距离d 等于半径r .即d =3542+32=7=r ,故所求圆的方程为x 2+y 2=49. 故选D.答案:D3.解析:联立方程组⎩⎪⎨⎪⎧x 2+y 2-4=0x 2+y 2-4x +4y -12=0, 得x -y +2=0.已知圆x 2+y 2-4=0的圆心(0,0),半径r 为2,且圆心(0,0)到直线x -y +2=0的距离d =22=2, 则公共弦长为2r 2-d 2=24-2=2 2.答案:22 题组三1.解析:已知圆的圆心坐标为(2,1),半径r =2. 则圆心到直线l 的距离为d =|2-1+m |2≤r =2. 解得-22-1≤m ≤22-1. 故选D. 答案:D2.解析:已知圆的圆心坐标为(1,0),半径r =2, 则圆心到直线的距离d =|1+m |2<2,解得-3<m <1,则-3<m <1的一个充分不必要条件是0<m <1或-1<m <0. 故选AB. 答案:AB3.解析:由题意知P 在圆外,当切线斜率不存在时,切线方程为x =3,满足题意;当切线斜率存在时,设斜率为k ,所以切线方程为y -1=k (x -3),即kx -y +1-3k =0,所以|k ×0-0+1-3k |k 2+1=3,解得k =-43,所以切线方程为4x +3y -15=0.综上,切线方程为x =3或4x +3y -15=0.答案:x =3或4x +3y -15=0课堂题型讲解题型一例1 解析:(1)法一 (代数法)由⎩⎪⎨⎪⎧mx -y +1-m =0,x 2+(y -1)2=5,消去y 得(1+m 2)x 2-2m 2x +m 2-5=0. 因为Δ=16m 2+20>0, 所以直线l 与圆相交.法二 (几何法)由题意知,圆心(0,1)到直线l 的距离d =|-m |m 2+1<1<5,故直线l 与圆相交.法三 易得直线l 过定点(1,1).把点(1,1)代入圆的方程有1+0< 5.∴点(1,1)在圆的内部,故直线l 与圆C 相交.(2)计算得圆心到直线l 的距离为22=2>1,如图,直线l :x -y -2=0与圆相交,l 1,l 2与l 平行,且与直线l 的距离为1,故可以看出,圆的半径应该大于圆心到直线l 2的距离2+1.故选A.答案:(1)A (2)A巩固训练1 解析:(1)因为M (a ,b )在圆O :x 2+y 2=1外,所以a 2+b 2>1,而圆心O到直线ax +by =1的距离d =1a 2+b2<1.所以直线与圆相交.故选B.(2)∵x 2+y 2-2x -2y +b =0表示圆, ∴8-4b >0,即b <2.∵直线ax +y +a +1=0过定点(-1,-1), ∴点(-1,-1)在圆x 2+y 2-2x -2y +b =0的内部, ∴6+b <0,解得b <-6,∴b 的取值范围是(-∞,-6). 答案:(1)B (2)(-∞,-6) 题型二例2 解析:(1)解法一 因为直线y =kx +b (k >0)与圆x 2+y 2=1,圆(x -4)2+y 2=1都相切,所以|b |1+k 2=|4k +b |1+k 2=1,得k =33,b =-233. 解法二 因为直线y =kx +b (k >0)与圆x 2+y 2=1,圆(x -4)2+y 2=1都相切,所以直线y =kx +b 必过两圆心连线的中点(2,0),所以2k +b =0.设直线y =kx +b 的倾斜角为θ,则sin θ=12,又k >0,所以θ=π6,所以k =tan π6=33,b =-2k =-233. (2)如图:圆C :x 2+y 2+4x +4y +7=0的标准方程为:(x +2)2+(y +2)2=1.圆心C (-2,-2),半径r =1.∴圆心到直线l :x +y -1=0的距离|CP |=|-2-2-1|2=522,则切线长的最小值为:|CP |2-|CQ |2=252-1=462.答案:(1)33 -233 (2)462巩固训练2 解析:(1)根据题意,圆(x -1)2+(y -1)2=1的圆心为(1,1),半径r =1.过点P (2,4)引圆(x -1)2+(y -1)2=1的切线,若切线的斜率不存在,此时切线的方程为x =2,符合题意;若切线的斜率存在,设此时切线的斜率为k ,则其方程为y -4=k (x -2),即kx -y -2k +4=0,则有|3-k |k 2+1=1,解得k =43,则切线的方程为4x -3y +4=0.综上可得,切线的方程为x =2或4x -3y +4=0.故选BC.(2)圆x 2+y 2=4在点(-1,3)处的切线为l :-x +3y =4,即l :x -3y +4=0,点P 是圆(x -2)2+y 2=1上的动点,圆心(2,0)到直线l :x -3y +4=0的距离d =|2-0+4|1+3=3,∴点P 到直线l 的距离的最小值等于d -1=3-1=2.答案:(1)BC (2)2例3 解析:(1)圆C 的圆心坐标为(-3,3),半径为6,所以弦长AB 的最大值为圆C 的直径12.又直线y =kx -1过点P (0,-1),当直线CP 与直线y =kx -1垂直时,弦长AB 最短,此时|AB |=262-|CP |2=262-52=211,所以211≤|AB |≤12,故选BC.(2)圆的标准方程为(x -1)2+(y -3)2=10,则圆心(1,3),半径r =10,由题意知AC ⊥BD ,且|AC |=210,|BD |=210-5=25,所以四边形ABCD 的面积为S =12|AC |·|BD |=12×210×25=10 2.故选B.(3)由题意得,圆心(0,0)到直线x -3y +8=0的距离d =82=4,因此r 2=d 2+|AB |22=25,又r >0,∴r =5.答案:(1)BC (2)B (3)5巩固训练3 解析:(1)将圆的方程x 2+y 2-6x =0化为标准方程(x -3)2+y 2=9,设圆心为C ,则C (3,0),半径r =3.设点(1,2)为点A ,过点A (1,2)的直线为l ,因为(1-3)2+22<9,所以点A (1,2)在圆C 的内部,则直线l 与圆C 必相交,设交点分别为B ,D .易知当直线l ⊥AC 时,直线l 被该圆所截得的弦的长度最小,设此时圆心C 到直线l 的距离为d ,则d =|AC |=(3-1)2+(0-2)2=22,所以|BD |min =2r 2-d 2=232-(22)2=2,即弦的长度的最小值为2,故选B.(2)将圆的方程化为标准形式为:(x -1)2+(y -1)2=4,所以圆心为C (1,1),圆的半径r =2,当直线l 的斜率不存在时,直线l 的方程为x =0,圆心到直线l 的距离为d =1,所以|AB |=24-1=23,符合题意;当直线l 的斜率存在时,设直线l 的方程为y =kx +3,易知圆心C (1,1)到直线y =kx +3的距离d =|k -1+3|k 2+1=|k +2|k 2+1,因为d 2+|AB |22=r 2,所以(k +2)2k 2+1+3=4,解得k =-34,所以直线l 的方程为y =-34x +3.即3x +4y -12=0.综上,直线l 的方程为3x +4y -12=0或x =0,故选BC.(3)记圆C 与y 轴的两个交点分别是A ,B ,由圆心C 到y 轴的距离为1,|CA |=|CB |=2可知,圆心C (1,2)到直线2x -y +b =0的距离也等于1才符合题意,于是|2×1-2+b |5=1,解得b =± 5.答案:(1)B (2)BC (3)±5 题型三例4 解析:两圆的标准方程分别为(x -1)2+(y -3)2=11,(x -5)2+(y -6)2=61-m , 圆心分别为M (1,3),N (5,6), 半径分别为11和61-m .(1)当两圆外切时, (5-1)2+(6-3)2 =11+61-m .解得m =25+1011.(2)当两圆内切时,因定圆的半径11小于两圆圆心间距离,故只有61-m -11=5.解得m =25-1011.因为k MN =6-35-1=34,所以两圆公切线的斜率是-43.设切线方程为y =-43x +b ,则有43×1+3-b 432+1=11.解得b =133±5113.容易验证,当b =133+5113,直线与后一圆相交,舍去.故所求公切线方程为y =-43x +133-5311,即4x +3y +511-13=0.(3)两圆的公共弦所在直线的方程为(x 2+y 2-2x -6y -1)-(x 2+y 2-10x -12y +45)=0, 即4x +3y -23=0.由圆的半径、弦长、弦心距间的关系,得公共弦的长为 2×(11)2-|4+3×3-23|42+322=27.巩固训练4 解析:(1)圆C 1:x 2+y 2+2x +3y +1=0,即(x +1)2+y +322=94,∴C 1-1,-32,圆C 1的半径r 1=32.圆C 2:x 2+y 2+4x -3y -36=0,即(x +2)2+y -322=1694, ∴C 2-2,32,圆C 2的半径r 2=132.∴两圆的圆心距|C 1C 2|=(-2+1)2+32+322=10.又∵r 1+r 2=32+132=8,r 2-r 1=132-32=5,∴|C 1C 2|=10<r 2-r 1=5,故两圆内含.故选B.(2)由题意易得∠APO =12∠APB =30°,|OP |=|OA |sin ∠APO =1sin 30°=2,∴点P 在以O 为圆心,2为半径的圆上,∴此圆与圆M 有公共点,∴2-1≤|OM |≤2+1,即1≤|OM |2≤9.∵|OM |2=a 2+(a -3)2=2a 2-6a +9,∴1≤2a 2-6a +9≤9,即⎩⎪⎨⎪⎧2a 2-6a +8≥0,2a 2-6a ≤0,解得0≤a ≤3,∴a 的取值范围是[0,3]. (3)两圆作差得公共弦所在直线方程为a 2+ay -6=0.原点到a 2+ay -6=0的距离为d =6a-a .∵公共弦长为2 3.∴a 2=(3)2+6a-a 2,∴a 2=4,a =±2.答案:(1)B (2)[0,3] (3)±2高考命题预测预测1 解析:如图所示,由圆的切线的性质,得|P A |2=|PC 1|2-1,|PB |2=|PC 2|2-1.又|P A |=|PB |,所以|PC 1|=|PC 2|,所以点P 在线段C 1C 2的垂直平分线上.因为C 1C 2的垂直平分线为y =-21(x -1)+12,即y =-2x +52,点P (x 0,y 0)在y =-2x +52上,所以点P 的坐标满足y 0=-2x 0+52,所以x 20+y 20=x 20+-2x 0+522=5(x 0-1)2+54≥54,所以x 20+y 20的最小值为54.故选B. 答案:B预测2 解析:∵圆M 与直线x +y +2=0相切于点A (0,-2),∴直线AM 与直线x +y +2=0垂直,∴直线AM 的斜率为1,则点M 在直线y =x -2,即x -y -2=0上,A 正确;设M (a ,a -2),∴圆M 的半径r =|AM |=a 2+(a -2+2)2=2|a |,∴圆M 被x 轴截得的弦长为2r 2-(a -2)2=2a 2+4a -4=2,解得a =-5或a =1,当a =-5时,圆M 的面积最大,为πr 2=50π,B 正确;当a =1时,圆M 的半径最小,为2,C 错误;满足条件的所有圆M 的半径之积为52×2=10,D 正确.故选ABD.答案:ABD。
河北省邢台市沙河市高考数学总复习第4讲直线与圆、圆与圆的位置关系基础巩固题组(无答案)
第4讲直线与圆、圆与圆的位置关系基础巩固题组一、选择题1.若直线ax+by=1与圆x2+y2=1相交,则P(a,b)()A.在圆上B.在圆外C.在圆内D.以上都有可能2.圆x2+y2-4x=0在点P(1,3)处的切线方程为( )A.x+错误!y-2=0 B.x+错误!y-4=0C.x-错误!y+4=0 D.x-错误!y+2=03.(2015·甘肃诊断考试)已知圆O1:(x-a)2+(y-b)2=4,O2:(x-a-1)2+(y-b-2)2=1(a,b∈R),则两圆的位置关系是( )A.内含B.内切C.相交D.外切4.过点(3,1)作圆(x-1)2+y2=1的两条切线,切点分别为A,B,则直线AB的方程为()A.2x+y-3=0 B.2x-y-3=0C.4x-y-3=0 D.4x+y-3=05.若直线y=kx与圆(x-2)2+y2=1的两个交点关于直线2x+y+b=0对称,则k,b的值分别为()A.k=错误!,b=-4 B.k=-错误!,b=4C.k=错误!,b=4 D.k=-错误!,b=-4二、填空题6.直线y=2x+1被圆x2+y2=1截得的弦长为________.7.过点P(1,1)的直线,将圆形区域错误!分为两部分,使得这两部分的面积之差最大,则该直线的方程为________.8.已知直线x-y+a=0与圆心为C的圆x2+y2+2x-4y-4=0相交于A,B两点,且AC⊥BC,则实数a的值为________.三、解答题9.已知点P(0,5)及圆C:x2+y2+4x-12y+24=0.若直线l过P且被圆C截得的线段长为4错误!,求l的方程.10.已知直线l:y=kx+1,圆C:(x-1)2+(y+1)2=12.(1)试证明:不论k为何实数,直线l和圆C总有两个交点;(2)求直线l被圆C截得的最短弦长.尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文稿在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4讲 直线与圆、圆与圆的位置关系
基础巩固题组
一、选择题
1.若直线ax +by =1与圆x 2
+y 2
=1相交,则P (a ,b )( )
A .在圆上
B .在圆外
C .在圆内
D .以上都有可能
2.圆x 2
+y 2
-4x =0在点P (1,3)处的切线方程为( ) A .x +3y -2=0 B .x +3y -4=0 C .x -3y +4=0
D .x -3y +2=0
3.(2015·甘肃诊断考试)已知圆O 1:(x -a )2
+(y -b )2
=4,O 2:(x -a -1)2
+(y -b -2)2
=1(a ,b ∈R ),则两圆的位置关系是( )
A .内含
B .内切
C .相交
D .外切
4.过点(3,1)作圆(x -1)2
+y 2
=1的两条切线,切点分别为A ,B ,则直线AB 的方程为( )
A .2x +y -3=0
B .2x -y -3=0
C .4x -y -3=0
D .4x +y -3=0
5.若直线y =kx 与圆(x -2)2
+y 2
=1的两个交点关于直线2x +y +b =0对称,则k ,b 的值分别为( )
A .k =1
2,b =-4
B .k =-1
2,b =4
C .k =1
2,b =4
D .k =-1
2
,b =-4
二、填空题
6.直线y =2x +1被圆x 2
+y 2
=1截得的弦长为________.
7.过点P (1,1)的直线,将圆形区域{} x ,y |x 2
+y 2
≤4分为两部分,使得这两部分的面积之差最
大,则该直线的方程为________.
8.已知直线x -y +a =0与圆心为C 的圆x 2
+y 2
+2x -4y -4=0相交于A ,B 两点,且AC ⊥BC ,则实数a 的值为________. 三、解答题
9.已知点P (0,5)及圆C :x 2
+y 2
+4x -12y +24=0.若直线l 过P 且被圆C 截得的线段长为43,求l 的方程.
10.已知直线l:y=kx+1,圆C:(x-1)2+(y+1)2=12.
(1)试证明:不论k为何实数,直线l和圆C总有两个交点;
(2)求直线l被圆C截得的最短弦长.。
