数的整除知识点总结
整除知识点总结与练习

整除知识点总结与练习一、整除的定义整除是指对于两个整数a和b,如果a能够被b整除,即a除以b的结果是一个整数,则称a能够被b整除,记作b|a。
其中a称为被除数,b称为除数,整数的除法结果称为商。
例如,6÷3=2,6除以3的结果是2,因此6能够被3整除,即3|6。
整除的定义表明了整除的两个基本特点:1. 整数a能够被整数b整除的定义是a÷b的结果是一个整数。
2. 整除的概念是具有传递性的,即如果a能够被b整除,b能够被c整除,则a能够被c整除。
二、整除的判定在计算整除时,通常需要用到整除的判定方法。
整除的判定方法主要有以下几种:1. 除法判定法:即直接计算被除数除以除数的结果是否为整数。
2. 因数判定法:利用被除数和除数的因数来判断整除关系。
3. 余数判定法:如果a能够被b整除,那么a÷b的余数为0。
4. 分解质因数判定法:将被除数和除数分解质因数,如果被除数分解后能够完全包含除数分解质因数的情况,那么a能够被b整除。
下面通过一些实例来说明整除的判定方法:例1:判断24能否被6整除?方法一:除法判定法,直接计算24÷6=4,结果为整数,因此24能够被6整除。
方法二:因数判定法,24的因数包括1、2、3、4、6、8、12,其中6是24的因数,因此24能够被6整除。
方法三:余数判定法,24÷6=4余0,余数为0,因此24能够被6整除。
方法四:分解质因数判定法,24=2³×3,6=2×3,24的分解质因数包含6的分解质因数,因此24能够被6整除。
综上所述,24能够被6整除。
例2:判断35能否被5整除?方法一:除法判定法,35÷5=7,结果为整数,因此35能够被5整除。
方法二:因数判定法,35的因数包括1、5、7、35,其中5是35的因数,因此35能够被5整除。
方法三:余数判定法,35÷5=7余0,余数为0,因此35能够被5整除。
数的整除知识点总结

数的整除知识点总结数的整除是数论中的一个基本概念,也是初等数学中的重要内容。
它与因数、倍数和约数等概念密切相关,对于解题和推理都有着重要的作用。
下面将对数的整除进行详细总结。
一、定义:如果整数a能够被整数b整除,即a/b是整数,那么称a是b的倍数,b是a的因数。
可以用数学表达式a=b*k来表示,其中k是整数。
二、性质:1.任何一个整数都是它自身的倍数,也是它自身的因数,即a是a的倍数,a是a的因数。
2.任何一个正整数都是1的倍数,即对于任何整数a,都有a是1的倍数。
3.任何一个整数都是它自身的因数,即对于任何整数a,都有a是a的因数。
4.如果a是b的倍数,b是c的倍数,那么a也是c的倍数,即若a是b的倍数且b是c的倍数,则a是c的倍数。
5.如果a是b的倍数,b是a的倍数,那么a和b是互为倍数,即a是b的倍数且b是a的倍数,则a和b互为倍数。
6.如果a是b的因数,b是c的因数,那么a也是c的因数,即若a是b的因数且b是c的因数,则a是c的因数。
三、判断一个数能否整除另一个数的方法:1.因式分解法:将被除数和除数都分解成质因数的乘积形式,然后进行比较。
如果被除数的质因数包含除数的质因数,并且对应质因数的指数均大于等于相应的质因数的指数,则被除数能够整除除数。
2.试商法:用除数去除被除数,如果商是整数且余数为0,则被除数能够整除除数,否则不能整除。
四、整除的性质:1.整除关系具有传递性,即如果a能够整除b,b能够整除c,则a 能够整除c。
2.整除关系具有反对称性,即如果a能够整除b,b能够整除a,则a 和b相等或互为相反数。
3.整除关系具有自反性,即任何一个数都能整除它本身。
4.整除关系具有非传递性,即如果a能够整除b,b能够整除c,但a 不能整除c。
例如:2能整除4,4能整除8,但2不能整除8五、整数的混合运算与整除的关系:1.若a整除b,b整除c,则a整除c。
2. 若a整除b,b整除c,则a整除bc。
数的整除 整除、因数和倍数

1 / 7第四讲 数的整除 整除、因数和倍数【知识点】一、整除的意义1、零和正整数统称为自然数。
正整数、零、负整数统称为整数。
2. 整数a 除以整数b ,如果除得的商是整数而余数为零,我们就说a 能被b 整除,或者说b 能整除a 。
用式子表示:如果 a ÷b=c(其中a 、b ,c 都为整数)称a 能被b 整除或b 能整除a 。
(区分两种表述)3. 整除的条件:1)除数,被除数都为整数2)被除数除以除数,商是整数而且余数为零。
二、因数和倍数1. 整数a 被整数b 整除,a 叫b 的倍数,b 叫a 的因数(也称为约数)2.注意:只有在整除的条件下,才有因数和倍数的概念。
倍数和因数是相互依存的,不能单独存在,这里包含两层意思:第一,讲倍数和因数时,只能说谁是谁的倍数,或者谁是谁的因数,不能说谁是倍数,谁是因数。
第二,两个整数存在倍数和因数关系是相互,如果a 是b 的倍数,那么b 一定是a 的因数。
一个数的因数的个数是有限的,一个数的最小的因数是1,最大的因数是它本身。
3.求一个数的因数的方法(1).列乘法运算:根据因数的意义,有序的写出某数的所有两个数乘积的乘法算式,乘法算式中的因数就是该数的因数。
(2).列除法运算:用此数除以任意数,所得商是整数且没有余数,这些除数和商都是该数的因数。
4.求一个数的倍数的方法求一个数的倍数,就是用这个数,依次与非零自然数相乘,所得之数就是这个数的倍数。
三、奇数和偶数1.整数中能被2整除的整数叫做偶数(2k),余下的整数都是奇数[(2k+1)或(2k-1)]2.奇数+奇数=偶数偶数+偶数=偶数奇数+偶数=奇数奇数-奇数=偶数偶数-偶数=偶数奇数-偶数=奇数奇数×奇数=奇数偶数×偶数=偶数奇数×偶数=偶数3. 能被2整除的数的特征:个位上的数是0,2,4,6,8能被5整除的数的特征:个位上的数是0,5能被10整除(既能被2整除又能被5整除)的数的特征:个位上的数是0能被3整除的数的特征:各位上的数字的和能被3整除能被9整除的数的特征:各位上的数字的和能被9整除【典型例题】2 / 73 / 7 一、整除例1. 什么是整数?什么是自然数?在8,-10,0,0.25,-50,73,100,-8.5中, 正整数有 ,自然数有 ,整数有例2.最小的自然数是思考:非负整数,如小于3的非负整数有例 3.下列各组数中,第一个数能被第二个数整除的是 __________________________,第二个数能整除第一个数的是12和24;39和13;54和27;46和4;17和51;84和7例4. 12÷3=4,那么 能被 整除; 能整除例5: 小明认为2.5能被5整除。
数的整除知识点总结
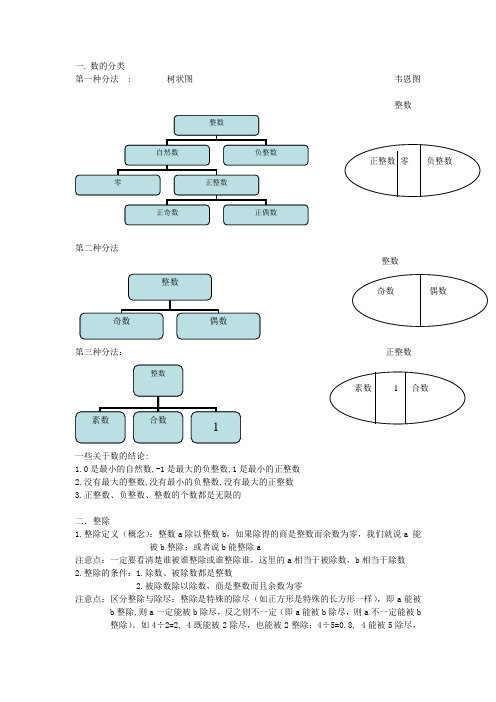
一. 数的分类第一种分法 : 树状图 韦恩图整数第二种分法 整数第三种分法: 正整数一些关于数的结论:1.0是最小的自然数,-1是最大的负整数,1是最小的正整数2.没有最大的整数,没有最小的负整数,没有最大的正整数3.正整数、负整数、整数的个数都是无限的二.整除1.整除定义(概念):整数a 除以整数b ,如果除得的商是整数而余数为零,我们就说a 能被b 整除;或者说b 能整除a注意点:一定要看清楚谁被谁整除或谁整除谁,这里的a 相当于被除数,b 相当于除数2.整除的条件:1.除数、被除数都是整数2.被除数除以除数,商是整数而且余数为零注意点:区分整除与除尽:整除是特殊的除尽(如正方形是特殊的长方形一样),即a 能被b 整除,则a 一定能被b 除尽,反之则不一定(即a 能被b 除尽,则a 不一定能被b 整除)。
如4÷2=2, 4既能被2除尽,也能被2整除;4÷5=0.8, 4能被5除尽,却不能说4能被5整除三.因数与倍数1.因数与倍数的定义:整数a能被整数b整除,a 就叫做b的倍数,b就叫做a的因数(约数)。
注意点:1.因数和倍数是相互依存的,不能简单的说某个数是因数,某个数是倍数。
如: 6÷3=2,不能说6是倍数,3是因数;要说6是3的倍数,3是6的因数。
2.因数与倍数是建立在整除的基础上的,所以如4÷0.2=20,一般是不说4是0.2的倍数,0.2是4的因数。
2.因数与倍数的特点:一个整数的因数中最小的因数是1,最大的因数是它本身。
一个数的倍数中最小的倍数是这个数本身,没有最大的倍数。
因数的个数是有限的,都能一一列举出来,倍数的个数是无限的。
3.求一个数因数的方法:利用积与因数的关系一对一对找,找出哪两个数的乘积等于这个数,那么这两个数就是这个数的因数。
如16=1×16=2×8=4×4,那么16的因数就有1、2、4、8、16,计算时一定不要忘了1和这个数本身都是它的因数,注意按照一定的顺序以防遗漏。
数的整除知识点总结数的整除知识整理

数的整除知识点总结数的整除知识整理数的整除知识点总结如下:1. 除数和被除数:一个数被另一个数整除时,被除数称为整数,除数称为除数。
2. 整除关系:如果一个数a能被另一个数b整除,即a ÷ b = c,则称a能被b整除,或者说b能整除a,记作b|a。
3. 余数:当一个数a被另一个数b整除时,如果除完后还有剩余部分,即a ÷ b = c 余 r(0 ≤ r < |b|),则r称为数a除以b的余数。
4. 因数:对于一个数a,如果存在一个数b,使得b能整除a,即a = b × c,则称b 是a的因数,c是a的倍数。
a的因数包括1和a本身。
5.倍数:对于一个数a,如果存在一个数b,使得a能整除b,即b = a × c,则称b 是a的倍数,c是a的因数。
a的倍数包括0和任意正负整数。
6.公约数:对于两个数a和b,如果存在一个数c,既能整除a又能整除b,即c|a 且c|b,则称c是a和b的公约数。
7.最大公约数:对于两个数a和b的公约数中,最大的一个公约数称为a和b的最大公约数,记作gcd(a, b)。
8.最小公倍数:对于两个数a和b的公倍数中,最小的一个公倍数称为a和b的最小公倍数,记作lcm(a, b)。
9.质数:一个大于1的自然数,除了1和它本身外,无法被其他自然数整除的数称为质数。
质数只有两个因数,即1和该数本身。
10.合数:一个自然数,除了1和它本身外,还有其他因数的数称为合数。
合数有多个因数。
11.互质:两个数的最大公约数为1时,称这两个数互质。
12.互质数性质:互质数的乘积等于它们的最小公倍数。
13.素数分解:将一个合数分解成质数的乘积的过程,这个过程叫做素数分解。
这些是数的整除的基本知识点。
数的整除知识点

数的整除知识点数的整除问题,容丰富,思维技巧性强。
它是小学数学中的重要课题,也是小学数学竞赛命题的容之一。
数的整除1.整除——因数和倍数例如:15÷3=5,63÷7=9一般地,如a、b、c为整数,b≠0,且a÷b=c,即整数a除以整除b(b不等于0),除得的商c正好是整数而没有余数(或者说余数是0),我们就说,a能被b整除(或者说b能整除a)。
记作b|a.如果整数a能被整数b整除,a就叫做b的倍数,b就叫做a 的因数。
例如:在上面算式中,15是3的倍数,3是15的因数;63是7的倍数,7是63的因数。
2.数的整除性质性质1:如果a、b都能被c整除,那么它们的和与差也能被c 整除。
即:如果c|a,c|b,那么c|(a±b)。
例如:如果2|10,2|6,那么2|(10+6),并且2|(10—6)。
性质2:如果b与c的积能整除a,那么b与c都能整除a.即:如果bc|a,那么b|a,c|a。
性质3:如果b、c都能整除a,且b和c互质,那么b与c 的积能整除a。
即:如果b|a,c|a,且(b,c)=1,那么bc|a。
例如:如果2|28,7|28,且(2,7)=1,那么(2×7)|28。
性质4:如果c能整除b,b能整除a,那么c能整除a。
即:如果c|b,b|a,那么c|a。
例如:如果3|9,9|27,那么3|27。
3.数的整除特征①能被2整除的数的特征:个位数字是0、2、4、6、8的整数.“特征”包含两方面的意义:一方面,个位数字是偶数(包括0)的整数,必能被2整除;另一方面,能被2整除的数,其个位数字只能是偶数(包括0).下面“特征”含义相似。
②能被5整除的数的特征:个位是0或5。
③能被3(或9)整除的数的特征:各个数位数字之和能被3(或9)整除。
④能被4(或25)整除的数的特征:末两位数能被4(或25)整除。
例如:1864=1800+64,因为100是4与25的倍数,所以1800是4与25的倍数.又因为4|64,所以1864能被4整除.但因为2564,所以1864不能被25整除.⑤能被8(或125)整除的数的特征:末三位数能被8(或125)整除。
数的整除知识点整理

数的整除知识点整理
一、基本概念和符号:
1、整除:如果一个整数a,除以一个自然数b,得到一个整数商c,而且没有余数,那么叫做a能被b整除或b能整除a,记作b|a。
2、常用符号:整除符号“|”,不能整除符号“ ”;因为符号“∵”,所以的符号“∴”;
二、整除判断方法:
1.能被2、5整除:末位上的数字能被2、5整除。
2.能被4、25整除:末两位的数字所组成的数能被4、25整除。
3.能被8、125整除:末三位的数字所组成的数能被8、125整除。
4.能被3、9整除:各个数位上数字的和能被3、9整除。
5.能被7整除:
①末三位上数字所组成的数与末三位以前的数字所组成数之差能被7整除。
②逐次去掉最后一位数字并减去末位数字的2倍后能被7整除。
6.能被11整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被11整除。
②奇数位上的数字和与偶数位数的数字和的差能被11整除。
③逐次去掉最后一位数字并减去末位数字后能被11整除。
7.能被13整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之差能被13整除。
②逐次去掉最后一位数字并减去末位数字的9倍后能被13整除。
三、整除的性质:
1.如果a、b能被c整除,那么(a+b)与(a-b)也能被c整除。
2.如果a能被b整除,c是整数,那么a乘以c也能被b整除。
3.如果a能被b整除,b又能被c整除,那么a也能被c整除。
4.如果a能被b、c整除,那么a也能被b和c的最小公倍数整除。
整除重点知识点总结

整除重点知识点总结一、整除的概念1. 整除的定义:如果一个整数a除另一个整数b(且b≠0)的商仍为整数,那么我们说a 能被b整除,记作b|a。
即$a\%b=0$2. 被除数、除数、商、余数:(1)被除数:被除数是指被除数的整数(2)除数:除数是指除数的整数(3)商:商是指商的整数(4)余数:当被除数能被除数整除时,商为整数,余数为零当被除数不能被除数整除时,商不为整数,余数不为零二、整除的性质1. 0的整除性:0是任何整数的倍数。
2. 正整数的整除性:(1)整数c能被整数a、b整数:若c既能被a整数,又能被b整数,则c能被a,b的最小交集整数整除。
(2)整除的传递性:若a能被b整数,b能被c整数,则a能被c整数。
3. 负整数的整除性:(1)整数c能被整数a整数:若c能被a整数,c能被-a、-b整数。
(2)整除的传递性:若a能被b整数,b能被c整数,则a能被c整数。
三、整除的判断方法1. 用倍数表示:若整数a能被整数b整数,则整数a是整数b的倍数(倍数是指数字b 的n倍,n是整数)。
2. 用因数表示:若整数a能被整数b整数,则整数a是整数b的因数(因数是指a能被整数b整数)。
3. 用除法表示:若整数a能被整数b整数,则整数a÷整数b=商。
若商是整数,则整数a 能被整数b整数。
四、整除的应用1. 整数的奇偶性判断:一个数能够被2整数,称为偶数;一个数不能被2整数,称为奇数。
2. 整数的哪些整除:(1)整数判断:整数5能被整数2整数,因为5÷2=2余1;整数3不能被整数2整数,因为3÷2=1余1。
(2)一元一次方程:整数代表数的值,整除代表数的比值。
五、整除的解题方法1. 整除的运算规则:整除的加减乘除法规则。
2. 整数的乘法和除法:整数的乘法、整数的除法。
3. 整数的乘法和除法法则:整数的乘法、整数的除法法则。
4. 整数的乘法和除法法则:整数的乘法、整数的除法法则。
解整分是整数中的一个重要知识点,通过综合上述知识点的学习,我们可以更好地应用整除知识解决实际问题,提高数学解题的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数的整除知识点总结
导读:数的整除知识点总结1
数的整除知识点总结2
一、基本概念和符号:
1、整除:如果一个整数a,除以一个自然数b,得到一个整数商c,而且没有余数,那么叫做a能被b整除或b能整除a,记作b|a。
2、常用符号:整除符号“|”,不能整除符号“”;因为符号“∵”,所以的符号“∴”;
二、整除判断方法:
1. 能被2、5整除:末位上的数字能被2、5整除。
2. 能被4、25整除:末两位的数字所组成的数能被4、25整除。
3. 能被8、125整除:末三位的数字所组成的数能被8、125整除。
4. 能被3、9整除:各个数位上数字的和能被3、9整除。
5. 能被7整除:
①末三位上数字所组成的数与末三位以前的数字所组成数之差
能被7整除。
②逐次去掉最后一位数字并减去末位数字的2倍后能被7整除。
6. 能被11整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之
差能被11整除。
②奇数位上的数字和与偶数位数的数字和的差能被11整除。
③逐次去掉最后一位数字并减去末位数字后能被11整除。
7. 能被13整除:
①末三位上数字所组成的数与末三位以前的数字所组成的数之
差能被13整除。
②逐次去掉最后一位数字并减去末位数字的9倍后能被13整除。
三、整除的性质:
1. 如果a、b能被c整除,那么(a+b)与(a-b)也能被c整除。
2. 如果a能被b整除,c是整数,那么a乘以c也能被b整除。
3. 如果a能被b整除,b又能被c整除,那么a也能被c整除。
4. 如果a能被b、c整除,那么a也能被b和c的最小公倍数整除。
【数的整除知识点总结】
1.数的整除教学总结反思
2.数的整除教案
3.数的整除教学反思
4.数的整除参考教案
5.数的整除的教学反思
6.数学数的整除复习题
7.能被3整除的数的教学与反思
8.数的整除复习优秀教案
上文是关于数的整除知识点总结,感谢您的阅读,希望对您有帮助,谢谢。
