2020年高考数学(理科)模拟试卷一附答案解析
2020年河北省石家庄市高考数学一模试卷(理科)
2020年河北省石家庄市高考数学一模试卷（理科）一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知复数3213iz i-+=++，则复数z 在复平面内对应的点在( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．（5分）设集合{|||3}P x x =>，2{|4}Q x x =>，则下列结论正确的是( ) A ．QP B ．P Q C ．P Q = D ．P Q R =3．（5分）若2242(),log 3,log 63a b c ===，则a ，b ，c 的大小关系是( )A ．a b c <<B ．a c b <<C ．c b a <<D ．b c a <<4．（5分）若x ，y 满足约束条件02636,x y x y +⎧⎨-⎩则2z x y =+的最大值为( )A ．10B ．8C ．5D ．35．（5分）“斗拱”是中国古代建筑中特有的构件，从最初的承重作用，到明清时期集承重与装饰作用于一体．在立柱顶、额枋和檐檩间或构架间，从枋上加的一层层探出成弓形的承重结构叫拱拱与拱之间垫的方形木块叫斗．如图所示，是“散斗”（又名“三才升” )的三视图（三视图中的单位：分米），现计划用一块长方体的海南黄花梨木料加工成该散斗，则长方体木料的最小体积为( )立方分米．A ．40B ．853C ．30D ．7336．（5分）不透明的袋中装有8个大小质地相同的小球，其中红色的小球6个，白色的小球2个，从袋中任取2个小球，则取出的2个小球中有1个是白色小球另1个是红色小球的概率为( )A ．314B ．37C ．67D ．13287．（5分）已知F 是抛物线2:8C y x =的焦点，M 是C 上一点，MF 的延长线交y 轴于点N ．若2MF FN =，则||MF 的值为( )A ．8B ．6C ．4D ．28．（5分）某函数的部分图象如图，则下列函数中可以作为该函数的解析式的是( )A ．sin 2sin 2x xy e = B ．cos2cos2x xy e = C ．cos2|cos2|xx y e =D ．cos |cos |xx y e =9．（5分）如图，某中学数学兴趣小组要测量底部不能到达的某铁塔AB 的高度（如图），铁塔AB 垂直于水平面，在塔的同一侧且与塔底部B 在同一水平面上选择C ，D 两观测点，且在C ，D 两点测得塔顶的仰角分别为45︒，30︒并测得120BCD ∠=︒，C ，D 两地相距600m ，则铁塔AB 的高度是( )A ．300 mB ．600 mC ．3003mD ．6003m10．（5分）已知函数()2|cos |sin sin 2f x x x x =+，给出下列三个命题： ①函数()f x 的图象关于直线4x π=对称；②函数()f x 在区间[,]44ππ-上单调递增；③函数()f x 的最小正周期为π． 其中真命题的个数是( ) A ．0B ．1C ．2D ．311．（5分）已知ABC ∆是由具有公共直角边的两块直角三角板(Rt ACD ∆与Rt BCD)∆组成的三角形，如左图所示．其中，45CAD ∠=︒，60BCD ∠=︒现将Rt ACD ∆绕斜边AC 旋转至△1D AC 处1(D 不在平面ABC 上）．若M 为BC 的中点，则在ACD ∆旋转过程中，直线1AD 与DM 所成角(θ )A ．(0,45)θ∈︒︒B ．(0θ∈︒，45]︒C ．(0θ∈︒，60]︒D ．(0,60)θ∈︒︒12．（5分）设符号{min x ，y ，}z 表示x ，y ，z 中的最小者，已知函数(){|2|f x min x =-，2x ，|2|}x +则下列结论正确的是( )A ．[0x ∀∈，)+∞，(2)()f x f x ->B ．[1x ∀∈，)+∞，(2)()f x f x ->C ．x R ∀∈，(())()f f x f xD ．x R ∀∈，(())()f f x f x >二、填空题：本大题共4小题，每小题5分，把答案填在答题卡中对应题号后的横线上. 13．（5分）函数y x lnx =+在点(1,1)处的切线方程为 ．14．（5分）已知向量a ，b 满足||2a =，||1b =，若()()a a b b a b ++-的最大值为1，则向量a ，b 的夹角θ的最小值为 ，|2|a b +的取值范围为 ．15．（5分）飞镖锦标赛的赛制为投掷飞镖3次为一轮，一轮中投掷3次飞镖至少两次投中9环以上，则评定该轮投掷飞镖的成绩为优秀．某选手投掷飞镖每轮成绩为优秀的概率为45，则该选手投掷飞镖共三轮，至少有一轮可以拿到优秀成绩的概率是16．（5分）已知双曲线C 的方程为2218y x -=，右焦点为F ，若点(0,6)N ，M 是双曲线C的左支上一点，则FMN ∆周长的最小值为三、解答题：解答应写出文字说明、证明过程或演算步骤.（一）必考题：共60分. 17．（12分）已知数列{}n a 为等差数列，n S 是数列{}n a 的前n 项和，且22a =，36S a =，数列{}n b 满足：2124b b ==，当3n ，*n N ∈时，1122(22)2n n n a b a b a b n b ++⋯+=-+． （1）求数列{}n a ，{}n b 的通项公式； （2）令*,nn na c n Nb =∈，证明：122n c c c ++⋯+<． 18．（12分）如图，在四棱锥P ABCD -中，已知PA ⊥平面ABCD ，且四边形ABCD 为直角梯形，2ABC BAD π∠=∠=，2PA AD ==，1AB BC ==，点M ，E 分别是PA ，PD 的中点．（1）求证：//CE 平面BMD ；（2）点Q 为线段BP 中点，求直线PA 与平面CEQ 所成角的余弦值．19．（12分）已知椭圆2222:1(0))x y C a b a b +=>>的左、右顶点分别为A 、B ，且||4AB =，椭圆C 3．（1）求椭圆C 的标准方程；（2）已知点(1M ，)(0)m m ≠在椭圆C 内，直线AM 与BM 分别与椭圆C 交于E 、F 两点，若AM F ∆面积是BM E ∆面积的5倍，求m 的值．20．（12分）BMI 指数是用体重公斤数除以身高米数的平方得出的数值，是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准．对于高中男体育特长生而言，当BMI 数值大于或等于20.5时，我们说体重较重，当BMI 数值小于20.5时，我们说体重较轻，身高大于或等于170cm 时，我们说身高较高，身高小于170cm 时，我们说身高较矮．某中小学生成长与发展机构从某市的320名高中男体育特长生中随机选取8名，其身高和体重的数据如表所示： 编号 1 2 3 4 5 6 7 8 身高()i cm x166167160173178169158173体重()i kg y57 58 53 61 66 57 50 66（1）根据最小二乘法的思想与公式求得线性回归方程ˆ0.875.9yx =-．利用已经求得的线性回归方程，请完善下列残差表，并求解释变量（身高）对于预报变量（体重）变化的贡献值2R （保留两位有效数字）；（2）通过残差分析，对于残差的最大（绝对值）的那组数据，需要确认在样本点的采集中是否有人为的错误．已知通过重新采集发现，该组数据的体重应该为58()kg ．请重新根据最小二乘法的思想与公式，求出男体育特长生的身高与体重的线性回归方程．参考公式：2211()1(nii i n ii yy R y==-=-∑∑．1122211()()ˆ()nnix i yi ix yi i nnixixi i xy x yn bxxn----==--==---==--∑∑∑∑，ˆˆa y bx =-．ˆˆˆi i ie y bx a =--． 参考数据：8178880i i i x y ==∑，281226112i i x ==∑，168x =，58.5y =，821()226i i y y =-=∑．21．（12分）已知函数()2()f x ln ax b =+，其中a ，b R ∈．（1）当0a >时，若直线y x =是曲线()y f x =的切线，求ab 的最大值；（2）设1b =，函数2()(1)(1)()(g x ax a ax f x a R =+++-∈，0)a ≠有两个不同的零点，求a 的最大整数值．（参考数据5:0.223)4ln ≈请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.[选修4--4：坐标系与参数方程]22．（10分）极坐标系于直角坐标系xOy 有相同的长度单位，以原点O 为极点，以x 正半轴为极轴．已知曲线1C 的极坐标方程为4cos()3πρθ=-，曲线2C 的极坐标方程为cos()3a πρθ-=，射线6πθα=-，θα=，3πθα=+，2πθα=+与曲线1C 分别交异于极点O 的四点A ，B ，C ，D ．（1）若曲线1C 关于曲线2C 对称，求a 的值，并把曲线1C 和2C 化成直角坐标方程； （2）设()||||||||f OA OB OC OD α=+，当63ππα时，求()f α的值域．[选修4-5：不等式选讲]23．已知函数()|21||1|f x x x =-+-． （Ⅰ）求不等式()4f x 的解集；（Ⅱ）设函数()f x 的最小值为m ，当a ，b ，c R +∈，且a b c m ++=时，求2020年河北省石家庄市高考数学一模试卷（理科）参考答案与试题解析一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知复数3213iz i-+=++，则复数z 在复平面内对应的点在( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限【解答】解：复数3(13)2221313i i i z i i i-++=+=+=+++，则复数z 在复平面内对应的点(2,1)在第一象限． 故选：A ．2．（5分）设集合{|||3}P x x =>，2{|4}Q x x =>，则下列结论正确的是( ) A ．QP B ．P Q C ．P Q = D ．P Q R =【解答】解：集合{|||3}{|3P x x x x =>=<-或3}x >，2{|4}{|2Q x x x x =>=<-或2}x >，P Q ∴，故选：B ．3．（5分）若2242(),log 3,log 63a b c ===，则a ，b ，c 的大小关系是( )A ．a b c <<B ．a c b <<C ．c b a <<D ．b c a <<【解答】解：由 可得49a =，42log 6log c == 则 可知，1bc a >>>， 故选：B ．4．（5分）若x ，y 满足约束条件02636,x y x y +⎧⎨-⎩则2z x y =+的最大值为( )A ．10B ．8C ．5D ．3【解答】解：由约束条件02636,x y x y +⎧⎨-⎩作出可行域如图，化目标函数2z x y=+为直线方程的斜截式，122zy x=-+，由图可知，当直线122zy x=-+过(3,0)A时，直线在y轴上的截距最大，z有最大值为3．故选：D．5．（5分）“斗拱”是中国古代建筑中特有的构件，从最初的承重作用，到明清时期集承重与装饰作用于一体．在立柱顶、额枋和檐檩间或构架间，从枋上加的一层层探出成弓形的承重结构叫拱拱与拱之间垫的方形木块叫斗．如图所示，是“散斗”（又名“三才升”)的三视图（三视图中的单位：分米），现计划用一块长方体的海南黄花梨木料加工成该散斗，则长方体木料的最小体积为()立方分米．A．40B．853C．30D．733【解答】解：由三视图还原原几何体如图，要加工成如图所示散斗，则长方体木料长的最小值为4，宽的最小值为4，高的最小值为52， 则则长方体木料的最小体积为544402⨯⨯=立方分米． 故选：A ．6．（5分）不透明的袋中装有8个大小质地相同的小球，其中红色的小球6个，白色的小球2个，从袋中任取2个小球，则取出的2个小球中有1个是白色小球另1个是红色小球的概率为( ) A ．314B ．37C ．67D ．1328【解答】解：不透明的袋中装有8个大小质地相同的小球，其中红色的小球6个，白色的小球2个，从袋中任取2个小球，基本事件总数2828n C ==，取出的2个小球中有1个是白色小球另1个是红色小球包含的基本事件个数：116212m C C ==，则取出的2个小球中有1个是白色小球另1个是红色小球的概率为123287m p n ===． 故选：B ．7．（5分）已知F 是抛物线2:8C y x =的焦点，M 是C 上一点，MF 的延长线交y 轴于点N ．若2MF FN =，则||MF 的值为( )A ．8B ．6C ．4D ．2【解答】解：由抛物线的方程可得焦点(2,0)F ，准线方程为：2x =-，作MA 垂直于y 轴交于A ，因为2MF FN =，所以可得F 为线段MN 的三等分点，即13NF MN =，由NFO NMA ∆∆∽，所以13OF MA =，即3326MA OF ==⨯=，所以||628MF =+=， 故选：A ．8．（5分）某函数的部分图象如图，则下列函数中可以作为该函数的解析式的是( )A ．sin 2sin 2x xy e = B ．cos2cos2x xy e = C ．cos2|cos2|xx y e =D ．cos |cos |xx y e =【解答】解：由图象可知，当0x =时，0y ≠，故排除选项A ； 又对任意的x ，函数值0y ，故排除选项B ； 对选项D ，当12x π=>时，0y =，这与图象矛盾，综上，选项C 满足题意． 故选：C ．9．（5分）如图，某中学数学兴趣小组要测量底部不能到达的某铁塔AB 的高度（如图），铁塔AB 垂直于水平面，在塔的同一侧且与塔底部B 在同一水平面上选择C ，D 两观测点，且在C ，D 两点测得塔顶的仰角分别为45︒，30︒并测得120BCD ∠=︒，C ，D 两地相距600m ，则铁塔AB 的高度是( )A ．300 mB ．600 mC ．3003mD ．6003m【解答】解：设AB x =，由图利用直角三角形的性质可得：BC AB x ==，3BD x =， 在BCD ∆中，由余弦定理可得：22236002600cos120x x x =+-⨯︒，化为：23001800000x x --=，解得600x =． 故选：B ．10．（5分）已知函数()2|cos |sin sin 2f x x x x =+，给出下列三个命题： ①函数()f x 的图象关于直线4x π=对称；②函数()f x 在区间[,]44ππ-上单调递增；③函数()f x 的最小正周期为π． 其中真命题的个数是( ) A ．0 B ．1C ．2D ．3 【解答】解：332cos sin sin 2,[2,2]0,[2,2]2222()2|cos |sin sin 2,2cos sin sin 2,[2,2)2sin 2,[2,2)2222x x x x k k x k k f x x x x k Zx x x x k k x x k k ππππππππππππππππ⎧⎧-+∈++∈++⎪⎪⎪⎪=+==∈⎨⎨⎪⎪+∈-++∈-++⎪⎪⎩⎩，其大致图象如图所示，①()f x 的图象不关于直线4x π=对称，即①错误；②()f x 在区间[,]44ππ-上单调递增，即②正确； ③()f x 的最小正周期为2π，即③错误． 所以真命题只有②， 故选：B ．11．（5分）已知ABC ∆是由具有公共直角边的两块直角三角板(Rt ACD ∆与Rt BCD)∆组成的三角形，如左图所示．其中，45CAD ∠=︒，60BCD ∠=︒现将Rt ACD ∆绕斜边AC 旋转至△1D AC 处1(D 不在平面ABC 上）．若M 为BC 的中点，则在ACD ∆旋转过程中，直线1AD 与DM 所成角(θ )A ．(0,45)θ∈︒︒B ．(0θ∈︒，45]︒C ．(0θ∈︒，60]︒D ．(0,60)θ∈︒︒【解答】解：作//AP DM ，1AD 可以看成以AC 为轴线，以45︒为平面角的圆锥的母线， 由题意知1AD 与AP 落在同一个轴截面上时， 1PAD ∠取得最大值，则1PAD ∠的最大值为60︒，此时，1D ∈平面ABC ，1D 不在平面ABC 上，1(0,60)PAD ∴∠∈︒︒，∴在ACD ∆旋转过程中，直线1AD 与DM 所成角(0,60)θ∈︒︒．故选：D ．12．（5分）设符号{min x ，y ，}z 表示x ，y ，z 中的最小者，已知函数(){|2|f x min x =-，2x ，|2|}x +则下列结论正确的是( )A ．[0x ∀∈，)+∞，(2)()f x f x ->B ．[1x ∀∈，)+∞，(2)()f x f x ->C ．x R ∀∈，(())()f f x f xD ．x R ∀∈，(())()f f x f x >【解答】解：如图所示：由题意可得A 中，2,[0,1]()|2|,(1,)x x f x x x ⎧∈=⎨-∈+∞⎩B 中，当12x 时，120x --，(2)(2)2()f x f x x f x -=--=，当23x <时，021x <-，(2)2()f x x f x --=，当34x <时，122x <-，(2)2(2)42()f x x x x f x -=--=--=，当4x ，22x -，恒有(2)()f x f x -<，所以B 不正确，A 也不正确；C 中，从图象上看，[0x ∈，)+∞，()f x x ，令()t f x =，则0t ，所以()f t t ，即(())()f f x f x ，故C 正确，D 不正确． 故选：C ．二、填空题：本大题共4小题，每小题5分，把答案填在答题卡中对应题号后的横线上. 13．（5分）函数y x lnx =+在点(1,1)处的切线方程为 210x y --= ． 【解答】解：1y x nx =+，∴11y x'=+， 1|112x k y =∴='=+=，∴函数1y x nx =+在点(1,1)处的切线方程为12(1)y x -=-，整理，得210x y --=． 故答案为：210x y --=．14．（5分）已知向量a ，b 满足||2a =，||1b =，若()()a a b b a b ++-的最大值为1，则向量a ，b 的夹角θ的最小值为23π，|2|a b +的取值范围为 ． 【解答】解：设向量a ，b 的夹角为θ，则[0θ∈，]π； 又||2a =，||1b =，所以22()()421cos 12cos 134cos a a b b a b a a b b a b θθθ++-=++-=+⨯⨯+⨯⨯-=+， 即34cos 1θ+， 解得1cos 2θ-； 则向量a ，b 的夹角θ的最小值为23π； 即2[3πθ∈，]π； 所以222(2)444421cos 488cos a b a a b b θθ+=++=+⨯⨯⨯+=+， 又cos [1θ∈-，1]2-，所以88cos [0θ+∈，4]，所以|2|a b +的取值范围是[0，2]． 故答案为：23π，[0，2]． 15．（5分）飞镖锦标赛的赛制为投掷飞镖3次为一轮，一轮中投掷3次飞镖至少两次投中9环以上，则评定该轮投掷飞镖的成绩为优秀．某选手投掷飞镖每轮成绩为优秀的概率为45，则该选手投掷飞镖共三轮，至少有一轮可以拿到优秀成绩的概率是 124125【解答】解：飞镖锦标赛的赛制为投掷飞镖3次为一轮，一轮中投掷3次飞镖至少两次投中9环以上，则评定该轮投掷飞镖的成绩为优秀． 某选手投掷飞镖每轮成绩为优秀的概率为45， 则该选手投掷飞镖共三轮，至少有一轮可以拿到优秀成绩的概率是： 0033411241()()55125P C =-=． 故答案为：124125．16．（5分）已知双曲线C 的方程为21x =，右焦点为F ，若点(0,6)N ，M 是双曲线C的左支上一点，则FMN ∆周长的最小值为 2【解答】解：双曲线的标准方程为2218y x -=，设双曲线的左焦点为F '，由双曲线C 可得(3,0)F ，(3,0)F '-，||NF =MNF ∆周长为||||||||||MN MF NF MN MF ++=++，由双曲线的定义可得||||22MF MF a '-==， 即有||||||||2MN MF MN MF '+=++， 当P 在左支上运动到M ，N ，F '共线时，||||MN MF '+取得最小值||NF '=则有MNF ∆周长的最小值为22=．故答案为：2．三、解答题：解答应写出文字说明、证明过程或演算步骤.（一）必考题：共60分. 17．（12分）已知数列{}n a 为等差数列，n S 是数列{}n a 的前n 项和，且22a =，36S a =，数列{}n b 满足：2124b b ==，当3n ，*n N ∈时，1122(22)2n n n a b a b a b n b ++⋯+=-+． （1）求数列{}n a ，{}n b 的通项公式； （2）令*,nn na c n Nb =∈，证明：122n c c c ++⋯+<． 【解答】解：（1）数列{}n a 为等差数列，n S 是数列{}n a 的前n 项和，且22a =，36S a =， 设数列的首项为1a ，公差为d ， 则：1112335a d a d a d+=⎧⎨+=+⎩，解得：111a d =⎧⎨=⎩，所以1(1)n a n n =+-=．数列{}n b 满足：2124b b ==，1122(22)2n n n a b a b a b n b ++⋯+=-+．① 所以1122111(24)2n n n a b a b a b n b ---++⋯+=-+．② ①-②得：1(22)(24)n n n n a b n b n b -=---， 由于n a n =， 整理得12nn b b -=（常数）， 所以数列{}n b 是以12b =为首项，2为公比的等比数列． 所以1222n n n b -=⨯=． 由于首项符合通项公式， 所以2n n b =．证明：（2）由（1）得2n n n n a nc b ==， 所以212222n n nT =++⋯+①， 故2311122222n n nT +=++⋯+② ①-②得：211111(1)1111122()112222222212n n n n n n n n n n T +++-=++⋯+-=-=---， 所以112222n n n nT -=--<． 即122n c c c ++⋯+<．18．（12分）如图，在四棱锥P ABCD -中，已知PA ⊥平面ABCD ，且四边形ABCD 为直角梯形，2ABC BAD π∠=∠=，2PA AD ==，1AB BC ==，点M ，E 分别是PA ，PD 的中点．（1）求证：//CE 平面BMD ；（2）点Q 为线段BP 中点，求直线PA 与平面CEQ 所成角的余弦值．【解答】（1）证明：连接ME ，因为点M ，E 分别是PA ，PD 的中点，所以12ME AD =，//ME AD ，所以//BC ME ，BC ME =，所以四边形BCEM 为平行四边形， 所以//CE BM ．又因为BM ⊂平面BMD ，CE ⊂/平面BMD ， 所以//CE 平面BMD ．⋯⋯⋯⋯⋯⋯⋯⋯（6分）（2）如图，以A 为坐标原点建立空间坐标系O xyz -，则又1(2CQ =-，1-，1)，(1CE =-，0，1)，设平面CEQ 的法向量为(n x =，y ，)z ，列方程组00n CQ n CE ⎧=⎪⎨=⎪⎩，可得：120x y z x z ⎧--+=⎪⎨⎪-+=⎩其中一个法向量为(2n =，1，2)，设直线PA 与平面CEQ 所成角大小为θ，于是22sin 3414001θ==++++， 进而求得5cos θ=（15分） 19．（12分）已知椭圆2222:1(0))x y C a b a b +=>>的左、右顶点分别为A 、B ，且||4AB =，椭圆C 3．（1）求椭圆C 的标准方程；（2）已知点(1M ，)(0)m m ≠在椭圆C 内，直线AM 与BM 分别与椭圆C 交于E 、F 两点，若AM F ∆面积是BM E ∆面积的5倍，求m 的值．【解答】解：（1）由题意可得：222243a ca ab c=⎧⎪⎪=⎨⎪=+⎪⎩，解得213a b c ⎧=⎪=⎨⎪=⎩，∴椭圆C 的标准方程为：2214x y +=；（2）(1,)M m ，(2,0)A -，(2,0)B ，∴直线AM 的斜率3AM m k =， ∴直线AM 的方程为：(2)3my x =+， 联立方程22(2)314m y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩，解得21294E m y m =+， 同理可得2414F my m =+，5AMF BME S S ∆∆=，即()5()ABF ABM ABE ABM S S S S ∆∆∆∆-=-， 54ABF ABE ABM S S S ∆∆∆∴=-，∴22412||5||4||1494m mm m m=-++，又0m ≠， 42161630m m ∴-+=，解得214m =或34， 点M 在椭圆内，∴234m <， ∴214m =， 12m ∴=±．20．（12分）BMI 指数是用体重公斤数除以身高米数的平方得出的数值，是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准．对于高中男体育特长生而言，当BMI 数值大于或等于20.5时，我们说体重较重，当BMI 数值小于20.5时，我们说体重较轻，身高大于或等于170cm 时，我们说身高较高，身高小于170cm 时，我们说身高较矮．某中小学生成长与发展机构从某市的320名高中男体育特长生中随机选取8名，其身高和体重的数据如表所示：（1）根据最小二乘法的思想与公式求得线性回归方程ˆ0.875.9yx =-．利用已经求得的线性回归方程，请完善下列残差表，并求解释变量（身高）对于预报变量（体重）变化的贡献值2R （保留两位有效数字）；（2）通过残差分析，对于残差的最大（绝对值）的那组数据，需要确认在样本点的采集中是否有人为的错误．已知通过重新采集发现，该组数据的体重应该为58()kg ．请重新根据最小二乘法的思想与公式，求出男体育特长生的身高与体重的线性回归方程．参考公式：22121()1()nii i n ii yy R yy ==-=--∑∑．1122211()()ˆ()nnix i yi ix yi i nnixixi i xy x yn bxxn----==--==---==--∑∑∑∑，ˆˆa y bx =-．ˆˆˆi i ie y bx a =--． 参考数据：8178880i i i x y ==∑，281226112i i x ==∑，168x =，58.5y =，821()226i i y y =-=∑．【解答】解：（1）由题意知线性回归方程为ˆ0.875.9y x =-， 计算6ˆ570.816975.9 2.3e=-⨯+=-， 7ˆ500.815875.90.5e=-⨯+=-， 8ˆ660.817375.9 3.5e=-⨯+=； 完善下列残差表如下，计算22121()111(0.010.090.81 2.250.25 5.290.2512.25)10.090.90226()nii i n ii yy R yy ==-=-=-⨯+++++++≈-=-∑∑；所以解释变量（身高）对于预报变量（体重）变化的贡献值20.90R ≈． （2）通过残差分析知，残差的最大（绝对值）的那组数据为第8组，且858y =，由8178880i i i x y ==∑，计算修订后8178880173661735877496i i i x y ='=-⨯+⨯=∑，又281226112i ix ==∑，168x =，修订后1(858.56658)57.58y '=⨯⨯-+=，所以1222177496816857.5ˆ0.6752261128168ni ix yi nixi x yn bxn --=-=--⨯⨯===-⨯-∑∑，ˆˆ57.50.67516855.9ay bx ='-=-⨯=-； 所以x 关于y 的线性回归方程是ˆ0.67555.9yx =-． 21．（12分）已知函数()2()f x ln ax b =+，其中a ，b R ∈．（1）当0a >时，若直线y x =是曲线()y f x =的切线，求ab 的最大值；（2）设1b =，函数2()(1)(1)()(g x ax a ax f x a R =+++-∈，0)a ≠有两个不同的零点，求a 的最大整数值．（参考数据5:0.223)4ln ≈【解答】解：（1）设直线y x =与()y f x =相切于点0(P x ，02())ln ax b +， 2()af x ax b '=+， 002()1af x ax b '∴==+，02ax b a ∴+= (0)a >，又点P 在切线y x =上，002()ln ax b x ∴+=， 022ln a x ∴=，02222b a ax a aln a ∴=-=-，因此22222ab a a ln a =-(0)a >，设g （a ）22222a a ln a =-，0a >，g '∴（a ）2422(122)a aln a a ln a =-=-，令g '（a ）0>得，0a <<g '（a ）o <得，a > g ∴（a）在上单调递增，在，)+∞上单调递减， g ∴（a）的最大值为4e g =， ab ∴的最大值为4e ； （2）函数2()(1)(1)()(g x ax a axf x a R =+++-∈，0)a ≠有两个不同的零点，等价于方程22(1)(1)(1)ln ax ax a ax +=+++有两个不相等的实根，设1t ax =+，则等价于方程220lnt t at --= (0)t >有两个不同的解，即关于t 的方程22lnt t a t-= (0)t >有两个不同的解， 设22()lnt t h t t -=，则2222()t lnt h t t --'=， 设2()22m t t lnt =--，由0t >可知()m t '=-， ()m t ∴在(0,)+∞上单调递减，又m （1）10=>，575()204164m ln =-<， ∴存在05(1,)4t ∈使得0()0m t =，即200220t lnt --=，∴20022lnt t +=， ∴当0(0,)t t ∈时，()0m t >，()0h t '>，函数()h t 单调递增；当0(t t ∈，)+∞时，()0m t <，()0h t '<，函数()h t 单调递减，∴函数()h t 的极大值为220000000022229()2(,0)10lnt t t h t t t t t --===-∈-， 要使得关于t 的方程22lnt t a t-= (0)t >有两个不同的解，则0()a h t <， 当1a =-时，设2()2p t lnt t t =-+， 则2()21p t t t'=-+，可知()p t在上单调递增，在，)+∞上单调递减， 又p （1）0=，0p >，p （e ）220e e =-+<， ()p t ∴有两个不同的零点，符合题意，a ∴的最大整数值为1-．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.[选修4--4：坐标系与参数方程]22．（10分）极坐标系于直角坐标系xOy 有相同的长度单位，以原点O 为极点，以x 正半轴为极轴．已知曲线1C 的极坐标方程为4cos()3πρθ=-，曲线2C 的极坐标方程为cos()3a πρθ-=，射线6πθα=-，θα=，3πθα=+，2πθα=+与曲线1C 分别交异于极点O 的四点A ，B ，C ，D ．（1）若曲线1C 关于曲线2C 对称，求a 的值，并把曲线1C 和2C 化成直角坐标方程；（2）设()||||||||f OA OB OC OD α=+，当63ππα时，求()f α的值域．【解答】解：（1）1:4cos()3C πρθ=-，即22cos sin ρρθθ=+，化为直角坐标方程为22(1)(4x y -+=把2C 的方程化为直角坐标方程为20x a -=，因为曲线1C 关于曲线2C 对称，故直线20a =经过圆心(1，解得2a =，故2C 的直角坐标方程为0x =．（2）由题意可得，当63ππα时，||4sin OA α=；||4cos()3OB πα=-；||4cos OC α=；||4sin()3OD πα=-， ∴设2()||||||||16sin cos 16cos()sin()8sin 28sin(2)12sin 2)3336f OA OB OC OD ππππαααααααααα=+=+--=--=+=+，当63ππα时，52266πππα+， 383sin(2)836πα+，故()f α的值域为[选修4-5：不等式选讲]23．已知函数()|21||1|f x x x =-+-．（Ⅰ）求不等式()4f x 的解集；（Ⅱ）设函数()f x 的最小值为m ，当a ，b ，c R +∈，且a b c m ++=时，求【解答】解：（Ⅰ）1()42324x f x x ⎧<⎪⇔⎨⎪-+⎩或1124x x ⎧<⎪⎨⎪⎩或1324x x ⎧⎨-⎩， 解得223x -， 故不等式()4f x 的解集为2{|2}3x x -（Ⅱ）132,21(),1232,1x x f x x x x x ⎧-+<⎪⎪⎪=<⎨⎪-⎪⎪⎩，1()2min f x ∴=，即12m =， 又a ，b ，c R +∈且12a b c ++=，z 则2221a b c ++=，设x =yz =， 222x y xy +，2222121222xy x y a b a b +=+++=++，同理：2222yz a c ++，2222xz c a ++，2222222222228xy yz xz a b b c c a ∴++++++++++=，2222()222212121812x y z x y z xy yz xz a b c ∴++=+++++++++++=， 23x y z ∴++，即123，当且仅当16a b c ===时，取得最大值．。
2020年四川省宜宾市高考数学一诊试卷(理科)试题及答案(解析版)
∴ 时，g（x）取得最小值 ，
解 得，a≥4，显然a＜4和a＞4时，都不满足f（x）在（0，2）上是减函数，只有a＝4时满足f（x）在（0，2）上是减函数，
∴满足条件的a的集合是{4}．
故答案为：{4}．
三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17-21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分.
2020年四川省宜宾市高考数学一诊试卷（理科）
参考答案与试题解析
一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合要求的．
1．已知集合U＝{1，2，3，4，5，6}，A＝{1，3，4}，则∁UA＝（ ）
A．{5，6}B．{1，2，3，4}C．{2，5，6}D．{2，3，4，5，6}
（1）讨论f（x）在其定义域内的单调性；
（2）若a＝1，且f（x1）＝f（x2），其中0＜x1＜x2，求证：x1+x2+x1x2＞3．
（二）选考题：共10分.请考生在第22、23题中选一题作答．如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]
22．如图所示，“8”是在极坐标系Ox中分别以 和 为圆心，外切于点O的两个圆．过O作两条夹角为 的射线分别交⊙C1于O、A两点，交⊙C2于O、B两点．
∴cos∠AOB＝ ，即∠AOB＝60°．
（1）若λ＞0，μ＞0，
设 ＝2 ， ＝2 ，则 ＝ + ，
∵|λ|+|μ|＝λ+μ≤2，故当λ+μ＝2时，E，F，P三点共线，
故点P表示的区域为△OEF，
2023高考数学模拟卷(一)(含答案解析)
9.已知抛物线 的焦点为 ，准线为 ， 是 上一点，直线 与抛物线交于 两点，若 ，则
A B.8C.16D.
10.已知函数 的图象过点 ，且在 上单调，同时 的图象向左平移 个单位之后与原来的图象重合，当 ，且 时， ，则
A. B.-1C.1D.
11.下图是某四棱锥的三视图，网格纸上小正方形的边长为1，则该四棱锥的外接球的表面积为
20.已知椭圆 的一个焦点为 ，离心率为 .不过原点的直线 与椭圆 相交于 两点，设直线 ，直线 ，直线 的斜率分别为 ，且 成等比数列.
（1）求 的值；
（2）若点 在椭圆 上，满足 直线 是否存在？若存在，求出直线 的方程；若不存在，请说明理由.
21.已程 的两个实数根为 ，求证： ；
设M（x1，y1），N（x2，y2），M，N到准线的距离分别为dM，dN，
由抛物线的定义可知|MF|=dM=x1+1，|NF|=dN=x2+1，于是|MN|=|MF|+|NF|=x1+x2+2．
∵ ，
∴ ，即 ，∴ .
∴ ,∴直线AB的斜率为 ，
∵F（1，0），∴直线PF的方程为y= （x﹣1），
将y= （x﹣1），代入方程y2=4x，得3（x﹣1）2=4x，化简得3x2﹣10x+3=0，
A. B. C. D.
6.已知 展开式中 的系数为0，则正实数
A.1B. C. D.2
7.已知数列 的前 项和 ，若 ，则
A. B.
C. D.
8.如图是正四面体的平面展开图， 分别是 的中点，在这个正四面体中：① 与 平行；② 与 为异面直线；③ 与 成60°角；④ 与 垂直.以上四个命题中，正确命题的个数是（）
高考数学(理科)模拟试题含答案(一)精编版
高考数学(理科)模拟试题含答案(一)精编版高考理科数学模拟试题精编(一)注意事项：1.作答选择题时，在答题卡上涂黑对应选项的答案信息点。
如需改动，先擦干净再涂其他答案。
不得在试卷上作答。
2.非选择题用黑色钢笔或签字笔作答，写在答题卡指定区域内。
如需改动，先划掉原答案再写新答案。
不得用铅笔或涂改液。
不按要求作答无效。
3.答题卡需整洁无误。
考试结束后，交回试卷和答题卡。
第Ⅰ卷一、选择题(本大题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项符合题目要求。
)1.设全集Q={x|2x²-5x≤0，x∈N}，且P⊆Q，则满足条件的集合P的个数是()A。
3B。
4C。
7D。
82.若复数z=m(m-1)+(m-1)i是纯虚数，其中m是实数，则z=()A。
iB。
-iC。
2iD。
-2i3.已知等差数列{an}的公差为5，前n项和为Sn，且a1，a2，a5成等比数列，则S6=()A。
80B。
85C。
90D。
954.XXX每天上学都需要经过一个有交通信号灯的十字路口。
已知十字路口的交通信号灯绿灯亮的时间为40秒，黄灯5秒，红灯45秒。
如果XXX每天到路口的时间是随机的，则XXX上学时到十字路口需要等待的时间不少于20秒的概率是()A。
4/5B。
3/4C。
2/3D。
3/56.已知p：a=±1，q：函数f(x)=ln(x+a²+x²)为奇函数，则p 是q成立的()A。
充分不必要条件B。
必要不充分条件C。
充分必要条件D。
既不充分也不必要条件7.(省略了一个选项) 327.(1+x²+4x)²的常数项为()A。
120B。
160C。
200D。
2408.我们可以用随机模拟的方法估计π的值，如图所示的程序框图表示其基本步骤(函数RAND是产生随机数的函数，它能随机产生(0,1)内的任何一个实数)，若输出的结果为521，则由此可估计π的近似值为()A。
3.119B。
全国卷Ⅰ新高考理科数学仿真模拟试卷含答案解析 (4)
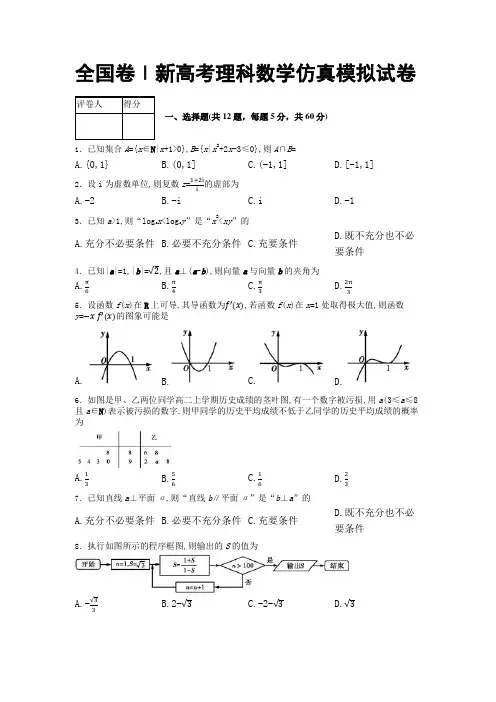
全国卷Ⅰ新高考理科数学仿真模拟试卷一、选择题(共12题，每题5分，共60分)1．已知集合A={x∈N|x+1>0},B={x|x2+2x-3≤0},则A∩B=A.{0,1}B.(0,1]C.(-1,1]D.[-1,1]2．设i为虚数单位,则复数z=1+2ii的虚部为A.-2B.-iC.iD.-13．已知a>1,则“log a x<log a y”是“x2<xy”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4．已知|a|=1,|b|=√2,且a⊥(a-b),则向量a与向量b的夹角为A.π6B.π4C.π3D.2π35．设函数f(x)在R上可导,其导函数为f′(x),若函数f(x)在x=1处取得极大值,则函数y=−x f′(x)的图象可能是A. B. C. D.6．如图是甲、乙两位同学高二上学期历史成绩的茎叶图,有一个数字被污损,用a(3≤a≤8且a∈N)表示被污损的数字.则甲同学的历史平均成绩不低于乙同学的历史平均成绩的概率为A.13B.56C.16D.237．已知直线a⊥平面α,则“直线b∥平面α”是“b⊥a”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8．执行如图所示的程序框图,则输出的S的值为A.-√33B.2-√3C.-2-√3D.√39．已知各项均为正数的数列{a n }的前n 项和为S n ,且a n 2-9=4(S n -n ),数列{1a n ·a n+1}的前n 项和为T n ,则T 10=A.13B.17C.235D.22510．已知椭圆C 1:x 2a 2+y 2b 2=1(a >b >0),双曲线C 2:x 2b 2−y 2a 2-2b 2=1,F 1,F 2分别为C 2的左、右焦点,P为C 1和C 2的交点,若三角形PF 1F 2的内切圆的圆心的横坐标为2,C 1和C 2的离心率之积为32,则该内切圆的半径为A.4√2-2√6B.4√2-2√3C.4√3-2√6D.4√6-2√311．已知函数f (x )= A sin(x +π3)+b (A >0)的最大值、最小值分别为3和-1,关于函数f (x )有如下四个结论:①A =2,b =1;②函数f (x )的图象C 关于直线x =-5π6对称;③函数f (x )的图象C 关于点(2π3,0)对称;④函数f (x )在区间(π6,5π6)内是减函数.其中,正确结论的个数是A.1B.2C.3D.412．如图,正方体ABCD-A 1B 1C 1D 1的棱长为1,线段B 1D 1上有两个动点E,F,且EF=12,则下列结论中错误的是___.A.AC⊥BEB.EF∥平面ABCDC.三棱锥A-BEF 的体积为定值D.△AEF 的面积与△BEF 的面积相等第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题(共4题，每题5分，共20分)13．曲线f (x )=sin(x +π2)在点P (π2,f (π2))处的切线方程为 .14．已知在等比数列{a n }中,a n >0且a 3+a 4=a 1+a 2+3,记数列{a n }的前n 项和为S n ,则S 6-S 4的最小值为 .15．某统计调查组从A ,B 两市各随机抽取了6个大型商品房小区调查空置房情况,并记录他们的调查结果,得到如图所示的茎叶图.已知A 市被调查的商品房小区中空置房套数的平均数为82,B 市被调查的商品房小区中空置房套数的中位数为77,则x -y = .16．已知抛物线y 2=2px (p >0)的焦点为F ,准线与x 轴的交点为Q ,双曲线x 2a 2−y 2b2=1(a >0,b >0)的一条渐近线被抛物线截得的弦为OP ,O 为坐标原点.若△PQF 为直角三角形,则该双曲线的离心率等于 .三、解答题(共7题，共70分)17．(本题12分)在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,sin 2A +sin 2B =4sin A sin B cosC.(1)求角C 的最大值;(2)若b =2,B =π3,求△ABC 的面积.18．(本题12分)如图,在直三棱柱ABC -A 1B 1C 1中,D 为BC 的中点,AB =AC ,BC 1⊥B 1D.求证:(1)A 1C ∥平面ADB 1; (2)平面A 1BC 1⊥平面ADB 1.19．(本题12分)某车床生产某种零件的不合格率为p (0<p <1),要求这部车床生产的一组5个零件中,有2个或2个以上不合格品的概率不大于0.05.为了了解该车床每天生产零件的利润,现统计了该车床100天生产的零件组数(1组5个零件),得到的条形统计图如下.现以记录的100天的日生产零件组数的频率作为日生产零件组数的概率. (1)设平均每天可以生产n 个零件,求n 的值; (2)求p 的最大值p 0;(3)设每个零件的不合格率是p 0,生产1个零件的成本是20元,每个合格零件的出厂价为120元,不合格的零件不得出厂,不计其他成本.假设每天该机床生产的零件数为n ,X 表示这部车床每天生产零件的利润,求X 的数学期望E (X ). (参考数据:0.924×1.32的取值为0.95)20．(本题12分)在平面直角坐标系xOy 中,椭圆C :x 2a 2+y 2b 2=1(a >b >0)经过点(-1,32),且它的右焦点为F (1,0).直线l :y =kx +1与椭圆C 有两个不同的交点A ,B. (1)求椭圆C 的方程;(2)设点M 在y 轴上(M 不在l 上),且满足S1S 2=|AM||BM|,其中S 1,S 2分别为△OAM ,△OBM 的面积,求点M 的坐标.21．(本题12分)已知函数f (x )=e x -12ax 2+b (a >0),函数f (x )的图象在x =0处的切线方程为y =x +1.(1)当a =1时,求函数f (x )在[0,2]上的最小值与最大值; (2)若函数f (x )有两个零点,求a 的值.请考生在第 22、23 三题中任选二道做答，注意：只能做所选定的题目。
2020年高考理科数学模拟考(一)
模拟考(一) 高考仿真模拟冲刺卷(A)第Ⅰ卷 (选择题 共60分)一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．[2019·陕西模拟]设集合M ＝{x ||x －1|≤1}，N ＝{x |y ＝lg(x 2－1)}，则M ∩∁R N ＝( )A ．[1,2]B ．[0,1]C ．(－1,0)D ．(0,2) 答案：B解析：M ＝{x ||x －1|≤1}＝{x |0≤x ≤2}，N ＝{x |y ＝lg(x 2－1)}＝{x |x ＞1或x ＜－1}，∴M ∩∁R N ＝{x |0≤x ≤1}，故选B.2．[2019·陕西模拟]已知复数z 满足z (1－i)2＝1＋i(i 为虚数单位)，则|z |为( )A.12B.22C. 2 D ．1 答案：B解析：因为复数z 满足z (1－i)2＝1＋i ，所以z ＝1＋i(1－i )2＝1＋i－2i＝－12＋12i ，所以|z |＝22，故选B.3．要计算1＋12＋13＋…＋12 017的结果，如图所示的程序框图的判断框内可以填( )A ．n <2 017B ．n ≤2 017C ．n ＞2 017D ．n ≥2 017sin x ＋cos x ≤2”是真命题，所以綈p 是假命题，故D 错误．故选A.6．[2018·全国卷Ⅰ]在长方体ABCD -A 1B 1C 1D 1中，AB ＝BC ＝2，AC 1与平面BB 1C 1C 所成的角为30°，则该长方体的体积为( )A ．8B ．6 2C ．8 2D ．8 3 答案：C解析：如图，连接AC 1，BC 1，AC .∵ AB ⊥平面BB 1C 1C ，∴ ∠AC 1B 为直线AC 1与平面BB 1C 1C 所成的角，∴ ∠AC 1B ＝30°.又AB ＝BC ＝2，在Rt △ABC 1中，AC 1＝2sin 30°＝4，在Rt △ACC 1中，CC 1＝AC 2 1－AC 2＝42－(22＋22)＝22，∴ V 长方体＝AB ×BC ×CC 1 ＝2×2×22＝8 2.故选C.7．[2019·江西联考]已知实数x ，y 满足不等式组⎩⎪⎨⎪⎧x ≤1，x －y ＋m 2≥0，x ＋y －1≥0，若目标函数z ＝－2x ＋y 的最大值不超过4，则实数m 的取值范围是( )A ．(－3，3)B ．[0，3]C ．[－3，0]D ．[－3，3] 答案：D解析：将z ＝－2x ＋y 化为y ＝2x ＋z ，作出可行域和目标函数在z ＝0时的直线y ＝2x (如图所示)，当直线y ＝2x ＋z 向左上方平移时，直线y ＝2x ＋z 在y 轴上的截距z 增大，由图象可知，当直线y ＝2x ＋z 过点A 时，z取得最大值，联立⎩⎨⎧x －y ＋m 2＝0，x ＋y －1＝0，得A ⎝ ⎛⎭⎪⎪⎫1－m 22，1＋m 22，则－2×1－m 22＋1＋m 22≤4，解得－3≤m ≤3，故选D.8．已知数列{a n }，{b n }，其中{a n }是首项为3，公差为整数的等差数列，且a 3>a 1＋3，a 4<a 2＋5，a n ＝log 2b n ，则{b n }的前n 项和S n ＝( )A ．8(2n －1)B ．4(3n －1) C.83(4n －1) D.43(3n －1) 答案：C解析：设数列{a n }的公差为d (d ∈Z )，由题意，得a n ＝3＋(n －1)d ，由a 3>a 1＋3，a 4<a 2＋5可得⎩⎨⎧2d >3，2d <5，所以d ＝2，所以a n ＝2n ＋1.因为a n ＝log 2b n ，即2n ＋1＝log 2b n ，所以b n ＝22n ＋1＝8×4n －1，所以数列{b n }是以8为首项，4为公比的等比数列，所以S n ＝8(1－4n )1－4＝83(4n －1)，故选C.9．[2019·河南开封模拟]函数f (x )＝x 2ln|x ||x |的图象大致是( )答案：D解析：由解析式可知函数为偶函数，当x >0时，f (x )＝x ln x ，f ′(x )＝1＋ln x ，即0<x <1e 时，函数f (x )单调递减；当x >1e ，函数f (x )单调递增．故选D.10．[2019·四川绵阳南山中学诊断]若圆x 2＋y 2＋4x －4y －10＝0上至少有三个不同的点到直线l ：ax ＋by ＝0的距离为22，则直线l 的斜率的取值范围是( )A ．[2－3，2＋3]B ．[－2－3，3－2]C ．[－2－3，2＋3]D ．[－2－3，2－3] 答案：B解析：圆x 2＋y 2＋4x －4y －10＝0可化为(x ＋2)2＋(y －2)2＝18，则圆心为(－2,2)，半径为32，则由圆x 2＋y 2＋4x －4y －10＝0上至少有三个不同点到直线l ：ax ＋by ＝0的距离为22，得圆心到直线l ：ax ＋by ＝0的距离d ≤32－22＝2，即|－2a ＋2b |a 2＋b 2≤2，则a 2＋b 2－4ab ≤0，若b ＝0，则a ＝0，故不成立，故b ≠0，则上式可化为1＋⎝ ⎛⎭⎪⎫a b 2－4·a b ≤0，由直线l 的斜率k ＝－a b ，则上式可化为k 2＋4k ＋1≤0，解得－2－3≤k ≤－2＋ 3.故选B.11．[2019·广西两校联考]在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若bc ＝1，b ＋2c cos A ＝0，则当角B 取得最大值时，△ABC 的周长为( )A ．2＋ 3B ．2＋ 2C ．3D ．3＋ 2 答案：A解析：解法一 由题意可得，sin B ＋2sin C cos A ＝0，即sin(A ＋C )＋2sin C cos A ＝0，得sin A cos C ＝－3sin C cos A ，即tan A ＝－3tan C .又cos A＝－b2c <0，所以A 为钝角，于是tan C >0.从而tan B ＝－tan(A ＋C )＝－tan A ＋tan C1－tan A tan C ＝2tan C 1＋3tan 2C＝21tan C ＋3tan C，由基本不等式，得1tan C ＋3tan C ≥21tan C ×3tan C ＝23，当且仅当tan C ＝33时等号成立，此时角B 取得最大值，且tan B ＝tan C ＝33，tan A ＝－3，即b ＝c ，A ＝120°，又bc ＝1，所以b ＝c ＝1，a ＝3，故△ABC 的周长为2＋ 3.解法二 由已知b ＋2c cos A ＝0，得b ＋2c ·b 2＋c 2－a 22bc ＝0，整理得2b 2＝a 2－c 2.由余弦定理，得cos B ＝a 2＋c 2－b 22ac ＝a 2＋3c 24ac ≥23ac 4ac ＝32，当且仅当a ＝3c 时等号成立，此时角B 取得最大值，将a ＝3c 代入2b 2＝a 2－c 2可得b ＝c .又bc ＝1，所以b ＝c ＝1，a ＝3，故△ABC 的周长为2＋ 3.故选A.12．[2019·安徽淮南模拟]已知函数f (x )＝x 2e x ，若函数g (x )＝[f (x )]2－kf (x )＋1恰有4个零点，则实数k 的取值范围是( )A ．(－∞，－2)∪(2，＋∞) B.⎝ ⎛⎭⎪⎫4e 2＋e 24，＋∞ C.⎝ ⎛⎭⎪⎫8e 2，2 D.⎝ ⎛⎭⎪⎫2，4e 2＋e 24 答案：B解析：f ′(x )＝2x e x ＋x 2e x ＝x (x ＋2)e x ，令f ′(x )＝0，解得x ＝0或x ＝－2.∴当x <－2或x >0时，f ′(x )>0；当－2<x <0时，f ′(x )<0. ∴f (x )在(－∞，－2)上单调递增，在(－2,0)上单调递减，在(0，＋∞)上单调递增，∴当x ＝－2时，函数f (x )取得极大值f (－2)＝4e 2， 当x ＝0时，f (x )取得极小值f (0)＝0.∵f (x )＝x 2e x ≥0，∴作出f (x )的大致图象如右图所示．令f (x )＝t ，则当t ＝0或t >4e 2时，关于x 的方程f (x )＝t 只有1个解；当t ＝4e 2时，关于x 的方程f (x )＝t 有2个解；当0<t <4e 2时，关于x 的方程f (x )＝t 有3个解．∵g (x )＝[f (x )]2－kf (x )＋1恰有4个零点，∴关于t 的方程t 2－kt ＋1＝0在⎝ ⎛⎭⎪⎫0，4e 2上有1个解，在⎝ ⎛⎭⎪⎫4e 2，＋∞∪{0}上有1解，显然t ＝0不是方程t 2－kt ＋1＝0的解，∴关于t 的方程t 2－kt ＋1＝0在⎝ ⎛⎭⎪⎫0，4e 2和⎝ ⎛⎭⎪⎫4e 2，＋∞上各有1个解，∴16e 4－4k e 2＋1<0，解得k >4e 2＋e 24.故选B.第Ⅱ卷(非选择题 共90分)二、填空题：本大题共4小题，每小题5分，共20分．把答案填在相应题号后的横线上．13．[2019·郑州测试]在⎝⎛⎭⎪⎫x ＋3x n 的展开式中，各项系数和与二项式系数和之比为32：1，则x 2的系数为________．答案：90解析：令x ＝1，则⎝ ⎛⎭⎪⎫x ＋3x n ＝4n，所以⎝⎛⎭⎪⎫x ＋3x n 的展开式中，各项系数和为4n ，又二项式系数和为2n，所以4n2n ＝2n ＝32，解得n ＝5.二项展开式的通项T r ＋1＝C r 5x 5－r ⎝ ⎛⎭⎪⎫3x r ＝C r 53r x 35-r2，令5－32r ＝2，得r ＝2，所以x 2的系数为C 2532＝90.14．在△ABC 中，若(AB →－2AC →)⊥AB →，(AC →－2AB →)⊥AC →，则△ABC的形状为________．答案：等边三角形解析：(AB →－2AC →)⊥AB →⇒(AB →－2AC →)·AB →＝0，即AB →·AB →－2AC →·AB →＝0.(AC →－2AB →)⊥AC →，即(AC →－2AB →)·AC →＝0，即AC →·AC →－2AB →·AC→＝0，∴sin B ＝1－cos 2B ＝1－13＝63.由正弦定理知a sin A ＝b sin B ，∴b ＝a sin B sin A ＝2×6332＝423，∴b ＝423.18．(本小题满分12分)[2019·云南昆明一中模拟]某校为了解本校2万名学生的汉字书写水平，在全校范围内进行了汉字听写考试，发现其成绩服从正态分布N (69,49)，现从该校随机抽取了50名学生，将所得成绩整理后，绘制出如图所示的频率分布直方图．(1)估算该校50名学生成绩的平均值x －(同一组中的数据用该组区间的中点值作代表)；(2)求这50名学生成绩在[80,100]内的人数；(3)现从该校50名考生成绩在[80,100]的学生中随机抽取两人，该两人成绩排名(从高到低)在全市前26名的人数记为X ，求X 的分布列和数学期望．参考数据：若X ～N (μ，σ2)，则P (μ－σ<X ≤μ＋σ)＝0.682 6，P (μ－2σ<X ≤μ＋2σ)＝0.954 4，P (μ－3σ<X ≤μ＋3σ)＝0.997 4.解析：(1)x －＝45×0.08＋55×0.2＋65×0.32＋75×0.2＋85×0.12＋95×0.08＝68.2.(2)(0.008＋0.012)×10×50＝10(名)． (3)P (μ－3σ<X ≤μ＋3σ)＝0.997 4， 则P (X ≥90)＝1－0.997 42＝0.001 3. 0．001 3×20 000＝26，所以该市前26名的学生听写考试成绩在90分以上．上述50名考生成绩中90分以上的有0.08×50＝4人． 随机变量X ＝0,1,2.于是P (X ＝0)＝C 26C 210＝13，P (X ＝1)＝C 16·C 14C 210＝815，P (X ＝2)＝C 24C 210＝25.所以X 的分布列为X0 1 2 P13815215数学期望E (X )＝0×13＋1×815＋2×225＝45. 19．(本小题满分12分)[2019·合肥市质检]如图所示，在四棱台ABCD －A 1B 1C 1D 1中，AA 1⊥底面ABCD ，四边形ABCD 为菱形，∠BAD ＝120°，AB ＝AA 1＝2A 1B 1＝2.(1)若M 为CD 中点，求证：AM ⊥平面AA 1B 1B ； (2)求直线DD 1与平面A 1BD 所成角的正弦值． 解析：(1)证明：四边形ABCD 为菱形，∠BAD ＝120°，连接AC ，如图，则△ACD 为等边三角形，又M 为CD 中点，∴AM ⊥CD ，由CD ∥AB 得，AM ⊥AB ，∵AA 1⊥底面ABCD ，AM ⊂平面ABCD ，∴AM ⊥AA 1，又AB ∩AA 1＝A ，∴AM ⊥平面AA 1B 1B .。
2020年安徽省高考数学(理科)模拟试卷(1)
2020年安徽省高考数学（理科）模拟试卷（1）一．选择题（共12小题，满分60分，每小题5分）1．（5分）已知集合A ＝{x ∈N |x ＞1}，B ＝{x |x ＜5}，则A ∩B ＝（ ） A ．{x |1＜x ＜5}B ．{x |x ＞1}C ．{2，3，4}D ．{1，2，3，4，5}2．（5分）复数z ＝（1+2i ）2（i 为虚数单位）的共轭复数z 在复平面内对应的点在（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．（5分）“纹样”是中国艺术宝库的瑰宝，“火纹”是常见的一种传统纹样．为了测算某火纹纹样（如图阴影部分所示）的面积，作一个边长为3的正方形将其包含在内，并向该正方形内随机投掷200个点，已知恰有80个点落在阴影部分，据此可估计阴影部分的面积是（ ）A ．165B ．325C ．10D ．1854．（5分）为得到y ＝2sin （3x −π3）的图象，只需要将y ＝2cos3x 函数的图象（ ） A ．向左平移π6个单位B ．向右平移π6个单位C ．向左平移5π18个单位 D ．向右平移5π18个单位5．（5分）已知函数f(x)=√x 2+x +a 的定义域为R ，则实数a 的取值范围是（ ） A ．（0，14]B ．（﹣∞，14]C ．[14，+∞）D ．[1，+∞）6．（5分）已知抛物线y 2＝2px （p ＞0）与圆x 2+y 2＝5交于A ，B 两点，且|AB |＝4，则p ＝（ ） A ．√2B ．1C ．2D ．47．（5分）若直线y ＝ax +2a 与不等式组{x −y +6≥0x ≤3x +y −3≥0表示的平面区域有公共点，则实数a的取值范围是（ ）A ．[0，95]B ．[0，9]C ．[0，+∞]D ．[﹣∞，9]8．（5分）函数y ＝2x +2x−1（x ＞1）的最小值是（ ） A ．2B ．4C ．6D ．89．（5分）已知sin(π+α)=45，且sin2α＜0，则tan （α−π4）的值为（ ） A ．7B ．﹣7C ．17D ．−1710．（5分）设a ＝30.1，b ＝log 0.30.5，c ＝log 60.3，则a ，b ，c 的大小关系是（ ） A ．a ＜b ＜cB ．c ＜b ＜aC ．c ＜a ＜bD ．b ＜c ＜a11．（5分）把一个已知圆锥截成一个圆台和一个小圆锥，已知圆台的上、下底面半径之比为1：3，母线长为6cm ，则已知圆锥的母线长为（ ）cm ． A ．8B ．9C ．10D ．1212．（5分）如图，F I ，F 2是双曲线C ：x 22−y 23=1(a ＞0)的左、右焦点，点P 是双曲线上位于第一象限内的一点，且直线F 2P 与y 轴的正半轴交于点A ，△APF 1的内切圆与边PF 1切于点Q ，且|PQ |＝4，则双曲线C 的离心率为（ ）A ．2B ．√72C ．2√33D ．√194二．填空题（共4小题，满分20分，每小题5分）13．（5分）如图，在平行四边形ABCD 中，AB ＝2，AD ＝1．则AC →⋅BD →的值为 ．14．（5分）化简：tan(3π−α)cos(4π+α)sin(π2−α)cos(−α−π)sin(−5π−α)= ．15．（5分）已知（1﹣x ）6＝a 0+a 1x +a 2x 2+…+a 6x 6，则a 2＝ ，a 0﹣a 1+a 2﹣a 3+a 4﹣a 5+a 6＝ ．16．（5分）在三棱锥P ﹣ABC 中，P A ＝PC ＝2√3，BA ＝BC =√3，∠ABC ＝90°，若P A 与底面ABC 所成的角为60°，则三棱锥P ﹣ABC 的外接球的表面积 ． 三．解答题（共6小题）17．已知数列{a n }是等差数列，满足a 2＝5，a 4＝9，数列{b n +a n }是公比为3的等比数列，且b 1＝3．（1）求数列{a n }和{b n }的通项公式； （2）求数列{b n }的前n 项和S n ．18．已知函数f(x)=sinx ⋅sin(x +π3)−14(x ∈R)． （1）求f(π3)的值和f （x ）的最小正周期；（2）设锐角△ABC 的三边a ，b ，c 所对的角分别为A ，B ，C ，且f(A2)=14，a ＝2，求b +c 的取值范围．19．如图，在四棱锥P ﹣ABCD 中，底面ABCD 为矩形，侧面P AB ⊥底面ABCD ，H 为棱AB 的中点，E 为棱DC 上任意一点，且不与D 点、C 点重合．AB ＝2，AD ＝P A ＝1，PH =√2． （Ⅰ）求证：平面APE ⊥平面ABCD ；（Ⅱ）是否存在点E 使得平面APE 与平面PHC 所成的角的余弦值为√63？若存在，求出点E 的位置；若不存在，请说明理由．20．已知一堆产品中有一等品2件，二等品3件，三等品4件，现从中任取3件产品． （1）求一、二、三等品各取到一个的概率；（2）记X 表示取到一等品的件数，求X 的分布列和数学期望． 21．已知f （x ）＝（x ﹣m ）e x ．（1）当m ＝2时，求函数f （x ）在点（0，f （0））处的切线方程；（2）若函数f （x ）在区间（﹣1，0）上有极小值点，且总存在实数m ，使函数f （x ）的极小值与e 2m +2am 2(a+1)e互为相反数，求实数a 的取值范围．22．已知动圆C 与圆C 1：(x −2)2+y 2=1外切，又与直线l ：x ＝﹣1相切．设动圆C 的圆心的轨迹为曲线E ． （1）求曲线E 的方程；（2）在x 轴上求一点P （不与原点重合），使得点P 关于直线y =12x 的对称点在曲线E 上．2020年安徽省高考数学（理科）模拟试卷（1）参考答案与试题解析一．选择题（共12小题，满分60分，每小题5分）1．（5分）已知集合A ＝{x ∈N |x ＞1}，B ＝{x |x ＜5}，则A ∩B ＝（ ） A ．{x |1＜x ＜5}B ．{x |x ＞1}C ．{2，3，4}D ．{1，2，3，4，5}【解答】解：∵集合A ＝{x ∈N |x ＞1}，B ＝{x |x ＜5}， ∴A ∩B ＝{x ∈N |1＜x ＜5}＝{2，3，4}． 故选：C ．2．（5分）复数z ＝（1+2i ）2（i 为虚数单位）的共轭复数z 在复平面内对应的点在（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限【解答】解：因为z ＝（1+2i ）2＝1+4i +4i 2＝﹣3+4i ； ∴z =−3﹣4i ；∴z 在复平面内对应的点在第三象限； 故选：C ．3．（5分）“纹样”是中国艺术宝库的瑰宝，“火纹”是常见的一种传统纹样．为了测算某火纹纹样（如图阴影部分所示）的面积，作一个边长为3的正方形将其包含在内，并向该正方形内随机投掷200个点，已知恰有80个点落在阴影部分，据此可估计阴影部分的面积是（ ）A ．165B ．325C ．10D ．185【解答】解：由题意可得：S 阴影S 正方形=80200，∴S 阴影=25×32=185． 故选：D ．4．（5分）为得到y ＝2sin （3x −π3）的图象，只需要将y ＝2cos3x 函数的图象（ ） A ．向左平移π6个单位B ．向右平移π6个单位C ．向左平移5π18个单位D ．向右平移5π18个单位【解答】解：将y ＝2cos3x ＝2sin （3x +π2）的图象，向右平移5π18个单位，可得函数的图象得到y ＝2sin （3x −π3）的图象， 故选：D ．5．（5分）已知函数f(x)=√x 2+x +a 的定义域为R ，则实数a 的取值范围是（ ） A ．（0，14]B ．（﹣∞，14]C ．[14，+∞）D ．[1，+∞）【解答】解：∵f （x ）的定义域为R ， ∴x 2+x +a ≥0的解集为R ， ∴△＝1﹣4a ≤0，解得a ≥14， ∴实数a 的取值范围是[14，+∞)． 故选：C ．6．（5分）已知抛物线y 2＝2px （p ＞0）与圆x 2+y 2＝5交于A ，B 两点，且|AB |＝4，则p ＝（ ） A ．√2B ．1C ．2D ．4【解答】解：抛物线y 2＝2px （p ＞0）与圆x 2+y 2＝5交于A ，B 两点，且|AB |＝4， 由抛物线和圆都关于x 轴对称，可得A ，B 的纵坐标为2，﹣2， 可设A （2p ，2），代入圆的方程可得4p 2+4＝5，可得p ＝2．故选：C ．7．（5分）若直线y ＝ax +2a 与不等式组{x −y +6≥0x ≤3x +y −3≥0表示的平面区域有公共点，则实数a的取值范围是（ ） A ．[0，95]B ．[0，9]C ．[0，+∞]D ．[﹣∞，9]【解答】解：画出不等式组表示的平面区域，如图所示{x −y +6=0x +y −3=0⇒{x =−32y =92；∴C （−32，92），直线y ＝a （x +2）过定点A （﹣2，0），直线y ＝a （x +2）经过不等式组表示的平面区域有公共点 则a ＞0，k AC =92−0(−32)−(−2)=9，∴a ∈[0，9]． 故选：B ．8．（5分）函数y ＝2x +2x−1（x ＞1）的最小值是（ ） A ．2B ．4C ．6D ．8【解答】解：因为y ＝2x +2x−1（x ＞1）， ＝2（x ﹣1）+2x−1+2≥2√2(x −1)⋅2x−1+2=6， 当且仅当2（x ﹣1）=2x−1即x ＝2时取等号，此时取得最小值6． 故选：C ．9．（5分）已知sin(π+α)=45，且sin2α＜0，则tan （α−π4）的值为（ ） A ．7B ．﹣7C ．17D ．−17【解答】解：∵sin(π+α)=45， ∴可得sin α=−45，又∵sin2α＝2sin αcos α＜0，可得cos α＞0，∴可得cosα=√1−sin2α=35，tanα=sinαcosα=−43，∴tan（α−π4）=tanα−11+tanα=−43−11−43=7．故选：A．10．（5分）设a＝30.1，b＝log0.30.5，c＝log60.3，则a，b，c的大小关系是（）A．a＜b＜c B．c＜b＜a C．c＜a＜b D．b＜c＜a【解答】解：∵a＝30.1＞30＝1，∴a＞1；∵log0.31＜b＝log0.30.5＜log0.30.3＝1，∴0＜b＜1；∵c＝log50.3＜log51＝0，∴c＜0，∴a＞b＞c，故选：B．11．（5分）把一个已知圆锥截成一个圆台和一个小圆锥，已知圆台的上、下底面半径之比为1：3，母线长为6cm，则已知圆锥的母线长为（）cm．A．8B．9C．10D．12【解答】解：由题意画出轴截面图形，可知CDAB =SDSB=13，BD＝6，可得SD＝2，所以圆锥的母线长为：2+6＝8（cm）．故选：A．12．（5分）如图，F I，F2是双曲线C：x2a2−y23=1(a＞0)的左、右焦点，点P是双曲线上位于第一象限内的一点，且直线F2P与y轴的正半轴交于点A，△APF1的内切圆与边PF1切于点Q，且|PQ|＝4，则双曲线C的离心率为（）A ．2B ．√72C ．2√33D ．√194【解答】解：PQ ＝PF 1﹣F 1Q ＝PF 1﹣F 1M ＝PF 1﹣NF 2＝PF 1﹣（PF 2+PQ ） ⇒PQ =12(PF 1−PF 2)=a ，∴a ＝4，b =√3，∴c =√19， 所以双曲线的离心率为：e =√194．故选：D ．二．填空题（共4小题，满分20分，每小题5分）13．（5分）如图，在平行四边形ABCD 中，AB ＝2，AD ＝1．则AC →⋅BD →的值为 ﹣3 ．【解答】解：∵AB ＝2，AD ＝1， ∴AC →⋅BD →=(AB →+AD →)⋅(BA →+BC →) =(AB →+AD →)⋅(AD →−AB →) =AD →2−AB →2 ＝1﹣4 ＝﹣3． 故答案为：﹣3．14．（5分）化简：tan(3π−α)cos(4π+α)sin(π2−α)cos(−α−π)sin(−5π−α)= 1 ．【解答】解：tan(3π−α)cos(4π+α)sin(π2−α)cos(−α−π)sin(−5π−α)=(−tanα)cosαcosα(−cosα)sinα=1．故答案为：1．15．（5分）已知（1﹣x）6＝a0+a1x+a2x2+…+a6x6，则a2＝15，a0﹣a1+a2﹣a3+a4﹣a5+a6＝64．【解答】解：由（1﹣x）6的通项为T r+1=C6r(−x)r可得，令r＝2，即x2项的系数a2为C62=15，即a2＝15，由（1﹣x）6＝a0+a1x+a2x2+…+a6x6，取x＝﹣1，得a0﹣a1+a2﹣a3+a4﹣a5+a6＝[1﹣（﹣1）]6＝64，故答案为：15，64．16．（5分）在三棱锥P﹣ABC中，P A＝PC＝2√3，BA＝BC=√3，∠ABC＝90°，若P A与底面ABC所成的角为60°，则三棱锥P﹣ABC的外接球的表面积15π．【解答】解：因为P A＝PC＝2√3，BA＝BC=√3，所以P在底面的投影在∠ABC的角平分线上，设为E，再由若P A与底面ABC所成的角为60°可得AE＝P A•cos60°＝2√3⋅12=√3，可得E，B重合，PB＝P A•sin60°＝2√3⋅√32=3，即PB⊥面ABC，由∠ABC＝90°可得，将三棱锥P﹣ABC放在长方体中，由长方体的对角线为外接球的直径2R可得：4R2＝32+（√3）2+（√3）2＝15，所以外接球的表面积S＝4πR2＝15π，故答案为：15π．三．解答题（共6小题）17．已知数列{a n}是等差数列，满足a2＝5，a4＝9，数列{b n+a n}是公比为3的等比数列，且b1＝3．（1）求数列{a n}和{b n}的通项公式；（2）求数列{b n}的前n项和S n．【解答】解：（1）数列{a n}是公差为d的等差数列，满足a2＝5，a4＝9，可得a1+d＝5，a1+3d＝9，解得a1＝3，d＝2，即有a n＝3+2（n﹣1）＝2n+1；数列{b n+a n}是公比为3的等比数列，且b1＝3，可得b n+a n＝6•3n﹣1＝2•3n，则b n＝2•3n﹣（2n+1）；（2）前n项和S n＝（6+18+…+2•3n）﹣（3+5+…+2n+1）=6(1−3n)1−3−12n（3+2n+1）＝3n+1﹣3﹣n（n+2）．18．已知函数f(x)=sinx⋅sin(x+π3)−14(x∈R)．（1）求f(π3)的值和f（x）的最小正周期；（2）设锐角△ABC的三边a，b，c所对的角分别为A，B，C，且f(A2)=14，a＝2，求b+c的取值范围．【解答】解：（1）函数f(x)=sinx⋅sin(x+π3)−14(x∈R)．所以f(π3)=√32×√32−14=12．所以f（x）=sinx(12sinx+√32cosx)=1−cos2x4+√34sin2x−14=12sin(2x−π6)，所以函数f（x）的最小正周期为π；（2）设锐角△ABC的三边a，b，c所对的角分别为A，B，C，且f(A2)=14，所以sin(A−π6)=12，解得A=π3．利用正弦定理asinA =bsinB=csinC，解得b=3，c=3sin(2π3−B)，所以b+c=3+sin(2π3−B)]=4sin(B+π6)，由于{0＜B＜π20＜C=2π3−B＜π2，解得π6＜B＜π2，所以B+π6∈(π3，2π3)，所以b+c∈(2√3，4]．19．如图，在四棱锥P﹣ABCD中，底面ABCD为矩形，侧面P AB⊥底面ABCD，H为棱AB 的中点，E为棱DC上任意一点，且不与D点、C点重合．AB＝2，AD＝P A＝1，PH=√2．（Ⅰ）求证：平面APE⊥平面ABCD；（Ⅱ）是否存在点E 使得平面APE 与平面PHC 所成的角的余弦值为√63？若存在，求出点E 的位置；若不存在，请说明理由．【解答】解：（Ⅰ）证明：∵AB ＝2，H 为AB 中点， ∴AH ＝1，又PA =1，PH =√2，∴P A 2+AH 2＝PH 2，则P A ⊥AH ，又侧面P AB ⊥底面ABCD ，侧面P AB ∩底面ABCD ＝AB ， ∴P A ⊥平面ABCD ， 又P A 在平面APE 内， ∴平面APE ⊥平面ABCD ；（Ⅱ）由（Ⅰ）可知，以A 为坐标原点，AD ，AB ，AP 所在直线分别为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系，则A （0，0，0），P （0，0，1），H （0，1，0），C （1，2，0），假设存在点E （1，y ，0）满足题意，则AP →=(0，0，1)，AE →=(1，y ，0)，PH →=(0，1，−1)，HC →=(1，1，0)，设平面APE 的一个法向量为m →=(a ，b ，c)，则{m →⋅AP →=c =0m →⋅AE →=a +by =0，设a ＝1，则m →=(−1，1y ，0)，设平面PHC 的一个法向量为n →=(p ，k ，t)，则{n →⋅PH →=k −t =0n →⋅HC →=p +k =0，设k ＝1，则n →=(−1，1，1)，∵平面APE 与平面PHC 所成的角的余弦值为√63， ∴|cos ＜m →，n →＞|=|m →⋅n →||m →||n →|=|1+1y |√1+1y2⋅√3=√63，∴y ＝1，即存在点E 为CD 的中点，使得平面APE 与平面PHC 所成的角的余弦值为√63． 20．已知一堆产品中有一等品2件，二等品3件，三等品4件，现从中任取3件产品． （1）求一、二、三等品各取到一个的概率；（2）记X 表示取到一等品的件数，求X 的分布列和数学期望．【解答】解：（1）一堆产品中有一等品2件，二等品3件，三等品4件，现从中任取3件产品．基本事件总数n =C 93=84，一、二、三等品各取到一个包含的基本事件个数m ＝2×3×4＝24， ∴一、二、三等品各取到一个的概率p =m n =2484=27． （2）记X 表示取到一等品的件数，则X 的可能取值为0，1，2， P （X ＝0）=C 73C 93=512， P （X ＝1）=C 21C 72C 93=12， P （X ＝2）=C 22C 71C 93=112，∴X 的分布列为：X 012 P51212112数学期望E （X ）=0×512+1×12+2×112=23． 21．已知f （x ）＝（x ﹣m ）e x ．（1）当m ＝2时，求函数f （x ）在点（0，f （0））处的切线方程；（2）若函数f （x ）在区间（﹣1，0）上有极小值点，且总存在实数m ，使函数f （x ）的极小值与e 2m +2am 2(a+1)e互为相反数，求实数a 的取值范围．【解答】解：（1）f '（x ）＝[x ﹣（m ﹣1）]e x ．当m ＝2时，f （x ）＝（x ﹣2）e x ，f '（x ）＝（x ﹣1）e x ． ∴f （0）＝﹣2，f '（0）＝﹣1，所以，函数f （x ）在点（0，f （0））处的切线方程为y +2＝﹣（x ﹣0），即x +y +2＝0． （2）f '（x ）＝[x ﹣（m ﹣1）]e x 得x ∈（﹣∞，m ﹣1）时，f '（x ）＜0，x ∈（m ﹣1，+∞）时，f '（x ）＞0，∴函数f （x ）在区间（﹣∞，m ﹣1）上单调递减，在区间（m ﹣1，+∞）单调递增， 函数f （x ）的极小值点为m ﹣1． 由已知﹣1＜m ﹣1＜0，∴0＜m ＜1.f(x)极小=f(m −1)=−e m−1 故在区间（0，1）上存在m ，使得e 2m +2am 2(a+1)e−e m−1=0．∴2a =e 2m −2e m e m −m （0＜m ＜1）．设g(m)=e 2m −2e me m −m．∴当0＜m ＜1时，g ′(m)=(e m −1)[e 2m +2(1−m)e m ](e m −m)2＞0，∴函数g （m ）在区间（0，1）上递增， ∴当0＜m ＜1时，g （0）＜g （m ）＜g （1），即−1＜2a ＜e 2−2e e−1，∴−12＜a ＜e 2−2e 2e−2，所以，实数a 的取值范围是(−12，e 2−2e2e−2)．22．已知动圆C 与圆C 1：(x −2)2+y 2=1外切，又与直线l ：x ＝﹣1相切．设动圆C 的圆心的轨迹为曲线E ． （1）求曲线E 的方程；（2）在x 轴上求一点P （不与原点重合），使得点P 关于直线y =12x 的对称点在曲线E 上．【解答】解：解法一：（1）依题意得圆心C 到于直线x ＝﹣2的距离等于到圆C 1圆心的距离，所以C 的轨迹是（2，0）为焦点，以直线x ＝﹣2为准线的抛物线， 设其方程y 2＝2px （p ＞0），则p2=2，p ＝4，所以曲线E 的方程为y 2＝8x ．（2）设P （t ，0），P 关于直线y =12x 的对称点为P 1（m ，n ），则{nm−t=−2，n 2=12(m+t 2)，即{2m +n =2t ，2n −m =t ，解得{m =35t ，n =35t.代入曲线E 得1625t 2=245t ，解得t ＝0（舍去），t =152，即点P 的坐标为(152，0)． 解法二：（1）设圆心C （x ，y ），依题意x ≥﹣1， 因为圆C 与直线l ：x ＝﹣1相切，所以r ＝x +1， 又圆C 与圆C 1外切，所以|CC 1|＝r +1， 即√(x −2)2+y 2=x +2， 化简得曲线E 的方程为y 2＝8x ． （2）同解法．。
2020年高考模拟内蒙古高考数学模拟试卷(理科)(3月份) 含解析
2020年高考模拟高考数学模拟试卷（理科）（3月份）一、选择题1．设复数z的共轭复数为，i为虚数单位，若z＝1﹣i，则（3+2）i＝（）A．﹣2﹣5i B．﹣2+5i C．2+5i D．2﹣5i2．已知集合M＝{x|x2﹣2x﹣3＜0}，N＝{x|x2﹣mx＜0}，若M∩N＝{x|0＜x＜1}，则m的值为（）A．1B．﹣1C．±1D．23．已知等差数列{a n}中，S n为其前n项的和，S4＝24，S9＝99，则a7＝（）A．13B．14C．15D．164．如图所示，四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形，若直角三角形中较小的锐角为θ，现在向该正方形区域内随机地投掷一枚飞镖，则飞镖落在小正方形内的概率是（）A．1﹣sin 2θB．C．1﹣sinθD．5．函数f（x）＝ln|x|+|sin x|（﹣π≤x≤π且x≠0）的图象大致是（）A．B．C．D．6．从6名女生3名男生中，选出3名学生组成课外小组，如果按性别比例分层抽样，则不同的抽取方法数为（）A．45种B．120 种C．30种D．63种7．已知一个三棱锥的三视图如图所示，其中俯视图是等腰直角三角形，则该三棱锥的外接球表面积（）A．B．2C．4D．12π8．设F1，F2分别是椭圆E的左、右焦点，过点F1的直线交椭圆E于A，B两点，A在x轴上方，且满足|AF1|＝3|F1B|，，则A点位于（）A．第一象限B．第二象限C．y轴上D．都有可能9．已知函数，函数y＝f（x）﹣a有四个不同的零点，从小到大依次为x1，x2，x3，x4，则x1+x2+x3+x4的最大值为（）A．1+e B．4+e C．1﹣e D．1+2e10．O为△ABC内一点，且，若B，O，D三点共线，则t的值为（）A．B．C．D．11．已知F1、F2分别是双曲线（a＞0，b＞0）的左、右焦点，过点F2与双曲线的一条渐近线平行的直线交叉双曲线另一条渐近线于点M，若点M在以线段F1F2为直径的圆内，则双曲线离心的取值范围是（）A．（，+∞）B．（2，+∞）C．（，2）D．（1，2）12．定义在R上的偶函数f（x）的导函数为f′（x），且当x＞0时，xf′（x）+2f（x）＜0．则（）A．B．9f（3）＞f（1）C．D．二、填空题（共4小题，每小题5分，满分20分）13．设x，y满足，则z＝2x+y的最小值为．14．在等比数列{a n}中，已知a2+a4＝8，a6+a8＝4，则a10+a12+a14+a16＝．15．“砥砺奋进的五年”，首都经济社会发展取得新成就．自2012年以来北京城乡居民收入稳步增长．随着扩大内需，促进消费等政策的出台，居民消费支出全面增长，消费结构持续优化升级，城乡居民人均可支配收人快速增长，人民生活品质不断提升．右图是北京市2012﹣2016年城乡居民人均可支配收人实际增速趋势图（例如2012年，北京城镇居民收人实际增速为7.3%，农村居民收人实际增速为8.2%）．从2012﹣2016五年中任选两年，则至少有一年农村和城镇居民收入实际增速均超过7%的概率为．16．在棱长为a的正方体内有一个和各面都相切的球，过正方体中两条互为异面直线的棱的中点作直线，则该直线被球面截在球内的弦长为．三、解答题（共5小题，满分60分）17．已知，2sin x），＝（sin，，函数．（1）求函数f（x）的零点；（2）已知在△ABC中，角A，B，C所对的边分别为a，b，c，且f（A）＝2，△ABC 的外接圆半径为，求△ABC周长的最大值．18．如图，在平行四边形ABCD中，AB＝2，AD＝1，∠BAD＝60°，EDBF是矩形，DE ＝a，平面EDBF⊥平面ABCD．（1）若a＝1，求证：AE⊥CF；（2）若二面角A﹣EF﹣B的余弦值为，求a的值．19．设动圆P（圆心为P）经过定点（0，2），被x轴截得的弦长为4，P的轨迹为曲线E．（1）求曲线E的方程；（2）直线l：y ＝x+m（m∈R）与曲线E交于不同的两点A、B，线段AB的垂直平分线与y轴交于点M，若tan∠AMB＝﹣2，求m的值．20．某种产品的质量以其质量指标值衡量，并依据质量指标值划分等级如表：M≥205质量指标值m m＜185185≤m＜205等级三等品二等品一等品从某企业生产的这种产品中抽取200件，检测后得到如右的频率分布直方图：（1）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一等品至少要占全部产品50%”的规定？（2）在样本中，按产品等级用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；（3）该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值X近似服从正态分布N（216，139），则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？21．已知函数f（x）＝x﹣2+ae x（e为自然对数的底数）（1）讨论f（x）的单调性；（2）设x1，x2是f（x）的两个零点，证明：x1+x2＞6．请考生在第22、23二题中任选一题作答，如果多做，则按所做的第一题记分.解答时请写清题号.[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，直线l的参数方程为；在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为（1）若a＝1，求C与l交点的直角坐标；（2）若C上的点到l的距离的最大值为，求a．[选修4-5：不等式选讲]23．已知函数f（x）＝|x﹣1|﹣|x﹣a|．（1）当a＝﹣2时，求不等式0＜f（x）≤3的解集；（2）若a≤0，∃x∈（0，+∞）使f（x）≤a2﹣3成立，求a的取值范围．参考答案一、选择题（共12小题，每小题5分，满分60分）1．设复数z的共轭复数为，i为虚数单位，若z＝1﹣i，则（3+2）i＝（）A．﹣2﹣5i B．﹣2+5i C．2+5i D．2﹣5i【分析】把z＝1﹣i代入（3+2）i，再由复数代数形式的乘除运算化简得答案．解：由z＝1﹣i，得（3+2）i＝（3+2+2i）i＝（5+2i）i＝﹣2+5i．故选：B．2．已知集合M＝{x|x2﹣2x﹣3＜0}，N＝{x|x2﹣mx＜0}，若M∩N＝{x|0＜x＜1}，则m的值为（）A．1B．﹣1C．±1D．2【分析】可以求出M＝{x|﹣1＜x＜3}，从而可以根据M∩N＝{x|0＜x＜1}即可得出N＝{x|0＜x＜m}，从而得出m＝1．解：∵M＝{x|﹣1＜x＜3}，N＝{x|x2﹣mx＜0}，M∩N＝{x|0＜x＜1}，∴N＝{x|0＜x＜m}，∴m＝1．故选：A．3．已知等差数列{a n}中，S n为其前n项的和，S4＝24，S9＝99，则a7＝（）A．13B．14C．15D．16【分析】由已知结合等差数列的求和公式可求d，a1，然后结合等差数列的通项公式即可求解．解：因为S4＝24，S9＝99，，解可得，a1＝3，d＝2则a7＝a1+6d＝15．故选：C．4．如图所示，四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形，若直角三角形中较小的锐角为θ，现在向该正方形区域内随机地投掷一枚飞镖，则飞镖落在小正方形内的概率是（）A．1﹣sin 2θB．C．1﹣sinθD．【分析】分别求出小正方形的面积及大正方形的面积，然后根据几何概率的求解公式即可．解：由题意可知，小正方形的边长为2（cosθ﹣sinθ），面积S1＝4（cosθ﹣sinθ）2＝4（1﹣sin2θ），大正方形的面积S＝2×2＝4，故镖落在小正方形内的概率P＝（1﹣sin2θ）．故选：A．5．函数f（x）＝ln|x|+|sin x|（﹣π≤x≤π且x≠0）的图象大致是（）A．B．C．D．【分析】利用函数的奇偶性排除选项，通过函数的导数求解函数的极值点的个数，求出f（π）的值，推出结果即可．解：函数f（x）＝ln|x|+|sin x|（﹣π≤x≤π且x≠0）是偶函数排除A．当x＞0时，f（x）＝lnx+sin x，可得：f′（x）＝+cos x，令+cos x＝0，作出y＝与y＝﹣cos x图象如图：可知两个函数有一个交点，就是函数有一个极值点．f（π）＝lnπ＞1，故选：B．6．从6名女生3名男生中，选出3名学生组成课外小组，如果按性别比例分层抽样，则不同的抽取方法数为（）A．45种B．120 种C．30种D．63种【分析】6名女生3名男生中，选出3名学生组成课外小组，根据分层抽样要求，应选出2名女生，1名男生．利用组合数的意义、乘法原理即可得出．解：6名女生3名男生中，选出3名学生组成课外小组，根据分层抽样要求，应选出2名女生，1名男生．∴不同的抽取方法数＝•＝45．故选：A．7．已知一个三棱锥的三视图如图所示，其中俯视图是等腰直角三角形，则该三棱锥的外接球表面积（）A．B．2C．4D．12π【分析】首先把三视图转换为几何体，进一步利用几何体的表面积公式的应用求出结果．解：根据几何体的三视图，把几何体转换为：所以：该几何体的球心为O，R＝，．故选：D．8．设F1，F2分别是椭圆E的左、右焦点，过点F1的直线交椭圆E于A，B两点，A在x轴上方，且满足|AF1|＝3|F1B|，，则A点位于（）A．第一象限B．第二象限C．y轴上D．都有可能【分析】设|BF2|＝k，题意开发其他的焦半径的值，再由余弦定理可得a与k的关系，进而可得|AF2|＝3k＝|AF1|，可得A在y轴上．解：设|BF1|＝k，则|AF1|＝3k由椭圆的定义可得：|AF2|＝2a﹣3k，|BF2|＝2a﹣k，|AB|＝4k，在△ABF2中，由余弦定理可得：|AB|2＝|AF2|2+|BF﹣2|AF2|•|BF2|cos∠AF2B，即16k2＝（2a﹣3k）2+（2a﹣k）2﹣2（2a﹣3k）（2a﹣k），整理可得a＝3k，所以|AF2|＝3k＝|AF1|，|BF2|＝5k，F1A⊥F2A，即△AF1F2为等腰直角三角形，所以A在y轴上，故选：C．9．已知函数，函数y＝f（x）﹣a有四个不同的零点，从小到大依次为x1，x2，x3，x4，则x1+x2+x3+x4的最大值为（）A．1+e B．4+e C．1﹣e D．1+2e【分析】作出函数f（x）的图象，结合题意，利用根与系数的关系利用函数的单调性得解．解：若函数y＝f（x）﹣a有四个不同的零点，则有a∈（1，e]，当x＞0时，f（x）＝x+﹣3≥2﹣3＝1，可得f（x）在x＞2递增，在0＜x＜2处递减，由f（x）＝，x≤0，x＜﹣1时，f（x）递减；﹣1＜x＜0时，f（x）递增，可得x＝﹣1处取得极小值1，作出f（x）的图象，以及直线y＝a，可得＝＝＝，即有x1+1+x2+1＝0，可得x1+x2＝﹣2，x3，x4是方程﹣3＝a的两根，即x2﹣（3+a）x+4＝0的两个根，∴x3+x4＝3+a，则x1+x2+x3+x4＝﹣2+3+a＝a+1≤e+1，故最大值为e+1，故选：A．10．O为△ABC内一点，且，若B，O，D三点共线，则t的值为（）A．B．C．D．【分析】根据即可得出，而根据B，O，D三点共线，可设，从而可得出，这样根据平面向量基本定理即可得出，解出t即可．解：由得，，∴，∵B，O，D三点共线，∴可设，且，∴，∴，解得．故选：D．11．已知F1、F2分别是双曲线（a＞0，b＞0）的左、右焦点，过点F2与双曲线的一条渐近线平行的直线交叉双曲线另一条渐近线于点M，若点M在以线段F1F2为直径的圆内，则双曲线离心的取值范围是（）A．（，+∞）B．（2，+∞）C．（，2）D．（1，2）【分析】确定M，F1，F2的坐标，进而由•＜0，结合a、b、c的关系可得关于ac的不等式，利用离心率的定义可得范围．解：设直线方程为y＝（x﹣c），与双曲线（a＞0，b＞0）联立，可得交点坐标为P（，﹣）∵F1（﹣c，0），F2（c，0），∴＝（﹣，），＝（，），由题意可得•＜0，即＜0，化简可得b2＜3a2，即c2﹣a2＜3a2，故可得c2＜4a2，c＜2a，可得e＝＜2，∵e＞1，∴1＜e＜2故选：D．12．定义在R上的偶函数f（x）的导函数为f′（x），且当x＞0时，xf′（x）+2f（x）＜0．则（）A．B．9f（3）＞f（1）C．D．【分析】构造函数g（x）＝x2f（x），结合已知条件及导数与单调性关系可判断g（x）的单调性及奇偶性，从而可求解．解：令g（x）＝x2f（x），当x＞0时，xf′（x）+2f（x）＜0，则g′（x）＝2xf（x）+x2f′（x）＝x[2f（x）+f′（x）]＜0即g（x）在（0，+∞）上单调递减，因为f（﹣x）＝f（x），所以g（﹣x）＝（﹣x）2f（﹣x）＝x2f（x）＝g（x）即g（x）为偶函数，根据偶函数的对称性可知，g（x）在（﹣∞，0）上单调递增，g（e）＞g（3），所以＝，故选：D．二、填空题（共4小题，每小题5分，满分20分）13．设x，y满足，则z＝2x+y的最小值为﹣6．【分析】由约束条件作出可行域，数形结合得到最优解，求出最优解的坐标，代入目标函数得答案．解：由x，y满足作出可行域如图，化目标函数z＝2x+y为y＝﹣2x+z，由图可知，当直线y＝﹣2x+z过B（﹣2，﹣2）时直线在y轴上的截距最小，z最小z＝﹣2×2﹣2＝﹣6．故答案为：﹣6．14．在等比数列{a n}中，已知a2+a4＝8，a6+a8＝4，则a10+a12+a14+a16＝3．【分析】由已知结合等比数列的通项公式可求公比q，然后结合等比数列的性质即可求解．解：设等比数列的公比为q，则，解可得q4＝，所以a10+a12+a14+a16＝+（a6+a8）q8＝8×＝3．故答案为：3．15．“砥砺奋进的五年”，首都经济社会发展取得新成就．自2012年以来北京城乡居民收入稳步增长．随着扩大内需，促进消费等政策的出台，居民消费支出全面增长，消费结构持续优化升级，城乡居民人均可支配收人快速增长，人民生活品质不断提升．右图是北京市2012﹣2016年城乡居民人均可支配收人实际增速趋势图（例如2012年，北京城镇居民收人实际增速为7.3%，农村居民收人实际增速为8.2%）．从2012﹣2016五年中任选两年，则至少有一年农村和城镇居民收入实际增速均超过7%的概率为．【分析】设至少有一年农村和城镇居民实际收入增速均超7%为事件B，这五年中任选两年，利用列举法能出至少有一年农村和城镇居民收入实际增速均超过7%的概率．解：设至少有一年农村和城镇居民实际收入增速均超7%为事件B，这五年中任选两年，有（2012，2013），（2012，2014），（2012，2015），（2012，2016），（2013，2014），（2013，2015），（2013，2016），（2014，2015），（2014，2016），（2015，2016）共10种情况，其中至少有一年农村和城镇居民实际收入增速均超过7%的为前9种情况，所以至少有一年农村和城镇居民收入实际增速均超过7%的概率P（B）＝，故答案为：．16．在棱长为a的正方体内有一个和各面都相切的球，过正方体中两条互为异面直线的棱的中点作直线，则该直线被球面截在球内的弦长为．【分析】由题意画出图形，利用直线与圆的位置关系及垂径定理求解．解：如图，M，N是正方体中两条互为异面直线的棱的中点，直线MN与球O的表面交于E，F两点，连接MO，并延长交于P，则P为对棱的中点，取EF的中点G，则OG∥PN，且OG＝＝．在Rt△OGE中，OE＝，则EF＝2EG＝2．故答案为：．三、解答题（共5小题，满分60分）17．已知，2sin x），＝（sin，，函数．（1）求函数f（x）的零点；（2）已知在△ABC中，角A，B，C所对的边分别为a，b，c，且f（A）＝2，△ABC 的外接圆半径为，求△ABC周长的最大值．【分析】（1）根据向量数量积的定义求出f（x），结合零点的定义进行求解即可．（2）根据条件先求出A和a的大小，结合余弦定理，以及基本不等式的性质进行转化求解即可．解：（1）f（x）＝＝2cos x sin（x﹣）+2sin x cos（x﹣）＝2sin（2x﹣），由f（x）＝0得2x﹣＝kπ，k∈Z，得x＝+，即函数的零点为x＝+，k∈Z．（2）∵f（A）＝2，∴f（A）＝2sin（2A﹣）＝2，得sin（2A﹣）＝1，即2A﹣＝2kπ+，即A＝kπ+，在三角形中，当k＝0时，A＝，满足条件，∵△ABC的外接圆半径为，∴＝2，即a＝2×＝3，由余弦定理得a2＝b2+c2﹣2bc cos A＝b2+c2﹣bc＝（b+c）2﹣3bc≥＝（b+c）2﹣（b+c）2＝（b+c）2，即（b+c）2≤4×9＝36，即b+c≤6当且仅当b＝c时取等号，则a+b+c≤9，即三角形周长的最大值为9．18．如图，在平行四边形ABCD中，AB＝2，AD＝1，∠BAD＝60°，EDBF是矩形，DE ＝a，平面EDBF⊥平面ABCD．（1）若a＝1，求证：AE⊥CF；（2）若二面角A﹣EF﹣B的余弦值为，求a的值．【分析】（1）根据勾股定理判断AD⊥BD，AE⊥EF，AE⊥EC，得到AE⊥平面EFC，最后得出结论；（2）以D为原点，DA，DB，DE分别为x，y，z轴建立空间直角坐标系，求出平面AEF 和平面DEFB的法向量，利用夹角公式列方程，求出a．解：（1）连接AC，在三角形ABD中AB＝2，AD＝1，∠BAD＝60°，由余弦定理得BD＝，AD2+BD2＝AB2，故AD⊥BD，EDBF是矩形，DE＝1，平面EDBF⊥平面ABCD，故BF⊥平面ABCD，DE⊥平面ABCD，则AF＝，AE2+EF2＝AF2，故AE⊥EF，由AC＝，EC＝，AE＝，得AE2+EC2＝AC2，故AE⊥EC，EC∩EF＝E，所以AE⊥平面EFC，FC⊂平面EFC，所以AE⊥FC；（2）以D为原点，DA，DB，DE分别为x，y，z轴建立空间直角坐标系，则A（1，0，0），E（0，0，a），F（0，），，设平面AEF的法向量为，由，得，平面DEFB的法向量为，由cos＜＞＝，得a＝．19．设动圆P（圆心为P）经过定点（0，2），被x轴截得的弦长为4，P的轨迹为曲线E．（1）求曲线E的方程；（2）直线l：y＝x+m（m∈R）与曲线E交于不同的两点A、B，线段AB的垂直平分线与y轴交于点M，若tan∠AMB＝﹣2，求m的值．【分析】（1）设动圆P的圆心为（x，y），半径为r，根据题意列出方程组化简即可得到曲线E的方程；（2）设A（x1，y1），B（x2，y2），线段AB的中点坐标C（x3，y3），M（0，y0），联立直线l与抛物线方程，利用韦达定理求出C的坐标为（2，4+m），利用弦长公式求出|AB|＝4，所以|AC|＝2，又y0＝6+m，所以|MC|＝，再利用二倍角的正切公式求出tan，所以tan∠AMC＝＝＝，即可解出m的值．解：（1）设动圆P的圆心为（x，y），半径为r，被x轴截得的弦长为|AB|，依题意得：，化简整理得：x2＝4y，∴曲线E的方程为：x2＝4y；（2）设A（x1，y1），B（x2，y2），线段AB的中点坐标C（x3，y3），M（0，y0），联立方程，整理得：，∴△＝16×2+4×4m＝32+16m＞0，∴m＞﹣2，∴，x1x2＝﹣4m，，∴，y3＝4+m，∴线段AB的中点C的坐标为（2，4+m），又|AB|＝＝＝4，∴|AC|＝2，又AB的垂直平分线方程为：y﹣（4+m）＝﹣，∴y0＝6+m，∴|MC|＝，∵CM垂直平分AB，∴∠AMB＝2∠AMC，又tan∠AMB＝＝﹣2，解得tan或﹣（舍去），∴在Rt△AMC中，tan∠AMC＝＝＝，∴m＝0，满足m＞﹣2，∴m的值为0．20．某种产品的质量以其质量指标值衡量，并依据质量指标值划分等级如表：M≥205质量指标值m m＜185185≤m＜205等级三等品二等品一等品从某企业生产的这种产品中抽取200件，检测后得到如右的频率分布直方图：（1）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一等品至少要占全部产品50%”的规定？（2）在样本中，按产品等级用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；（3）该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值X近似服从正态分布N（216，139），则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？【分析】（1）根据抽样调查数据，求得一等品所占比例的估计值为0.375，由于该估计值小于0.5，故不能认为该企业生产的这种产品符合“一等品至少要占全部产品50%”的规定；（2）由直方图知，一、二、三等品的频率，求得在样本中用分层抽样的方法抽取的8件产品中，一等品3件，二等品4件，三等品1件，然后利用古典概型概率计算公式求解；（3）求出“质量提升月”活动前，该企业这种产品的质量指标值的均值，再由“质量提升月”活动后，产品质量指标值X近似满足X～N（216，139），得质量指标的均值约为216，作差得答案．解：（1）根据抽样调查数据，一等品所占比例的估计值为0.260+0.090+0.025＝0.375．由于该估计值小于0.5，故不能认为该企业生产的这种产品符合“一等品至少要占全部产品50%”的规定；（2）由直方图知，一、二、三等品的频率分别为：0.375，0.5，0.125．故在样本中用分层抽样的方法抽取的8件产品中，一等品3件，二等品4件，三等品1件，再从这8件产品中抽取4件，一、二、三等品都有的情形由2种．①一等品2件，二等品1件，三等品1件．②一等品1件，二等品2件，三等品1件．P＝；（3）“质量提升月”活动前，该企业这种产品的质量指标值的均值约为：170×0.025+180×0.1+190×0.2+200×0.3+210×0.26+220×0.09+230×0.025＝200.4．“质量提升月”活动后，产品质量指标值X近似满足X～N（216，139），即质量指标的均值约为216．所以，“质量提升月”活动后的质量指标值的均值比活动前大约提升了15.6．21．已知函数f（x）＝x﹣2+ae x（e为自然对数的底数）（1）讨论f（x）的单调性；（2）设x1，x2是f（x）的两个零点，证明：x1+x2＞6．【分析】（1）对函数求导，然后结合导数与单调性的关系对a进行分类讨论确定导数符号，即可求解函数单调性；（2）由零点存在的条件，结合函数的性质，把所要证明的不等式转换为函数的单调性与大小关系的比较．解：（1）f′（x）＝1+ae x，当a≥0时，f′（x）＞0，则f（x）在R上单调递增，当a＜0时，令f′（x）＝0可得x＝ln（﹣），故函数的单调递增区间为（﹣），单调递减区间（ln（﹣），+∞），（2）证明：由f（x）＝0可得a＝，设g（x）＝，则，当x＜3时，g′（x）＜0，函数单调递减，当x＞3时，g′（x）＞0，函数单调递增，当x＝3时，g（x）取得最小值g（3）＝﹣，当x＞时，g（x）＜0，当x＜2时，g（x）＞0，不妨设x1＜x2，则x1∈（2，3），x2∈（3，+∞），所以6﹣x1＞3，且g（x）在（3，+∞）上单调递增，要证x1+x2＞6，只要证x2＞6﹣x1＞3，故只要证g（x2）＞g（6﹣x1），因为g（x1）＝g（x2）＝a，只要证g（x1））＞g（6﹣x1），即，即证（x1﹣4）+x﹣2＜0，令h（x）＝e2x﹣6（x﹣4）+x﹣2，2＜x＜3，则h′（x）＝e2x﹣6（2x﹣7）+1，令m（x）＝h′（x），则m′（x）＝4e2x﹣6（x﹣3）＜0，所以m（x）在（2，3）上单调及，h′（x）＞h′（3）＝0，故h（x）在（2，3）上单调递增，h（x）＜h（3）＝0，即e2x﹣6（x﹣4）+x﹣2＜0，从而：x1+x2＞6．请考生在第22、23二题中任选一题作答，如果多做，则按所做的第一题记分.解答时请写清题号.[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，直线l的参数方程为；在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为（1）若a＝1，求C与l交点的直角坐标；（2）若C上的点到l的距离的最大值为，求a．【分析】（1）求出曲线C的普通方程和当a＝1时，直线l的普通方程，列方程组能求出C与l的交点的直角坐标．（2）直线l的普通方程是x+y﹣1﹣a＝0，C上的点（2cos θ，sin θ）到l的距离为，由此利用C上的点到l的距离的最大值为，能求出a．解：（1）∵曲线C的极坐标方程为，∴曲线C的普通方程为，∵直线l的参数方程为，∴当a＝1时，直线l的普通方程为x+y﹣2＝0．由解得或从而C与l的交点的直角坐标是．（2）直线l的普通方程是x+y﹣1﹣a＝0，故C上的点（2cos θ，sin θ）到l的距离为，当a≥﹣1时，d的最大值为．由题设得，所以当a＜﹣1时，d的最大值为.由题设得，所以．综上，．[选修4-5：不等式选讲]23．已知函数f（x）＝|x﹣1|﹣|x﹣a|．（1）当a＝﹣2时，求不等式0＜f（x）≤3的解集；（2）若a≤0，∃x∈（0，+∞）使f（x）≤a2﹣3成立，求a的取值范围．【分析】（1）当a＝﹣2时，利用绝对值不等式得f（x）＝|x﹣1|﹣|x+2|≤|（x﹣1）﹣（x+2）|＝3，即f（x）≤3的解集为R；再由f（x）＞0，得|x﹣1|＞|x+2|，解之，即可得到不等式0＜f（x）≤3的解集；（2）当a≤0，x∈（0，+∞）时，可求得f（x）＝|x﹣1|﹣x+a的最小值为f（1）＝a﹣1，解不等式a2﹣3≥a﹣1即可得到答案．解：（1）当a＝﹣2时，因为f（x）＝|x﹣1|﹣|x+2|≤|（x﹣1）﹣（x+2）＝3，|所以f（x）≤3的解集为R；由f（x）＞0，得|x﹣1|＞|x+2|，解得x＜﹣，故不等式0＜f（x）≤3的解集为（﹣∞，﹣）；（2）当a≤0，x∈（0，+∞）时，f（x）＝|x﹣1|﹣x+a＝，则f（x）min＝f（1）＝a﹣1，故a2﹣3≥a﹣1，解得：a≥2或a≤﹣1，又a≤0，所以a≤﹣1．所以a的取值范围是（﹣∞，﹣1]．。
2020年高考模拟重庆市直属校(3月)高考(理科)数学模拟测试卷 含解析
2020年高考模拟高考数学模拟试卷（理科）（3月份）一、选择题1．设集合A＝{x|x2＜9}，B＝{﹣3，﹣2，﹣1，0，1，2}，则A∩B＝（）A．{0，1，2}B．{﹣1，0，1，2}C．{﹣2，﹣1，0，1，2}D．{﹣2，﹣1，0}2．设（1+i）（a+bi）＝2，其中a，b是实数，i为虚数单位，则|3a+bi|＝（）A．2B．C．D．3．已知数列{a n}是各项均为正数的等比数列，a1＝2，a3＝2a2+16，则log2a9＝（）A．15B．16C．17D．184．若实数x，y满足约束条件，则z＝x+y的最小值为（）A．﹣8B．﹣6C．1D．35．我国古代有着辉煌的数学研究成果，其中《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》有着丰富多彩的内容，是了解我国古代数学的重要文献．这5部专著中有3部产生于汉、魏、晋、南北朝时期．现拟从这5部专著中选择2部作为学生课外兴趣拓展参考书目，则所选2部专著中至少有一部不是汉、魏、晋、南北朝时期专著的概率为（）A．B．C．D．6．如图，四棱柱ABCD﹣A1B1C1D1中，ABCD为平行四边形，E，F分别在线段DB，DD1上，且，G在CC1上且平面AEF∥平面BD1G，则＝（）A．B．C．D．7．在直角坐标系xOy中，半径为lm的⊙C在t＝0时圆心C与原点O重合，⊙C沿x轴以1m/s的速度匀速向右移动，⊙C被y轴所截的左方圆弧长记为x，令y＝cos x，则y关于时间t（0≤t≤l，单位：s）的函数的图象大致为（）A．B．C．D．8．的展开式中，各二项式系数和为32，各项系数和为243，则展开式中x3的系数为（）A．40B．30C．20D．109．设函数f（x）＝cos（ωx+φ）（x∈R）（ω＞0，﹣π＜φ＜0）的部分图象如图所示，如果，x1≠x2，且f（x1）＝f（x2），则f（x1+x2）＝（）A．B．C．D．10．已知三棱锥P﹣ABC的四个顶点在球O的球面上，球O的半径为4，△ABC是边长为6的等边三角形，记△ABC的外心为O1．若三棱锥P﹣ABC的体积为则PO1＝（）A．B．C．D．11．设双曲线）的左顶点为A，右焦点为F（c，0），若圆A：（x+a）2+y2＝a2与直线bx﹣ay＝0交于坐标原点O及另一点E，且存在以O为圆心的圆与线段EF相切，切点为EF的中点，则双曲线的离心率为（）A．B．C．D．312．函数f（x）＝，若关于x的方程f2（x）﹣af（x）+a﹣a2＝0有四个不等的实数根，则a的取值范围是（）A．B．（﹣∞，﹣1）∪[1，+∞）C．（﹣∞，﹣1）∪{1}D．（﹣1，0）∪{1}二、填空题：（共4小题，每小题5分，共20分）13．已知向量与的夹角为120°，且，则＝．14．已知函数f（x）＝3|x﹣a|（a∈R）满足f（x）＝f（4﹣x），则实数a的值为．15．设各项均为正数的数列{a n}的前n项和S n满足S n2﹣（n2+n﹣2）S n﹣2（n2+n）＝0，n∈N*，则数列的前2020项和T2020＝．16．设抛物线y2＝2x的焦点为F，准线为1，弦AB过点F且中点为M，过点F，M分别作AB的垂线交l于点P，Q，若|AF|＝3|BF|，则|FP|•|MQ|＝．三、解答题：（共70分）17．在△ABC中，角A，B，C的对边分别为a，b，c，且满足．（Ⅰ）求角B的大小；（Ⅱ）若a＝4，且BC边上的高为，求△ABC的周长．18．如图，四边形ABCD为平行四边形，点E在AB上，AE＝2EB＝2，且DE⊥AB．以DE为折痕把△ADE折起，使点A到达点F的位置，且∠FEB＝60°．（Ⅰ）求证：平面BFC⊥平面BCDE；（Ⅱ）若直线DF与平面BCDE所成角的正切值为，求二面角E﹣DF﹣C的正弦值．19．为了保障某治疗新冠肺炎药品的主要药理成分在国家药品监督管理局规定的值范围内，武汉某制药厂在该药品的生产过程中，检验员在一天中按照规定从该药品生产线上随机抽取20件产品进行检测，测量其主要药理成分含量（单位：mg）．根据生产经验，可以认为这条药品生产线正常状态下生产的产品的主要药理成分含量服从正态分布N（μ，σ2）．在一天内抽取的20件产品中，如果有一件出现了主要药理成分含量在（μ﹣3σ，μ+3σ）之外的药品，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对本次的生产过程进行检查．（Ⅰ）下面是检验员在2月24日抽取的20件药品的主要药理成分含量：9.7810.049.9210.1410.049.2210.139.919.959.969.8810.019.989.9510.0510.059.9610.12经计算得＝x i＝9.96，s＝＝≈0.19其中x i为抽取的第i件药品的主要药理成分含量，i＝1，2，…，20．用样本平均数作为μ的估计值，用样本标准差s作为σ的估计值，利用估计值判断是否需对本次的生产过程进行检查？（Ⅱ）假设生产状态正常，记X表示某天抽取的20件产品中其主要药理成分含量在（μ﹣3σ，μ+3σ）之外的药品件数，求P（X＝1）及X的数学期望．附：若随机变量Z服从正态分布N（μ，σ2），则P（μ﹣3σ＜Z＜μ+3σ）≈0.9974，0.997419≈0.95．20．已知椭圆的左、右焦点分别为F1，F2，过点F1的直线与C 交于A，B两点．△ABF2的周长为，且椭圆的离心率为．（Ⅰ）求椭圆C的标准方程：（Ⅱ）设点P为椭圆C的下顶点，直线PA，PB与y＝2分别交于点M，N，当|MN|最小时，求直线AB的方程．21．已知函数f（x）＝e ax﹣x﹣1，且f（x）≥0．（Ⅰ）求a；（Ⅱ）在函数f（x）的图象上取定两点A（x1，f（x1）），B（x2，f（x2））（x1＜x2），记直线AB的斜率为k，问：是否存在x0∈（x1，x2），使f'（x0）＝k成立？若存在，求出x0的值（用x1，x2表示）；若不存在，请说明理由．请从下面所给的22、23两题中选定一题作答，并用2B铅笔在答题卡上将所选题目对应的题号方框涂黑，按所涂题号进行评分；不涂、多涂均按所答第一题评分；多答按所答第一题评分.[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，以O为极点，x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程为ρ2（cos2θ+3sin2θ）＝12，直线l的参数方程为（t为参数），直线l与曲线C交于M，N两点．（Ⅰ）若点P的极坐标为（2，π），求|PM|•|PN|的值；（Ⅱ）求曲线C的内接矩形周长的最大值．[选修4-5：不等式选讲]23．已知函数f（x）＝x|x﹣a|，a∈R．（Ⅰ）当f（2）+f（﹣2）＞4时，求a的取值范围；（Ⅱ）若a＞0，∀x，y∈（﹣∞，a]，不等式f（x）≤|y+3|+|y﹣a|恒成立，求a的取值范围．参考答案一、选择题：（共12小题，每小题5分，共60分）1．设集合A＝{x|x2＜9}，B＝{﹣3，﹣2，﹣1，0，1，2}，则A∩B＝（）A．{0，1，2}B．{﹣1，0，1，2}C．{﹣2，﹣1，0，1，2}D．{﹣2，﹣1，0}【分析】可以求出集合A，然后进行交集的运算即可．解：∵A＝{x|﹣3＜x＜3}，B＝{﹣3，﹣2，﹣1，0，1，2}，∴A∩B＝{﹣2，﹣1，0，1，2}．故选：C．2．设（1+i）（a+bi）＝2，其中a，b是实数，i为虚数单位，则|3a+bi|＝（）A．2B．C．D．【分析】根据复数的基本运算法则进行化简即可．解：由题意可知：，∴a＝1，b＝﹣1，∴3a+bi＝3﹣i，∴|3a+bi|＝|3﹣i|＝，故选：D．3．已知数列{a n}是各项均为正数的等比数列，a1＝2，a3＝2a2+16，则log2a9＝（）A．15B．16C．17D．18【分析】由等比数列的能项公式得2q2＝2×2q+16，且q＞0，解得q＝4，由此能求出log2a9的值．解：∵数列{a n}是各项均为正数的等比数列，a1＝2，a3＝2a2+16，∴2q2＝2×2q+16，且q＞0，解得q＝4，∴log2a9＝＝17．故选：C．4．若实数x，y满足约束条件，则z＝x+y的最小值为（）A．﹣8B．﹣6C．1D．3【分析】由题意作平面区域，），从而求最小值解：由题意作平面区域如下，由解得，A（﹣4，﹣2），z＝x+y经过可行域的A时，目标函数取得最小值．故z＝x+y的最小值是﹣6，故选：B．5．我国古代有着辉煌的数学研究成果，其中《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》有着丰富多彩的内容，是了解我国古代数学的重要文献．这5部专著中有3部产生于汉、魏、晋、南北朝时期．现拟从这5部专著中选择2部作为学生课外兴趣拓展参考书目，则所选2部专著中至少有一部不是汉、魏、晋、南北朝时期专著的概率为（）A．B．C．D．【分析】基本事件总数n＝＝10，所选2部专著中至少有一部不是汉、魏、晋、南北朝时期专著包含的基本事件个数m＝＝7，由此能求出所选2部专著中至少有一部不是汉、魏、晋、南北朝时期专著的概率．解：我国古代有着辉煌的数学研究成果，其中《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、《缉古算经》有着丰富多彩的内容，这5部专著中有3部产生于汉、魏、晋、南北朝时期．现拟从这5部专著中选择2部作为学生课外兴趣拓展参考书目，基本事件总数n＝＝10，所选2部专著中至少有一部不是汉、魏、晋、南北朝时期专著包含的基本事件个数m＝＝7，则所选2部专著中至少有一部不是汉、魏、晋、南北朝时期专著的概率为p＝＝．故选：B．6．如图，四棱柱ABCD﹣A1B1C1D1中，ABCD为平行四边形，E，F分别在线段DB，DD1上，且，G在CC1上且平面AEF∥平面BD1G，则＝（）A．B．C．D．【分析】推导出EF∥BD1，平面ADD1A1∥平面BCC1B1，由G在CC1上且平面AEF∥平面BD1G，得AF∥BG，从而＝＝．解：∵四棱柱ABCD﹣A1B1C1D1中，ABCD为平行四边形，E，F分别在线段DB，DD1上，且，∴EF∥BD1，平面ADD1A1∥平面BCC1B1，∵G在CC1上且平面AEF∥平面BD1G，∴AF∥BG，∴＝＝．故选：B．7．在直角坐标系xOy中，半径为lm的⊙C在t＝0时圆心C与原点O重合，⊙C沿x轴以1m/s的速度匀速向右移动，⊙C被y轴所截的左方圆弧长记为x，令y＝cos x，则y关于时间t（0≤t≤l，单位：s）的函数的图象大致为（）A．B．C．D．【分析】根据题意，由特殊值法分析：令t＝0、、1，求出对应的y的值，据此分析即可得答案．解：根据题意，⊙C的半径为1，则其周长l＝2π，当t＝0时，⊙C被y轴所截的左方圆弧长记为x＝π，此时y＝cosπ＝﹣1；当t＝时，⊙C被y轴所截的左方圆弧长记为x＝，此时y＝cos＝﹣＜0；当t＝1时，⊙C被y轴所截的左方圆弧长记为x＝2π，此时y＝cos2π＝1；据此排除BCD；故选：A．8．的展开式中，各二项式系数和为32，各项系数和为243，则展开式中x3的系数为（）A．40B．30C．20D．10【分析】由题意利用二项式系数的性质求出n、m的值，再利用二项展开式的通项公式，求出展开式中x3的系数．解：∵的展开式中，各二项式系数和为2n＝32，∴n＝5．再令x＝1，可得各项系数和为（m+1）5＝243＝35，∴m＝2，则展开式中的通项公式为T r+1＝•m5﹣r•，令5﹣＝3，可得r＝4，故展开式中x3的系数为•2＝10，故选：D．9．设函数f（x）＝cos（ωx+φ）（x∈R）（ω＞0，﹣π＜φ＜0）的部分图象如图所示，如果，x1≠x2，且f（x1）＝f（x2），则f（x1+x2）＝（）A．B．C．D．【分析】由周期求出ω，由五点法作图求出φ的值，可得f（x）的解析式，再利用余弦函数的图象的对称性求得x1+x2的值，可得f（x1+x2）的值．解：根据函数f（x）＝cos（ωx+φ）（x∈R）（ω＞0，﹣π＜φ＜0）的部分图象，可得＝﹣，∴ω＝2．再根据五点法作图可得2•+φ＝﹣，∴φ＝﹣，∴f（x）＝cos（2x﹣）．如果，x1≠x2，则2x1﹣∈（﹣，），2x2﹣∈（﹣，），∵f（x1）＝f（x2），∴2x1﹣+（2x2﹣）＝0，∴x1+x2＝，则f（x1+x2）＝cos（﹣）＝cos＝﹣cos＝﹣，故选：B．10．已知三棱锥P﹣ABC的四个顶点在球O的球面上，球O的半径为4，△ABC是边长为6的等边三角形，记△ABC的外心为O1．若三棱锥P﹣ABC的体积为则PO1＝（）A．B．C．D．【分析】由题意可得：S△ABC＝＝9，O1A＝2，O1O＝2．设点P到平面BAC的高为h，由＝×h×9，解得h．可得点P所在小圆⊙O2（⊙O1与⊙O2所在平面平行）上运动，即可得出．解：由题意可得：S△ABC＝＝9，O1A＝2，O1O＝2．设点P到平面BAC的高为h，由＝×h×9，解得h＝4．∴点P所在小圆⊙O2（⊙O1与⊙O2所在平面平行）上运动，OO2＝2．∴O2P＝2．∴PO1＝＝2．故选：D．11．设双曲线）的左顶点为A，右焦点为F（c，0），若圆A：（x+a）2+y2＝a2与直线bx﹣ay＝0交于坐标原点O及另一点E，且存在以O为圆心的圆与线段EF相切，切点为EF的中点，则双曲线的离心率为（）A．B．C．D．3【分析】联立．⇒E（﹣，﹣），由OE＝OF，e＝．解：联立．⇒E（﹣，﹣），∵OE＝OF，∴，∴4a4＝c4⇒e＝．故选：B．12．函数f（x）＝，若关于x的方程f2（x）﹣af（x）+a﹣a2＝0有四个不等的实数根，则a的取值范围是（）A．B．（﹣∞，﹣1）∪[1，+∞）C．（﹣∞，﹣1）∪{1}D．（﹣1，0）∪{1}【分析】利用导数先判断出函数f（x）的图象，条件可转化为关于t的方程t2﹣at+a﹣a2＝0有两个实数根t1＝0，t2＝1或t1∈（0，1），t2∈（﹣∞，0）∪（1，+∞），分情况讨论即可解：当x≥0时，f′（x）e1﹣x（1﹣x），所以当0＜x＜1时，f′（x）＞0，f（x）单调递增；当x＞1时，f′（x）＜0，f（x）单调递减，且f（0）＝0，当x→+∞时，f（x）→0，当x＜0时，f（x）单调递减，所以f（x）的图象如图所示：令t＝f（x），则由上图可知当t＝0或1时，方程t＝f（x）有两个实根；当t∈（0，1）时，方程t＝f（x）有3个实数根；当t∈（﹣∞，0）∪（1，+∞）时，方程t＝f（x）有一个实数根，所以关于x的方程程f2（x）﹣af（x）+a﹣a2＝0有四个不等的实数根等价于关于t的方程t2﹣at+a﹣a2＝0有两个实数根t1＝0，t2＝1或t1∈（0，1），t2∈（﹣∞，0）∪（1，+∞），当t1＝0，t2＝1时，a＝1，当t1∈（0，1），t2∈（﹣∞，0）∪（1，+∞）时，（02﹣a×0+a﹣a2）（12﹣a×1+a﹣a2）＜0，解得﹣1＜a＜0，综上所述，a∈（﹣1，0）∪{1}．故选：D．二、填空题：（共4小题，每小题5分，共20分）13．已知向量与的夹角为120°，且，则＝﹣5．【分析】由题意可得向量的模长，再直接代入数量积可得．解：因为向量与的夹角为120°，且，所以：||＝＝；则＝××cos120°＝10×（﹣）＝﹣5；故答案为：﹣5．14．已知函数f（x）＝3|x﹣a|（a∈R）满足f（x）＝f（4﹣x），则实数a的值为2．【分析】结合指数函数的性质，建立指数方程进行求解即可．解：∵f（x）＝f（4﹣x），∴函数关于x＝2对称，即f（a）＝f（4﹣a），即3|a﹣a|＝3|4﹣a﹣a|，即30＝3|4﹣2a|即|4﹣2a|＝0，得2a﹣4＝0，得a＝2，故答案为：215．设各项均为正数的数列{a n}的前n项和S n满足S n2﹣（n2+n﹣2）S n﹣2（n2+n）＝0，n∈N*，则数列的前2020项和T2020＝．【分析】本题先对题干中的等式进行因式分解，根据题意可得S n的表达式，然后根据公式a n＝可计算出数列{a n}的通项公式，即可计算出数列的通项公式，然后运用裂项相消法即可计算出前2020项和T2020的值．解：依题意，由S n2﹣（n2+n﹣2）S n﹣2（n2+n）＝0，n∈N*，可得[S n﹣（n2+n）]（S n+2）＝0．∵数列{a n}的各项均为正数，∴S n＞0．∴S n＝n2+n，n∈N*．当n＝1时，a1＝S1＝12+1＝2，当n≥2时，a n＝S n﹣S n﹣1＝n2+n﹣[（n﹣1）2+（n﹣1）]＝2n．∴a n＝2n，n∈N*．∴＝＝（﹣）．∴T2020＝++…+＝（1﹣）+（﹣）+…+（﹣）＝（1﹣+﹣+…+﹣）＝（1﹣）＝．故答案为：．16．设抛物线y2＝2x的焦点为F，准线为1，弦AB过点F且中点为M，过点F，M分别作AB的垂线交l于点P，Q，若|AF|＝3|BF|，则|FP|•|MQ|＝．【分析】作BF⊥l于F，作AE⊥l于E，令准线于x轴交点为S，AB交准线于K．设BH＝m，则AF＝3m，可得∠HKB＝，FK＝2，QM＝MK•tan30°＝4m×tan30°．＝，即可求解．解：如图，作BF⊥l于F，作AE⊥l于E，令准线于x轴交点为S，AB交准线于K．设BH＝m，则AF＝3m，∵，∴BK＝2m则sin∠HKB＝，∴∠HKB＝30°．∵，∴，∴，∴FK＝2．∴．QM＝MK•tan30°＝4m×tan30°．＝则|FP|•|MQ|＝．故答案为：．三、解答题：（共70分）17．在△ABC中，角A，B，C的对边分别为a，b，c，且满足．（Ⅰ）求角B的大小；（Ⅱ）若a＝4，且BC边上的高为，求△ABC的周长．【分析】（Ⅰ）由正弦定理，两角和到正弦函数公式化简已知等式可得sin A cos B＝sin B sin A，结合sin A＞0，可得cos B＝sin B，结合范围B∈（0，π），可求B的值．（Ⅱ）由已知可求c的值，在△ABC中，由余弦定理可求b到值，即可得解△ABC的周长．解：（Ⅰ）∵．∴由正弦定理可得：sin C＝sin B（cos A+sin A），∵sin C＝sin（A+B）＝sin A cos B+cos A sin B，∴可得：sin A cos B＝sin B sin A，∵A∈（0，π），sin A＞0，∴cos B＝sin B，∵B∈（0，π），∴tan B＝，B＝．（Ⅱ）如图，AD＝，B＝，则c＝AB＝＝2，又a＝4，在△ABC中，由余弦定理b2＝a2+c2﹣2ac cos B＝4，可得b＝2，可得△ABC的周长为a+b+c＝6+2．18．如图，四边形ABCD为平行四边形，点E在AB上，AE＝2EB＝2，且DE⊥AB．以DE为折痕把△ADE折起，使点A到达点F的位置，且∠FEB＝60°．（Ⅰ）求证：平面BFC⊥平面BCDE；（Ⅱ）若直线DF与平面BCDE所成角的正切值为，求二面角E﹣DF﹣C的正弦值．【分析】（Ⅰ）由DE⊥AB，得DE⊥EB，DE⊥EF，从而DE⊥平面BEF，进而DE⊥BF，FB⊥EB，BF⊥平面BCDE，由此能证明平面BFC⊥平面BCDE．（Ⅱ）以B为原点，BA为x轴，在平面ABCD中过点B作AB的垂线为y轴，BF为z 轴，建立空间直角坐标系，利用向量法能求出二面角E﹣DF﹣C的正弦值．解：（Ⅰ）证明：∵DE⊥AB，∴DE⊥EB，DE⊥EF，∴DE⊥平面BEF，∴DE⊥BF，∵AE＝2EB＝2，∴EF＝2，EB＝1，∵∠FEB＝60°，∴由余弦定理得BF＝＝，∴EF2＝EB2+BF2，∴FB⊥EB，由①②得BF⊥平面BCDE，∴平面BFC⊥平面BCDE．（Ⅱ）解：以B为原点，BA为x轴，在平面ABCD中过点B作AB的垂线为y轴，BF 为z轴，建立空间直角坐标系，设DE＝a，则D（1，a，0），F（0，0，），＝（﹣1，﹣a，），∵直线DF与平面BCDE所成角的正切值为，∴直线DF与平面BCDE所成角的正弦值为，平面BCDE的法向量＝（0，0，1），∴|cos＜＞|＝＝＝，解得a＝2，∴D（1，2，0），C（﹣2，2，0），∴＝（0，2，0），＝（﹣1，﹣2，），设平面EDF的法向量＝（x，y，z），则，取z＝1，得＝（），同理得平面DFC的一个法向量＝（0，，2），∴cos＜＞＝＝，∴二面角E﹣DF﹣C的正弦值为sin＜＞＝＝．19．为了保障某治疗新冠肺炎药品的主要药理成分在国家药品监督管理局规定的值范围内，武汉某制药厂在该药品的生产过程中，检验员在一天中按照规定从该药品生产线上随机抽取20件产品进行检测，测量其主要药理成分含量（单位：mg）．根据生产经验，可以认为这条药品生产线正常状态下生产的产品的主要药理成分含量服从正态分布N（μ，σ2）．在一天内抽取的20件产品中，如果有一件出现了主要药理成分含量在（μ﹣3σ，μ+3σ）之外的药品，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对本次的生产过程进行检查．（Ⅰ）下面是检验员在2月24日抽取的20件药品的主要药理成分含量：9.7810.049.9210.1410.049.2210.139.919.959.969.8810.019.989.9510.0510.059.9610.12经计算得＝x i＝9.96，s＝＝≈0.19其中x i为抽取的第i件药品的主要药理成分含量，i＝1，2，…，20．用样本平均数作为μ的估计值，用样本标准差s作为σ的估计值，利用估计值判断是否需对本次的生产过程进行检查？（Ⅱ）假设生产状态正常，记X表示某天抽取的20件产品中其主要药理成分含量在（μ﹣3σ，μ+3σ）之外的药品件数，求P（X＝1）及X的数学期望．附：若随机变量Z服从正态分布N（μ，σ2），则P（μ﹣3σ＜Z＜μ+3σ）≈0.9974，0.997419≈0.95．【分析】（I）由＝9.96，s＝0.19．可得：＝9.96，＝0.19，由样品数据看出有一样药品的主要药理成分（9.22）含量在（μ﹣3σ，μ+3σ）＝（9.39，10.53）之外的药品，即可判断出结论．（II）抽取的一件药品中其主要药理成分含量在（μ﹣3σ，μ+3σ）之内的概率为0.9974，而主要药理成分含量在（μ﹣3σ，μ+3σ）之内的概率为0.0026，可得X～B（20，0.0026），可得P（X＝1），及其E（X）．解：（I）由＝9.96，s＝0.19．可得：＝9.96，＝0.19，由样品数据看出有一样药品的主要药理成分（9.22）含量在（μ﹣3σ，μ+3σ）＝（9.39，10.53）之外的药品，因此需对本次的生产过程进行检查．（II）抽取的一件药品中其主要药理成分含量在（μ﹣3σ，μ+3σ）之内的概率为0.9974，而主要药理成分含量在（μ﹣3σ，μ+3σ）之内的概率为0.0026，故X～B（20，0.0026），∴P（X＝1）＝0.997419×0.0026≈0.0494．X的数学期望E（X）＝20×0.0026≈0.052．20．已知椭圆的左、右焦点分别为F1，F2，过点F1的直线与C 交于A，B两点．△ABF2的周长为，且椭圆的离心率为．（Ⅰ）求椭圆C的标准方程：（Ⅱ）设点P为椭圆C的下顶点，直线PA，PB与y＝2分别交于点M，N，当|MN|最小时，求直线AB的方程．【分析】（Ⅰ）由题意可得4a＝4，结合离心率即可求出c，再利用b2＝a2﹣c2即可求出b2，从而求出椭圆C的方程；（Ⅱ）点P（0，﹣1），F1（﹣1，0），设A（x1，y1），B（x2，y2），显然直线AB与x轴不重合，设直线AB的方程为：x＝my﹣1，则可知m≠﹣1，与椭圆方程联立，利用韦达定理可求|MN|＝6，当m＝0时，|MN|＝6，当m≠0时利用基本不等式求得|MN|的最小值为6＜6，在m＝1处取得，所以当|MN|最小时，直线AB的方程为：x＝y﹣1，即x﹣y+1＝0．解：（Ⅰ）由题意可得：4a＝4，，∴a＝，c＝1，∴b2＝a2﹣c2＝1，∴椭圆C的方程为：；（Ⅱ）点P（0，﹣1），F1（﹣1，0），设A（x1，y1），B（x2，y2），显然直线AB与x轴不重合，设直线AB的方程为：x＝my﹣1，则可知m≠﹣1，联立方程，消去y得：（m2+2）y2﹣2my﹣1＝0，∴，，直线PA的方程为：（y1+1）x﹣x1y﹣x1＝0，可得，同理，|MN|＝||＝3||＝3＝3＝6，当m＝0时，|MN|＝6，当m≠0时，|MN|＝6，由于m+∈（﹣∞，﹣2）∪[2，+∞），则，此时|MN|的最小值为6＜6，在m＝1处取得，综上所述，当|MN|最小时，直线AB的方程为：x＝y﹣1，即x﹣y+1＝0．21．已知函数f（x）＝e ax﹣x﹣1，且f（x）≥0．（Ⅰ）求a；（Ⅱ）在函数f（x）的图象上取定两点A（x1，f（x1）），B（x2，f（x2））（x1＜x2），记直线AB的斜率为k，问：是否存在x0∈（x1，x2），使f'（x0）＝k成立？若存在，求出x0的值（用x1，x2表示）；若不存在，请说明理由．【分析】（I）结合已知先对函数求导，然后结合已知导数可求函数的单调性，进而可求函数的最小值，解不等式可求；（II）结合直线的斜率公式及函数的性质及零点判定定理即可求解．解：（1）若a≤0，则对一切x＞0，f（x）＝）＝e ax﹣x﹣1＜0，不符合题意，若a＞0，f′（x）＝ae ax﹣1，令f′（x）＝ae ax﹣1＝0可得x＝，当x＜时，f′（x）＜0，函数f（x）单调递减，当x＞时，f′（x）＞0，函数f（x）单调递增，故当x＝﹣时，函数取得最小值f（﹣）＝，由题意可得，有≥0①，令g（t）＝t﹣tlnt﹣1，则g′（t）＝﹣lnt，当0＜t＜1时，g′（t）＞0，g（t）单调递增，当t＞1时，g′（t）＜0，g（t）单调递减，故当t＝1时，g（t）取得最大值g（1）＝0，当且仅当＝1即a＝1时①成立，综上a＝1；（II）由题意可知，k＝＝﹣1，令t（x）＝f′（x）﹣k＝e x﹣，则可知y＝t（x）在[x1，x2]上单调递增，且t（x1）＝[﹣（x2﹣x1）﹣1]，t（x2）＝[e﹣（x1﹣x2）﹣1]，由（I）可知f（x）＝e x﹣x﹣1≥0，x＝0时取等号，∴﹣（x2﹣x1）﹣1≥0，e﹣（x1﹣x2）﹣1≥0，∴t（x1）＜0，t（x2）＞0，由零点判定定理可得，存在x0∈（x1，x2），使得t（x0）＝0且，综上可得，存在x0∈（x1，x2），使f'（x0）＝k成立请从下面所给的22、23两题中选定一题作答，并用2B铅笔在答题卡上将所选题目对应的题号方框涂黑，按所涂题号进行评分；不涂、多涂均按所答第一题评分；多答按所答第一题评分.[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，以O为极点，x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程为ρ2（cos2θ+3sin2θ）＝12，直线l的参数方程为（t为参数），直线l与曲线C交于M，N两点．（Ⅰ）若点P的极坐标为（2，π），求|PM|•|PN|的值；（Ⅱ）求曲线C的内接矩形周长的最大值．【分析】（Ⅰ）直接利用转换关系的应用，把参数方程极坐标方程和直角坐标方程之间进行转换．（Ⅱ）利用一元二次方程根和系数关系式的应用和三角函数关系式的恒等变换和正弦型函数的性质的应用求出结果．解：（Ⅰ）曲线C的极坐标方程为ρ2（cos2θ+3sin2θ）＝12，转换为直角坐标方程为．点P的极坐标为（2，π），转换为直角坐标为（﹣2，0）由于点P（﹣2，0）在直线l 上，所以直线l的参数方程为（t为参数），转化为（t为参数），所以代入曲线的方程为，整理得，所以|PM|•|PN|＝|t1t2|＝4．（Ⅱ）不妨设Q（），（），所以该矩形的周长为4（）＝16sin（）．当时，矩形的周长的最大值为16．[选修4-5：不等式选讲]23．已知函数f（x）＝x|x﹣a|，a∈R．（Ⅰ）当f（2）+f（﹣2）＞4时，求a的取值范围；（Ⅱ）若a＞0，∀x，y∈（﹣∞，a]，不等式f（x）≤|y+3|+|y﹣a|恒成立，求a的取值范围．【分析】（1）求得关于a的不等式，由绝对值的意义，去绝对值，解不等式，求并集即可；（2）原不等式等价为f（x）max≤（|y+3|+|y﹣a|）min，运用家的孩子不等式的性质和二次函数的最值求法，分别求得最值，解不等式可得所求范围．解：（1）f（2）+f（﹣2）＞4，可得2|2﹣a|﹣2|2+a|＞4，即|a﹣2|﹣|a+2|＞2，则或或，解得a≤﹣2或﹣2＜a＜﹣1或a∈∅，则a的范围是（﹣∞，﹣1）；（2）f（x）≤|y+3|+|y﹣a|恒成立，等价为f（x）max≤（|y+3|+|y﹣a|）min，其中当x，y∈（﹣∞，a]，|y+3|+|y﹣a|≥|y+3+a﹣y|＝|a+3|＝a+3，当且仅当﹣3≤y≤a取得等号，而f（x）＝﹣x（x﹣a）＝﹣（x﹣）2+≤，当且仅当x＝a时取得等号．所以≤a+3，解得0＜a≤6．。
高考理科数学(1卷)：答案详细解析(最新)
2020年普通高等学校招生全国统一考试理科数学（I 卷）答案详解一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.（复数）若1z i =+,则22z z -=A.0B.1 D.2【解析】∵1z i =+，∴222(2)(1)(1)12z z z z i i i -=-=+-=-=-，∴2=22z z -.【答案】D2.（集合）设集合{}240A x x =-≤，{}20B x x a =+≤，且{}21A B x x =-≤≤ ，则a =A.－4B.－2C.2D.4【解析】由已知可得{}22A x x =-≤≤，2a B x x ⎧⎫=≤-⎨⎬⎩⎭，∵{}21A B x x =-≤≤ ，∴12a -=，解得2a =-.【答案】B 3.（立体几何，同文3）埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为A.14- B.12 C.14+ D.12+【解析】如图A3所示，设正四棱锥底面的边长为a ，则有22221212h am a h m ⎧=⎪⎪⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩整理得22420m am a --=，令m t a =，则有24210t t --=，∴114t +=，214t -=（舍去），即14m a +=.图A3【答案】C4.（解析几何）已知A 为抛物线2:2(0)C y px p =>上一点，点A 到C 的焦点的距离为12，到y 轴的距离为9，则p =A ．2B ．3C ．6D ．9【解析】设A 点的坐标为(m ,n )，∵点A 到C 的焦点的距离为12，∴m =9，∵点A 到C 的焦点的距离为12，∴122p m +=，解得6p =.【答案】C5.（概率统计，同文5）某校一个课外学习小组为研究某作物种子的发芽率y 和温度x （单位：C ）的关系，在20个不同的温度条件下进行种子的发芽实验，由实验数据,)(i i x y i =（1,2,…,20)得到下面的散点图：由此散点图，在10C 至40C 之间，下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是A.y a bx =+B.2y a bx =+C.x y a be =+D.ln y a b x=+【解析】根据散点图的趋势和已学函数图象可知，本题的回归方程类型为对数函数，故选D 选项.【答案】D6.（函数）函数43()2f x x x =-的图像在点(1,(1))f 处的切线方程为A ．21y x =--B ．21y x =-+C ．23y x =-D ．21y x =+【解析】32()46f x x x '=-，∴函数()f x 的图像在点(1,(1))f 处的切线斜率为(1)2k f '==-，又∵(1)1f =-，∴所求的切线方程为12(1)y x +=--，化简为21y x =-+.【答案】B7.（三角函数，同文7）设函数()cos()6f x x πω=+在[]ππ-，的图像大致如下图，则()f x 的最小正周期为A.109πB.76πC.43πD.32π【解析】∵函数过点4π,09⎛⎫- ⎪⎝⎭，∴4ππcos()=096x ω-+，∴4πππ=962x ω-+-，解得23=ω，∴()f x 的最小正周期为3π4π2==ωT .【答案】C 8.（概率统计）25()()y x x y x++的展开式中33x y 的系数为A.5 B.10 C.15 D.20【解析】∵5()x y +展开式的通项公式为55C r r r x y -(r =0,1,2,3,4,5)，∴1r =时，2141335C 5y x y x y x=，∴3r =时，323335C 10x x y x y =，∴展开式中的33x y 系数为5+10=15.【答案】C9.（三角函数）已知(0,)α∈π，且3cos28cos 5αα-=，则sin α=A.53 B.23 C.13 D.59【解析】应用二倍角公式2cos22cos 1αα=-，将3cos28cos 5αα-=化简为，23cos 4cos 40αα--=，解得2cos 3α=-或cos 2α=（舍去），又∵(0,)α∈π，∴5sin 3α=.【答案】A 10.（立体几何，同文12）已知A ，B ，C 为球O 的球面上的三个点，1O 为△ABC 的外接圆.若 1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为A ．64πB ．48πC ．36πD ．32π【解析】由题意可知， 1O 为的半径r =2，由正弦定理可知，24sin ==AB r C，则14sin 4sin 60==== OO AB C ，∴球O 的半径4R ==，∴球O 的表面积为24π64πR =．图A10【答案】A11.（解析几何）已知22:2220M x y x y +---= ，直线:20+=l x y ，p 为l 上的动点.过点p 作M 的切线PA ，PB ，切点为,A B ，当PM AB 最小时，直线AB 的方程为A.210x y --= B.210x y +-=C.210x y -+= D.210x y ++=【解析】222:(1)(1)2-+-= M x y ， M 的半径r =2，圆心(1,1)M ，由几何知识可知，⊥PM AB ，故1||||=2=||||2||2∆=⋅⋅==四边形APM APBM S PM AB S AP AM AP ，∴⋅PM AB 最小，即PM 最小，此时直线PM ⊥l ，即直线PM 的斜率为12=m k ，故直线PM 的方程为11(1)2-=-y x ，化简为1122=+y x ，∴直线PM 与l 的交点P 的坐标为(1,0)-P ，直线AB 为过点P 作 M 的切线所得切点弦AB 所在的直线，其方程为(11)(1)(01)(1)4---+--=x y ，化简得210++=x y ．图A11【答案】D注：过圆外一点00(,)P x y 作222:()()O x a y b r -+-= 的切线所得切点弦所在直线方程为200()()()()x a x a y b y b r --+--=.特别当0a b ==时，切点弦所在直线方程为200x x y y r +=.（具体推到过程，可到百度搜索）12.（函数）若242log 42log +=+a b a b 则A.a >2bB.a <2bC.a >b 2D.a <b 2【解析】由指数和对数运算性质，原等式可化为2222log 2log a b a b +=+，∵222log 1log log 2b b b <+=，∴22222log 2log 2b b b b +<+，∴2222log 2log 2a b a b +<+，设2()2log x f x x =+，则有()(2)f a f b <，由指数函数和对数函数的单调性可知()f x 在(0,)+∞单调递增，∴2a b <.【答案】B二、填空题：本题共4小题，每小题5分，共20分。
2020年北京市朝阳区高考数学一模试卷(理科)含答案解析
2020年北京市朝阳区高考数学一模试卷（理科）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．1．i是虚数单位，=（）A．1﹣i B．﹣1﹣i C．1+i D．﹣1+i2．已知全集U=R，函数y=ln（x﹣1）的定义域为M，集合N={x|x2﹣x＜0}，则下列结论正确的是（）A．M∩N=N B．M∩（∁U N）=∅C．M∪N=U D．M⊆（∁U N）3．“”是“e a＞e b”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件4．执行如图所示的程序框图，输出的S值为（）A．42 B．19 C．8 D．35．在△ABC中，角A，B，C，的对边分别为a，b，c，若（a2+c2﹣b2）tanB=ac，则角B的值为（）A．B．或C．D．或6．某工厂一年中各月份的收入、支出情况的统计如图所示，下列说法中错误的是（）（注：结余=收入﹣支出）A．收入最高值与收入最低值的比是3：1B．结余最高的月份是7月C．1至2月份的收入的变化率与4至5月份的收入的变化率相同D．前6个月的平均收入为40万元7．某三棱锥的三视图如图所示，则该三棱锥的体积是（）A．B．C．1 D．8．若圆x2+（y﹣1）2=r2与曲线（x﹣1）y=1没有公共点，则半径r的取值范围是（）A．0＜r＜B．0＜r＜C．0＜r＜D．0＜r＜二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．9．二项式（x2+）5的展开式中含x4的项的系数是_______（用数字作答）．10．已知等差数列{a n}（n∈N*）中，a1=1，a4=7，则数列{a n}的通项公式a n=_______；a2+a6+a10+…+a4n+10=_______．11．在直角坐标系xOy中，曲线C1的方程为x2+y2=2，曲线C2的参数方程为（t为参数）．以原点O为极点，x轴非负半轴为极轴，建立极坐标系，则曲线C1与C2的交点的极坐标为_______．12．不等式组所表示的平面区域为D．若直线y=a（x+1）与区域D有公共点，则实数a的取值范围是_______．13．已知M为△ABC所在平面内的一点，且．若点M在△ABC的内部（不含边界），则实数n的取值范围是_______．14．某班主任在其工作手册中，对该班每个学生用十二项能力特征加以描述．每名学生的第i（i=1，2，…，12）项能力特征用x i表示，，若学生A，B的十二项能力特征分别记为A=（a1，a2，…，a12），B=（b1，b2，…，b12），则A，B两名学生的不同能力特征项数为_______（用a i，b i表示）．如果两个同学不同能力特征项数不少于7，那么就说这两个同学的综合能力差异较大．若该班有3名学生两两综合能力差异较大，则这3名学生两两不同能力特征项数总和的最小值为_______．三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．已知函数，ω＞0．（Ⅰ）若ω=1，求f（x）的单调递增区间；（Ⅱ）若，求f（x）的最小正周期T的表达式并指出T的最大值．16．为了解学生暑假阅读名著的情况，一名教师对某班级的所有学生进行了调查，调查结果如表．1 2 3 4 5男生 1 4 3 2 2女生0 1 3 3 1（Ⅰ）从这班学生中任选一名男生，一名女生，求这两名学生阅读名著本数之和为4的概率？（Ⅱ）若从阅读名著不少于4本的学生中任选4人，设选到的男学生人数为X，求随机变量X的分布列和数学期望；（Ⅲ）试判断男学生阅读名著本数的方差与女学生阅读名著本数的方差的大小（只需写出结论）．17．如图，在直角梯形AA1B1B中，∠A1AB=90°，A1B1∥AB，AB=AA1=2A1B1=2．直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到，且使得平面AA1C1C⊥平面AA1B1B．M为线段BC的中点，P为线段BB1上的动点．（Ⅰ）求证：A1C1⊥AP；（Ⅱ）当点P是线段BB1中点时，求二面角P﹣AM﹣B的余弦值；1（Ⅲ）是否存在点P，使得直线A1C∥平面AMP？请说明理由．18．已知函数f（x）=x+alnx，a∈R．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）当x∈[1，2]时，都有f（x）＞0成立，求a的取值范围；（Ⅲ）试问过点P（1，3）可作多少条直线与曲线y=f（x）相切？并说明理由．19．已知点和椭圆C：．（Ⅰ）设椭圆的两个焦点分别为F1，F2，试求△PF1F2的周长及椭圆的离心率；（Ⅱ）若直线l：与椭圆C交于两个不同的点A，B，直线PA，PB 与x轴分别交于M，N两点，求证：|PM|=|PN|．20．已知等差数列{a n}的通项公式．设数列{b n}为等比数列，且．（Ⅰ）若b1=a1=2，且等比数列{b n}的公比最小，（ⅰ）写出数列{b n}的前4项；（ⅱ）求数列{k n}的通项公式；（Ⅱ）证明：以b1=a2=5为首项的无穷等比数列{b n}有无数多个．2020年北京市朝阳区高考数学一模试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项．1．i是虚数单位，=（）A．1﹣i B．﹣1﹣i C．1+i D．﹣1+i【考点】复数代数形式的乘除运算．【分析】两个复数代数形式的乘除法，两个复数相除，分子和分母同时乘以分母的共轭复数，运算求得结果．【解答】解：===1+i，故选C．2．已知全集U=R，函数y=ln（x﹣1）的定义域为M，集合N={x|x2﹣x＜0}，则下列结论正确的是（）A．M∩N=N B．M∩（∁U N）=∅C．M∪N=U D．M⊆（∁U N）【考点】交、并、补集的混合运算．【分析】分别解出关于M，N的范围，然后判断即可．【解答】解：由x﹣1＞0，解得：x＞1，故函数y=ln（x﹣1）的定义域为M=（1，+∞），由x2﹣x＜0，解得：0＜x＜1，故集合N={x|x2﹣x＜0}=（0，1），∴∁U N={x|x≥1或x≤0}，∴M⊆（∁U N），故选：D．3．“”是“e a＞e b”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】“”等价于a＞b，可得“e a＞e b”，反之不成立，例如取a=2，b=﹣1．即可判断出结论．【解答】解：∵“”⇔a＞b⇒“e a＞e b”，反之不成立，例如取a=2，b=﹣1．∴“”是“e a＞e b”的充分不必要条件．故选：A．4．执行如图所示的程序框图，输出的S值为（）A．42 B．19 C．8 D．3【考点】程序框图．【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，依次写出每次循环得到的S，i的值，当i=4时不满足条件i＜4，退出循环，输出S的值为19．【解答】解：模拟执行程序，可得i=1，S=1满足条件i＜4，S=3，i=2满足条件i＜4，S=8，i=3满足条件i＜4，S=19，i=4不满足条件i＜4，退出循环，输出S的值为19．故选：B．5．在△ABC中，角A，B，C，的对边分别为a，b，c，若（a2+c2﹣b2）tanB=ac，则角B的值为（）A．B．或C．D．或【考点】余弦定理．【分析】利用余弦定理表示出cosB，整理后代入已知等式，利用同角三角函数间基本关系化简，求出sinB的值，即可确定出B的度数．【解答】解：∵cosB=，∴a2+c2﹣b2=2accosB，代入已知等式得：2ac•cosBtanB=ac，即sinB=，则B=或．故选：B．6．某工厂一年中各月份的收入、支出情况的统计如图所示，下列说法中错误的是（）（注：结余=收入﹣支出）A．收入最高值与收入最低值的比是3：1B．结余最高的月份是7月C．1至2月份的收入的变化率与4至5月份的收入的变化率相同D．前6个月的平均收入为40万元【考点】函数的图象与图象变化．【分析】根据折现统计图即可判断各选项．【解答】解：由图可知，收入最高值为90万元，收入最低值为30万元，其比是3：1，故A正确，由图可知，结余最高为7月份，为80﹣20=60，故B正确，由图可知，1至2月份的收入的变化率为与4至5月份的收入的变化率相同，故C正确，由图可知，前6个月的平均收入为（40+60+30+30+50+60）=45万元，故D错误，故选：D．7．某三棱锥的三视图如图所示，则该三棱锥的体积是（）A．B．C．1 D．【考点】由三视图求面积、体积．【分析】由三视图可知：该几何体为如图所示的三棱锥，CB⊥侧面PAB．利用体积计算公式即可得出．【解答】解：由三视图可知：该几何体为如图所示的三棱锥，CB⊥侧面PAB．该几何体的体积V=××1=．故选：A．8．若圆x2+（y﹣1）2=r2与曲线（x﹣1）y=1没有公共点，则半径r的取值范围是（）A．0＜r＜B．0＜r＜C．0＜r＜D．0＜r＜【考点】圆与圆锥曲线的综合．【分析】求得圆的圆心和半径，设圆与曲线y=相切的切点为（m，n），代入曲线的方程，求出函数的导数和切线的斜率，由两点的斜率公式和两直线垂直的条件：斜率之积为﹣1，解方程可得切点，进而得到此时圆的半径，结合图象即可得到所求范围．【解答】解：圆的圆心为（0，1），半径为r，设圆与曲线y=相切的切点为（m，n），可得n=，①y=的导数为y′=﹣，可得切线的斜率为﹣，由两点的斜率公式可得•（﹣）=﹣1，即为n﹣1=m（m﹣1）2，②由①②可得n4﹣n3﹣n﹣1=0，化为（n2﹣n﹣1）（n2+1）=0，即有n2﹣n﹣1=0，解得n=或，则有或．可得此时圆的半径r==．结合图象即可得到圆与曲线没有公共点的时候，r的范围是（0，）．故选：C．二、填空题：本大题共6小题，每小题5分，共30分．把答案填在答题卡上．9．二项式（x2+）5的展开式中含x4的项的系数是10（用数字作答）．【考点】二项式定理．【分析】先求出二项式（x2+）5的展开式中通项公式，令x的系数等于4，求出r的值，即可求得展开式中含x4的项的系数．【解答】解：二项式（x2+）5的展开式中通项公式为T r+1=x10﹣2r x﹣r=x10﹣3r．令10﹣3r=4，可得r=2，∴展开式中含x4的项的系数是=10，故答案为10．10．已知等差数列{a n}（n∈N*）中，a1=1，a4=7，则数列{a n}的通项公式a n=2n﹣1；a2+a6+a10+…+a4n+10=（n+3）（4n+11）．【考点】等差数列的前n项和．【分析】利用等差数列的通项公式求出首项和公差，由此能求出结果．【解答】解：∵等差数列{a n}（n∈N*）中，a1=1，a4=7，∴a4=1+3d=7，解得d=2，∴a n=1+（n﹣1）×2=2n﹣1，∴a2=1+2=3，a6=1+5×2=11，a6﹣a2=8，∴a2+a6+a10+…+a4n+10=×3+×8=（n+3）（4n+11）．故答案为：2n﹣1，（n+3）（4n+11）．11．在直角坐标系xOy中，曲线C1的方程为x2+y2=2，曲线C2的参数方程为（t 为参数）．以原点O为极点，x轴非负半轴为极轴，建立极坐标系，则曲线C1与C2的交点的极坐标为（，）．【考点】简单曲线的极坐标方程；直线与圆的位置关系．【分析】将曲线C2的参数方程代入曲线C1的方程，可得t=1，再由x=ρcosθ，y=ρsinθ，tanθ=，求得ρ，θ，即可得到所求坐标．【解答】解：将曲线C2的参数方程（t为参数）代入曲线C1的方程为x2+y2=2，可得（2﹣t）2+t2=2，解得t=1，可得交点的直角坐标为（1，1），由x=ρcosθ，y=ρsinθ，tanθ=，可得ρ==，tanθ=1，0＜θ＜，可得θ=．可得交点的极坐标为（，）．故答案为：（，）．12．不等式组所表示的平面区域为D．若直线y=a（x+1）与区域D有公共点，则实数a的取值范围是．【考点】简单线性规划．【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合进行求解即可．【解答】解：作出不等式组对应的平面区域图示：因为y=a（x+1）过定点C（﹣1，0）．当a≤0时，直线y=a（x+1）与区域D有公共点，满足条件．当a＞0时，当直线y=a（x+1）过点A时，由公共点，由得，即A（3，3），代入y=a（x+1）得4a=3，a=，又因为直线y=a（x+1）与平面区域D有公共点．此时0＜a≤．综上所述，a≤．故答案为：．13．已知M为△ABC所在平面内的一点，且．若点M在△ABC的内部（不含边界），则实数n的取值范围是（0，）．【考点】向量在几何中的应用．【分析】根据题意可作出图形，将，带入并进行向量的数乘运算便可以得出，这样根据向量加法的平行四边形法则及向量数乘的几何意义便可得到，从而便可得出实数n的取值范围．【解答】解：如图，由得：；∴；∴；∴；∴；∴实数n的取值范围是．故答案为：．14．某班主任在其工作手册中，对该班每个学生用十二项能力特征加以描述．每名学生的第i（i=1，2，…，12）项能力特征用x i表示，，若学生A，B的十二项能力特征分别记为A=（a1，a2，…，a12），B=（b1，b2，…，b12），则A，B两名学生的不同能力特征项数为（用a i，b i表示）．如果两个同学不同能力特征项数不少于7，那么就说这两个同学的综合能力差异较大．若该班有3名学生两两综合能力差异较大，则这3名学生两两不同能力特征项数总和的最小值为22．【考点】函数模型的选择与应用；分段函数的应用．【分析】根据A，B两名学生的每一项的特征数是否相同，进行求解计算即可．【解答】解：若第i（i=1，2，…，12）项能力特征相同，则差为0，特征不相同，绝对值为1，则用x i表示A，B两名学生的不同能力特征项数为=|a1﹣b1|+|b2﹣c2|+…+|c12﹣a12|=，设第三个学生为C=（c1，c2，…，c12），则d i=|a i﹣b i|+|b i﹣c i|+|c i﹣a i|，1≤i≤12，∵d i的奇偶性和（a i﹣b i）+（b i﹣c i）+（c i﹣a i）=0一样，∴d i是偶数，3名学生两两不同能力特征项数总和为S=d1+d2+…+d12为偶数，又S≥7×3=21．则S≥22，取A=（0，1，1，0，1，1，0，1，1，0，1，1），B=（1，0，1，1，0，1，1，0，1，1，0，1），C=（1，1，0，1，1，0，1，1，0，1，1，1），则不同能力特征数总和恰好为22，∴最小值为22，故答案为：，22三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．已知函数，ω＞0．（Ⅰ）若ω=1，求f（x）的单调递增区间；（Ⅱ）若，求f（x）的最小正周期T的表达式并指出T的最大值．【考点】三角函数中的恒等变换应用；三角函数的周期性及其求法；正弦函数的单调性．【分析】（Ⅰ）当ω=1时，利用两角和与差以及二倍角公式化简函数的解析式，然后求解函数的单调区间．（Ⅱ）化简函数的解析式为：f（x）=．通过，求出．然后求解T的最大值．【解答】（本小题满分13分）解：（Ⅰ）当ω=1时，==．令．解得．所以f（x）的单调递增区间是．…（Ⅱ）由==．因为，所以．则，n∈Z．解得．又因为函数f（x）的最小正周期，且ω＞0，所以当ω=时，T的最大值为4π．…16．为了解学生暑假阅读名著的情况，一名教师对某班级的所有学生进行了调查，调查结果如表．1 2 3 4 5男生 1 4 3 2 2女生0 1 3 3 1（Ⅰ）从这班学生中任选一名男生，一名女生，求这两名学生阅读名著本数之和为4的概率？（Ⅱ）若从阅读名著不少于4本的学生中任选4人，设选到的男学生人数为X，求随机变量X的分布列和数学期望；（Ⅲ）试判断男学生阅读名著本数的方差与女学生阅读名著本数的方差的大小（只需写出结论）．【考点】离散型随机变量的期望与方差；极差、方差与标准差；列举法计算基本事件数及事件发生的概率；离散型随机变量及其分布列．【分析】（Ⅰ）设事件A：从这个班级的学生中随机选取一名男生，一名女生，这两名学生阅读本数之和为4．由此能求出这两名学生阅读名著本数之和为4的概率．（Ⅱ）阅读名著不少于4本的学生共8人，其中男学生人数为4人，故X的取值为0，1，2，3，4．分别求出相应的概率，由此能求出随机变量X的分布列和数学期望．（Ⅲ）．【解答】（本小题满分13分）解：（Ⅰ）设事件A：从这个班级的学生中随机选取一名男生，一名女生，这两名学生阅读本数之和为4．由题意可知，．…（Ⅱ）阅读名著不少于4本的学生共8人，其中男学生人数为4人，故X的取值为0，1，2，3，4．由题意可得，，，，．所以随机变量X的分布列为X 0 1 2 3 4P随机变量X的均值．…（Ⅲ）．…17．如图，在直角梯形AA1B1B中，∠A1AB=90°，A1B1∥AB，AB=AA1=2A1B1=2．直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到，且使得平面AA1C1C⊥平面AA1B1B．M为线段BC的中点，P为线段BB1上的动点．（Ⅰ）求证：A1C1⊥AP；（Ⅱ）当点P是线段BB1中点时，求二面角P﹣AM﹣B的余弦值；1（Ⅲ）是否存在点P，使得直线A1C∥平面AMP？请说明理由．【考点】二面角的平面角及求法；直线与平面平行的判定；直线与平面垂直的性质．【分析】（Ⅰ）证明AC⊥AB．结合AC⊥AA1，证明AC⊥平面AA1B1B．推出A1C1⊥平面AA1B1B．即可证明A1C1⊥AP．（Ⅱ）以AC，AB，AA1为x轴、y轴、z轴建立空间直角坐标系，求出平面ABM的一个法向量，平面APM的一个法向量，利用空间向量的数量积求解二面角P﹣AM﹣B的余弦值．（Ⅲ）存在点P，使得直线A1C∥平面AMP．设P（x1，y1，z1），求出平面AMP的一个法向量，求出，利用．求出λ，即可证明结果．【解答】（本小题满分14分）解：（Ⅰ）证明：由已知∠A1AB=∠A1AC=90°，且平面AA1C1C⊥平面AA1B1B，所以∠BAC=90°，即AC⊥AB．又因为AC⊥AA1且AB∩AA1=A，所以AC⊥平面AA1B1B．由已知A1C1∥AC，所以A1C1⊥平面AA1B1B．因为AP⊂平面AA1B1B，所以A1C1⊥AP．…（Ⅱ）由（Ⅰ）可知AC，AB，AA1两两垂直．分别以AC，AB，AA1为x轴、y轴、z轴建立空间直角坐标系如图所示．由已知AB=AC=AA1=2A1B1=2A1C1=2，所以A（0，0，0），B（0，2，0），C（2，0，0），B1（0，1，2），A1（0，0，2）．因为M为线段BC的中点，P为线段BB1的中点，所以．易知平面ABM的一个法向量=（0，0，1）．设平面APM的一个法向量为=（x，y，z），由，得取y=2，得=（﹣2，2，﹣3）．由图可知，二面角P﹣AM﹣B的大小为锐角，所以===．所以二面角P﹣AM﹣B的余弦值为．…（Ⅲ）存在点P，使得直线A1C∥平面AMP．设P（x1，y1，z1），且，λ∈[0，1]，则（x1，y1﹣2，z1）=λ（0，﹣1，2），所以x1=0，y1=2﹣λ，z1=2λ．所以．设平面AMP的一个法向量为=（x0，y0，z0），由，得取y0=1，得（显然λ=0不符合题意）．又，若A1C∥平面AMP，则．所以．所以．所以在线段BB1上存在点P，且时，使得直线A1C∥平面AMP．…18．已知函数f（x）=x+alnx，a∈R．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）当x∈[1，2]时，都有f（x）＞0成立，求a的取值范围；（Ⅲ）试问过点P（1，3）可作多少条直线与曲线y=f（x）相切？并说明理由．【考点】利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．【分析】（Ⅰ）求出函数f（x）的定义域，函数的导函数，通过（1）当a≥0时，（2）当a ＜0时，当0＜x＜﹣a时，当x＞﹣a时，导函数的符号，判断函数的单调性．（Ⅱ）（1）当﹣a≤1时，（2）当1＜﹣a＜2时，（3）当﹣a≥2时，分别求解函数的最值．（Ⅲ）设切点为（x0，x0+alnx0），则切线斜率，求出切线方程，切线过点P（1，3），推出关系式，构造函数（x＞0），求出导函数，（1）当a＜0时，判断g（x）单调性，说明方程g（x）=0无解，切线的条数为0．（2）当a＞0时，类比求解，推出当a＞0时，过点P（1，3）存在两条切线．（3）当a=0时，f（x）=x，说明不存在过点P（1，3）的切线．【解答】解：（Ⅰ）函数f（x）的定义域为{x|x＞0}．．（1）当a≥0时，f′（x）＞0恒成立，函数f（x）在（0，+∞）上单调递增；（2）当a＜0时，令f′（x）=0，得x=﹣a．当0＜x＜﹣a时，f′（x）＜0，函数f（x）为减函数；当x＞﹣a时，f′（x）＞0，函数f（x）为增函数．综上所述，当a≥0时，函数f（x）的单调递增区间为（0，+∞）．当a＜0时，函数f（x）的单调递减区间为（0，﹣a），单调递增区间为（﹣a，+∞）．…（Ⅱ）由（Ⅰ）可知，（1）当﹣a≤1时，即a≥﹣1时，函数f（x）在区间[1，2]上为增函数，所以在区间[1，2]上，f（x）min=f（1）=1，显然函数f（x）在区间[1，2]上恒大于零；（2）当1＜﹣a＜2时，即﹣2＜a＜﹣1时，函数f（x）在[1，﹣a）上为减函数，在（﹣a，2]上为增函数，所以f（x）min=f（﹣a）=﹣a+aln（﹣a）．依题意有f（x）min=﹣a+aln（﹣a）＞0，解得a＞﹣e，所以﹣2＜a＜﹣1．（3）当﹣a≥2时，即a≤﹣2时，f（x）在区间[1，2]上为减函数，所以f（x）min=f（2）=2+aln2．依题意有f（x）min=2+aln2＞0，解得，所以．综上所述，当时，函数f（x）在区间[1，2]上恒大于零．…（Ⅲ）设切点为（x0，x0+alnx0），则切线斜率，切线方程为．因为切线过点P（1，3），则．即．…①令（x＞0），则．（1）当a＜0时，在区间（0，1）上，g′（x）＞0，g（x）单调递增；在区间（1，+∞）上，g′（x）＜0，g（x）单调递减，所以函数g（x）的最大值为g（1）=﹣2＜0．故方程g（x）=0无解，即不存在x0满足①式．因此当a＜0时，切线的条数为0．（2）当a＞0时，在区间（0，1）上，g′（x）＜0，g（x）单调递减，在区间（1，+∞）上，g′（x）＞0，g（x）单调递增，所以函数g（x）的最小值为g（1）=﹣2＜0．取，则．故g（x）在（1，+∞）上存在唯一零点．取，则=．设，u（t）=e t﹣2t，则u′（t）=e t﹣2．当t＞1时，u′（t）=e t﹣2＞e﹣2＞0恒成立．所以u（t）在（1，+∞）单调递增，u（t）＞u（1）=e﹣2＞0恒成立．所以g（x2）＞0．故g（x）在（0，1）上存在唯一零点．因此当a＞0时，过点P（1，3）存在两条切线．（3）当a=0时，f（x）=x，显然不存在过点P（1，3）的切线．综上所述，当a＞0时，过点P（1，3）存在两条切线；当a≤0时，不存在过点P（1，3）的切线．…19．已知点和椭圆C：．（Ⅰ）设椭圆的两个焦点分别为F1，F2，试求△PF1F2的周长及椭圆的离心率；（Ⅱ）若直线l：与椭圆C交于两个不同的点A，B，直线PA，PB 与x轴分别交于M，N两点，求证：|PM|=|PN|．【考点】直线与圆锥曲线的综合问题；椭圆的标准方程．【分析】（Ⅰ）利用椭圆的方程，求出a，b，c．通过椭圆的定义求解三角形的周长，求解椭圆的离心率．（Ⅱ）联立，利用直线l与椭圆C有两个交点，求出﹣4＜m＜0或0＜m＜4．设A（x1，y1），B（x2，y2），结合韦达定理，求解AB坐标，设直线PA与PB的斜率分别为k1，k2，推出k1+k2=0，即可证明|PM|=|PN|．【解答】解：（Ⅰ）由题意可知，a2=4，b2=2，所以c2=2．因为是椭圆C上的点，由椭圆定义得|PF1|+|PF2|=4．所以△PF1F2的周长为．易得椭圆的离心率．…（Ⅱ）证明：由得．因为直线l与椭圆C有两个交点，并注意到直线l不过点P，所以解得﹣4＜m＜0或0＜m＜4．设A（x1，y1），B（x2，y2），则，，，．显然直线PA与PB的斜率存在，设直线PA与PB的斜率分别为k1，k2，则======．因为k1+k2=0，所以∠PMN=∠PNM．所以|PM|=|PN|．…20．已知等差数列{a n}的通项公式．设数列{b n}为等比数列，且．（Ⅰ）若b1=a1=2，且等比数列{b n}的公比最小，（ⅰ）写出数列{b n}的前4项；（ⅱ）求数列{k n}的通项公式；（Ⅱ）证明：以b1=a2=5为首项的无穷等比数列{b n}有无数多个．【考点】等差数列与等比数列的综合．【分析】（Ⅰ）（ⅰ）写出数列{a n}的前若干项，观察可得等比数列{b n}的公比最小为4，即可得到所求；（ⅱ）由（ⅰ）可知{b n}的通项公式，由等差数列的通项公式可得．证明k n为正整数即可；（Ⅱ）设数列{c n}是数列{a n}中包含的一个无穷等比数列，求出c1，c2，求得公比q，只要证是数列{a n}的项，运用归纳法，即可得证．【解答】解：（Ⅰ）观察数列{a n}的前若干项：2，5，8，11，14，17，20，23，26，29，32，35，…．因为数列{a n}是递增的整数数列，且等比数列以2为首项，显然最小公比不能是，最小公比是4．（ⅰ）以2为首项，且公比最小的等比数列的前四项是2，8，32，128．（ⅱ）由（ⅰ）可知b1=2，公比q=4，所以．又，所以，即．再证k n为正整数．显然k1=1为正整数，n≥2时，，即，故为正整数．所以，所求通项公式为；（Ⅱ）证明：设数列{c n}是数列{a n}中包含的一个无穷等比数列，且，，所以公比．因为等比数列{c n}各项为整数，所以q为整数．取k2=5m+2（m∈N*），则q=3m+1，故．只要证是数列{a n}的项，即证3k n﹣1=5•（3m+1）n﹣1．只要证（n∈N*）为正整数，显然k1=2为正整数．又n≥2时，，即，又因为k1=2，5m（3m+1）n﹣2都是正整数，故n≥2时，k n也都是正整数．所以数列{c n}是数列{a n}中包含的无穷等比数列，其公比q=3m+1有无数个不同的取值，对应着不同的等比数列，故数列{a n}所包含的以a2=5为首项的不同无穷等比数列有无数多个．2020年9月12日。
2020年普通高等学校招生全国统一考试数学试题 理(全国卷1,含解析)
绝密★启用前2020年普通高等学校招生全国统一考试课标1理科数学2020年全国1高考数学与2020全国1高考数学难度方面相对持平，在选择题和填空题方面难度有所提升，解答题方面难度有所减缓.在保持稳定的基础上，进行适度创新，尤其是选择填空压轴题.试卷内容上体现新课程理念，贴近中学数学教学，坚持对基础性的考查，同时加大了综合性、应用性和创新性的考查，如理科第2、3、10、11、12、16、19题，文科第2、4、9、12、19题.1.体现新课标理念，重视对传统核心考点考查的同时，增加了对数学文化的考查，如理科第2题，文科第4题以中国古代的太极图为背景，考查几何概型.2.关注通性通法.试卷淡化了特殊的技巧，全面考查通性通法，体现了以知识为载体，以方法为依托，以能力考查为目的的命题要求.3.考查了数学思想、数学能力、数学的科学与人文价值，体现了知识与能力并重、科学与人文兼顾的精神.如理科第6、10、13、15题，文科第5、12、13、16题对数形结合思想的考查；理科第11，文科第9题对函数与方程思想的考查；理科第12、16题对数学的科学与人文价值的考查.4.体现了创新性，如理科第19题，文科第19题立意新、情景新、设问新，增强了学生数学应用意识和创新能力.命题趋势：（1）函数与导数知识：以函数性质为基础，考查函数与不等式综合知识，如理科第5题，；以基本初等函数为背景考查构造新函数解决比较大小问题，如理科第11题；对含参单调性以及零点问题的考查，如理科21题，比较常规.（2）三角函数与解三角形知识：对三角函数图像与性质的考查，如理科第9题；；对解三角形问题的考查，如理科第17题.重视对基础知识与运算能力的考查.（3）数列知识：对数列性质的考查，如理科第4题；突出了数列与现实生活的联系，考查学生分析问题的能力，如理科第12题，难点较大.整体考查比较平稳，没有出现偏、怪的数列相关考点.（4）立体几何知识：对立体几何图形的认识与考查，如理科第7题，试题难度不大，比较常规；对简单几何体的体积知识的考查，如理科第16题，用到函数知识进行解决，体现了综合性，难度较大，立体几何解答题的考查较常规，如理科对二面角的考查.（5）解析几何知识：对圆锥曲线综合知识的考查，如理科第15题，难度偏大；解答题考查较为常规，考查直线与圆锥曲线的位置关系，难度中等，重视对学生运算能力的考查.【试卷解析】一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A ={x |x <1}，B ={x |31x <}，则 A ．{|0}A B x x =<I B ．A B =R U C ．{|1}A B x x =>UD ．A B =∅I【答案】A2．如图，正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是A ．14 B ．π8 C ．12D ．π4【答案】B 【解析】试题分析：设正方形边长为a ，则圆的半径为2a ，则正方形的面积为2a ，圆的面积为24a π.由图形的对称性可知，太极图中黑白部分面积相等，即各占圆面积的一半.由几何概型概率的计算公式得，此点取自黑色部分的概率是221248a a ππ⋅=，选B. 秒杀解析：由题意可知，此点取自黑色部分的概率即为黑色部分面积占整个面积的比例，由图可知其概率1142p <<，故选B.【考点】几何概型【名师点睛】对于几何概型的计算，首先确定事件类型为几何概型并确定其几何区域（长度、面积、体积或时间），其次计算基本事件区域的几何度量和事件A 区域的几何度量，最后计算()P A . 3．设有下面四个命题1p ：若复数z 满足1z ∈R ，则z ∈R ；2p ：若复数z 满足2z ∈R ，则z ∈R ；3p ：若复数12,z z 满足12z z ∈R ，则12z z =；4p ：若复数z ∈R ，则z ∈R .其中的真命题为 A.13,p pB ．14,p pC ．23,p pD ．24,p p【答案】B4．记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为A ．1B ．2C ．4D ．8【答案】C 【解析】试题分析：设公差为d ，45111342724a a a d a d a d +=+++=+=，611656615482S a d a d ⨯=+=+=，联立112724,61548a d a d +=⎧⎨+=⎩解得4d =，故选C.秒杀解析：因为166346()3()482a a S a a +==+=，即3416a a +=，则4534()()24168a a a a +-+=-=，即5328a a d -==，解得4d =，故选C. 【考点】等差数列的基本量求解【名师点睛】求解等差数列基本量问题时，要多多使用等差数列的性质，如{}n a 为等差数列，若m n p q +=+，则m n p q a a a a +=+.5．函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足21()1x f --≤≤的x 的取值范围是 A ．[2,2]-B ．[1,1]-C ．[0,4]D ．[1,3]【答案】D6．621(1)(1)x x++展开式中2x 的系数为 A ．15B ．20C ．30D ．35【答案】C 【解析】试题分析：因为6662211(1)(1)1(1)(1)x x x x x++=⋅++⋅+，则6(1)x +展开式中含2x 的项为2226115C x x ⋅=，621(1)x x⋅+展开式中含2x 的项为44262115C x x x ⋅=，故2x 前系数为151530+=，选C. 【考点】二项式定理【名师点睛】对于两个二项式乘积的问题，第一个二项式中的每项乘以第二个二项式的每项，分析好2x 的项共有几项，进行加和.这类问题的易错点主要是未能分析清楚构成这一项的具体情况，尤其是两个二项式展开式中的r 不同.7．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10 B．12 C．14 D．16【答案】B8．右面程序框图是为了求出满足3n−2n>1000的最小偶数n，那么在和两个空白框中，可以分别填入A．A>1 000和n=n+1B．A>1 000和n=n+2C．A≤1 000和n=n+1D．A≤1 000和n=n+2【答案】D9．已知曲线C1：y=cos x，C2：y=sin (2x+2π3)，则下面结论正确的是A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2C．把C1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2D．把C1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2 【答案】D 【解析】试题分析：因为12,C C 函数名不同，所以先将2C 利用诱导公式转化成与1C 相同的函数名，则222:sin(2)cos(2)cos(2)3326C y x x x ππππ=+=+-=+，则由1C 上各点的横坐标缩短到原来的12倍变为sin 2y x =，再将曲线向左平移12π个单位得到2C ，故选D. 【考点】三角函数图像变换.【名师点睛】对于三角函数图像变换问题，首先要将不同名函数转换成同名函数，利用诱导公式，需要重点记住sin cos(),cos sin()22ππαααα=-=+；另外，在进行图像变换时，提倡先平移后伸缩，而先伸缩后平移在考试中经常出现，无论哪种变换，记住每一个变换总是对变量x 而言.10．已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为 A ．16B ．14C ．12D ．10【答案】A2222||sin cos()2p pDE παα==-，所以22222211||||4()cos sin cos sin p p AB DE αααα+=+=+ 2222222211sin cos 4()(cos sin )4(2)4(22)16cos sin cos sin αααααααα=++=++≥⋅+=11．设x 、y 、z 为正数，且235x y z ==，则A ．2x <3y <5zB ．5z <2x <3yC ．3y <5z <2xD ．3y <2x <5z【答案】D12．几位大学生响应国家的创业号召，开发了一款应用软件.为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推.求满足如下条件的最小整数N ：N >100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是 A ．440B ．330C ．220D ．110【答案】A【解析】试题分析：由题意得，数列如下：11,1,2,1,2,4,1,2,4,,2k -LL L则该数列的前(1)122k k k ++++=L 项和为 1(1)1(12)(122)222k k k k S k ++⎛⎫=+++++++=-- ⎪⎝⎭L L 要使(1)1002k k +>，有14k ≥，此时122k k ++<，所以2k +是之后的等比数列11,2,,2k +L 的部分和，即1212221t t k -+=+++=-L ，所以2314tk =-≥，则5t ≥，此时52329k =-=， 对应满足的最小条件为293054402N ⨯=+=，故选A. 【考点】等差数列、等比数列的求和.【名师点睛】本题非常巧妙的将实际问题和数列融合在一起，首先需要读懂题目所表达的具体含义，以及观察所给定数列的特征，进而判断出该数列的通项和求和.另外，本题的难点在于数列里面套数列，第一个数列的和又作为下一个数列的通项，而且最后几项并不能放在一个数列中，需要进行判断. 二、填空题：本题共4小题，每小题5分，共20分.13．已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则| a +2 b |= . 【答案】2314．设x，y满足约束条件2121x yx yx y+≤⎧⎪+≥-⎨⎪-≤⎩，则32z x y=-的最小值为.【答案】5-15．已知双曲线C：22221x ya b-=（a>0，b>0）的右顶点为A，以A为圆心，b为半径作圆A，圆A与双曲线C 的一条渐近线交于M、N两点.若∠MAN=60°，则C的离心率为________.23【考点】双曲线的简单性质.【名师点睛】双曲线渐近线是其独有的性质，所以有关渐近线问题受到出题者的青睐.做好这一类问题要抓住以下重点：①求解渐近线，直接把双曲线后面的1换成0即可；②双曲线的焦点到渐近线的距离是b；③双曲线的顶点到渐近线的距离是abc.16．如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形.沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥.当△ABC的边长变化时，所得三棱锥体积（单位：cm3）的最大值为_______.【答案】415【考点】简单几何体的体积【名师点睛】对于三棱锥最值问题，肯定需要用到函数的思想进行解决，本题解决的关键是设好未知量，利用图形特征表示出三棱锥体积.当体积中的变量最高次是2次时可以利用二次函数的性质进行解决，当变量是高次时需要用到求导得方式进行解决.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答. （一）必考题：共60分. 17．（12分）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为23sin a A（1）求sin B sin C ;（2）若6cos B cos C =1，a =3，求△ABC 的周长.【考点】三角函数及其变换.【名师点睛】在处理解三角形问题时，要注意抓住题目所给的条件，当题设中给定三角形的面积，可以使用面积公式建立等式，再将所有边的关系转化为角的关系，有时需将角的关系转化为边的关系；解三角形问题常见的一种考题是“已知一条边的长度和它所对的角，求面积或周长的取值范围”或者“已知一条边的长度和它所对的角，再有另外一个条件，求面积或周长的值”，这类问题通法思路是：全部转化为角的关系，建立函数关系式，如sin()y A x b ωϕ=++，从而求出范围，或利用余弦定理以及基本不等式求范围；求具体的值直接利用余弦定理和给定条件即可. 18.（12分）如图，在四棱锥P-ABCD 中，AB//CD ，且90BAP CDP ∠=∠=o .（1）证明：平面PAB ⊥平面PAD ；（2）若PA =PD =AB =DC ，90APD ∠=o ，求二面角A -PB -C 的余弦值.则3cos ,||||3⋅==-<>n m n m n m ， 所以二面角A PB C --的余弦值为33-. 【考点】面面垂直的证明，二面角平面角的求解【名师点睛】高考对空间向量与立体几何的考查主要体现在以下几个方面：①求异面直线所成的角，关键是转化为两直线的方向向量的夹角；②求直线与平面所成的角，关键是转化直线的方向向量和平面的法向量的夹角；③求二面角，关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键. 19．（12分）为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm ）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布2(,)N μσ．（1）假设生产状态正常，记X 表示一天内抽取的16个零件中其尺寸在(3,3)μσμσ-+之外的零件数，求(1)P X ≥及X 的数学期望；（2）一天内抽检零件中，如果出现了尺寸在(3,3)μσμσ-+之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．（ⅰ）试说明上述监控生产过程方法的合理性； （ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：9.95 10.12 9.969.96 10.01 9.92 9.98 10.04 10.269.9110.1310.029.2210.0410.059.95经计算得16119.9716i i x x ===∑，161622221111()(16)0.2121616i ii i s x x x x ===-=-≈∑∑，其中i x 为抽取的第i 个零件的尺寸，1,2,,16i =⋅⋅⋅．用样本平均数x 作为μ的估计值ˆμ，用样本标准差s 作为σ的估计值ˆσ，利用估计值判断是否需对当天的生产过程进行检查？剔除ˆˆˆˆ(3,3)μσμσ-+之外的数据，用剩下的数据估计μ和σ（精确到0.01）． 附：若随机变量Z 服从正态分布2(,)N μσ，则(33)0.997 4P Z μσμσ-<<+=，160.997 40.959 2=，0.0080.09≈．试题解析：（1）抽取的一个零件的尺寸在(3,3)μσμσ-+之内的概率为0.9974，从而零件的尺寸在(3,3)μσμσ-+之外的概率为0.0026，故~(16,0.0026)X B .因此(1)1(0)10.99740.0408P X P X ≥=-==-=.X 的数学期望为160.00260.0416EX =⨯=.20.（12分）已知椭圆C ：2222=1x y a b+（a >b >0），四点P 1（1,1），P 2（0,1），P 3（–1，32），P 4（1，32）中恰有三点在椭圆C 上. （1）求C 的方程；（2）设直线l 不经过P 2点且与C 相交于A ，B 两点.若直线P 2A 与直线P 2B 的斜率的和为–1，证明：l 过定点.（2）设直线P 2A 与直线P 2B 的斜率分别为k 1，k 2，如果l 与x 轴垂直，设l ：x =t ，由题设知0t ≠，且||2t <，可得A ，B 的坐标分别为（t ，24t -，（t ，24t -）. 则221242421t t k k ---++==-，得2t =，不符合题设. 从而可设l ：y kx m =+（1m ≠）.将y kx m =+代入2214x y +=得222(41)8440k x kmx m +++-=由题设可知22=16(41)0k m ∆-+>.设A （x 1，y 1），B （x 2，y 2），则x 1+x 2=2841kmk -+，x 1x 2=224441m k -+.而12121211y y k k x x --+=+121211kx m kx m x x +-+-=+ 1212122(1)()kx x m x x x x +-+=.由题设121k k +=-，故1212(21)(1)()0k x x m x x ++-+=.即222448(21)(1)04141m kmk m k k --+⋅+-⋅=++.解得12m k +=-. 当且仅当1m >-时，0∆>，欲使l ：12m y x m +=-+，即11(2)2m y x ++=--， 所以l 过定点（2，1-）【考点】椭圆的标准方程，直线与圆锥曲线的位置关系.【名师点睛】椭圆的对称性是椭圆的一个重要性质，判断点是否在椭圆上，可以通过这一方法进行判断；证明直线过定点的关键是设出直线方程，通过一定关系转化，找出两个参数之间的关系式，从而可以判断过定点情况.另外，在设直线方程之前，若题设中为告知，则一定要讨论直线斜率不存在和存在情况，接着通法是联立方程组，求判别式、韦达定理，根据题设关系进行化简. 21.（12分）已知函数2()(2)x xf x ae a e x =+--.（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围.（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分. 22．[选修4―4：坐标系与参数方程]（10分）在直角坐标系xOy 中，曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩（θ为参数），直线l 的参数方程为4,1,x a t t y t =+⎧⎨=-⎩（为参数）. （1）若a =−1，求C 与l 的交点坐标；（2）若C 上的点到l 17 a.【解析】试题分析：（1）先将曲线C 和直线l 化成普通方程，然后联立求出交点坐标；（2）直线l 的普通方程为440x y a +--=，设C 上的点(3cos ,sin )θθ，l 的距离为17d =.对a 进行讨23．[选修4—5：不等式选讲]（10分）已知函数f （x ）=–x 2+ax +4，g (x )=│x +1│+│x –1│.（1）当a =1时，求不等式f （x ）≥g （x ）的解集；（2）若不等式f （x ）≥g （x ）的解集包含[–1，1]，求a 的取值范围.【解析】试题分析：（1）将1a =代入，不等式()()f x g x ≥等价于2|1||1|40x x x x -+++--≤，对x 按1x <-，11x -≤≤，1x >讨论，得出最值的解集；（2）当[1,1]x ∈-时，()2g x =.若()()f x g x ≥的解集包含[1,1]-，。
2020年高考数学(理科)全国1卷高考模拟试卷(17)
2020年高考数学（理科）全国1卷高考模拟试卷（17）一．选择题（共12小题，满分60分，每小题5分）1．（5分）已知集合A ＝{x |x 2﹣x ﹣6＜0}，B ＝N ，则A ∩B ＝（ ） A ．{﹣1，0，1，2} B ．{0，1，2} C ．{﹣2，﹣1，0，1} D ．{0，1}2．（5分）已知i 是虚数单位，复数z 满足z⋅i 3+2i=1−i ，则z =（ ） A ．1+5iB ．﹣1﹣5iC ．1﹣5iD ．﹣1+5i3．（5分）已知平面α，直线m ，n 满足m ⊈α，n ⫋α，则“m ∥n ”是“m ∥α”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分也不必要条件4．（5分）已知数列{a n }满足a n +1•（1﹣a n ）＝1，且a 1=−12，则a 2020＝（ ） A ．3B ．−12C ．23D ．134525．（5分）根据如下样本数据：x 1 2 3 4 5 6 y54.53.532.52得到的线性回归方程为y =b x +a ，则（ ） A ．a ＞0，b ＜0B ．a ＞0，b ＞0C ．a ＜0，b ＜0D ．a ＜0，b ＞06．（5分）若直线y ＝ax +2a 与不等式组{x −y +6≥0x ≤3x +y −3≥0表示的平面区域有公共点，则实数a的取值范围是（ ） A ．[0，95]B ．[0，9]C ．[0，+∞]D ．[﹣∞，9]7．（5分）已知数列{a n }中，a 1=12，a n +1＝1−1a n，利用下面程序框图计算该数列的项时，若输出的是2，则判断框内的条件不可能是（ ）A ．n ≤2 015B ．n ≤2 018C ．n ≤2 020D ．n ≤2 0218．（5分）设向量CA →=2OB →，|OA →|＝2√5，OA →•OB →=1，则OA →•OC →=（ ） A ．14B ．16C ．18D ．209．（5分）函数f （x ）＝（3x ﹣3﹣x ）log 3x 2的图象大致为（ ）A ．B ．C ．D ．10．（5分）已知函数f(x)=2sinωx ⋅cos 2(ωx2−π4)−sin 2ωx +cosωx(ω＞0)的区间[0，π]上的最大值与最小值之和是0，则ω的最小值是（ ） A ．94B ．54C ．1D ．3411．（5分）若双曲线E ：x 2a 2−y 2b2=1(a ＞0，b ＞0)的一条渐近线被圆（x +3）2+y 2＝9所截得的弦长为3，则E 的离心率为（ ） A ．√2B ．√3C ．2D ．2√3312．（5分）已知定义在R 上的连续函数f （x ）满足f （x ）＝f （4﹣x ），且f （﹣2）＝0，f '（x ）为函数f （x ）的导函数，当x ＜2时，有f （x ）+f '（x ）＞0，则不等式x •f （x ）＞0的解集为（ ）A ．（0，6）B ．（﹣2，0）C ．（﹣∞，﹣2）D ．（﹣∞，﹣2）∪（0，6）二．填空题（共4小题，满分20分，每小题5分）13．（5分）已知抛物线y 2＝2px 的焦点为F ，准线与x 轴的交点为M ，N 为抛物线上的一点，且满足|MN |＝2|NF |，则∠NMF ＝ ． 14．（5分）若二项式(x −x)n的展开式中只有第4项的二项式系数最大，则展开式中常数项为 ．15．（5分）若无穷数列{cos （ωn ）}（ω∈R ）是等差数列，则其前10项的和为 ． 16．（5分）边长为1的正方体ABCD ﹣A 1B 1C 1D 1中，点M 为上底面A 1B 1C 1D 1的中心，N 为下底面ABCD 内一点，且直线MN 与底面ABCD 所成线面角的正切值为2，则点N 的轨迹围成的封闭图象的面积为 ．三．解答题（共5小题，满分60分，每小题12分）17．（12分）在三棱锥P ﹣ABC 中，AB ＝1，BC ＝2，AC =√5，PC =√2，P A =√5，PB =√6，E 是线段BC 的中点．（1）求点C 到平面APE 的距离d ； （2）求二面角P ﹣EA ﹣B 的余弦值．18．（12分）在平面直角坐标系xOy 中，设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且a +b =√3c ，2sin 2C ＝3sin A sin B ． （1）求C ；（2）设P （﹣1，cos A ），Q （﹣cos A ，1），且A ≤C ，OP →与OQ →的夹角为θ，求cos θ的值． 19．（12分）已知一堆产品中有一等品2件，二等品3件，三等品4件，现从中任取3件产品．（1）求一、二、三等品各取到一个的概率；（2）记X 表示取到一等品的件数，求X 的分布列和数学期望．20．（12分）已知椭圆C ：x 23+y 2b 2=1（b ＞0）的右焦点为F ，过F 作两条直线分别与圆O ：x 2+y 2＝r 2（r ＞0）相切于A ，B ，且△ABF 为直角三角形．又知椭圆C 上的点与圆O 上的点的最大距离为√3+1． （1）求椭圆C 及圆O 的方程；（2）若不经过点F 的直线l ：y ＝kx +m （其中k ＜0，m ＞0）与圆O 相切，且直线l 与椭圆C 交于P ，Q ，求△FPQ 的周长．21．（12分）已知函数f （x ）＝lnx ﹣x +2sin x ，f '（x ）为f （x ）的导函数． （Ⅰ）求证：f '（x ）在（0，π）上存在唯一零点； （Ⅱ）求证：f （x ）有且仅有两个不同的零点 四．解答题（共1小题，满分10分，每小题10分）22．（10分）在平面直角坐标系x 0y 中，直线l 1的参数方程为{x =t −√3y =kt （t 为参数），直线l 2的参数方程为{x =√3−my =m3k（m 为参数）．设直线l 1与l 2的交点为P ．当k 变化时点P 的轨迹为曲线C 1．（Ⅰ）求出曲线C 1的普通方程；（Ⅱ）以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，直线C 2的极坐标方程为ρsin(θ+π4)=3√2，点Q 为曲线C 1上的动点，求点Q 到直线C 2的距离的最大值． 五．解答题（共1小题）23．已知函数f （x ）＝|x +1|﹣|x ﹣2|． （1）求不等式f （x ）≥1的解集；（2）记f （x ）的最大值为m ，且正实数a ，b 满足1a+2b+12a+b=m ，求a +b 的最小值．2020年高考数学（理科）全国1卷高考模拟试卷（17）参考答案与试题解析一．选择题（共12小题，满分60分，每小题5分）1．（5分）已知集合A＝{x|x2﹣x﹣6＜0}，B＝N，则A∩B＝（）A．{﹣1，0，1，2}B．{0，1，2}C．{﹣2，﹣1，0，1}D．{0，1}【解答】解：∵A＝{x|x2﹣x﹣6＜0}＝[﹣2，3]，B＝N，则A∩B＝{0，1，2}．故选：B．2．（5分）已知i是虚数单位，复数z满足z⋅i3+2i=1−i，则z=（）A．1+5i B．﹣1﹣5i C．1﹣5i D．﹣1+5i【解答】解：因为z⋅i3+2i=1−i，所以z•i＝（1﹣i）•（3+2i）＝5﹣i，所以z=−1−5i，z−1+5i，故选：D．3．（5分）已知平面α，直线m，n满足m⊈α，n⫋α，则“m∥n”是“m∥α”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：m⊈α，n⫋α，“m∥n”⇒“m∥α”．∴m∥n”是“m∥α”的充分不必要条件．故选：A．4．（5分）已知数列{a n}满足a n+1•（1﹣a n）＝1，且a1=−12，则a2020＝（）A．3B．−12C．23D．13452【解答】解：数列{a n}满足a n+1•（1﹣a n）＝1，且a1=−1 2，a2=23，a3＝3，a4=−12，…，所以数列的周期为：3，则a2020＝a673×3+1＝a1=−1 2．故选：B．5．（5分）根据如下样本数据：x123456y 54.53.5 3 2.5 2得到的线性回归方程为y =b x +a ，则（ ） A ．a ＞0，b ＜0B ．a ＞0，b ＞0C ．a ＜0，b ＜0D ．a ＜0，b ＞0【解答】解：【方法一】根据表中数据，计算x =16×（1+2+3+4+5+6）＝3.5， y =16×（5+4.5+3.5+3+2.5+2）=4112≈3.4； 计算b =∑ 6i=1xi y i−6xy∑ 6i=1x i2−6x 2=(5+9+10.5+12+12.5+12)−6×3.5×3.4(1+4+9+16+25+36)−6×3.52≈−0.66＜0；a =y −b x =3.4﹣（﹣0.66）×3.5＝5.71＞0．【方法二】根据表中样本数据知，变量y 随x 的增大而减小， 所以线性回归方程y =b x +a 中，b ＜0； 又x ＞0，对应y ＞0，所以a ＞0． 故选：A ．6．（5分）若直线y ＝ax +2a 与不等式组{x −y +6≥0x ≤3x +y −3≥0表示的平面区域有公共点，则实数a的取值范围是（ ） A ．[0，95]B ．[0，9]C ．[0，+∞]D ．[﹣∞，9]【解答】解：画出不等式组表示的平面区域，如图所示 {x −y +6=0x +y −3=0⇒{x =−32y =92；∴C （−32，92），直线y ＝a （x +2）过定点A （﹣2，0），直线y ＝a （x +2）经过不等式组表示的平面区域有公共点 则a ＞0，k AC =92−0(−32)−(−2)=9，∴a ∈[0，9]． 故选：B ．7．（5分）已知数列{a n }中，a 1=12，a n +1＝1−1a n，利用下面程序框图计算该数列的项时，若输出的是2，则判断框内的条件不可能是（ ）A ．n ≤2 015B ．n ≤2 018C ．n ≤2 020D ．n ≤2 021【解答】解：因为a 1=12，a n +1＝1−1a n， 所以a 2=1−1a 1=1−2=−1，a 3=1−1a 2=1+1=2，a 4=1−1a 3=1−12=12， 所以数列{a n }是以3为周期的周期数列，循环的三项分别是12，−1，2，即输出的数字2是循环数列中的第三项，20153=671⋯⋯2，20183=672⋯⋯2，20203=673⋯⋯1，20213=673⋯⋯2，只有选项C 对应的余数是1，不是2， 故选：C ．8．（5分）设向量CA →=2OB →，|OA →|＝2√5，OA →•OB →=1，则OA →•OC →=（ ） A ．14B ．16C ．18D ．20【解答】解：∵CA →=OA →−OC →=2OB →， ∴OA →=2OB →+OC →，∴OA →2=OA →⋅(2OB →+OC →)=2OA →⋅OB →+OA →⋅OC →， ∴(2√5)2=2×1+OA →⋅OC →， ∴OA →⋅OC →=18． 故选：C ．9．（5分）函数f （x ）＝（3x ﹣3﹣x ）log 3x 2的图象大致为（ ）A ．B ．C ．D ．【解答】解：根据题意，函数f （x ）＝（3x ﹣3﹣x ）log 3x 2，其定义域为{x |x ≠0}， 且f （﹣x ）＝（3x ﹣3﹣x ）log 3x 2＝﹣（3x ﹣3﹣x ）log 3x 2）＝﹣f （x ），即函数f （x ）为奇函数，排除A 、C ，又由x →0时，（3x ﹣3﹣x ）→0，则f （x ）→0，排除D ；故选：B ．10．（5分）已知函数f(x)=2sinωx ⋅cos 2(ωx 2−π4)−sin 2ωx +cosωx(ω＞0)的区间[0，π]上的最大值与最小值之和是0，则ω的最小值是（ ） A ．94B ．54C ．1D ．34【解答】解：f(x)=2sinωx ⋅cos 2(ωx 2−π4)−sin 2ωx +cosωx(ω＞0) ＝2sin ωx ⋅1+cos(ωx−π2)2−1−cos2ωx 2+cosωx ＝sin ωx +sin ωx •sin ωx −12+12cos2ωx +cos ωx ＝sin ωx +sin 2ωx −12(1−cos2ωx)+cos ωx＝sin ωx +cos ωx =√2sin(ωx +π4)．由ωx +π4=π2+kπ，得x =π4ω+kπω，k ∈Z ； 由ωx +π4=3π2+kπ，得x =5π4ω+kπω，k ∈Z ． ∵f （x ）在区间[0，π]上的最大值与最小值之和是0，∴{π4ω≥05π4ω≤π，即ω≥54．∴ω的最小值是54．故选：B ．11．（5分）若双曲线E ：x 2a 2−y 2b2=1(a ＞0，b ＞0)的一条渐近线被圆（x +3）2+y 2＝9所截得的弦长为3，则E 的离心率为（ ） A ．√2B ．√3C ．2D ．2√33【解答】解：由圆C ：（x +3）2+y 2＝9可得圆心（﹣3，0），半径为3， 双曲线E ：x 2a 2−y 2b 2=1(a ＞0，b ＞0)的一条渐近线为：bx ﹣ay ＝0， 渐近线被圆（x +3）2+y 2＝9所截得的弦长为：3，圆心到直线的距离为：√a 2+b 2，由弦长公式可得32=√9−9b 2a 2+b 2，可得a 2a 2+b 2=14，即c 2a 2=4．可得e ＝2， 故选：C ．12．（5分）已知定义在R 上的连续函数f （x ）满足f （x ）＝f （4﹣x ），且f （﹣2）＝0，f '（x ）为函数f （x ）的导函数，当x ＜2时，有f （x ）+f '（x ）＞0，则不等式x •f （x ）＞0的解集为（ ） A ．（0，6） B ．（﹣2，0）C ．（﹣∞，﹣2）D ．（﹣∞，﹣2）∪（0，6）【解答】解：由f （x ）＝f （4﹣x ），且f （﹣2）＝0，可得f （6）＝0，且函数图象关于x ＝2对称，令g （x ）＝e x f （x ），则g ′（x ）＝e x [f （x ）+f ′（x ）]当，因为x ＜2时，有f （x ）+f '（x ）＞0，即g ′（x ）＞0，所以g （x ）在（﹣∞，2）上单调递增，根据函数的对称性可得f （x ）在（2，+∞）上单调递减，g （x ）的大致图象如图所示， 则不等式x •f （x ）＞0可化为x⋅g(x)e x＞0即x •g （x ）＞0，所以{x ＞0g(x)＞0，或{x ＜0g(x)＜0，可得，0＜x ＜6或x ＜﹣2．故不等式的解集（0，6）∪（﹣∞，﹣2） 故选：D ．二．填空题（共4小题，满分20分，每小题5分）13．（5分）已知抛物线y 2＝2px 的焦点为F ，准线与x 轴的交点为M ，N 为抛物线上的一点，且满足|MN |＝2|NF |，则∠NMF ＝π3．【解答】解：过点N 作NP ⊥准线，交准线于P ， 由抛物线定义知|NP |＝|NF |， ∴在Rt △MPN 中，∠MPN ＝90°， |MN |＝2|PN |， ∴∠PMN ＝30°， ∴∠NMF =π3． 故答案为：π3．14．（5分）若二项式(x −1√x )n 的展开式中只有第4项的二项式系数最大，则展开式中常数项为 15 ．【解答】解：由二项式(x −1√x )n展开式中只有第4项的二项式系数最大， 即展开式有7项，∴n ＝6； ∴展开式中的通项公式为T r +1=C 6r•（﹣1）r •x 6−32r ； 令6−32r ＝0，求得r ＝4，故展开式中的常数项为（﹣1）4•C 64=15．故答案为：15．15．（5分）若无穷数列{cos （ωn ）}（ω∈R ）是等差数列，则其前10项的和为 10 ． 【解答】解：∵无穷数列{cos （ωn ）}（ω∈R ）是等差数列， ∴ω＝0，∴cos （ωn ）＝1，∴无穷数列{cos （ωn ）}（ω∈R ）的前10项的和为：S 10＝10×1＝10． 故答案为：10．16．（5分）边长为1的正方体ABCD ﹣A 1B 1C 1D 1中，点M 为上底面A 1B 1C 1D 1的中心，N 为下底面ABCD 内一点，且直线MN 与底面ABCD 所成线面角的正切值为2，则点N 的轨迹围成的封闭图象的面积为π4．【解答】解：如图，由题意知，M 在底面ABCD 内的投影为底面ABCD 的中心O ，连接ON ，则∠MNO 即为直线MN 与底面ABCD 所成线面角， 所以tan ∠MNO =MO NO =2，则NO =12，所以N 的轨迹是以底面ABCD 的中心0为圆心，以12为半径的圆，则N 的轨迹围成的封闭图象的面积为S =π4． 故答案为：π4．三．解答题（共5小题，满分60分，每小题12分）17．（12分）在三棱锥P ﹣ABC 中，AB ＝1，BC ＝2，AC =√5，PC =√2，P A =√5，PB =√6，E 是线段BC 的中点．（1）求点C 到平面APE 的距离d ； （2）求二面角P ﹣EA ﹣B 的余弦值．【解答】解：∵AB 2+BC 2＝AC 2，PC 2+BC 2＝PB 2，P A 2+AB 2＝PB 2， ∴∠ABC =∠PCB =∠PAB =π2，过点P 作PO ⊥平面ABC ，垂足为O ，易得OP ＝1，且BC ⊥OC ，BA ⊥OA ， ∴四边形ABCO 为矩形，（1）以O 为坐标原点，建立如图所示的空间直角坐标系， 则C （1，0，0），E （1，1，0），A （0，2，0），P （0，0，1）， AP →=(0，−2，1)，AE →=(1，−1，0)，CE →=(0，1，0)， 设平面APE 的法向量为n →=(x ，y ，z)，则{n →⋅AP →=−2y +z =0n →⋅AE →=x −y =0，令x ＝1，则n →=(1，1，2)， ∴d =|CE →⋅n →||n →|=√66；（2）由（1）知平面APE 的法向量为n →=(1，1，2)，取平面ABE 的一个法向量m →=(0，0，1)，且二面角P ﹣EA ﹣B 为钝角，设其为θ，故cosθ=−|n →⋅m →||n →||m →|=−√63．18．（12分）在平面直角坐标系xOy 中，设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且a +b =√3c ，2sin 2C ＝3sin A sin B ． （1）求C ；（2）设P （﹣1，cos A ），Q （﹣cos A ，1），且A ≤C ，OP →与OQ →的夹角为θ，求cos θ的值． 【解答】解：（1）∵2sin 2C ＝3sin A sin B ， ∴sin 2C =32sinAsinB ， ∴由正弦定理得c 2=32ab ， ∵a +b =√3c ， ∴a 2+b 2+2ab ＝3c 2，根据余弦定理得：cosC =a 2+b 2−c 22ab =2c 2−2ab 2ab =ab 2ab =12，∴C =π3．（2）由（1）知C =π3，代入已知，并结合正弦定理得：{sinA +sinB =32sinAsinB =12，解得sinA =12或sin A ＝1（舍去）， 所以A ＝30°，B ＝90°， ∴OP →⋅OQ →=2cosA =√3，而|OP →|⋅|OQ →|=√1+cos 2A ⋅√cos 2A +1=1+cos 2A =74， ∴cosθ=2cosA 1+cos 2A =√374=4√37． 19．（12分）已知一堆产品中有一等品2件，二等品3件，三等品4件，现从中任取3件产品．（1）求一、二、三等品各取到一个的概率；（2）记X 表示取到一等品的件数，求X 的分布列和数学期望．【解答】解：（1）一堆产品中有一等品2件，二等品3件，三等品4件，现从中任取3件产品．基本事件总数n =C 93=84，一、二、三等品各取到一个包含的基本事件个数m ＝2×3×4＝24， ∴一、二、三等品各取到一个的概率p =m n =2484=27．（2）记X 表示取到一等品的件数，则X 的可能取值为0，1，2， P （X ＝0）=C 73C 93=512， P （X ＝1）=C 21C 72C 93=12， P （X ＝2）=C 22C 71C 93=112， ∴X 的分布列为：X 012 P51212112数学期望E （X ）=0×512+1×12+2×112=23． 20．（12分）已知椭圆C ：x 23+y 2b =1（b ＞0）的右焦点为F ，过F 作两条直线分别与圆O ：x 2+y 2＝r 2（r ＞0）相切于A ，B ，且△ABF 为直角三角形．又知椭圆C 上的点与圆O 上的点的最大距离为√3+1． （1）求椭圆C 及圆O 的方程；（2）若不经过点F 的直线l ：y ＝kx +m （其中k ＜0，m ＞0）与圆O 相切，且直线l 与椭圆C 交于P ，Q ，求△FPQ 的周长．【解答】解：（1）椭圆C 上的点与圆O 上的点的最大距离为√3+1， 可得√3+1⇒a +r =√3+1⇒r =1； △ABF 为直角三角形⇒c =√2r ⇒c =√2； 又b 2+c 2＝3⇒b ＝1．圆O 的方程为：x 2+y 2＝1；椭圆C 的方程为：x 2+y 2=1．（2）y＝kx+m与圆相切：则m2＝k2+1，设P（x1，y1），Q（x2，y2），由{x23+y2=1y=kx+m得（1+3k2）x2+6kmx+3m2﹣3＝0，由△＞0，得3k2+1＞m2…（※），且x1+x2=−6km1+3k2，x1x2=3m2−31+3k2，|PQ|=2√3√k2+1⋅√3k2−m2+13k2+1=−2√6k√k2+13k2+1，|PF|+|QF|=2a−e(x1+x2)=2√3+2√6k √k2+13k2+1，△FPQ的周长为|PQ|+|PF|+|QF|=2√3．21．（12分）已知函数f（x）＝lnx﹣x+2sin x，f'（x）为f（x）的导函数．（Ⅰ）求证：f'（x）在（0，π）上存在唯一零点；（Ⅱ）求证：f（x）有且仅有两个不同的零点【解答】解：（Ⅰ）设g(x)=f′(x)=1x−1+2cosx，当x∈（0，π）时，g′(x)=−2sinx−1x2＜0，∴g（x）在（0，π）上单调递减．又∵g(π3)=3π−1+1＞0，g(π2)=2π−1＜0，∴g（x）在(π3，π2)上有唯一的零点．（Ⅱ）①由（Ⅰ）知，当x∈（0，α）时，f'（x）＞0，f（x）在（0，α）上单调递增；当x∈（α，π）时，f'（x）＜0，f（x）在（α，π）上单调递减；∴f（x）在（0，π）上存在唯一的极大值点α(π3＜α＜π2)，∴f(α)＞f(π2)=lnπ2−π2+2＞2−π2＞0．∵f(12)=−2−12+2sin12＜−2−12+2＜0，∴f（x）在（0，α）上恰有一个零点．∵f（π）＝lnπ﹣π＜2﹣π＜0，∴f（x）在（α，π）上也恰有一个零点；②当x∈[π，2π）时，sin x≤0，f（x）≤lnx﹣x．设h（x）＝lnx﹣x，ℎ′(x)=1x−1＜0，∴h（x）在[π，2π）上单调递减，∴h（x）≤h（π）＜0，∴当x ∈[π，2π）时，f （x ）≤h （x ）≤h （π）＜0恒成立， ∴f （x ）在[π，2π）上没有零点．③当x ∈[2π，+∞）时，f （x ）≤lnx ﹣x +2， 设φ（x ）＝lnx ﹣x +2，φ′(x)=1x −1＜0，∴φ（x ）在[2π，+∞）上单调递减，∴φ（x ）≤φ（2π）＜0， ∴当x ∈[2π，+∞）时，f （x ）≤φ（x ）≤φ（2π）＜0恒成立， ∴f （x ）在[2π，+∞）上没有零点． 综上，f （x ）有且仅有两个零点．四．解答题（共1小题，满分10分，每小题10分）22．（10分）在平面直角坐标系x 0y 中，直线l 1的参数方程为{x =t −√3y =kt （t 为参数），直线l 2的参数方程为{x =√3−my =m3k（m 为参数）．设直线l 1与l 2的交点为P ．当k 变化时点P 的轨迹为曲线C 1．（Ⅰ）求出曲线C 1的普通方程；（Ⅱ）以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，直线C 2的极坐标方程为ρsin(θ+π4)=3√2，点Q 为曲线C 1上的动点，求点Q 到直线C 2的距离的最大值． 【解答】解：（Ⅰ）直线l 1的参数方程为{x =t −√3y =kt （t 为参数），转换为直角坐标方程为y =k(x +√3)①． 直线l 2的参数方程为{x =√3−m y =m3k（m 为参数）．转换为直角坐标方程为y =13k (√3−x)②． 所以①×②得到x 23+y 2=1（y ≠0）．（Ⅱ）直线C 2的极坐标方程为ρsin(θ+π4)=3√2，转换为直角坐标方程为x +y ﹣6＝0． 设曲线C 1的上的点Q （√3cosθ，sinθ）到直线x +y ﹣8＝0的距离d =|√3cosθ+sinθ−6|2=|2sin(θ+π3)−6|2，当sin(θ+π3)=−1时，d max =82=4√2． 五．解答题（共1小题）23．已知函数f （x ）＝|x +1|﹣|x ﹣2|．（1）求不等式f （x ）≥1的解集；（2）记f （x ）的最大值为m ，且正实数a ，b 满足1a+2b+12a+b=m ，求a +b 的最小值．【解答】解：（1）当x ≥2时，f （x ）＝x +1﹣（x ﹣2）＝3≥1恒成立，∴x ≥2， 当﹣1≤x ＜2时，f （x ）＝x +1+x ﹣2＝2x ﹣1≥1，解得1≤x ＜2， 当x ＜﹣1时，f （x ）＝﹣（x +1）+x ﹣2＝﹣3≥1不成立，无解， 综上，原不等式的解集为[1，+∞）； （2）由（1）知m ＝3，即1a+2b+12a+b=3，∴a +b =19[(a +2b)+(2a +b)(1a+2b +12a+b )=19(2+a+2b2a+b +2a+ba+2b )≥19(2+2√a+2b 2a+b ⋅2a+ba+2b )=49， 当且仅当a+2b 2a+b=2a+b a+2b ，即a =b =29时等号成立，∴a +b 的最小值是49．。
2020年高考模拟试卷广西高考数学一诊测试试卷(理科) 含解析
2020年高考模拟试卷高考数学一诊试卷（理科）一、选择题1．已知集合A＝{x|3x2﹣5x﹣2≥0}，则∁R A＝（）A．B．C．D．2．已知复数z满足z•|3﹣4i|＝2+5i（i为虚数单位），则在复平面内复数z对应的点的坐标为（）A．B．C．D．3．设x∈R，则“x3＞8”是“x＞2”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件4．已知双曲线C：x2﹣4y2＝k的焦距等于圆M：x2+y2+4x＝12的直径，则实数k＝（）A．B．C．或D．5．在区间[4，12]上随机地取一个实数a，则方程2x2﹣ax+8＝0有实数根的概率为（）A．B．C．D．6．已知等比数列{a n}的前n项和为S n，若a1＝a3﹣8，且S3＝13，则a2＝（）A．﹣3 B．3 C．D．3或7．某程序框图如图所示，则该程序的功能是（）A．输出3（1+2+3+4+…+2018）的值B．输出3（1+2+3+4+…+2017）的值C．输出3（1+2+3+4+…+2019）的值D．输出1+2+3+4+…+2018的值8．某几何体的三视图如图所示，其俯视图是一圆心角为45°的扇形，则该几何体的表面积为（）A．5π+24 B．C．3π+12 D．9．近两年为抑制房价过快上涨，政府出台了﹣﹣系列以“限购、限外、限贷、限价”为主题的房地产调控政策．各地房产部门为尽快实现稳定房价，提出多种方案，其中之一就是在规定的时间T内完成房产供应量任务Q．已知房产供应量Q与时间t的函数关系如图所示，则在以下四种房产供应方案中，供应效率（单位时间的供应量）逐步提高的是（）A．B．C．D．10．函数f（x）＝A sin（wx+φ）（A＞0，w＞0）的部分图象如图所示，则下列说法中错误的是（）A．f（x）的最小正周期是2πB．f（x）在上单调递增C．f（x）在上单调递增D．直线是曲线y＝f（x）的一条对称轴11．已知椭圆的左、右焦点分别为F1，F2，P是C上一点，且PF2⊥x轴，直线PF1与C的另一个交点为Q，若|PF1|＝4|F1Q|，则C的离心率为（）A．B．C．D．12．已知二次函数f（x）＝ax2﹣ax﹣1没有零点，g（x）＝f（x）+ax3﹣（a+3）x2+ax+2，若方程g（x）＝0只有唯一的正实数根，则实数a的取值范围是（）A．（﹣4，0）B．（﹣∞，﹣4）C．（﹣2，0）D．（﹣4，﹣2）二、填空题13．已知向量，若，则实数k＝．14．二项式的展开式中的常数项是．15．已知实数x，y满足不等式组则的最小值为．16．已知正三棱锥的底面边长为2，侧棱长为2，则该正三棱锥内切球的表面积为．三、解答题17．在△ABC中，角A，B，C所对的边分别为a，b，c，且a2﹣3c2＝ac，sin A cos C＝sin C （2﹣cos A）．（1）求角B的大小；（2）若△ABC的外接圆半径是，求△ABC的周长．18．如图，在四棱锥A﹣DBCE中，AD＝BD＝AE＝CE＝，BC＝4，DE＝2，DE∥BC，O，H分别为DE，AB的中点，AO⊥CE．（1）求证：DH∥平面ACE；（2）求直线DH与底面DBCE所成角的大小19．已知抛物线C：y2＝4x的焦点为F，过点P（2，0）的直线交抛物线C于A（x1，y1）和B（x2，y2）两点．（1）当x1+x2＝4时，求直线AB的方程；（2）若过点P且垂直于直线AB的直线l与抛物线C交于C，D两点，记△ABF与△CDF 的面积分别为S1，S2，求S1S2的最小值．20．在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分，并将其得分作为该选手的成绩，成绩大于等于60分的选手定为合格选手，直接参加第二轮比赛，大于等于90分的选手将直接参加竞赛选拔赛．已知成绩合格的100名参赛选手成绩的频率分布直方图如图所示，其中[60，70），[80，90），[90，100]的频率构成等比数列．（1）求a，b的值；（2）估计这100名参赛选手的平均成绩；（3）根据已有的经验，参加竞赛选拔赛的选手能够进入正式竞赛比赛的概率为，假设每名选手能否通过竞赛选拔赛相互独立，现有4名选手进入竞赛选拔赛，记这4名选手在竞赛选拔赛中通过的人数为随机变量X，求X的分布列和数学期望．21．已知函数f（x）＝e x+aln（x+1）（a∈R）的图象在点（0，f（0））处的切线与直线x+2y+1＝0垂直．（1）求f（x）的单调区间；（2）若当x∈[0，+∞）时，f（x）﹣mx﹣1≥0恒成立，求实数m的取值范围．（二）选考题：共10分.请考生在第22、23两题中任选一题作答.如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，直线l的参数方程为（t为参数）．以坐标原点为极点，x轴的非负半轴为极轴且取相同的单位长度建立极坐标系，曲线C的极坐标方程为ρ2+12ρcosθ+35＝0．（1）求直线l的普通方程和曲线C的直角坐标方程；（2）设A是曲线C上任意一点，直线l与两坐标轴的交点分别为M，N，求|AM|2+|AN|2最大值．[选修4-5：不等式选讲]23．（1）求不等式|x﹣4|﹣x＜0的解集；（2）设a，b∈（2，+∞），证明：（a2+4）（b2+4）＞8a2+8b2．参考答案一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A＝{x|3x2﹣5x﹣2≥0}，则∁R A＝（）A．B．C．D．【分析】先求出集合A，再利用补集的定义即可求出∁R A．解：易知，所以，故选：A．2．已知复数z满足z•|3﹣4i|＝2+5i（i为虚数单位），则在复平面内复数z对应的点的坐标为（）A．B．C．D．【分析】利用复数模的计算公式求|3﹣4i|，即可求得z，则答案可求．解：由题意，得z•5＝2+5i．则，其在复数平面内对应的点的坐标为．故选：B．3．设x∈R，则“x3＞8”是“x＞2”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件【分析】“x3＞8”⇔“x＞2”，即可判断出结论．解：“x3＞8”⇔“x＞2”，∴“x3＞8”是“x＞2”的充要条件．故选：C．4．已知双曲线C：x2﹣4y2＝k的焦距等于圆M：x2+y2+4x＝12的直径，则实数k＝（）A．B．C．或D．【分析】C圆M：x2+y2+4x＝12化为标准方程是（x+2）2+y2＝16，其半径为4．直径为8．对k分类讨论，可得双曲线的焦距，即可得出k．解：C圆M：x2+y2+4x＝12化为标准方程是（x+2）2+y2＝16，其半径为4．直径为8．当k＞0时，双曲线C：x2﹣4y2＝k化为标准方程，其焦距为，解得；当k＜0时，双曲线C：x2﹣4y2＝k化为标准方程是，其焦距为，解得．综上，或．故选：C．5．在区间[4，12]上随机地取一个实数a，则方程2x2﹣ax+8＝0有实数根的概率为（）A．B．C．D．【分析】根据一元二次方程有实数根△≥0，求出a的取值范围，再求对应的概率值．解：因为方程2x2﹣ax+8＝0有实数根，所以△＝（﹣a）2﹣4×2×8≥0，解得a≥8或a≤﹣8，所以方程2x2﹣ax+8＝0有实数根的概率为P＝＝．故选：D．6．已知等比数列{a n}的前n项和为S n，若a1＝a3﹣8，且S3＝13，则a2＝（）A．﹣3 B．3 C．D．3或【分析】由已知结合等比数列的通项公式及求和公式可求首项及公比，然后再结合等比数列的通项公式即可求解．解：设公比为q，易知q≠1．由得，解得或，当时，a2＝a1q＝3；当时，，所以a2＝3或，故选：D．7．某程序框图如图所示，则该程序的功能是（）A．输出3（1+2+3+4+…+2018）的值B．输出3（1+2+3+4+…+2017）的值C．输出3（1+2+3+4+…+2019）的值D．输出1+2+3+4+…+2018的值【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．解：模拟程序的运行，可得第一次运行时，k＝2，S＝3+3×2；第二次运行时，k＝3，S＝3+3×2+3×3；第三次运行时，k＝4，S＝3+3×2+3×3+3…，以此类推，第2017次运行时，k＝2018，S＝3+3×2+3×3+3×4+…+3×2018，此时刚好不满足k＜2018，则输出S＝3（1+2+3+4+…+2018），所以该程序的功能是“输出3（1+2+3+4+…+2018）的值．故选：A．8．某几何体的三视图如图所示，其俯视图是一圆心角为45°的扇形，则该几何体的表面积为（）A．5π+24 B．C．3π+12 D．【分析】直接把三视图转换为几何体，进一步求出几何体的表面积．解：由三视图可知，该几何体是个圆柱，其上下底面均为圆面，侧面由2个矩形和1个圆弧面构成，所以其表面积．故选：B．9．近两年为抑制房价过快上涨，政府出台了﹣﹣系列以“限购、限外、限贷、限价”为主题的房地产调控政策．各地房产部门为尽快实现稳定房价，提出多种方案，其中之一就是在规定的时间T内完成房产供应量任务Q．已知房产供应量Q与时间t的函数关系如图所示，则在以下四种房产供应方案中，供应效率（单位时间的供应量）逐步提高的是（）A．B．C．D．【分析】分析可知，图象应上升的，且越来越陡，由此即可得出选项．解：单位时间的供应量逐步提高时，供应量的增长速度越来越快，图象上切线的斜率随着自变量的增加会越来越大，则曲线是上升的，且越来越陡，所以函数的图象应一直下凹的．故选：B．10．函数f（x）＝A sin（wx+φ）（A＞0，w＞0）的部分图象如图所示，则下列说法中错误的是（）A．f（x）的最小正周期是2πB．f（x）在上单调递增C．f（x）在上单调递增D．直线是曲线y＝f（x）的一条对称轴【分析】由图象求出函数f（x）的解析式，然后逐个分析所给命题的真假．解：由图可知，A＝2，该三角函数的最小正周期，故A项正确；由，则f（x）＝2sin（x+φ）中，因为，所以该三角函数的一条对称轴为，将代入y＝2sin（x+φ），得，解得，所以，令，得，所以函数f（x）在上单调递增．故B项正确；令，得，所以函数f（x）在上单调递减．故C项错误；令，得，则直线是f（x）的一条对称轴．故D项正确．故选：C．11．已知椭圆的左、右焦点分别为F1，F2，P是C上一点，且PF2⊥x轴，直线PF1与C的另一个交点为Q，若|PF1|＝4|F1Q|，则C的离心率为（）A．B．C．D．【分析】本题根据题意可得|PF2|＝，然后过Q点作QE⊥x轴，垂足为点E，设Q（x0，y0），根据两个直角三角形相似可计算出点Q坐标，再将点Q坐标代入椭圆方程，结合b2＝a2﹣c2，可解出e的值．解：由题意，可将点P坐标代入椭圆C方程得+＝1，解得|PF2|＝．如图所示，过Q点作QE⊥x轴，垂足为点E，设Q（x0，y0），根据题意及图可知，Rt△PF2F1∽Rt△QEF1，∵＝4，∴＝＝4，∴|EF1|＝＝＝，∴x0＝﹣c﹣＝﹣．又∵y0＝﹣|QE|＝﹣＝﹣．∴点Q坐标为（﹣，﹣）．将点Q坐标代入椭圆方程，得．结合b2＝a2﹣c2，解得，故选：D．12．已知二次函数f（x）＝ax2﹣ax﹣1没有零点，g（x）＝f（x）+ax3﹣（a+3）x2+ax+2，若方程g（x）＝0只有唯一的正实数根，则实数a的取值范围是（）A．（﹣4，0）B．（﹣∞，﹣4）C．（﹣2，0）D．（﹣4，﹣2）【分析】根据已知二次函数f（x）＝ax2﹣ax﹣1没有零点，则a≠0且△＝a2+4a＜0；解得﹣4＜a＜0．再根据方程g（x）＝0只有唯一的正实数根，求导，分析函数y＝g（x）根的分布，列出不等式得出a的取值范围即可．解：因为二次函数f（x）＝ax2﹣ax﹣1没有零点，则a≠0且△＝a2+4a＜0，解得﹣4＜a ＜0．由g（x）＝f（x）+ax3﹣（a+3）x2+ax+2＝ax2﹣ax﹣1+ax3﹣（a+3）x2+ax+2＝a3x﹣3x2+1．则g'（x）＝3ax2﹣6x＝3x（ax﹣2），令g'（x）＝0，故x＝0或x＝；由于a＜0，所以x＜时，g'（x）＜0，g（x）单调递减；当＜x＜0时，g'（x）＞0，g（x）单调递增；当x＞0时，g'（x）＜0，g（x）单调递减；所以x＝有极小值，x＝0时，有极大值；因为g（0）＝1．当a＜0时，g（x）＝0只有唯一的正实数根，所以g（x）＝0在（﹣∞，0）上没有实数根．而当时，g（x）＝ax3﹣3x2+1在（﹣∞，0）上取得最小值，所以，解得a＞2（舍去）或a＜﹣2．综上所述，实数a 的取值范围是（﹣4，﹣2）．故选：D．二、填空题：本题共4小题，每小题5分，共20分.13．已知向量，若，则实数k＝ 2 ．【分析】根据两向量平行的坐标表示，列出方程求出k的值解：由题意，得，因为．所以1×（﹣3k﹣4）﹣5（﹣k）＝0，解得k＝2．故答案为2．14．二项式的展开式中的常数项是．【分析】先求得二项式展开式的通项公式，再令x的幂指数等于0，求得r的值，即可求得结论．解：二项式的展开式的通项是，令，解得r＝6．故二项式的展开式中的常数项是．故答案为：15．已知实数x，y满足不等式组则的最小值为．【分析】作出不等式对应的平面区域，利用线性规划的知识，转化为斜率问题即可求解．【解答】解作出不等式组表示的平面区域如图所示：由几何意义可知，目标函数表示可行域内的点（x，y）与点（﹣1，﹣1）组成的直线的斜率，目标函数在点C（4，0）处取得最小值，故答案为：．16．已知正三棱锥的底面边长为2，侧棱长为2，则该正三棱锥内切球的表面积为（4﹣）π．【分析】设底面正三角形BCD的中心为O，由三角形的知识可得棱锥的高和底面积，代入体积公式可得；设内切球的半径为R，则由等体积的方法可求半径，由球的表面积公式可得．解：正三棱锥的底面边长为2，侧棱长为2，由正弦定理可知，△BDC外接圆半径2r＝＝4及r＝2，所以三棱锥的高h＝＝4，又底面积S△BCD＝＝3，根据题意可知△ABC底BC边上的高h1＝＝，侧面积S＝3S△ABC＝3×＝3，设三棱锥的体积V＝＝4，设内切球的半径为R，则由等体积可得，（S△ABC+S△ACD+S△ABD+S△BCD）R＝4，所以R＝，故内切球的表面积S′＝4πR2＝（4﹣）π．故答案为：（4﹣）π．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.17．在△ABC中，角A，B，C所对的边分别为a，b，c，且a2﹣3c2＝ac，sin A cos C＝sin C （2﹣cos A）．（1）求角B的大小；（2）若△ABC的外接圆半径是，求△ABC的周长．【分析】（1）由sin A cos C＝sin C（2﹣cos A），可得sin A cos C＝2sin C﹣sin C cos A，利用和差公式可得：sin（A+C）＝2sin C，利用诱导公式、三角形内角和定理及其正弦定理可得b＝2c．根据已知a2﹣3c2＝ac，利用余弦定理即可得出B．（2）因为△ABC的外接圆半径是，由正弦定理，得．解得b．c．代入a2﹣3c2＝ac 中，得a，j即可得出△ABC的周长．解：（1）因为sin A cos C＝sin C（2﹣cos A），所以sin A cos C＝2sin C﹣sin C cos A，所以sin A cos C+sin C cos A＝2sin C，所以sin（A+C）＝2sin C，所以sin B＝2sin C．由正弦定理，得b＝2c．因为a2﹣3c2＝ac，由余弦定理，得，又因为B∈（0，π），所以（2）因为△ABC的外接圆半径是，则由正弦定理，得．解得b＝4．所以c＝2．将c＝2代入a2﹣3c2＝ac中，得a2﹣12＝2a，解得（舍去）或．所以△ABC的周长是．18．如图，在四棱锥A﹣DBCE中，AD＝BD＝AE＝CE＝，BC＝4，DE＝2，DE∥BC，O，H分别为DE，AB的中点，AO⊥CE．（1）求证：DH∥平面ACE；（2）求直线DH与底面DBCE所成角的大小【分析】（1）利用中位线的性质及平行线的传递性，可证四边形DEFH为平行四边形，由此即可得证；（2）关键是找出∠HDG是DH与底面DBCE所成的角，进而转化到三角形中解三角形即可．【解答】（1）证明：取线段AC的中点F，连接EF，HF．因为HF是△ABC的中位线，所以．又因为DE＝2，DE∥BC，所以HF＝DE，HF∥DE．所以四边形DEFH为平行四边形，所以EF∥HD．因为EF⊂平面ACE，DH⊄平面ACE．所以DH∥平面ACE．（2）解：连接OB，取OB的中点G，连接HG，DG．易知，易知HG是△AOB的中位线，所以HG∥AO且．因为AD＝AE，O为DE中点，AO⊥DE，又HG∥AO，所以HG⊥DE．因为AO⊥CE，HG∥AO，所以HG⊥CE．又DE∩CE＝E，DE，CE⊂平面DBCE，所以HG⊥底面DBCE．所以∠HDG是DH与底面DBCE所成的角．易求等腰梯形DBCE的高为所以DG＝1．在Rt△HDG中，由．得∠HDG＝45°．故直线DH与底面DBCE所成角的大小为45°．19．已知抛物线C：y2＝4x的焦点为F，过点P（2，0）的直线交抛物线C于A（x1，y1）和B（x2，y2）两点．（1）当x1+x2＝4时，求直线AB的方程；（2）若过点P且垂直于直线AB的直线l与抛物线C交于C，D两点，记△ABF与△CDF 的面积分别为S1，S2，求S1S2的最小值．【分析】（1）由直线AB过定点P（2，0），可设直线方程为x＝my+2．与抛物线方程联立消去x，得y2﹣4my﹣8＝0，利用根与系数的关系即可得出．（2）由（1），知△ABF的面积为＝，利用根与系数的关系代入可得．因为直线CD与直线AB垂直，对m分类讨论，m≠0时，推理可得：△CDF的面积．进而得出结论．解：（1）由直线AB过定点P（2，0），可设直线方程为x＝my+2．联立消去x，得y2﹣4my﹣8＝0，由韦达定理得y1+y2＝4m，y1y2＝﹣8，所以．因为x1+x2＝4．所以4m2+4＝4，解得m＝0．所以直线AB的方程为x＝2．（2）由（1），知△ABF的面积为＝．因为直线CD与直线AB垂直，且当m＝0时，直线AB的方程为x＝2，则此时直线l的方程为y＝0，但此时直线l与抛物线C没有两个交点，所以不符合题意，所以m≠0．因此，直线CD的方程为．同理，△CDF的面积．所以，当且仅当，即m2＝1，亦即m＝±1时等号成立．20．在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分，并将其得分作为该选手的成绩，成绩大于等于60分的选手定为合格选手，直接参加第二轮比赛，大于等于90分的选手将直接参加竞赛选拔赛．已知成绩合格的100名参赛选手成绩的频率分布直方图如图所示，其中[60，70），[80，90），[90，100]的频率构成等比数列．（1）求a，b的值；（2）估计这100名参赛选手的平均成绩；（3）根据已有的经验，参加竞赛选拔赛的选手能够进入正式竞赛比赛的概率为，假设每名选手能否通过竞赛选拔赛相互独立，现有4名选手进入竞赛选拔赛，记这4名选手在竞赛选拔赛中通过的人数为随机变量X，求X的分布列和数学期望．【分析】（1）由频率分布直方图的性质能求出a，b．（2）由频率分布直方图的性质能估计这100名选手的平均成绩．（3）由题意知X～B（4，），由此能求出X的分布列和数学期望．解：（1）由题意，得，解得a＝0.04，b＝0.02．（2）估计这100名选手的平均成绩为：＝65×0.1+75×0.3+85×0.2+95×0.4＝84．（3）由题意知X～B（4，），则P（X＝i）＝，（i＝0，1，2，3，4），∴X的分布列为：X 0 1 2 3 4PE（X）＝4×＝1．21．已知函数f（x）＝e x+aln（x+1）（a∈R）的图象在点（0，f（0））处的切线与直线x+2y+1＝0垂直．（1）求f（x）的单调区间；（2）若当x∈[0，+∞）时，f（x）﹣mx﹣1≥0恒成立，求实数m的取值范围．【分析】（1）先对函数求导，然后结合导数与单调性的关系即可求解；（2）构造函数g（x）＝f（x）﹣mx﹣1，对其求导，然后结合导数，对a进行分类讨论，结合函数的性质分析求解．解：（1）由已知得，则f'（0）＝e0+a＝a+1．又因为直线x+2y+1＝0的斜率为所以，解得a＝1．所以f（x）＝e x+ln（x+1），定义域为（﹣1，+∞），所以．所以函数f（x）的单调递增区间为（﹣1，+∞），无单调减区间．（2）令g（x）＝f（x）﹣mx﹣1．则令，则当x≥0时，，所以h'（x）≥0．所以函数y＝h（x）（x≥0）为增函数．所以h（x）≥h（0）＝2，所以g'（x）≥2﹣m．①当m≤2时，2﹣m≥0，所以当m≤2时，g'（x）≥0，所以函数y＝g（x）（x≥0）为增函数，所以g（x）≥g（0）＝0，故对∀x≥0，f（x）﹣mx﹣1≥0成立；②当m＞2时，m﹣1＞1，由x≥0时，，，当x∈（0，ln（m﹣1）），知e x+1﹣m＜0，即g'（x）＜0．所以函数y＝g（x），x∈（0，ln（m﹣1））为减函数．所以当0＜x＜ln（m﹣1）时，g（x）＜g（0）＝0．从而f（x）﹣mx﹣1＜0，这与题意不符．综上，实数m的取值范围为（﹣∞，2]．（二）选考题：共10分.请考生在第22、23两题中任选一题作答.如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，直线l的参数方程为（t为参数）．以坐标原点为极点，x轴的非负半轴为极轴且取相同的单位长度建立极坐标系，曲线C的极坐标方程为ρ2+12ρcosθ+35＝0．（1）求直线l的普通方程和曲线C的直角坐标方程；（2）设A是曲线C上任意一点，直线l与两坐标轴的交点分别为M，N，求|AM|2+|AN|2最大值．【分析】（1）直接利用转换关系的应用，把参数方程极坐标方程和直角坐标方程之间进行转换．（2）利用两点间的距离公式的应用和三角函数关系式的恒等变换及正弦型函数的性质的应用求出结果．解：（1）由直线l的参数方程为（t为参数）．转换为直角坐标方程为：3x﹣y+9＝0．所以：直线l的普通方程为3x﹣y+9＝0．曲线C的极坐标方程为ρ2+12ρcosθ+35＝0．转换为直角坐标方程为：x2+y2+12x+35＝0．故曲线C的直角坐标方程为x2+y2+12x+35＝0．（2）直线l3x﹣y+9＝0与坐标轴的交点依次为（﹣3，0），（0，9），不妨设M（﹣3，0），N（0，9），曲线C的直角坐标方程x2+y2+12x+35＝0化为标准方程是（x+6）2+y2＝1，由圆的参数方程，可设点A（﹣6+cosα，sinα），所以|AM|2+|AN|2最＝（﹣3+cosα）2+sin2α+（﹣6+cosα）2+（sinα﹣9）2＝﹣18（sin α+cosα）2+128＝﹣18，当，即时，最大值为18．[选修4-5：不等式选讲]23．（1）求不等式|x﹣4|﹣x＜0的解集；（2）设a，b∈（2，+∞），证明：（a2+4）（b2+4）＞8a2+8b2．【分析】（1）解绝对值不等式即可；（2）利用作差法比较大小．解：（1）由不等式|x﹣4|﹣x＜0，得|x﹣4|＜x，则，解得x＞2．故所求不等式的解集为（2，+∞）．证明：（2）（a2+4）（b2+4）﹣（8a2+8b2）＝（ab）2﹣4a2﹣4b2+16＝（ab）2﹣4a2﹣4b2+16＝（a2﹣4）（b2﹣4），因为a＞2，b＞2，所以a2＞4，b2＞4，所以（a2﹣4）（b2﹣4）＞0．所以原不等式（a2+4）（b2+4）＞8a2+8b2成立．。
2020年高考理科数学(1卷)：答案详细解析(客观题 最新)
2020年普通高等学校招生全国统一考试理科数学（I 卷）答案详解一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.（复数）若1z i =+,则22z z -=A.0B.1 D.2【解析】∵1z i =+，∴222(2)(1)(1)12z z z z i i i -=-=+-=-=-，∴2=22z z -.【答案】D2.（集合）设集合{}240A x x =-≤，{}20B x x a =+≤，且{}21A B x x =-≤≤ ，则a =A.－4B.－2C.2D.4【解析】由已知可得{}22A x x =-≤≤，2a B x x ⎧⎫=≤-⎨⎬⎩⎭，∵{}21A B x x =-≤≤ ，∴12a -=，解得2a =-.【答案】B 3.（立体几何，同文3）埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为A.514- B.512 C.514+ D.512+【解析】如图A3所示，设正四棱锥底面的边长为a ，则有22221212h am a h m ⎧=⎪⎪⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩整理得22420m am a --=，令m t a =，则有24210t t --=，∴114t +=，214t -=（舍去），即14m a +=.图A3【答案】C4.（解析几何）已知A 为抛物线2:2(0)C y px p =>上一点，点A 到C 的焦点的距离为12，到y 轴的距离为9，则p =A ．2B ．3C ．6D ．9【解析】设A 点的坐标为(m ,n )，∵点A 到C 的焦点的距离为12，∴m =9，∵点A 到C 的焦点的距离为12，∴122p m +=，解得6p =.【答案】C5.（概率统计，同文5）某校一个课外学习小组为研究某作物种子的发芽率y 和温度x （单位：C ）的关系，在20个不同的温度条件下进行种子的发芽实验，由实验数据,)(i i x y i =（1,2,…,20)得到下面的散点图：由此散点图，在10C 至40C 之间，下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是A.y a bx =+B.2y a bx =+C.x y a be =+D.ln y a b x=+【解析】根据散点图的趋势和已学函数图象可知，本题的回归方程类型为对数函数，故选D 选项.【答案】D6.（函数）函数43()2f x x x =-的图像在点(1,(1))f 处的切线方程为A ．21y x =--B ．21y x =-+C ．23y x =-D ．21y x =+【解析】32()46f x x x '=-，∴函数()f x 的图像在点(1,(1))f 处的切线斜率为(1)2k f '==-，又∵(1)1f =-，∴所求的切线方程为12(1)y x +=--，化简为21y x =-+.【答案】B7.（三角函数，同文7）设函数()cos()6f x x πω=+在[]ππ-，的图像大致如下图，则()f x 的最小正周期为A.109π B.76π C.43π D.32π【解析】∵函数过点4π,09⎛⎫- ⎪⎝⎭，∴4ππcos()=096x ω-+，∴4πππ=962x ω-+-，解得23=ω，∴()f x 的最小正周期为3π4π2==ωT .【答案】C 8.（概率统计）25()y x x y x++的展开式中33x y 的系数为A.5 B.10 C.15 D.20【解析】∵5()x y +展开式的通项公式为55C r r r x y -(r =0,1,2,3,4,5)，∴1r =时，2141335C 5y x y x y x=，∴3r =时，323335C 10x x y x y =，∴展开式中的33x y 系数为5+10=15.【答案】C9.（三角函数）已知(0,)α∈π，且3cos28cos 5αα-=，则sin α=A.53 B.23 C.13 D.59【解析】应用二倍角公式2cos22cos 1αα=-，将3cos28cos 5αα-=化简为，23cos 4cos 40αα--=，解得2cos 3α=-或cos 2α=（舍去），又∵(0,)α∈π，∴5sin 3α=.【答案】A10.（立体几何，同文12）已知A ，B ，C 为球O 的球面上的三个点， 1O 为△ABC 的外接圆.若 1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为A ．64πB ．48πC ．36πD ．32π【解析】由题意可知， 1O 为的半径r =2，由正弦定理可知，24sin ==AB r C，则14sin 4sin 60==== OO AB C ，∴球O 的半径4R ==，∴球O 的表面积为24π64πR =．图A10【答案】A11.（解析几何）已知22:2220M x y x y +---= ，直线:20+=l x y ，p 为l 上的动点.过点p 作M 的切线PA ，PB ，切点为,A B ，当PM AB 最小时，直线AB 的方程为A.210x y --= B.210x y +-=C.210x y -+= D.210x y ++=【解析】222:(1)(1)2-+-= M x y ， M 的半径r =2，圆心(1,1)M ，由几何知识可知，⊥PM AB ，故1||||=2=||||2||2∆=⋅⋅==四边形APM APBM S PM AB S AP AM AP ，∴⋅PM AB 最小，即PM 最小，此时直线PM ⊥l ，即直线PM 的斜率为12=m k ，故直线PM 的方程为11(1)2-=-y x ，化简为1122=+y x ，∴直线PM 与l 的交点P 的坐标为(1,0)-P ，直线AB 为过点P 作 M 的切线所得切点弦AB 所在的直线，其方程为(11)(1)(01)(1)4---+--=x y ，化简得210++=x y ．图A11【答案】D注：过圆外一点00(,)P x y 作222:()()O x a y b r -+-= 的切线所得切点弦所在直线方程为200()()()()x a x a y b y b r --+--=.特别当0a b ==时，切点弦所在直线方程为200x x y y r +=.（具体推到过程，可到百度搜索）12.（函数）若242log 42log +=+a b a b 则A.a >2bB.a <2bC.a >b 2D.a <b 2【解析】由指数和对数运算性质，原等式可化为2222log 2log a b a b +=+，∵222log 1log log 2b b b <+=，∴22222log 2log 2b b b b +<+，∴2222log 2log 2a b a b +<+，设2()2log x f x x =+，则有()(2)f a f b <，由指数函数和对数函数的单调性可知()f x 在(0,)+∞单调递增，∴2a b <.【答案】A二、填空题：本题共4小题，每小题5分，共20分。
2020年四川省绵阳市高考数学一诊试卷(理科)(解析版)
2020年四川省绵阳市高考数学一诊试卷（理科）一、选择题：本大题共12小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知A＝{x∈N*|x≤3}，B＝{x|x2﹣4x≤0}，则A∩B＝（）A．{1，2，3}B．{1，2}C．（0，3]D．（3，4]2．若b＜a＜0，则下列结论不正确的是（）A．B．ab＞a2C．|a|+|b|＞|a+b|D．3．下列函数中的定义域为R，且在R上单调递增的是（）A．f（x）＝x2B．C．f（x）＝ln|x|D．f（x）＝e2x 4．等差数列{a n}的前n项和为S n，若a3＝2，S3＝3，则a6＝（）A．4B．5C．10D．155．已知函数，若f（﹣m）＝2，则f（m）＝（）A．﹣2B．﹣1C．0D．6．已知命题p：函数的最小值为；命题q：若向量，，满足•＝•，则＝．下列正确的是（）A．￢p∧q B．p∨q C．p∧￢q D．￢p∧￢q 7．若，b＝3﹣0.8，c＝ln3，则a，b，c的大小关系（）A．b＞c＞a B．c＞a＞b C．c＞b＞a D．a＞c＞b8．已知x，y满足线性约束条件，则z＝2x+y的最小值为（）A．.4B．.2C．.1D．9．设函数f（x）＝ae x﹣lnx（其中常数a≠0）的图象在点（1，f（1））处的切线为l，则l 在y轴上的截距为（）A．1B．2C．ae﹣1D．1﹣2ae10．某数学小组进行社会实践调查，了解某公司为了实现1000万元利率目标，准备制定激励销售人员的奖励方案：在销售利润超过10万元时，按销售利润超过10万元时，按销售利润进行奖励，且奖金y（单位：万元）随销售利润x（单位：万元）的增加而增加，但奖金总数不超过5万元，同时奖金不超过利润的25%．同学们利用函数知识，设计了如下的函数模型，其中符合公司要求的是（参考数据：1.0021000≈7.37，lg7≈0.845）（）A．y＝0.25x B．y＝1.002xC．y＝log7x+1D．11．函数在上单调递增，且图象关于x＝﹣π对称，则ω的值为（）A．B．C．2D．12．在△ABC中，角A为，角A的平分线AD交BC于点D，已知，且，则在方向上的投影是（）A．1B．C．3D．二、选择题：本大题共4小题，每小题5分．共20分．13．已知函数f（x）的定义域为R，且满足f（x）＝f（x+2），当x∈[0，2]时，f（x）＝e x，则f（7）＝．14．已知向量＝（﹣2，2），向量的模为1，且|﹣2|＝2，则与的夹角为．15．2019年10月1日，在庆祝新中国成立70周年阅兵中，由我国自主研制的军用飞机和军用无人机等参阅航空装备分秒不差飞越天安门，状军威，振民心，令世人瞩目．飞行员高超的飞行技术离不开艰苦的训练和科学的数据分析．一次飞行训练中，地面观测站观测到一架参阅直升机以千米/小时的速度在同一高度向正东飞行，如图，第一次观测到该飞机在北偏西60°的方向上，1分钟后第二次观测到该飞机在北偏东75°的方向上，仰角为30°，则直升机飞行的高度为（结果保留根号）．16．若函数有且仅有一个零点，则实数m的取值范围．三、填空题：共70分．17．已知函数f（x）＝（cos x﹣sin x）2﹣2sin2x．（1）求函数f（x）的最小正周期与单调递减区间；（2）若f（x0）＝﹣1，且，求x0的值．18．已知数列{a n}满足，且a1＝1，a4＝7，数列{b n}的前n项和．（1）求数列{a n}{b n}的通项公式；（2）设，求数列{c n}的前n项和T n．19．已知△ABC中三个内角A，B，C满足．（1）求sin B；（2）若，b是角B的对边，，求△ABC的面积．20．已知函数．（1）求函数f（x）在区间[1，+∞）上的值域；（2）若实数x1，x2均大于1且满足，求f（x1x2）的最小值．21．已知函数f（x）＝e x﹣ax2，a∈R，x∈（0，+∞）．（1）若f（x）存在极小值，求实数a的取值范围；（2）若，求证：f（x）＞ax（lnx﹣x）．（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，曲线C的参数方程为（α为参数），以坐标原点0为极点，x的正半轴为极轴，取相同长度单位建立极坐标系，直线l的极坐标方程．（1）求曲线C的普通方程与极坐标方程；（2）设射线OM：与曲线C交于点A，与直线l交于点B，求线段AB的长．[选修4-5：不等式选讲]23．设函数f（x）＝|x﹣m|+|x+1|+5（m∈R）．（1）当m＝2时，求不等式f（x）≥0的解集；（2）若f（x）≥﹣2，求实数m的取值范围．2020年四川省绵阳市高考数学一诊试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知A＝{x∈N*|x≤3}，B＝{x|x2﹣4x≤0}，则A∩B＝（）A．{1，2，3}B．{1，2}C．（0，3]D．（3，4]【解答】解：由题意得：A＝{x∈N*|x≤3}＝{1，2，3}，B＝{x|x2﹣4x≤0}＝{x|0≤x≤4}，∴所以A∩B＝{1，2，3}，故选：A．2．若b＜a＜0，则下列结论不正确的是（）A．B．ab＞a2C．|a|+|b|＞|a+b|D．【解答】解：∵b＜a＜0，∴＜，ab＞a2，由函数y＝在R上单调递增，可得：＜．设a＝﹣2，b＝﹣1时，|a|+|b|＝|a+b|与C矛盾．因此只有C错误．故选：C．3．下列函数中的定义域为R，且在R上单调递增的是（）A．f（x）＝x2B．C．f（x）＝ln|x|D．f（x）＝e2x【解答】解：由f（x）＝的定义域为[0，+∞），不符合题意，C：函数的定义域x≠0，不符合题意，A：y＝x2在（﹣∞，0]单调递减，在[0，+∞）单调递增，不符合题意，故选：D．4．等差数列{a n}的前n项和为S n，若a3＝2，S3＝3，则a6＝（）A．4B．5C．10D．15【解答】解：由题意得，解得a1＝0，d＝1，∴a6＝a1+5d＝5．故选：B．5．已知函数，若f（﹣m）＝2，则f（m）＝（）A．﹣2B．﹣1C．0D．【解答】解：∵，∴f（﹣x）+f（x）＝+＝＝1，∵f（﹣m）＝2，∴f（m）＝﹣1．故选：B．6．已知命题p：函数的最小值为；命题q：若向量，，满足•＝•，则＝．下列正确的是（）A．￢p∧q B．p∨q C．p∧￢q D．￢p∧￢q【解答】解：由题意得：命题p：函数，由基本不等式成立的条件，y≥2＝2，知等号取不到，所以p命题是假的；命题q：若向量，，满足＝，∴，，有可能是零向量或者，所以q是错误的．∴￢p∧q，p∨q，p∧￢q，是假命题，￢p∧￢q为真命题；故选：D．7．若，b＝3﹣0.8，c＝ln3，则a，b，c的大小关系（）A．b＞c＞a B．c＞a＞b C．c＞b＞a D．a＞c＞b【解答】解：由指数函数y＝在R上单调递减，又，b＝3﹣0.8＝，∴1＞a＞b．c＝ln3∈（1，2）∴c＞a＞b．故选：B．8．已知x，y满足线性约束条件，则z＝2x+y的最小值为（）A．.4B．.2C．.1D．【解答】解：先根据x，y满足线性约束条件画出可行域，平移直线0＝2x+y，当直线z＝2x+y过点B（0，1）时，z取最小值为1．故选：C．9．设函数f（x）＝ae x﹣lnx（其中常数a≠0）的图象在点（1，f（1））处的切线为l，则l 在y轴上的截距为（）A．1B．2C．ae﹣1D．1﹣2ae【解答】解：由f（x）＝ae x﹣lnx，得，∴f′（1）＝ae﹣1，又x＝1时，f（1）＝ae，∴f（x）在点（1，f（1））处的切线方程为y﹣（ae）＝（ae﹣1）（x﹣1），取x＝0，得在y轴上截距y＝（ae﹣1）（0﹣1）+ae＝1．故选：A．10．某数学小组进行社会实践调查，了解某公司为了实现1000万元利率目标，准备制定激励销售人员的奖励方案：在销售利润超过10万元时，按销售利润超过10万元时，按销售利润进行奖励，且奖金y（单位：万元）随销售利润x（单位：万元）的增加而增加，但奖金总数不超过5万元，同时奖金不超过利润的25%．同学们利用函数知识，设计了如下的函数模型，其中符合公司要求的是（参考数据：1.0021000≈7.37，lg7≈0.845）（）A．y＝0.25x B．y＝1.002xC．y＝log7x+1D．【解答】解：由题意得：有两个条件①奖金y≤5；②奖金y≤0.25x．且10≤x≤1000．A选项，当x≥20时，y≥5，不符合题意．B选项，当x＝1000时，1.0021000≈7.37，也超出了5，不符合题意．D选项，当x＝1000时，＝y＝tan（2）是一个负数，不符合题意．故选：C．11．函数在上单调递增，且图象关于x＝﹣π对称，则ω的值为（）A．B．C．2D．【解答】解：要使函数的递增，则，化简得：，已知在单增，所以．又因为图象关于x＝﹣π对称，，所以，因为ω＞0，此时k＝﹣1，所以，故选：A．12．在△ABC中，角A为，角A的平分线AD交BC于点D，已知，且，则在方向上的投影是（）A．1B．C．3D．【解答】解：由λ＝﹣可得：＝λ+，∵B，C，D三点共线，故λ+＝1，即λ＝．∴＝+．以A为原点，以AB为x轴建立平面直角坐标系如图所示，则D（3，），设B（m，0），C（n，n），由＝+得：，解得m＝3，n＝3．故B（3，0），∴在上的投影为|AB|cos30°＝．故选：D．二、选择题：本大题共4小题，每小题5分．共20分．13．已知函数f（x）的定义域为R，且满足f（x）＝f（x+2），当x∈[0，2]时，f（x）＝e x，则f（7）＝e．【解答】解：因为f（x）＝f（x+2），周期T＝2，当x∈[0，2]时，f（x）＝e x，∴f（7）＝f（1）＝e．故答案为：e．14．已知向量＝（﹣2，2），向量的模为1，且|﹣2|＝2，则与的夹角为．【解答】解：由已知得：||＝2，||＝1，|﹣2|＝2，2﹣4+42＝4，∴设与的夹角为θ，θ∈[0，π]，＝2＝2•1•cosθ，∴cosθ＝，θ＝，故答案为：．15．2019年10月1日，在庆祝新中国成立70周年阅兵中，由我国自主研制的军用飞机和军用无人机等参阅航空装备分秒不差飞越天安门，状军威，振民心，令世人瞩目．飞行员高超的飞行技术离不开艰苦的训练和科学的数据分析．一次飞行训练中，地面观测站观测到一架参阅直升机以千米/小时的速度在同一高度向正东飞行，如图，第一次观测到该飞机在北偏西60°的方向上，1分钟后第二次观测到该飞机在北偏东75°的方向上，仰角为30°，则直升机飞行的高度为（结果保留根号）．【解答】解：如图由题上条件可得线AC平行于东西方向，∠ABD＝60°，∠CBD＝75°；AC＝72；∴∠ABC＝135°；∠BAC＝30°；在△ABC中，＝⇒＝⇒BC＝＝72．如图D1C⊥平面ABC，在直角△BD1C中，tan∠D1BC＝＝⇒h＝BC•tan∠D1BC＝72×tan∠30°＝．故答案为：．16．若函数有且仅有一个零点，则实数m的取值范围{m|m＝﹣或m≥0}．【解答】解：令u（x）＝x﹣lnx，x＞0；则u'（x）＝，∴0＜x＜1时，u'（x）＜0；x＞1时，u'（x）＞0；于是u（x）＝x﹣lnx在（0，1）上递减，在（1，+∞）上递增；最小值为u（1）＝1＞0，∴∀x∈（0，+∞），x﹣lnx＞0；由f（x）＝0，即+m（lnx﹣x）﹣x＝0，解得：m＝；设g（x）＝，y＝m；由于函数有且仅有一个零点；所以直线y＝m与函数g（x）有且只有一个交点；由g'（x）＝，此时不能完全判断导函数值的正负；再令h（x）＝x+2﹣2lnx，得h'（x）＝，当x∈（0，2）时，h'（x）＜0；当x∈（2，+∞）时，h'（x）＞0；于是，h（x）在（0，2）上递减，（2，+∞）上递增．那么h（x）≥h（2）＝2（2﹣ln2）＞0．由此，g'（x）的正负只同x﹣1有关，由此得g（x）在（0，1）上递减，在（1，+∞）上递增，且g（x）的极小值为g（1）＝﹣；又x→0时，g（x）→0；x→+∞时，g（x）→+∞；g（x）图象大值如图所示，结合g（x）的图象，得m≥0或m＝﹣．故答案为：{m|m＝﹣或m≥0}．三、填空题：共70分．17．已知函数f（x）＝（cos x﹣sin x）2﹣2sin2x．（1）求函数f（x）的最小正周期与单调递减区间；（2）若f（x0）＝﹣1，且，求x0的值．【解答】解：（1）函数f（x）＝（cos x﹣sin x）2﹣2sin2x＝1﹣2sin x cos x﹣2•＝cos2x﹣sin2x＝cos（2x+），所以函数f（x）的最小正周期为T＝＝π，又函数y＝cos x的单调减区间为[2kπ，2kπ+π]，k∈Z；令2kπ≤2x+≤2kπ+π，k∈Z；解得kπ﹣≤x≤kπ+，k∈Z；所以f（x）的单调递减区间为[kπ﹣，kπ+]，k∈Z；（2）若f（x0）＝﹣1，则cos（2x0+）＝﹣1，即cos（2x0+）＝﹣，再由，可得2x0+∈（﹣，﹣）；所以2x0+＝﹣，解得x0＝﹣．18．已知数列{a n}满足，且a1＝1，a4＝7，数列{b n}的前n项和．（1）求数列{a n}{b n}的通项公式；（2）设，求数列{c n}的前n项和T n．【解答】解：（1）数列{a n}满足，可得a n+2﹣a n+1＝a n+1﹣a n，即{a n}为等差数列，a1＝1，a4＝7，可得公差d＝＝2，则a n＝1+2（n﹣1）＝2n﹣1；数列{b n}的前n项和，可得b1＝S1＝4﹣2＝2；n≥2时，b n＝S n﹣S n﹣1＝2n+1﹣2﹣2n+2＝2n，则b n＝2n，n∈N*；（2）＝22n﹣1+n，则前n项和T n＝（2+8+…+22n﹣1）+（1+2+…+n）＝+n（n+1）＝（4n﹣1）+（n2+n）．19．已知△ABC中三个内角A，B，C满足．（1）求sin B；（2）若，b是角B的对边，，求△ABC的面积．【解答】解：（1）∵．sin（A+C）＝sin B，∴cos B＝sin B+1，又sin2B+cos2B＝1，化为：3sin2B+2sin B﹣1＝0，1＞sin B＞0．联立解得sin B＝．（2），又A+B+C＝π，可得：2A＝﹣B，C为钝角．∴sin2A＝cos B．又，∴＝＝＝3，∴a＝3sin A，c＝3sin C，B为锐角，∴cos B＝．∴△ABC的面积S＝ac sin B＝×3sin A×3sin C×＝sin A sin（+A）＝sin A cos A＝sin2A＝cos B＝×＝．∴∴△ABC的面积S为．20．已知函数．（1）求函数f（x）在区间[1，+∞）上的值域；（2）若实数x1，x2均大于1且满足，求f（x1x2）的最小值．【解答】解：（1）由题意得f（x）＝，由x≥1，知lnx≥0，于是lnx+2≥2，∴0＜，即﹣2≤﹣，∴﹣1≤1﹣＜1，∴f（x）的值域为[﹣1，1）．（2）f（x1）+f（x2）＝1﹣+1﹣＝，所以，又x1＞1，x2＞1，∴lnx1x2＝lnx1+lnx2＝lnx1+2+lnx2+2﹣4＝，＝≥，当且仅当，即x1＝x2时，取“＝”，故（x1x2）min＝e，∵f（x）在（1，+∞）上是增函数，∴f（x1x2）min＝．21．已知函数f（x）＝e x﹣ax2，a∈R，x∈（0，+∞）．（1）若f（x）存在极小值，求实数a的取值范围；（2）若，求证：f（x）＞ax（lnx﹣x）．【解答】解：（1）：∵f′（x）＝e x﹣2ax＝x（﹣2a），令H（x）＝，则H′（x）＝，当0＜x＜1时，H′（x）＜0，H（x）单调递减，且x→0时，H（x）→+∞，当x＞1时，H′（x）＞0，H（x）单调递增，且x→+∞时，H（x）→+∞，∴H（x）min＝H（1）＝e，①当2a≤e即a时，f′（x）≥0，f（x）在（0，+∞）上单调递增，没有极值，②当a＞时，存在0＜x1＜1＜x2，使得f′（x1）＝f′（x2）＝0，当x∈（0，x1），（x2，+∞）时，f′（x）＞0，f（x）单调递增，当x∈（x1，x2）时，f′（x）＜0，f（x）单调递减，∴x2是f（x）的极小值，综上可得，a（2）要证f（x）＞ax（lnx﹣x），即证e x＞axlnx，①当0＜x≤1时，e x＞1，axlnx≤0，显然成立，②当x＞1时，xlnx＞0，结合已知0＜a可得，0＜axlnx，于是问题转化为，即证，令g（x）＝，则g′（x）＝，令h（x）＝2e x﹣2（x﹣1）﹣x，则h′（x）＝2xe x﹣2﹣1，且在（0，+∞）上单调递增，∵＜0，h′（2）＝3＞0，存在x0∈（1，2）使得h（x0）＝0，即＝1，∴h（x）在（1，x0）上单调递减，在（x0，+∞）上单调递增，又h（1）＝﹣1＜0，h（2）＝0，故当x∈（1，2）时，g′（x）＜0，g（x）单调递减，当x∈（2，+∞）时，g′（x）＞0，g（x）单调递增，∴g（x）≥g（2）＝1﹣ln2＞0，故g（x）＞0，得证．（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．在平面直角坐标系xOy中，曲线C的参数方程为（α为参数），以坐标原点0为极点，x的正半轴为极轴，取相同长度单位建立极坐标系，直线l的极坐标方程．（1）求曲线C的普通方程与极坐标方程；（2）设射线OM：与曲线C交于点A，与直线l交于点B，求线段AB的长．【解答】解：（1）由，两边平方作和得，，∴曲线C的普通方程为x2+y2＝4．∵x2+y2＝ρ2，∴ρ2＝4，则ρ＝2；（2）把代入，可得，解得．即B点的极径为．由（1）得ρA＝2，∴|AB|＝|ρA﹣ρB|＝．[选修4-5：不等式选讲]23．设函数f（x）＝|x﹣m|+|x+1|+5（m∈R）．（1）当m＝2时，求不等式f（x）≥0的解集；（2）若f（x）≥﹣2，求实数m的取值范围．【解答】解：（1）当m＝2时，f（x）＝|x﹣2|+|x+1|＝5，当x≤﹣1，f（x）＝﹣（x﹣2）﹣（x+1）﹣5≥0，解得x≤﹣2；当﹣1＜x＜2，f（x）＝﹣（x﹣2）+x+1﹣5≥0，无解；当x≥2时，f（x）＝x﹣2+x+1﹣5≥0，解得x≥3；综上，不等式的解集为（﹣∞，﹣2]∪[3，+∞）．（2）由f（x）＝|x﹣m|+|x+1|﹣5≥|（x﹣m）﹣（x+1）|﹣5＝|m+1|﹣5≥﹣2，所以|m+1|≥3，即m≥2或者m≤﹣4．。
2020年(理科数学)(新课标Ⅰ)试卷真题+参考答案+详细解析
2020年全国统一高考数学试卷（理科）（新课标Ⅰ）一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．（5分）若1z i =+，则2|2|(z z -= ) A ．0B ．1C ．2D ．22．（5分）设集合2{|40}A x x =-，{|20}B x x a =+，且{|21}A B x x =-，则(a = )A ．4-B ．2-C ．2D ．43．（5分）埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为( )A 51-B 51-C 51+D 51+4．（5分）已知A 为抛物线2:2(0)C y px p =>上一点，点A 到C 的焦点的距离为12，到y 轴的距离为9，则(p = ) A ．2B ．3C ．6D ．95．（5分）某校一个课外学习小组为研究某作物种子的发芽率y 和温度x （单位：C)︒的关系，在20个不同的温度条件下进行种子发芽实验，由实验数据()(1,i i x y i =，2，⋯，20)得到下面的散点图：由此散点图，在10C ︒至40C ︒之间，下面四个回归方程类型中最适宜作为发芽率y 和温度x 的回归方程类型的是( ) A ．y a bx =+B ．2y a bx =+C ．x y a be =+D ．y a blnx =+6．（5分）函数43()2f x x x =-的图象在点(1,(1))f 处的切线方程为( ) A ．21y x =--B ．21y x =-+C ．23y x =-D ．21y x =+7．（5分）设函数()cos()6f x x πω=+在[,]ππ-的图象大致如图，则()f x 的最小正周期为( )A ．109πB ．76π C ．43π D ．32π 8．（5分）25()()y x x y x++的展开式中33x y 的系数为( )A ．5B ．10C ．15D ．209．（5分）已知(0,)απ∈，且3cos28cos 5αα-=，则sin (α= ) A 5B ．23 C ．13D 5 10．（5分）已知A ，B ，C 为球O 的球面上的三个点，1O 为ABC ∆的外接圆．若1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为( )A ．64πB ．48πC ．36πD ．32π11．（5分）已知22:2220M x y x y +---=，直线:220l x y ++=，P 为l 上的动点．过点P 作M 的切线PA ，PB ，切点为A ，B ，当||||PM AB 最小时，直线AB 的方程为( ) A ．210x y --=B ．210x y +-=C ．210x y -+=D ．210x y ++=12．（5分）若242log 42log a b a b +=+，则( ) A ．2a b >B ．2a b <C ．2a b >D ．2a b <二、填空题：本题共4小题，每小题5分，共20分。
2020-2021学年高三数学（理科）第一次高考模拟考试试题及答案解析
2020-2021学年⾼三数学（理科）第⼀次⾼考模拟考试试题及答案解析@学⽆⽌境！@绝密★启⽤前试卷类型：A 最新第⼀次⾼考模拟考试数学试卷（理科）本试卷分选择题和⾮选择题两部分，共4页，满分150分，考试时间120分钟。
注意事项：1．答卷前，考⽣要务必填写答题卷上的有关项⽬。
2．选择题每⼩题选出答案后，⽤2B 铅笔把答案填在答题卡相应的位置上。
3．⾮选择题必须⽤⿊⾊字迹的钢笔或签字笔作答，答案必须写在答题卷各题⽬指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使⽤铅笔和涂改液. 不按以上要求作答的答案⽆效。
4．考⽣必须保持答题卷的整洁，考试结束后，将答题卷交回。
第Ⅰ卷（选择题，共60分）⼀.选择题：本⼤题共12⼩题，每⼩题5分，共60分.在每⼩题给出的四个选项中，只有⼀项是符合题⽬要求的. 1.复数i215-（i为虚数单位）的虚部是（）A. 2iB. 2i -C. 2-D. 22. 下列函数在其定义域上既是奇函数⼜是减函数的是（）A ．()2x f x =B ．()sin f x x x =C ．1()f x x =D ．()||f x x x =- 3.已知()=-παcos 12，πα-<<，则tan α=（）A.B.C. D.4.设双曲线2214y x -=上的点P到点的距离为6，则P点到(0,的距离是（）@学⽆⽌境！@A ．2或10 B.10 C.2 D.4或85. 下列有关命题说法正确的是（）A. 命题p ：“sin +cos =2x x x ?∈R ，”，则?p 是真命题 B ．21560x x x =---=“”是“”的必要不充分条件 C ．命题2,10x x x ?∈++的否定是：“210x x x ?∈++D ．“1>a ”是“()log (01)(0)a f x x a a =>≠+∞，在，上为增函数”的充要条件6. 将函数-=32sin )(πx x f 的图像向右平移3π个单位得到函数)(x g 的图像,则)(x g 的⼀条对称轴⽅程可以为（） A. 43π=x B. 76x π= C. 127π=x D. 12π=x 7．2015年⾼中⽣技能⼤赛中三所学校分别有3名、2名、1名学⽣获奖，这6名学⽣要排成⼀排合影，则同校学⽣排在⼀起的概率是（）A ．130 B ．115 C ．110 D ．158．执⾏如图8的程序框图，若输出S 的值是12，则a 的值可以为（）A ．2014B ．2015C ．2016D ．20179．若某⼏何体的三视图(单位：cm )如图所⽰，则该⼏何体的体积（）A.310cmB.320cmC.330cmD.340cm10．若nx x ??? ?-321的展开式中存在常数项，则n 可以为（） A ．8 9 C ．10 D. 11 11．=∠=?==?C CA A B CA BC ABC 则中在,60,6,8, （）A ．?60B ．C ．?150D ．?120 12. 形如)0,0(||>>-=b c cx by 的函数因其图像类似于汉字中的“囧”字，故我们把其⽣动地称为“囧函数”．若函数()()2log 1a f x x x =++)1,0(≠>a a 有最⼩值，则当,c b 的值分别为⽅程222220x y x y +--+=中的,x y 时的“囧函数”与函数||log x y a =的图像交点个数为（）．A ．1B ．2C ．4D ．6第Ⅱ卷（⾮选择题，共90分）⼆.填空题：本⼤题共4⼩题，每⼩题 5分，共20分.13．⼀个长⽅体⾼为5，底⾯长⽅形对⾓线长为12，则它外接球的表⾯积为@学⽆⽌境！@14．如图，探照灯反射镜的纵截⾯是抛物线的⼀部分，光源在抛物线的焦点F 处，灯⼝直径AB 为60cm ，灯深（顶点O 到反射镜距离）40cm ，则光源F 到反射镜顶点O 的距离为15.已知点()y x P ,的坐标满⾜条件>-+≤≤02221y x y x ，那么()221y x ++的取值范围为 16．CD CB AD AC AD AB ，AB D ABC 3,,3,===?且的⼀个三等分点为中在，则B cos =三.解答题：本⼤题共5⼩题，每题12分共60分.解答应写出⽂字说明，证明过程或演算步骤.17．（本⼩题满分12分）已知{}n b 为单调递增的等差数列，168,266583==+b b b b ,设数列{}n a 满⾜n b n n a a a a 2222233221=++++(1)求数列{}n b 的通项； (2)求数列{}n a 的前n 项和n S 。
2020届高考全国卷1数学(理)模拟试卷含答案详解-202全国卷1数学
第 1 页 共 8 页 2020年普通高等学校招生全国统一考试理科数学模拟试题卷注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其它答案标号。
回答非选择题时，将答案写在答题卡上。
写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题（本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知集合}02|{2<--=x x x A ，}log |{2m x x B >=，若B A ⊆，则实数m 的取值范围（ ）A ．]21,(-∞ B ．]4,0( C ．]1,21( D ．]21,0( 2. 若复数z 满足232z z i +=-，其中i 为虚数单位，则z=（ ）A ．1+2iB ．1﹣2iC ．﹣1+2iD ．﹣1﹣2i 3．在等差数列{}n a 中，810112a a =+，则数列{}n a 的前11项和11S =( ) A. 8 B. 16 C. 22 D. 444． 某几何体的三视图如图（其中侧视图中的圆弧是半圆），则该几何体的表面积为A ．9214π+B ．8214π+C ．9224π+D ．8224π+5．若)()1(*3N n xx x n ∈+ 的展开式中存在常数项，则下列选项中n 可为( ) A ．9 B ．10 C ．11 D ．12 6．某地区高考改革，实行“3+1+2”模式，即“3”指语文、数学、外语三门必考科目，“1”指在物理、历史两门科目中必选一门，“2”指在化学、生物、政治、地理以及除了必选一门以外的历史或物理这五门学科中任意选择两门学科，则一名学生的不同选科组合有( )A. 8种B. 12种C. 16种D. 20种7. 已知抛物线C: 28=x y ，定点A （0，2），B （0，2-），点P 是抛物线C 上不同于顶点的动点，则∠PBA 的取值范围为 （ ） A. 0,4π⎛⎤ ⎥⎝⎦ B. 42，ππ⎡⎫⎪⎢⎣⎭ C. 0,3π⎛⎤ ⎥⎝⎦D. 32，ππ⎡⎫⎪⎢⎣⎭8． 若0>ω，函数)3cos(πω+=x y 的图象向右平移3π个单位长度后与函数x y ωsin =图象重合，则ω的最小值为A.211B.25C.21D. 23 9．抛掷两枚骰子，当至少有一枚5点或6点出现时，就说这次试验成功，则在9次试验中成功次数的均值为（ ）。
2020年河南省、广东省等五岳联考高考数学模拟试卷(理科)(4月份)(附答案详解)
2020年河南省、广东省等五岳联考高考数学模拟试卷（理科）（4月份）一、单选题（本大题共12小题，共60.0分）1. 设集合M ={x|x 2−2x −3<0,x ∈Z}，则集合M 的真子集个数为( )A. 8B. 7C. 4D. 32. 已知i 是虚数单位，则化简(1+i1−i )2020的结果为( )A. iB. −iC. −1D. 13. 若干年前，某教师刚退休的月退休金为4000元，月退休金各种用途占比统计图如下面的条形图该教师退休后加强了体育锻炼，目前月退休金的各种用途占比统计图如下面的折线图．已知目前的月就医费比刚退休时少100元，则目前该教师的月退休金为( )A. 4500元B. 5000元C. 5500元D. 6000元4. 将包括甲、乙、丙在内的8人平均分成两组参加文明交通”志愿者活动，其中一组指挥交通，一组分发宣传资料，则甲、乙至少一人参加指挥交通且甲、丙不在同一组的概率为( )A. 27B. 37C. 17D. 3145. 已知抛物线y 2=4x 的焦点为F ，过点F 和抛物线上一点M(3,2√3)的直线l 交抛物线于另一点N ，则|NF|：|NM|等于( )A. 1：2B. 1：3C. 1：4D. 1：√36. 在所有棱长都相等的直三棱柱ABC −A 1B 1C 1中，D ，E 分别为棱CC 1，AC 的中点，则直线AB 与平面B 1DE 所成角的余弦值为( )A. √3010B. √3020C. √13020D. √70107. 已知点A(4,3)，点B 为不等式组{y ≥0x −y ≤0x +2y −6≤0所表示平面区域上的任意一点，则|AB|的最小值为( )A. 5B. 4√55C. √5D. 2√558. 给出下列说法①定义在[a,b]上的偶函数f(x)=x 2−(a +4)x +b 的最大值为20； ②“x =π4”是“tanx =1”的充分不必要条件；③命题“∃x 0∈(0,+∞),x 0+1x 0≥2”的否定形式是“∀x ∈(0,+∞),x +1x <2”其中正确说法的个数为( )A. 0B. 1C. 2D. 39. 已知log m 3>0,a =m log 42,b =m log 32,c =m 20.5，则a ，b ，c 间的大小关系为( )A. a <b <cB. b <a <cC. c <a <bD. b <c <a10. 元代数学家朱世杰在《算学启蒙》中提及如下问题：今有银一秤一斤十两(1秤=15斤，1斤=16两)，令甲、乙、丙从上作折半差分之，问：各得几何？其意思是：现有银一秤一斤十两，现将银分给甲、乙、丙三人，他们三人每一个人所得是前一个人所得的一半．若银的数量不变，按此法将银依次分给7个人，则得银最少的一个人得银( )A. 9两B. 266127两C.26663两 D. 250127两11. 在△ABC 中，角A 、B 、C 的对边分别是a 、b 、c ，若acosB −bcosA =c3，则acosBacosA+bcosB的最大值为( )A. √2B. √22 C. √32 D. 2√3312. 已知f(x)为奇函数，g(x)为偶函数，且f(x)+g(x)=log 3(3x +1)，不等式3g(x)−f(x)−t ≥0对x ∈R 恒成立，则t 的最大值为( )A. 1B. 3−2log 32C. 2D. 32log 32−1二、单空题（本大题共4小题，共20.0分）13. 已知向量a ⃗ =(2,−√5)，b ⃗ =(1,2√5)，则b ⃗ 在a ⃗ 方向上的投影等于______． 14. 在△ABC 中，∠B =2π3，A 、B 是双曲线E 的左、右焦点，点C 在E 上，且BC =12AB ，则E 的离心率为______．15. 已知函数f(x)=cos(ωx +φ)(ω>0,0≤φ≤π)是奇函数，且在[−π6,π4]上单调递减，则ω的最大值是 ．16. 已知三棱锥A −BCD 中，平面ABD ⊥平面BCD ，BC ⊥CD ，BC =CD =2，AB =AD =√6，则三棱锥A −BCD 的外接球的体积为______．三、解答题（本大题共7小题，共82.0分）17.已知数列{a n}的前n项和为S n，且S n=12na n+a n−1．(1)求数列{a n}的通项公式；(2)若数列{2a n2}的前n项和为T n，证明：T n<32．18.如图，在以A，B，C，D，E，F为顶点的五面体中，四边形ABEF为正方形，AF⊥DF，AF=2√2FD，∠DFE=∠CEF=45．(1)证明：DC//FE；(2)求二面角D−BE−C的平面角的余弦值．19.已知点P在圆O：x2+y2=9上运动，点P在x轴上的投影为Q，动点M满足4PQ⃗⃗⃗⃗⃗ = 3√2MQ⃗⃗⃗⃗⃗⃗⃗ ．(1)求动点M的轨迹E的方程；(2)设G(−3,0)，H(3,0)，过点F(1,0)的动直线l与曲线E交于A、B两点．问：直线AG与BH的斜率之比是否为定值？若为定值，求出该定值；若不为定值，试说明理由．20.某县为了帮助农户脱贫致富，鼓励农户利用荒地山坡种植果树，某农户考察了三种不同的果树苗A、B、C.经过引种实验发现，引种树苗A的自然成活率为0.7，引种树苗B、C的自然成活率均为p(0.6≤p≤0.8)．(1)任取树苗A、B、C各一棵，估计自然成活的棵数为X，求X的分布列及其数学期望；(2)将(1)中的数学期望取得最大值时p的值作为B种树苗自然成活的概率，该农户决定引种n棵B种树苗，引种后没有自然成活的树苗有75%的树苗可经过人栽培技术处理，处理后成活的概率为0.8，其余的树苗不能成活．①求一棵B种树苗最终成活的概率；②若每棵树苗引种最终成活可获利400元，不成活的每棵亏损80元该农户为了获利期望不低于10万元，问至少要引种种树苗多少棵？21.已知函数f(x)=(a−1)x+xlnx的图象在点A(e2,f(e2))(e为自然对数的底数)处的切线斜率为4．(1)求实数a的值；(2)若m∈Z，且m(x−1)<f(x)+1对任意x>1恒成立，求m的最大值．22.以坐标原点为极点，以x轴的非负半轴为极轴建立极坐标系，已知曲线C的极坐标方程为ρ=√2(θ∈[−π2,π2])，直线l的参数方程为{x=−2+tcosαy=−4+tssinα(t为参数)．(1)点A在曲线C上，且曲线C在点A处的切线与直线：x+2y+1=0垂直，求点A的直角坐标；(2)设直线l与曲线C有且只有一个公共点，求直线l的斜率的取值范围．23.设函数f(x)=|x−1|+2|x+1|，x∈R．(1)求不等式f(x)<5的解集；(2)若关于x的不等式f(x)+2<|2t−1|在实数范围内解集为空集，求实数t的取值范围．答案和解析1.【答案】B【解析】解：集合M={x|x|x2−2x−3<0,x∈Z}={x|−1<x<3,x∈Z}={0,1,2}，所以集合M的真子集个数为：23−1=7个．故选：B．由列举法得到集合A中的元素个数，再由结论：含有n个元素的集合的真子集数共有：2n−1个，即得答案本题主要考查了集合的子集，一般地，含有n个元素的集合的真子集数共有：2n−1个．2.【答案】D【解析】解：∵1+i1−i =(1+i)2(1−i)(1+i)=i，∴(1+i1−i)2020=i2020=i4×505=1．故选：D．利用复数代数形式的乘除运算化简1+i1−i，再由虚数单位i的运算性质得答案．本题考查复数的代数形式的乘除运算，考查虚数单位i的运算性质，是基础题．3.【答案】B【解析】解：设目前该教师的月退休金为x元，则有10%x=4000×15%−100，解之得x=5000，故选：B．根据题中目前的月就医费比刚退休时少100元可列等式，求出即可．本题考查对条形图，折线图的数据整合能力，属于基础题．4.【答案】B【解析】解：①甲指挥交通，乙不指挥交通，是丙不能指挥交通，故有C52=10种方法，②乙指挥交通，甲不指挥交通，则丙必须指挥交通，故有C52=10种方法，③甲、乙都指挥交通，则丙不能指挥交通，故有C52=10种方法，∴甲、乙至少一人参加指挥交通且甲、丙不在同一组的概率为： p =3C 52C 84=37．故选：B ．①甲指挥交通，乙不指挥交通，是丙不能指挥交通，故有C 52=10种方法，乙指挥交通，甲不指挥交通，则丙必须指挥交通，故有C 52=10种方法，甲、乙都指挥交通，则丙不能指挥交通，故有C 52=10种方法，由此能求出甲、乙至少一人参加指挥交通且甲、丙不在同一组的概率．本题考查概率的求法，考查分类讨论思想、列举法等基础知识，考查运算求解能力，是基础题．5.【答案】C【解析】解：抛物线y 2=4x 的焦点为F(1,0)，所以k FM =2√33−1=√3，由{y 2=4x y =√3(x −1)，可得3x 2−10x +3=0，所以x 1=3，x 2=13， 所以|FN||MN|=x 2+p2x 1+x 2+p=13+13+13+2=14．故选：C ．求出抛物线的焦点坐标，通过直线与抛物线方程联立，求出MN 的坐标，然后转化求解|NF|：|NM|即可．本题考查抛物线的焦点弦，抛物线的简单性质以及数形结合的思想的应用，是中档题．6.【答案】C【解析】 【分析】本题考查了利用空间向量求线面角的问题，属于中档题．根据题意，建立空间直角坐标系，将所求的角转化为直线AB 与平面B 1DE 的法向量的夹角来求即可． 【解答】解：因为是所有棱长都相等的直三棱柱ABC −A 1B 1C 1． ∴该棱柱的上下底面是正三角形，侧面都是正方形，设各棱长均为2，取AB 的中点为原点，直线OC ，OB 分为x ，y 轴建立如图所示的空间直角坐标系．则O(0,0,0)，B(0,1,0)，E(√32,−12,0)，D(√3,0,1)，B 1(0,1,2)． ∴ED⃗⃗⃗⃗⃗ =(√32,12,1)，EB 1⃗⃗⃗⃗⃗⃗⃗ =(−√32,32,2)， 设平面B 1DE 的法向量m ⃗⃗⃗ =(x,y,z)， ∴{m ⃗⃗⃗ ⋅ED⃗⃗⃗⃗⃗ =0m ⃗⃗⃗ ⋅EB 1⃗⃗⃗⃗⃗⃗⃗ =0，∴{√32x +12y +z =0−√32x +32y +2z =0，令x =2，得m ⃗⃗⃗ =(2,6√3,−4√3)．∵OB ⃗⃗⃗⃗⃗⃗ =(0,1,0)且AB ⃗⃗⃗⃗⃗ //OB ⃗⃗⃗⃗⃗⃗ ． 设所求角为θ，则sinθ=|m⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ |m ⃗⃗⃗ |OB⃗⃗⃗⃗⃗⃗ |=3√3020， ∴cosθ=√13020． 故选：C ．7.【答案】C【解析】解：不等式组{y ≥0x −y ≤0x +2y −6≤0的可行域如图：则|AB|的最小值为A 到B 的距离． 由{x −y =0x +2y −6=0解得B(2,2)， |AB|的最小值：√(4−2)2+(3−2)2=√5， 故选：C ．画出约束条件的可行域，利用已知条件求解距离的最小值即可．本题考查线性规划的简单应用，是基本知识的考查，考查数形结合以及点到直线的距离公式的应用．8.【答案】D【解析】解：①定义在[a,b]上的偶函数f(x)=x2−(a+4)x+b，所以有f(−x)=f(x)，即a=−4，定义域为[a,b]，所以b=4，所以函数f(x)在x=±4时取得最大值为20，正确；②由充要条件的定义“x=π4”能推出“tanx=1”成立，而“tanx=1”不能推出“x=π4”成立，所以“x=π4”是“tanx=1”的充分不必要条件正确；③由特称量词命题的否定定义可得命题“∃x0∈(0,+∞),x0+1x0≥2”的否定形式是“∀x∈(0,+∞),x+1x<2”正确；其中正确说法的个数为①②③三个，故选：D．①利用函数的奇偶性和最值可得答案，②由充要条件定义可判断，③由命题的否定定义可判断，从而可得结论．本题考查命题真假判断及充要条件，函数的奇偶性和最值，命题的否定，属基础题．9.【答案】A【解析】【分析】本题考查对数函数和指数函数的性质，属于基础题．利用对数函数和指数函数的性质求解．【解答】解：∵log m3>0，∴m>1，∵0<log42<log32<1，20.5>1，∴a<b<c，故选：A．10.【答案】B【解析】解：由题意共有银：16×16+10=266两，设分银最少的为a两，则7人的分银量构成以a为首项，2为公比的等比数列，则a(1−27)1−2=266，解得a=266127．故选：B．共有银：16×16+10=266两，设分银最少的为a两，则7人的分银量构成以a为首项，2为公比的等比数列，由此利用等比数列前n项和公式能求出结果．本题考查等比数列的首项的求法，考查等比数列的性质等基础知识，考查运算求解能力，是基础题．11.【答案】B【解析】解：因为acosB−bcosA=c3，由正弦定理可得，sinAcosB−sinBcosA=13sinC=13(sinAcosB+sinBcosA)，化简可得，tanA=2tanB，则acosBacosA+bcosB=sinAcosBsinAcosA+sinBcosB=1cosAcosB+sinBsinA≤2√sinAcosB，当且仅当cosAcosB=sinBsinA时取等号，=2√tanBtanA =√22，即最大值√22，故选：B．由已知结合正弦定理及和差角公式化简可得tanA=2tanB，然后对所求式子进行化简，结合基本不等式即可求解．本题主要考查了正弦定理及三角恒等变形在求解三角形中的应用，还考查了基本不等式求解最值的应用，属于中档试题．12.【答案】B【解析】解：f(x)为奇函数，g(x)为偶函数，可得f(−x)=−f(x)，g(−x)=g(x)，由f(x)+g(x)=log3(3x+1)，①可得f(−x)+g(−x)=log3(3−x+1)，即为−f(x)+g(x)=log3(3−x+1)，②联立①②可得f(x)=12x，g(x)=log3(3x+1)−12x，由不等式3g(x)−f(x)−t≥0对x∈R恒成立，可得t ≤3g(x)−f(x)=3log 3(3x+1)−2x =log 3(3x +1)332x恒成立，设ℎ(x)=(3x +1)332x，ℎ′(x)=ln3⋅32x (1+3x )2(3x −2)34x，当x >log 32时，ℎ′(x)>0，ℎ(x)递增，当x <log 32时，ℎ′(x)<0，ℎ(x)递减， 可得x =log 32处ℎ(x)取得极小值，且为最小值3−2log 32， 则t ≤3−2log 32， 故选：B ．运用奇偶性的定义，将x 换为−x ，联立两个方程求得f(x)，g(x)，由题意可得t ≤3g(x)−f(x)的最小值，构造函数ℎ(x)，求得导数和单调性、极值和最小值，可得所求范围． 本题考查函数的奇偶性的定义和函数恒成立问题解法，注意运用参数分离和构造函数法，运用导数求得单调性和最值，考查化简运算能力和推理能力，属于中档题．13.【答案】−83【解析】解：向量a ⃗ =(2,−√5)，b ⃗ =(1,2√5)， 则b ⃗ 在a⃗ 方向上的投影为|b ⃗|cosθ=a ⃗ ⋅b ⃗ |a ⃗ |=√5×2√5√22+(−√5)2=−83．故答案为：−83．根据平面向量投影的定义，计算即可．本题考查了平面向量投影的定义与计算问题，也考查了平面向量的坐标运算问题，是基础题．14.【答案】√7+13【解析】解：由题得，AB =2c ，BC =c ，∠B =23π， 则根据余弦定理可得AC =√AB 2+BC 2−2AB ⋅BC ⋅cosB =√4c 2+c 2−2×2c ×(−12)=√7c ，所以√7c −c =2a ，解得e =√7+13，故答案为√7+13．根据余弦定理可得AC =√7c ，结合双曲线定义，则有√7c −c =2a ，即可解出e ．本题考查双曲线离心率的求法，考查余弦定理的应用，属于中档题．15.【答案】2【解析】【分析】本题考查了奇函数的定义，奇函数在原点有定义时，原点处的函数值为0，三角函数的诱导公式，正弦型函数的单调性，考查了计算能力．根据f(x)是奇函数即可得出φ=π2，进而得出f(x)=−sinωx，然后根据题意即可得出[−π6,π4]⊆[−π2ω,π2ω]，然后即可得出0<ω≤2，从而得出ω的最大值．【解答】解：∵f(x)是R上的奇函数，∴f(0)=cosφ=0，且0≤φ≤π，∴φ=π2，∴f(x)=cos(ωx+π2)=−sinωx，且ω>0，f(x)在[−π6,π4]上单调递减，∴[−π6,π4]⊆[−π2ω,π2ω]，∴π2ω≥π4且−π2ω⩽−π6，解得0<ω≤2，∴ω的最大值是2．故答案为：2．16.【答案】9π2【解析】解：∵AB=AD，取BD中点E，则AE⊥BD ∵平面ABD⊥平面BCD，则AE⊥BD，故AE⊥平面BCD，则球心O在AE上，且BD=2√2，EB=√2，AE=√AD2−BE2=2，设外接球的半径R，则OB2=OE2+EB2，∴R2=2+(2−R)2，解可得，R=32，V=4πR33=43×(32)3=9π2．根据四棱锥的性质可先求出球心的位置，然后根据勾股定理可求半径R，然后代入球的体积公式可求．本题主要通过空间几何体的外接球问题，考查了考生的空间想象能力，推理论证能力，属于中档试题．17.【答案】解：(1)当n=1时，S1=12a1+a1−1=a1，得a1=2，当n≥2时，由S n=12na n+a n−1得，S n−1=12(n−1)a n−1+a n−1−1，作差得，a n=12na n+a n−1−12a n−1−a n−1+1，化简得，na n=(n+1)a n−1，即a na n−1=n+1n，由a n=a na n−1⋅a n−1a n−2…a2a1⋅a1=n+1n⋅nn−1…32⋅2=n+1，综上，a n=n+1(n∈N∗)；(2)证明：根据(1)得，当n=1时，2a12=12，当n≥2时，2a n2=2(n+1)2<2n(n+1)=2(1n−1n+1)，所以T n=222+232+242+⋯+2(n+1)2<12+2(12−13+13−14+⋯+1n−1n+1)=12+1−2n+1<32，故命题成立．【解析】(1)当n=1时，S1=12a1+a1−1=a1，得a1=2，当n≥2时，由S n=12na n+a n−1得，S n−1=12(n−1)a n−1+a n−1−1，作差化简求出a n的通项公式；(2)根据(1)得，当n=1时，2a12=12，当n≥2时，2a n2=2(n+1)2<2n(n+1)=2(1n−1n+1)，根据裂项相消法和放缩法，证明结论成立．本题考查了数列递推式求数列的通项公式和前n项和公式，考查运算能力，中档题．18.【答案】解：(1)证明：∵四边形ABEF 为正方形，∴AB//FE ，∵AB ⊄平面EFDC ，FE ⊂平面EFDC ，∴AB//平面EFDC ， ∵AB ⊂平面ABCD ，平面ABCD ∩平面EFDC =DC ， ∴DC//AB ，∴DC//FE ．(2)解：∵AF ⊥EF ，AF ⊥DF ，∴AF ⊥平面EFDC ， ∴平面ABEF ⊥平面EFDC ，作DG ⊥EF ，垂足为G ，则DG ⊥平面ABEF ，∴以G 为原点，GF 为x 轴，在平面ABEF 中，过G 作EF 的垂线为y 轴，GD 为z 轴，建立空间直角坐标系，则题意得∠DFG =∠CEF =45°，设AB =4， 则D(0,0,1)，E(−3,0,0)，C(−2,0,1)，B(−3,4,0)，BD ⃗⃗⃗⃗⃗⃗ =(3,−4,1)，ED ⃗⃗⃗⃗⃗ =(3,0,1)，BC ⃗⃗⃗⃗⃗ =(1,−4,1)，EC ⃗⃗⃗⃗⃗ =(1,0,1)， 设平面DBE 的法向量m⃗⃗⃗ =(x,y,z)， 则{m ⃗⃗⃗ ⋅BD⃗⃗⃗⃗⃗⃗ =3x −4y +z =0m ⃗⃗⃗ ⋅ED ⃗⃗⃗⃗⃗ =3x +z =0，取x =1，得m⃗⃗⃗ =(1,0,−3)， 设平面BEC 的法向量n⃗ =(a,b,c)， 则{n ⃗ ⋅BC ⃗⃗⃗⃗⃗ =a −4b +c =0n ⃗ ⋅EC ⃗⃗⃗⃗⃗ =a +c =0，取a =1，得n ⃗ =(1,0,−1)， 设二面角D −BE −C 的平面角为θ， 则二面角D −BE −C 的平面角的余弦值为： cosθ=|m ⃗⃗⃗ ⋅n ⃗⃗ ||m ⃗⃗⃗ |⋅|n ⃗⃗ |=1√10⋅√2=2√55．【解析】(1)推导出AB//FE ，从而AB//平面EFDC ，进而DC//AB ，由此能证明DC//FE ． (2)由AF ⊥EF ，AF ⊥DF ，得AF ⊥平面EFDC ，从而平面ABEF ⊥平面EFDC ，作DG ⊥EF ，垂足为G ，则DG ⊥平面ABEF ，以G 为原点，GF 为x 轴，在平面ABEF 中，过G 作EF 的垂线为y 轴，GD 为z 轴，建立空间直角坐标系，利用向量法能证明二面角D −BE −C 的平面角的余弦值．本题考查线线平行的证明，考查二面角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．19.【答案】解：(1)设M(x,y)，P(x 0,y 0)，Q(x 0,0)， 则由4PQ ⃗⃗⃗⃗⃗ =3√2MQ ⃗⃗⃗⃗⃗⃗⃗ ，得 4(0,−y 0)=3√2(x 0−x,−y)，∴x 0=x ，y 03√24y ，代入圆O ：x 2+y 2=9，可得x 29+y 28=1．∴动点M 的轨迹E 的方程为x 29+y 28=1；(2)直线AG 与BH 的斜率之比为定值12． 证明如下：设直线l 为x =my +1，A(x 1,y 1)，B(x 2,y 2).联立{x =my +1x 29+y 28=1，得(8m 2+9)y 2+16my −64=0．则y 1+y 2=−16m 8m 2+9，y 1y 2=−648m 2+9． ∴my 1y 2=4(y 1+y 2)， 则k AGk BH=y 1x 1+3⋅x 2−3y 2=y 1(my 2−2)(my 1+4)y 2=my 1y 2−2y 1my 1y 2+4y 2=4(y 1+y 2)−2y 14(y 1+y 2)+4y 2=2y 1+4y 24y 1+8y 2=12．【解析】(1)设M(x,y)，P(x 0,y 0)，Q(x 0,0)，则由4PQ ⃗⃗⃗⃗⃗ =3√2MQ⃗⃗⃗⃗⃗⃗⃗ ，得x 0=x ，y 03√24y ，代入圆O ：x 2+y 2=9，可得动点M 的轨迹E 的方程；(2)设直线l 为x =my +1，A(x 1,y 1)，B(x 2,y 2)，联立直线方程与椭圆方程，利用根与系数的关系即可求得直线AG 与BH 的斜率之比为定值12．本题考查轨迹方程的求法，考查直线与椭圆的位置关系，考查计算能力，属于中档题．20.【答案】解：(1)X 的所有可能取值为0，1，2，3，则P(X =0)=0.3(1−p)2=0.3−0.6p +0.3p 2，P(X =1)=0.7(1−p)2+0.3×2p(1−p)=0.1p 2−0.8p +0.7， P(X =2)=2×0.7p(1−p)+0.3p 2=−1.1p 2+1.4p ， P(X =3)=0.7p 2， 所以X 的分布列为所以E(X)=1×0.1p 2−0.8p +0.7+2×−1.1p 2+1.4p +3×0.7p 2=2p +0.7． (2)因为0.6≤p ≤0.8，由(1)可知，当p =0.8时，E(X)取得最大值， ①一棵B 种树苗最终成活的概率为0.8+(1−0.8)×0.75×0.8=0.92， ②记Y 为n 棵树苗的成活棵数，则Y ～B(n,0.92)，E (Y)=0.92n ， ∴(0.92×400−0.08×80)n ≥100000， 解得n ≥100000361.6≈276.55，∴n ≥277，∴该农户至少要种植277棵树苗，才可获利不低于10万元．【解析】(1)X 的所有可能取值为0，1，2，3，然后用p 分别表示出每个X 的取值所对应的概率即可得分布列和数学期望；(2)先结合p 的取值范围和(1)中的结论确定p 的取值，然后就能得到一颗B 种树苗成活的概率；记Y 为n 棵树苗的成活棵数，则Y ～B(n,0.92)，再结合二项分布的性质，列出关于n 的不等式，解之并取整即可．本题考查了随机变量的分布列、数学期望等基础知识点，考查了学生数学建模的能力，即把实际问题转化为数学问题，再运算求解的能力，对于考生的综合分析能力提出较高要求，属于中档题．21.【答案】解：(1)∵f(x)=(a −1)x +xlnx ，∴f′(x)=a +lnx ，∵函数f(x)=(a −1)x +xlnx 的图象在点A(e 2,f(e 2))处的切线斜率为4， ∴f′(e 2)=a +lne 2=4，∴a =2．(2)由(1)知f(x)=x +xlnx ，∵m(x −1)<f(x)+1对任意x >1恒成立，∴m <f(x)+1x−1对任意x >1恒成立， 令g(x)=f(x)+1x−1，则g′(x)=(lnx+2)(x−1)−(x+xlnx+1)(x−1)2=x−lnx−3(x−1)2．令μ(x)=x −lnx −3，则μ′(x)=1−1x ，∵x >1，∴μ′(x)>0，∴μ(x)=x −lnx −3在(1,+∞)为增函数． ∵μ(4)=1−ln4<0，μ(5)=2−ln5>0， ∴∃x 0∈(4,5)，使得μ(x 0)=x 0−lnx 0−3=0，∴x ∈(1,x 0)时，g′(x)<0，g(x)单调递减，x ∈(x 0,+∞)时，g′(x)>0，g(x)单调递增， ∴g(x)min =g(x 0)=x 0+x 0lnx 0+1x 0−1=x 0+x 0(x 0−3)+1x 0−1=x 0−1，故有m <x 0−1对x >1都成立，∵x 0∈(4,5)，x 0−1∈(3,4)，∴m 的最大值为3．【解析】(1)f(x)=(a −1)x +xlnx ⇒f′(x)=a +lnx ，依题意，f′(e 2)=a +lne 2=4，可求得a 的值；(2)由(1)知f(x)=x +xlnx ，∀x >1，m(x −1)<f(x)+1⇔m <f(x)+1x−1对任意x >1恒成立，构造函数g(x)=f(x)+1x−1，求g′(x)=x−lnx−3(x−1)2，再令μ(x)=x −lnx −3，分析得到∃x 0∈(4,5)，使得μ(x 0)=x 0−lnx 0−3=0，g(x)min =g(x 0)=x 0−1∈(3,4)，从而可求得m 的最大值．本题第(1)问考查切线问题，第(2)问考查恒成立问题，通过分离参数后，构造函数，利用导数解决问题，考查转化思想与运算能力，对学生要求较高，属于难题．22.【答案】解：(1)已知曲线C 的极坐标方程为ρ=√2(θ∈[−π2,π2])，转换为直角坐标方程为x 2+y 2=2(x ≥0)，A 在曲线C 上，且曲线C 在点A 处的切线与直线：x +2y +1=0垂直， 所以{x 2+y 2=2y =−12xx ≥0，解得{x =2√105y =−√105，即A(2√105,−√105). (2)直线l 的直角坐标方程为y =−4+k(x +2)与半圆x 2+y 2=2(x ≥0)有且只有一个交点， 故√1+k 2=√2，整理得k 2−8k +7=0，解得k =1或7，由于B(0,√2)，C(0,−√2)P(−2,−4)， 所以k PB =4+√22，k PC =4−√22， 所以直线l 的斜率的范围为(4−√22,4−√22]∪{1}．【解析】(1)直接利用参数方程极坐标方程和直角坐标方程之间的转换的应用求出结果． (2)利用直线和曲线的位置关系的应用建立等量关系，进一步求出范围的值． 本题考查的知识要点：参数方程极坐标方程和直角坐标方程之间的转换，点到直线的距离公式的应用，三角函数关系式的恒等变换，正弦型函数的性质的应用，主要考查学生的运算能力和转换能力及思维能力，属于中档题型．23.【答案】解：(1)函数f(x)={−3x −1,x <−1x +3,−1≤x ≤13x +1,x >1，则{x <−1−3x −1<5或{x >13x +1<5或{−1≤x ≤1x +3<5， 解得−2<x <−1或1<x <43或−1≤x ≤1， 则原不等式的解集为(−2,43)；(2)关于x 的不等式f(x)+2<|2t −1|在实数范围内解集为空集， 等价为(f(x)+2)min ≥|2t −1|， 由(1)可得f(x)的最小值为f(−1)=2，则2+f(x)的最小值为4，则|2t −1|≤4，解得−32≤t ≤52， 则t 的取值范围是[−32,52].【解析】(1)将f(x)写成分段函数的形式，f(x)<5等价为一次不等式组，解不等式，求并集，可得所求解集；(2)由题意可得(f(x)+2)min ≥|2t −1|，由f(x)的解析式可得f(−1)为最小值，再由绝对值不等式的解法可得所求范围．本题考查绝对值不等式的解法和不等式恒成立问题解法，注意运用转化思想和分类讨论思想，考查化简运算能力和推理能力，属于中档题．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2018年高考数学(理科)模拟试卷(一) (本试卷分第Ⅰ卷和第Ⅱ卷两部分．满分150分，考试时间120分钟)第Ⅰ卷(选择题满分60分)一、选择题：本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2016年四川)设集合A＝{x|1≤x≤5}，Z为整数集，则集合A∩Z中元素的个数是( )A．6 B. 5 C．4 D．31.B 解析：由题意，A∩Z＝{1,2,3,4,5}，故其中的元素的个数为5.故选B.2．(2016年山东)若复数z满足2z＋z＝3－2i, 其中i为虚数单位，则z＝( )A．1＋2i B．1－2iC．－1＋2i D．－1－2i2．B 解析：设z＝a＋b i(a，b∈R)，则2z＋z＝3a＋b i＝3－2i，故a＝1，b＝－2，则z＝1－2i.故选B.3．(2015年北京)某四棱锥的三视图如图M11，该四棱锥最长棱的棱长为( )图M11A．1 B. 2 C. 3 D．23．C 解析：四棱锥的直观图如图D188：由三视图可知，SC⊥平面ABCD，SA是四棱锥最长的棱，SA ＝SC 2＋AC 2＝SC 2＋AB 2＋BC 2＝ 3.故选C.图D1884．曲线y ＝x 3－2x ＋4在点(1,3)处的切线的倾斜角为( ) A.π6 B.π3 C.π4 D.π2 4．C 解析：f ′(x )＝3x 2－2，f ′(1)＝1，所以切线的斜率是1，倾斜角为π4.5．设x ∈R ，[x ]表示不超过x 的最大整数. 若存在实数t ，使得[t ]＝1，[t 2]＝2，…，[t n ]＝n 同时成立，则正整数n 的最大值是( )A ．3B ．4C ．5D ．65．B 解析：因为[x ]表示不超过x 的最大整数．由[t ]＝1，得1≤t <2，由[t 2]＝2，得2≤t 2<3.由[t 3]＝3，得3≤t 3<4.由[t 4]＝4，得4≤t 4<5.所以2≤t 2< 5.所以6≤t 5<45.由[t 5]＝5，得5≤t 5<6，与6≤t 5<45矛盾，故正整数n 的最大值是4.6．(2016年北京)执行如图M12所示的程序框图，若输入的a 值为1，则输出的k 值为( )图M12A ．1B ．2C ．3D ．46．B 解析：输入a ＝1，则k ＝0，b ＝1；进入循环体，a ＝－12，否，k ＝1，a ＝－2，否，k ＝2，a ＝1，此时a ＝b ＝1，输出k ，则k ＝2.故选B.7．某市重点中学奥数培训班共有14人，分为两个小组，在一次阶段考试中两个小组成绩的茎叶图如图M13，其中甲组学生成绩的平均数是88，乙组学生成绩的中位数是89，则m ＋n 的值是( )图M13A ．10B ．11C ．12D ．137．C 解析：由题意，得78＋88＋84＋86＋92＋90＋m ＋957＝88，n ＝9.所以m ＋n＝12.故选C.8．(2015年陕西)某企业生产甲、乙两种产品均需用A ，B 两种原料．已知分别生产1吨甲、乙产品需原料及每天原料的可用限额如表所示，如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得最大利润为( )项目甲 乙 原料限额 A /吨 3 2 12 B /吨128A.12万元 B ．16C．17万元D．18万元8．D 解析：设该企业每天生产甲、乙两种产品分别为x吨、y吨，则利润z＝3x＋4y.由题意可得⎩⎪⎨⎪⎧3x＋2y≤12，x＋2y≤8，x≥0，y≥0.其表示如图D189阴影部分区域：图D189当直线3x＋4y－z＝0过点A(2,3)时，z取得最大值，所以z max＝3×2＋4×3＝18.故选D.9．(2016年新课标Ⅲ)定义“规范01数列”{a n}如下：{a n}共有2m项，其中m项为0，m 项为1，且对任意k≤2m，a1，a2，…，a k中0的个数不少于1的个数．若m＝4，则不同的“规范01数列”共有( )A．18个B．16个C．14个D．12个9．C 解析：由题意，必有a1＝0，a8＝1，则具体的排法列表如下：10．(2016年天津)已知函数f (x )＝sin 2ωx 2＋12sin ωx －12(ω>0)，x ∈R .若f (x )在区间(π，2π)内没有零点，则ω的取值范围是( )A.⎝ ⎛⎦⎥⎤0，18B.⎝ ⎛⎦⎥⎤0，14∪⎣⎢⎡⎭⎪⎫58，1 C.⎝ ⎛⎦⎥⎤0，58 D.⎝ ⎛⎦⎥⎤0，18∪⎣⎢⎡⎦⎥⎤14，58 10.D 解析：f (x )＝1－cos ωx2＋sin ωx 2－12＝22sin ⎝ ⎛⎭⎪⎫ωx －π4，f (x )＝0⇒sin ⎝⎛⎭⎪⎫ωx －π4＝0，所以x ＝k π＋π4ω(π，2π)，(k ∈Z )．因此ω⎝ ⎛⎭⎪⎫18，14∪⎝ ⎛⎭⎪⎫58，54∪⎝ ⎛⎭⎪⎫98，94∪…＝⎝ ⎛⎭⎪⎫18，14∪⎝ ⎛⎭⎪⎫58，＋∞⇒ω∈⎝ ⎛⎦⎥⎤0，18∪⎣⎢⎡⎦⎥⎤14，58.故选D.11．四棱锥P ABCD 的底面ABCD 为正方形，PA ⊥底面ABCD ，AB ＝2，若该四棱锥的所有顶点都在体积为243π16的同一球面上，则PA ＝( )A ．3 B.72C ．23 D.9211．B 解析：如图D190，连接AC ，BD 交于点E ，取PC 的中点O ，连接OE ，则OE ∥PA ，所以OE ⊥底面ABCD ，则O 到四棱锥的所有顶点的距离相等，即O 为球心，12PC ＝12PA 2＋AC 2＝12PA 2＋8，所以由球的体积可得43π⎝ ⎛⎭⎪⎫12PA 2＋83＝243π16，解得PA ＝72.故选B.图D19012．已知F 为抛物线y 2＝x 的焦点，点A 、B 在该抛物线上且位于x 轴两侧，若OA →·OB →＝6(O 为坐标原点)，则△ABO 与△AOF 面积之和的最小值为( )A ．4 B.3132 C.17 24D.1012．B 解析：设直线AB 的方程为x ＝ty ＋m ，点A (x 1，y 1)，B (x 2，y 2)，直线AB 与x 轴的交点为M (m,0)，将直线方程与抛物线方程联立，可得y 2－ty －m ＝0，根据韦达定理有y 1·y 2＝－m ，因为OA →·OB →＝6，所以x 1·x 2＋y 1·y 2＝6，从而(y 1·y 2)2＋y 1·y 2－6＝0，因为点A ，B 位于x 轴的两侧，所以y 1·y 2＝－3，故m ＝3，不妨令点A 在x 轴上方，则y 1>0，又F ⎝ ⎛⎭⎪⎫14，0，所以S △ABO＋S △AFO ＝12×3×(y 1－y 2)＋12×14y 1＝138y 1＋92y 1≥2138·y 1·92·1y 1＝3132，当且仅当13y 18＝92y 1，即y 1＝61313时取等号，故其最小值为3 132.故选B.第Ⅱ卷(非选择题 满分90分)本卷包括必考题和选考题两部分．第13～21题为必考题，每个试题考生必须作答．第22～23题为选考题，考生根据要求作答．二、填空题：本大题共4小题，每小题5分．13．平面向量a ＝(1,2)，b ＝(4,2)，c ＝m a ＋b (m ∈R )，且c 与a 的夹角等于c 与b 的夹角，则m ＝________.13．2 解析：a ＝(1,2)，b ＝(4,2)，则c ＝m a ＋b ＝(m ＋4,2m ＋2)，|a |＝5，|b |＝25，a ·c ＝5m ＋8，b ·c ＝8m ＋20.∵c 与a 的夹角等于c 与b 的夹角，∴c·a |c|·|a|＝c·b|c|·|b|.∴5m ＋85＝8m ＋202 5.解得m ＝2.14．设F 是双曲线C ：x 2a 2－y 2b2＝1的一个焦点，若C 上存在点P ，使线段PF 的中点恰为其虚轴的一个端点，则C 的离心率为__________．14.5 解析：根据双曲线的对称性，不妨设F (c,0)，虚轴端点为(0，b )，从而可知点(－c,2b )在双曲线上，有c 2a2－4b 2b 2＝1，则e 2＝5，e ＝ 5.15．(2016年北京)在(1－2x )6的展开式中，x 2的系数为________．(用数字作答)15．60 解析：根据二项展开的通项公式T r ＋1＝C r 6·(－2)r x r 可知，x 2的系数为C 26(－2)2＝60，故填60.16．在区间[0，π]上随机地取一个数x ，则事件“sin x ≤12”发生的概率为________．16.13 解析：由正弦函数的图象与性质知，当x ∈⎣⎢⎡⎦⎥⎤0，π6∪⎣⎢⎡⎦⎥⎤5π6，π时，sin x ≤12. 所以所求概率为⎝ ⎛⎭⎪⎫π6－0＋⎝⎛⎭⎪⎫π－5π6π＝13.三、解答题：解答应写出文字说明，证明过程或演算步骤．17．(本小题满分12分)已知{a n }是各项均为正数的等比数列，{b n }是等差数列，且a 1＝b 1＝1，b 2＋b 3＝2a 3，a 5－3b 2＝7.(1)求{a n }和{b n }的通项公式；(2)设c n ＝a n b n ，n ∈N *，求数列{c n }的前n 项和．17．解：(1)设{a n }的公比为q ，{b n }的公差为d ，由题意知q >0.由已知，有⎩⎪⎨⎪⎧2q 2－3d ＝2，q 4－3d ＝10.消去d ，得q 4－2q 2－8＝0.解得q ＝2，d ＝2.所以{a n }的通项公式为a n ＝2n －1，n ∈N *， {b n }的通项公式为b n ＝2n －1，n ∈N *.(2)由(1)有c n ＝(2n －1)2n －1，设{c n }的前n 项和为S n ， 则S n ＝1×20＋3×21＋5×22＋…＋(2n －1)×2n －1， 2S n ＝1×21＋3×22＋5×23＋…＋(2n －1)×2n .两式相减，得－S n ＝1＋22＋23＋…＋2n －(2n －1)×2n ＝－(2n －3)×2n －3. 所以S n ＝(2n －3)·2n ＋3，n ∈N *.18．(本小题满分12分)(2014年大纲)设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6，0.5，0.5,0.4，各人是否需使用设备相互独立．(1)求同一工作日至少3人需使用设备的概率；(2)X 表示同一工作日需使用设备的人数，求X 的数学期望．18．解：记A 1表示事件：同一工作日乙、丙中恰有i 人需使用设备，i ＝0,1,2.B 表示事件：甲需使用设备．C 表示事件：丁需使用设备．D 表示事件：同一工作日至少3人需使用设备．(1)因为P (B )＝0.6，P (C )＝0.4，P (A i )＝C i 2×0.52，i ＝0,1,2，所以P (D )＝P (A 1·B ·C ＋A 2·B ＋A 2·B ·C )＝P (A 1·B ·C )＋P (A 2·B )＋P (A 2·B ·C ) ＝P (A 1)P (B )P (C )＋P (A 2)P (B )＋P (A 2)P (B )P (C )＝0.31. (2)X 的可能取值为0,1,2,3,4，其分布列为P (X ＝0)＝P (B ·A 0·C )＝P (B )P (A 0)P (C ) ＝(1－0.6)×0.52×(1－0.4) ＝0.06，P (X ＝1)＝P (B ·A 0·C ＋B ·A 0·C ＋B ·A 1·C )＝P (B )P (A 0)P (C )＋P (B )P (A 0)P (C )＋P (B )P (A 1)P (C )＝0.6×0.52×(1－0.4)＋(1－0.6)×0.52×0.4＋(1－0.6)×2×0.52×(1－0.4)＝0.25，P (X ＝4)＝P (A 2·B ·C )＝P (A 2)P (B )P (C )＝0.52×0.6×0.4＝0.06，P (X ＝3)＝P (D )－P (X ＝4)＝0.25，P (X ＝2)＝1－P (X ＝0)－P (X ＝1)－P (X ＝3)－P (X ＝4)＝1－0.06－0.25－0.25－0.06＝0.38，所以E (X )＝0×P (X ＝0)＋1×P (X ＝1)＋2×P (X ＝2)＋3×P (X ＝3)＋4×P (X ＝4) ＝0.25＋2×0.38＋3×0.25＋4×0.06＝2.19．(本小题满分12分)(2016年四川)如图M14，在四棱锥P ABCD 中，AD ∥BC ，∠ADC ＝∠PAB ＝90°，BC ＝CD ＝12AD ，E 为边AD 的中点，异面直线PA 与CD 所成的角为90°.(1)在平面PAB 内找一点M ，使得直线CM ∥平面PBE ，并说明理由； (2)若二面角P CD A 的大小为45°，求直线PA 与平面PCE 所成角的正弦值．图M1419．解：(1)在梯形ABCD 中，AB 与CD 不平行．延长AB ，DC ，相交于点M (M ∈平面PAB )，点M 即为所求的一个点．理由如下： 由已知，BC ∥ED ，且BC ＝ED ， 所以四边形BCDE 是平行四边形． 所以CD ∥EB . 从而CM ∥EB .又EB ⊂平面PBE ，CM 平面PBE ， 所以CM ∥平面PBE .(说明：延长AP 至点N ，使得AP ＝PN ，则所找的点可以是直线MN 上任意一点) (2)方法一，由已知，CD ⊥PA ，CD ⊥AD ，PA ∩AD ＝A ， 所以CD ⊥平面PAD . 从而CD ⊥PD .所以∠PDA 是二面角P CD A 的平面角． 所以∠PDA ＝45°.设BC ＝1，则在Rt △PAD 中，PA ＝AD ＝2.如图D191，过点A 作AH ⊥CE ，交CE 的延长线于点H ，连接PH . 易知PA ⊥平面ABCD ， 从而PA ⊥CE .于是CE ⊥平面PAH . 所以平面PCE ⊥平面PAH .过A 作AQ ⊥PH 于Q ，则AQ ⊥平面PCE . 所以∠APH 是PA 与平面PCE 所成的角． 在Rt △AEH 中，∠AEH ＝45°，AE ＝1， 所以AH ＝22.在Rt △PAH 中，PH ＝PA 2＋AH 2＝3 22，所以sin ∠APH ＝AH PH ＝13.图D191 图D192方法二，由已知，CD ⊥PA ，CD ⊥AD ，PA ∩AD ＝A ， 所以CD ⊥平面PAD . 于是CD ⊥PD .从而∠PDA 是二面角P CD A 的平面角． 所以∠PDA ＝45°.由PA ⊥AB ，可得PA ⊥平面ABCD . 设BC ＝1，则在Rt △PAD 中，PA ＝AD ＝2.作Ay ⊥AD ，以A 为原点，以AD → ，AP →的方向分别为x 轴，z 轴的正方向，建立如图D192所示的空间直角坐标系Axyz ，则A (0,0,0)，P (0,0,2)，C (2,1,0)，E (1,0,0)，所以PE →＝(1,0，－2)，EC →＝(1,1,0)，AP →＝(0,0,2) 设平面PCE 的法向量为n ＝(x ，y ，z )， 由⎩⎨⎧n ·PE →＝0，n ·EC→＝0， 得⎩⎪⎨⎪⎧x －2z ＝0，x ＋y ＝0.设x ＝2，解得n ＝(2，－2,1)． 设直线PA 与平面PCE 所成角为α，则sin α＝|n ·AP →||n |·|AP →|＝22×22＋－22＋12＝13.所以直线PA 与平面PCE 所成角的正弦值为13.20．(本小题满分12分)(2016年新课标Ⅲ)设函数f (x )＝ln x －x ＋1. (1)讨论f (x )的单调性； (2)证明当x ∈(1，＋∞)时，1<x －1ln x<x ；(3)设c >1，证明当x ∈(0,1)时，1＋(c －1)x >c x .20．解：(1)由题设，f (x )的定义域为(0，＋∞)，f ′(x )＝1x－1，令f ′(x )＝0，解得x ＝1.当0<x <1时，f ′(x )>0，f (x )单调递增； 当x >1时，f ′(x )<0，f (x )单调递减．(2)由(1)知，f (x )在x ＝1处取得最大值，最大值为f (1)＝0. 所以当x ≠1时，ln x <x －1.故当x ∈(1，＋∞)时，ln x <x －1，ln 1x <1x －1，即1<x －1ln x <x .(3)由题设c >1，设g (x )＝1＋(c －1)x －c x ， 则g ′(x )＝c －1－c x ln c .令g ′(x )＝0，解得x 0＝lnc －1ln cln c.当x <x 0时，g ′(x )>0，g (x )单调递增； 当x >x 0时，g ′(x )<0，g (x )单调递减． 由(2)知，1<c －1ln c<c ，故0<x 0<1.又g (0)＝g (1)＝0，故当0<x <1时，g (x )>0. 所以x ∈(0,1)时，1＋(c －1)x >c x .21．(本小题满分12分)(2016年广东广州综合测试一)已知椭圆C 的中心在坐标原点，焦点在x 轴上，左顶点为A ，左焦点为F 1(－2, 0)，点B (2，2)在椭圆C 上，直线y ＝kx (k ≠0)与椭圆C 交于E ，F 两点，直线AE ，AF 分别与y 轴交于点M ，N .(1)求椭圆C 的方程；(2)以MN 为直径的圆是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由．21．解：(1)设椭圆C 的方程为x 2a 2＋y 2b2＝1(a >b >0)，因为椭圆的左焦点为F 1(－2,0)，所以a 2－b 2＝4.① 因为点B (2，2)在椭圆C 上，所以4a 2＋2b2＝1.②由①②，解得a ＝2 2，b ＝2.所以椭圆C 的方程为x 28＋y 24＝1.(2)因为椭圆C 的左顶点为A ，则点A 的坐标为(－22，0)．因为直线y ＝kx (k ≠0)与椭圆x 28＋y 24＝1交于两点E ，F ，设点E (x 0，y 0)(不妨设x 0>0)，则点F (－x 0，－y 0)．联立方程组⎩⎪⎨⎪⎧y ＝kx ，x 28＋y24＝1消去y ，得x 2＝81＋2k 2.所以x 0＝2 21＋2k 2，则y 0＝22k1＋2k 2.所以直线AE 的方程为y ＝k1＋1＋2k 2(x ＋2 2)．因为直线AE ，AF 分别与y 轴交于点M ，N ，令x ＝0得y ＝ 22k1＋1＋2k 2，即点M ⎝ ⎛⎭⎪⎪⎫0，2 2k 1＋1＋2k 2.同理可得点N ⎝ ⎛⎭⎪⎪⎫0，2 2k 1－1＋2k 2.所以|MN |＝⎪⎪⎪⎪⎪⎪⎪⎪2 2k 1＋1＋2k 2－ 2 2k 1－1＋2k 2＝221＋2k 2|k |.设MN 的中点为P ，则点P 的坐标为P ⎝ ⎛⎭⎪⎪⎫0，－2k .则以MN 为直径的圆的方程为x 2＋⎝ ⎛⎭⎪⎪⎫y ＋2k 2＝⎝⎛⎭⎪⎪⎫21＋2k 2|k |2，即x 2＋y 2＋2 2k y ＝4.令y ＝0，得x 2＝4，即x ＝2或x ＝－2.故以MN 为直径的圆经过两定点P 1(2,0)，P 2(－2,0)，请考生在第(22)(23)两题中任选一题作答．注意：只能作答在所选定的题目上．如果多做，则按所做的第一个题目计分．22．(本小题满分10分)选修44：极坐标与参数方程已知曲线C 的参数方程是⎩⎪⎨⎪⎧x ＝2cos θ，y ＝sin θ(θ为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，A 、B 的极坐标分别为A (2，π)、B ⎝⎛⎭⎪⎫2，4π3.(1)求直线AB 的直角坐标方程；(2)设M 为曲线C 上的动点，求点M 到直线AB 距离的最大值．22．解：(1)将A 、B 化为直角坐标为A (2cos π，2sin π)，B ⎝⎛⎭⎪⎫2cos 4π3，2sin 4π3，即A ，B 的直角坐标分别为A (－2,0)，B (－1，－3)，k AB ＝－3－0－1＋2＝－3，∴直线AB 的方程为y －0＝－3(x ＋2)，即直线AB 的方程为3x ＋y ＋23＝0.(2)设M (2cos θ，sin θ)，它到直线AB 的距离d ＝|2 3cos θ＋sin θ＋23|2＝|13sin θ＋φ＋23|2，∴d max ＝13＋2 32.23．(本小题满分10分)选修45：不等式选讲 已知函数f (x )＝|x －2|－|2x －a |，a ∈R . (1)当a ＝3时，解不等式f (x )>0；(2)当x ∈(－∞，2)时，f (x )<0恒成立，求a 的取值范围． 23．解：(1)当a ＝3时，f (x )>0，即|x －2|－|2x －3|>0， 等价于⎩⎪⎨⎪⎧x ≤32，x －1>0，或⎩⎪⎨⎪⎧32<x <2，－3x ＋5>0，或⎩⎪⎨⎪⎧x ≥2，－x ＋1>0.解得1<x ≤32，或32<x <53.所以原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1<x <53.(2)f (x )＝2－x －|2x －a |，所以f (x )<0可化为|2x －a |>2－x ， ① 即2x －a >2－x ，或2x －a <x －2.①式恒成立等价于(3x －2)min >a 或(x ＋2)max <a ， ∵x ∈(－∞，2)，∴a ≥4.。