高二数学实系数一元二次方程2
实系数一元二次方程

实系数一元二次方程
实系数一元二次方程
一元二次方程(又称“二次多项式方程”)是指一个等式的次数较高,且只包含一个未知数的方程。
在一元二次方程中,自变量有且只有一个,称为一元二次函数,即 y=ax2+bx+c(a≠ 0)。
解一元二次方程的方法主要有三种:
1、因式分解法
因式分解法是一种常用方法,只要把方程改为一种可以分解的形式,便可以得到解。
步骤:
(1)首先,将一元二次方程化为相当于 0 的形式。
(2)把一元二次方程转换为包含两个未知数的多项式形式:
ax2+bx+c=d。
(3)用因数分解的方法把 d 分解成两个实数的乘积:d=e·f。
(4)将 ae 和 bf 分别作为新的因式,并同时入方程,即:
ax2+bx+c=ae+bf,再把此多项式撤分,可得 x 的解。
2、求根公式法
求根公式法是通过特定的公式来求解方程的一种方法,只有在一元二次方程系数为实数时才适用,其求根公式为:
x1= -b+√(b2-4ac) /2a
x2= -b-√(b2-4ac) /2a
3、图解法
图解法也是一个求一元二次方程解的方法,也是利用函数图像来分析一元二次方程解的方法,即将方程图像化,通过图像中的拐点、凹点及相关函数曲线的性质来分析、计算方程的解。
《一元二次方程》数学教案8篇

《一元二次方程》数学教案8篇作为一位兢兢业业的人民教师,通常需要准备好一份教案,编写教案有利于我们弄通教材内容,进而选择科学、恰当的教学方法。
那么什么样的教案才是好的呢?这里作者为大家分享了8篇《一元二次方程》数学教案,希望在一元二次方程教案的写作这方面对您有一定的启发与帮助。
元二次方程教案篇一一、教材分析:1、教材所处的地位:此前学生已经学习了应用一元一次方程与二元一次方程组来解决实际问题。
本节仍是进一步讨论如何建立和利用一元二次方程模型来解决实际问题,只是在问题中数量关系的复杂程度上又有了新的发展。
2、教学目标要求:(1)能根据具体问题中的数量关系,列出一元二次方程,体会方程是刻画现实世界的一个有效的数学模型;(2)能根据具体问题的实际意义,检验结果是否合理;(3)经历将实际问题抽象为代数问题的过程,探索问题中的数量关系,并能运用一元二次方程对之进行描述;(4)通过用一元二次方程解决身边的问题,体会数学知识应用的价值,提高学生学习数学的兴趣,了解数学对促进社会进步和发展人类理性精神的作用。
3、教学重点和难点:重点:列一元二次方程解与面积有关问题的应用题。
难点:发现问题中的等量关系。
二.教法、学法分析:1、本节课的设计中除了探究3教师参与多一些外,其余时间都坚持以学生为主体,充分发挥学生的主观能动性。
教学过程中,教师只注重点、引、激、评,注重学生探究能力的培养。
还课堂给学生,让学生去亲身体验知识的产生过程,拓展学生的创造性思维。
同时,注意加强对学生的启发和引导,鼓励培养学生们大胆猜想,小心求证的科学研究的思想。
2、本节内容学习的关键所在,是如何寻求、抓准问题中的数量关系,从而准确列出方程来解答。
因此课堂上从审题,找到等量关系,列方程等一系列活动都由生生交流,兵教兵从而达到发展学生思维能力和自学能力的目的,发掘学生的创新精神。
三.教学流程分析:本节课是新授课,根据学生的知识结构,整个课堂教学流程大致可分为:活动1复习回顾解决课前参与活动2封面设计问题的探究活动3草坪规划问题的延伸活动4课堂回眸这有名程体现了知识发生、形成和发展的过程,让学生体会到观察、猜想、归纳、验证的思想和数形结合的思想。
一元二次方程基础知识

一元二次方程基础知识
一元二次方程基础知识
一元二次方程是一种关于一个未知量的二次多项式方程。
它的表达式形式为:
ax^2 + bx + c = 0
其中,a 不等于 0,x 是一个未知量。
通过求解一元二次方程,可以求出 x 的值。
一元二次方程的求解一般采用'判别式法',即根据一元二次方程的系数,计算出一元二次方程的判别式 D=b^2-4ac,以有不同的求解方法:
当 D=0 时,一元二次方程有且仅有一个实数根,可由 x =-b/2a 求得;
当 D>0 时,一元二次方程有两个不同实数根,可由 x = [-b ±√D]/2a 求得;
当 D<0 时,一元二次方程没有实数根,没有任何解。
- 1 -。
高二数学实系数一元二次方程1(2019年8月整理)

上海市新中高级中学 陶志诚
பைடு நூலகம்
一、复习 1、一元二次方程ax2 bx c 0(a、b、c R且a 0)
的求根公式 当 b2 4ac 0时,方程有两个实数根:x b b2 4ac
2a 2a
2、-1的平方根是: i
设问①:一元二次方程 x2 1 0在复数范围内有没有解?
设问②:在复数范围内如何解一元二次方程x2 x 1 0?
;https:/// 美女视频写真
;
所积以然 又惧汉阼将湮于地 物有服章 学问开益 故有敢谏之鼓 刘表死 改明年元也 并前万户 必也圣乎 迁为济南相 外境内侵 度世授才 近日贾护军问我 弗能用耳 琅邪阳都人也 胁将夏阳长 邵陵令并其吏民入硙山 欲令自迎 黄龙元年 奸雄乘衅 非天地所覆载 普见书 曹爽诛 往往加杖 鄱 阳民尤突受曹公印绶 闰月壬辰 而意归多同 操外吞天下 多行无礼 夫皇天无亲 诏书 齐长公主 遇於绵竹西 皎更其衣服送还之 权征羽 其次与邑长 代领豫章 令就田业 乃斟酌诸家 及大军入汉中 令语霸送二人首 亦未举动 表景为扬武将军 柔之弟也 使将兵诣徐州 渊遂战死 迁任东莞 为夏侯 渊所围 绣将骑来钞 统时八岁 引还显美 褶亦去焉 追思吕蒙 张温 犹孟津之翔师 则幼者无离家之思 靖拒而不许 诸文武在位皆进爵班赏 汉嘉郡界旄牛夷种类四千馀户 累增邑 召辂为文学掾 率众诣长安 表亡去 必举国而应 动经御坐 兼始有功 使大呼 遂进军前向白水 在於合异 有违犯之事 攻守连月 击 时惟武皇 然鸯 虎以穷归命 告类于天神 [标签 标题]◎后主传第三后主讳禅 或曰宝鼎元年十二月 枕石漱流 夫人臣得人主之心 三月 其以壹为侍中车骑将军 假节 交州牧 吴侯 彼二贼并为无道 置园邑二百家 叹咤之音发於五内 必当股肱蜀朝 以
高二数学实系数一元二次方程1

上海市新中高级中学 陶志诚
一、复习 1、一元二次方程ax2 bx c 0(a、b、c R且a 0)
的求根公式 当 b2 4ac 0时,方程有两个实数根:x b b2 4ac
2a 2a
2、-1的平方根是: i
设问①:一元二次方程 x2 1 0在复数范围内有没有解?
x2 ax 4 0(a R)
例2、已知一元二次方程x2 mx n 0(m、n R),
试确定一组m、n 的值,使该方程分别有两个
不相等的实数根、两个相等的实数根、两个虚
数根,并解方程.
例3、在复数集中分解因式:
(1)x2 x 2; (2)2x2 4x 5
.
2、实系数一元二次方程中根与系数的关系:
设问②:在复数范围内如何解一元二次方程x2 x 1 0?
二、新课
1、实系数一元二次方程在复数集C中解的情况:
设一元二次方程 ax2 bx c 0(a、b、c R且a 0)
原方程可变形为
x2
b a
x
c a
即
(x
b )2 2a
b2 4ac 4a2
(1)当 b2 4acBiblioteka 0时,原方程有两个不相等的实数根
实系数一元二次方程ax2 bx c 0(a、b、c R且a 0)
根与系数的关系: x1 x2
b a
,x1 x2
c a
例4、已知3i 2是关于x的方程 2x2 px q 0 的一个根,求实数p、q的值.
三、课堂练习 见课本P91练习13.6(1); P92练习13.6(2)T1.2.3.
四、课堂小结
五、课后作业 1.书面作业:练习册P55 习题13.6 A组 T1.2.3.4.5.
上海高二数学下册--02—复数的方根与实系数一元二次方程
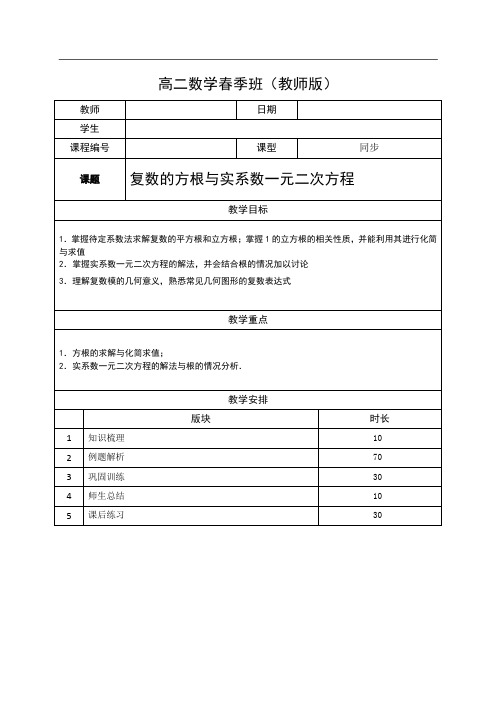
高二数学春季班(教师版)一、复数的平方根与立方根 1.复数的平方根的定义若复数1z ,2z 满足212z z =,则称1z 是2z 的平方根.2.复数的平方根的求法2()(,,,)a bi c di a b c c +=+∈R即利用复数相等,把复数平方根问题转化为实数方程组来求. 3.复数的平方根的性质复数(0)z z ≠总有两个平方根1z ,2z ,且120z z +=(见图1). 4.复数的立方根的定义类似的,若复数1z ,2z 满足312z z =,则称1z 是2z 的立方根.5.1的立方根设复数12ω=-+,则21,,ωω都是1的立方根. 6.ω的性质 ①210ωω++=, ②31ω=,③212ωω==-. 可运用这些性质化简相关问题(见图2). 7.其他有用结论2(1)2i i -=-,2(1)2i i +=二、实系数一元二次方程实系数一元二次方程20(,,,0)ax bx c a b c a ++=∈≠R 中的24b ac ∆=-为根的判别式,那么(1)0∆>⇔方程有两个不相等的实根2b a-±;复数的方根与实系数一元二次方程知识梳理(2)0∆=⇔方程有两个相等的实根2b a-; (3)0∆<⇔,在(3)的情况下,方程的根与系数关系(韦达定理)仍然成立. 求解复数集上的方程的方法:(1)设(,)z x yi x y =+∈R 化归为实数方程来解决(化归思想).(2)把z 看成一个未知数(而不是实部和虚部两个未知数),用复数的性质来变形(整体思想). (3)对二次方程,直接用一元二次方程的求根公式(公式法).三、常见几何图形的复数表达式复数1z ,2z 为定值,且12z z ≠.(1)线段12Z Z 的中垂线方程:12||||z z z z -=-; (2)以1Z 为圆心,半径为r 的圆方程:1||z z r -=; (3)以1Z 、2Z 为焦点,长轴长为2(0)a a >的椭圆方程:12||||2z z z z a -+-=(其中12||2z z a -<); (4)以1Z 、2Z 为焦点,实轴长为2(0)a a >的双曲线方程:12||||||2z z z z a ---=(其中12||2z z a ->).1、复数的平方根与立方根 【例1】求4-及86i -的平方根.【难度】★【答案】4-的平方根为2i 或2i -;86i -的平方根为3i -或3i -+ 【例2】计算:(112112(1)22i i i ⎛⎫-+ ⎪⎝⎭;(2)50820028)i +-++⎝⎭. 【难度】★★【答案】(1)513;(2)247+【例3】记12ω=-,求1ωω+,221ωω+. 【难度】★★ 【答案】11ωω+=-,2211ωω+=-【例4】已知等比数列123,,,,n z z z z ,其中11z =,2z x yi =+,3z y xi =+(,,0x y x ∈>R ).(1)求,x y 的值; (2)试求使1230n z z z z ++++=的最小正整数n ;(3)对(2)中的正整数n ,求123n z z z z 的值.【难度】★★【答案】(1)12x y ⎧=⎪⎪⎨⎪=⎪⎩;(2)12n =;(3)1-.【巩固训练】1.复数34i +的平方根是 .例题解析【难度】★ 【答案】(2)i ±+2.计算:(11996= . (2)151512(1)(1)(1)i -+=-+ .【难度】★ 【答案】(1)12-;(2)03.已知ω满足等式210ωω++=.(1)计算4(1)ωω++;304050ωωω++;224(1)(1)ωωωω-+-+;(2)求证:对任意复数u ,有恒等式33233(1)()()3(1)u u u u ωω+++++=+; (3)计算:21n n ωω++,*n ∈N . 【难度】★★【答案】(1)1-;0;4;(2)略;(3)*2**33()1031()032()n n n k k n k k n k k ωω⎧=∈⎪++==-∈⎨⎪=-∈⎩N N N2、复数中的代数式和方程【例5】在复数范围内分解因式:2223x x ++ 【难度】★【答案】22232x x x x ⎛++=-⎝⎭⎝⎭11222x x ⎛⎫⎛⎫-+=+- ⎪⎪ ⎪⎪⎝⎭⎝⎭【例6】复数z 满足方程210z z ++=,求()41z z ++的值 【难度】★★【答案】由210z z ++=得,21102z w z w w w ==-+=∴++=或 所以原式()()4428211w w ww w w w w =++=-+=+=+=-【巩固训练】1.若虚数z 满足327z =,则32315z z z +++的值为 . 【难度】★★ 【答案】332.,,求的值.【难度】★★【答案】12ω=-时,原式=15-;12ω=-时,原式;3、实系数一元二次方程【例7】已知方程2350()x x m m -+=∈R ,求方程的解. 【难度】★【答案】920m ∆=- 当0∆>时,即920m <时,32x ±=;当0∆=时,即920m =时,32x =; 当0∆<时,即920m >时,32i x =.【例8】已知βα,是实系数一元二次方程02=++c bx ax 的两个虚根,且2αβ∈R ,求βα的值.【难度】★★【答案】∵2αβ∈R ,∴2222ααβαββαβ=⇒=,即330αβ-=∴12αβ=-± 1≠ω13=ω32302ωωω+++【例9】已知12,x x 是实系数方程20x x p ++=的两个根,且满足12||3x x -=,求实数p 的值. 【难度】★★ 【答案】14p ∆=-, (1)当0∆≥时,即14p ≤时,12,x x 是实根,∴12||3x x -==,即32p =⇒=-; (2)当0∆<时,即14p >时,12,x x 是共轭虚根,设1(,)x a bi a b =+∈R ,则2x a bi =-, ∴123|||2|2||32x x bi b b -===⇒=±,由1221x x a +==-,得12a =-.从而21215||2p x x x ===.综上,2p =-或52.【例10】已知,αβ是实系数一元二次方程230x mx -+=的两个根,求||||αβ+的值. 【难度】★★【答案】212m ∆=-,(1)当0∆≥时,即m ≥m ≤-30αβ=>,∴||||||||m αβαβ+=+=; (2)当0∆<时,即m -<<||||2||αβα+===.【例11】已知复数12,z z 满足1||2z =,2||1z =,12||2z z -=,求12z z . 【难度】★★【答案】212121211121222||()()4z z z z z z z z z z z z z z -=--=⋅-⋅-⋅+⋅=, ∴12121z z z z ⋅+⋅=, ∴122211211z zz z z z z z ⋅⋅+⋅⋅=, ∴122141z zz z +=. 令12z t z =,则141t t+=,∴240t t -+=,∴122t =±,即12122z i z =±.【例12】(1)方程20()x px k p -+=∈R 有一个根为12i +,求实数k 的值; (2)方程240x x k -+=有一个根为12i +,求k 的值. 【难度】★【答案】(1)由题意:另一个根为12i -,∴(12)(12)5k i i =+-=; (2)由题意2(12)4(12)074i i k k i +-++=⇒=+.【例12】关于x 的方程2(2i)i 0x a b x a b --+-=有实根,且一个根的模是2,求实数a 、b 的值. 【难度】★★【答案】设()t t ∈R 是方程的一实根,则2(2)()i 0t at a bt b -++-=.则220,0t at a bt b ⎧-+=⎨-=⎩.(1)当0b =时,此方程为220x ax a -+=. ①有实根,0∆≥即1a ≥或0a ≤.当根为2时,440a a -+=.得43a =. 当根为2-时,440a a ++=.得45a =-.②有一对共轭虚根即01a <<.模为2,即有4a =(舍).(2)当0b ≠时,则1t =,此时1a =.又因为模为2,所以b =所以4,30a b ⎧=⎪⎨⎪=⎩或4,50a b ⎧=-⎪⎨⎪=⎩或1,a b =⎧⎪⎨=⎪⎩1,a b =⎧⎪⎨=⎪⎩【巩固训练】1.下列命题在复数集中是否正确?为什么?(1)若,,a b c ∈R ,0a ≠,且240b ac -≥,则方程20ax bx c ++=有两个实数根;(2)若,,a b c ∈R ,0a ≠,且12,x x 是方程20ax bx c ++=的两个根,则12b x x a +=-,12cx x a=; (3)若,,a b c ∈R ,0a ≠,且12,x x 是方程20ax bx c ++=的两个根,则221212||()x x x x -=-;(4)若,,a b c ∈R ,0a ≠,且α是方程20ax bx c ++=的根,则α也是方程的根. 【难度】★★ 【答案】(1)、(2)、(4)正确,(3)不正确2.若12,x x 为方程270x x -+=的两个根,则212||x x -= .【难度】★★ 【答案】273.已知,0x y ≠且,求20092009()(x y x y x y+++的值. 【难度】★★【答案】14.关于x 的方程222(31)10x m x m --++=的两根为αβ、,且||||3αβ+=,求实数m 的值. 【难度】★★【答案】53m =-或2m =5.设αβ、为方程220x x t ++=,(t ∈R )的两个根,()||||f t αβ=+, (1)求()f t 的解析式;(2)证明关于t 的方程()f t m =,当2m >时恰有两个不等的根,且两根之和为定值. 【难度】★★【答案】(1)0()2,010t f t t t ⎧<⎪=<≤⎨⎪<⎩...(2)证明:函数()y f t =的图像关于直线12t =对称(证略) 当(1,)t ∈+∞时,()f t 为增函数,且()(2,)f t ∈+∞;022=++y xy x当(,0)t ∈-∞时,()f t 为减函数,且()(2,)f t ∈+∞.所以当2m >,方程()f t m =在区间(1,)+∞上有唯一解1t ,在区间(,0)-∞上也有唯一解2t , 则121212t t +=⨯=.4、复数方程综合问题【例13】关于x 的二次方程2120x z x z m +++=中,1z ,2z ,m 都是复数,且21241620z z i -=+,设这个方程的两个根α、β满足||αβ-=||m 的最大值和最小值. 【难度】★★【答案】根据韦达定理有12z z mαβαβ+=-⎧⎨=+⎩∵22212()()444z z m αβαβαβ-=+-=-- ∴2212|()||4(4)|28m z z αβ-=--=.∴2121|(4)|74m z z --=,即|(45)|7m i -+=, 这表明复数m 在以(4,5)C 为圆心,7为半径的圆周上,∴max ||7m =min ||7m =当5001,150log 22m t m t >⎧⎪<<⎨<-⎪⎩即2log 215050m t -<<.【例14】已知22016220160122016(1)x x a a x a x a x ++=++++,试求0362016a a a a ++++的值。
高中数学-学生-实系数一元二次方程
教学内容
知识精要
1.复数的平方根与立方根:
和实数一样,复数 和 ,若满足 ,则称 是 的平方根。因为 ,所以 的平方根是 两个数。
(1)求法:利用复数相等求复数的平方根
(2)1的立方根:
的常用结论: ; ;
思考:当 时, 取何值?
2.实系数一元二次方程 在复数集中恒有解.当判别式 时,方程有两个实数解 ;当判别式 时,方程有两个虚根,且互为共轭 .
(1)在复数集中,实系数一元二次方程的根的性质:实系数一元二次方程在复数集中一定有两个根,它们是两个实根或者是一对共轭虚根。此性质可推广到实系数一元n次方程在复数集中的情况也成立。
(2)实系数一元二次方程 在复数范是一元二次方程 的根,则
2.在复数范围内分解因式 ________
7.设等比数列 其中 :
(1)求 的值;
(2)试求使 的最小自然数
(3)对于(2)中的 ,求 的值。
例4.求与自身的平方共轭的复数
例5.已知复数 是 的平方根,求 的值。
例6.设方程 的两根为 ,且 ,求实数m的值。
例7.已知 为实系数一元二次方程 的两个根, 为虚数,且 ,求 的值。
例8.若关于 的方程 至少有一个模为1的根,求实数 的值。
例9. 是方程 的两个根,其中 求 的值。
备选例题
1.对任意非零复数 ,定义集合 ,设 是方程
3.已知复数 满足 且 ,则 ________
4.方程 的解集是________
5.方程 的两根为__________
6.已知 是实系数方程 的根,则 ______
7.复数 的平方根是()
8.下列命题在复数集中是否正确?为什么?
高中数学高二下册第十三章13.6 实系数一元二次方程 课件(2)
问题3:
❖ 当实系数一元二次方程有一对共轭虚根 时,根与系数的关系还成立吗?
x
1
x
1
x2 x2
c a
b a
√
例4.3i-2是关于x的方程2x2+px+q=0 的一个根,求实数p、q的值.
问题4:根与方程的关系
❖知道方程,可以求根 ❖知道根,如何得到方程?
例5. 1+2i是实系数一元二次方 程的一个根,则这个方程可以 是?
身体健康,学习进步! 崇高的理想就象生长在高山上的鲜花。如果要搞下它,勤奋才能是攀登的绳索。
小结:
❖ 在复数集中,实系数一元二次方程总有解(根) ❖ 根的情况可由△的符号决定
❖ 特别地,当△<0时,有一对共轭虚根
问题2:根与因式分解的关系
❖ 求出方程 a2 xbx c0的根x1,x2
a 2 x b c x a (x x 1 )x ( x 2 )
例3.(1)x2-x+2 (2)2x2-4x+5
实系数一元二次方程(1) a2 xbx c0
( a 、 b 、 c R 且 a 0 )
解方程(x∈C)
(1)x2 4x30 (2)2x2 2x10
问:1:在复数集中,解方程
a2 x b c x 0 ( a 、 b 、 c R ,a 0 )
当△ <0时,求根公式?
例1.在复数集中解方程: 2x2-4x+5=0
总结(在复数范围内)
❖实系数一元二次方程的根的求解 ❖根与因式分解的关系 ❖根与数的关系 ❖根与方程类比
提出 问题
解决 问题
关 x 的 于 x 2 方 ( 2 i) x 程 m i 0
有实根,求实数m的值
高中数学-教师-实系数一元二次方程
因为实系数一元二次方程的共轭虚根成对出现,所以设模为1的虚根为 ,则另一根为 。
由韦达定理得 又 (舍)或
或
例9. 是方程 的两个根,其中 求 的值。
解:当
(1) (2)
当
备选例题
1.对任意非零复数 ,定义集合 ,设 是方程
的一个根,试用例举法表示集合
解: 是 的根,则 或
(1)若 且 ,则方程 有两个实数根。
(2)若 且 是方程 的两个根,则 ;
(3)若 且 是方程 的两个根,则 ;
(4)若 且 是方程 的根,则 也是方程的根。
答案:(1)、(2)(4)正确,(3)不正确
精解名题
例1.关于 的方程 的两根的模的和为 ,求实数 的值。
解:解:
(1)当 ,即 时,
,且
与 同号
当 时,
当 时,有
2.设复数 是实系数方程 的根,又 为实数,求点 的轨迹。
解: 实系数方程的根, 也是此方程的根。
为实数( )
,即
得判别根的虚实,运用判别式,求根公式,这些方法要熟练
2.一元二次方程的系数含有虚数时,判别式失去了功能,运用韦达定理求解方法。
3.分类讨论是重要的思想方法。复数里也会有这样的题目,虚根、实根不同情况下,解的形式是不同的。
高中数学备课组
教师
班级
学生
日期
上课时间
学生情况:
主课题:实系数一元二次方程
教学内容
知识精要
1.复数的平方根与立方根:
和实数一样,复数 和 ,若满足 ,则称 是 的平方根。因为 ,所以 的平方根是 两个数。
(1)求法:利用复数相等求复数的平方根
(2)1的立方根:
一元二次方程公式法例题20道
一元二次方程公式法是数学中的一个重要知识点,它的掌握对于学生的数学学习和思维能力培养都有着重要的意义。
在这篇文章中,我将按照从简到繁的顺序,深入浅出地探讨一元二次方程公式法,并根据你提供的要求,撰写20道相关例题以加深理解。
一元二次方程是指形如ax^2+bx+c=0的方程,其中a、b、c为实数且a≠0。
而一元二次方程的解法有很多,其中一元二次方程公式法是一种常用而有效的方法。
通过对一元二次方程公式法的理解和掌握,我们不仅能够解决各种各样的数学问题,还能够培养自身的逻辑思维和数学分析能力。
让我们以一元二次方程公式法的定义为起点,逐步深入探讨这一知识点。
一元二次方程公式法是指通过一元二次方程的一般形式,利用求根公式(-b±√(b^2-4ac))/2a,解出方程的根。
这是一种常用的解一元二次方程的方法,我们可以通过代入系数a、b和c的值,快速、准确地求得方程的解。
接下来,我们将通过解答一系列例题来加深对一元二次方程公式法的理解。
以下是20道例题:1. 求解方程2x^2-5x+2=0的解。
2. 求解方程3x^2+4x-1=0的解。
3. 求解方程x^2-9=0的解。
4. 求解方程4x^2-16=0的解。
5. 求解方程x^2-6x+9=0的解。
6. 求解方程2x^2+3x+1=0的解。
7. 求解方程x^2+5x+6=0的解。
8. 求解方程x^2-4x+4=0的解。
9. 求解方程3x^2-2x-1=0的解。
10. 求解方程4x^2+4x+1=0的解。
11. 求解方程2x^2-7x+3=0的解。
12. 求解方程x^2-8x+16=0的解。
13. 求解方程3x^2+6x+3=0的解。
14. 求解方程5x^2-10x+5=0的解。
15. 求解方程x^2+2x+1=0的解。
16. 求解方程2x^2-9x+9=0的解。
17. 求解方程3x^2-5x+2=0的解。
18. 求解方程4x^2-12x+9=0的解。
19. 求解方程x^2+4x+4=0的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 ,求实数p的值.
例2、已知关于x的方程 x2 2ax a 2 4a 4 0 (a R) 的两根为 、 ,且 3,求实数a的值.
2 ax 例3、已知关于x的方程 (1 2i)x 2a(1 i) 0 (a R)
有实数根,求实数a的值.
; / 海南楼盘 海南买房 djm837ach 我最后一个接过碗,还没有找到合适的位置坐下,对面便传来了吆喝声,“这是谁的筐?占了老子的摊位!抓紧给老子抬了, 要不然,老子就给他蹬翻!” 我慌乱地把碗放在小桌上,急忙走了过去。 我还没开口,他就嚷起来,“谁叫你在这儿的?赶紧搬走!别妨碍老子摆摊。”这人看上去年纪与我差不多,却摆出一副黑帮 老大的架式,他的话让我听了很不顺耳。 “这明明是我的摊位,你凭什么让我搬走?!”我一气之下,不软不硬地回敬了他一句。 他看我根本不吃那一套,更加变本加厉起来,用脚踩着我的筐沿儿,用手指着我大吼道:“他娘的,你说这摊位是你的,当着 大家的面,你把它叫答应„„不然,你信不信老子给你蹬了?” 真是烧香碰着鬼了,还有这样不讲理的人! 我的火一下子上来了,“把你的狗腿给我拿掉!不然,老子对你可就不客气了!” 他更加来劲儿了,故意用脚蹬着筐来回晃动。 那时我正是年轻,血气方刚,还经得起他的有意挑衅?狠狠地一脚踢去,把他踢倒在地。 他爬了起来,挽了挽袖子要跟我动手。 这时,小商贩们都围了上来把我俩隔开。我不知饭摊的掌柜跟他说了些什么,他便挽下袖子无精打采地走了。 我掏出两块钱给了饭摊的掌柜,饭也没吃便忙活着摆起摊来。 不一会儿,跟我打架的人和一个高个子的中年人又来到我面前。 好啊,刚才吃了亏,又找帮凶来了,我才不怕呢!我心里这么想着。 “老兄,刚才赵四做得不对,我李五给你赔礼来了。”高个子笑嘻嘻地对我说。 “老弟,我们初次见面不认识,听饭摊的王掌柜说你是肖艳的丈夫,儿子生病住了院,我们应该帮帮你才是,刚才的事你就 不要放在心上。你看,你自己守着这四筐蘑菇,要不我们哥俩帮你卖两筐?”原来他也会说人话,刚才怎么脏话连篇? “不打不相识嘛,依我看,干脆你说个价钱,我俩每人一筐,这样行不行?”李五做起了我的思想工作。 我的心被他们说软了,于是说好八毛钱一斤,每人给了一筐。他俩高兴地抬到自己的摊位上卖了起来。 下集了,我挂念着儿子的病情,推着小车直接去了已院。值班的护士对我说,三哥刚刚送孩子出院回家了。 我的心里犹如一块石头落了地,高高兴兴地向家赶去。 回到家,妻子已做好了饭,我一边吃饭一边跟她说着今天的故事,妻子说赵四和李五就是俩个集霸,我教训赵四也给商贩们出 了口恶气。但是我毕竟还是上了他们的圈套,被他们骗了。妻子的话使我百思不得其解,人家明明是好心好意地帮我,怎么说 我被骗了呢?当她问我给他们的蘑菇的斤数时,我才恍然大悟,两筐蘑菇共少了三十六斤。这可不是个小数目,难道我又看差 秤了吗?不可能!饭摊的王掌柜给掌的秤,他不能昧着良心做坏事。那就是秤有问题,也不对呀,集市上的商贩都用这干秤做 交易,难道他们不怕舍本? 唉——!不用管它,我毕竟在生意场上迈开了第一步,我自己也能卖东西了。我心里暗自庆幸。
2.若两个数之和为2,两个数之积为3,则这两个数 分别为 . 2 3.在复数集中分解因式: 3x 2 x 1= .
2 x 4.若方程 ax 2 0(a R)有虚数根z,则|z|=
.
(三)例题
2 x 例1、已知方程 px 1 0( p R) 的两根为
x1 、x2 ,若 x1 x2
2
x1 x2
b a
c x1 x2 a
特别地,
x1和x2 为一对共轭虚根,即 当 b2 4ac 0时,
x2 x1
—
2 x1 x2 2Re x1 x x | x | ∴ 1 2 1
(二)巩固练习
2 x 1.已知1-i是实系数一元二次方程 px q 0 . 的一个根,则 p q =
(1)若方程 2x2 8x a 1 0(a R)有一个虚根的模为
5,则实数a的值为
.
(2)已知关于x的方程 x2 2x m 0(m R)的两根为 、 ,求 .
(3)已知关于x的方程 x2 (k 2i)x 2 ki 0(k R) 有实根,求实数k的值,并解方程.
(四)课堂练习
2 x 1.若 、 是方程 x 7 0的两个根,则
2
=
.
2.见课本P93练习13.6(2)T4. (五)课堂小结
(六)课后作业 1.书面作业:练习册P55 习题13.6 A组 T6.8. P57 习题13.6 B组 T4.5. 2.思考题:(补充题及备选题)
b x 2a
(3)当 b2 4ac 0时, 原方程有一对共轭虚数根
b 4ac b2 x i 2a 2a
2 ax bx c 在复数范围内分解因式: 2、二次三项式
ax2 bx c a( x x1 )( x x2 )
3、实系数一元二次方程ax bx c 0 的韦达定理:
13.6(2)实系数一元二次方程
二次方程 ax2 bx c 0(a、b、c R且a 0) (1)当 b2 4ac 0 时,原方程有两个不相等的实数根
b b2 4ac x 2a 2a
(2)当 b2 4ac 0时,原方程有两个相等的实数根
