matlab二分法求根例题
matlab 二分法汇总

二分法的matlab主程序function [k,x,wuca,yx]=erfen(a,b,abtol)a(1)=a; b(1)=b;ya=fun(a(1)); yb=fun(b(1)); %程序中调用的fun.m 为函数if ya* yb>0,disp('注意:ya*yb>0,请重新调整区间端点a和b.'), return endmax1=-1+ceil((log(b-a)- log(abtol))/ log(2)); % ceil是上取整for k=1: max1+1a;ya=fun(a); b;yb=fun(b); x=(a+b)/2;yx=fun(x); wuca=abs(b-a)/2; k=k-1;[k,a,b,x,wuca,ya,yb,yx]if yx==0a=x; b=x;elseif yb*yx>0b=x;yb=yx;elsea=x; ya=yx;endif b-a< abtol , return, endendk=max1; x; wuca; yx=fun(x);区间二分法:与对分查找法相同1 区间二分法求出的仅仅是方程的一个单根,如果方程有重根或者多个根时,在做区间二分法时就会出现分叉,这样方程有几个根,就会产生几个实数序列,每一个实数序列的极限便是方程的一个根2 通常用区间二分法为一些迭代法提供靠近x^*的初始选代值;3 区间二分法的缺点是不能求方程的复数根。
format longa=5;b=6;x1=a;x2=b;f1=4*cos(x1)+4*sin(x1)+0.5*x1-2; f2=4*cos(x2)+4*sin(x2)+0.5*x2-2;step=0.000001;ii=0;while abs(x1-x2)>stepii=ii+1;x3=(x1+x2)/2;f3=4*cos(x3)+4*sin(x3)+0.5*x3-2;if f3~=0if f1*f3<0x2=x3;elsex1=x3;endendendx3f=[4*cos(x3)+4*sin(x3)+0.5*x3] disp(['迭代次数:',num2str(ii),'次'])牛顿迭代法求解:在方程f(x)=0有实数根的情况下,若能够将方程等价地转化成x=g(x)的形式,然后取一个初始值x0代入x=g(x)的右端,算得x1=g(x0),再计算x2=g(x1),这样依次类推x(k+1)=g(x(k))可以得到一个序列xk,通常称g(x)为迭代函数,序列xk为由迭代函数产生得迭代序列,x0为迭代初始值。
数值计算作业

数值计算作业1:方程求根的二分法第一步:在MATLAB 软件中,建立一个实现二分法的MATLAB 函数文件xy01.m 如下: function [x_star,k]=xy01(fun,a,b,e) if nargin<4;endfa=feval(fun,a);fb=feval(fun,b);if fa*fb>0 x_star=[fa,fb];k=0;return;end k=1;while abs(b-a)/2>ex=(a+b)/2;fx=feval(fun,x); if fx*fa<0b=x;fb=fx; elsea=x;fa=fx; end k=k+1; endx_star=(a+b)/2; 第二步:(1)在MATLAB 命令窗口求解方程sinx+9x-2=0在自变量区间[0,1]上的近似实根,并使误差不超过0.5×10−3。
输入并得到结果如下图即结果为0.1997,二分次数为11次。
(2)改变输入参数,计算误差不超过100.510-⨯的近似实根,并给出二分的次数,输入并得到结果如下图:即结果为0.2001,二分次数为35次。
实验分析与结论:由上面二分法的实验结果,我们可以得出这样的结论:二分法要循环k=11次,才能达到精度为0.5×10−3的要求。
要循环35次,才能达到精度为0.5×10−10的要求。
作业2:方程求根的迭代法第一步:在MATLAB软件中,建立一个实现二分法的MATLAB函数文件xy02.m如下:function [z,k]=xy02(fun,x0,ep,Nmax)if nargin<4Nmax=500;endif nargin<3ep=1e-5;endx=x0;x0=x+2*ep;k=0;while abs(x0-x)>ep&k<Nmaxx0=x;x=feval(fun,x0)k=k+1endz=x;if k==Nmax waring;end第二步:(1)在MATLAB命令窗口求解方程sinx+9x-2=0在自变量区间[0,1]上的近似实根,并使误差不超过0.5×10−3。
计算方法 实验一 方程求根

实验一方程求根(1)二分法
1、实验程序
实现二分法的MATLAB函数文件agui_bisect.m
2. 在MATLAB命令窗口输入及实验结果及操作界面
(2)迭代法
1、实验程序
实现二分法的MATLAB函数文件agui_iterative.m
2、在MATLAB命令窗口输入及实验结果及操作界面
(3)牛顿法
1、实验程序
实现二分法的MATLAB函数文件agui_newton.m
2、在MATLAB命令窗口输入及实验结果及操作界面
结果分析:
由上面的对二分法、迭代法、牛顿法三种方法的三次实验结果,我们可以得出这样的结论:
二分法要循环k=10次,迭代法要迭代k=4次,牛顿法要迭代k=2次才能达到精度为0.5*10^-3的要求,而且方程0210=-+x e x
的精确解经计算,为0.0905250,由此可知,牛顿法和迭代法的精确度要优越于二分法。
而这三种方法中,牛顿法不仅计算量少,而且精确度高。
从而可知牛顿迭代法收敛速度明显加快,但由所学的内容可知,其收敛性与初值有关,它是局部收敛的。
二分法收敛虽然是速度最慢,但也常用于求精度不高的近似根。
而迭代法是逐次逼近的方法,原理简单,但存在收敛性和收敛速度的问题。
总之各种方法都各有优劣,适用于不同的情况中,须具体情况具体分析。
matlab方程求解实例

方程求根一、二分法1.用二分法求方程[]5.1,1013在区间=--x x 内的一个实根,要求两次近似值之间的误差不超过0.001。
解:用MA TLAB 求解:function rtn=bisection(fx,xa,xb,n,delta)x=xa;fa=eval(fx);x=xb;fb=eval(fx);disp(' [ n xaxb xc fc ]'); for i=1:nxc=(xa+xb)/2;x=xc;fc=eval(fx);X=[i,xa,xb,xc,fc];disp(X),if fc*fa<0xb=xc;else xa=xc;endif (xb-xa)<delta,break,endend输入:f='x^3-x-1';bisection(f,1,1.5,20,10^(-3))运行得:x0 =144 169 225y0 =12 13 15y =13.2302[ n xa xbxc fc ] 1.0000 1.0000 1.50001.2500 -0.29692.0000 1.2500 1.50001.3750 0.22463.0000 1.2500 1.37501.3125 -0.05154.0000 1.3125 1.37501.3438 0.08265.0000 1.3125 1.34381.3281 0.01466.0000 1.3125 1.3281 1.3203 -0.01877.0000 1.3203 1.3281 1.3242 -0.00218.0000 1.3242 1.3281 1.3262 0.00629.0000 1.3242 1.3262 1.3252 0.00202.求方程01)(3=--=x x x f 在区间[1,2]内的根,取精度510-=ε。
解:MATBLE 编程:function [x_star,it]=bisect(fun,a,b,ep)%%fun 为求根函数%%ep 为精度要求%%a ,b 为初始区间端点if nargin<4 ep=1e-5;endfa=feval(fun,a);fb=feval(fun,b);if fa*fb>0errorendk=0while abs(b-a)/2>=epx=(a+b)/2;fx=feval(fun,x);if fx==0breakendif fx*fa<0b=x;fb=fxelsea=x;fa=fxendk=k+1endx_star=(a+b)/2it=k输入:fun =@(x)(x^3-x-1);[x_star,it]=bisect(fun,1,2)运行得:x_star=1.3274It=16二、迭代法1.一般迭代法求解方程:.105.101)(5-03===--=ε附近的根,取精度在x x x x f 解:MATBLE 编程:function [x_star,it]=iterate(phi, x, ep, it_max) %% phi ()为迭代函数, %%x 为起始点, %%ep 为精度要求, %%it_max 为最大迭代次数。
数值计算方法matlab 第二章 求根

1第二章作业问题描述:不同温度的两种流体进入混合器混合,流出时具有相同的温度。
流体A 和B 的热容(单位:cal/(mol ·K))分别为:2623.381 1.80410 4.30010pA c T T --=+⨯-⨯ 1528.592 1.29010 4.07810pB c T T --=+⨯-⨯焓变(单位:cal/mol )为21T p T H c dT ∆=⎰。
A 进入混合器的温度为400℃,B 进入混合器的温度为700℃,A 的量(mol )是B 的量(mol )的两倍,试确定流体离开混合器的温度。
问题分析: 初始情况下,气体A 的温度比气体B 的温度低,故在混合过程中,气体A 温度升高,气体B 温度降低。
由于没有外界加热或者做功,混合气体整体的焓变应该为零。
设A 有2mol ,B 有1mol ,根据焓变公式计算得到:21-262400-22632= 6.762+3.608108.60010)6.762 1.80410 2.867105407.712T TA pA T H c dT T T dTT T T --∆=⨯-⨯=+⨯-⨯-⎰⎰(21-152700-1253=+1.29010 4.07810)0.64510 1.3591032958.030T TB pB T H c dT T T dTT T T --∆=⨯-⨯=+⨯-⨯-⎰⎰(8.5928.592而0A B H H ∆+∆=,故该问题最后变成求解方程2263()15.3548.2541016.4571038365.742f T T T T --=+⨯-⨯-的根的问题。
接下来将采用二分法、试位法以及牛顿法进行改方程的求解。
方程保存为f.m ,可在压缩文件中找到。
一、 二分法二分法的基本思想为,确定有根区间,然后不断将区间二等分,通过判断f(x)的符号,逐步将区间缩小,直到有根区间足够小,便可满足精度要求的近似根。
本例中,可以清楚的得到有根区间为(400,700)。
数值分析作业MATLAB

1.用二分法解方程 x-lnx=2 在区间【2 ,4】内的根方法: 二分法算法:f=inline('x-2-log(x)');a=2;b=4;er=b-a; ya=f(a);er0=.00001;while er>er0x0=.5*(a+b);y0=f(x0);if ya*y0<0b=x0;elsea=x0;ya=y0;enddisp([a,b]);er=b-a;k=k+1;end求解结果:>> answer13 43.0000 3.50003.0000 3.25003.1250 3.25003.1250 3.18753.1250 3.15633.1406 3.15633.1406 3.14843.1445 3.1484 3.1445 3.1465 3.1455 3.1465 3.1460 3.1465 3.1460 3.1462 3.1461 3.1462 3.1462 3.14623.1462 3.1462 3.1462 3.1462 3.1462 3.1462 最终结果为: 3.14622.试编写MATLAB 函数实现Newton 插值,要求能输出插值多项式。
对函数141)(2+=x x f 在区间[-5,5]上实现10次多项式插值。
Matlab 程序代码如下:%此函数实现y=1/(1+4*x^2)的n 次Newton 插值,n 由调用函数时指定 %函数输出为插值结果的系数向量(行向量)和插值多项式 算法:function [t y]=func5(n) x0=linspace(-5,5,n+1)'; y0=1./(1.+4.*x0.^2); b=zeros(1,n+1); for i=1:n+1 s=0; for j=1:i t=1; for k=1:iif k~=jt=(x0(j)-x0(k))*t;end;end;s=s+y0(j)/t;end;b(i)=s;end;t=linspace(0,0,n+1);for i=1:ns=linspace(0,0,n+1);s(n+1-i:n+1)=b(i+1).*poly(x0(1:i));t=t+s;end;t(n+1)=t(n+1)+b(1);y=poly2sym(t);10次插值运行结果:[b Y]=func5(10)b =Columns 1 through 4-0.0000 0.0000 0.0027 -0.0000Columns 5 through 8-0.0514 -0.0000 0.3920 -0.0000Columns 9 through 11-1.1433 0.0000 1.0000Y =- (7319042784910035*x^10)/147573952589676412928 + x^9/18446744073709551616 + (256*x^8)/93425 -x^7/1152921504606846976 -(28947735013693*x^6)/562949953421312 -(3*x^5)/72057594037927936 + (36624*x^4)/93425 -(5*x^3)/36028797018963968 -(5148893614132311*x^2)/4503599627370496 +(7*x)/36028797018963968 + 1b为插值多项式系数向量,Y为插值多项式。
二分法matlab程序(推荐文档)

二分法二分法基本思路一般地,对于函数f(x),如果存在实数c,当x=c 时,若f(c)=0,那么把x=c 叫做函数f(x)的零点。
解方程即要求f(x)的所有零点。
假定f(x)在区间(x ,y )上连续先找到a 、b 属于区间(x ,y ),使f(a),f(b)异号,说明在区间(a,b)内一定有零点,然后求f[(a+b)/2],现在假设f(a)<0,f(b)>0,a<b① 如果f[(a+b)/2]=0,该点就是零点,如果f[(a+b)/2]<0,则在区间((a+b)/2,b)内有零点,(a+b)/2>=a ,从①开始继续使用 ② 中点函数值判断。
如果f[(a+b)/2]>0,则在区间(a,(a+b)/2)内有零点,(a+b)/2<=b ,从①开始继续使用 中点函数值判断。
这样就可以不断接近零点。
通过每次把f(x)的零点所在小区间收缩一半的方法,使区间的两个端点逐步迫近函数的零点,以求得零点的近似值,这种方法叫做二分法。
从以上可以看出,每次运算后,区间长度减少一半,是线形收敛。
另外,二分法不能计算复根和重根。
二分法步骤用二分法求方程()0f x =的根*x 的近似值k x 的步骤① 若对于a b <有()()0f a f b <,则在(,)a b 内()0f x =至少有一个根。
② 取,a b 的中点12a b x +=计算1()f x ③ 若1()0f x =则1x 是()0f x =的根,停止计算,运行后输出结果*1x x =若1()()0f a f x <则在1(,)a x 内()0f x =至少有一个根。
取111,a a b x ==;若1()()0f a f x >,则取111,a x b b ==;④ 若12k k b a ε-≤(ε为预先给定的要求精度)退出计算,运行后输出结果*2k k a b x +≈,反之,返回步骤1,重复步骤1,2,3 二分法Mtalab 程序syms x;fun=input('(输入函数形式)fx=');a=input('(输入二分法下限)a=');b=input('(输入二分法上限)b=');d=input('输入误差限 d=')%二分法求根%f=inline(x^2-4*x+4);%修改需要求解的inline 函数的函数体f=inline(fun);%修改需要求解的inline 函数的函数体e=b-a; k=0 ;while e>dc=(a+b)/2;if f(a)*f(c)<0b=c;elseif f(a)*f(c)>0a=c;elsea=c;b=cende=e/2; k=k+1;endx=(a+b)/2;x%x 为答案 k%k 为次数例题:用二分法计算方程4324100x x x -++=在(-2,2)内的实根的近似值,要求精度为0.0001解:(输入函数形式)fx=x^4-2*x^3+4*x+10(输入二分法下限)a=-2(输入二分法上限)b=2输入误差限 d=0.0001得到结果d =1.0000e-004x =2.0000k =16>>。
借助Matlab使用二分法求解方程的根
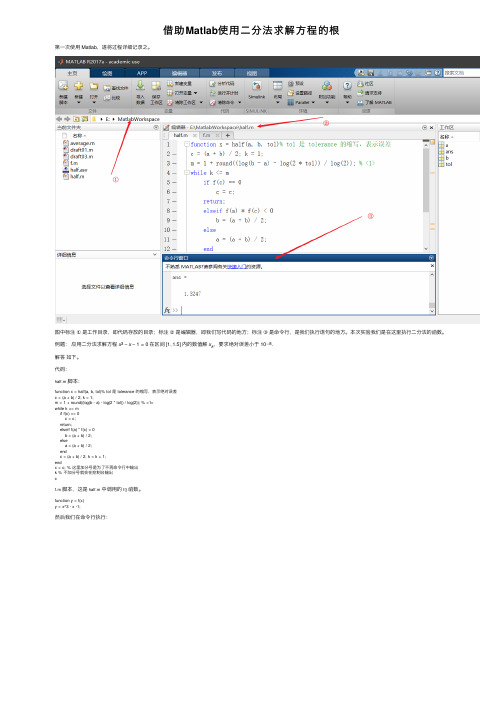
借助Matlab使⽤⼆分法求解⽅程的根第⼀次使⽤ Matlab,遂将过程详细记录之。
图中标注①是⼯作⽬录,即代码存放的⽬录;标注②是编辑器,即我们写代码的地⽅;标注③是命令⾏,是我们执⾏语句的地⽅。
本次实验我们是在这⾥执⾏⼆分法的函数。
例题:应⽤⼆分法求解⽅程x3−x−1=0 在区间 [1,1.5] 内的数值解x k,要求绝对误差⼩于 10−8.解答如下。
代码:half.m脚本:function x = half(a, b, tol)% tol 是 tolerance 的缩写,表⽰绝对误差c = (a + b) / 2; k = 1;m = 1 + round((log(b - a) - log(2 * tol)) / log(2)); % <1>while k <= mif f(c) == 0c = c;return;elseif f(a) * f(c) < 0b = (a + b) / 2;elsea = (a + b) / 2;endc = (a + b) / 2; k = k + 1;endx = c; % 这⾥加分号是为了不再命令⾏中输出k % 不加分号就会在控制台输出cf.m脚本,这是half.m中调⽤的f()函数。
function y = f(x)y = x^3 - x -1;然后我们在命令⾏执⾏:可以看出,最后求解得到的x=1.3247,即输出的ans,迭代次数k=27.关于代码half.m中的标注<1>,有如下解释:注意,在 Matlab 中,log()函数的底是e.补充例题(感兴趣的朋友可以⾃⾏测试):Processing math: 100%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab二分法求根例题
标题: MATLAB二分法求根例题
正文:
二分法是解决函数零点问题的一种常用方法。
在MATLAB中,可以使用
`root()`函数进行二分法求根。
下面是一个示例:
假设我们有一个函数`f(x)`,它在[-1,1]上零点为`(-1,0)`,现在我们希望使用二分法找到一个根。
我们可以使用以下步骤:
1. 使用二分法求导数,得到二分点的斜率`k`。
2. 计算二分点的横坐标`x_2`,满足`f(x_2) = f(x_1) + k`。
3. 使用二分法求导数,得到二分点的斜率`k`。
4. 计算二分点的横坐标`x_2`,满足`f(x_2) = f(x_1) + k`。
5. 重复步骤3和步骤4,直到求出的根不再重复。
下面是MATLAB代码实现:
```matlab
% 定义函数
f = -1 : 1 : 2;
% 求二分点
x_1 = min(f);
x_2 = max(f);
% 计算斜率
k = f(x_2) - f(x_1);
% 计算根
root = x_2 - (1 / k);
% 输出结果
disp(["二分法求根结果:" num2str(root)]);
```
在上面的代码中,我们首先定义了一个包含零点的函数`f(x)`,然后使用二分法求导数得到二分点的斜率`k`。
接着,我们计算二分点的横坐标`x_2`,并满足`f(x_2) = f(x_1) + k`。
最后,我们使用二分法求导数,得到二分点的斜率`k`,并计算二分点的横坐标`x_2`,满足`f(x_2) = f(x_1) + k`。
最后,我们重复步骤3和步骤4,直到求出的根不再重复,并输出结果。
需要注意的是,二分法求根可能会遇到无穷级数的情况。
这种情况下,我们需要使用一些技巧来避免无限递归。
具体来说,可以使用二分法求解函数的局部零点,或者使用二分法求解函数的极值点,然后在此基础上继续求根。
