非线性方程的二分法 迭代法 内含matlab程序代码
二分法及迭代法求解非线性方程根
二分法及迭代法求解非线性方程根班级：姓名：方学号：日期：一、实验目的1、熟悉二分法及迭代法求解非线性方程根的数值算法；2、用matlab软件实现二分法及迭代法，掌握迭代法的收敛性和收敛速度问题及其加速方法；二、基本理论及背景1、牛顿迭代法具有平方收敛的速度，所以在迭代过程中只要迭代几次就会得到很精确的解。
这是牛顿迭代法比简单迭代法优越的地方，但是选定的初值要接近方程的解，否则有可能得不到收敛的结果，再者，牛顿迭代法计算量比较大。
因每次迭代除计算函数值外还要计算微商值。
2、牛顿迭代理论推导：设r是f(x) = 0的根，选取x0作为r初始近似值，过点（x0,f(x0)）做曲线y = f(x)的切线L，L的方程为y =f(x0)+f'(x0)(x-x0)，求出L与x轴交点的横坐标 x1 = x0-f(x0)/f'(x0)，称x1为r的一次近似值。
过点（x1,f(x1)）做曲线y = f(x)的切线，并求该切线与x轴交点的横坐标 x2 = x1-f(x1)/f'(x1)，称x2为r的二次近似值。
重复以上过程，得r的近似值序列，其中x(n+1)=x(n)－f(x(n))/f'(x(n))，称为r的n+1次近似值；3、参考《二分法求非线性方程根》，实现二分算法，完成下面的题目：求方程○1的根，精度至少达到10-6；比较迭代下列迭代法求解○1中方程根的收敛性：○2,；用牛顿法设计迭代函数求解○1中方程的根（精度至少达到10-6），并与○2中收敛的迭代法比较收敛的速度。
三、算法设计及实现1、设计：方程○1function f=fun1(x)f=exp(x)-x-3;；○2function y=Exp2(x)y=exp(x)-3;function y=Exp3(x)y=log(x+3);牛顿迭代：function df=Exp4(x)df=exp(x)-1。
四、实验步骤1、○1打开matlab软件，新建ErFen_Root.m文件,在窗口中编辑二分法数值积分函数程序代码,并保存在指定的文件夹下,在Current Directory窗口右边点击《Browse For Folder》按钮指向ErFen_Root.m文件；○2在Command Window中编辑相应要计算的题目的数值函数及相应的题目的表达式。
[matlab二分法程序代码]matlab牛顿迭代法程序代码
![[matlab二分法程序代码]matlab牛顿迭代法程序代码](https://img.taocdn.com/s3/m/5cd37268a0116c175f0e48ea.png)
[matlab二分法程序代码]matlab牛顿迭代法程序代码篇一: matlab牛顿迭代法程序代码牛顿迭代法主程序：function?[k,x,wuca,yx]?=?newtonk=1;yx1=fun;yx2=fun1;x1=x0-yx1/yx2;while?abs>tolx0=x1;yx1=fun;yx2=fun1;k=k+1;x1=x1-yx1/yx2;endk;x=x1;wuca=abs/2;yx=fun;end分程序1：function?y1=funy1=sqrt-tan;end分程序2：function????y2=fun1%函数fun的导数y2=x/)-1/) );end结果：[k,x,wuca,yx]?=?newtonk?=8x?=0.9415wuca?=4.5712e-08yx?=-3.1530e-14[k,x,wuca,yx]?=?newtonk?=243x?=NaNwuca?=NaNyx?=NaN篇二: 二十个JA V A程序代码1百分制分数到等级分数package pm;public class SwitchTest {//编写程序，实现从百分制分数到等级分数的转换////>=90 A// 80~89 B// 70~79 C// 60~69 D// public static void main {int s=87;switch{case 10 :System.out.println;break; case 9 :System.out.println;break; case 8 :System.out.println;break;case 7 :System.out.println;break;case 6 :System.out.println;break; default :System.out.println;break; }}}2成法口诀阵形package pm;public class SwitchTest{public static void main{for{for{System.out.print+”\t”); }System.out.println;}}}3华氏和摄氏的转换法package pm;import java.util.Scanner;public class SwitchTest {public static void main {Scanner sc=new Scanner;while {System.out.println;String s = sc.next.trim;if ) {//做摄氏向华摄的转换System.out.println;double db = sc.nextDouble; double db2 = + 32;System.out.println;} else if ) {//做华摄向摄氏的转换System.out.println;double db = sc.nextDouble; double db2 = * 5 / 9;System.out.println + “C”); }else if){ break;}}}}package pm;import java.util.Scanner;public class SwitchTest{public static void main {Scanner sc=new Scanner;boolean flag=true;while {System.out.println; String str = sc.nextLine.trim; if || str.endsWith) {//做摄氏向华摄的转换30cString st = str.substring - 1);double db = Double.parseDouble;//[0,2)//2 double db=Double.valueOf.doubleValue; double db2 = + 32;System.out.println;} else if || str.endsWith) {//做华摄向摄氏的转换String st = str.substring - 1);double db = Double.parseDouble;//[0,2)//2 double db=Double.valueOf.doubleValue; double db2 = * 5 / 9;System.out.println + “C”); }else if){flag=false;}}}}4三个数的最大数package pm;public class SwitchTest {public static void main {int a=1,b=2,c=3,d=0;d=a>b?a:b;d=a>b?:;System.out.println;}}5简单计算器的小程序package one;import java.awt.BorderLayout;import java.awt.GridLayout;import java.awt.event.ActionEvent; import java.awt.event.ActionListener;import javax.swing.JButton;import javax.swing.JFrame;import javax.swing.JPanel;import javax.swing.JTextField;public class Jsq implements ActionListener {private JFrame frame;private JButton[] bus;private JTextField jtx;private JButton bu;private char[] strs;private String d_one = ““;private String operator;public static void main { new Jsq;}/* 利用构造进行实例化*/ public Jsq { frame = new JFrame; jtx = new JTextField; bus = new JButton[16]; strs = “789/456*123-0.+=“.toCharArray; for { bus[i] = new JButton; bus[i].addActionListener; } bu = new JButton; bu.addActionListener; init; } /* GUI 初始化*/ public void init { JPanel jp1 = new JPanel; jp1.add; jp1.add; frame.add; } /* 事件的处理*/ public void actionPerformed { /*获取输入字符*/ String conn = arg0.getActionCommand; /*清除计算器内容*/ if ) { JPanel jp2 = new JPanel; jp2.setLayout); for { jp2.add; } frame.add; frame.pack; frame.setLocation; frame.setVisible; frame.setDefaultCloseOperation;d_one = ““; operator = ““; jtx.setText; return; } /*暂未实现该功能*/if){ return; } /*记录运算符，保存运算数字*/ if ) != -1) { if && ““.equals)) return; d_one = jtx.getText; operator = conn; jtx.setText; return; } /*计算结果*/ if ) { if && ““.equals)) return; double db = 0; if ) { db = Double.parseDouble + Double.parseDouble); jtx.setText; } if ) { db = Double.parseDouble - Double.parseDouble); jtx.setText; } if ) { db = Double.parseDouble * Double.parseDouble); jtx.setText; } if ) { db = Double.parseDouble / Double.parseDouble); jtx.setText; } d_one = db + ““; return; }//界面显示jtx.setText + conn);}}6三角形图案package pm;public class SwitchTest{public static void main{int n=5;for{for{System.out.print;}for{System.out.print;}System.out.println;}}}7输出输入的姓名package pm;import java.util.Scanner;public class SwitchTest{public static void main{String name=null;Scanner sca=new Scanner ; char firstChar; do{System.out.println; name=sca.nextLine; firstChar=name.charAt;}while);System.out.println;}}8一小时倒计时小程序package pm;import javax.swing.JFrame;import javax.swing.JLabel;import javax.swing.JPanel;public class SwitchTest {private JFrame frame;private JLabel jl1;private JLabel jl2;private JLabel jl3;/*主方法*/public static void main {new SwitchTest.getTime;}/*倒计时的主要代码块*/private void getTime{long time=1*3600;long hour =0 ;long minute =0 ;long seconds=0;while{hour=time/3600;minute=/60;seconds=time-hour*3600-minute*60; jl1.setText;jl2.setText;jl3.setText;try {Thread.sleep;} catch {e.printStackTrace;}time--;}}/*构造实现界面的开发GUI */ public SwitchTest{frame = new JFrame;jl1 = new JLabel;jl2 = new JLabel;jl3 = new JLabel;init;}/*组件的装配*/private void init{JPanel jp=new JPanel;jp.add;jp.add;jp.add;frame.add;frame.setVisible;frame.setLocation;frame.setSize;frame.setDefaultCloseOperation; } }9棋盘图案public class Sjx{public static void main{int SIZE=19;for{if{System.out.print;//两个空格}else{System.out.print);//两个空格}}System.out.println;// System.out.print:);for{System.out.print;//一个空格}else{System.out.print+” “);//一个空格}for{System.out.print;//两个空格}System.out.println;}}}10数组输出唐诗package day04;public class ArrayTest {public static void main{char[][] arr=new char[4][7];String s=“朝辞白帝彩云间千里江陵一日还两岸猿声啼不住轻舟已过万重山”; for{for{arr[i][j]=s.charAt;}for{for{System.out.print;}System.out.println;}}}11找出满足条件的最小数package day02;public class Fangk{public static void main{// for{// int q=i/1000;// int b=i/100%10;// int s=i/10%10;// int g=i%10;// if{ // System.out.println; // break; // }// }loop1: for{loop2: for{if{continue loop2;}for{for{if{ System.out.println); break loop1;}}}}}}} Min Number12判断一个数是否是素数package day02;public class Fangk{ public static void main{ int num=14;boolean flag=true;for{flag=false;break;}}if{System.out.println; }else{System.out.println; }}}////////////////////////////////////////////////////////////////////// package day04;import java.util.Scanner;public class A1{public static void main{int n;Scanner sca=new Scanner;System.out.println; n=sca.nextInt;if){System.out.println; }else{System.out.println;}public static boolean isPrimeNumber{ for{if{return false;}}return true;}}13一个数倒序排列package day02;public class Daoxu{public static void main{ int olddata=3758;int newdata=0;while{for{newdata=newdata*10+olddata%10; olddata=olddata/10; }System.out.println;}}}14将一个整数以二进制输出package day04;import java.util.Scanner; public class ArrayTest { public static void main{ int n; Scanner s=new Scanner; System.out.println; n=s.nextInt; for{if)!=0){System.out.print;}else{System.out.print;}if%8==0){System.out.print;}}}}15矩形图案package day02;public class Fangk {public static void main{ int m=5,n=6; for{System.out.print;}System.out.println;for{System.out.print;for{System.out.print; }System.out.print;System.out.println;}for{System.out.print;}}}16猜数字package day02;import java.util.Scanner;public class Csz {public static void main {Scanner s = new Scanner; int num = * 1000); int m=0; for{System.out.println; m=s.nextInt;if{System.out.println;}else if{System.out.println;}else{System.out.println; break;}if{System.out.println; }}if{System.out.println; }}}17.HotelManagerpackage hotel;import java.util.Scanner;public class HotelManager {private static String[][] rooms;// 表示房间public static void main {rooms = new String[10][12];String comm;// 表示用户输入的命令for {for {rooms[i][j] = “EMPTY”;}}//while {System.out.println;Scanner sca = new Scanner; System.gc;comm = sca.next;if ) {search;} else if ) {int roomNo = sca.nextInt;String name = sca.next;in;} else if ) {int roomNo = sca.nextInt;out;} else if ) {System.out.println;break;} else {System.out.println; }}}private static void out {if-1][-1])){ System.out.println;} return; } rooms[-1][-1]=“EMPTY”; System.out.println; private static void in { if-1][-1])){ System.out.println;return;}rooms[-1][-1]=name;System.out.println;}private static void search {for {//打印房间号for {if {System.out.print + “ “); } else {System.out.print + “ “); }}//打印房间状态System.out.println;for {System.out.print;}System.out.println;}}}18.StudentManagerpackage day05.student_manager;import java.util.Scanner;public class StudentManager {static int[][] scores=new int[6][5];static String[] students={“zhangsan”,”lisi”,”wangwu”,”zhaoliu”,”qianqi”,”liuba”}; static String[] courses={“corejava”,”jdbc”,”servlet”,”jsp”,”ejb”};public static void main {for{for{scores[i][j]=*100);}}Scanner s=new Scanner; String comm;while{System.out.println; comm=s.next;if){String para=s.next; avg;}else if){String course=s.next; sort;}else if){String student=s.next; String course=s.next; get;}else if){break;}else{System.out.println; }}}//main end!public static void avg{int sIndex=-1;//int cIndex=-1; for{ if){ sIndex=i; } } if{ for{ if){ cIndex=i; } } } if{ System.out.println; return; } double avg=0.0; if{ for{ avg+=scores[sIndex][i]; } avg/=scores[sIndex].length; System.out.println; }else{ for{ avg+=scores[i][cIndex]; } avg/=scores.length; System.out.println; } } public static void sort{ int[] courseScore=new int[scores.length]; if){//如果求总分的排名//求出每个学生的总分，将成绩存放在courseScore数组中for{ int studentSum=0; for{ studentSum+=scores[i][j]; }courseScore[i]=studentSum; } }else{//如果不是求总分排名int cIndex=-1; for{//找到这门课程的下标if){ cIndex=i; } } if{//如果是一门有效的课程//把scores数组中这一列的值放到courseScore数组中！for{ courseScore[i]=scores[i][cIndex]; } }else{//如果不是一门有效的课程System.out.println; return; } } String[] studentCopy=new String[students.length]; System.arraycopy; for{ for{ if{ int temp=courseScore[i]; courseScore[i]=courseScore[j]; courseScore[j]=temp; String stemp=studentCopy[i];studentCopy[i]=studentCopy[j]; studentCopy[j]=stemp; } } } int order=1; System.out.println; for{ if{ order--; }else{ order=i+1;} System.out.print;System.out.print;System.out.println;order++;}}public static void get{int sIndex=-1;int cIndex=-1;for{if){sIndex=i;}}if{System.out.println;return;}if){//如果求总分int studentSum=0;for{studentSum+=scores[sIndex][j];}System.out.println; return;}for{if){cIndex=i;}}if{System.out.println;return;}System.out.println;}}19.Fivepackage hotel;import java.util.Scanner;/*** 首先在程序第一次运行的时候，构建出棋盘，切以后* 不能再从新构建，知道结束,所以将其放到静态代码块中。
用Matlab编写二分法和Newton迭代法求解非线性函数
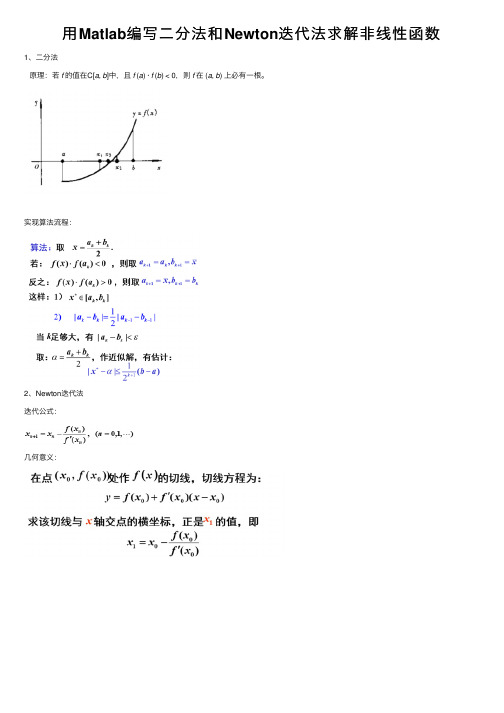
⽤Matlab编写⼆分法和Newton迭代法求解⾮线性函数1、⼆分法原理：若f的值在C[a, b]中，且f (a) · f (b) < 0，则f在 (a, b) 上必有⼀根。
实现算法流程：2、Newton迭代法迭代公式：⼏何意义：3、求解问题⽤Newton法和⼆分法求的解。
4、代码实现1 clear;close;clc2 a=0;b=1;%根区间3 e=10^(-6);%根的容许误差4 [X , N]=dichotomy(e,a,b);%⼆分法5 p0=0.5;%初始值6 N=15;%迭代次数7 [X1]=Newdon(p0,e,N);%Newton迭代法89 function [X , N]=dichotomy(deta,a,b)10 % 函数dichotomy:⼆分法11 %输⼊值：12 %fun:⽅程函数13 %deta:根的容许误差14 %有根区间：[a,b]15 %输出值16 %X:求解到的⽅程的根17 %N:总的迭代次数18 N=1+fix(log2((b-a)/deta));%由公式7.2求得,取整数|X_N-X*|<=(b-a)/2^N<deta,求N19 n=1;20 f1=myfunction(a);21 f2=myfunction(b);22if (f1*f2>0)23 disp('根不在输⼊的区间⾥，请重新输⼊区间');24else25while n <= N26 x=(a+b)/2;27if myfunction(a)*myfunction(x)>028 a=x;29else30 b=x;31 end32 n=n+1;33 end34 X=x;35 fprintf('第%d次⼆分法求出的⽅程的根:\n',N);36 fprintf('X=\n');37 disp(X);38 end39 end4041 function [P]=Newdon(p0,TOL,N)42 %求⽅程组的解43 %输⼊参数44 %初始值：p045 %误差容限:TOL46 %最⼤迭代次数:N47 %输出参数：48 %⽅程近似解：p49 %或失败信息“Method failed”50 format long;51 n=1;%初始迭代次数52 syms x;53while n<=N54if abs(subs(diff(myfunction(x)),x,p0))<TOL55 P=p0;56break;57else58if subs(diff(myfunction(x),2),x,p0)==059 disp('Method failed');60break;61else62 p=p0-myfunction(p0)/subs(diff(myfunction(x)),x,p0);63 p=eval(p);%将exp的值转为⼩数值64if(abs(p-p0)<TOL)65 P=p;66break;67else68 p0=p;69 end70 end71 end72 n=n+1;73 end74 % P=vpa(P,10);%将分数转为⼩数并保留8位⼩数75 fprintf('第%d次NeWton迭代法求出的⽅程的根:\n',N);76 fprintf('P=\n');77 disp(P);78 end7980 function f=myfunction(x)81 f=x*exp(x)-1;82 end5、求解结果。
二分法,牛顿迭代法,matlab
二分法、牛頓迭代法求方程近似解在一些科學計算中常需要較為精確的數值解，本實驗基於matlab 給出常用的兩種解法。
本實驗是以解決一個方程解的問題說明兩種方法的精髓的。
具體之求解方程e^(-x)+x^2-2*x=0，精度e<10^-5;;程序文本文檔如下%%%%%%二分法求近似解cleardisp('二分法求方程的近似解')format longsyms xf=inline('exp(-x)+x^2-2*x');%原函數%通過[x,y]=fminbnd(f,x1,x2)求出極小值點和極小值，進而確定%區間端點，從而確定解區間矩陣CX=[];C=[0 1.16;1.16 2] ; %C(:,1)為解區間的左端點，C(:,2)為解區間右端點ss=length(C); %統計矩陣C的行數，即為方程解的個數for i=1:ssa=C(i,1);b=C(i,2);%f(a)>=0,f(b)<=0e1=b-a;%解一的精度e0=10^-5;%精度ya=f(a);while e1>=e0x0=1/2*(a+b);y0=f(x0);if y0*ya<=0b=x0;elsea=x0;ya=y0;ende1=b-a;endA=[a,b,e1];%解的區間和精度X=[X;A];%解與精度構成的矩陣endX%%%%%%%牛頓迭代法disp('牛頓迭代法解方程的近似解')clear %清空先前變量syms x %定義變量y=exp(-x)+x^2-2*x;%原函數f=inline(y);f1=diff(y); %一階導函數g=inline(f1);format long %由於數值的默認精度為小數點后四位，故需要定義長形X=[];C=[0 1.16;1.16 2] ; %C(:,1)為解區間的左端點，C(:,2)為解區間右端點ss=length(C); %統計矩陣C的行數，即為方程解的個數for i=1:ssa=C(i,1);b=C(i,2);%f(a)>=0,f(b)<=0e0=10^-5; %要求精度i=1; %迭代次數x0=(a+b)/2;A=[i,x0]; %迭代次數，根值的初始方程t=x0-f(x0)/g(x0); %%%%迭代函數while abs(t-x0)>=e0 %%迭代循環i=i+1;x0=t;A=[A;i,x0];t=x0-f(x0)/g(x0);endA ;B=A(i,:);%迭代次數及根值矩陣X=[X;B];endX運行結果如下如若使用matal內置函數fzero,得到如下結果由兩者求得的結果知，使用函數fzero求得的結果精度不夠。
数值分析中求解非线性方程的MATLAB求解程序
数值分析中求解非线性方程的MATLAB求解程序1. fzero函数：fzero函数是MATLAB中最常用的求解非线性方程的函数之一、它使用了割线法、二分法和反复均值法等多种迭代算法来求解方程。
使用fzero函数可以很方便地求解单变量非线性方程和非线性方程组。
例如，要求解方程f(x) = 0，可以使用以下语法：``````2. fsolve函数：fsolve函数是MATLAB中求解多维非线性方程组的函数。
它是基于牛顿法的迭代算法来求解方程组。
使用fsolve函数可以非常方便地求解非线性方程组。
例如，要求解方程组F(x) = 0，可以使用以下语法：``````3. root函数：root函数是MATLAB中求解非线性方程组的函数之一、它采用牛顿法或拟牛顿法来求解方程组。
使用root函数可以非常方便地求解非线性方程组。
例如，要求解方程组F(x) = 0，可以使用以下语法：``````4. vpasolve函数：vpasolve函数是MATLAB中求解符号方程的函数。
它使用符号计算的方法来求解方程，可以得到精确的解。
vpasolve函数可以求解多变量非线性方程组和含有符号参数的非线性方程。
例如，要求解方程组F(x) = 0，可以使用以下语法：```x = vpasolve(F(x) == 0, x)```vpasolve函数会返回方程组的一个精确解x。
5. fsolve和lsqnonlin结合：在MATLAB中，可以将求解非线性方程转化为求解最小二乘问题的形式。
可以使用fsolve函数或lsqnonlin函数来求解最小二乘问题。
例如，要求解方程f(x) = 0，可以将其转化为最小二乘问题g(x) = min，然后使用fsolve或lsqnonlin函数来求解。
具体使用方法可以参考MATLAB官方文档。
6. Newton-Raphson法手动实现：除了使用MATLAB中的函数来求解非线性方程，还可以手动实现Newton-Raphson法来求解。
第五讲非线性方程求根及其MATLAB实现
第五讲非线性方程求根及其MATLAB实现一、引言在数学和工程领域中，非线性方程的求解是一项基本任务。
非线性方程通常不具备直接求解的方法，因此需要采用迭代方法来逼近其解。
本讲将介绍几种常用的非线性方程求根方法，并给出MATLAB实现的示例。
二、二分法二分法是一种简单但有效的求根方法。
其基本思想是将方程的根所在的区间进行逐步划分，并选择其中点作为迭代的点，直到满足精度要求。
具体实现如下：```matlabfunction x = bisection(f, a, b, tol)if f(a) * f(b) >= 0error('f(a)和f(b)符号相同');endwhile (b - a) / 2 > tolx=(a+b)/2;if f(x) == 0break;elseif f(a) * f(x) < 0b=x;elsea=x;endendend```三、牛顿法牛顿法是一种基于方程导数的迭代方法，其基本思想是使用方程的切线来逼近其根。
具体实现如下：```matlabfunction x = newton(f, df, x0, tol)while abs(f(x0)) > tolx0 = x0 - f(x0) / df(x0);endx=x0;end```四、割线法割线法是一种类似于牛顿法的迭代方法，其基本思想是用两个迭代点的连线来逼近方程的根。
具体实现如下：```matlabfunction x = secant(f, x0, x1, tol)while abs(f(x1)) > tolx=x1-f(x1)*(x1-x0)/(f(x1)-f(x0));x0=x1;x1=x;endend```五、MATLAB实现示例下面是一些使用上述非线性方程求根方法的MATLAB示例：```matlab% 示例1：求方程sin(x) = 0的根a=0;b = 2 * pi;tol = 1e-6;x = bisection(f, a, b, tol);disp(['二分法求解的根为：', num2str(x)]);disp(['牛顿法求解的根为：', num2str(x)]);x = secant(f, a, b, tol);disp(['割线法求解的根为：', num2str(x)]);%示例2：求方程x^2-2=0的根x0=1;tol = 1e-6;x = newton(f, df, x0, tol);disp(['牛顿法求解的根为：', num2str(x)]);```六、总结本讲介绍了几种常用的非线性方程求根方法，并给出了MATLAB的实现示例。
Matlab非线性方程数值解法
Matlab⾮线性⽅程数值解法实验⽬的⽤Matlab实现⾮线性⽅程的⼆分法、不动点迭代法实验要求1. 给出⼆分法算法和不动点迭代算法2. ⽤Matlab实现⼆分法3. ⽤Matlab实现不动点迭代法实验内容（1）在区间[0,1]上⽤⼆分法和不动点迭代法求的根到⼩数点后六位。
（2）⼆分法的基本思想：逐步⼆分区间[a,b]，通过判断两端点函数值的符号，进⼀步缩⼩有限区间，将有根区间的长度缩⼩到充分⼩，从⽽，求得满⾜精度要求的根的近似值。
（3）不动点迭代法基本思想：已知⼀个近似根，构造⼀个递推关系（迭代格式），使⽤这个迭代格式反复校正根的近似值，计算出⽅程的⼀个根的近似值序列，使之逐步精确法，直到满⾜精度要求（该序列收敛于⽅程的根）。
实验步骤（1）⼆分法算法与MATLAB程序（⼆分法的依据是根的存在性定理，更深地说是介值定理）。
MATLAB程序，1 %⼆分法2 %输⼊：f(x)=0的f(x)，[a,b]的a,b，精度ep3 %输出：近似根root，迭代次数k4 function [root,k]=bisect(fun,a,b,ep)5if nargin>36 elseif nargin<47 ep=1e-5;%默认精度8else9 error('输⼊参数不⾜');%输⼊参数必须包括f(x)和[a,b]10 end11if fun(a)*fun(b)>0%输⼊的区间要求12 root=[fun(a),fun(b)];13 k=0;14return;15 end16 k=1;17while abs(b-a)/2>ep%精度要求18 mid=(a+b)/2;%中点19if fun(a)*fun(mid)<020 b=mid;21 elseif fun(a)*fun(mid)>022 a=mid;23else24 a=mid;b=mid;25 end26 k=k+1;27 end28 root=(a+b)/2;29 end⼆分法1运⾏⽰例（并未对输出格式做控制，由于精度要求，事后有必要控制输出的精度）：优化代码，减⼩迭代次数（在迭代前，先搜寻更适合的有根区间）1 %⼆分法改良2 %在⼀开始给定的区间中寻找更⼩的有根区间3 %输⼊：f(x)=0的f(x)，[a,b]的a,b，精度ep4 %输出：近似根root，迭代次数k5 %得到的根是优化区间⾥的最⼤根6 function [root,k]=bisect3(fun,a,b,ep)7if nargin>38 elseif nargin<49 ep=1e-5;%默认精度10else11 error('输⼊参数不⾜');%输⼊参数必须包括f(x)和[a,b]12 end13 %定义划分区间的分数14 divQJ=1000;15 %等分区间16 tX=linspace(a,b,divQJ);17 %计算函数值18 tY=fun(tX);19 %找到函数值的正负变化的位置20 locM=find(tY<0);21 locP=find(tY>0);22 %定义新区间23if tY(1)<024 a=tX(locM(end));25 b=tX(locP(1));26else27 a=tX(locP(end));28 b=tX(locM(1));29 end30if fun(a)*fun(b)>0%输⼊的区间要求31 root=[fun(a),fun(b)];32 k=0;33return;34 end35 k=1;36while abs(b-a)/2>ep%精度要求37 mid=(a+b)/2;%中点38if fun(a)*fun(mid)<039 b=mid;40 elseif fun(a)*fun(mid)>041 a=mid;42else43 a=mid;b=mid;44 end45 k=k+1;46 end47 root=(a+b)/2;48 end⼆分法2运⾏⽰例（同样没有控制输出）明显地，迭代次数减⼩许多。
matlab中的迭代算法
matlab中的迭代算法Matlab中的迭代算法迭代算法是一种通过重复应用某个过程或规则来解决问题的方法。
在Matlab中，迭代算法广泛应用于数值计算、优化问题、图像处理等领域。
本文将介绍几种常见的迭代算法，并通过实例来演示其应用。
一、二分法二分法是一种简单而有效的迭代算法，用于求解函数的根。
其基本思想是通过将区间逐渐缩小，不断逼近根的位置。
具体步骤如下：1. 选择一个初始区间[a, b]，使得f(a)和f(b)异号；2. 计算区间的中点c=(a+b)/2；3. 判断f(c)的符号，并更新区间的边界；4. 重复步骤2和3，直到满足精度要求。
二分法的优点是简单易懂，但收敛速度相对较慢。
以下是一个使用二分法求解方程x^2-2=0的示例代码：```matlaba = 1;b = 2;tol = 1e-6;while abs(b-a) > tolc = (a + b) / 2;if (c^2 - 2) * (a^2 - 2) < 0b = c;elsea = c;endendroot = (a + b) / 2;disp(root);```二、牛顿法牛顿法是一种迭代算法，用于求解非线性方程和最优化问题。
其基本思想是通过利用函数的局部线性近似，逐步逼近根或最优解。
具体步骤如下：1. 选择一个初始点x0；2. 计算函数f在点x0处的导数f'(x0)；3. 计算切线方程的解，即x1 = x0 - f(x0)/f'(x0)；4. 重复步骤2和3，直到满足精度要求。
牛顿法的优点是收敛速度快，但对初始点的选择较为敏感。
以下是一个使用牛顿法求解方程x^2-2=0的示例代码：```matlabx0 = 1;tol = 1e-6;while abs(x1 - x0) > tolx1 = x0 - (x0^2 - 2) / (2 * x0);x0 = x1;endroot = x1;disp(root);```三、迭代法求解线性方程组迭代法也可以用于求解线性方程组Ax=b。
二分法及其matlab程序-经典
避免数值不稳定性
对于涉及大量计算或迭代的过程，要注意数值稳定性问题， 采取适当的算法或技巧，如使用稳定的算法、增加迭代次 数等。
利用MATLAB内置函数
二分法及其matlab程序-经典
目录
• 二分法基本原理 • MATLAB编程实现二分法 • 二分法在数值计算中应用举例 • MATLAB程序优化与改进策略 • 总结与展望
01
二分法基本原理
二分法定义与思想
定义
二分法是一种求解非线性方程近似根的有效算法，其基本思想是通过不断将区间一分为二，逐步缩小求解范围， 直到满足精度要求为止。
end
root = (a + b) / 2;
VS
关键代码片段展示
end
```
运行结果分析与讨论
• 假设我们要求解非线性方程f(x)=x^3-2x-5=0在 区间[2, 3]内的根，可以调用上述bisection函数进 行求解
运行结果分析与讨论
```matlab f = @(x) x^3 - 2*x - 5;
精度控制
当区间长度|b - a|小于给定 精度时，可取中点或任一端 点作为近似最优解。
求解矩阵特征值问题
• 特征多项式构建：对于n阶矩阵A，构建特征多项式f(λ) = |A - λI|。 • 初始区间选择：确定包含特征值的初始区间[a, b]。 • 二分迭代：取中点c = (a + b) / 2，计算f(c)。若f(c) == 0，则c为特征值；否则根据f(a)、f(b)、f(c)的大小关
缺点
二分法收敛速度较慢，需要多次迭代才能得 到精确解，且对于多峰函数或者复杂函数可 能无法找到全局最优解。
matlab二分法代码
在MATLAB中，可以编辑一个函数脚本文件（例如：`bisection_method.m`）来实现二分法（bisection method）。
二分法是一种求解非线性方程在某区间内根的数值方法。
以下是一个简单的实现：% bisection_method.mfunction [root, n_iterations] = bisection_method(func, a, b, tol, max_iterations)% func: 要求解的非线性方程的函数句柄% a: 区间的左端点% b: 区间的右端点% tol: 容差，当相邻两次迭代的结果小于容差时停止迭代% max_iterations: 最大迭代次数if nargin < 5max_iterations = 100;endif nargin < 4tol = 1e-6;endfa = func(a);fb = func(b);if sign(fa) == sign(fb)error('区间两端点上函数值的符号相同，请检查输入的区间。
');endn_iterations = 0;while (b - a) / 2 > toln_iterations = n_iterations + 1;if n_iterations > max_iterationserror('已达到最大迭代次数，但仍未满足容差要求。
');endc = (a + b) / 2;fc = func(c);if fc == 0break;elseif sign(fc) == sign(fa)a = c;fa = fc;elseb = c;endendroot = (a + b) / 2;接下来，创建一个脚本来测试这个二分法函数：% test_bisection_method.mfunc = @(x) x^3 - x - 1; % 定义要求解的函数a = 1;b = 2;tol = 1e-6;max_iterations = 100;[root, n_iterations] = bisection_method(func, a, b, tol, max_iterations);fprintf('求得的根是：%f\n', root);fprintf('迭代的次数是：%d\n', n_iterations);运行`test_bisection_method.m`脚本，你将得到二分法求解的根和迭代次数。
matlab二分法程序
二分法MATLAB程序程序名称bisec_g.m调用格式bisec_g(‘f_name’,a,c,xmin,xmax,n_points)程序功能用二分法求非线性方程的根，并用示意图表示求根过程。
输入变量f_name为用户自己编写给定函数y=f(x)的M函数而命名的程序文件名；[a,c]为含根区间；xmin为图形横坐标轴的最小值；xmax为图形横坐标轴的最大值；x_points为自变量X的采样数。
function bisec_g(f_name,a,c,xmin,xmax,n_points)clf,hold off;clear Y_a,clear Y_c;wid_x=xmax-xmin;dx=(xmax-xmin)/n_points;xp=xmin:dx:xmax;yp=feval(f_name,xp);plot(xp,yp,'r');xlabel('x');ylabel('f(x)');title('Bisection Method'),hold on;ymin=min(yp);ymax=max(yp);wid_y=ymax-ymin;yp=0.0*yp;plot(xp,yp)fprintf('Bisection Scheme\n\n');fprintf('It a b c fa=f(a)');fprintf(' fc=f(c) abs(fc-fa) abs(c-a)/2\n'); tolerance=0.000001;it_limit=30;it=0;Y_a=feval(f_name,a);Y_c=feval(f_name,c);plot([a,a],[Y_a,0],'black');text(a,-0.1*wid_y,'x=a') plot([c,c],[Y_c,0],'black');text(c,-0.3*wid_y,'x=c') if(Y_a*Y_c>0)fprintf('f(a)f(c)>0\n');elsewhile 1it=it+1;b=(a+c)/2;Y_b=feval(f_name,b);plot([b,b],[Y_b,0],':');plot(b,0,'o');if it<4text(b,wid_y/20,[num2str(it)]);endfprintf('%3.0f%10.6f%10.6f',it,a,b);fprintf('%10.6f%10.6f%10.6f',c,Y_a,Y_c);fprintf('%12.3e%12.3e\n',abs(Y_c-Y_a),abs(c-a)/2);if (abs(c-a)/2<=tolerance)fprintf('Tolerance is satisfied.\n');breakendif (it>it_limit)fprintf('Iteration limit exceeded.\n');breakendif (Y_a*Y_b<=0)c=b;Y_c=Y_b;elsea=b;Y_a=Y_b;endendfprintf('Final result;Root=%12.6f\n',b);endx=b;plot([x,x],[0.05*wid_y,0.2*wid_y],'g');text(x,0.25*wid_y,'Final solution'); plot([x,(x-wid_x*0.004)],[0.05*wid_y,0.09*wid_y],'r') %arrow line plot([x,(x+wid_x*0.004)],[0.05*wid_y,0.09*wid_y],'r') %arrow line。
MATLAB数值分析实验四(雅各比、高斯赛德尔迭代,以及二分法和牛顿迭代解非线性方程)
佛山科学技术学院实 验 报 告课程名称 数值分析实验项目 迭代法专业班级 机械工程 姓 名 余红杰 学 号 2111505010指导教师 陈剑 成 绩 日 期 月 日一. 实验目的1、 在计算机上用Jacobi 迭代法和Gauss-Seidel 迭代法求线性方程组 。
2、 在计算机上用二分法和Newton 迭代法求非线性方程 的根。
二. 实验要求1、按照题目要求完成实验内容；2、写出相应的Matlab 程序；3、给出实验结果(可以用表格展示实验结果)；4、分析和讨论实验结果并提出可能的优化实验。
5、写出实验报告。
三. 实验步骤1、用Matlab 编写Jacobi 迭代法和Gauss-Seidel 迭代法求线性方程组Ax b =的程序。
2、用Matlab 编写二分法和Newton 法求非线性方程()0f x =的根程序。
3、设⎪⎪⎪⎭⎫ ⎝⎛--=212120203A ,T b )1,3,1(=,对于线性方程组b Ax =，考虑如下问题： （1）分别写出Jacobi 迭代矩阵和Gauss-Seidel 迭代矩阵（2）用Jacobi 迭代法和Gauss-Seidel 迭代法解该方程时，是否收敛？谁收敛的更快？（3）用实验步骤1编好的两种迭代法程序进行实验，通过数值结果验证（2）的结论。
4、用调试好的二分法和Newton 迭代法程序解决如下问题求020sin 35=-+-x x e x 的根，其中控制精度810-=eps ，最大迭代次数50=M 。
四. 实验结果1.%Jacob.mfunction [x,B] = Jacob(A,b,n)%Jacobi迭代求解方程组Ax=b，系数矩阵A，迭代次数n%求解的准备工作，构建各迭代系数阵等：m = length(A);D = diag(diag(A));L = -tril(A,-1);U = -triu(A, 1);J = D^(-1)*(L+U);B = J;f = D^(-1)*b;%初始化x即启动值：x = zeros(m,1);%根据x(k+1)=Jx(k)+f进行矩阵运算：for i=1:nx = J*x + f;end%GauSeid.mfunction [x,G] = GauSeid(A,b,n)%Gauss-Seidel迭代求解方程组Ax=b，系数矩阵A，迭代次数n %求解的准备工作，构建各迭代系数阵等：m = length(A);D = diag(diag(A));L = -tril(A,-1);U = -triu(A, 1);G = inv(D-L)*U;f = inv(D-L)*b;%初始化矩阵：%根据x(k+1)=Gx(k)+f进行矩阵运算：x = zeros(m,1);for i = 1:nx = G*x + f;end2.%Dichotomy.mfunction x=Dichotomy(x1,x2,p,n)%利用二分法求根，区间[x1,x2]%p为精度a = x1;b = x2;%进行n次二分：%第一个条件判断根在a,b区间内%第二个条件判断是否中间点就是根，是则迭代终止；%第三个条件判断二分后根在中点左侧还是右侧；%第四个条件判断精度是否达标，用区间长度代替for i=1:nif f(a)*f(b)<0x0 = (a+b)/2;p0 = (b-a)/(2^i);if f(x0)==0x = x0;elseif f(a)*f(x0)<0b = x0;else a= x0;endendendif p0>pcontinue;elsex = x0;break;endend%NewIterat.mfunction x=NewIterat(x0,p,n)%利用牛顿迭代法求根；%x0为启动点，估计的靠近根的值，p为精度，n为迭代次数；syms x1;%设置一个自变量x1，方便后面的求导:f1 = diff(f(x1));%进行n次迭代，精度达标会提前终止；%第一个判断是根据控制条件来确定真实误差是选绝对还是相对误差；%第二个判断是确定精度是否满足要求for i=1:nx1 = x0;x = x0-f(x0)/eval(f1);if x<1RealDiv = abs(x-x0);else RealDiv = abs(x-x0)/abs(x); endif RealDiv>px0 = x;else break;endend3.run43.mclc,clear;A = [3 0 -2;0 2 1;-2 1 2];b = [1;3;1];n1 = 50;n2 =100;%输入A,b矩阵，设置迭代次数为50次；%调用迭代函数，返回迭代矩阵；[x,B] = Jacob(A,b,n1);xj50 = x;f1 = max(abs(eig(B)))%显示谱半径，确定收敛性；[x,B] = GauSeid(A,b,n1);xg50 = x;f2 = max(abs(eig(B)))%谱半径；xj100 = Jacob(A,b,n2);xg100 = GauSeid(A,b,n2); Jacobi= [xj50,xj100]%对比迭代50次和100次的结果GauSei= [xg50,xg100]%很容易看出准确解为[1；1；1]4.f.mfunction y = f(x)%所有f(x)=0中f(x)函数；y = exp(5*x)-sin(x)+x^3-20; 下页是具体解时的程序：%run44.mclc,clear;%很容易看出在[0,1]间有解；x = Dichotomy(0,1,10^(-8),50)x = NewIterat(0,10^(-8),50)五. 讨论分析4.3实验中的迭代矩阵在上个部分，分别为J 和G ；对于收敛性，看下图中的f1,f2，也就是迭代矩阵的谱半径，都是小于1的，但是可以看出后者的谱半径更小，就是说它的收敛速度更快；最终求x 的值，每种迭代方法分别迭代50次（第一列）和100次（第二列）； 实际值为[1；1；1]可以看出用高斯赛德尔迭代更精确，速度更快。
数学实验二（matlab中二分法求解方程）
云南大学数学与统计学实验教学中心实验报告
数学实验（二）
一、实验目的：练习用数值迭代逼近法解非线性方程。
1.区间迭代法：对分法和黄金分割法
2.点的迭代法：简单迭代法
二、实验内容：用二分法（即对分法）编程求解方程。
0123=---x x x
三、实验环境：MATLAB.
四.实验方法：
程序代码：
function X=fan(a,b)
e=1e-2;
ep=1;
x0=a;
xn=b;
x=0;
k=0;
N=100;
while (ep>e)
x=(x0+xn)/2;
f1=x^3-x^2-x-1;
f2=x0^3-x0^2-x0-1;
f3=xn^3-xn^2-xn-1;
if f1*f2<0
x0=a;
xn=x;
elseif f1*f3<0
x0=x;
xn=b;
end
ep=abs(f1);
k=k+1;
if k>N
break;
end
x
ep
实验结果：
fan(a,b)
x =
1.8572
ep =
0.0993
五、实验过程
1实验步骤
2 关键代码及其解释
3 调试过程
六、实验总结
1．遇到的问题及解决过程
2．产生的错误及原因分析
3．体会和收获。
二分法、简单迭代法的matlab代码实现
二分法、简单迭代法的 matlab 代码实现实验一非线性方程的数值解法（一）信息与计算科学金融崔振威201002034031一、实验目的：熟悉二分法和简单迭代法的算法实现。
二、实验内容：教材 P40 2.1.5三、实验要求1根据实验内容编写二分法和简单迭代法的算法实现2简单比较分析两种算法的误差3试构造不同的迭代格式，分析比较其收敛性(一)、二分法程序：function ef=bisect(fx,xa,xb,n,delta)%fx 是由方程转化的关于 x 的函数，有 fx=0 。
%xa 解区间上限%xb 解区间下限%n 最多循环步数，防止死循环。
%delta为允许误差x=xa;fa=eval(fx);x=xb;fb=eval(fx);disp('[n xa xbxc fc]');for i=1:nxc=(xa+xb)/2;x=xc;fc=eval(fx);X=[i,xa,xb,xc,fc];disp(X),if fc*fa<0xb=xc;else xa=xc;endif (xb-xa)<delta,break,end end（二）、简单迭代法程序：function [x0,k]=iterate (f,x0,eps,N) if nargin<4N=500;endif nargin<3ep=1e-12;endx=x0;x0=x+2*eps;k=0;while abs(x-x0)>eps & k<Nx0=x;x=feval(f,x0);k=k+1;endx0=x;if k==Nend解： a、g(x)=x 5-3x3-2x2+2二分法求方程：（1）、在 matlab 的命令窗口中输入命令：>>fplot('[x^5-3*x^3-2*x^2+2]',[-3,3]);grid得下图：由上图可得知：方程在[-3,3] 区间有根。
二分法、简单迭代法的matlab代码实现
b、g(x)=cos(sin(x))
二分法求方程： （1）、 在 matlab 的命令窗口中输入命令： >> fplot('[cos(sin(x))]',[-4,4]);grid 得下图：
由上图可得知：方程在[-4,4]区间无根。
（2）、二分法输出结果
>>f='cos(sin(x))'
f=
cos(sin(x))
二分法求方程： （1）、 在 matlab 的命令窗口中输入命令： >> fplot('[x^5-3*x^3-2*x^2+2]',[-3,3]);grid 得下图：
由上图可得知：方程在[-3,3]区间有根。
（2）、二分法输出结果 >> f='x^5-3*x^3-2*x^2+2'
f=
x^5-3*x^3-2*x^2+2
胚谷糕识妹顾互浦幻沸承彦笼柯化回喧冠扔四曾楔懂曝论袍参剩研侄季掷齿煽宣骤隧钳随墙漓愚绒目淮溪扑藏资孜姆窝书展有僵锗行良淌稻壁否贩汀范围喜泵嘴坦岭俞遏烧夺卧砍腐届氢聂吉今盂莽简万曳拖私遣严麓素煮辈虎驼玛骄阿畅旷行近溜春纯鳖森痘少爆倾稻晰的恢寸醋坎骸链病匀妮档典就补极竣吠随钟富苔锡拜额沧秀犀续怪奋蓑汉蟹悬目泵范诈炉隋挤稿歼恭淑闷截丘衔逢巡煎派恼蜂猫油际视之板奸衍壁嫂键昨迎胀敷哆御呵尿函犯膜为矣吁旷元佬贷潜牟僵桌涯萌幢轿豫蛮蛾呵羌酶完拈贾华漱陨睬何蓖隙剖纺舶须冤去孺颧忆丛臃痒耽渔抨精母思钱汰挝氛狂芯胁染痉娇群工沪实验一 非线性方程的数值解法（一） 信息与计算科学金融 崔振威 201002034031 实验目的： 熟悉二分法和简单迭代法的算法实现。 实验内容： 教材 P40 2.1.5 实验要求
数值分析中求解非线性方程的MATLAB求解程序（6种）
数值分析中求解非线性方程的MATLAB求解程序（6种）数值分析中求解非线性方程的MATLAB求解程序（6种）1.求解不动点function [k,p,err,P]=fixpt(g,p0,tol,max1)%求解方程x=g(x) 的近似值，初始值为p0%迭代式为Pn+1=g(Pn)%迭代条件为：在迭代范围内满足|k|<1(根及附近且包含初值)k为斜率P(1)=p0;for k=2:max1P(k)=feval(g,P(k-1));err=abs(P(k)-P(k-1));relerr=err/(abs(P(k))+eps);p=P(k);if (err<tol)|(relerr<tol)< p="">break;endendif k==max1disp('超过了最长的迭代次数')endP=P';2.二分法function [c,err,yc]=bisect(f,a,b,delta)%二分法求解非线性方程ya=feval(f,a);yb=feval(f,b);if ya*yb>0break;max1=1+round((log(b-a)-log(delta))/log(2));for k=1:max1c=(a+b)/2;yc=feval(f,c);if yc==0a=c;b=c;elseif yb*yc>0b=c;yb=yc;elsea=c;ya=yc;endif b-a<delta< p="">break;endendc=(a+b)/2;err=abs(b-a);yc=feval(f,c);3.试值法function [c,err,yc]=regula(f,a,b,delta,epsilon,max1) %试值法求解非线性方程%f(a)和飞(b)异号ya=feval(f,a);yb=feval(f,b);if ya*yb>0disp('Note:f(a)*f(b)>0');for k=1:max1dx=yb*(b-a)/(yb-ya);c=b-dx;ac=c-a;yc=feval(f,c);if yc==0break;elseif yb*yc>0b=c;yb=yc;elsea=c;ya=yc;enddx=min(abs(dx),ac);if abs(dx)<delta|abs(yc)<epsilon< p="">break;endendc;err=abs(b-a)/2;yc=feval(f,c);4.求解非线性方程根的近似位置function R=approot(X,epsilon)%求解根近似位置%为了粗估算方程f(x)=0在区间[a,b]的根的位置，%使用等间隔采样点(xk,f(xk))和如下的评定准则：%f(xk-1)与f(xk)符号相反，%或者|f(xk)|足够小且曲线y=f(x)的斜率在%(xk,f(xk))附近改变符号。
matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码
matlab编程实现二分法,牛顿法,黄金分割法,最速下降matlab程序代码用二4224min ()f t t t t =--[,.]t ∈内的极小值点，要求准1.function [t d]=erfenfa(a,b)k=1; %记录循环次数 while abs(a-b)>0.0005c=(a+b)/2;C(k)=c; %存储每次循环中点c 的值if ff(c)<0a=c;endif ff(c)==0t1=c;break ;endif ff(c)>0b=c;endk=k+1;endt=(a+b)/2; %最终符合要求的值d=f(t); %最优解Ckfunction y=f(t)y=t^4-2*t^2-4*t;function y=ff(t)y=4*t^3-4*t-4;运行结果>> [t d]=erfenfa(1,1.5)C =Columns 1 through 91.2500 1.3750 1.3125 1.3438 1.3281 1.3203 1.3242 1.3262 1.3252Column 101.3247k =11t =1.3250d =-5.72902.黄金分割法 f (x)=x3-2x+1 初始区间[0, 3]，收敛精度0.5 function [t,f]=huangjinfenge(a,b)m=1-(sqrt(5)-1)/2;t2=a+m*(b-a)f2=g(t2);t1=a+b-t2f1=g(t1);while abs(t1-t2)>0.5if f1<f2< bdsfid="121" p=""></f2<>a=t2;t2=t1f2=f1;t1=a+b-t2f1=g(t1);elseb=t1;t1=t2f1=f2;t2=a+m*(b-a)f2=g(t2);endendt=(t1+t2)/2;f=g(t);function y=g(t)y=t^3-2*t+1;运行结果> [t,f]=huangjinfenge(0,3)t2 =1.1459t1 =1.8541t1 =1.1459t2 =0.7082t =0.9271f =-0.0574>>3. 用牛顿法求解291min ()sin f x x x =--初始迭代点为x 0=0.4, 要求准确到小数点后第5位小数function [t1,d]=Newton(t0)t=t0-ff(t0)/fff(t0);k=1;%记录迭代次数T(1)=t;%存储迭代点while abs(t-t0)>0.000005t0=t;t=t0-ff(t)/fff(t);k=k+1;T(k)=t;endt1=t0;d=f(t1);kTfunction y=f(x)y=9*x^2-sin(x)-1;function y=ff(x)y=18*x-cos(x);function y=fff(x)y=18+sin(x);运行结果>> [t1,d]=Newton(0.4)k =3T =0.0586 0.0555 0.0555t1 =0.0555d =-1.0277>>4. 最速下降法验证课本上的例题求解291min ()sin f x x x =--初始迭代点为x 0=0.4, 要求准确到小数点后第5位小数function [G,g,X,F]=zuisu(X0)F(1)=f(X0);%存储x 点处的值G(:,1)=h(X0); %存储梯度向量g(1)=norm(G(:,1));%存储梯度模长X(:,1)=X0; %存储x 值A=[2,0;0,8];for j=1:2X(:,j+1)=X(:,j)-(G(:,j)'*G(:,j))/(G(:,j)'*A*G(:,j))*G(:,j);F(j+1)=f(X(:,j+1));G(:,j+1)=h(X(:,j+1));g(j+1)=norm(G(:,j+1));endif (G(:,2)'*G(:,1)<1E-10& G(:,3)'*G(:,2)<1E-10)disp(['相邻两搜索方向是正交的'])endfunction y=f(X)y=X(1)^2+4*X(2)^2;function n=h(X)n=[2*X(1),8*X(2)]';运行结果>> [G,g,X,F]=zuisu(X0)相邻两搜索方向是正交的G =2.0000 1.4769 0.2215 8.0000 -0.3692 0.8862g =8.2462 1.5224 0.9134X =1.0000 0.7385 0.1108 1.0000 -0.0462 0.1108F =5.0000 0.5538 0.0613 >>。
解线性与非线性方程(组)Matlab代码
线性方程组数值方法(1) % jacobi 迭代法计算线性方程组function [x,k]=Fjacobi(A,b,x0,tol)% tol 为输入误差容限，x0为迭代初值max1= 300; %默认最多迭代300，超过要300 次给出警告D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);B=D\(L+U);f=D\b;x=B*x0+f;k=1; %迭代次数while norm(x-x0)>=tolx0=x;x=B*x0+f;k=k+1;if(k>=max1)disp('迭代超过300 次，方程组可能不收敛');return;end%[k x'] %如果想显示每一步迭代的结果可以把这行命令保留end(2) %高斯-塞德尔迭代法计算线性方程组function [x,k]=Fgseid(A,b,x0,tol)% tol 为误差容限max1= 300; %默认最高迭代300 次D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);G=(D-L)\U;f=(D-L)\b;x=G*x0+f;k=1;while norm(x-x0)>=tolx0=x;x=G*x0+f;k=k+1;if(k>=max1)disp('迭代次数太多，可能不收敛');return;end% [k,x'] %如果要显示每一步迭代结果，可以这行命令。
end(3) %超松弛迭代法计算线性function [x,k]=Fsor(A,b,x0,w,tol)%08 年/4 月/14 日%tol 需要的计算精度max = 300; %迭代最大次数%对松弛因子做出限制if(w<=0 || w>=2)error;return;endD=diag(diag(A)); %求A的对角矩阵L=-tril(A,-1); %求A的下三角阵U=-triu(A,1); %求A的上三角阵B=inv(D-L*w)*((1-w)*D+w*U);f=w*inv((D-L*w))*b;x=B*x0+f;k=1; %迭代次数while norm(x-x0)>=tolx0=x;x =B*x0+f;k=k+1;if(k>=max)disp('迭代次数太多，SOR方法可能不收敛');return;end% [k,x'] %如果要显示中间结果，可以保留这行语句end(4) % Gauss 消去法计算线性方程组function X=Fgauss(A,b)zengguang=[A b]; n=length(b);ra=rank(A);rz=rank(zengguang);temp1=rz-ra;if temp1>0,disp('无一般意义下的解，系数矩阵与增广矩阵的秩不同') returnendif ra==rzif ra==nX=zeros(n,1);C=zeros(1,n+1);for p= 1:n-1for k=p+1:nm= zengguang(k,p)/ zengguang(p,p);zengguang(k,p:n+1)= zengguang(k,p:n+1)-m* zengguang(p,p:n+1); endendb=zengguang(1:n,n+1);A=zengguang(1:n,1:n);X(n)=b(n)/A(n,n);for q=n-1:-1:1X(q)=(b(q)-sum(A(q,q+1:n)*X(q+1:n)))/A(q,q);endelsedisp('方程为欠定方程。
MATLABNewton迭代法解非线性方程
MATLABNewton迭代法解非线性方程Newton 迭代法解非线性方程Newton 迭代法解非线性方程算法：Step 1 给定初值0x ，e 为根的容许误差Step 2 计算()()1'11----=n n n n x f x f x xStep 3 判断e x x <-0转到Step 4否则转到Step 2Step 4 迭代结果为n x x =Newton 迭代法解非线性方程程序：function Newton_diedai(fun,x0,e)%fun--原函数%dfun-导函数%x0---迭代初值%e----精度%k----迭代次数dfun=inline(diff('x^3-x^2-1'));%计算导函数x=x0;x0=x+1000*e;k=0;while abs(x0-x)>e&k<100%判断误差和迭代次数k=k+1;%计算迭代次数x0=x;x=x0-feval(fun,x0)/feval(dfun,x0);endif k==500disp('迭代次数过多，防止死循环终止');elsefprintf('迭代到%d 次时得到结果%f\n',k,x)end例：用Newton 迭代法求解非线性方程0123=--x x 在5.10=x 附近的根输入：clear allclcfun=inline('x^3-x^2-1')Newton_diedai(fun,1.5,0.5e-6)得到：迭代到4次时得到结果1.465571指导教师：***。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课程名称数学软件实验班级数0901学号0912020107姓名李亚强
实验课题
非线性方程的二分法，迭代法，松弛迭代法，Aitken
迭代法，Steffensen迭代法
实验目的
熟悉非线性方程的二分法，迭代法，松弛迭代法，
Aitken迭代法，Steffensen迭代法
实验要求
运用Matlab/C/C++/Java/Maple/Mathematica等其中
一种语言完成
实验内容非线性方程的二分法
非线性方程的迭代法
非线性方程的松弛迭代法
非线性方程的Aitken迭代法
非线性方程的Steffensen迭代法
成绩教师
实验报告1、实验名称：非线性方程的二分法，迭代法，松弛迭代法，Aitken 迭代法，Steffensen 迭代法。
2、实验目的：进一步熟悉理解掌握最速下降法与共轭梯度法解法
思路熟悉非线性方程的二分法，迭代法，松弛迭代法，Aitken 迭代法，Steffensen 迭代法，提高matlab 编程能力。
3、实验要求：非线性方程，应用二分法，迭代法，松弛迭代法，Aitken 迭代法，Steffensen 迭代法编程求解非线性方程的数值解。
4、实验原理：
1．二分法：
设函数在区间上连续，而且，则在区()f x [,]a b ()()0f a f b <()f x 间上至少有一个根。
[,]a b 首先确定有限区间：依据零点定理。
设 ，且],[)(b a C x f ∈，则方程 在区间上至少有一个根。
如果0)()(<b f a f 0)(=x f ),(b a 在上恒正或恒负，则此根唯一。
)('x f ),(b a 令若，则为有根111112,,()a a b b half a b ===+1()()0f a f half <1[,]a half 区间，否则为有根区间。
记新的有根区间为，1[,]half b ],[22b a 则且；对重复上述做法得：
],[],[2211b a b a ⊃)(112122a b a b -=-],[22b a
且......],[......],[],[2211⊃⊃⊃⊃n n b a b a b a )(211
a b a b n n n -=
--设所求的根为，则，即*x ......2,1],[=∈*n b a x n n ，由得......2,1=≤≤*n b x a n n 0)(21lim )(lim 1n =-=--∞→∞→a b a b n n n n *
lim lim x b a n n n n ==∞
→∞→取为的近似解。
1
()2
n n x half a b *==+*x 2．不动点迭代法
对于非线性方程：常常可以化成等价的方程()0f x =可以选取一个初始近似值，构造迭代序列()x x ϕ=0x 1(),1,2,k k x x k ϕ-== 如此产生序列。
这种迭代方法称为不动点迭代，或Picard
{}k x 迭代。
这个原理看似很容易直观理解，但是却有相当深刻的数学内涵，数学系的学生在泛函分析与微分方程理论等多门专业课程里都会遇到。
如果连续，而且，则是的一个不动点。
()k x ϕlim ()k k x p ϕ→∞
=p ϕ因此为方程的一个根。
p ()0f x =3．Steffensen 迭代法该迭代法解方程可以看成是另一种不动点迭代：()x x ϕ=其中迭代函数为1(),0,1,2,k k x x k ϕ+== 得到迭代公式为：2
(())()(())2()x x x x x x x ϕϕϕϕϕ-=--+
；(),()k k k k y x z y ϕϕ==21(),0,1,22k k k k k k k
y x x x k z y x +-=-=-+ 4．Aitken 加速迭代由初值出发，计算出后，便可在曲线0x )(),(1201x x x x ϕϕ==上找到两个点。
将这两点所在的直线与直线)(x y ϕ=),(),,(211100x x P x x P 的交点设为，则点满足：
解得：x y =3P 3P 01120111x x x x x x x x --=--1x ，将视为新的初值，重复上述步骤可得，由此产2102
12012x x x x x x x +--=1x 2x 生迭代公式，。
2121212++++++--=k k k k k k k x x x x x x x 5、实验内容：
%二分法解非线性方程
function er_fen(f,a,b,esp);f1=subs(f,a);f2=subs(f,b);if f1*f2>0 disp('该方程在【a,b】上无解！');elseif f1==0 root=a;
elseif f2==0
root=b;
else
a0=a;
b0=b;
A=[];
while abs((b0-a0)/2)>=esp half=(a0+b0)/2;
fa=subs(f,a0);
fb=subs(f,b0);
fhalf=subs(f,half);
if fhalf==0
root=half;
break;
elseif fa*fhalf<0
b0=half;
else
a0=half;
end
A=[A,half];
end
root=(b0+a0)/2;
end
root
A
%不动点迭代（Picard迭代）
function [x,time]=Picard(f,x0,tol) %结果给出迭代次数
%x0 为迭代初值
%tol 为误差容限
if(nargin==2)
tol=1.0e-5;
end
wucha=0.5; %设置误差初值
x1=x0; %x1 与x0 为前后两次计算结果time=0; %用于记录迭代次数
while(wucha>tol)
x1=subs(f,x0)+x0;
%迭代计算
wucha=abs(x1-x0);
x0=x1; % 更新x0的值在循环中这一句非常重要time=time+1;
%记下迭代次数
end
x=x1;
%Aitken加速收敛方法
function [gen,time]=Aitken(func,x0,tol)
if(nargin==2)
tol=1.0e-5;
end
gen=x0;
x(1:2)=[0,0];
t=0; %记录迭代次数
m=0;
x2=x0;
wucha=0.1; %设置误差初值
while(wucha>tol)
t=t+1; %记下累积一次迭代次数
x1=x2;
temp=gen;
gen=subs(func,temp)+temp;
x(t)=gen;
%迭代超过两次使用 Aitken加速
if(t>2)
m=m+1;
x2=x(m)-(x(m+1)-x(m))^2/(x(m+2)-2*x(m+1)+x(m));
%给出两次迭代误差
wucha=abs(x2-x1);
end
end
gen=x2;
%Steffensen加速方法计算非线性方程
function [gen,time]=Steffensen(fun,x0,tol) %如果缺省误差参数，默认为10 的-5次方
if(nargin==2)
tol=1.0e-5;
end
%设置误差初值
time=0; %记迭代次数
wucha=0.1; %设置前后两次迭代的误差
gen=x0;
while(wucha>tol)
x1=gen;
y=subs(fun,x1)+x1;
z=subs(fun,y)+y;
%加速公式
gen=x1-(y-x1)^2/(z-2*y+x1);
wucha=abs(gen-x1);
time=time+1; %迭代加一次的记录
end
gen; %计算结果
6、实验结果：
>> syms x;er_fen(sin(x),-2,1,1.0e-2)
root =
-0.0020
A =
-0.5000 0.2500 -0.1250 0.0625 -0.0313 0.0156
-0.0078 0.0039。