图形推理之折纸盒
公考行测图形推理之折、拆纸盒问题
折、拆纸盒问题空间形式图形推理是近几年考查热点。
而在空间形式图形推理的考查中，折纸盒与拆纸盒问题，更是常见考点。
折纸盒，泛指题干为平面展开图，四个选项均为立体图形，提问方式一般为“将题干图形折叠后，得到的图形是？”拆纸盒，泛指题干为立体图形，四个选项均为平面展开图，提问方式一般为“将题干图形展开后应为？”针对这一类问题，根据选项情况可采用区分相邻面及相对面、时针法、标点法来应对。
一、区分相邻面及相对面平面图形中相邻的两个面折成立体图形后也相邻，立体图形中相对的两个面拆成平面图形后不相邻，区别相邻面与相对面往往能快速排除错误选项，得出符合要求的答案。
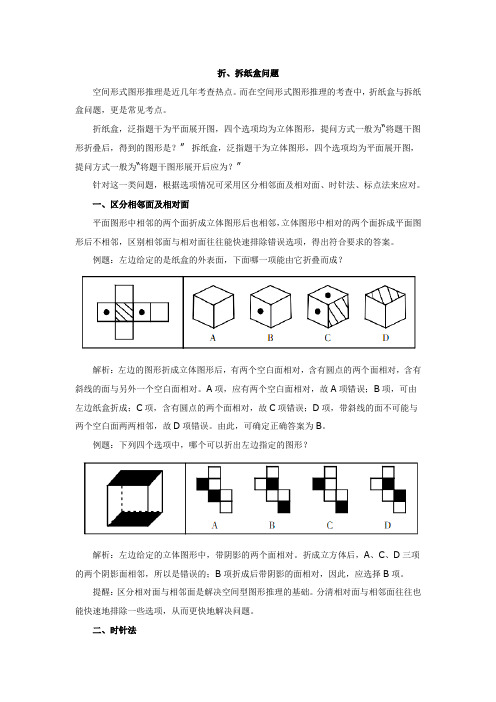
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？解析：左边的图形折成立体图形后，有两个空白面相对，含有圆点的两个面相对，含有斜线的面与另外一个空白面相对。
A项，应有两个空白面相对，故A项错误；B项，可由左边纸盒折成；C项，含有圆点的两个面相对，故C项错误；D项，带斜线的面不可能与两个空白面两两相邻，故D项错误。
由此，可确定正确答案为B。
例题：下列四个选项中，哪个可以折出左边指定的图形？解析：左边给定的立体图形中，带阴影的两个面相对。
折成立方体后，A、C、D三项的两个阴影面相邻，所以是错误的；B项折成后带阴影的面相对，因此，应选择B项。
提醒：区分相对面与相邻面是解决空间型图形推理的基础。
分清相对面与相邻面往往也能快速地排除一些选项，从而更快地解决问题。
二、时针法对于立方体纸盒，折成后只能看到图形的三个面，时针法就是比较这三个面在立体图形与平面图形中的旋转方向来判断选项的正确与否。
时针法只适用于解决面中的小图形不涉及方向的折纸盒问题。
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？解析：首先通过相对面与相邻面可排除C项，C项中1和2应为相对的面，不可能相邻。
A项，按1-4-6的顺序，顺时针旋转，题干平面图形中1-4-6则按逆时针旋转，如下图所示，两者的旋转方向不一致，则A项不能由左边的图形折成；同理可判定B项可由左边图形折成，D项不能由左边图形折成。
B3逻辑组专题(三)——图形重构 教程
B3逻辑组专题（三）——图形重构教你用“描点法”解决折纸盒问题在公考的图形推理的试题中，总会有那么一题是关于折纸盒的。
或者要你判断哪个是展开图形所折成的纸盒；或这要你判断纸盒摊开了会是什么样的图形等等。
而且，由于现在出的题目会出现内容相似或者是相同的面，用以前的“相对面相邻面”的解题方法会越来越费时间。
“折纸盒”的是指就是一个点与点重合，边与边重合的过程，当确定两个点重合时，这个立体图形也就确定了。
描点法就是根据已知的点确定由这个点出发的线条的情况，从而判定“纸盒”的样式。
也就是说，一个标准的正方体纸盒会有8个顶点，每个顶点负责引出3条边，也就是说1个点可以连接着3个面（听不明白？看看试题的备选答案，是不是只能看到三个面？还不明白？不要紧，下面会配合例题讲解的）。
下图就是一个标准的正方体纸盒的展开图，上面就标出了，在折合的过程中，哪些点会重合。
从上图可以看出。
单是A这个点，就有AD,DA,AE三条线。
从而引出了□BACD、□DAHE、□ABEF三个面。
而“折纸盒”问题，就是考察这个点引出的三个面各自的相对关系。
所以“描点法”的关键，就是要根据选项，找出选项里面的点所在平面图的位置，从位置上判断三个面的相对关系，从而得出答案。
好！下面根据例题来讲解一下“描点法”的具体用法。
【例1】：【解析】题干是一个我称之为“标准护翼型”的图形，所有的正方体纸盒，都可以化成“标准护翼型”来使我们观察“点”更加方便。
我们先看A选项。
根据黑三角形和有“点”的那个面的相对位置。
我们找到了原图中的红色点，由原图看，黑色三角形的一条直角边在白面上方，另外一条在“点”面上方，所以纸盒是可以折成A的形状的。
再看B，B 选项的这个顶点，在原图上面是找不到相对应的点的，因为以“点”面为中心，上下两个黑色三角形的直角边都与“点”面有一条公共边，B选项这样，没有公共边的情况是不存在的，所以原图不能折成B的样子。
答案就是B。
C、D两个选项的点，我也用不同的颜色标出来了，大家可以看看。
空间型图形推理-折纸盒问题
折、拆纸盒问题折纸盒，泛指题干为平面展开图，四个选项均为立体图形，提问方式一般为“将题干图形折叠后，得到的图形是？”拆纸盒，泛指题干为立体图形，四个选项均为平面展开图，提问方式一般为“将题干图形展开后应为？”针对这一类问题，根据选项情况可采用区分相邻面及相对面、时针法、标点法来应对。
一、区分相邻面及相对面平面图形中相邻的两个面折成立体图形后也相邻，立体图形中相对的两个面拆成平面图形后不相邻，区别相邻面与相对面往往能快速排除错误选项，得出符合要求的答案。
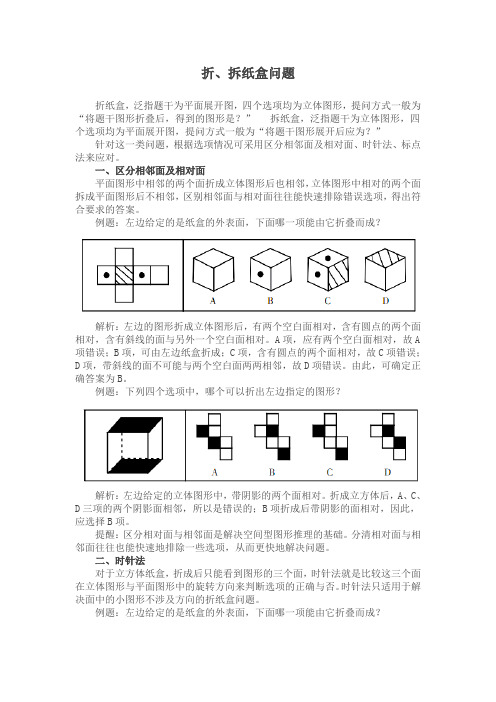
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？解析：左边的图形折成立体图形后，有两个空白面相对，含有圆点的两个面相对，含有斜线的面与另外一个空白面相对。
A项，应有两个空白面相对，故A 项错误；B项，可由左边纸盒折成；C项，含有圆点的两个面相对，故C项错误；D项，带斜线的面不可能与两个空白面两两相邻，故D项错误。
由此，可确定正确答案为B。
例题：下列四个选项中，哪个可以折出左边指定的图形？解析：左边给定的立体图形中，带阴影的两个面相对。
折成立方体后，A、C、D三项的两个阴影面相邻，所以是错误的；B项折成后带阴影的面相对，因此，应选择B项。
提醒：区分相对面与相邻面是解决空间型图形推理的基础。
分清相对面与相邻面往往也能快速地排除一些选项，从而更快地解决问题。
二、时针法对于立方体纸盒，折成后只能看到图形的三个面，时针法就是比较这三个面在立体图形与平面图形中的旋转方向来判断选项的正确与否。
时针法只适用于解决面中的小图形不涉及方向的折纸盒问题。
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？解析：首先通过相对面与相邻面可排除C项，C项中1和2应为相对的面，不可能相邻。
A项，按1-4-6的顺序，顺时针旋转，题干平面图形中1-4-6则按逆时针旋转，如下图所示，两者的旋转方向不一致，则A项不能由左边的图形折成；同理可判定B项可由左边图形折成，D项不能由左边图形折成。
2019-2020年公务员考试备考行测《图形推理》试题精选含答案解析(八十七)[四川]
![2019-2020年公务员考试备考行测《图形推理》试题精选含答案解析(八十七)[四川]](https://img.taocdn.com/s3/m/ef7bb33e168884868762d6af.png)
2019-2020年公务员考试备考行测《图形推理》试题精选含答案解析(八十七)[四川]一、第1题：将左图折叠成一个立方体，得到的图形是（____ ）。
A.B.C.D.【答案】：B【来源】：暂无【解析】本题考查折纸盒。
根据相对面不能相邻的规则，带有箭头的两面不能相邻，带有方块和带有圆形的两面不能相邻，排除C、D两项。
A项图形错在折叠后箭头的方向应该指向右下方。
故正确答案为B。
二、第2题：A.如图所示B.如图所示C.如图所示D.如图所示【答案】：D【来源】：2011年北京【解析】本题同时考查图形的旋转与相加运算。
题干中前三个图形中前两个图叠加并旋转90°后形成第三个图，后两个图形相加并旋转90°，为选项D。
因此，本题答案为D选项。
三、第3题：从所给四个选项中，选项最合适的一个填入问号处，使之呈现一定的规律性（____）A.如图所示B.如图所示C.如图所示D.如图所示【答案】：C【来源】：2015年天津公务员考试《行测》真题卷【解析】本题主要考查图形叠加，第一组图中，相对应位置叠加为：黑＋黑＝黑，白＋黑＝白，白＋白＝黑，黑＋白＝白。
按照此规律，第二组图进行叠加后，符合要求的为C 项。
故答案为C 。
四、 第4题：命题可以分为四种：①伪命题，指的是无真假可言的命题；②永真命题，指的是不论在何种情况下都不可能假的命题；③永假命题，指的是不论在何种情况下都不可能真的命题；④可满足命题，指的是在有。
四面体折纸盒解题技巧
四面体折纸盒解题技巧
1. 嘿，四面体折纸盒解题有个超棒的技巧你知道不？就好比搭积木一样，要找到关键的那块！像这个纸盒，看着复杂吧，但咱只要找到几个特殊面，一下子就清晰啦！例子嘛，就比如这个有个明显图案的面，那就是关键呀！
2. 哇塞，四面体折纸盒解题，一定要学会看相邻面啊！这就跟交朋友一样，熟悉了他们之间的关系，解题就不难喽。
你看这个例子，这几个面的相邻关系搞清楚，答案不就呼之欲出啦！
3. 哎呀呀，四面体折纸盒的时候要注意方向哦！就好像走路不能走反了方向呀。
来看看这个例子，方向搞对了，那肯定不会错呀！
4. 嘿，别忘了用排除法呀！这可是个大法宝呢，就好像在一堆苹果里挑出坏的一样。
比如这个例子，有些选项明显不符合实际，一下就可以排除掉啦！
5. 哇，四面体折纸盒还要会想象呀！把它在脑子里展开，是不是很神奇？瞧这个例子，想象一下它展开后的样子，解题就轻松多啦！
6. 哎呀，注意相对面哦，它们可不能在同一面出现呀！就像水火不容一样。
看看这个例子，很明显那个相对面出现就不对啦！
7. 嘿，仔细观察细节啊！有时候一个小图案就能决定答案呢。
像这个例子里，那个小小的标记，就是解题的关键呀！
8. 哇塞，有时候可以标记一下呢，这样就不容易混乱啦，跟做标记记路线一样。
看这个例子，标记后是不是清楚很多呀！
9. 四面体折纸盒解题技巧可真重要啊，掌握了这些，那解起题来就得心应手啦！你学会了吗？。
图形推理的折叠纸盒秘籍.doc
图形推理的折叠纸盒秘籍。
[共享]立方体折叠主题一个接一个。
确定给定的平面图形是否属于立方体表面。
图1。
中间最长的行(或列)可以是2、3、4、4以上或不在中间的长排不是立方体表面膨胀。
2.在每一行(或列)的两边，每一边只能有一个正方形与之相连，多于一个则不行。
3.规则:(1)每个顶点最多有3个相邻面，不会有4个或更多。
(2)在排列成“一”形的三个面中，两端的面必须是相对的，具有相同的字母。
(3)在以“L”形排列的三个面中，没有相同的字母，即没有相对的面，只有相邻的面。
2.快速确定立方体“反面”的公式是:交替相位和“Z”端与下图相反。
让我们首先统一以下理解:图1中所示的或由它们旋转的图统称为“I”型图。
(2)、(3)和(4)中所示的或在给定平面图中由它们旋转的图形统称为“Z”型图形。
结论:如果给定的平面图形可以折叠成立方体，则平面图形中包含的“I”或“Z”型图形两端的正方形(阴影部分)在折叠成立方体后必须是相对的一侧。
应用上述结论，我们可以快速确定立方体的“反面”。
例1。
如图所示，一个汉字写在一个立方体的每一边，它的平面展开图如图所示，那么立方体中与“超级”相对的单词是。
分析:自信-下沉-着陆-超越形成一个垂直的z形，所以“自我”对应于“超越”，所以“自我”应该填写。
3两个相邻面的角知道被两个小正方形分开或者三个边的角是立方体的相邻面。
例2。
如图所示，有一个立方体纸盒，在其三面分别画有三角形、正方形和圆形，用一把剪刀沿其边缘剪成一个平面图，展开后的图可以()分析:我们将圆的边称为平面A，正方形阴影边称为平面B，三角形阴影边称为平面C。
在选项A中，Z形结构用于知道与已知立方体bc 不相邻的B和C的相对边，应将其排除在外。
在选项B中，平面B和平面C被平面A分开，平面B和平面C 是相对的，这也应该排除在外。
在选项D中，虽然三个面A、B和C形成一个角形状，并且是立方体的三个相邻面，面B作为上面，面A作为前面，但是面C应该在立方体的左侧，这与原始图像不一致，应该被排除。
行测推行推理之折纸盒——相对面
行测推行推理之折纸盒——相对面【答题妙招】折纸盒问题是图形推理试题中的常青树，在解答这类题目时，一定要抓住相对面的图形特征，从而快速通过排除法选择正确答案。
【例1】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成（）【答案】C。
解析：根据相对面特征快速排除A.B项：空白面和有一条对角线的面是相对面，根据相对不相邻原则，排除A；同理，有圆形的面与有两条对角线的面也是相对面，不能同时出现。
此外，D项中的顶面应该是梯形面，也应该排除，故答案选择C。
【例2】如白、灰、黑三种颜色的油漆为正方体盒子的6个面上色，且两个相对面上的颜色都一样，以下哪一个不可能是该盒子外表图的展开图（）【答案】C。
解析：在平面图形中，判定相对面的方法是：（1）相间排列；（2）位于“Z”字型的两端，选项A.B.D都符合相对面“颜色相同”的要求，只有C不符合，正确答案为C。
【例3】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成（）【答案】B。
解析：左边的图形折成立体图形后，有两个空白面相对，含有圆点的两个面相对，含有斜线的面与另外一个空白面相对。
A项，应有两个空白面相对，故A项错误；B项，可由左边纸盒折成；C项，含有圆点的两个面相对，故C项错误；D项，带斜线的面不可能与两个空白面两两相邻，故D项错误。
由此，可确定正确答案为B。
【考点链接】（一）相对面的判定1.相间面是相对面一个平面展开图中，几个面处在同一直线上，则其中间隔一个面的两个面是一对相对面，在折成的立体图形中不可能相邻。
上面的四个面中，“1”和“3”是相对面，“2”和“4”是相对面；注意：相间的面只能是两者之间间隔一个面。
3和5，2和6不属于相对面，因为他们不在一条直线上。
2.“Z”字型的两个端点处的面是相对面上面三幅图形中，每一个图形中的两个阴影面是一对相对的面，即“Z”字的两端处的两个面是一对相对面，不可能相邻，并且要注意“Z”的两端的距离是相等的。
（二）相对面的特性1.相对面不相邻，相邻面不相对2.一组相对面能且只能看到其中一个面。
图形推理之折纸盒秘籍
【分享】立方体折叠专题一一.判断给定的平面图形是否属正方体表面展开图1．最长的一行（或列）在中间，可为2、3、4个，超过4•个或长行不在中间的不是正方体表面展开图．2．在每一行（或列）的两旁，每旁只能有1个正方形与其相连，超过1个就不是．3．规律：①每一个顶点至多有3个邻面，不会有4个或更多个．②“一”形排列的三个面中，两端的面一定是对面，字母相同．③“L”形排列的三个面中，没有相同的字母，即没有对面，只有邻面．二.快速确定正方体的“对面” 口诀是：相间、“Z”端是对面如下图，我们先来统一以下认识：把含有图（1）所示或可由其作旋转后的图形统称为“I”型图；把所给平面图中含有（2）、（3）、（4）所示或可由其作旋转后的图形统称为“Z ”型图。
结论：如果给定的平面图形能折叠成一个正方体，那么在这个平面图形中所含的“I”型图或“Z”型图两端的正方形（阴影部分）必为折成正方体后的对面。
应用上面的结论，我们可以迅速地确定出正方体的“对面”。
例1．如图，一个正方体的每个面上都写有一个汉字，其平面展开图如图所示，那么在该正方体中，和“超”相对的字是．分析：自—信—沉—着—超，构成了竖着的Z字型，所以“自”与“超”对应，故应填“自”．三. 间二、拐角邻面知中间隔着两个小正方形或拐角型的三个面是正方体的邻面．例2.如图，有一个正方体纸盒，在它的三个侧面分别画有三角形、正方形和圆，现用一把剪刀沿着它的棱剪开成一个平面图形，则展开图可以是（）分析：我们把画有圆的一面记为a面，正方形阴影面记为b面，三角形阴影面记为c 面．在选项A中，由Z字型结构知b与c对面，与已知正方体bc相邻不符，应排除；在选项B中，b面与c面隔着a面，b面与c面是对面，也应排除；在选项D中，虽然a、b、c三面成拐角型，是正方体的三个邻面，b面作为上面，a面为正面，则c面应在正方体的左面，与原图不符，应排除，故应选（C）．四. 正方体展开图：相对的两个面涂上相同颜色五. 找正方体相邻或相对的面1．从展开图找．（1）正方体中相邻的面，在展开图中有公共边或公共顶点．如，•或在正方形长链中相隔两个正方形．如中A与D．（2）在正方体中相对的面，在展开图中同行（或列）中，中间隔一个正方形．如ABCD中，A与C，B与D，或和中间一行（或列）•均相连的两正方形亦相对．例1 右图中哪两个字所在的正方形，在正方体中是相对的面．解“祝”与“似”，“你”和“程”，“前”和“锦”相对．例2在A、B、C内分别填上适当的数．使得它们折成正方体后，对面上的数互为倒数，则填入正方形A、B、C•的三数依次是：（A）12，13，1 （B）13，12，1（C）1，12，13（D）12，1，13分析A与2，B与3中间都隔一个正方形，C与1分处正方形链两边且与其相连，选（A）．例3 在A、B、C内分别填上适当的数，使它们折成正方体后，对面上的数互为相反数．分析A与0，B与2，C和-1都分处正方形链两侧且与其相连，∴A─0，B─-2，C─1．例4 找出折成正方体后相对的面．解A和C，D和F，B和E是相对的面．2．从立体图找．例5 正方体有三种不同放置方式，问下底面各是几？分析先找相邻的面，余下就是相对的面．上图出现最多的是3，和3相连的有2、4、5、6，余下的1就和3相对．再看6，•和6相邻的有2、3、4，和3相对的是1，必和6相邻，故6和5相对，余下是4和2相对，•下底面依次是2、5、1．例6由下图找出三组相对的面．分析和2相连的是1、3、5、6，相对的是4，和3相连的是2、4、5、6，相对的是1，和6相连的是1、2、3、4，相对的是5．五. 由带标志的正方体图去判断是否属于它的展开图例7 如下图，正方体三个侧面分别画有不同图案，它的展开图可以是（）．分析基本方法是先看上下，后定左右，图A图B都是□和+两个面相对，不合题意，图C“□”和“○”之上，从立体图看“＋”在右，符合要求．图D•“□”和“＋”之上，“○”在右，而立体图“○”应在左，不合要求，故选（C）．例8 下面各图都是正方体的表面展开图，若将它们折成正方体，•则其中两个正方体各面图案完全一样，它们是（）．分析首先找出上下两底，（1）是+和*，（2）是+和*，（3）（4）都是□和×，排除（1）（2），再检查侧面，（3）（4）顺序相同，所以选（3）（4）．【分享】立方体折叠专题二专题一的知识主要是介绍了如何寻找各种正方体及其展开图的对面。
人大早培第四讲 立体图形规律与推理
第四讲立体图形规律与推理【一】专题精讲一、“折纸盒”与“拆纸盒”折纸盒，泛指题干为平面展开图，四个选项均为立体图形，提问方式一般为“将题干图形折叠后，得到的图形是？” 拆纸盒，泛指题干为立体图形，四个选项均为平面展开图，提问方式一般为“将题干图形展开后应为？”针对这一类问题，根据选项情况可采用区分相邻面及相对面、时针法、小图形特征判定法，二面定位法，标点法来应对。
同时结合选项运用排除法。
1、区分相邻面及相对面平面图形中相邻的两个面折成立体图形后也相邻，立体图形中相对的两个面拆成平面图形后不相邻，区别相邻面与相对面往往能快速排除错误选项，得出符合要求的答案。
2、时针旋转法对于立方体纸盒，折成后只能看到图形的三个面，时针法就是比较这三个面在立体图形与平面图形中的旋转方向来判断选项的正确与否。
时针法只适用于解决面中的小图形不涉及方向的折纸盒问题。
3、小图形特征判定法根据面中小图形的指向、线条交点的位置，相交边来判定正确与否。
4、二面定位法假定其中两个面的方位正确，判断第三个面的方位正确与否，从而来确定答案。
5、标点法折、拆纸盒的实质就是一个点与点重合、边与边重合的过程，当确定两个点重合并确定该点放置的位置时，该纸盒也就确定了。
标点法就是根据已知点确定由这个点出发的线条的情况，从而确定“纸盒”的形式。
二、正方体展开图1）．141型，中间一行4个作侧面，上下两个各作为上下底面，共有六种基本图形2）．132型，中间3个作侧面，共3中基本图形3）．222型，两行只能有1个正方形相连4）．33型，两行只能有一个正方形相连一共11种三、棱柱的表面展开图是两个完全相同的多边形(作底面)和几个长方形(作侧面)四、棱锥的展开图是由一个多边形(作底)和几个三角形(作侧面)组成的五、长方体的展开图【二】经典例题【例1】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?（）【例2】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?（）【例3】左边给定的是纸盒的外表面，下面哪一项不能由它折叠而成?（）【例4】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成? （）【例5】右边哪个正方体不是由左边的展开图折成的？（）【例6】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成? （）【例8】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成? （）【例9】右边哪个正方体不是由左边的展开图折成的？（）【例10】下图左边的正方体，如果把它展开，可以是选项哪个图形?（）【例12】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成? （）【例13】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？（）【例14】下列四个选项中，哪个可以折出左边指定的图形?（）【例15】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?（）【例16】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?（）【例17】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?（）【例18】左边给定的是纸盒的外表面，下面哪一项不能由它折叠而成？（）【例19】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？（）【例20】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?（）【例21】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？（）【例22】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？（）【例23】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？（）【例24】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？（）【例25】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？（）【例26】选出最合适的一项填到问号处。
公务员行测三种方法应对折、拆纸盒问题
一、区分相邻面及相对面平面图形中相邻的两个面折成立体图形后也相邻，立体图形中相对的两个面拆成平面图形后不相邻，区别相邻面与相对面往往能快速排除错误选项，得出符合要求的答案。
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?解析：左边的图形折成立体图形后，有两个空白面相对，含有圆点的两个面相对，含有斜线的面与另外一个空白面相对。
A项，应有两个空白面相对，故A项错误;B项，可由左边纸盒折成;C项，含有圆点的两个面相对，故C项错误;D项，带斜线的面不可能与两个空白面两两相邻，故D项错误。
由此，可确定正确答案为B。
例题：下列四个选项中，哪个可以折出左边指定的图形?解析：左边给定的立体图形中，带阴影的两个面相对。
折成立方体后，A、C、D三项的两个阴影面相邻，所以是错误的;B项折成后带阴影的面相对，因此，应选择B项。
提醒：区分相对面与相邻面是解决空间型图形推理的基础。
分清相对面与相邻面往往也能快速地排除一些选项，从而更快地解决问题。
二、时针法对于立方体纸盒，折成后只能看到图形的三个面，时针法就是比较这三个面在立体图形与平面图形中的旋转方向来判断选项的正确与否。
时针法只适用于解决面中的小图形不涉及方向的折纸盒问题。
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?解析：首先通过相对面与相邻面可排除C项，C项中1和2应为相对的面，不可能相邻。
A项，按1-4-6的顺序，顺时针旋转，题干平面图形中1-4-6则按逆时针旋转，如下图所示，两者的旋转方向不一致，则A项不能由左边的图形折成;同理可判定B项可由左边图形折成，D项不能由左边图形折成。
三、标点法折、拆纸盒的实质就是一个点与点重合、边与边重合的过程，当确定两个点重合并确定该点放置的位置时，该纸盒也就确定了。
标点法就是根据已知点确定由这个点出发的线条的情况，从而确定“纸盒”的形式。
下面介绍标点法的具体应用。
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?如上图所示，分析中间的平面图形，我们可发现折成纸盒后，重合的点为A与M、B 与L、C与K、D与J、E与I、F与H。
折纸盒题目秒杀技巧
折纸盒题目秒杀技巧
嘿，朋友们！今天咱就来讲讲折纸盒题目秒杀技巧哈。
就说我上次遇到一道折纸盒题，那可真是把我给难住了。
题目上画了个奇奇怪怪的展开图，我瞅了半天，脑袋都快大了也没整明白。
然后我就开始琢磨呀，这要是有个啥简单的法子就好了。
嘿，你还别说，我突然就想到一个招。
我就先找那些相对位置特别明显的面，把它们给标记出来，然后呢，再根据其他面和这些面的关系来判断。
就像侦探破案一样，一点点去分析线索。
比如说，有个面旁边肯定得挨着另一个特定的面，那要是不符合的选项，直接就给它 pass 掉。
我就这么一试，哎呀妈呀，还真就好用多了。
一下子就排除了好多错误选项，感觉就像找到了宝藏的钥匙一样。
而且呀，我发现只要耐心点，仔细去观察那些细节，就能找到关键所在。
所以呀，遇到折纸盒题目别慌张，就用咱这小技巧，先标记，再分析，保准能快速找到正确答案。
哈哈，以后再碰到这种题，咱可就不怕啦！这就是我发现的折纸盒题目秒杀小技巧，大家也快去试试吧！。
历年国考行测高频题型解读之折纸盒题
历年国考行测高频题型解读之折纸盒题图形推理是公务员考试中非常常见的一类问题，而在这其中，立体图形问题，尤其是折纸盒问题，考察的频率越来越高。
通常情况下，如果考生第一次遇到这种类型的题目，往往要思考比较长的时间，从而耽误了考试整体的进度，中公教育在这里就给考生几个关于解决折纸盒问题的小技巧，相信对于考生在解决此类问题时有所帮助和启发。
我们先拿一个正六面体体纸盒的外表面举例子。
如上图，任何的一个正六面体的外表面，都可以画成四块排成一行，上下各有一块的形式，我们就以这个图为例子来进行讲解折纸盒的一些性质。
一、相对的不相邻。
图中的六块图形，有三组是永远不会相邻的，折成纸盒之后，他们会成为相对的两个面。
这三组分别为：“A和C”、“B和D”、“E和F”。
可以通过这条性质根据选项，来迅速的做排除法，从而得到答案或者缩小范围。
二、相邻的相对位置不变。
如果两块图形相邻，那么无论怎样转动这个折成的纸盒，他们俩的相对位置永远不会变化。
例如，“A和B”这两块图形的顺序是并排的，那么，下面三幅图形都是“A和B”的正确顺序，他们无论怎样转动，相对位置都是不变的。
我们也可以根据这条性质来进一步做排除法。
三、上下两块可以分别在上下区域转动。
仍然以最开始给出的纸盒来说,若折成纸盒的话，被红色线标注的两条边其实应为纸盒的同一条楞于是我们可以得到下右图的变换。
因为通常给出的选项为呈现出3面的立体图形，这样的变化可以有效的变换成我们想要的那三块相邻的图块，直接与选项进行比对即可得到答案,例如CDE 这三块，就可以得到如下右的立体图形，从而得到答案。
四、四块并排的左右可直接移动。
例子中的六面体，虽然折成纸盒后A和D 是连在一起的，但是从平面上来看，无法直观的进行想象，而有的时候，可能选项中会出现A、D在一起的情况，这时候只需要直接的把A移动到最右端或者D 移动到最左端即可。
相信通过以上几条性质，考生们可以把需要空间想象力的折纸盒问题变的更加的直观，更加的容易操作。
省考行测立体图形之折纸盒问题最佳五种解法
省考行测立体图形之折纸盒问题最佳五种解法在公务员行测考试中，图形推理均是判断推理部分的必考版块之一，而其中的立体图形的折叠问题(折纸盒问题)是常考考点。
所谓折纸盒问题即题干左面给大家一个正方体的平面展开图形，右面给大家四个选项，让大家从中找出一个可以由左面的平面图形折成的立体图形。
对于这种题型，很多空间想象能力不高的同学经常感觉一头雾水、无从下手。
鉴于此，中公教育专家给大家提供几种解题思路，保证大家在考场上看到这类题目便喜笑颜开。
方法一：根据相对面法则排除法相对面法则即在立体图形中，比如正方体、长方体等都有六个面，而这六个面中有三组相对面。
而在平面中表现立体图形时往往只能表现三个相邻面。
因此，三组相对的两个面在选项中的立体图形中必须出现而且只能出现一个面。
相对面如何判断?以下给大家列举几种常见的情况。
下图中的两个阴影面均属于相对面，折成立体图形后，相对的两个面不能相邻。
例：根据相对面排除法可知，两个阴影面是相对关系，所以可以排除A、C、D，选B。
方法二：时针法对于立方体纸盒，折成后只能看到图形的三个面。
所谓时针法就是比较这三个面在立体图形与平面图形中的旋转方向来判断选项的正确与否。
然而并非任意三个面都可以画时针，时针法应用的前提有两点：1、画时针的三个面必须不存在平行面;2、画时针的时候必须保证这三个面至少两对面两两有交点。
如在下面两个图中，两个平面图中的1、2、3三个面都不平行，满足了时针法的第一个前提。
此外，第一个图形中1、2两个面有两个交点(红点)，2、3两个面有一个交点(蓝点);第二个图形中1、2两个面的交点为a、b，1、3两个面的交点为b、c，2、3两个面的交点为b。
第一个图形中两对面两两有交点，第二个图形中三对面都两两有交点，所以满足时针法的第二个前提。
因此，这两个图都可以用时针法解决的。
方法三：公共顶点法在平面中相交于同一个公共顶点下的三个面，其面上的图形与公共顶点的位置关系保持不变。
图形推理 折叠
一、关于内外折的问题：我通常是由外向内折，但是也存在有些题是由内向外折的，所以没有固定的向内还是向外，如果向内有2个正解，而向外恰好1个正解的话，自然是向外折了。
二、折纸盒正确选项的特征：一定有2个数是相邻的或是可以头尾相接的，剩下的那1个数在由前两数连成的直线的两旁。
三、折纸盒题错误选项的特征：3个数在同一直线上，2个数在同一数的两边时。
四、时针法：（假定为由外向内叠，且大部分真题模拟题都是由外向内叠的）
1.找出两个相邻的数，或是头尾接的数，如图A中2,64相邻，（那么剩下的那个数一定不再2,64所在的32—4—64—2这条直线上，而在这条直线的两旁如，16或8）
2.时针法：A中由2到64，再由64到8，是顺时针转的，那么回到前面的那个十字架上同样由2开始沿着64,8的顺序转，它的转动是逆时针转，所以一个顺时针，一个逆时针，两图不同向转，不选
B由2到64,64到16顺时针转，回十字架上，2到64，到16也是顺时针转，两图同向转，是符合的，所以选B
C，2,4在同一个数64两旁，符合错误项特征，不选
D由64到4,4到8顺时针转，回前面的图，64到4，4到8是逆时针转，两图转向不同，不选。
附加：如果出现首位连接的话，把尾上的数写到头上数上面再转（效果图如下面的那个没有框的十字架），首尾接的例子：如果选项中有这样3个数的组合（32在上，2在左，16
在右）那么32到16，16到2是顺时针转，在十字架上把2放到32上，即32到16在到2是逆时针转动，不选。
2
32
8 4 16
64
（2）被剪到上面去了
当然纸盒子的四种平面图如下：
折好后，前与后，左与右，上与下是不可能同时看见的，时针法基本能做出大部分不涉及方向的折纸盒题了。
判断---四面体-公共边法
四面体-公共边法
折纸盒问题一直是行测图形推理中一个非常重要的考点。
很多考生遇到折纸盒问题的时候,感觉做题慢，就会抱怨、放弃，特别是四面体可能根本想不到怎么去折叠。
今天我们就一起来帮大家解决四面体的折纸盒问题。
不需要你的空间想象能力,只要平面的知识降这一问题会迎刃而解,下面就跟大家一起来看四面体的折纸盒：
一、什么是四面体
1.四面体的立体图和展开图：由四面组成，每三个面都含有公共顶点。
2.四面体的展开图中如何判断四面体相邻面：
（1）展开图中构成一条直线的两条边是同一条边
（2）平行四边形两个短边是同一条边
图1 图2
展开图中构成一条直线的两条边是同一条边：图1中标蓝色、绿色、黑色的两条边均是同一条边；图2中标绿色、黄色的两条边是同一条边。
平行四边形两个短边是同一条边：图2的外框是平行四边形，两端蓝色的短边是同一条边。
二、解题思维：排除错误选项，即用平面的思维去做题，排除掉错误的选项，剩下的就是正确答案。
三、四面体解题方法：公共边法
公共边法：两个相邻面的公共边与两个面的相对位置不变
图1 图2
图2中的两个面分别是图1中的面2和面3，面2和面3的公共边在展开图中与面3的箭头并不垂直，但是在立体图中，面3的箭头垂直于面2和面3的公共边，所以展开图与平面图不一致，可以排除。
题型示例：
左边给定的是纸盒外表面的展开图，右边哪一项能够由它折叠而成：
四个选项中都是面2和面4，所以可以画出面2和面4的公共边，面2的虚线与公共边相交却不垂直，可以排除C、D两个选项，面4的两个短线与公共边都相交，排除B项，所以选择A项。
判断---四面体-画边法
四面体-画边法折纸盒问题一直是行测图形推理中一个非常重要的考点。
很多考生遇到折纸盒问题的时候,感觉做题慢，就会抱怨、放弃，特别是四面体可能根本想不到怎么去折叠。
今天我们就一起来帮大家解决四面体的折纸盒问题。
不需要你的空间想象能力,只要平面的知识降这一问题会迎刃而解,下面就跟大家一起来看四面体的折纸盒：一、什么是四面体1.四面体的立体图和展开图：由四面组成，每三个面都含有公共顶点。
2.四面体的展开图中如何判断四面体相邻面：（1）展开图中构成一条直线的两条边是同一条边（2）平行四边形两个短边是同一条边图1 图2展开图中构成一条直线的两条边是同一条边：图1中标蓝色、绿色、黑色的两条边均是同一条边；图2中标绿色、黄色的两条边是同一条边。
平行四边形两个短边是同一条边：图2的外框是平行四边形，两端蓝色的短边是同一条边。
二、解题思维：排除错误选项，即用平面的思维去做题，排除掉错误的选项，剩下的就是正确答案。
三、四面体解题方法：画边法画边法：1.找到同一个面的唯一点（起点）2.按同一个方向（顺/逆时针）给唯一点所在的面的三个边标号3.结合选项排除图1 图2 图3找唯一点：如图1的左右有2个红点，但这2个红点在图3中不容易区分，找不到对应的红点；如果将上面的顶点标红（图2），则能很容易在图3中找到对应的点（与直线相交的点），即唯一点（能马上识别出来的点）。
图4 图5按同一个方向（顺/逆时针）给唯一点所在的面的三个边标号，展开图和立体图形的方向要保持一致。
直线面上与直线相交的顶点是唯一点，以该点作为起点，在直线面上沿着顺时针方向转一圈，标记1、2、3（如图4），图5的立体图按照相同的方式标号。
结合选项排除：图4的边1对应的是箭头面，图5的边1对应两条直线的面，与图4不一致，可以排除。
题型示例：左边给定的是纸盒外表面的展开图，右边哪一项能够由它折叠而成：本题通过相对位置不容易观察，展开图中有直线面，与顶点的交点比较容易确认，可以作为唯一点，且选项均有该面，找到唯一点后，顺时针画一圈标记1、2、3。
3种方法对应折纸盒问题
三种方法应对折、拆纸盒问题例题：下列四个选项中，哪个可以折出左边指定的图形?解析：左边给定的立体图形中，带阴影的两个面相对。
折成立方体后，A、C、D三项的两个阴影面相邻，所以是错误的;B项折成后带阴影的面相对，因此，应选择B项。
提醒：区分相对面与相邻面是解决空间型图形推理的基础。
分清相对面与相邻面往往也能快速地排除一些选项，从而更快地解决问题。
二、时针法对于立方体纸盒，折成后只能看到图形的三个面，时针法就是比较这三个面在立体图形与平面图形中的旋转方向来判断选项的正确与否。
时针法只适用于解决面中的小图形不涉及方向的折纸盒问题。
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?解析：首先通过相对面与相邻面可排除C项，C项中1和2应为相对的面，不可能相邻。
A项，按1-4-6的顺序，顺时针旋转，题干平面图形中1-4-6则按逆时针旋转，如下图所示，两者的旋转方向不一致，则A项不能由左边的图形折成;同理可判定B项可由左边图形折成，D项不能由左边图形折成。
三、标点法折、拆纸盒的实质就是一个点与点重合、边与边重合的过程，当确定两个点重合并确定该点放置的位置时，该纸盒也就确定了。
标点法就是根据已知点确定由这个点出发的线条的情况，从而确定“纸盒”的形式。
下面介绍标点法的具体应用。
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?如上图所示，分析中间的平面图形，我们可发现折成纸盒后，重合的点为A与M、B 与L、C与K、D与J、E与I、F与H。
A项，看右上角的立体图形，我们先确定右侧面为平面图形中的面③，根据前面判断的点重合情况，可得出顶面为平面图形中的面④(MLGF)，正面为平面图形中的面①(ABCN)，由此得出A项不正确。
B项，看左下角的立体图形，我们先确定顶面的方位为平面图形中的面③，根据前面判断的点重合情况，可得出正面为平面图形中的面②(CDEN)，右侧面为平面图形中的面⑥(HI JG)，由此得出B项不正确。
2022国家公务员考试真题由2022年国家公务员考试真题分析折纸盒问题
2022国家公务员考试真题由2022年国家公务员考试真
题分析折纸盒问题
华图公务员研究中心研究员针对2022年国家公务员真题，对国考中
折纸盒问题进行了深入分析。
空间折叠问题(也叫折纸盒问题)是图形推理模块中比较难的一类题目，涉及到比较多的知识点，也需要考生有一定的空间想象能力。
下题是
2022年国考行测考试第80题。
这个题比较具有代表性，考察了空间折叠问题的两个知识点。
如果考
生不具备相关的知识结构体系，那么在解决这一类问题将会非常困难。
下面华图考试研究中心以此题为例，详细讲解空间折叠问题。
为了指
代方面，我们将各个面进行定义如下：
知识点1：相对面
比较容易看出来，其中1、3为相对面，2、5为相对面，4、6为相对面。
由2、5是相对面，只能在立体图中出现其中的一个，可以排除选项A;
由4、6是相对面，只能在立体图中出现其中的一个，可以排除选项B;
知识点2：时针方向
共点的三个面，不管是平面展开图，还是立体图，其时针方向是不变的。
在选项D中，3、4、5三个面的时针方向是逆时针方向的;在左边的平面图中，3、4、5三个面的时针方向是顺时针的，因此D错误，如下图所示。
在选项C中，1、5、6三个面的时针方向是逆时针方向的;在左边的平面图中，1、5、6三个面的时针方向也是逆时针的，因此C正确，如下图所示。
综上所述，本题的答案为C。
在更加复杂的空间折叠问题中，可能还会考察到相邻边的关系，也可能考察的对象并不是立方体而是其他的立体图形，这就需要考生在掌握基本知识点的基础上，多做练习，面对空间折叠问题时才能得心应手。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
图形推理之折纸盒、拆纸盒问题
一般来说，图形推理题目可以按照图形数量变化来划分，可以按照图形位置变化来划分，可以按照图形形状变化来划分。
但是，近年来，图形推理题目出现了一个新的趋势，那就是按照图形的立体变化来出题目。
立体变化，顾名思义，就是利用图形在空间中的“平面——立体”、“立体——平面”变化来考察考生的空间想象能力。
平面图形与立体图形的这两种相互转化，我们分别称之为折纸盒问题——平面图形的空间还原、拆纸盒问题——立体图形的平面展开。
一、折纸盒问题——平面图形的空间还原
平面图形的空间还原，就是给出一个平面图形，即立体图形的平面展开图，让考生将这个平面图形还原成空间图形。
这类题型经常出现在智商测验中，公务员考试借鉴此类题型来测查考生的空间想象能力等基本素质。
由平面到立体的这种本质性的变化直接对考生的能力提出了挑战，要想做好此类题目必须要多加练习，熟悉题目的特点，找出其中的解题技巧和规律。
下面，我们来看几道题目。
【例题1】
【答案】D
【解析】这个题目相当简单，通过观察可知只有D可以由左边的纸板折叠而成。
因为侧面没有阴影。
因此，正确答案是D。
【例题2】右边四个选项中的哪个不是左边图形折叠而成的。
()
【答案】A
【解析】这个题目不是很难，5的四个临面是4、2、3、1，而且1和4是平行面，2和3是平行面，故答案选择A，因为2和3不可能是临面。
【例题3】(2008年中央)
下面四个所给的选项中，哪—个选项的盒子不能由左边给定的图形做成( )
【答案】C
【解析】这个题目和上个题目有点类似都是选择不符合的项，由于题干中没有只给出一条对角线的面，故不能由左边的图形折成，因此答案选择C。
【例题4】(2010年中央)
左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?
【答案】B
【解析】自己用折纸法，得出是B。
空白面与横线面应该在对面的面上，所以排除C、D。
A项中上表面的对角线应该与右表面的对角线相交在一个顶点上。
故答案选择B项。
【例题5】(2010年中央)
左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?
【答案】C
【解析】首先排除D项，顶面的横线和有两条横线的侧面中的横线不可能平行，把B项掉转过来看，和A项是同样的图形，所以都排除，剩下的只有C项
【例题6】
【答案】A
【解析】两个小的黑方块的一定是相对的，和两个小黑方块所在面相对的面一定是阴影的。
故答案只能选择A。
【例题7】
【答案】B
【解析】这个题目比较简单，两个黑点的面和上下连个空白面市平行的，以此可以排除A和C，因为阴影边的两个空白面是平行的，因此D也排除，故答案选择B。
【例题8】不能折成的图形是()
【答案】B
【解析】有一“横”所在的面和阴影所在的面应该是相平行的，不能相邻。
错误的是B。
二、拆纸盒问题——立体图形的平面展开
与上面的折纸盒问题相对的另一种题型就是拆纸盒问题，即题目给出一个立体图形，让考生从四个平面图形选项中选出一个可以折成给定的立体图形的答案。
所以，这类题目给很多考生带来了困然。
其实，无论是从平面图形转化为立体图形还是从立体图形转化为平面图形，遵循的规律都是一样的，只要抓住对面和邻面这两个关键点，再经过认真的训练，这类貌似非常困难的题目都将变成纸老虎。
下面我们就看几道拆纸盒问题的题目来让大家训练一下，增加对此类题目的敏感程度。
【例题1】有一个正方体纸盒，在它的三个侧面分别画有三角形、正方形和圆，现用一把剪刀沿着它的棱剪开成一个平面图形，则展开图可以是()
【答案】C
【解析】我们把画有圆的一面记为a面，正方形阴影面记为b面，三角形阴影面记为c面. 在选项A中，由Z字型结构知b与c对面，与已知正方体bc相邻不符，应排除;在选项B中，b面与c面隔着a 面，b面与c面是对面，也应排除;在选项D中，虽然a、b、c三面成拐角型，是正方体的三个邻面，b 面作为上面，a面为正面，则c面应在正方体的左面，与原图不符，应排除，故答案选择C。
【例题2】
正方体三个侧面分别画有不同图案，它的展开图可以是( ).
【答案】C
【解析】基本方法是先看上下，后定左右，图A图B都是□和+两个面相对，不合题意，图C“□”和“○”之上，从立体图看“+”在右，符合要求.图D “□”和“+”之上，“○”在右，而立体图“○”应在左，不合要求，故答案选择C。
【例题3】(2009年中央)
下面四个所给的选项中，哪一项能折成左边给定的图形：( )
【答案】B
【解析】国家公务员考试中之前出现的都是由平面图形折成立体图形，而这道题中是已知立体图形，再拆成平面图形，这就给很多考生造成了困扰。
其实不管是由平面到立体还是由立体到平面，遵循的规律都是一样的。
因此在本题中，很显然原图中的虚线就是我们解题的关键，要使两个黑色三角形的顶点相对，显然应该使这两个顶点位于同一条线上，因此A、C、D项均不符合定义，而B项粗略一看也不符合，但是如果折起来的话两个黑色三角形的顶点是可以位于一条线段上的，因此B项为正确答案。