行测图形推理之折纸盒、拆纸盒问题_189
公考行测图形推理之折、拆纸盒问题
折、拆纸盒问题空间形式图形推理是近几年考查热点。
而在空间形式图形推理的考查中，折纸盒与拆纸盒问题，更是常见考点。
折纸盒，泛指题干为平面展开图，四个选项均为立体图形，提问方式一般为“将题干图形折叠后，得到的图形是？”拆纸盒，泛指题干为立体图形，四个选项均为平面展开图，提问方式一般为“将题干图形展开后应为？”针对这一类问题，根据选项情况可采用区分相邻面及相对面、时针法、标点法来应对。
一、区分相邻面及相对面平面图形中相邻的两个面折成立体图形后也相邻，立体图形中相对的两个面拆成平面图形后不相邻，区别相邻面与相对面往往能快速排除错误选项，得出符合要求的答案。
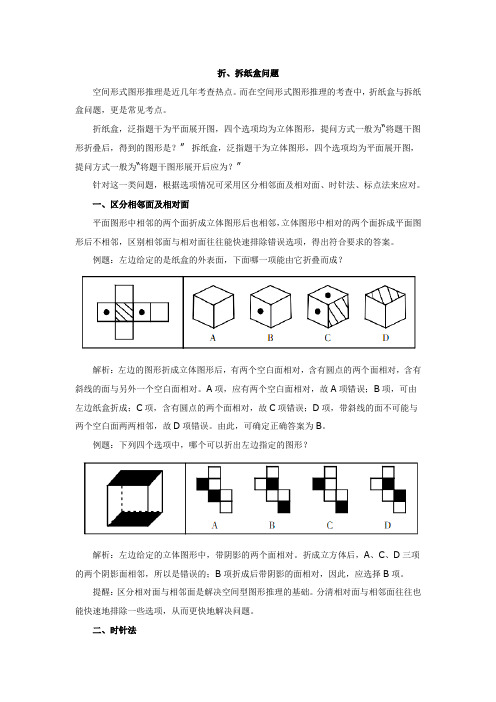
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？解析：左边的图形折成立体图形后，有两个空白面相对，含有圆点的两个面相对，含有斜线的面与另外一个空白面相对。
A项，应有两个空白面相对，故A项错误；B项，可由左边纸盒折成；C项，含有圆点的两个面相对，故C项错误；D项，带斜线的面不可能与两个空白面两两相邻，故D项错误。
由此，可确定正确答案为B。
例题：下列四个选项中，哪个可以折出左边指定的图形？解析：左边给定的立体图形中，带阴影的两个面相对。
折成立方体后，A、C、D三项的两个阴影面相邻，所以是错误的；B项折成后带阴影的面相对，因此，应选择B项。
提醒：区分相对面与相邻面是解决空间型图形推理的基础。
分清相对面与相邻面往往也能快速地排除一些选项，从而更快地解决问题。
二、时针法对于立方体纸盒，折成后只能看到图形的三个面，时针法就是比较这三个面在立体图形与平面图形中的旋转方向来判断选项的正确与否。
时针法只适用于解决面中的小图形不涉及方向的折纸盒问题。
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？解析：首先通过相对面与相邻面可排除C项，C项中1和2应为相对的面，不可能相邻。
A项，按1-4-6的顺序，顺时针旋转，题干平面图形中1-4-6则按逆时针旋转，如下图所示，两者的旋转方向不一致，则A项不能由左边的图形折成；同理可判定B项可由左边图形折成，D项不能由左边图形折成。
2017黑龙江烟草局招聘笔试备考之判断推理
2017黑龙江烟草局招聘笔试备考之判断推理行政职业能力测验主要测查与职业密切相关的、适合通过客观化纸笔测验方式进行考查的基本素质和能力要素，包括言语理解与表达、数量关系、判断推理、资料分析和常识判断等部分。
【考点一】折纸盒问题区别相邻面与向对面。
平面图形中相邻的两个面折成立体图形后也相邻，立体图形中相对的两个面拆成平面图形后不相邻，区别相邻面与相对面往往能快速排除错误选型，得出符合要求的答案。
时针法。
对于立方体纸盒，折成后只能看到图形的三个面，时针法就是比较这三个面在立体图形与平面图形中的旋转方向来判断选型的正确与否。
时针法只适用于解决面中的小图形不涉及方向的折纸盒问题。
【例题精讲】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？【答案】B。
解析：A项，由左图得出白圆与白心属于相对面，两面不能相邻，排除；C项，由左图得出黑圆与黑心属于相对面，两面不能相邻，排除；D 项，固定白三角与黑圆位置，逆时针观察，顶面应为白圆面，排除。
故答案选择B。
【考点二】假言命题1.含义：假言命题是在假设的基础上得出结论的复言命题。
即假定某一条件存在，从而推出某一结果存在的命题。
2.常见关联词：如果……那么，若……则，只要……就，只有……才，除非……否则3.矛盾命题：A且非B4.推理规则：A→B的逆否命题就是非B→非A。
注意：假言命题只有肯前推肯后、否后推否前是成立的，其他如：否前推否后，肯后推肯前都是不成立的。
【例题精讲】如果工资提高或者物价上涨，那么将发生通货膨胀。
如果发生通货膨胀，则政府必须限制通货膨胀，否则人民将遭受损失。
如果人民遭受损失，那么政府就会失掉民心。
实际情况是政府既没有限制通货膨胀也没有失掉民心。
根据以上陈述，可以得出：A.工资提高了，物价没有上涨B.工资没有提高，但是物价上涨C.工资没有提高，物价也没有上涨D.工资提高了，但是物价也上涨了【答案】C。
解析：题干推理关系为工资提高或者物价上涨→发生通货膨胀→政府必须限制通货膨胀，人民没遭受损失→政府限制通货膨胀，人民遭受损失→政府就会失掉民心，因为政府既没有限制通货膨胀也没有失掉民心，肯前则肯后，否后则否前，所以没有发生通货膨胀，工资没有上涨且物价没有上涨，C项正确。
图形推理之折纸盒
图形推理之折纸盒、拆纸盒问题一般来说，图形推理题目可以按照图形数量变化来划分，可以按照图形位置变化来划分，可以按照图形形状变化来划分。
但是，近年来，图形推理题目出现了一个新的趋势，那就是按照图形的立体变化来出题目。
立体变化，顾名思义，就是利用图形在空间中的“平面——立体”、“立体——平面”变化来考察考生的空间想象能力。
平面图形与立体图形的这两种相互转化，我们分别称之为折纸盒问题——平面图形的空间还原、拆纸盒问题——立体图形的平面展开。
一、折纸盒问题——平面图形的空间还原平面图形的空间还原，就是给出一个平面图形，即立体图形的平面展开图，让考生将这个平面图形还原成空间图形。
这类题型经常出现在智商测验中，公务员考试借鉴此类题型来测查考生的空间想象能力等基本素质。
由平面到立体的这种本质性的变化直接对考生的能力提出了挑战，要想做好此类题目必须要多加练习，熟悉题目的特点，找出其中的解题技巧和规律。
下面，我们来看几道题目。
【例题1】【答案】D【解析】这个题目相当简单，通过观察可知只有D可以由左边的纸板折叠而成。
因为侧面没有阴影。
因此，正确答案是D。
【例题2】右边四个选项中的哪个不是左边图形折叠而成的。
()【答案】A【解析】这个题目不是很难，5的四个临面是4、2、3、1，而且1和4是平行面，2和3是平行面，故答案选择A，因为2和3不可能是临面。
【例题3】(2008年中央)下面四个所给的选项中，哪—个选项的盒子不能由左边给定的图形做成( )【答案】C【解析】这个题目和上个题目有点类似都是选择不符合的项，由于题干中没有只给出一条对角线的面，故不能由左边的图形折成，因此答案选择C。
【例题4】(2010年中央)左边给定的是纸盒的外表面，下面哪一项能由它折叠而成?【答案】B【解析】自己用折纸法，得出是B。
空白面与横线面应该在对面的面上，所以排除C、D。
A项中上表面的对角线应该与右表面的对角线相交在一个顶点上。
故答案选择B项。
2014年国家公务员考试行测：空间还原问题
2014年国家公务员考试行测：空间还原
问题
空间还原类题目主要使用拆（折）纸盒的方法进行解答。
折纸盒主要是针对平面图形变为立体图形的题目，而拆纸盒则是针对立体图形转化为平面图形的题目。
对于这类题目，简单直观的方法就是快速地找到特殊面或者特殊边，然后根据这个面或者边的位置进行折叠，从而分析得出试题的答案。
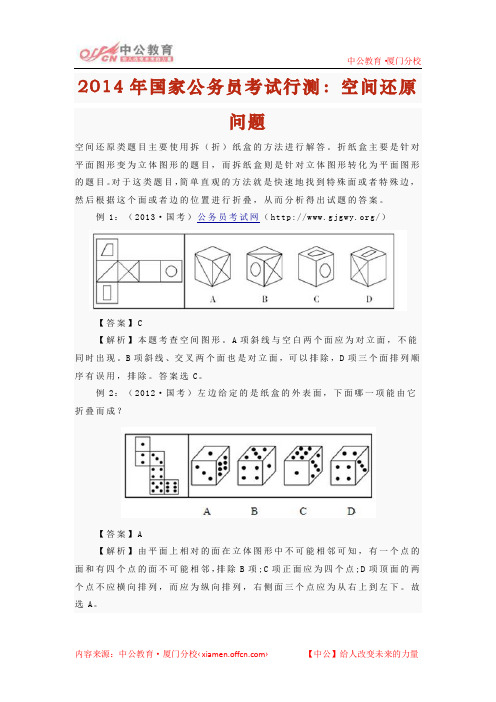
例1：（2013·国考）公务员考试网（/）
【答案】C
【解析】本题考查空间图形。
A项斜线与空白两个面应为对立面，不能同时出现。
B项斜线、交叉两个面也是对立面，可以排除，D项三个面排列顺序有误用，排除。
答案选C。
例2：（2012·国考）左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？
【答案】A
【解析】由平面上相对的面在立体图形中不可能相邻可知，有一个点的面和有四个点的面不可能相邻，排除B项;C项正面应为四个点;D项顶面的两个点不应横向排列，而应为纵向排列，右侧面三个点应为从右上到左下。
故选A。
以上是解决此类问题的常规分析方法，如果有部分考生实在不擅长分析，可以考虑在考场演示的方式，这样更为直观。
只要是能够真正解决问题的方法，都是可行的方法。
2014年国家公务员考试公告备考资料：
/html/guojiagongwuyu an/。
B3逻辑组专题(三)——图形重构 教程
B3逻辑组专题（三）——图形重构教你用“描点法”解决折纸盒问题在公考的图形推理的试题中，总会有那么一题是关于折纸盒的。
或者要你判断哪个是展开图形所折成的纸盒；或这要你判断纸盒摊开了会是什么样的图形等等。
而且，由于现在出的题目会出现内容相似或者是相同的面，用以前的“相对面相邻面”的解题方法会越来越费时间。
“折纸盒”的是指就是一个点与点重合，边与边重合的过程，当确定两个点重合时，这个立体图形也就确定了。
描点法就是根据已知的点确定由这个点出发的线条的情况，从而判定“纸盒”的样式。
也就是说，一个标准的正方体纸盒会有8个顶点，每个顶点负责引出3条边，也就是说1个点可以连接着3个面（听不明白？看看试题的备选答案，是不是只能看到三个面？还不明白？不要紧，下面会配合例题讲解的）。
下图就是一个标准的正方体纸盒的展开图，上面就标出了，在折合的过程中，哪些点会重合。
从上图可以看出。
单是A这个点，就有AD,DA,AE三条线。
从而引出了□BACD、□DAHE、□ABEF三个面。
而“折纸盒”问题，就是考察这个点引出的三个面各自的相对关系。
所以“描点法”的关键，就是要根据选项，找出选项里面的点所在平面图的位置，从位置上判断三个面的相对关系，从而得出答案。
好！下面根据例题来讲解一下“描点法”的具体用法。
【例1】：【解析】题干是一个我称之为“标准护翼型”的图形，所有的正方体纸盒，都可以化成“标准护翼型”来使我们观察“点”更加方便。
我们先看A选项。
根据黑三角形和有“点”的那个面的相对位置。
我们找到了原图中的红色点，由原图看，黑色三角形的一条直角边在白面上方，另外一条在“点”面上方，所以纸盒是可以折成A的形状的。
再看B，B 选项的这个顶点，在原图上面是找不到相对应的点的，因为以“点”面为中心，上下两个黑色三角形的直角边都与“点”面有一条公共边，B选项这样，没有公共边的情况是不存在的，所以原图不能折成B的样子。
答案就是B。
C、D两个选项的点，我也用不同的颜色标出来了，大家可以看看。
空间型图形推理-折纸盒问题
折、拆纸盒问题折纸盒，泛指题干为平面展开图，四个选项均为立体图形，提问方式一般为“将题干图形折叠后，得到的图形是？”拆纸盒，泛指题干为立体图形，四个选项均为平面展开图，提问方式一般为“将题干图形展开后应为？”针对这一类问题，根据选项情况可采用区分相邻面及相对面、时针法、标点法来应对。
一、区分相邻面及相对面平面图形中相邻的两个面折成立体图形后也相邻，立体图形中相对的两个面拆成平面图形后不相邻，区别相邻面与相对面往往能快速排除错误选项，得出符合要求的答案。
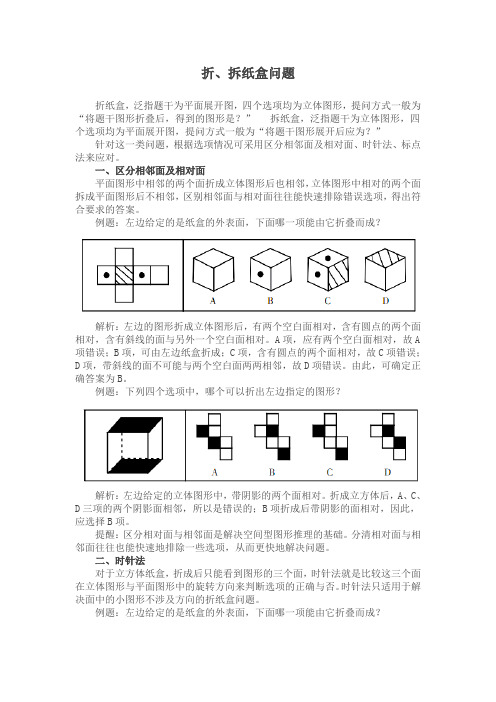
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？解析：左边的图形折成立体图形后，有两个空白面相对，含有圆点的两个面相对，含有斜线的面与另外一个空白面相对。
A项，应有两个空白面相对，故A 项错误；B项，可由左边纸盒折成；C项，含有圆点的两个面相对，故C项错误；D项，带斜线的面不可能与两个空白面两两相邻，故D项错误。
由此，可确定正确答案为B。
例题：下列四个选项中，哪个可以折出左边指定的图形？解析：左边给定的立体图形中，带阴影的两个面相对。
折成立方体后，A、C、D三项的两个阴影面相邻，所以是错误的；B项折成后带阴影的面相对，因此，应选择B项。
提醒：区分相对面与相邻面是解决空间型图形推理的基础。
分清相对面与相邻面往往也能快速地排除一些选项，从而更快地解决问题。
二、时针法对于立方体纸盒，折成后只能看到图形的三个面，时针法就是比较这三个面在立体图形与平面图形中的旋转方向来判断选项的正确与否。
时针法只适用于解决面中的小图形不涉及方向的折纸盒问题。
例题：左边给定的是纸盒的外表面，下面哪一项能由它折叠而成？解析：首先通过相对面与相邻面可排除C项，C项中1和2应为相对的面，不可能相邻。
A项，按1-4-6的顺序，顺时针旋转，题干平面图形中1-4-6则按逆时针旋转，如下图所示，两者的旋转方向不一致，则A项不能由左边的图形折成；同理可判定B项可由左边图形折成，D项不能由左边图形折成。
公务员考试行测技巧：空间折叠抓住最核心
公务员考试行测技巧：空间折叠抓住最核心_空间折叠类图形推理题一直以来都有同学反映特别难，解题需要很强的空间感。
其实不然，Z字型法和相邻面法可以解决大部分问题。
同学们的之所以认为难，主要有两点，一点在于直接求证哪一个选项才能真正折出原图。
其实克服这点的办法就是用排除法，有时候不需要证明哪个选项是对的，只需要证明其他选项是错的即可。
另外一点在于，面对不能完全证明错误的选项，很多同学总是思考多种可能性，意图将所有可能涵盖进去。
其实，如果提出一种可能，最简单的办法就是用反证法。
先假设这种可能性为真，最后推出一个矛盾的结论，即证明了前提为假。
我们可以通过2010年64题来看看如何在图形推理的空间折叠类题型中使用排除和反证方法。
【例题】左边给定的是纸盒的外表面，下面哪一项能由它折叠而成? （）【答案】B【解析】可以看到，该图属于空间重构类题型，题干给出一个立方体的展开图，而选项中给出一系列折叠而成的空间图形。
该题需要一定水平的空间想象能力才能完成，但用我们的图形推理知识体系也可以快速解决。
本题要直接推出答案是很难的，因此可以考虑用排除法。
首先，我们注意到原图（即展开图）中大部分面都是拥有对角线的面，因此不太好定位，可以较好定位的是A面，即被一条直线平均分割为两个长方形的那个面，与D面下方的一白面。
此两面特征较为明显，可以考虑作为推理的起点。
由Z字型法可以看到，以上所强调的两个特正面可以画个Z字，因此该两特征面是相对面，而根据相对面原理，我们可以知道，这两个面（即A面与白面）在空间图中能且只能看到一个。
因此，可以迅速排除C, D两个选项，因为这两个选项中，两个本是相对面的特征面同时出现了，而在逻辑上这是绝对不可能的。
本题关键是在A与B两个选项中纠结，因为我们已无法用Z字法排除了。
但，可以注意到，选项A与原图很像，在选项A中，A面的位置与原图一样，如果把原图的B面往内折，则可以得到一个与A选项空间图类似的结构。
行测纸盒折叠方法解题技巧
行测纸盒折叠方法解题技巧
在行测中，纸盒折叠方法经常出现在空间关系题或者折纸题中。
以下是一些解题技巧：
1.熟悉基本结构：了解常见的纸盒结构，例如长方体、立方体、正方形盒等。
熟悉这些结构可以帮助你快速理解题目中给出的折叠纸片在拼合成纸盒时的变换方式。
2.注意角度和方向：观察题目中给出的示意图或者折叠纸片的图形，注意线段的角度和方向。
通过细致观察，你可以找出图形中的对称性和平行关系，从而确定纸片在折叠时的方向和位置。
3.利用纸盒的关键特征：对于给定的纸片图形，找到关键特征，例如边长、角度等，并观察这些特征之间的关系。
这些特征可以是题目中给出的具体数值，或者通过图形上的比例关系来确定。
4.图形拆分和重叠：对于复杂的折叠纸片图形，可以尝试将其拆分成简单的几何图形，例如三角形、矩形等。
然后分析这些简单图形的拼合方式，最后再将它们合并成整体纸盒的形状。
5.反推和验证：当你完成了纸盒折叠的步骤，尝试反推回原始纸片的形状，以验证你的答案是否正确。
同时，还可以验证纸盒的各个面的长度、角度以及其他关键特征是否满足题目中的要求。
6.灵活运用数学知识：在解题过程中，可以适当运用数学知识，例如几何图形的性质、投影关系等。
灵活运用这些知识可以帮助你更好地理解和解决纸盒折叠问题。
总的来说，纸盒折叠方法的解题技巧主要包括熟悉基本结构、观察角度和方向、利用关键特征、图形拆分和重叠、反推和验证以及灵活运用数学知识。
通过不断练习和掌握这些技巧，你可以更加高效地解决行测中的纸盒折叠问题。