第四讲数学
第四讲印度与阿拉伯的数学

2007年9月
印度与阿拉伯的数学
2
一、印度数学
印度数学的发展可以划分为3个重要时期: Ⅰ雅利安人入侵以前的达罗毗荼人时期(约公元前
3000-前1400),史称河谷文化; Ⅱ吠陀时期(约公元前10世纪-前3世纪); Ⅲ悉檀多时期(5世纪-12世纪)。
第四讲 印度与阿拉伯的数学
印度数学
⒈古代《绳法经》 ⒉“巴克沙利手稿”与零号 ⒊“悉檀多”时期的印度 数学
阿拉伯数学
⒈阿拉伯的代数 ⒉阿拉伯的三角学与几何 学
2007年9月
印度与阿拉伯的数学
1
一、印度数学
公元前3000年左右,印度土著居民达罗毗荼人创造 了“哈拉帕文明”。大约到了公元前2000年中叶, 操印度语的游牧民族雅利安人入侵印度,征服了 达罗毗荼人,印度土著文化从此衰微不振。
2007年9月
印度与阿拉伯的数学
20
二、阿拉伯数学 2、主要成果
代数方面
《代数学》约1140年被英国彻斯特地方的罗伯特译 成拉丁文,作为一种标准的数学课本在欧洲行用 了数百年,引导了16世纪意大利数学家在三、四 次方程求解方面的突破。
2007年9月
印度与阿拉伯的数学
21
二、阿拉伯数学 2、主要成果
几何学方面
几何方面的工作主要是对希腊几何的翻译与保存, 并传给了欧洲。在评注《几何原本》的过程中, 对第五公设引起了注意。对非欧几何的诞生产生 了一定的影响。
(无理量概念,确定立体体积的穷竭原理)
2007年9月
印度与阿拉伯的数学
24
二、阿拉伯数学 3、主要思想方法
总结概括文献方法(观察法、实验法),逻辑思维 方法
数学文化第四讲 数学的魅力

*
一、渔网的几何规律
用数学方法可以证明,无论你用什么绳索织一片 网,无论你织一片多大的网,它的结点数(V),网眼 数(F),边数(E)都必定适合下面的公式:
V + F– E = 1
*
多面体的欧拉公式
• V + F– E =2
*
数学就有这样的本领,能够把看起来复杂 的事物变得简明,把看起来混乱的事物理出 规律。
*
• 1879年,一位英国律师肯泊在《美国数学杂志》上 发表论文,宣布证明了“四色猜想”。
• 但十一年后,一位叫希伍德的年轻人指出,肯泊的 证明中有严重错误。
*
• 一个看来简单,且似乎容易说清楚的问题,居然如此困难, 这引起了许多数学家的兴趣,体现了该问题的魅力。 • 实际上,对于地图着色来说,各个地区的形状和大小并不重要 ,重要的是它们的相互位置。 • 下图中的三个地图对地图着色来说都是等价的。从数学上看, 问题的实质在于地图的“拓扑结构”。
*
拉姆塞(Ramsay)理论
拉姆塞是位天才的英国科学家,只活 了26岁。在他去世的1930年,他发表了 一篇学术论文,其副产物就是所谓拉姆 塞理论。
• 在一个集会上,两个人或者彼此认识,或 者彼此不认识,拉姆塞得出结果是说,当 集会人数大于或等于6时,则必定有3个人 ,他们或者彼此者认识或者彼此都不认识 。6称为拉姆塞数,记r(3,3)。 • 进一步当集会人数大于或等于18时,则必 定有4个人,他们或者彼此都认识或者彼此 都不认识,用记号表示就是r(4,4)=18。
*
练习
• 向量组的秩 • 矩阵的秩 • 线性空间的维数
*
• 三角形有多种多样,“三角形三内角之和等 于180度”也是“变中有不变”的性质。 • 陈省身说“不好”是相对的,有层次的区别。 “变中有不变”也是有层次的。 • 我们在学习和科学研究中,要善于抓住“变 中有不变”的性质,要有这样的素养!
4、第四讲 四年级数学简便算法

第四讲四年级数学简便算法4―1、四年级加减混合运算(一)、加法运算定律①、加法交换律。
它是指两个数相加,交换加数的位置,其和不变。
现用字母a 和b分别表示两个加数,可以写成下面的形式:a +b = b + a②、加法结合律。
它是指三个数相加,再同第三个数相加;或者先把后两个数相加,再同第一个数相加,它们的和不变。
现用a、b、c分别表示三个加数,可以写成下面的形式:a +b +c = a +(b + c)(二)、加减法运算性质①、减法性质是指一个数分别减去两个数,等于从这个数里减去这两个数的和。
现用a、b、c表示被减数和减数,可以写成:a–b–c = a–(b + c)②、a + b–c = a – c + b③、a(b–c)= a + b–c④、a–b–c = a–c–b⑤、a–(b–c)= a–b + c = a + c–b这些运算定律和性质,可以看成是一些数学公式,则可从左到右顺着用,也可从右到左逆着用。
切注意:此时要求被减数不小于减数。
(三)、加减混合运算例题例4-1-1、计算下列各题:(a)572 + 159 + 28 (b)348–69 + 652(c)348 + 69 - 48 (d)827–129 - 271[思路分析]:上面各题是加减法混合运算,应根据数字的特点,综合运用加减法混合运算中可交换和结合的性质,先把一些数凑成整百、整千,从而使计算更加简便。
(a)、572 + 159 + 28= 572 + 28 + 159= 600 + 159= 759(b)、348–69 + 652= 348 + 652 - 69= 1000 - 69= 931(c)、348 + 69 -48= 348–48 + 69= 300 + 69= 369(d)、827 -129 -271= 827 -(129 +271)= 827 + 400= 427例4-1-2、计算下列各题:(a)627 -(186 + 327)(b)546 -(289 - 154)(c)281 +(719 - 588)[思路分析]:上面各题仍运用加减法混合运算的定律和性质,先把括号去掉,再把能凑成整百、整千的数交换结合到一起算,从而达到巧算的目的。
第四讲 数学归纳法证明不等式 知识归纳 课件(人教A选修4-5)

由(1)、(2)知,对任意n∈N+原命题成立.
[例 4]
1 设 0<a<1,定义 a1=1+a,an+1=a +a,求证: n
1 对一切正整数 n∈N+,有 1<an< . 1-a
[证明] 命题成立.
1 (1)当 n=1 时,a1>1,又 a1=1+a< , 1-a
(2)假设 n=k(k∈N+)时,命题成立, 1 即 1<ak< . 1-a ∴当 n=k+1 时,由递推公式,知 1 ak+1=a +a>(1-a)+a=1. k
1-a2 1 1 同时,ak+1=a +a<1+a= < , 1-a 1-a k 1 ∴当 n=k+1 时,命题也成立,即 1<ak+1< . 1-a 1 综合(1)、 (2)可知, 对一切正整数 n, 1<an< 有 . 1-a
点击下图进入阶段质量检测
[例3]
除.
用数学归纳法证明:n(n+1)(2n+1)能被6整
[证明](1)当n=1时,1×2×3显然能被6整除. (2)假设n=k时,命题成立, 即k(k+1)(2k+1)=2k3+3k2+k能被6整除.
当n=k+1时,(k+1)(k+2)(2k+3)=
2k3+3k2+k+6(k2+2k+1) 因为2k3+3k2+k,6(k2+2k+1)都能被6整除,所以2k3 +3k2+k+6(k2+2k+1)能被6整除,即当n=k+1时命题 成立.
tank+1α-tan α 1 = [ ][1+tan(k+1)α· α]-k tan tan α 1+tank+1α· α tan 1 = [tan(k+1)α-tan α]-k tan α tank+1α = -(k+1), tan α 所以当 n=k+1 时,等式也成立. 由(1)和(2)知,n≥2,n∈N+时等式恒成立.
初中数学复习第四讲——整式与分式
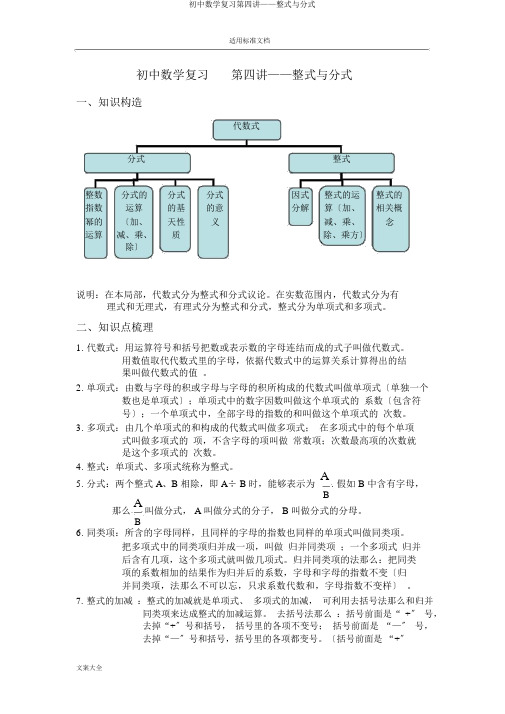
适用标准文档初中数学复习第四讲——整式与分式一、知识构造代数式分式整式整数分式的分式分式因式整式的运整式的指数运算的基的意分解算〔加、相关概幂的〔加、天性义减、乘、念运算减、乘、质除、乘方〕除〕说明:在本局部,代数式分为整式和分式议论。
在实数范围内,代数式分为有理式和无理式,有理式分为整式和分式,整式分为单项式和多项式。
二、知识点梳理1.代数式:用运算符号和括号把数或表示数的字母连结而成的式子叫做代数式。
用数值取代代数式里的字母,依据代数式中的运算关系计算得出的结果叫做代数式的值。
2.单项式:由数与字母的积或字母与字母的积所构成的代数式叫做单项式〔单独一个数也是单项式〕;单项式中的数字因数叫做这个单项式的系数〔包含符号〕;一个单项式中,全部字母的指数的和叫做这个单项式的次数。
3.多项式:由几个单项式的和构成的代数式叫做多项式;在多项式中的每个单项式叫做多项式的项,不含字母的项叫做常数项;次数最高项的次数就是这个多项式的次数。
4.整式:单项式、多项式统称为整式。
5.分式:两个整式 A、B 相除,即 A÷ B 时,能够表示为A. 假如 B 中含有字母,B那么A叫做分式, A 叫做分式的分子, B 叫做分式的分母。
B6.同类项:所含的字母同样,且同样的字母的指数也同样的单项式叫做同类项。
把多项式中的同类项归并成一项,叫做归并同类项;一个多项式归并后含有几项,这个多项式就叫做几项式。
归并同类项的法那么:把同类项的系数相加的结果作为归并后的系数,字母和字母的指数不变〔归并同类项,法那么不可以忘,只求系数代数和,字母指数不变样〕。
7.整式的加减:整式的加减就是单项式、多项式的加减,可利用去括号法那么和归并同类项来达成整式的加减运算。
去括号法那么:括号前面是“+〞号,去掉“+〞号和括号,括号里的各项不变号;括号前面是“—〞号,去掉“—〞号和括号,括号里的各项都变号。
〔括号前面是“+〞号,去掉括号不变号;括号前面是“—〞号,去掉括号都变号。
数学:第四讲《容斥原理》讲义

【例 4】(难度★★) (第 11 届保良局小学数学世界 邀请赛个人赛)针对 100 人做问 卷调查,结果有 28 人阅读 A 杂志;30 人读 B 杂志;42 人读 C 杂志;8 人同时阅读 A 与 B 杂 志;10 人同时阅读 A 与 C 杂志; 5 人同时阅读 B 与 C 杂志; 有 3 人同时阅读这三种杂志.请 问有多少人没有阅读上 述三种杂志中的任何一种? 【分析】28+30+42-8-10-5+3=80
堡又带了芝土蛋糕。问:三种都
带了的有几人?
【分析】
⑴24+28+26-12-9-14+5=48(人) ⑵如图,用K + 6圆表示带汉堡的 人,K 圆表示带鸡腿的人,K = 5 圆表示带芝士蛋糕的人。根据包 含排除法,总人数2带汉堡的人 数4带鸡腿的人数4带芝士蛋糕 的人数10带汉堡、鸡腿的人数22 带汉堡、芝士蛋糕的人数37带鸡 腿、芝士蛋糕的人数4三种都带 了的人数,即 10=(6 + 6 + 4) − (3 + 2 +1)三种都 带了的人数,得三种都带了的人 数为:4(人)。
只有红、蓝两种小旗的有 3 人, 那么这个班共有多少人? 【分析】如图,用3 + 3 =6圆表示 手中有红旗的,3 + 6 =9圆表示 手中有黄旗的,2 + 4 + 2 + 4 =12 圆表示手中有蓝旗的.如果用手 中有红旗的、有黄旗的与有蓝旗 的相加,发现手中只有红、黄两 种小旗的各重复计算了一次,应 减去,手中有三种颜色小旗的重 复计算了二次,也应减去,那么, 全班人数为:3 + 3 =63 + 6 =9 (人)
【例 7】(难度★★★★) 在一根长木棍上,有三种刻度线, 第一种刻度线将木棍分成十等 份;第二种将木棍分成十二等份; 第三种将木棍分成十五等份;如 果沿每条刻度线将木棍锯断,则 木棍总共被锯成多少段? 【分析】假设木棍长 60cm,则 沿第一种刻度线锯成的木棍每 段长b = 3,沿第二种刻度线锯成 的木棍每段长+,沿第三种刻度 线锯成的木棍每段长2S= 35 +。
第四讲 重点小学数学 盈亏问题

第四讲盈亏问题(一)把一定数量的物品平均分给若干对象,如果每个对象少分,则表示物品有剩余;如果每个对象多分,则表示物品不够分。
分物时会出现盈(有余)、亏(不足)或尽(恰好分完)三种情况,这类问题称为盈亏问题。
常用的几个公式:一盈一亏类:(盈数+亏数)÷两次分配数量差=分配对象的个数;×一盈一尽类:例1.6本。
例2.4粒,例3.7支。
例4.例5.2组。
例6.例7.4台;例8.20元。
这两种鱼每条的价格相差2元1角。
问:这两种鱼的单价各是多少?巩固提高1.将一批糖果分给幼儿园大班小朋友,如果没人分3粒,就剩余17粒;如果没人分5粒,就缺少13粒。
问:幼儿园大班小朋友有多少人?这批糖果一共有多少粒?2.学习分发学习工具,每班发10盒还剩14盒,每班发12盒还剩2盒。
学校把学习工具发给几个班级?一共有多少盒学习工具?3.小玲买7千克苹果,还差18元;如果买5千克苹果,还差2元。
问每千克苹果多少元?小玲带了多少元?4.某校学生参加劳动,先分成若干组,每组8人,后来把每组改成12人,因此少了2组。
问:参加劳动的学生共有多少人?5.用一根绳子绕树5圈正好,如果绕树4圈还多4尺。
问:树的周长是几尺?6.五(一)班同学去划船,若每条船坐6人,则少4个空位;若每条船坐5人,则有4人没有座位。
那么,一共租了几条船?五(一)班一共去了多少人?7.学生搬砖,如果每人搬4块,其中5人要搬2次;如果每人搬5块,就有2人没有砖可搬。
那么,搬砖的学生有多少人?一共有多少块转?8.每千克面粉比每千克大米贵8元,一顾客若买40千克大米还缺40元;若不买大米而买30千克面粉则还缺20元。
这位顾客带了多少元钱?9.某小学学生剩车去春游,如果每车坐65人,就有15人没有座位;如果每车多坐5人,恰好多余1辆车。
问:一共有几辆车?有多少学生去春游?10.学校新建了一栋宿舍楼,如果每间寝室住8人,则有22人没有床位;如果每间寝室住10人,又恰好空出3间寝室。
数学分析第四讲 实数系的6个定理的等价证明

(1) [ak1, bk1] [ak , bk ], k 1, 2,
(2)
lim
k
|
bk
ak
|
0
(3){[ak , bk ]}中每个区间都含有E的无穷多个点
由闭区间套定理存在唯一 [ak , bk ].
k 1
实数的连续不完备性讨论
根据
lim
n
an
lim
n
bn
,得到
0, N1 N * ,k N1 : ak
N2 N * ,k
N2
:
bk
0, N1 N * ,k N1 : ak +
N2 N * ,k N2 :
单调有 界定理
确界 定理
闭区间 套定理
柯西 收敛定理
列紧性 定理
有限覆 盖定理
聚点 定理
实数的连续不完备性讨论
定理:用闭区间套定理证明柯西收敛定理
证明充分性: 0, k N * ,n, m k : xm xn . 0, N k 1,m N : xm xN xN xm xN
用数列极限观点分析
实数集=有理数集+无理数集 有理数集在实数集稠密 无理数集在实数集稠密
著名数学家希尔伯特说:“无穷是人类最伟大的朋友,也是人类心 灵最宁静的敌人”说明极限是数学最重要的概念.
希尔伯特(David Hilbert, 1862-1943)德国数学家, 19世 纪和20世纪初最具影响力的数学家之一. 1900年在巴黎第二界国际 数学家大会上提出的23个数学问题(称希尔伯特问题),激发了整个 数学界的想象力. 现在这些问题约有一半已得到囿满解决. 其中第八 个问题,就是广为人知的“哥德巴赫猜想”他的杰出工作在整个数学 版图上留下了巨大显赫的名字:希尔伯特空间,希尔伯特丌等式, 希尔伯特算子,被尊为数学世界的亚历山大.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二教育
第四讲解简易方程
学法指导:
解稍复杂的方程,要先加以变形,变为较简单的简易方程。
变形常用的方法是:
1、运用乘法分配律,去掉括号。
2、两边是分数形式的方程,运用交叉相乘法,转化为不是分数形式的方程。
3、方程的两边都加上或减去相等的数或相等的式子,等式仍然成立,这是等式的性质。
利用这个性质可以化简方程。
4、方程的两边都乘以或除以相等的数或相等的式子(这些数与式子不能为0),这也是等式的性质。
利用这个性质也可以花间方程。
解方程的步奏要规范,求出得数后要简易检验。
