典型例题及答案
高中数学第十章概率典型例题(带答案)

高中数学第十章概率典型例题单选题1、“某彩票的中奖概率为1100”意味着( )A .购买彩票中奖的可能性为1100 B .买100张彩票能中一次奖 C .买100张彩票一次奖也不中 D .买100张彩票就一定能中奖 答案:A分析:根据概率的定义,逐项判定,即可求解.对于A 中,根据概率的定义,概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小,由某彩票的中奖概率为1100,可得购买彩票中奖的可能性为1100,所以A 正确;对于B 、C 中,买任何1张彩票的中奖率都是1100,都具有偶然性,可能中奖,还可能中奖多次,也可能不中奖,故B 、C 错误;对于D 选项、根据彩票总数目远大于100张,所以买100张也不一定中一次奖,故D 错误. 故选:A.2、北京2022年冬奥会新增了女子单人雪车、短道速滑混合团体接力、跳台滑雪混合团体、男子自由式滑雪大跳台、女子自由式滑雪大跳台、自由式滑雪空中技巧混合团体和单板滑雪障碍追逐混合团体等7个比赛小项,现有甲、乙两名志愿者分别从7个比赛小项中各任选一项参加志愿服务工作,且甲、乙两人的选择互不影响,那么甲、乙两名志愿者选择同一个比赛小项进行志愿服务工作的概率是( ) A .249B .649C .17D .27 答案:C分析:根据古典概型概率的计算公式直接计算.由题意可知甲、乙两名志愿者分别从7个比赛小项中各任选一项参加志愿服务工作共有7×7=49种情况, 其中甲、乙两名志愿者选择同一个比赛小项进行志愿服务工作共7种,所以甲、乙两名志愿者选择同一个比赛小项进行志愿服务工作的概率是749=17,故选:C.3、某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是()A.62%B.56%C.46%D.42%答案:C分析:记“该中学学生喜欢足球”为事件A,“该中学学生喜欢游泳”为事件B,则“该中学学生喜欢足球或游泳”为事件A+B,“该中学学生既喜欢足球又喜欢游泳”为事件A⋅B,然后根据积事件的概率公式P(A⋅B)=P(A)+P(B)−P(A+B)可得结果.记“该中学学生喜欢足球”为事件A,“该中学学生喜欢游泳”为事件B,则“该中学学生喜欢足球或游泳”为事件A+B,“该中学学生既喜欢足球又喜欢游泳”为事件A⋅B,则P(A)=0.6,P(B)=0.82,P(A+B)=0.96,所以P(A⋅B)=P(A)+P(B)−P(A+B)=0.6+0.82−0.96=0.46所以该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例为46%.故选:C.小提示:本题考查了积事件的概率公式,属于基础题.4、若随机事件A,B互斥,且P(A)=2−a,P(B)=3a−4,则实数a的取值范围为()A.(43,32]B.(1,32]C.(43,32)D.(12,43)答案:A分析:根据随机事件概率的范围以及互斥事件概率的关系列出不等式组,即可求解.由题意,知{0<P(A)<1 0<P(B)<1P(A)+P(B)≤1,即{0<2−a<10<3a−4<12a−2≤1,解得43<a≤32,所以实数a的取值范围为(43,32].故选:A.5、甲、乙两人投篮,投中的概率分别为0.6,0.7,若两人各投2次,则两人投中次数不等的概率是()A.0.6076B.0.7516C.0.3924D.0.2484答案:A分析:先求出两人投中次数相等的概率,再根据对立事件的概率公式可得两人投中次数不相等的概率.两人投中次数相等的概率P=0.42×0.32+C21×0.6×0.4×C21×0.7×0.3+0.62×0.72=0.3924,故两人投中次数不相等的概率为:1﹣0.3924=0.6076.故选:A.小提示:本题考查了对立事件的概率公式和独立事件的概率公式,属于基础题.6、下列各对事件中,不互为相互独立事件的是()A.掷一枚骰子一次,事件M“出现偶数点”;事件N“出现3点或6点”B.袋中有3白、2黑共5个大小相同的小球,依次有放回地摸两球,事件M“第一次摸到白球”,事件N“第二次摸到白球”C.袋中有3白、2黑共5个大小相同的小球,依次不放回地摸两球,事件M“第一次摸到白球”,事件N“第二次摸到黑球”D.甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,事件M“从甲组中选出1名男生”,事件N“从乙组中选出1名女生”答案:C分析:利用对立事件和相互独立事件的概念求解.解:对于选项A,事件M={2,4,6},事件N={3,6},事件MN={6},基本事件空间Ω={1,2,3,4,5,6},所以P(M)=36=12,P(N)=26=13,P(MN)=16=12×13,即P(MN)=P(N)P(M),因此事件M与事件N是相互独立事件;对于选项B,袋中有3白、2黑共5个大小相同的小球,依次有放回地摸两球,事件M“第一次摸到白球”,事件N“第二次摸到白球”,则事件M发生与否与N无关,同时,事件N发生与否与M无关,则事件M与事件N是相互独立事件;对于选项C,袋中有3白、2黑,5个大小相同的小球,依次不放回地摸两球,事件M“第一次摸到白球”,事件N “第二次摸到黑球”, 则事件M 发生与否和事件N 有关,故事件M 和事件N 与不是相互独立事件;对于选项D ,甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲、乙两组中各选1名同学参加演讲比赛,事件M “从甲组中选出1名男生”,事件N “从乙组中选出1名女生”,则事件M 发生与否与N 无关,同时,事件N 发生与否与M 无关,则事件M 与事件N 是相互独立事件; 故选:C.7、2021年12月9日,中国空间站太空课堂以天地互动的方式,与设在北京、南宁、汶川、香港、澳门的地面课堂同步进行.假设香港、澳门参加互动的学生人数之比为5:3,其中香港课堂女生占35,澳门课堂女生占13,若主持人向这两个分课堂中的一名学生提问,则该学生恰好为女生的概率是( ) A .18B .38C .12D .58答案:C分析:利用互斥事件概率加法公式计算古典概型的概率即可得答案.解:因为香港、澳门参加互动的学生人数之比为5:3,其中香港课堂女生占35,澳门课堂女生占13, 所以香港女生数为总数的58×35=38,澳门女生数为总数的38×13=18,所以提问的学生恰好为女生的概率是38+18=12. 故选:C.8、某学校共有教职工120人,对他们进行年龄结构和受教育程度的调查,其结果如下表:60% B .该教职工具有研究生学历的概率超过50% C .该教职工的年龄在50岁以上的概率超过10%D .该教职工的年龄在35岁及以上且具有研究生学历的概率超过10% 答案:D分析:根据表中数据,用频率代替概率求解.A.该教职工具有本科学历的概率p=75120=58=62.5%>60%,故错误;B.该教职工具有研究生学历的概率p=45120=38=37.5%<50%,故错误;C.该教职工的年龄在50岁以上的概率p=10120=112≈8.3%<10%,故错误;D.该教职工的年龄在35岁及以上且具有研究生学历的概率p=15120=18=12.5%>10%,故正确.小提示:本题主要考查概率的求法,还考查了分析求解问题的能力,属于基础题.多选题9、下列有关古典概型的说法中,正确的是()A.试验的样本空间的样本点总数有限B.每个事件出现的可能性相等C.每个样本点出现的可能性相等D.已知样本点总数为n,若随机事件A包含k个样本点,则事件A发生的概率P(A)=kn答案:ACD分析:根据古典概型的定义逐项判断即可.由古典概型概念可知:试验的样本空间的样本点总数有限;每个样本点出现的可能性相等.故AC正确;每个事件不一定是样本点,可能包含若干个样本点,所以B不正确;根据古典概型的概率计算公式可知D正确.故选:ACD10、某学校为调查学生迷恋电子游戏情况,设计如下调查方案,每个被调查者先投掷一枚骰子,若出现向上的点数为3的倍数,则如实回答问题“投掷点数是不是奇数?”,反之,如实回答问题“你是不是迷恋电子游戏?”.已知被调查的150名学生中,共有30人回答“是”,则下列结论正确的是()A.这150名学生中,约有50人回答问题“投掷点数是不是奇数?”B.这150名学生中,必有5人迷恋电子游戏C.该校约有5%的学生迷恋电子游戏D.该校约有2%的学生迷恋电子游戏答案:AC分析:先由题意计算出回答问题一的人数50人,再计算出回答问题一“是”的人数25人,故可得到回答问题二“是”的人数5人,最后逐一分析四个选项即可.由题意可知掷出点数为3的倍数的情况为3,6,故掷出点数为3的倍数的概率为13,故理论上回答问题一的人数为150×13=50人.掷出点数为奇数的概率为12,理论上回答问题一的50人中有25人回答“是”,故回答问题二的学生中回答“是”的人数为30-25=5人.对于A, 抽样调查的这150名学生中,约有50人回答问题一,故A正确.对于B, 抽样调查的这150名学生中,约有5人迷恋电子游戏,“必有”过于绝对,故B错.对于C,抽样调查的150名学生中,50名学生回答问题一,故有100名学生回答问题二,有5名学生回答“是”,故该校迷恋电子游戏的学生约为5100=5%,故C正确.对于D,由C可知该校迷恋电子游戏的学生约为5100=5%,故D错.故选:AC.11、不透明的口袋内装有红色、绿色和蓝色卡片各2张,一次任意取出2张卡片,则与事件“2张卡片都为红色”互斥而不对立的事件有()A.2张卡片都不是红色B.2张卡片恰有一张红色C.2张卡片至少有一张红色D.2张卡片都为绿色答案:ABD分析:列举出所有情况,然后再利用互斥事件和对立事件的定义判断.解:6张卡片中一次取出2张卡片的所有情况有:“2张都为红色”、“2张都为绿色”、“2张都为蓝色”、“1张为红色1张为绿色”、“1张为红色1张为蓝色”、“1张为绿色1张为蓝色”,选项中给出的四个事件中与“2张都为红色”互斥而非对立的事件是:“2张都不是红色”,“2张恰有一张红色”,“2张都为绿色”,其中“2张至少一张为红色”包含事件“2张都为红色”,二者并非互斥.故选:ABD.12、设A,B分别为随机事件A,B的对立事件,已知0<P(A)<1,0<P(B)<1,则下列说法正确的是()A.P(B|A)+P(B|A)=1B.P(B|A)+P(B|A)=0C.若A,B是相互独立事件,则P(A|B)=P(A)D.若A,B是互斥事件,则P(B|A)=P(B)答案:AC分析:计算得AC正确;当A,B是相互独立事件时,P(B|A)+P(B|A)=2P(B)≠0,故B错误;因为A,B 是互斥事件,得P(B|A)=0,而P(B)∈(0,1),故D错误.解:P(B|A)+P(B|A)=P(AB)+P(AB)P(A)=P(A)P(A)=1,故A正确;当A,B是相互独立事件时,则P(B|A)+P(B|A)=2P(B)≠0,故B错误;因为A,B是相互独立事件,则P(AB)=P(A)P(B),所以P(A|B)=P(AB)P(B)=P(A),故C正确;因为A,B是互斥事件,P(AB)=0,则根据条件概率公式P(B|A)=0,而P(B)∈(0,1),故D错误.故选:AC.13、袋中有红球3个,白球2个,黑球1个,从中任取2个,则互斥的两个事件是()A.至少有一个白球与都是白球B.恰有一个红球与白、黑球各一个C.至少一个白球与至多有一个红球D.至少有一个红球与两个白球答案:BD分析:根据互斥事件的定义和性质判断.袋中装有红球3个、白球2个、黑球1个,从中任取2个,在A中,至少有一个白球和都是白球两个事件能同时发生,不是互斥事件,故A不成立.在B中,恰有一个红球和白、黑球各一个不能同时发生,是互斥事件,故B成立;在C中,至少一个白球与至多有一个红球,能同时发生,故C不成立;在D中,至少有一个红球与两个白球两个事件不能同时发生,是互斥事件,故D成立;故选:BD.小提示:本题考查互斥事件的判断,根据两个事件是否能同时发生即可判断,是基础题. 填空题14、甲、乙两队进行篮球决赛,采取三场二胜制(当一队赢得二场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以2:1获胜的概率是_____. 答案:0.3解析:甲队以2:1获胜的是指甲队前两场比赛中一胜一负,第三场比赛甲胜,利用独立事件的概率乘法公式和概率的加法公式能求出甲队以2:1获胜的概率. 甲队的主客场安排依次为“主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立, 甲队以2:1获胜的是指甲队前两场比赛中一胜一负,第三场比赛甲胜, 则甲队以2:1获胜的概率是:P =0.6×0.5×0.6+0.4×0.5×0.6=0.3. 所以答案是:0.3.小提示:本题考查概率的求法,考查相互独立事件概率乘法公式和互斥事件概率加法公式等基础知识,考查运算求解能力,是基础题.15、已知事件A ,B ,C 相互独立,若P (AB )=16,P(BC)=14,P(ABC)=112,则P (A )=______. 答案:13分析:根据相互独立事件的概率公式,列出P (A ),P (B ),P(C),P(B)的等式,根据对立逐一求解,可求出P (A )的值.根据相互独立事件的概率公式,可得{ P (A )P (B )=16P(B)P (C )=14P (A )P (B )P(C)=112,所以P (A )=13. 所以答案是:13.16、在一个口袋中有大小和质地相同的4个白球和3个红球,若不放回的依次从口袋中每次摸出一个球,直到摸出2个红球就停止,则连续摸4次停止的概率等于______.答案:935分析:根据题设写出基本事件,再应用互斥事件加法公式求概率.由题意知,连续依次摸出的4个球分别是:白白红红,白红白红,红白白红共3种情况,第一种摸出“白白红红”的概率为47×36×35×12=335,第二种摸出“白红白红”的概率为47×36×35×12=335,第三种摸出“红白白红”的概率为37×46×35×12=335,所以连续摸4次停止的概率等于935.所以答案是:935解答题17、数学兴趣小组设计了一份“你最喜欢的支付方式”的调查问卷(每人必选且只能选一种支付方式),在某商场随机调查了部分顾客,并将统计结果绘制成如下所示的两幅不完整的统计图,请结合图中所给的信息解答下列问题:(1)将条形统计图补充完整,在扇形统计图中表示“现金”支付的扇形圆心角的度数为多少?(2)若之前统计遗漏了15份问卷,已知这15份问卷都是采用“支付宝”进行支付,问重新统计后的众数所在的分类与之前统计的情况是否相同,并简要说明理由;(3)在一次购物中,嘉嘉和琪琪随机从“微信,支付宝,银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.答案:(1)条形统计图见解析,90∘;(2)不同,理由见解析;(3)13.分析:(1)由两幅图可知,用现金、支付宝、其他支付共有人数110人,所占比例为1-15%-30%=55%,可得共调查了多少人,再根据用银行卡、微信支付的百分比可得答案(2)根据原数据的众数所在的分类为微信,加上遗漏的15份问卷后,数据的众数所在的分类为微信、支付宝可得答案;(3)将微信记为A 、支付宝记为B 、银行卡记为C ,画出树状图根据古典概型概率计算公式可得答案. (1)由条形统计图可知,用现金、支付宝、其他支付共有人数110人, 所占比例为1-15%-30%=55%,所以共调查了1100.55=200人,所以用银行卡支付的人有200×0.15=30人,用微信支付的人有200×0.3=60人, 用现金支付所占比例为50200=0.25,所以0.25×360∘=90∘,在扇形统计图中表示“现金”支付的扇形圆心角的度数为90°,补全统计图如图所示:(2)重新统计后的众数所在的分类与之前统计的情况不同,理由如下:原数据的众数所在的分类为微信,而加上遗漏的15份问卷后,数据的众数所在的分类为微信、支付宝. (3)将微信记为A 、支付宝记为B 、银行卡记为C ,画树状图如下:∵共有9种等可能的结果,其中两人恰好选择同一种支付方式的有3种, ∴两人恰好选择同一种支付方式的概率为39=13.18、某田径队有三名短跑运动员,根据平时训练情况统计甲、乙、丙三人100米跑(互不影响)的成绩在13s 内(称为合格)的概率分别为25,,13.若对这三名短跑运动员的100跑的成绩进行一次检测,则求:(Ⅰ)三人都合格的概率;34(Ⅱ)三人都不合格的概率;(Ⅲ)出现几人合格的概率最大.答案:(Ⅰ)110;(Ⅱ)110;(Ⅲ)1人. 分析:记甲、乙、丙三人100米跑成绩合格分别为事件A ,B ,C ,显然事件A ,B ,C 相互独立,则P(A)=25,P(B)=34,P(C)=13,从而根据不同事件的概率求法求得各小题.记甲、乙、丙三人100米跑成绩合格分别为事件A ,B ,C ,显然事件A ,B ,C 相互独立,则P(A)=25,P(B)=34,P(C)=13 设恰有k 人合格的概率为P k (k =0,1,2,3).(Ⅰ)三人都合格的概率:P 3=P(ABC)=P(A)⋅P(B)⋅P(C)=25×34×13=110(Ⅱ)三人都不合格的概率:P 0=P(ABC)=P(A)⋅P(B)⋅P(C)=35×14×23=110.(Ⅲ)恰有两人合格的概率:P 2=P(ABC)+P(ABC)+P(ABC)=25×34×23+25×14×13+35×34×13=2360. 恰有一人合格的概率:P 1=1−P 0−P 2−P 3=1−110−2360−110=2560=512.因为512>2360>110,所以出现1人合格的概率最大.。
初中物理功、功率、机械效率例题及详细解析

初中物理功、功率、机械效率例题及详细解析【典型例题】类型一、基础知识1、下面情况中,人对物体做功的是()A. 举重运动员举着杠铃不动B. 人用力却没有把重物提起C. 某同学提着水桶在水平路面匀速行走D. 旅客提着行李走上楼梯【思路点拨】本题要抓住做功的两个必要因素:1.作用在物体上的力;2.物体在力的方向上通过的距离;二者缺一不可。
【答案】D【解析】A、B均属于“不动无功”型,有力作用但没通过距离;C属于“劳而无功”型,桶运动方向与施力方向垂直;D具备做功的两个必要因素,人对行李施力,行李沿拉力方向有移动距离,D选项中人对行李箱用向上的力,并且在力的方向上移动了距离,所以人对物体做了功。
【总结升华】做功要满足的两个要素是:作用在物体上的力;在力的方向上通过的距离。
举一反三:【变式】(多选)小车重200N,人用30N的水平力推小车沿水平路面匀速前进50m的过程中,下列判断正确的是()A.重力没做功B.人对车做功10000JC.人对车做功1500J D.小车受到的阻力是230N【答案】AC2、某人用50N的力,将重30N的铅球抛到7m远处,这个人对铅球做的功为()A、350JB、210JC、0D、无法计算【思路点拨】人推铅球,对铅球施加了力,并且铅球在该力的方向上移动了距离,根据功的公式W=Fs分析判断。
【答案】D【解析】铅球的运动可以分为两个阶段:第一个阶段是人推铅球,第二个阶段是铅球在空中飞行。
在第一个阶段人用力推动铅球,对铅球做功;在第二个阶段,铅球离开了人,人不再对铅球做功。
注意:在第一个阶段,在人推力的作用下,铅球移动了一段距离,但这个距离不是7m;具体是多少,题中未给出,无法判断。
【总结升华】本题考查了学生对功的公式的掌握和运用,关键是掌握做功的两个必要条件(一是力,二是在力的方向上移动的距离)。
举一反三:【变式】(2015•无锡)现有30包大米,总质量为150kg,小明想尽快将它们搬上10m高处的库房,如图为小明可以提供的用于搬动物体的功率与被搬运物体质量之间的关系图象,由图可知他可以提供的最大功率为_____W;为尽可能快地将大米搬上库房,他每次应搬_____包,若每次下楼时间是上楼时间的一半,则他最快完成搬运任务并返回原地所用的时间是_____s。
牛顿运动定律 典型例题 参考答案

牛顿运动定律典型例题参考答案一、连接体问题(整体法与隔离法):1.二体连接问题例题1:F=(M+m)g F=(M+m)g F=(M+m)g F=(M+m)g例题2:例题3:2.多体连接问题:例题4:例题5:二、 超失重问题:例题1:BC例题2:A 例题3:C 例题4:A例题5:D三、 等环境问题(力的质量分配原则):例题1.例题2.D四、 临界值问题: 例题1. 解析:(1)ma sin N cos T =α-αmg cos N sin T =α+α当g 31a =时,N=68.4(N ) T=77.3(N ) (2) 若N=0,则有'm a cos T =αm g sin T =α )s /m (17g 3gctg 'a ==α=例题2.五、 瞬时值问题:例题1:解析:分析物体在某一时刻的瞬时加速度,关键是分析瞬时前后的受力情况及运动状态,再由牛顿第二定律求出瞬时加速度。
此类问题应注意两种模型的建立。
先分析剪断细线前两个物体的受力如图2,据平衡条件求出绳或弹簧上的弹力。
可知,F mg 2=,F F mg mg 122=+='。
剪断细线后再分析两个物体的受力示意图,如图2,绳中的弹力F 1立即消失,而弹簧的弹力不变,找出合外力据牛顿第二定律求出瞬时加速度,则图2剪断后m 1的加速度大小为2g ,方向向下,而m 2的加速度为零。
例题2:C例题3,D 例题4: (a=gsinθ ,a=gtanθ ) 例题5、BD 六、 分离问题:例题1:例题2:设物体与平板一起向下运动的距离为x 时,物体受重力mg ,弹簧的弹力F=kx 和平板的支持力N 作用。
据牛顿第二定律有:mg-kx-N=ma 得N=mg-kx-ma ,当N=0时,物体与平板分离,所以此时ka g m x )(-= 因为221at x =,所以kaa g m t )(2-= 例题3:七、 相对滑动问题:例题1:例题2:BC 例题3:ABC例题4:例题5:例题6:例题7:八、 传送带问题:例题1:D例题2:解析: 物体放上传送带以后,开始一段时间,其运动加速度2m/s 10cos sin =+=m mg mg a θμθ。
典型例题(有答案)
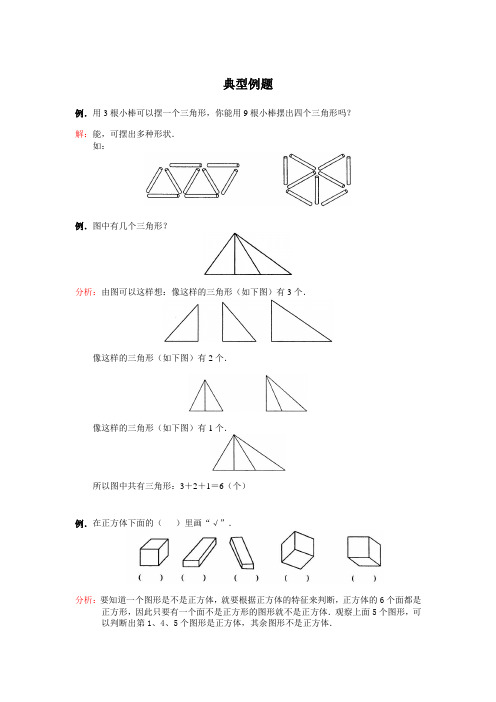
典型例题
例.用3根小棒可以摆一个三角形,你能用9根小棒摆出四个三角形吗?
解:能,可摆出多种形状.
如:
例.图中有几个三角形?
分析:由图可以这样想:像这样的三角形(如下图)有3个.
像这样的三角形(如下图)有2个.
像这样的三角形(如下图)有1个.
所以图中共有三角形:3+2+1=6(个)
例.在正方体下面的()里画“√”.
分析:要知道一个图形是不是正方体,就要根据正方体的特征来判断,正方体的6个面都是正方形,因此只要有一个面不是正方形的图形就不是正方体.观察上面5个图形,可以判断出第1、4、5个图形是正方体,其余图形不是正方体.
解:
例.数一数下面的图(1)中有多少个三角形?
分析:先观察图,从图中很容易看出上面有1个三角形,中间有1个三角形,下面左、右两边各有一个三角形,合起来共有4个小三角形,如图(2)所示.
假如把中间三角形的三条边去掉,那么图形就变成了一个大三角形,如图(3)所示.因此,图中就有小三角形4个,大三角形1个,合起来是5个三角形.
解:此图形中有5个三角形.
例.仔细观察小松鼠在几个长方形中.
分析:这样想:小松鼠所在的长方形有以下几种形状:
所以:小松鼠在4个长方形中.
解:小松鼠在4个长方形中.
例.先剪三张正方形纸片,如图所示,再用这三张正方形纸片拼出不同的图形.
分析与参考答案:可以拼出的图形很多,下面是其中的几种:。
向心力典型例题(附答案详解)

向心力典型例题(附答案详解)一、选择题【共12道小题】1、如图6-7-7所示,半径为r的圆筒,绕竖直中心轴OO′转动,小物块a靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ,现要使a不下滑,则圆筒转动的角速度ω至少为()图6-7-7A. B. C. D.您的答案:参考答案与解析:解析:要使a不下滑,则a受筒的最大静摩擦力作用,此力与重力平衡,筒壁给a的支持力提供向心力,则N=mrω2,而f m=mg=μN,所以mg=μmrω2,故.所以A、B、C均错误,D正确.答案:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用2、下面关于向心力的叙述中,正确的是()A.向心力的方向始终沿着半径指向圆心,所以是一个变力B.做匀速圆周运动的物体,除了受到别的物体对它的作用外,还一定受到一个向心力的作用C.向心力可以是重力、弹力、摩擦力中的某个力,也可以是这些力中某几个力的合力,或者是某一个力的分力D.向心力只改变物体速度的方向,不改变物体速度的大小您的答案:参考答案与解析:解析:向心力是按力的作用效果来命名的,它可以是物体受力的合力,也可以是某一个力的分力,因此,在进行受力分析时,不能再分析向心力.向心力时刻指向圆心与速度方向垂直,所以向心力只改变速度的方向,不改变速度的大小,即向心力不做功.答案:ACD主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用3、关于向心力的说法,正确的是()A.物体由于做圆周运动而产生了一个向心力B.向心力不改变圆周运动物体速度的大小C.做匀速圆周运动的物体其向心力即为其所受的合外力D.做匀速圆周运动的物体其向心力大小不变您的答案:参考答案与解析:解析:向心力并不是物体受到的一个特殊力,它是由其他力沿半径方向的合力或某一个力沿半径方向的分力提供的.因为向心力始终与速度方向垂直,所以向心力不会改变速度的大小,只改变速度的方向.当质点做匀速圆周运动时,向心力的大小保持不变.答案:BCD主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用4、在光滑水平面上相距20 cm的两点钉上A、B两个钉子,一根长1 m的细绳一端系小球,另一端拴在A钉上,如图6-7-8所示.已知小球质量为0.4 kg,小球开始以2 m/s的速度做水平匀速圆周运动,若绳所能承受的最大拉力为4 N,则从开始运动到绳拉断历时为()图6-7-8A.2.4π sB.1.4π sC.1.2π sD.0.9π s您的答案:参考答案与解析:解析:当绳子拉力为4 N时,由F=可得r=0.4 m.小球每转半个周期,其半径就减小0.2 m,由分析知,小球分别以半径为1 m,0.8 m和0.6 m各转过半个圆周后绳子就被拉断了,所以时间为t==1.2π s.答案:C主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用5、如图6-7-9所示,质量为m的木块,从半径为r的竖直圆轨道上的A点滑向B点,由于摩擦力的作用,木块的速率保持不变,则在这个过程中()图6-7-9A.木块的加速度为零B.木块所受的合外力为零C.木块所受合外力大小不变,方向始终指向圆心D.木块所受合外力的大小和方向均不变您的答案:参考答案与解析:解析:木块做匀速圆周运动,所以木块所受合外力提供向心力.答案:C主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用6、甲、乙两名溜冰运动员,M甲=80 kg,M乙=40 kg,面对面拉着弹簧秤做圆周运动的溜冰表演,如图6-7-9所示,两个相距0.9 m,弹簧秤的示数为9.2 N,下列判断正确的是()图6-7-9A.两人的线速度相同,约为40 m/sB.两人的角速度相同,为6 rad/sC.两人的运动半径相同,都是0.45 mD.两人的运动半径不同,甲为0.3 m,乙为0.6 m您的答案:参考答案与解析:解析:甲、乙两人绕共同的圆心做圆周运动,他们间的拉力互为向心力,他们的角速度相同,半径之和为两人的距离.设甲、乙两人所需向心力为F向,角速度为ω,半径分别为r甲、r乙.则F向=M甲ω2r甲=M乙ω2r乙=9.2 N ①r甲+r乙=0.9 m ②由①②两式可解得只有D正确答案:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用7、如图6-7-6所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,下列说法正确的是()图6-7-6A.物体所受弹力增大,摩擦力也增大B.物体所受弹力增大,摩擦力减小C.物体所受弹力减小,摩擦力也减小D.物体所受弹力增大,摩擦力不变您的答案:参考答案与解析:解析:物体在竖直方向上受重力G与摩擦力F,是一对平衡力,在向心力方向上受弹力F N.根据向心力公式,可知F N=mω2r,当ω增大时,F N增大,所以应选D.答案:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用8、用细绳拴住一球,在水平面上做匀速圆周运动,下列说法中正确的是()A.当转速不变时,绳短易断B.当角速度不变时,绳短易断C.当线速度不变时,绳长易断D.当周期不变时,绳长易断您的答案:参考答案与解析:解析:由公式a=ω2R=知,当角速度(转速)不变时绳长易断,故A、B 错误.周期不变时,绳长易断,故D正确.由,当线速度不变时绳短易断,C错.答案:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用9、如图6-7-9,质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块的速率不变()图6-7-9A.因为速率不变,所以木块的加速度为零B.木块下滑的过程中所受的合外力越来越大C.木块下滑过程中的摩擦力大小不变D.木块下滑过程中的加速度大小不变,方向时刻指向球心您的答案:参考答案与解析:解析:木块做匀速圆周运动,所受合外力大小恒定,方向时刻指向圆心,故选项A、B不正确.在木块滑动过程中,小球对碗壁的压力不同,故摩擦力大小改变,C错.答案:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用10、如图6-7-10所示,在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M的两球,两球用轻细线连接.若M>m,则()图6-7-10A.当两球离轴距离相等时,两球相对杆不动B.当两球离轴距离之比等于质量之比时,两球相对杆都不动C.若转速为ω时,两球相对杆都不动,那么转速为2ω时两球也不动D.若两球相对杆滑动,一定向同一方向,不会相向滑动您的答案:参考答案与解析:解析:由牛顿第三定律可知M、m间的作用力相等,即F M=F m,F M=Mω2r M,F m=mω2r m,所以若M、m不动,则r M∶r m=m∶M,所以A、B不对,C对(不动的条件与ω无关).若相向滑动,无力提供向心力,D对.答案:CD主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用11、一物体以4m/s的线速度做匀速圆周运动,转动周期为2s,则物体在运动过程的任一时刻,速度变化率的大小为()A.2m/s2B.4m/s2C.0D.4π m/s2您的答案:参考答案与解析:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用12、在水平路面上安全转弯的汽车,向心力是()A.重力和支持力的合力B.重力、支持力和牵引力的合力C.汽车与路面间的静摩擦力D.汽车与路面间的滑动摩擦力您的答案:参考答案与解析:C主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用二、非选择题【共3道小题】1、如图6-7-5所示,半径为R的半球形碗内,有一个具有一定质量的物体A,A与碗壁间的动摩擦因数为μ,当碗绕竖直轴OO′匀速转动时,物体A刚好能紧贴在碗口附近随碗一起匀速转动而不发生相对滑动,求碗转动的角速度.图6-7-5错题收藏参考答案与解析:思路分析:物体A随碗一起转动而不发生相对滑动,物体做匀速圆周运动的角速度ω就等于碗转动的角速度ω.物体A做匀速圆周运动所需的向心力方向指向球心O,故此向心力不是重力而是由碗壁对物体的弹力提供,此时物体所受的摩擦力与重力平衡.解析:物体A做匀速圆周运动,向心力:F n=mω2R而摩擦力与重力平衡,则有μF n=mg即F n=由以上两式可得:mω2R=即碗匀速转动的角速度为:ω=.答案:主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用2、汽车沿半径为R的水平圆跑道行驶,路面作用于车的摩擦力的最大值是车重的分1[]10式,要使汽车不致冲出圆跑道,车速最大不能超过多少?错题收藏参考答案与解析:解析:跑道对汽车的摩擦力提供向心力,,所以要使汽车不致冲出圆跑道,车速最大值为v=.答案:车速最大不能超过主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用3、一质量m=2 kg的小球从光滑斜面上高h=3.5 m处由静止滑下,斜面的底端连着一个半径R=1 m 的光滑圆环(如图6-7-15所示),则小球滑至圆环顶点时对环的压力为_____________,小球至少应从多高处静止滑下才能通过圆环最高点,h min=_________(g=10 m/s2).图6-7-16错题收藏参考答案与解析:解析:①设小球滑至圆环顶点时速度为v1,则mgh=mg·2R+F n+mg=得:F n=40 N②小球刚好通过最高点时速度为v2,则mg=又mgh′=mg2R+得h′=2.5R答案:40 N;2.5R主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用。
定积分典型例题20例标准答案

定积分典型例题20例答案例1 求33322321lim(2)n n n n n®¥+++.分析 将这类问题转化为定积分主要是确定被积函数和积分上下限.若对题目中被积函数难以想到,可采取如下方法:先对区间[0,1]n 等分写出积分和,再与所求极限相比较来找出被积函数与积分上下限.找出被积函数与积分上下限.解 将区间[0,1]n 等分,则每个小区间长为1i x nD =,然后把2111n n n =×的一个因子1n 乘入和式中各项.于是将所求极限转化为求定积分.即入和式中各项.于是将所求极限转化为求定积分.即33322321lim (2)n n n n n ®¥+++=333112lim ()n n n n nn ®¥+++=13034xdx =ò.例2 2202x x dx -ò=_________.解法1 由定积分的几何意义知,2202x x dx -ò等于上半圆周22(1)1x y -+= (0y ³) 与x 轴所围成的图形的面积.故2202x x dx -ò=2p. 解法2 本题也可直接用换元法求解.令1x -=sin t (22t pp-££),则,则222x x dx -ò=2221sin cos t tdt pp --ò=22021sin cos t tdt p-ò=2202cos tdt pò=2p例3 (1)若22()x t x f x e dt -=ò,则()f x ¢=___;(2)若0()()xf x xf t dt =ò,求()f x ¢=___.分析 这是求变限函数导数的问题,利用下面的公式即可这是求变限函数导数的问题,利用下面的公式即可()()()[()]()[()]()v x u x d f t dt f v x v x f u x u x dx ¢¢=-ò.解 (1)()f x ¢=422x x xee---;(2) 由于在被积函数中x 不是积分变量,故可提到积分号外即0()()xf x x f t dt =ò,则可得可得()f x ¢=()()xf t dt xf x +ò.例4 设()f x 连续,且31()x f t dt x -=ò,则(26)f =_________.解 对等式310()x f t dt x -=ò两边关于x 求导得求导得32(1)31f x x -×=,故321(1)3f x x-=,令3126x -=得3x =,所以1(26)27f =.例5 函数11()(3)(0)xF x dt x t =->ò的单调递减开区间为_________.解 1()3F x x ¢=-,令()0F x ¢<得13x>,解之得109x <<,即1(0,)9为所求.为所求. 例6 求0()(1)arctan xf x t tdt =-ò的极值点.的极值点. 解 由题意先求驻点.于是()f x ¢=(1)arctan x x -.令()f x ¢=0,得1x =,0x =.列表如下:如下: 故1x =为()f x 的极大值点,0x =为极小值点.为极小值点. 例7 已知两曲线()y f x =与()y g x =在点(0,0)处的切线相同,其中处的切线相同,其中2arcsin 0()xt g x e dt -=ò,[1,1]x Î-,试求该切线的方程并求极限3lim ()n nf n ®¥.分析 两曲线()y f x =与()y g x =在点(0,0)处的切线相同,隐含条件(0)(0)f g =,(0)(0)f g ¢¢=.解 由已知条件得由已知条件得2(0)(0)0tf g e dt -===ò,且由两曲线在(0,0)处切线斜率相同知处切线斜率相同知2(arcsin )2(0)(0)11x x e f g x-=¢¢===-.故所求切线方程为y x =.而.而3()(0)3lim ()lim33(0)330n n f f n nf f n n®¥®¥-¢=×==-.例8 求 22sin lim(sin )x x x tdt t t t dt®-òò;分析 该极限属于型未定式,可用洛必达法则.型未定式,可用洛必达法则. 解 22000sin lim (sin )x x xtdtt t t dt ®-òò=2202(sin )lim(1)(sin )x x x x x x ®-××-=220()(2)lim sin x x x x ®-×-=304(2)lim 1cos x x x ®-×- =2012(2)lim sin x x x®-×=0.注 此处利用等价无穷小替换和多次应用洛必达法则.此处利用等价无穷小替换和多次应用洛必达法则.x (,0)-¥(0,1)1 (1,)+¥()f x ¢-+-例9 试求正数a 与b ,使等式2021lim1sin xx t dt x b x a t®=-+ò成立.成立.分析 易见该极限属于型的未定式,可用洛必达法则. 解 20201lim sin x x t dt x b x a t ®-+ò=220lim 1cos x x a x b x ®+-=22001lim lim 1cos x x x b x a x ®®×-+201lim 11cos x x b xa ®==-,由此可知必有0lim(1cos )0x b x ®-=,得1b =.又由.又由 2012lim11cos x x xaa®==-,得4a =.即4a =,1b =为所求.为所求. 例10 设sin 20()sin xf x t dt =ò,34()g x x x =+,则当0x ®时,()f x 是()g x 的(的(). A .等价无穷小..等价无穷小. B .同阶但非等价的无穷小..同阶但非等价的无穷小. C .高阶无穷小..高阶无穷小.D .低阶无穷小. 解法1 由于由于 22300()sin(sin )cos lim lim ()34x x f x x x g x x x ®®×=+ 2200cos sin(sin )lim lim 34x x x x x x ®®=×+ 22011lim 33x x x ®==. 故()f x 是()g x 同阶但非等价的无穷小.选B .解法2 将2sin t 展成t 的幂级数,再逐项积分,得到的幂级数,再逐项积分,得到sin223370111()[()]sin sin 3!342x f x t t dt x x =-+=-+ò,则344340001111sin (sin )sin ()1342342lim lim lim ()13x x x x x x f xg x x x x ®®®-+-+===++.例11 计算21||x dx -ò.分析 被积函数含有绝对值符号,应先去掉绝对值符号然后再积分.解 21||x dx -ò=0210()x dx xdx --+òò=220210[][]22x x --+=52.注 在使用牛顿-莱布尼兹公式时在使用牛顿-莱布尼兹公式时,,应保证被积函数在积分区间上满足可积条件.如应保证被积函数在积分区间上满足可积条件.如 33222111[]6dx x x --=-=ò,则是错误的.错误的原因则是由于被积函数21x 在0x =处间断且在被积区间内无界积区间内无界. .例12 设()f x 是连续函数,且1()3()f x x f t dt =+ò,则()________f x =.分析 本题只需要注意到定积分()baf x dx ò是常数(,a b 为常数).解 因()f x 连续,()f x 必可积,从而1()f t dt ò是常数,记1()f t dt a =ò,则,则()3f x x a =+,且11(3)()x a dx f t dt a +==òò.所以所以2101[3]2x ax a +=,即132a a +=,从而14a =-,所以,所以 3()4f x x =-.例13 计算2112211x xdx x-++-ò. 分析 由于积分区间关于原点对称,因此首先应考虑被积函数的奇偶性. 解2112211x x dx x -++-ò=211112221111xxdx dx x x--++-+-òò.由于22211x x +-是偶函数,而211xx +-是奇函数,有112011x dx x-=+-ò, 于是于是 2112211x xdx x-++-ò=212411x dx x+-ò=2212(11)4x x dx x--ò=11200441dx x dx --òò由定积分的几何意义可知12014x dx p-=ò, 故2111022444411x xdx dx x p p -+=-×=-+-òò.例14 计算22()x d tf x t dt dx -ò,其中()f x 连续.连续. 分析 要求积分上限函数的导数,要求积分上限函数的导数,但被积函数中含有但被积函数中含有x ,因此不能直接求导,因此不能直接求导,必须先换必须先换元使被积函数中不含x ,然后再求导.,然后再求导.解 由于由于220()xtf x t dt -ò=22201()2xf x t dt -ò.故令22x t u -=,当0t =时2u x =;当t x =时0u =,而2dt du =-,所以,所以22()x tf x t dt -ò=201()()2xf u du -ò=21()2x f u du ò,故220()x d tf x t dt dx -ò=201[()]2x d f u du dx ò=21()22f x x ×=2()xf x . 错误解答 22()x d tf x t dt dx -ò22()(0)xf x x xf =-=.错解分析 这里错误地使用了变限函数的求导公式,公式这里错误地使用了变限函数的求导公式,公式()()()xa d x f t dt f x dx¢F ==ò中要求被积函数()f t 中不含有变限函数的自变量x ,而22()f x t -含有x ,因此不能直接求导,而应先换元.导,而应先换元. 例15 计算3sin x xdx pò.分析 被积函数中出现幂函数与三角函数乘积的情形,通常采用分部积分法.被积函数中出现幂函数与三角函数乘积的情形,通常采用分部积分法. 解 3s i n x x d x pò3(c o s )x d x p=-ò330[(c o s )](co s )x x x d x pp=×---ò 30cos 6xdx pp=-+ò326p=-. 例16 计算1200ln(1)(3)x dx x +-ò. 分析 被积函数中出现对数函数的情形,可考虑采用分部积分法.被积函数中出现对数函数的情形,可考虑采用分部积分法.解 120ln(1)(3)x dx x +-ò=101ln(1)()3x d x +-ò=1100111[ln(1)]3(3)(1)x dx x x x +-×--+ò =101111ln 2()2413dx x x-++-ò 11ln 2ln324=-.例17 计算20sin x e xdx pò.分析 被积函数中出现指数函数与三角函数乘积的情形通常要多次利用分部积分法. 解 由于2sin xe xdx pò20sin xxde p=ò220[sin ]cos xxe x e xdx p p=-ò220cos xe e xdx p p=-ò,(1) 而2cos xe xdx pò20cos xxde p=ò2200[cos ](sin )xxe x e x dx p p=-×-ò 2sin 1xe xdx p=-ò, (2)将(将(22)式代入()式代入(11)式可得)式可得2sin xe xdx pò220[sin 1]xe e xdx p p=--ò,故20sin xe xdx pò21(1)2e p=+.例18 计算10arcsin x xdx ò.分析 被积函数中出现反三角函数与幂函数乘积的情形,通常用分部积分法.被积函数中出现反三角函数与幂函数乘积的情形,通常用分部积分法.解10arcsin x xdx ò210arcsin ()2x xd =ò221100[arcsin ](arcsin )22x x x d x =×-ò 21021421x dx x p=--ò. (1) 令sin x t =,则,则2121x dx x-ò2202sin sin 1sin t d t tp =-ò220sin cos cos t tdt tp=×ò220sin tdt p=ò 201cos 22t dt p-==ò20sin 2[]24t t p-4p =. (2) 将(将(22)式代入()式代入(11)式中得)式中得1arcsin x xdx =ò8p .例19设()f x [0,]p 上具有二阶连续导数,()3f p ¢=且0[()()]cos 2f x f x xdx p¢¢+=ò,求(0)f ¢.分析分析 被积函数中含有抽象函数的导数形式,可考虑用分部积分法求解.被积函数中含有抽象函数的导数形式,可考虑用分部积分法求解. 解 由于0[()()]cos f x f x xdx p ¢¢+ò00()sin cos ()f x d x xdf x p p¢=+òò[]0000{()sin ()sin }{[()cos ]()sin }f x x f x xdx f x x f x xdx pppp¢¢¢=-++òò()(0)2f f p ¢¢=--=. 故 (0)f ¢=2()235f p ¢--=--=-.例20 计算2043dx x x +¥++ò. 分析 该积分是无穷限的的反常积分,用定义来计算.解 2043dx x x +¥++ò=20lim 43t t dx x x ®+¥++ò=0111lim ()213t t dx x x ®+¥-++ò =011lim [ln ]23t t x x ®+¥++=111lim (ln ln )233t t t ®+¥+-+ =ln 32.。
典型例题(有答案).DOC

典型例题
例 如图1,请你根据格子中的数,从1开始横着数或者竖着数,按照1,2,3,4,5,6,7,8,9,10的顺序数到10,如图2是其中的一种数法,你还有其他的吗?请你试一试.
分析与参考答案:
有以下几种不同的数法:
例.填空.
54)(=- 8)(10=- 分析:解答这组题可以想数的组成与分解.如54)(=-,想4和5组成几,4和5组成9,
所以括号里填9.8)(10=-,想10可以分成几和8,10可以分成2和8,所以括号里填2.根据加减法算式中各数的关系(即整体与部分的关系)来计算未知数也是
可以的,如
5
4
)
(=
-,想4加5等于几,4加5等9,所以括号里填9.8
)
(
10=
-,
想10减8等于几,10减8等于2,所以括号里填2.
答案:
5
4
)9(=
-8
)2(
10=
-
例.连线.
分析:第(1)题的意思是:左边算式的结果是几就应该和右边相应的数连起来.如:左边7+2=9,应该和右边的9连起来.
第(2)题是把左边和右边的结果相同的算式连起来,如:左边7+3=10,右边5+5=10,应该把这两个算式连起来.
例.在□里填上合适的数.
分析:做这道题要对数的组成比较熟悉.另外还要掌握解题技巧,按一定的顺序做,如:可以按从左往右,即10的分解来想.由于10的分解中右边的数又是7的组成中的一部分,因此所填的数必须比7小,即1、2、3、4、5、6,那么在7的组成中,右边的□所填的数相应是6、5、4、3、2、1.也可以按从右往左或从下往上,方法同上.
答案:略.。
牛顿第二定律经典例题及答案

牛顿第二定律经典例题及答案
例题:如图,质量的小车停放在光滑水平面上,在小车右端施加一水平恒力F=8N。
当小车向右运动速度达到3m/s时,在小车的右端轻放一质量m=2kg的小物块,物块与小车间的动摩擦因数μ=0.2,假定小车足够长,问:
(1)经过多长时间物块停止与小车间的相对运动?
(2)小物块从放在车上开始经过t0=3s 所通过的位移是多少?(g 取10m/s2)
【分析与解答】:
(1)依据题意,物块在小车上停止运动时,物块与小车保持相对静止,应具有共同的速度。
设物块在小车上相对运动时间为t,物块、小车受力分析如图:
物块放上小车后做初速度为零加速度为a1的匀加速直线运动,小车做加速度a2的匀加速运动。
其中对物块:由μmg=ma1,
有a1=μg=2m
对小车:F-μmg=Ma2
∴a2=0.5m/s2物块在小车上停止相对滑动时,速度相同
则有:a1t1=v0+a2t1
故答案为:
(1)经多2s物块停止在小车上相对滑动;
(2)小物块从放在车上开始,经过t=3.0s,通过的位移是8.4m.本文网络搜索,如有侵权联系删除。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
典型例题:1)数据库管理系统是()。
(2009-9 -8)A)操作系统的一部分B)在操作系统支持下的系统软件C)一种编译系统D)一种操作系统答案:B解析:数据库管理系统是指位于用户与操作系统之间的数据库管理软件。
数据库管理系统为数据的建立,使用和维护而配置的软件。
2)数据库设计的四个阶段是:需求分析、概念设计、逻辑设计和()。
(2006-9-5)A)编码设计B)测试阶段C)运行阶段D)物理设计答案:D解析:课本14页3)下列描述中错误的是()。
(2007-4-10)A)在数据库系统中,数据的物理结构必须与逻辑结构一致B)数据库技术的根本目标是要解决数据的共享问题C)数据库设计是指在已有数据库管理系统的基础上建立数据库D)数据库系统需要操作系统的支持4)数据库中有A、B 两表,均有相同字段C,在两表中C 字段都设为主键。
当通过C 字段建立两表关系时,则该关系为()。
(2009-3 -12)A)一对一B)一对多C)多对多D)不能建立关系解析:A)两个表之间是由相同的主键建立联系的,也就是主键和主键之间的联系,主键是唯一的,所以是一对一的关系。
5)有三个关系R,S 和T 如下:(2009-9 -10)其中关系T由关系R 和S通过某种操作得到,该操作为()。
A)选择B)投影C)交D)并解析:D)两个相同结构关系的并是由属于这两个关系的元组组成的集合。
6)在下列关系运算中,不改变关系表中的属性个数但能减少元组个数的是()。
(2007-4-8)A)并B)交C)投影D)笛卡儿乘积答案:B)解析:关系R与S经交运算所得到的关系是由那些既在R内又在S内的有序组所组成。
不改变关系表中的属性个数,但能减少元组个数的是关系表之间的交运算。
而投影是挑出若干属性,会改变属性个数。
考点二;数据库和表典型例题:1)以下关于 Access表的叙述中,正确的是(2006-9-14)A)表一般包含一到两个主题的信息B)表的数据表视图只用于显示数据C)表设计视图的主要工作是设计表的结构D)在表的数据表视图中,不能修改字段名称答案:C)解析:本题考查表的基础知识。
Access表是数据实际存储的对象,实现了逻辑上的关系。
一个表一般只包含一个主题信息,在表中数据表视图中,用户可以浏览,查找,添加,删除和修改记录;表的设计一般用来创建表或者修改表的结构。
在数据表视图中可以通过双击字段名的方式来修改字段名。
2)下列关于 OLE 对象的叙述中,正确的是()。
(2009-9-16)A)用于输入文本数据B)用于处理超级链接数据C)用于生成自动编号数据D)用于链接或内嵌 Windows 支持的对象答案:D)解析:本题考查OLE对象的相关知识(此类题几乎每年必考,考生要尤其注意)。
OLE对象是指字段允许单独地“链接”或“嵌入”OLE对象,如WORD文档,EXCEL表格、图像、声音、或者其他二进制数据。
3)下列关于空值的叙述中,正确的是()。
(2009-3-15)A)空值是双引号中间没有空格的值B)空值是等于 0 的数值C)空值是使用 Null 或空白来表示字段的值D)空值是用空格表示的值答案:C)解析:使用NULL或者空白来表示字段的空值。
空值是缺值或还没有值。
4)若设置字段的输入掩码为“####-######”,该字段正确的输入数据是()。
(2008-9-12)A)0755-123456B)0755-abcdefC)abcd-123456D)####-######答案:A)解析:输入“#”号表示可以选择输入数据或空格。
5)对数据表进行筛选操作,结果是()。
(2008-9-13)A)只显示满足条件的记录,将不满足条件的记录从表中删除B)显示满足条件的记录,并将这些记录保存在一个新表中C)只显示满足条件的记录,不满足条件的记录被隐藏D)将满足条件的记录和不满足条件的记录分为两个表进行显示答案:C)解析:本题考查表的基本操作的知识。
在Access中可以利用排序记录来根据当前表中一个或多个字段的值对整个表进行升序或者降序的排列;利用筛选来从所有数据中部分满足某些条件的数据进行处理并且只显示这部分数据,不满足条件的记录将被隐藏。
6)在数据表中,对指定字段查找匹配项,按下图“查找与替换”对话框中的设置,查找的结果是(2008-9-14)A)定位简历字段中包含了字符串“组织能力强”的记录B)定位简历字段仅为“组织能力强”的记录C)显示符合查询内容的第一条记录D)显示字符查询内容的所有记录答案:B)解析:本题考查数据表视图中查找操作的基本知识。
在Access数据表视图中,如果当查询某字段的值时选择了匹配“整个字段”,则会仅定位字段值和要查找的值精确相等的结果。
然每次点击“查找下一个”按扭只会定义一条记录,但该记录不一定是第一条记录,而是当前光标处的下一条记录。
7)ACCESS数据库中,为了保持表之间的关系,要求在主表中修改相关记录时,子表相关记录随之更改,为此需要定义参照完整性关系的(2008-4-19)A)级联更新相关字段B)级联删除相关字段C)级联修改相关字段D)级联插入相关字段答案:A)解析:本题考查参照完整性的知识。
参照完整性是指两个逻辑上有关系的表,表里面的数据必须满足它们之间的关系。
例如,主表中没有相关记录就不能将记录添加到相关表,此时需要设置级联插入相关字段;相关表中的记录删除时主表之间的先关记录随之删除,此时需要设置级联删除相关字段;相关表中的记录更新时主表的相关记录随之更新,此时需要设置级联更新相关字段。
考点三:查询考点三:查询1)在 Access 中,查询的数据源可以是(2007-9-18)A)表B)查询C)表和查询D)表、查询和报表答案:C)解析:本题考查查询数据源的知识。
查询的数据源可以是表或者视图,也可以是另一个查询,但是不能为报表。
2)在显示查询结果时,如果要将数据表中的“籍贯”字段名,显示为“出生地”,可在查询设计视图中改动()。
(2008-9-14)A)排序B)字段C)条件D)显示答案:B)解析:本题考查查询设计视图的知识。
查询的设计试图分为上下两个部分,上半部分为字段列表,下半部分为设计网络。
其中的设计网格中有若干行,其中的“字段”可以显示选定的字段名,也可以由设计者添加或输入字段名。
3)如果在查询的条件中使用了通配符方括号“[ ]”,它的含义是(2007-9-20)A)通配任意长度的字符B)通配不在括号内的任意字符C)通配方括号内列出的任一单个字符D)错误的使用方法答案:C)解析:本题考查通配符的知识。
ACCESS中的模糊查询和有效性规则设计中经常要用到通配符,常见的通配符有:“*”代表0个或多个任意字符;“?”代表一个任意字符;“#”代表一个任意数字字符;“[]”代表与[]内任意一个字符匹配;“!”代表与任意一个不在方括号内的字符匹配,必须与[]一起使用。
4)下面显示的是查询设计视图的“设计网络”部分:从所显示的内容中可以判断出该查询要查找的是(2006-9-19)A)性别为“女”并且 1980 年以前参加工作的记录B)性别为“女”并且 1980 年以后参加工作的记录C)性别为“女”或者 1980 年以前参加者作的记录D)性别为“女”或者 1980 年以后参加工作的记录答案:A)解析:本题考查查询的条件的基本知识。
由图中可以看出,两个查询条件位于同一行,说明两个条件之间是“与”的关系;Year(工作时间)<1980,说明工作时间是在1980年以前。
综合两个方面A选项正确。
5)在数据库中已有同名的表,要通过查询覆盖原来的表,应该使用的查询类型是(2008-4-17)A)删除B )追加C)生成表D)更新答案:C)解析:本题考查操作查询的知识。
操作查询,也叫动作查询,共有四种类型:追加查询,删除查询,更新查询和生成表查询。
利用这几种查询可以完成为源表追加数据,更新、删除源表中的数据,以及生成表操作。
本题中要求覆盖原来的表,应该是生成表查询,若为追加查询将会追加到原来表中原有的记录的后面。
6)在下列查询语句中,与SELECT TABL* FROM TAB1 WHERE InStr([简历],"篮球")<>0 功能相同的语句是()。
(2008-9-22)A)SELECT TAB1.* FROM TAB1 WHERE TAB1.简历 Like"篮球"B)SELECT TAB1.* FROM TAB1 WHERE TAB1.简历 Like"*篮球"C)SELECT TAB1.* FROM TAB1 WHERE TAB1.简历 Like"*篮球*"D)SELECT TAB1.* FROM TAB1 WHERE TAB1.简历 Like"篮球*"答案:C)解析:本题考查字符串函数的基本知识。
本体看似是考查SQL语句,实际上考查的是字符串函数InStr。
InStr函数的格式为InStr(字符表达式1,字符表达式2)[ ,数值表达式])其功能是检索字符表达式2在字符表达式1中最早出现的位置,返回一整型数,若没有找到则返回0,所以实际上这个查询的条件是在简历字段中最早出现了“篮球”二字。
使用关键词“Like”;另外在“篮球”的前后都加上“*”,代表要查找的是“篮球”前面或后面有多个或0个字符,也就是简历中包含“篮球”的记录。
7)在 Access 中已建立了“学生”表,表中有“学号”、“姓名”、“性别”和“入学成绩”等字段。
执行如下 SQL 命令:Select性别, avg(入学成绩) From学生 Group by性别其结果是(2007-4-20)A)计算并显示所有学生的性别和入学成绩的平均值B)按性别分组计算并显示性别和入学成绩的平均值C)计算并显示所有学生的入学成绩的平均值D)按性别分组计算并显示所有学生的入学成绩的平均值答案:B)解析:本题考查SQL查询的知识。
这个SQL查询由于有Group By子句,是一个分组查询,在Group By后面的就是分组字段,也就是按性别分组计算并显示性别和入学成绩的平均值。
考点四:窗体典型例题:1)窗体由多个部分且成,每个部分称为一个___________。
(2007-9-(9))答案:节解析:本题考查窗体组成的知识。
窗体除了能够放置控件和编写事件代码以外,还可以像报表一样设置若干节。
在窗体中可以使用5种节,分别是窗体页眉,窗体页脚,页面页眉,页面页脚和主体。
2)窗口事件是指操作窗口时所引发的事件。
下列事件中,不属于窗口事件的是(2007-4-21)A)打开B)关闭C)加载D)取消答案:D)解析:本题考查的是窗口事件的基本知识。
窗口事件是在打开、调账或关闭窗口的时发生的,包括Open(打开)、Close(关闭)、Load(加载)、Unload(卸载)、Resize(改变大小),并没有取消。
