穆斯堡尔谱学及其应用
穆斯堡尔效应

主要内容:
1
2
穆斯堡尔效应 穆斯堡尔谱学 穆斯堡尔实验技术
3
4 5
穆斯堡尔谱学的应用
穆斯堡尔谱学的发展
1.穆斯堡尔效应
have discovered an unexpected effect which now bears your name. You have explained this effect experimentally and theoretically, and thereby created a device which is of fundamental importance in numerous realms of physics, and which is nowadays being investigated and put to use in a large number of physical laboratories. By your discovery it has become possible to examine precisely, numerous important phenomena formerly beyond or at the limit of attainable accuracy of measurement.
引力红移是三个验证爱因斯坦 广义相对论的基本效应之一(光 线在太阳附近的偏折、行星近日 点的进动)。
穆斯堡尔学与核物理
(2ቤተ መጻሕፍቲ ባይዱ利用超精细相互作用测量相关系数
超 精 细 相 互 作 用
Ⅰ.电单极相互作用
同质异能移
Ⅱ.电四极相互作用
四极分裂
Ⅲ.磁偶极相互作用
磁超精细分裂
穆斯堡尔谱

V (r ) =
V (r ) =
Ze r
Ze R r (3 (4)
(r ≤ R )
因此,有限体积原子核的静电能量为
E=
Zeρ R
∫
R
0
2 2 2π r R (3 2 − 2 R 2 − r ) 4πr dr = − 5 ZeρR =
2
2π 5
Ze 2 R 2 φ (0)
俘获一个 K 层电子时,形成处于高激发态的 57Fe,它分别有 9%和 91%的概率辐 射 137keV 和 123keV 的γ射线跃迁至第一激发态和基态。 当 57Fe 原子核由第一激发 态跃迁至基态时,辐射出穆斯堡尔实验所需的 14.4keV 的γ射线。119mSn 源是通过 中子辐照 118Sn 来获得的。 亚稳态的 119mSn 衰变到处于激发态的 119Sn, 然后跃迁到 基态发射出 23.875keV 的 γ 射线为穆斯堡尔实验所用。 为了观测到无反冲的γ射线 吸收现象,一般采用将穆斯堡尔源的放射性同位素扩散到固体晶格(基质材料) 中,对于
2
(5)
其中 Ze 为 核电荷, φ (0) 为核处的电子波函数, ρ 为电子密度。 原子核在激发态和基态时的半径不同, 因此原子核在激发态与基态之间的跃迁 中,由于静电相互作用所引起的γ射线能量改变为
∆E = δE e − δE g =
2π 5
2 Ze 2 φ (0) ( Re2 − R g )
2
γ 射线吸收强度随着温度降低而增强这一与当时共振吸收观点不一致的 “反常” 现
象。穆斯堡尔及时敏锐地抓住这个“反常”现象,以严谨的科学态度从实验上进 行了多次重复,证实了其实验结果的可靠性,最终认识到在他的实验中共振原子 核是置于紧束缚的晶格中,部分原子核在发射和吸收 γ 射线时,消除了反冲能量 的损失,实现了无反冲共振吸收。他在两年多的时间内从实验上和理论上对这一 “反常”现象进行了解释,攻下这个当时许多物理学家为之努力近三十年而未能 解决的难题。穆斯堡尔实验非常精确,具有非常高的能量灵敏度,利用它可方便 地研究共振核与周围环境的超精细相互作用,为研究物质的微观结构提供了十分 重要的信息,而且对设备的要求相对简单,可以在一般大学实验室中进行。因此, 在很短时间内,这个效应便得到公认,并付诸于应用。由于穆斯堡尔本人在这方 面做出的杰出贡献, γ 射线无反冲共振发射和吸收现象被命名为穆斯堡尔效应, 并 于 1961 年被授予诺贝尔物理学奖。利用穆斯堡尔效应研究物质微观结构已经发展 成为一门独立的学科穆斯堡尔谱学,它是迄今为止能量分辨本领最高的物理研 究手段。经过四十多年的发展,穆斯堡尔谱学已在物理学、化学、生物学、地质 学、冶金学、材料科学、环境科学以及考古学等科学的领域中得到了广泛的应用。 3.11.18.1 穆斯堡尔效应无反冲 γ 射线共振发射和吸收 共振吸收是自然界存在的一种普遍现象。在 1929 年后的二十多年的时间内, 不断有人试图通过实验来观测 γ 射线共振吸收现象,但是都没有成功,其原因是 由于他们没有考虑和解决自由原子核在发射 γ 射线时存在反冲作用所产生的影 响。 自由的激发态原子核在发射γ射线时将发生反冲,其反冲能量 E R 为 ER ≅
试验10穆斯堡尔谱学试验
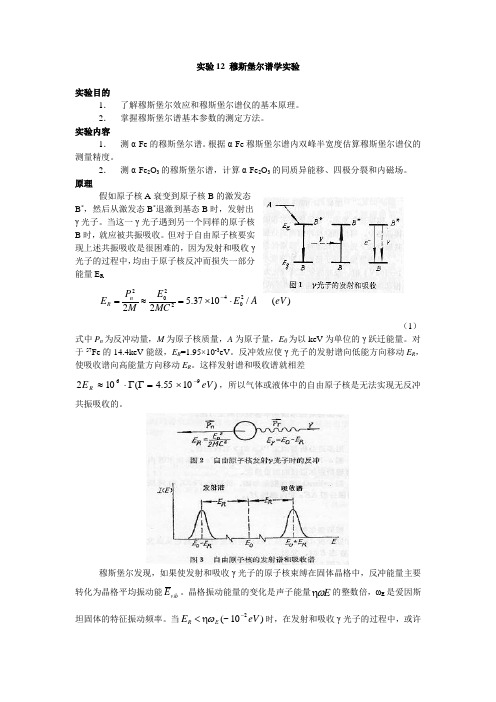
实验12 穆斯堡尔谱学实验实验目的1. 了解穆斯堡尔效应和穆斯堡尔谱仪的基本原理。
2. 掌握穆斯堡尔谱基本参数的测定方法。
实验内容1. 测α-Fe 的穆斯堡尔谱。
根据α-Fe 穆斯堡尔谱内双峰半宽度估算穆斯堡尔谱仪的测量精度。
2. 测α-Fe 2O 3的穆斯堡尔谱,计算α-Fe 2O 3的同质异能移、四极分裂和内磁场。
原理假如原子核A 衰变到原子核B 的激发态B *,然后从激发态B *退激到基态B 时,发射出γ光子。
当这一γ光子遇到另一个同样的原子核B 时,就应被共振吸收。
但对于自由原子核要实现上述共振吸收是很困难的,因为发射和吸收γ光子的过程中,均由于原子核反冲而损失一部分能量E R)(/1037.5222042202eV A E MC E M P E n R ⋅⨯=≈=- (1)式中P n 为反冲动量,M 为原子核质量,A 为原子量,E 0为以keV 为单位的γ跃迁能量。
对于57Fe 的14.4keV 能级,E R =1.95×10-3eV 。
反冲效应使γ光子的发射谱向低能方向移动E R ,使吸收谱向高能量方向移动E R 。
这样发射谱和吸收谱就相差)1055.4(10296eV E R -⨯=ΓΓ⋅≈,所以气体或液体中的自由原子核是无法实现无反冲共振吸收的。
穆斯堡尔发现,如果使发射和吸收γ光子的原子核束缚在固体晶格中,反冲能量主要转化为晶格平均振动能vib E 。
晶格振动能量的变化是声子能量E ω 的整数倍,ωE 是爱因斯坦固体的特征振动频率。
当)10(~2eV E E R -<ω 时,在发射和吸收γ光子的过程中,或许激发声子,或者不激发,其中不激发声子的几率f ,又叫无反冲分数。
由理论计算给出:)exp(22><-=x k f (2)其中k 是γ光子的波矢,<x 2>是原子振幅的均方值。
如采用德拜固体模型,我们可得到无反冲分数的下述表达式:⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-⎪⎪⎭⎫ ⎝⎛+-=⎰T x D D B R D dx e x T k E f /021416exp θθθ (3) 当T<<θD 时 ⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛Γ+-=22223exp D D B R k E f θπθ (4) 当T>θD 时⎥⎦⎤⎢⎣⎡-=26exp D B R k T E f θ (5) 式中k B 为玻尔兹曼常数,B D D k /ωθ =为德拜温度。
论穆斯堡尔谱效应及其在陶瓷领域中的应用

论穆斯堡尔谱效应及其在陶瓷领域中的应用摘要:本文简单介绍了穆斯堡尔效应、57Fe穆斯堡尔谱仪的结构与基本原理,以及在陶瓷领域中的应用。
把穆斯堡尔的方法运用到陶瓷领域中,将为陶瓷界带来更多的益处。
关键词:穆斯堡尔谱;效应;原理;陶瓷;应用1前言2穆斯堡尔效应穆斯堡尔效应是由德国科学家穆斯堡尔(R﹒L﹒Mssbauer)于1957年发现的。
在1961年获得了诺贝尔物理学奖。
这个效应实质上是无反冲核的γ射线共振吸收效应。
它是核能级之间跃迁产生的,具有一定能量的γ射线辐射的一种共振吸收现象。
2.1共振吸收共振吸收是常见的物理现象。
例如,两个固有频率相同的音叉放在一起时,如果一个音叉受到击打而发出声音,那么另一个未受击打的音叉也会吸收前一个音叉的能量,跟着振动,并发出相同的声音,这就是共振吸收现象。
同样,当具有一定能量的γ射线辐射到含有某种原子核的物质上时,当这个能量恰好等于该物质原子核的基态与激发态之间的能量差时,则这个原子核就会对辐射的γ射线产生共振吸收(如图1)。
2.2多普勒效应多普勒效应也是一种物理现象。
在科学意义上,多普勒效应定义是:当一个发射电磁波或声音的辐射体,由于它相对于观察者运动而改变了辐射体电磁波或声音的频率。
也就是说改变了辐射体电磁波或声音的能量。
这种改变的现象即为多普勒效应。
这个效应运用到能量为Er的γ射线辐射体时,如果这个辐射体放在运动着的载体上,那么它辐射γ射线的能量就会发生改变,其改变的能量数值为:ΔEs=(V0/C)·Er。
显然,辐射γ射线的能量的改变与辐射体载体的运动速度V0与光速C之比成正比。
2.3反冲现象与反冲能量当炮弹从炮管发射时,会产生后推的反冲力,同时使炮弹运动的能量相应有所减少,这就是反冲现象。
同样,当原子核发射γ射线时,原子核本身会受到反冲作用,并产生反冲能量。
这样,发射出来的γ射线能量Er将等于原子核激发态与基态之间的跃迁能量减去反冲的能量,即Er=(Ee-Eg)-ER(式中,Er为γ射线辐射的能量,Ee为原子核的激发态能量,Eg为原子核的基态能量,ER为反冲能量)。
穆斯堡尔谱

2、同质异能核 (1)电荷数与质量相同但能态不同的核,如:Fe, Fe+, Fe 2+,Fe 3+, Fe 6+ 。 (2)如用放射性核57Fe为标样,它发出能量为A=hv 的γ射线;(γ射线是不稳定的原子核从能量较高的激 发态跃迁到能量较低的能级或基态时,放出的电磁波) 含铁样品中Fe 的能级差为B; 设ΔE=A-B
穆斯堡尔谱
讲解人: 徐飞 汤惠芬 PPT制作:胡静
内容概要:
一、穆斯堡尔谱的原理和获得的信息 二、穆斯堡尔谱研究对象 三、穆斯堡尔谱的特点 四、穆斯堡尔仪器大致结构 五、制样要求 六、应用举例
一、穆 多普勒效应: 如一个幅射源相对接收者运动, 则对接收者而言, 幅射波长(频率、 能量)随二者的相对运动方向与速度而变化:
2、利用穆斯堡尔谱可方便地研究原子核与其周围环境间的超 精细相互作用,可以灵敏地获得原子核周围的物理和化学环 境的信息,为物质微观结构的分析提供重要的信息。
3、不足之处是:只有有限数量的核有穆斯堡尔效应,目前只有57Fe 和119Sn等少数的穆斯堡尔核得到了充分的应用。
四、仪器的大致结构
五、制样要求
(3)当标样相对含铁样品运动,则样品接受的γ射线能量为hv+/ΔE; (4)当速度达到某值, 使: B= hv+/-ΔE=A+/-VE/C;则形成共振吸收, 就得到Mossbauer谱
穆斯堡尔谱图:
穆斯堡尔谱图横坐标为放射源的运动速度,单位为 mm/s; 纵坐标为吸收率(或者透射率),为电压脉 冲信号经放大、分析而记录出来。
六、应用举例
1、硅酸盐矿物中Fe2+-Mg有序-无序的测定 2、矿物固相反应的研究 3、价态的研究 4、配位数与晶格占位的研究
穆斯堡尔谱原理及应用

为了获得准确的实验结果,需要控制实验环境的 温度、压力等因素,以减少外部因素对实验结果 的影响。
03 穆斯堡尔谱在材料科学中 应用
金属与合金材料研究
相变研究
利用穆斯堡尔谱可以研究金属与 合金中的相变过程,如马氏体相 变、贝氏体相变等,揭示相变过 程中的原子结构和化学键变化。
缺陷与扩散研究
02
原子核能级的精细结 构
穆斯堡尔效应揭示了原子核能级的精细 结构,这种结构使得不同原子核在相同 条件下吸收或发射的γ射线能量有所不 同。
03
原子核与周围环境的 相互作用
原子核所处的化学环境、电子环境等 都会对其能级结构产生影响,进而影 响穆斯堡尔效应。
穆斯堡尔谱定义
01
γ射线能量与吸收系数的关系
穆斯堡尔谱与能级结构的关系
通过分析穆斯堡尔谱的峰位、峰宽和峰强等参数,可以了解原子核的能级结构以及其与周围环境的相互 作用等信息。这些信息对于研究原子核的性质和核反应机制具有重要意义。
02 穆斯堡尔谱实验技术
放射源与探测器
放射源
通常使用穆斯堡尔同位素作为放射源,如57Fe、119Sn等。这些同位素能发射 出具有特定能量的γ射线,用于穆斯堡尔谱的测量。
06 穆斯堡尔谱在其他领域应 用
地球科学中同位素年代测定
测定岩石和矿物的 形成年代
利用穆斯堡尔谱可以测定岩石 和矿物中放射性同位素的衰变 产物,从而推算出它们的形成 年代,为地质年代学研究提供 重要依据。
研究地球化学过程
通过分析不同地质体中同位素 的分布和组成,可以揭示地球 化学过程的机制和演化历史, 如壳幔相互作用、板块运动等 。
05 穆斯堡尔谱在生物医学中 应用
药物作用机制研究
穆斯堡尔光谱

Mössbauer 光谱
穆斯堡尔效应:固体中的某些放射性原子核 有一定的几率能够无反冲地发射γ射线,γ光 子携带了全部的核跃迁能量。而处于基态的 固体中的同种核对前ቤተ መጻሕፍቲ ባይዱ发射的γ射线也有一定 的几率能够无反冲地共振吸收。这种原子核 无反冲地发射或共振吸收γ射线的现象。
Mössbauer 光谱
穆斯堡尔谱:穆斯堡尔效应对环境的依赖性 非常高,常利用多普勒效应对γ射线光子的能 量进行调制,通过调整γ射线辐射源和吸收体 之间的相对速度使其发生共振吸收。吸收率 (或者透射率)与相对速度之间的变化曲线。
穆斯堡尔谱仪 :由放射源(γ光源)射出的γ光子 被样品中存在的穆斯堡尔核(如57Fe,119Sn) 所吸收,形成共振吸收谱,样品中穆斯堡尔核与 核外化学环境的相互作用会引起共振吸收谱线的 位置、形状、数目的 变化。反过来利用所测穆谱 的这些变化推出穆核周围化学环境的信息。
穆斯堡尔谱仪方法的特点是: ①有极高的分辨率,以57Fe的γ共振吸收为例,γ能量(E0)为14.4 千电子伏,谱线自然宽度(Γ)为4.6×10-9电子伏,Γ/E0~3.2×1013,分辨率达1013分之一。 ②穆斯堡尔效应对核外化学环境的变化十分灵敏,适用于研究固 态物质的精细结构及超精细结构。 ③由于是特定核(如57Fe,119Sn)的共振吸收,穆斯堡尔效应不 受其他核和元素的干扰。 ④穆斯堡尔效应受核外环境影响的作用范围一般小于 2.0nm(限 于相邻二、三层离子之内),特别适用于细晶和非晶态物质。 因此,穆斯堡尔谱仪已广泛用来研究地质样品。已发现的穆 斯堡尔核有数十种,但在一般条件(常温)下仅能观察到57Fe、 119Sn的穆谱。所以,仪器适用于含一定量Fe、Sn的样品,可以提 供价态,化学键性,阳离子占位和有序-无序分布、配位结构、 磁性和相分析等方面的信息。
穆斯堡尔效应的应用

指一种原子核无反冲的γ射线共振散射或吸收的现象。
德国物理学家R.L.穆斯堡尔于 1957年~1958年间在观察19 1Ir(129keV)的γ射线共振本底时首先发现这种现象,并在理论上作了解释。
一个自由原子核发射或吸收γ光子时,原子核要受到反冲,反冲能量损失,发射谱或吸收谱便产生偏差,对大部分核辐射,难以实现共振吸收。
若原子核被束缚在晶体点阵上,晶体质量远大于一个原子核的质量,发射或吸收γ光子时,整个晶体反冲,反冲能量将显著减小,容易观察到共振吸收现象。
这就是所谓无反冲γ共振吸收。
但实际上点阵振动状态是量子化的,在反冲能量小于点阵振动的能级间隔时,它将被整个晶体吸收。
所以穆斯堡尔效应又称零声子发射和吸收。
迄今为止,已经观察到的穆斯堡尔效应有40多种元素,80多种核素,100多条穆斯堡尔跃迁线。
这些核素称为穆斯堡尔核。
其中最常用的是57Fe(14.4keV)和119Sn(23.8keV),括号内为γ光子的能量。
无反冲γ射线最主要特点是谱线的宽度接近于核能级宽度,这表明它具有极高的γ射线能量分辨率,因此能观察到原子核能级的超精细结构。
在共振实验中,由于源同吸收体的化学环境的差异,原子核外s电子电荷密度发生变化,它与原子核电荷的相互作用使跃迁能量相应变化,其差值表现为能量位移。
称为同质异能位移或化学位移。
自旋大于 1/2的核,电荷分布非球形对称,核具有电四极矩,它与核所处的电场梯度发生相互作用,核能级便产生四级分裂。
自旋大于零的核,具有核磁矩,它与核所处的内磁场相互作用,核能级就产生分裂。
在穆斯堡尔谱中可以清楚地分辨这些超精细相互作用引起的位移和分裂。
若已知核周围环境的电磁结构,则可以研究核的特性;反之,若核的性质已知,由测量结果可以推得核周围环境的电磁结构,即利用穆斯堡尔核,能探测物质的微观结构。
利用多普勒速度扫描可以实现共振吸收测量,这种装置称为穆斯堡尔谱仪。
由该仪器能获得穆斯堡尔谱——透过吸收体的γ射线光子数对多普勒速度的函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录摘要 (1)1 穆斯堡尔效应背景介绍 (1)2 穆斯堡尔效应原理 (2)2.1 γ射线的产生与谱线的自然线宽 (2)2.2原子核对γ射线的有反冲共振吸收现象 (3)2.3原子核对γ射线的无反冲共振吸收现象(穆斯堡尔效应) (4)2.4多普勒效应和穆斯堡尔谱 (5)3 原子核中的超精细相互作用以及核能级的超精细结构 (6)3.1 原子核的相关属性 (6)3.2核与环境间的超精细相互作用 (7)3.3 同质异能移与电单极相互作用 (7)3.4 四极劈裂与核电四极相互作用 (8)3.5 磁偶极相互作用 (9)4 穆斯堡尔谱仪装置和实验方法 (11)4.1穆斯堡尔谱仪实验装置: (12)4.2 数据处理方法: (13)4.3 能谱调试: (13)4.4 多定标方式: (14)浅谈穆斯堡尔谱学效应实验[摘要] 本文主要由四个部分组成。
第一个部分是斯堡尔效应的背景回顾与阐述。
第二个部分主要介绍穆斯堡尔效应原理,其中包括γ射线的产生与谱线的自然线宽、原子核对γ射线的有反冲共振吸收现象和原子核对γ射线的无反冲共振吸收现象(穆斯堡尔效应)等方面。
第三个部分主要阐述原子核中的超精细相互作用以及核能级的超精细结构。
最后一个部分对穆斯堡尔谱仪装置和实验方法进行论述。
1 穆斯堡尔效应背景介绍穆斯堡尔效应是γ射线对原子核的无反冲共振发射和吸收现象。
1957年德国青年物理学家穆斯堡尔首先发现了这一现象,并因此而命名,为此他获得了1961年诺贝尔奖,而且这个实验被称为“二十世纪物理学的里程碑实验”。
穆斯堡尔效应具有极高的能量分辨率,达到激发态能级的自然宽度,即10-9eV的量级,能够反映原子核与核外环境间超精细相互作用造成的能量细微变化,能量选择性非常好,而且它的实验设备相对简单,这使它迅速形成一门交叉学科——穆斯堡尔谱学。
现在,穆斯堡尔效应已在物理、化学、材料、生物、地质矿物、冶金、考古等学科领域得到广泛的应用,而且研究领域还在不断拓宽,尤其在材料物理和固体物理研究中,架起了原子核物理与凝聚态物理间的一座桥梁,成为核固体物理学中重要的一部分。
在基础研究方面,曾经利用穆斯堡尔谱学方法测量光子从放射源到达吸收体时由于重力势能的增加所造成的光子引力红移,以及在实验上验证爱因斯坦的质能等效原理,这些都是一些典型的例子。
目前已观察到100多种同位素具有穆斯堡尔效应,而可利用的穆斯堡尔跃迁已达到130多个。
室温下能观察到效应的只有57Fe、83Kr、119Sn、149Sm、151Eu、161Dy、169Tm、和181Ta 等十余个同位素,而大多数穆斯堡尔核素只有在低温下才能观察到效应,其中使用最广泛的是57Fe的14.4keV跃迁(57Fe原子核从I=3/2激发态到I=1/2基态的跃迁)和119Sn的23.8keV跃迁。
本实验采用的是57Fe的14.4keV跃迁。
2 穆斯堡尔效应原理2.1 γ射线的产生与谱线的自然线宽γ射线是波长极短的电磁波。
和原子类似,原子核也可以处与不同的能量状态,即我们常说的能级。
当不稳定的原子核从具有较高能量的激发态能级跃迁到较低能级(例如基态)时,就会放射出γ射线。
反之,如果原子核可以吸收具有某一个特定能量的γ射线,则可以从一个较低的能量状态跃迁回到一个较高能量状态。
由于原子核的激发态存在有限长的寿命τ,则它跃迁后发射的γ射线能量不是唯一值,表现为能量谱线具有洛伦兹分布,而且对应的能量谱线具有一定宽度。
已知光子的能量谱线强度和光子频率ω之间的关系是)(ωI ∝220)21()(1τωω+- (1) 考虑到光子的能量E= ω,( 为约化普朗克常数),得到谱线强度按照能量的分布:)(E I ∝220)21()(1τωω+- (2) 当E-E 0=± /2τ时,可以计算出谱线的强度下降为最大值的一半。
这时我们可以将对应的谱线半高宽称为γ射线的自然线宽Γ。
而且根据海森堡的测不准关系易知τ和Γ满足:Γ τ~ (3)图1为典型的洛伦兹型吸收谱线,线宽为Γ。
而对于发射谱线和吸收谱线均具有类似上式的能量分布图1)(E I ∝220)2()(1Γ+-E E (4)2.2原子核对γ射线的有反冲共振吸收现象AbsorberEmitter0R 0RAbsorberEmitter0R 0R 0正如前面所述,原子核中由高到低的能级跃迁可以放出γ射线,反之如果能够吸收合适能量的γ射线,也可以从低能级跃迁到高能级。
这种不同能量状态之间的跃迁就是我们熟悉的γ辐射和γ吸收现象。
考虑到原子核的质量比较小,而放射或者吸收的γ射线的能量又比较大(通常在keV 到MeV 量级),因此在放射和吸收过程中必须要考虑到原子核的反冲现象对放射和吸收谱线的影响。
假设原子核的质量为m ,初速度为零,激发态E e 和基态E g 的能级差为E 0=E e -E g ,辐射γ射线时为了保证动量守恒,原子核的反冲动量mu R 应该等于发射γ射线的动量P γ,即mu R =P γ=E γ /c 。
根据能量守恒定律:E 0=E γ+E R ,可得原子核的反冲动能2222222mc E m P mu E R R γγ===,因此原子核反冲会导致实际发射的γ射线能量为E 0-E R =(E e -E g )-E R ,小于能级差E 0,而消耗的能量在原子核的反冲动能E R 上。
反之在原子核的共振吸收时也会碰到同样的现象:如果需要从基态跃迁到激发态,γ射线所需要提供的能量为(E e -E g )+E R ,多出的能量使共振原子核有一个反冲能E R 。
因此发射谱和吸收谱就会产生2E R 的偏移,如图2 (a)所示。
这个反冲能能量E R 与原子核的质量和γ射线的能量有关,在某些特定情况下比自然线图2宽Γ大得多,以我们的实验中用的57Fe 原子核为例,E 0=14.41 keV ,则E R ≈2×10-3eV,而对应的自然线宽为10-8eV 量级,因此造成吸收谱和发射谱之间的重叠很少,应该看不到共振吸收现象。
在上面的讨论中,我们假设原子是孤立的、自由的和静止的。
实际情况是原子核有热运动,因此也会由热运动提供一定的多普勒能量,使发射谱和吸收谱有很大展宽,而不等于自然线宽,这种谱线的增宽称为多普勒增宽,展宽后的谱线宽度为E d =2R K E E ,其中E K =2T K B 为一个原子核每个自由度平均动能。
图2(b)中的E d 大约在10-2eV 的量级,这样会使吸收和发射谱线可能会有一定的重叠。
所以原则上讲,可以通过提高测量温度是原子核热运动加快,产生较多的谱线重叠,以获得有反冲的原子核对γ射线的共振吸收。
在发现穆斯堡尔效应之前,通常使用的办法主要就是采用加热和加速的办法补偿反冲时的能量损失,而且由于总的重叠面积较小,要想观察这种原子核的有反冲共振吸收总是比较困难。
2.3原子核对γ射线的无反冲共振吸收现象(穆斯堡尔效应)前面考虑的均为有反冲共振吸收现象,那么如果有一种办法可以使原子核被牢牢固定,应该可以减小反冲能E d ,甚至使之趋向于零,这样发射谱线和吸收谱线的叠加将明显增加,共振效应也易观察到。
具体讲来,如果把发射核和吸收核均牢牢地固定在固体晶格中,当发射或吸收γ射线时,需要考虑的反冲能222'Mc E E R γ=,其中M 为晶体的质量,远远大于单个原子核的质量m,因此反冲能急剧减小,甚至可以看为0。
这样发射谱线和吸收谱线可以认为完全重合,可以获得非常大的重合面积,很容易发生共振吸收现象。
但是实际上的过程比前面所说的要复杂的多,因为晶格的振动是一种量子化的体系,根据爱因斯坦模型如果提供 ω,2 ω,3 ω等能量就可以改变晶格的振动状态,即激发出声子,声子的频率为ω。
如果在这个过程中不产生或者吸收声子,那么发射和吸收γ射线的能量就不会改变,因此原子核不会产生反冲能量损耗。
这种没有反冲能量损耗的γ射线发射或者吸收过程的概率就被称为无反冲分数f 。
实际上爱因斯坦模型过于简单,更接近实际的是晶格振动的德拜模型,但仍然可以获得类似结果。
所以一句话来说,穆斯堡尔效应就是原子核对γ射线的零声子无反冲共振和吸收效应。
在晶格振动的爱因斯坦模型下,可计算出固体中有关和产生穆斯堡尔效应的几率即无反冲分数])/(exp[222c x E f ><-=γ,实际是固体中的穆斯堡尔核在发射或吸收γ光子时不激发或吸收声子(零声子)过程的几率,又被称为穆斯堡尔分数。
其中<x 2>为穆斯堡尔原子在γ射线传播方向上的均方振幅。
要易于观察到穆斯堡尔效应,f 必须尽可能的大,这就要求γ光子的能量不能太高(低能的γ辐射),穆斯堡尔原子与基质原子间的束缚要强,实验温度不能太高(这点恰好和原子核的有反冲共振吸收的实验现象相反,也正是穆斯堡尔发现这个效应的根源)。
此式表明:在液体、气体中,因><2x 很大,以至难以观察到穆斯堡尔效应。
当然并不是发射核或吸收核只要存在于固体之中就必定发生穆斯堡尔效应,但只有在固体之中的核才有可能产生穆斯堡尔效应。
凡有穆斯堡尔效应的原子核我们称之为穆斯堡尔核。
例如,在室温下57Fe 的无反冲分数可高达0.7-0.8。
此外119Sn 的23.87 keV 的γ跃迁在室温下有较大的无反冲分数,这两者是应用最为广泛的穆斯堡尔核。
而目前发现的有穆斯堡尔效应的43种元素,80多种同位素的100多个核跃迁大多数需要在低温下才能观察到,因此使用并不广泛。
在无反冲共振吸收时,γ射线的能量宽度为激发态的自然宽度,测得的穆斯堡尔谱线的宽度近似等于谱线的自然宽度,其值一般是相当小的。
仍然以57Fe(14.41 keV )为例,Γ~4.6×10-9 eV,而Γ/E γ~3.2×10-13,这就是通常所说的穆斯堡尔谱的能量分辨率。
因此可以看出,这种方法具有很高的能量分辨率。
如果原子核的能级由于某种原因有非常细小的变化,也可能会使我们无法观测到无反冲共振吸收现象,这样我们可以通过观察谱线的移动测量相应的能级移动。
所以说穆斯堡尔效应的发现,不仅仅使我们能够很容易的观察到核的共振吸收现象,更重要的是我们能够利用它的高能量分辨率特性来研究原子核的超精细结构。
2.4多普勒效应和穆斯堡尔谱一个光源发射的光子频率为ω,当它以速度V 向观察者移动时,即发射光子的方向和V 的方向一致,则观察者接收到的光子频率有一个增加,而且满足Δω/ω=V /c 。
如果V 和发射γ光子的方向有一个夹角θ,则吸收体接收到γ射线的能量存在一个移动为θγcos E cv E d =,而这时候发射出的γ射线的能量为E γ=E 0-E R +E d , 在前面原子核的有反冲共振吸收中谈过的多普勒热展宽也是由于多普勒效应的影响。
