穆斯堡尔效应及其应用
穆斯堡尔

穆斯堡尔当一种原子核发射的电磁辐射(g辐射)作用于同一种原子核上时,一般不会发生共振吸收,这是因为原子核要受到反冲,g辐射的能量和频率将会减少在穆思堡尔效应被发现以前,一般采用补偿反冲能量损失的办法来研究g辐射的共振吸收,但是,这样观察到的共振谱线的宽度远大于核谱线的自然宽度,共振吸收的信号太弱,本底太强,使得核谱线共振吸收技术的应用受到很大限制。
1958年,穆思堡尔在研究铱低温g辐射共振吸收实验时发现:如果发射或吸收g辐射的原子核束缚在晶体的晶格中,便可以消除原子核反冲及其对波长的影响。
这种无反冲的g辐射共振吸收效应就被称为穆思堡尔效应。
1960年,人们利用穆思堡尔效应成功地验证了爱因斯坦在相对论中预言的引力红移。
现在,穆思堡尔效应应用十分广泛,除了是研究固态物理微观结构的一种有力工具外,它的应用几乎遍及物理学的各个部门,甚至在化学、分子生物学、地质学和医学等方面也都起着广泛和重要的作用。
穆斯堡尔谱学给出的信息:穆斯堡尔谱学主要论述的是具有一定体积的原子核与其周围环境电或磁的相互作用。
这种相互作用的一方是原子核,它具有电荷、电四极距和磁偶极距,相互作用的另一方面是环境在核处形成的电荷分布、电场梯度和磁场。
所谓环境通常是指原子核的核外电子、近邻原子的电荷和磁距。
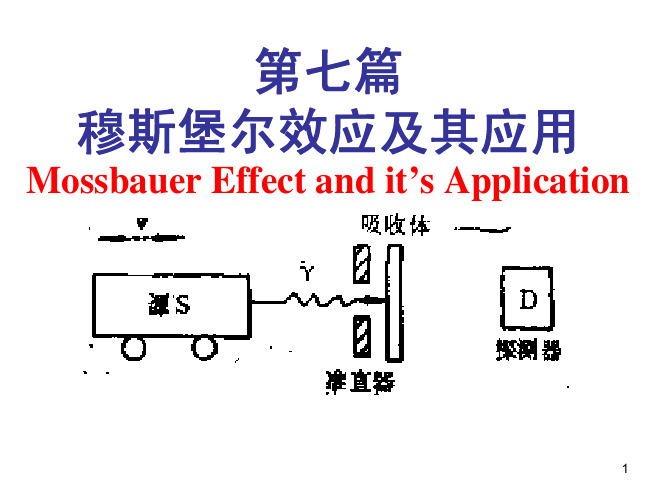
穆斯堡尔仪器的基本构成和原理。
穆斯堡尔效应是一种无反冲的γ射线的共振吸收或共振散射效应。
当穆斯堡尔放射源在振子中获得多普勒速度补偿时,它就有可能和吸收体(样品)产生共振吸收。
在共振吸收时,探测器探测到的γ射线强度明显下降,从而可得到样品的共振吸收谱线。
如典型的α-Fe样品谱线共有六个峰,对应于不同的速度值,即不同的补偿能量值。
通用接口送出步进信号给函数产生器。
函数产生器将此序列脉冲分频,获得对称的方波信号,经积分后得到三角波信号,并作为基准信号被送入功率放大器。
同时,对应于三角波的谷点输出正同步信号给通用接口。
振动子处拾波线圈感应的信号也加入到功率放大器,功率放大器放大基准信号和感应信号的差值,将其送入到振动子的驱动线圈上。
第7章穆斯堡尔效应剖析

E E0 ER
E0为激发态和基态的能量差。
6
核分析基础及应用
第一节 穆斯堡尔效应及穆斯堡尔谱
一、穆斯堡尔效应
同理,自由的、静止的原子核在吸收γ射线时,原子核也受 到反冲,因此光子的能量不是全部被用来激发原子核,有 一部分提供为核的反冲能ER,即要将吸收和从基态激发到 激发态所需的γ射线能量为:
14
核分析基础及应用
第一节 穆斯堡尔效应及穆斯堡尔谱
二、基本原理
➢穆斯堡尔谱学的特点: ①穆斯堡尔谱具有极高的能量分辨本领,很容易探测出原子 核能级的变化。 ②利用穆斯堡尔谱可以方便地研究原子核与其周围环境间的 超精细相互作用,可以灵敏地获得原子核周围的物理和化学 环境的信息。
15
核分析基础及应用
34
核分析基础及应用
第三节 穆斯堡尔实验装置
5.其它附属设备 ➢为使共振吸收效应显著,有时需在低温条件下实验,因此 要有附属的低温装置来冷却源和吸收体(或只冷却其中之一)。 ➢为研究穆斯堡尔参数随温度的变化关系,又常需要附属的 加温设备。
35
核分析基础及应用
第三节 穆斯堡尔实验装置
6.样品(吸收体)的制备 ➢对金属和合金材料,先要经锻造或轧制后制成较小的棒状、
20
核分析基础及应用
第二节 穆斯堡尔参数
2.四极矩分裂 ②四极矩分裂是穆斯堡尔谱的一个重要参数,通过分裂谱 可以了解原子核的对称性,即电子云分布情况和电子云的 分布梯度。如表面原子相对本体原子有较低的对称性,根 据这个差别可以区分这两种不同原子。 表面化学吸附物质的存在可以改变电场 梯度,而这又与化学吸附键的强度以及 化学吸附物质相对于表面原子的位置有 关。因此,测量四极矩分裂的大小变化, 可以提供表面状况的信息。
穆斯堡尔谱解析

穆斯堡尔谱解析穆斯堡尔谱解析穆斯堡尔效应是指铁族元素或其同位素的核自发辐射与晶格震动相互作用时发生的一种物理现象。
穆斯堡尔效应在化学、物理、材料学等领域具有广泛应用,可以提供原子、分子、离子的详细结构信息。
而穆斯堡尔谱谱图解析对于这些领域研究的进展至关重要。
1. 穆斯堡尔谱的基本原理穆斯堡尔谱是具有高分辨率、高灵敏度和高选择性的核磁共振技术。
其分析基本原理是通过核固有的自旋取向状态、核波矢的变化和与外部场的相互作用等,反映出核的周围电子和所嵌入的物质的性质。
2. 穆斯堡尔谱的特点穆斯堡尔谱谱图可以提供一些特定的定量信息,如原子核的价态、配位数、离子半径和联合程度等。
另外,穆斯堡尔谱不受样品形态和状态的限制,可以研究固体、液体、气体甚至是生物物质。
3. 穆斯堡尔谱解析的应用穆斯堡尔谱谱图解析在化学、物理、材料学等领域具有广泛应用。
常用于研究催化机理、氧化还原反应、电子转移、氧化剂和还原剂的定量分析、晶格缺陷及其影响等方面。
在材料学中,穆斯堡尔谱谱图解析可以解析纳米材料的晶格结构、表面化学和电子结构中的差异,研究材料的磁性、力学性质和温度依赖性质等。
4. 穆斯堡尔谱谱图解析的挑战穆斯堡尔谱谱图往往存在多峰性和线宽广的问题,因此解析谱图具有一定的挑战性。
针对这些问题,研究人员发展了多种定量分析方法和数据处理技术,如傅立叶变换、小波变换、能量拟合等。
5. 结语穆斯堡尔谱谱图解析是一项复杂而又具有广泛应用的技术,具有提供描述化学反应机制和研究材料性质的重要价值。
未来,在物理、化学、材料科学等领域中,穆斯堡尔谱谱图解析将会成为研究的关键手段。
论穆斯堡尔谱效应及其在陶瓷领域中的应用

论穆斯堡尔谱效应及其在陶瓷领域中的应用摘要:本文简单介绍了穆斯堡尔效应、57Fe穆斯堡尔谱仪的结构与基本原理,以及在陶瓷领域中的应用。
把穆斯堡尔的方法运用到陶瓷领域中,将为陶瓷界带来更多的益处。
关键词:穆斯堡尔谱;效应;原理;陶瓷;应用1前言2穆斯堡尔效应穆斯堡尔效应是由德国科学家穆斯堡尔(R﹒L﹒Mssbauer)于1957年发现的。
在1961年获得了诺贝尔物理学奖。
这个效应实质上是无反冲核的γ射线共振吸收效应。
它是核能级之间跃迁产生的,具有一定能量的γ射线辐射的一种共振吸收现象。
2.1共振吸收共振吸收是常见的物理现象。
例如,两个固有频率相同的音叉放在一起时,如果一个音叉受到击打而发出声音,那么另一个未受击打的音叉也会吸收前一个音叉的能量,跟着振动,并发出相同的声音,这就是共振吸收现象。
同样,当具有一定能量的γ射线辐射到含有某种原子核的物质上时,当这个能量恰好等于该物质原子核的基态与激发态之间的能量差时,则这个原子核就会对辐射的γ射线产生共振吸收(如图1)。
2.2多普勒效应多普勒效应也是一种物理现象。
在科学意义上,多普勒效应定义是:当一个发射电磁波或声音的辐射体,由于它相对于观察者运动而改变了辐射体电磁波或声音的频率。
也就是说改变了辐射体电磁波或声音的能量。
这种改变的现象即为多普勒效应。
这个效应运用到能量为Er的γ射线辐射体时,如果这个辐射体放在运动着的载体上,那么它辐射γ射线的能量就会发生改变,其改变的能量数值为:ΔEs=(V0/C)·Er。
显然,辐射γ射线的能量的改变与辐射体载体的运动速度V0与光速C之比成正比。
2.3反冲现象与反冲能量当炮弹从炮管发射时,会产生后推的反冲力,同时使炮弹运动的能量相应有所减少,这就是反冲现象。
同样,当原子核发射γ射线时,原子核本身会受到反冲作用,并产生反冲能量。
这样,发射出来的γ射线能量Er将等于原子核激发态与基态之间的跃迁能量减去反冲的能量,即Er=(Ee-Eg)-ER(式中,Er为γ射线辐射的能量,Ee为原子核的激发态能量,Eg为原子核的基态能量,ER为反冲能量)。
第七篇 穆斯堡尔效应及应用
( 14.413 × 10 MeV ) ≈ 1.96 × 10 -9 MeV E ER = = ≈ 2 2M R 2M RC 2 ( 57 × 938.8MeV )
p
2 γ 2 0 -3 2
Eγ = E0 - ER ≈ 14.4 KeV - 1.96 × 10 -6 KeV Eγ ≈ 14.4 KeV
E * = Eγ
Δx
探测器 移动辐射源
' Eγ = Eγ + E D
吸收体
E*
0.0
E*
0.0
Eγ = E *
v E D ≈ Eγ c
19
发射体对吸收体作相离运动, 发射光子能量小于吸收体跃迁能量,无共振吸收
20
发射体对吸收体相离速度变小, 发射光谱向吸收光谱靠拢,无重叠,无共振吸收
21
发射体对吸收体相离速度继续变小, 发射光谱与吸收光谱出现部分重叠,有共振吸收
四级分裂
1
ΔEQ
−ν
0
核能级和四级分裂
δ
相 对 透 射 率
2
+ν
速度(mm/s)
42
H ≠ 0 , V zz
0
6 5 4
3
3/2
1
2
1/2
同质异能位移 率 相 对 透 射 磁偶极分裂 1 2 3 4 5 6
速度(mm/s)
57Fe能级的磁分裂及相应的穆斯堡尔谱
43
红移效应 • 假设有个光源每隔时间T发出一个波列,即光源的 周期为T。当它静止时相邻两个波列时间间隔为 T, 距离间隔为 λ=cT • 当光源以速度V离开观察者时,在每两个相邻的波 列之间的时间里光源移动的距离为VT,于是下一个 波峰到达观察者所需的时间便增加了VT/c,所以, 相邻的两个波峰到达观察者那里所需的时间就为: T’=T+VT/c>T 相对于观察者而言,光波的周期变长了,频率变 低了;
穆斯堡尔谱原理及应用

为了获得准确的实验结果,需要控制实验环境的 温度、压力等因素,以减少外部因素对实验结果 的影响。
03 穆斯堡尔谱在材料科学中 应用
金属与合金材料研究
相变研究
利用穆斯堡尔谱可以研究金属与 合金中的相变过程,如马氏体相 变、贝氏体相变等,揭示相变过 程中的原子结构和化学键变化。
缺陷与扩散研究
02
原子核能级的精细结 构
穆斯堡尔效应揭示了原子核能级的精细 结构,这种结构使得不同原子核在相同 条件下吸收或发射的γ射线能量有所不 同。
03
原子核与周围环境的 相互作用
原子核所处的化学环境、电子环境等 都会对其能级结构产生影响,进而影 响穆斯堡尔效应。
穆斯堡尔谱定义
01
γ射线能量与吸收系数的关系
穆斯堡尔谱与能级结构的关系
通过分析穆斯堡尔谱的峰位、峰宽和峰强等参数,可以了解原子核的能级结构以及其与周围环境的相互 作用等信息。这些信息对于研究原子核的性质和核反应机制具有重要意义。
02 穆斯堡尔谱实验技术
放射源与探测器
放射源
通常使用穆斯堡尔同位素作为放射源,如57Fe、119Sn等。这些同位素能发射 出具有特定能量的γ射线,用于穆斯堡尔谱的测量。
06 穆斯堡尔谱在其他领域应 用
地球科学中同位素年代测定
测定岩石和矿物的 形成年代
利用穆斯堡尔谱可以测定岩石 和矿物中放射性同位素的衰变 产物,从而推算出它们的形成 年代,为地质年代学研究提供 重要依据。
研究地球化学过程
通过分析不同地质体中同位素 的分布和组成,可以揭示地球 化学过程的机制和演化历史, 如壳幔相互作用、板块运动等 。
05 穆斯堡尔谱在生物医学中 应用
药物作用机制研究
穆斯堡尔效应的应用

指一种原子核无反冲的γ射线共振散射或吸收的现象。
德国物理学家R.L.穆斯堡尔于 1957年~1958年间在观察19 1Ir(129keV)的γ射线共振本底时首先发现这种现象,并在理论上作了解释。
一个自由原子核发射或吸收γ光子时,原子核要受到反冲,反冲能量损失,发射谱或吸收谱便产生偏差,对大部分核辐射,难以实现共振吸收。
若原子核被束缚在晶体点阵上,晶体质量远大于一个原子核的质量,发射或吸收γ光子时,整个晶体反冲,反冲能量将显著减小,容易观察到共振吸收现象。
这就是所谓无反冲γ共振吸收。
但实际上点阵振动状态是量子化的,在反冲能量小于点阵振动的能级间隔时,它将被整个晶体吸收。
所以穆斯堡尔效应又称零声子发射和吸收。
迄今为止,已经观察到的穆斯堡尔效应有40多种元素,80多种核素,100多条穆斯堡尔跃迁线。
这些核素称为穆斯堡尔核。
其中最常用的是57Fe(14.4keV)和119Sn(23.8keV),括号内为γ光子的能量。
无反冲γ射线最主要特点是谱线的宽度接近于核能级宽度,这表明它具有极高的γ射线能量分辨率,因此能观察到原子核能级的超精细结构。
在共振实验中,由于源同吸收体的化学环境的差异,原子核外s电子电荷密度发生变化,它与原子核电荷的相互作用使跃迁能量相应变化,其差值表现为能量位移。
称为同质异能位移或化学位移。
自旋大于 1/2的核,电荷分布非球形对称,核具有电四极矩,它与核所处的电场梯度发生相互作用,核能级便产生四级分裂。
自旋大于零的核,具有核磁矩,它与核所处的内磁场相互作用,核能级就产生分裂。
在穆斯堡尔谱中可以清楚地分辨这些超精细相互作用引起的位移和分裂。
若已知核周围环境的电磁结构,则可以研究核的特性;反之,若核的性质已知,由测量结果可以推得核周围环境的电磁结构,即利用穆斯堡尔核,能探测物质的微观结构。
利用多普勒速度扫描可以实现共振吸收测量,这种装置称为穆斯堡尔谱仪。
由该仪器能获得穆斯堡尔谱——透过吸收体的γ射线光子数对多普勒速度的函数。
论穆斯堡尔谱效应及其在陶瓷领域中的应用

图1γ射线共振吸收原理示意图γ射线辐射源吸收体共振吸收多普勒效应也是一种物理现象。
在科学意义上,多普勒效应定义是:当一个发射电磁波或声音的辐射体,由于图257Fe 的放射波宽度辐射能量示意图123137keV123keV14.4keV基态第一激发态第一激发态图357Fe 穆斯堡尔谱仪的基本结构示意图计数振动器57Co样品探测器多道分析记录器速度(毫米/秒)不同能量的γ射线辐射中,以第三种能量辐射作为观察穆斯堡尔效应的辐射源。
它是57Fe 核的基态到第一激发态的能级之间的辐射源。
357Fe 穆斯堡尔谱仪的结构与基本工作原理57Fe 穆斯堡尔谱仪的基本结构示意图如图3所示穆斯堡尔仪的工作原理是:辐射源57Co 与振动器联结在一起,使辐射的γ射线获得等加速运动(产生多普勒图5四极分裂图E 0E I γ射线E M计数-V+V第一激发态基态Q ·S±1/2±1/2±1/2图6磁分裂能级状态示意图及相应的共振吸收速度谱E 03γ射线460-V+V123/21/25346125图4同质异能位移能级状态示意图及共振吸收速度谱E 0E Sγ射线E 0E A计数0-V +VI ·SV '0同质异能位移(I ·S)在一些文献中也称为化学位移(C ·S),它的大小与Fe 的三种结构状态有关。
(1)与Fe 的氧化状态有关按规律性来说,三价Fe 3+离子的同质异能位移小于二四极分裂值的大小与Fe 的结构状态有如下关系。
(1)与Fe 氧化状态有关。
二价Fe 2+离子的四极分裂的共振吸收的速度值大于三价Fe 3+离子的数值。
前者一般都大于2mm/s,后者一般均小于1mm/s。
因此,根据四极分57Fe 穆斯堡尔谱在陶瓷领域中的应用. All Rights Reserved.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
穆斯堡尔效应及其应用摘要:穆斯堡尔效应是现代核物理技术的核心理论,也是解决空间测距精确程度的重要方法。
本文具体而清晰地阐述了穆斯堡尔效应及应用形式,也对相应的科学领域进行了针对性的概述。
关键词:穆斯堡尔效应γ光子发射谱吸收谱一.引言在1958年由德国青年物理学家穆斯堡尔首次发现由γ射线所发出的一种共振荧光现象,后来人们把这一种现象称为无反冲γ射线共振吸收效应又称穆斯堡尔效应。
这一效应发现之后马上引起了物理学界以及与物理学相关的科学界的重视,很快成为跨学科多门类的新兴技术,渗透到了物理学中的核物理、点阵动力学、超导物理、磁学;化学中的化学键、化合物的结构、催化;以及地质学、生物学、医学、工学、人文科学甚至到考古学、美术学都有广泛的应用。
换句话说,只要是与物质结构微观结构有关的研究学科,都有穆斯堡尔效应的踪迹。
因此,穆斯堡尔效应的应用探究直到现在仍然是一个十分重要的研究领域。
穆斯堡尔在完成他的硕士论文时首次观察了191Os经过β衰变成191Ir 以及187Re、177Hf、188Er等原子核无反冲γ共振吸收现象。
本文阐述穆斯堡尔效应之后,对穆斯堡尔效应的具体应用分几个方面进行阐述,现代很多技术都与穆斯堡尔效应有关,这一结果是十分令人满意的。
二.穆斯堡尔效应的理论诠释一个处于静止状态的自由原子核,根据动量守恒定律,释放一个γ光子时,将受到一个反冲动量,反冲动量为:P=mv=h c ν (1) 所以:R E =12m 2v =22m p =222m E c (2) 式中:m 为原子核的质量 E 为释放γ光子的能量 c 为真空的光速 这个动量应该由原子核的跃迁所释放的能量021E E E =-来提供,所以发射γ光子所需要的能量为:·¢E =h ν=0R E E -=2202m E E c- (3) 我们使发射谱线的中心发生偏移,使谱线不在0E 处,而在0R E E -处。
如果一个原子核发射的γ射线的有一个反冲,发出的γ射线相应的能量就会减少一部分:10R E E E -=另外一个吸收的原子核也具有一个反冲能量,所以,要产生共振荧光现象就应该提供相应的能量:20R E E E -=这样会导致发射谱和吸收谱产生相差为2R E 的距离,如图1;图1;原子核吸收γ光子的过程,同时也会获得光子所发射的反冲能量222R m E E c =,这种反冲动量一定是入射光子提供的,则:22Îü002R m E E E E E c=+=+ (4) 经过这样的操作,会使发射谱和吸收谱相距2R E 的距离,如图一;例如对于57Fe 来说,第一激发态释放14.4kev 的γ光子能量。
原子核所受到的反冲能量为R E =1.9⨯310-ev ,这样会使发射谱和吸收谱的间距等于2R E =3.8⨯310-ev ,此外,R E 与激发态的能级的自然宽度相比较确实是一个大量,遵循海森堡不确定关系即E t h ∆•∆≥,所以有寿命的激发态一定存在能级的自然宽度Γ。
例如:57Fe 能级的半衰期为9.8810-⨯s ,它的自然宽度为:94.710c c ττ-Γ===⨯ev (5)所以2R E 比n Γ大一百多万倍,这样就会导致一个自有存在的57Fe 原子核所发出的14.4kev 能量的光子,不能为另一个基态的57Fe 所吸收。
一般而言,自由原子核发射γ光子所获得的反冲能量大于410-ev ,而谱线能级的自然宽度在16191010--ev 范围内,前者远远大于后者,这就是实验观察不到自由原子核所发射的γ射线所产生共振荧光的内在本质。
三.穆斯堡尔效应的特征自从德国物理学家穆斯堡尔发现并观测穆斯堡尔效应以后,它的发展速度是十分惊人地。
由穆斯堡尔效应开展的学科和领域不断增大,它已经成为观测物质微观结构的非常重要的技术手段,这与穆斯堡尔效应的几个优点是密不可分的。
(1)微观探测性 穆斯堡尔效应发出的光子形成的谱线是有物质(固态、液态、气态)这里特别是固体物质的固有属性决定的,它是表征被测样品中特殊同位素所发出的能级谱线随外界的变化而引起谱线变化的情况。
这里说的不是大量物体在总体程度上的统计平均所引起的宏观现象,所以,通过穆斯堡尔效应的进一步研究,我们可以清楚的发现许多物质内部的微观结构以及微观结构与微观结构之间相互联系的内部机理,同时我们也可整合物质内部与外部的联系的有关资料,为以后研究新的科研技术打下坚实的基础。
(2)高分辨率我们知道穆斯堡尔谱线中的吸收谱和发射谱之间交叠区域是非常狭窄的。
因此,我们可以得到很高的分辨率,同时,我们也可以利用穆斯堡尔效应观察很多物质超精细结构的相互作用(例如:测量地月距离)。
表1,给出了穆斯堡尔谱线的分辨率以及其他几种光谱的分辨率供我们参考。
表1, 几种谱的分辨率110-310-810---691010--10141010(3)高度的选择性用已知的57Fe作为γ-射线源时,在待测样品中只有含有57Fe的样品才会出现穆斯堡尔效应,所以它具备程度较高的选择性,同时它可以运用到含有组分复杂物质的特定元素的确定以及所处化学环境的数据分析。
从穆斯堡尔效应的发现到1971年,短短的几年中,就已经观测到很多元素中都具有穆斯堡尔效应的特性。
(4)高度的灵敏性随着科学技术的不断发展仪器设备性能的不断优化以及信息储存技术的应用,使穆斯堡尔效应的探测和获取数据的程度都有很高的灵敏度。
例如,把穆斯堡尔效应应用到物质超精细结构的相互作用方面都取得了很大的成功。
(5)动态探测性因为穆斯堡尔效应具有高分辨率、高度的选择性和极高的灵敏度等特性。
所以在一定程度上可以利用穆斯堡尔效应来探究化学中物质反应速率及催化问题,以及相变和地质学中的陨石、月岩和其他的动力学过程。
(6)非破坏性探测在一般情况下,我们进行穆斯堡尔效应的探测时,有两个突出的优点:①.所需待测样品的数量极少。
②.不会对待测样品的物理和化学属性产生任何影响。
因为穆斯堡尔效应具有这样的突出优点,在化学中的催化问题占据很高的地位。
综上所述,正如哲学中所说的一样:“任何事物都是一个矛盾的个体。
”穆斯堡尔效应具有一定的优点但也具有一定的缺点。
例如,(1)穆斯堡尔效应只有在固体物质中才能应用,这样可以在一定程度上削弱光子反冲能量和热致增宽效应;(2)穆斯堡尔效应发展到今天,我们并不能观测所有物质的穆斯堡尔效应;(3)许多具有穆斯堡尔效应的元素都应该在极低温度的情况下进行观测。
四.在磁学上以及与磁学领域相关的应用对于穆斯堡尔效应发展速度是十分惊人的以及它的应用方面是十分广泛的。
它在磁学以及磁性物质等方面就占据相当重要的地位,这是由于在元素周期表中有一半的元素都具有穆斯堡尔效应。
我们所熟知的铁族它是与磁性物质关系非常紧密的元素,如:3d族、4f族和5f族共计有20种元素,38种同位素都具有穆斯堡尔效应,这就导致铁族元素在磁学中占有重要的地位。
像前文中我们所提出的57Fe 的14.4kev的γ-光子反冲跃迁表现的几个显著地特点:微观探测性的用途很广,可以在室温和高温情况下进行实验;有较长的半衰期(可达到270天);吸收谱和发射谱的交叠区域较窄和高分辨率等特点,这就使得57Fe在穆斯堡尔效应的研究应用中占据相当大的比重。
本小节将重点根据穆斯堡尔效应对磁学和磁性物质的探究中的几个突出的应用进行介绍。
(1)铁氧体和石榴石型铁氧体等磁性物质中阳离子的研究在固体物理学中我们熟知了晶体结构的有关知识了解的,铁氧体的种类不同从而阳离子的占位也会不同。
对于我们所研究的A型尖晶石型铁氧体和B型石榴石型铁氧体中的阳离子晶位就会不完全相同,第一种A型铁氧体中阳离子有两种晶位分别是:四面体和八面体;第二种是B型铁氧体的阳离子有三种晶位分别是:四面体,八面体和十二面体。
由于两种铁氧体的晶位取向和所处的化学环境不同,所以导致穆斯堡尔谱线的线性结构也会不同。
同时我们也可以利用谱线的强度的不同来测量阳离子在不同结构中的具体分布,对于多晶体的穆斯堡尔谱线,如图2给出的石榴石型铁氧体的谱线,由此我们可以推导出在室温下3Fe+原子核的两种晶位的超精细结构为390与485千奥。
图2(2)不同点阵铁氧体的磁化强度的探究 我们可以利用穆斯堡尔效应对不同点阵的原子核进行超精细结构的测定,对实验与理论的结果进行分析对比可知,次级点阵原子核的超精细磁场随着温度T 的变化所组成的对比曲线与同级次点阵磁化强度随着T 的变化所组成的对比曲线的曲线是完全重合的,由此我们可以利用穆斯堡尔效应的温度关系来计算次级点阵的磁化强度与T 的关系,这一关系是宏观测量法不能给出的。
此外,我们也可以利用核磁共振来测量次级点阵的磁化强度与T 的关系,图3.给出A 位和B 位铁氧体的超精细结构()(0)sf sf T HH 与fT 的函数关系。
图3(3)尖晶石型铁氧体和石榴石型铁氧体等磁性物质中对2Fe+Fe+与3离子的研究对于某些非正分铁氧体经常含有少量的二价亚铁离子,我们采用一些化学分析的方法,但是这种方法是比较麻烦的并且会花费很长的时间,也无法排除其他多种离子的干扰,如果我们采用穆斯堡尔效应的方法,当温度高于一个居里点的时候,这样就可以完全消除磁超精细结构的干扰,另外由于核外电子组态与化学环境的差异。
我们可以根据2Fe+和3Fe+呈现完全不同的同质异能位错,所以易于研究,如图4.(4)铁氧体等磁性材料中超精细结构的探究在磁性材料中有些有序材料的自旋磁结构的不同,在很多情况下都是根据穆斯堡尔效应进行探测的。
例如所熟知的α-Fe O在莫林点以下23称为反铁磁体,它的自旋取向沿着[]111三角形晶轴排布。
在莫林点以上称为弱亚铁磁体,它的自旋取向在(1 1 1)晶面内部,在奈耳点以上称为顺磁性铁磁体。
(5)铁磁性铁氧体的穆斯堡尔谱线与磁场超精细结构的探究对于金属磁性材料的穆斯堡尔效应的探究,可以得到相关的原子核的微观结构的有关知识并与宏观特性进行对比研究,这样可以有利于对磁性材料规律性的研究(6)非晶体磁性物质的穆斯堡尔效应的探究非晶体磁性物质的探究,不仅在基础应用磁学与磁性物质的研究中备受瞩目。
例如:在某些不具有周期性特点的磁性物质以及混磁性和散磁性的探究属于应用磁学的内容,对于非晶体磁泡材料的应用属于磁性物质的内容。
五.穆斯堡尔效应在其它领域的应用穆斯堡尔效应的应用有几点突出的优点,这也使得它的应用领域不断地进行扩展。
不仅在物理学科学方面得到深入和发展,也在化学、工学、农学和医学甚至在考古学和美术学等领域也彰显着独特的魅力和作用,备受人们关注。
下面我们对其他方面的应用进行简单的概述。
(1)穆斯堡尔效应在物理学领域的应用穆斯堡尔效应在物理学的各个分支中都拥有极其重要的作用。
例如:在核物理学方面可以测定原子核的均方半径、测定原子核的电四极矩和测定核磁矩与核g因数等;在超导物理学中的应用,可以计算超导体的自旋驰豫以及铁磁性与超导性的共存等;在固体物理学中测量晶体的镜像方式、离子的电子层结构、金属中的缺陷、相变等;在激光物理学方面的 -放射源的构想是非常引人关注的,由于此构想我们可能在不久的将来发现分子全息术。
