柔度系数ppt课件
结构动力学的刚度系数柔度系数汇总.
三、自由振动微分方程的解
y(t ) Asin( t )
四、结构的自振周期和频率
k 1 m m
T
2
五、例题
m
l /2 1 EI l /2
[例1] 计算图示结构的频率和周期。 （柔度法） 解：
1 m
l 48EI
ml 3 T 2 48EI
3
48 EI ml 3
1
k22 k2
k12 k2
k2
EI∞
k11 k1 k2
1
k1
k1 、k2 —— 楼层刚度（本楼层单位侧移所需的侧向力） k11 、k12 、k21 、k22 —— 位移法的刚度系数 kij
kij
—— 第j 个结点位移发生单位位移(其它结点位移均锁固)时， 在第i 个结点位移处产生的反力。
h EI EI
3EI 3EI 6EI k k左柱 k右柱 3 3 3 h h h
总侧移刚度：
h2
h1
i1
i2
k k左柱 k右柱
3 i1 3 i2 2 2 h1 h2
∞ h
总侧移刚度：
i1
i2
12 i1 12 i2 k k左柱 k右柱 2 2 h h
（刚度并联，两者叠加）
k
k11 k
EI
1
l
3EI l3
k11 m
3 EI
l3
k m
[例7]计算图示刚架的频率和周期。
1
m EI1= I I h
k
解： （刚度法）
由柱刚度并联 得：
12 EI 24 EI k 2 3 3 h h
k 24 EI m mh3
应力状态柔度系数
应力状态柔度系数一、前言应力状态柔度系数是材料力学中的一个重要概念，它可以描述材料在不同应力状态下的变形特性。
本文将从以下几个方面对应力状态柔度系数进行详细解析。
二、什么是应力状态柔度系数应力状态柔度系数（Compliance）是指材料在受到一定大小的外部载荷作用后所产生的变形量与外部载荷之间的比值。
它通常用符号S表示，单位为Pa^-1或m^2/N。
三、如何计算应力状态柔度系数对于弹性线性材料，在小变形条件下，其应力与应变之间存在线性关系。
因此，可以通过施加不同大小的外部载荷，并测量相应的变形量和应力值，从而计算出该材料在不同应力状态下的柔度系数。
具体而言，可以通过以下公式计算：S = ε/σ其中，S为柔度系数；ε为材料的相对变形量；σ为施加在材料上的外部载荷。
四、影响应力状态柔度系数的因素1. 材料类型：不同类型的材料其柔度系数也会有所差异。
例如，金属和聚合物等材料其柔度系数相差很大。
2. 应力状态：材料在不同应力状态下的柔度系数也会有所不同。
例如，材料在拉伸和压缩等不同应力状态下其柔度系数也会有所差异。
3. 温度：温度对材料的柔度系数也会产生影响。
通常情况下，温度越高，材料的柔度系数越大。
4. 湿度：湿度对一些特殊类型的材料，如纤维素等，其柔度系数也会产生影响。
五、应力状态柔度系数的应用1. 材料设计：通过测量材料在不同应力状态下的柔度系数，可以为新型材料的设计提供重要参考依据。
2. 材料测试：测量材料的柔度系数是评价其性能和质量的重要手段之一。
3. 工程应用：在工程实践中，经常需要考虑不同应力状态下材料变形情况。
因此，了解材料在不同应力状态下的柔度系数对于工程设计和分析具有重要意义。
六、结论通过本文对应力状态柔度系数进行详细解析，我们可以了解到该概念在材料力学中的重要性以及其计算方法、影响因素和应用等方面的知识。
在材料设计、测试和工程应用等领域中，应力状态柔度系数都具有重要的作用。
柔度系数符号
柔度系数符号1. 什么是柔度系数？柔度系数是一种用于描述材料柔软性的物理量。
它是指材料在受到外力作用后发生变形的程度。
柔度系数通常用符号表示，可以用于定量比较不同材料的柔软性。
2. 柔度系数的符号表示柔度系数一般用小写字母表示，常见的符号有：•ε：表示材料的应变（strain），是指材料在受到外力作用后相对于初始状态的变形程度。
应变可以是线性的，也可以是非线性的，取决于材料的性质。
•σ：表示材料的应力（stress），是指材料单位面积上受到的力的大小。
应力可以是拉伸应力、剪切应力等不同类型的应力。
•E：表示材料的弹性模量（Young’s modulus），是指材料在拉伸或压缩时的应力和应变之间的比例关系。
弹性模量可以用来描述材料的刚度。
•G：表示材料的剪切模量（shear modulus），是指材料在剪切应力下的变形程度。
剪切模量可以用来描述材料的刚度。
•ν：表示材料的泊松比（Poisson’s ratio），是指材料在拉伸或压缩时在垂直方向上的收缩或伸长程度与拉伸方向上的应变之间的比例关系。
3. 柔度系数的计算方法柔度系数可以通过应力和应变之间的关系来计算。
对于线性弹性材料，柔度系数可以用弹性模量和泊松比来表示：柔度系数 = 弹性模量 / (2 * (1 + 泊松比))对于非线性材料，柔度系数的计算相对复杂，需要考虑材料的应力-应变曲线。
4. 柔度系数的应用柔度系数在材料科学和工程中有广泛的应用。
它可以用来比较不同材料的柔软性，帮助工程师选择合适的材料。
柔度系数还可以用来设计和优化结构，以确保其在受力时具有良好的变形性能。
在纺织工业中，柔度系数可以用来评估织物的柔软性和弹性。
这对于设计舒适的服装和纺织品非常重要。
在建筑工程中，柔度系数可以用来评估建筑材料的变形能力和抗震性能。
它可以帮助工程师设计出更安全、更稳定的建筑结构。
在医学领域，柔度系数可以用来评估组织和器官的柔软性。
例如，在眼科学中，柔度系数可以用来评估角膜的弹性，帮助医生诊断角膜病变。
结构动力学的刚度系数柔度系数通用课件
扭曲刚度系数计算
扭曲刚度系数定义
01
扭曲刚度系数是衡量结构在扭曲载荷下抵抗变形的能力的系数。
扭曲刚度系数的计算公式
02
扭曲刚度系数可以通过结构材料的弹性模量和截面极惯性矩计
算得出。
扭曲刚度系数的物理意义
03
扭曲刚度系数越大，表示结构在扭曲载荷下的变形越小，结构
的抗扭能力越强。
复合受力下的刚度系数计算
分析方法
通过对处理后的数据进行统计分析、曲线拟合、模式识别等，可以进一步分析结构的动力学特性，包括固有频率、 阻尼比等参数。此外，还可以通过对比不同结构的响应数据，评估不同结构的动力学性能。
实验结果及讨论
实验结果
实验测得了不同结构在不同激振条件下的响 应数据，包括加速度和位移。通过对数据进 行处理和分析，得到了不同结构的刚度系数 和柔度系数以及相关的动力学参数。
刚度系数和柔度系数是结构动力学中两个重要的概念，可以反映结构的刚度和柔度性质。
本文通过理论和实例分析，对结构动力学中的刚度系数和柔度系数进行了详细阐述，并介绍了它们在工 程实际中的应用和意义。
对未来研究的展望
随着科学技术的发展，结构动力学的研究领域将不断扩大，对刚度系数和柔度系数 的认识也将更加深入。
复合受力下的柔度系数的计算
复合受力下的柔度系数可以通过结构在复合力作用下的变形量进行计算。
03
复合受力下的柔度系数的影响因素
复合受力下的柔度系数受到材料性质、截面形状、边界条件等因素的影
响。
04
刚度系数与柔度系数的应用
在结构设计中的应用
刚度系数
在结构设计中，刚度系数是用来衡量结构抵抗变形的能力。通过计算和分析刚度 系数，可以确定结构的稳定性、承载能力和振动特性。
结构动力学的刚度系数柔度系数
l /2
1
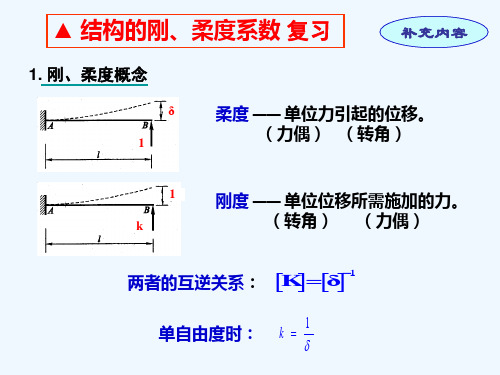
[例1] 计算图示结构的频率和周期。
解：（柔度法）
1 m
l3 48EI
48EI ml3
T 2 ml3 48EI
H
m
1
A,E,I
E,I
[例2] 计算图示结构的水平和竖向振动频率。
1
解：
V
H
1 m H
E,A
V
1 mV
其中
H
EA
l
[例3] 图示三根单跨梁，EI为常数，在梁中点有集中质量m ，
EI
总侧移刚度： kk左 柱 k右 柱 3 h E 3I3 h E 3I6 h E 3I
h1
i1
i 2 h2
∞
h i1
i2
总侧移刚度： kk左柱k右柱3h1i213hi222
总侧移刚度： kk左 柱k右 柱12 h2i112 h2i2
并联一般公式：
n
k kj j 1
（2）串联
Δ P h2 k2 Δ1
结束
（第二版）作业: 10 — 4、5
A
m E1I1=∞ m
EA=∞
A
m E1I1=∞ m
k
（等效图）
l /2
l /2
解：（刚度法） (2l)3 l3
48EI 6EI
EI l
k
1
6EI l3
1y 2
y
（位移几何关系）
ky
A
由∑MA=0
得： m (y)lm ylkyl0
22
化简得： 5m y4ky0
m(1 y) 2
my
（惯性力和弹力）
● 熟记几种简单情况的刚、柔度
δ 悬臂梁自由端：
结构动力学的刚度系数柔度系数
1 87.35 S1 m
a
10
[例5]求图示结构的自振圆频率。
h
Am
I→∞ EI
B l
1
h h
解：先求δ
C
1 lh2h lh2
EI 2 3 3EI
1 3EI m11 mlh2
a
11
[例6]求图示结构的自振频率。
解：先求k11
k11
k
3EI l3
（刚度并联，两者叠加）
22
化简得： 5m& y& 4ky0
m ( 1 &y&) 2
m &y&
（惯性力和弹力）
4k 24EI
5ma 5ml3
15
[例10] 建立图示结构的振动方程，并计算自振频率、周期。
k
k
m
EI
EI
Δ=1
l
6i/l
EA=∞
EI
EI
l
l
12i/l2
解：
刚度并联： k412i/l248lE 3I
振动方程
据此可得：ω1 ׃ω2 ׃ω3= 1 ׃1.512 ׃2
结构约束越强,则刚度越大, 其自振动频率也越大。
a
9
[例4] 图示桁架，E=206GPa , A=0.002m2 , mg=40KN , 计算自振频率。( g取10m/s2 )
1
m
4
4
解：（柔度法）
3
5 (Fn)i2li 243
k12=k21=－k2
k22=k2
a
5
3. 应用举例
求图示三层刚架的顶端侧移。
P
结构动力学的刚度系数柔度系数
my
（惯性力和弹力）
[例10] 建立图示结构的振动方程，并计算自振频率、EI
EA=∞ EI l
Δ=1
l
EI l
6i/l
12i/l2
2
48EI k 4 12i / l 3 刚度并联： 解： l 48EI ky 0 即 my 3 y 0 振动方程 my l
k
3EI l3
i
1 k
两端固支梁侧移刚度： 12 EI 12i k 3 2 l l
i
1
一固一铰支梁的侧移刚度:（同悬臂梁） 1 3EI 3i k 3 2 l l k 简支梁中点柔度、刚度：
l3 48EI 48EI k 3 l
δ
2. 柱的并联、串联刚度 （1）并联 总侧移刚度：
2
[例8]建立图示结构的振动方程，并计算自振频率。
A l /2
2m
EI=∞
m k
l /4
解： （刚度法） 由∑MA=0 得：
l /2
4 y （位移几何关系） 5 4 k ( y) 5 2m
k
2 y 5
2 l 5l 4 2m( y) my k ( y) l 0 5 2 4 5
l/2 l/2
3 l/ 16
l/2
l/2
P=1
l/2
l/2
1 ，先求δ 解： m
l 1 48EI
3
l/
2
3l /32 7l5 2 P=1 768EI
l3 3 192 EI
1
48 EI ml 3
3 192 EI 1 l 2 768 l EI 3l l 5l 7l 2 2 (2 3 )3 EI 6 2ml 16 2 32 768 EI 7 ml 3
结构动力学的刚度系数柔度系数
k21k2 1 k11k1k2
k22 k2
k12 k2
k1、k2 —— 楼层刚度（本楼层单位侧移所需的侧向力）
k11 、k12 、k21 、k22 —— 位移法的刚度系数 k i j
k i j —— 第j 个结点位移发生单位位移(其它结点位移均锁固)时，
在第i 个结点位移处产生的反力。
由图示可知： k11=k1+k2
48EI ml3
T 2 ml3 48EI
H
m
1
A,E,I
E,I
[例2] 计算图示结构的水平和竖向振动频率。
1
解：
V
H
1 m H
E,A
V
1 mV
其中
H
l3 3EI
其中
v
l EA
l
[例3] 图示三根单跨梁，EI为常数，在梁中点有集中质量m ，
不考虑梁的质量，试比较三者的自振频率。
m
m
m
l/2
l/2
1 k
k 12lE3 I 1l22i
一固一铰支梁的侧移刚度:（同悬臂梁）
i
1
1
k
k
3EI l3
3i l2
简支梁中点柔度、刚度：
δ
l3
48EI
48EI k l3
2. 柱的并联、串联刚度
（1）并联
h EI
EI
总侧移刚度： kk左 柱 k右 柱 3 h E 3I3 h E 3I6 h E 3I
h1
A
m E1I1=∞ m
EA=∞
A
m E1I1=∞ m
k
（等效图）
l /2
l /2
解：（刚度法） (2l)3 l3
结构动力学的刚度系数柔度系数
三、自由振动微分方程的解
y(t) Asin( t )
四、结构的自振周期和频率
静定结构，图乘法求δ
k 1 m m
T 2
五、例题
m EI
l /2
l /2
1
[例1] 计算图示结构的频率和周期。
解：（柔度法）
1 m
l3
48EI
48EI ml 3
T 2 ml3
▲ 结构的刚、柔度系数 复习
补充内容
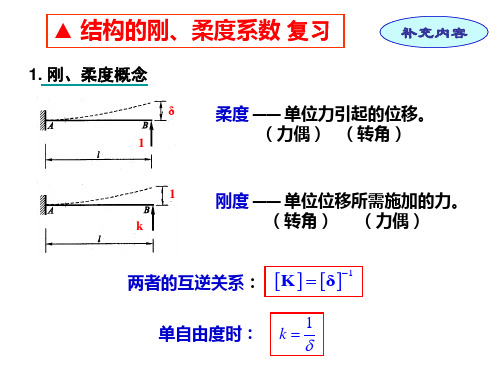
1. 刚、柔度概念
δ 1
柔度 —— 单位力引起的位移。 （力偶） （转角）
1 k
刚度 —— 单位位移所需施加的力。 （转角） （力偶）
两者的互逆关系： K δ1
单自由度时： k 1
● 熟记几种简单情况的刚、柔度
δ 悬臂梁自由端：
1
l3
24EI 5ml 3
1y 2
y
（位移几何关系）
ky
A
m(1 y) 2
my
（惯性力和弹力）
[例10] 建立图示结构的振动方程，并计算自振频率、周期。
k
k
m
EI
EI
Δ=1
l
6i/l
EA=∞
EI
EI
l
l
12i/l2
解：
刚度并联：
k
4 12i
/
l2
48 EI l3
48 EI 振动方程 my ky 0 即 my l 3 y 0
结构约束越强,则刚度越大, 其自振动频率也越大。
[例4] 图示桁架，E=206GPa , A=0.002m2 , mg=40KN , 计算自振频率。( g取10m/s2 )
柔度系数符号
柔度系数符号
摘要：
1.柔度系数符号的定义
2.柔度系数符号的性质
3.柔度系数符号的应用领域
4.柔度系数符号与其他相关概念的区别
正文：
柔度系数符号是用来表示材料、结构或系统的柔度性能的一种符号。
在工程、物理和数学等领域中，柔度系数符号被广泛应用。
柔度系数符号具有以下性质：它是一个无量纲的系数，表示单位力的作用下，材料、结构或系统的形变程度。
柔度系数符号的值越大，表示单位力作用下，对应的形变程度越大，即该材料、结构或系统的柔度性能越好。
柔度系数符号的应用领域非常广泛。
在工程领域，它被用来设计具有良好柔度性能的结构，以提高其稳定性和安全性。
在物理学中，柔度系数符号被用来描述弹簧、绳索等弹性材料的性能。
在数学中，柔度系数符号被用来描述非线性系统的动态行为。
柔度系数符号与其他相关概念的区别主要体现在以下几点：弹性模量是表示材料弹性性能的量，它描述的是单位应力作用下，材料的应变量；而刚度系数是表示材料、结构或系统的刚度性能的量，它描述的是单位力作用下，材料的形变量。
因此，柔度系数符号、弹性模量和刚度系数这三个概念在描述材料、结构或系统的性能时，所关注的方面是不同的。
总之，柔度系数符号是一个重要的无量纲系数，它在工程、物理和数学等领域中有着广泛的应用。
柔度系数ppt课件
i
1
1
k
k
3EI l3
3i l2
简支梁中点柔度、刚度：
δ
l3
48EI
k
48EI l3
2
2. 柱的并联、串联刚度
（1）并联
h EI
EI
总侧移刚度：
k
k左柱
k右柱
3EI h3
3EI h3
6EI h3
h1
i1
i2 h2
∞
h i1
i2
总侧移刚度：
k
k左柱
k右柱
3 h
i1
2 1
3 i2
h
2 2
总侧移刚度：
EI , m
2
39.84 l2
EI , m
3
88.83 l2
EI m
解得:1
9.80 l2
EI , m
解得 :1
9.86 l2
EI , m
2
38.2 l2
EI m
解得:1
9.865 l2
EI , m
2
39.2 l2
EI m
3
84.6 l2
EI m
(－0.7%）
(－0.1%） (－3.1%） (－0.05%） (－0.7%） (－4.8%）
据此可得：ω1 ׃ω2 ׃ω3= 1 ׃1.512 ׃2
结构约束越强,则刚度越大, 其自振动频率也越大。
8
m
l
ml
ml
ml
4
2
4
l/3
l/3
ml ml
ml
ml
63
3
6
l/3
l/3
l/3
柔度系数符号
柔度系数符号摘要：1.柔度系数的定义和意义2.柔度系数的符号表示3.柔度系数在工程中的应用4.提高柔度系数的方法5.总结正文：柔度系数是一个用于描述物体在受力过程中形变程度的物理量，它反映了材料的柔软程度或刚度。
在工程设计中，了解和掌握柔度系数至关重要，因为它可以直接影响到产品的使用寿命、性能和稳定性。
一、柔度系数的定义和意义柔度系数（Symbol: μ）是用来衡量材料在受力时的变形能力的物理量，它与材料的弹性模量（E）和泊松比（ν）有密切关系。
柔度系数μ越小，材料的柔软程度越高，抗变形能力越强；反之，μ越大，材料的刚度越高，抗变形能力越弱。
二、柔度系数的符号表示柔度系数通常用希腊字母μ（mu）表示，单位为1/Pa（帕斯卡）。
在实际工程中，柔度系数通常用符号C表示，单位为1/N（牛顿）。
它们之间的关系为：C = μ * ΔL / ΔF，其中ΔL表示受力后的变形量，ΔF表示所施加的力。
三、柔度系数在工程中的应用1.结构设计：在建筑、桥梁、机械等结构设计中，通过计算和比较不同材料的柔度系数，可以选择更适合的结构材料，提高结构的稳定性和使用寿命。
2.零部件选型：在机械零部件选型中，了解各部件的柔度系数，可以有效降低系统的振动、噪声和磨损，提高传动效率。
3.材料研究：通过研究材料的柔度系数，可以指导新材料的开发和优化，满足不同工程领域的应用需求。
四、提高柔度系数的方法1.选用高弹性模量的材料：提高材料的弹性模量可以降低柔度系数，提高抗变形能力。
2.调整材料结构：如采用纤维增强、网格结构等方式，可以提高材料的整体刚度，降低柔度系数。
3.改进设计方法：在结构设计中，采用合理的设计方法和优化算法，可以降低结构的柔度系数，提高稳定性。
五、总结柔度系数是一个重要的工程参数，它直接影响到产品的使用寿命、性能和稳定性。
了解和掌握柔度系数的符号、定义和应用，对于工程设计和材料研究具有重要的指导意义。
应力状态柔度系数
应力状态柔度系数一、什么是应力状态柔度系数应力状态柔度系数是弹性力学中的一个重要概念，用来描述材料在应力作用下的变形程度。
它反映了材料的柔韧性和变形能力。
二、应力状态柔度系数的定义应力状态柔度系数定义为材料的单位体积或单位面积上的应变与该处应力的比值，通常用符号J表示。
计算公式为：J = ε / σ其中，J为应力状态柔度系数，ε为应变，σ为应力。
三、应力状态柔度系数的计算方法应力状态柔度系数的计算方法根据具体材料和应变情况而定。
下面分别介绍几种常见的计算方法：1. 线性弹性材料的应力状态柔度系数对于线性弹性材料，应力和应变成正比，其应力状态柔度系数可以直接由应力-应变曲线得到。
根据应力-应变曲线的斜率，可以得到应变与应力的比值，即应力状态柔度系数。
2. 非线性材料的应力状态柔度系数对于非线性材料，其应力和应变之间的关系不再是简单的比例关系，需要使用更复杂的计算方法。
常见的方法有有限元法、试验测量法等。
这些方法可以通过实验或数值计算得到材料在不同应力条件下的应力状态柔度系数。
3. 剪切变形的应力状态柔度系数在剪切应变条件下，材料的应力状态柔度系数可以通过剪切刚度来计算。
剪切刚度是指单位面积上的剪切应力与剪切应变的比值。
四、应力状态柔度系数的意义和应用应力状态柔度系数有着重要的意义和应用。
它可以用来描述材料的各种力学特性，例如柔韧性、变形能力等。
以下是应力状态柔度系数的几个应用：1. 构建结构物的刚度分析在建筑、桥梁等工程中，需要对结构物的刚度进行分析和计算。
应力状态柔度系数可以用来描述材料的刚度，从而对结构物的整体强度和稳定性进行评估。
2. 材料选择和设计优化应力状态柔度系数可以用来评估不同材料的柔韧性和变形能力。
在材料选择和设计优化中，可以根据应力状态柔度系数来选择合适的材料，以达到设计要求。
3. 材料性能测试和质量控制应力状态柔度系数可以用来测试材料的力学性能，例如强度、刚度等。
通过对材料的应力状态柔度系数进行测试，可以评估材料的质量，并进行质量控制。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
m EI
l /2
l /2
1
例2.计算图示结构的水平和竖向振动频率。
H
1
m
1
V
l
A,E,I
E,I
E,A
l3
48 EI
48 EI ml 3
T 2
ml 3 48EI
例3.计算图示刚架的频率和周期。
m
6EI
EI1=
h2
I
Ih
12EI h3
6EI h2
H
1
m H
V
1
m
l/2
l/2
解：1）求δ
1
l3 48EI
m
l/2
l/2
3l/16
P=1
l/2
2
7l 3 768EI
5l/32
P=1
m
l/2
l/2
3
l3 192EI
1
1
m1
48EI ml3
21
E1Im1l622(2
l 2
77613m86l El3I2l
5l3 )
32
71l 3
7m68E3I
192EI ml3
据此可得：ω1 ׃ω2 ׃ω3= 1 ׃1.512 ׃2
i3
i2
i1
i3
k1
12i1 h12
2
k2
12i2 h22
2
k3
12i3 h32
2
i2
（柱并联）
2）计算楼顶点（侧移）柔度
i1
1 1 1 1
k k1 k2 k3
3）计算顶端侧移
P
P
1 k1
1 k2
1 k3
P
24
h12 i1
h22 i2
h32 i3
6
五、例题
m EI
l /2
l /2
mV
由截面平衡
1
6EI
k
k
24 EI h3
h2
12EI
h3
k m
24 EI mh 3
6EI h2
T 2 mh3
2EI 1
● 熟记几种简单情况的刚、柔度
δ 悬臂梁自由端：
1
l3
3EI
k
3EI l3
i
两端固支梁侧移刚度：
1 k
k
12EI l3
12i l2
一固一铰支梁的侧移刚度: （同悬臂梁）
据此可得：ω1 ׃ω2 ׃ω3= 1 ׃1.512 ׃2
结构约束越强,则刚度越大, 其自振动频率也越大。
8
m
l
ml
ml
ml
4
2
4
l/3
l/3
ml ml
ml
ml
63
3
6
l/3
l/3
l/3
ml ml ml ml ml
84 4
4
8
l/3 l/3 l/3 l/3
精确解 : 1
9.87 l2
1
[例1] 计算图示结构的频率和周期。
解：（柔度法）
1 m
l3
48EI
48EI
ml 3
T 2 ml3
48EI
H
m
1
A,E,I
E,I
[例2] 计算图示结构的水平和竖向振动频率。
1
解：
V
H
1
m H
E,A
V
1
mV
其中
H
l3 3EI
其中
v
l EA
7
l
[例3] 图示三根单跨梁，EI为常数，在梁中点有集中质量m ，
k11 、k12 、k21 、k22 —— 位移法的刚度系数 kij
kij —— 第j 个结点位移发生单位位移(其它结点位移均锁固)时，
在第i 个结点位移处产生的反力。
由图示可知： k11=k1+k2
k12=k21=－k2
k22=k2
5
3. 应用举例
求图示三层刚架的顶端侧移。
P
解： 1）计算各楼层（侧移）刚度
EI , m
2
39.84 l2
EI , m
3
88.83 l2
EI m
解得:1
9.80 l2
EI , m
解得 :1
9.86 l2
EI , m
2
38.2 l2
EI m
解得:1
9.865 l2
EI , m
2
39.2 l2
EI m
3
84.6 l2
EI m
(－0.7%）
(－0.1%） (－3.1%） (－0.05%） (－0.7%） (－4.8%）
不考虑梁的质量，试比较三者的自振频率。
m
m
m
l/2
l/2
解：
1
3l/16
，先求δ
m
1
l3 48EI
l/2
l/2
l/2
P=1
2
7l53l/32 768PE=I1
l/2
l/2
3
l3 192EI
1
48EI ml 3
2
E1I2
l2 (2
6
7726lm8El1336Il
l 2
352l)37678l1E39mI2lE3 I
结构约束越强,其刚度越大,刚度越大,其自振动频率也越大。
11
例6、求图示结构的自振频率。
解：求 k
k11
k11
3EI
m
k11
k
3EI l3
k l3
1
k
EI
l
k11 3EI l3 k
m
m
•对于静定结构一般计算柔度系数方便。 •如果让振动体系沿振动方向发生单位位移时，所有刚节点 都不能发生转动（如横梁刚度为∞刚架)计算刚度系数方便。
i
1
1
k
k
3EI l3
3i l2
简支梁中点柔度、刚度：
δ
l3
48EI
k
48EI l3
2
2. 柱的并联、串联刚度
（1）并联
h EI
EI
总侧移刚度：
kk左柱k右柱3EI h33EI h3
6EI h3
h1
i1
i2 h2
∞
h i1
i2
总侧移刚度：
k
k左柱
k右柱
3 h
i1
2 1
3 i2
h
2 2
总侧移刚度：
k
k左柱
k右柱
12 i1 h2
12 i2 h2
并联一般公式：
n
k kj j 1
3
（2）串联
Δ P h2 k2 Δ1
h1 k1
Δ2
1
Pg1
Pg1 k1
楼面刚度 为无穷大 视同刚臂
2
Pg 2
Pg1 k2
1
2
Pg1 k1
Pg1 k2
P
1 k1
1 k2
k1 、k2 — 楼层刚度
k1
12i1 h12
两端刚结的杆的侧移刚度为：
12EI l3
一端铰结的杆的侧移刚度为：
3EI
l3
12
9
例5、求图示结构的自振圆频率。
1
k Am
h
I→∞
EI
Bθ
l
1
h
解法1：求 k
θ=1/h
MBA=kh = MBC
3 EI 3EI
l lh
C
k
3EI lh2
k m
3EI mh 2l
解法2：求 δ
1 lh 2h lh2
EI 2 3 3EI
1
m11
3EI m lh2
10
例4、图示三根单跨梁，EI为常数，在梁中点有集中质量m， 不考虑梁的质量，试比较三者的自振频率。
k2
12i2 h22
总刚度： k P 1
1 k1
1 k2
串联一般公式：
1 1 1 L 1 n 1
k k1 k2
kn k j1 j
4
▲ 楼层刚度与位移法刚度系数的关系
EI∞
k2
EI∞
1 k1
k21 k2 1 k11 k1 k2
k22 k2
k12 k2
k1、k2 —— 楼层刚度（本楼层单位侧移所需的侧向力）