二年级奥数讲义学而思
学而思小学奥数知识点梳理

学而思小学奥数知识点梳理学而思教材编写组侍春雷前言小学奥数知识点梳理,对于学而思的小学奥数大纲建设尤其必要,不过,对于知识点的概括很可能出现以偏概全挂一漏万的现象,为此,本人参考了单尊主编的《小学数学奥林匹克》、中国少年报社主编的《华杯赛教材》、《华杯赛集训指南》以及学而思的《寒假班系列教材》和华罗庚学校的教材共五套教材,力图打破原有体系,重新整合划分,构建十七块体系(其第十七为解题方法汇集,可补充相应杂题),原则上简明扼要,努力刻画小学奥数知识的主树干。
概述一、计算1.四则混合运算繁分数⑴运算顺序⑵分数、小数混合运算技巧一般而言:①加减运算中,能化成有限小数的统一以小数形式;②乘除运算中,统一以分数形式。
⑶带分数与假分数的互化⑷繁分数的化简2.简便计算⑴凑整思想⑵基准数思想⑶裂项与拆分⑷提取公因数⑸商不变性质⑹改变运算顺序①运算定律的综合运用②连减的性质③ 连除的性质④ 同级运算移项的性质⑤ 增减括号的性质⑥ 变式提取公因数形如:1212......(......)n n a b a b a b a a a b ÷±÷±±÷=±±±÷3. 估算求某式的整数部分:扩缩法4. 比较大小① 通分a. 通分母b. 通分子② 跟“中介”比③ 利用倒数性质 若111a b c >>,则c>b>a.。
形如:312123m m m n n n >>,则312123n n n m m m <<。
5. 定义新运算6. 特殊数列求和运用相关公式:①()21321+=++n n n②()()612121222++=+++n n n n③()21n a n n n n =+=+④()()412121222333+=++=+++n n n n ⑤131171001⨯⨯⨯=⨯=abc abc abcabc⑥()()b a b a b a -+=-22⑦1+2+3+4…(n-1)+n+(n-1)+…4+3+2+1=n 2二、 数论1. 奇偶性问题奇±奇=偶 奇×奇=奇奇±偶=奇奇×偶=偶偶±偶=偶偶×偶=偶2.位值原则形如:abc=100a+10b+c3.数的整除特征:4.整除性质①如果c|a、c|b,那么c|(a±b)。
学而思小学奥数知识点梳理(大纲视图)资料讲解

⑷三视图与展开图
最短线路与展开图形状问题
⑸染色问题
几面染色的块数与“芯”、棱长、顶点、面数的关系。
四、
1
①开放型与封闭型
②间隔与株数的关系
2
外层边长数-2=内层边长数
(外层边长数-1)×4=外周长数
外层边长数2-中空边长数2=实面积数
3
①车长+桥长=速度×时间
②车长甲+车长乙=速度和×相遇时间
学而思小学奥数知识点梳理
学而思教材编写组侍春雷
前言
小学奥数知识点梳理,对于学而思的小学奥数大纲建设尤其必要,不过,对于知识点的概括很可能出现以偏概全挂一漏万的现象,为此,本人参考了单尊主编的《小学数学奥林匹克》、中国少年报社主编的《华杯赛教材》、《华杯赛集训指南》以及学而思的《寒假班系列教材》和华罗庚学校的教材共五套教材,力图打破原有体系,重新整合划分,构建十七块体系(其第十七为解题方法汇集,可补充相应杂题),原则上简明扼要,努力刻画小学奥数知识的主树干。
③车长甲+车长乙=速度差×追及时间
列车与人或骑车人或另一列车上的司机的相遇及追及问题
车长=速度和×相遇时间
车长=速度差×追及时间
4
差不变原理
5
假设法的解题思想
6
原有草量=(牛吃速度-草长速度)×时间
7
8
分析差量关系
9
10
11
12
还原法,从结果入手
13
列表消元法
等价条件代换
五、
1
路程和=速度和×相遇时间
n的约数个数:d(n)=(a1+1)(a2+1)....(ak+1)
学而思小学奥数知识点梳理

学而思小学奥数知识点梳理The final edition was revised on December 14th, 2020.学而思小学奥数知识点梳理学而思教材编写组前言小学奥数知识点梳理,对于学而思的小学奥数大纲建设尤其必要,不过,对于知识点的概括很可能出现以偏概全挂一漏万的现象,为此,本人参考了单尊主编的《小学数学奥林匹克》、中国少年报社主编的《华杯赛教材》、《华杯赛集训指南》以及学而思的《寒假班系列教材》和华罗庚学校的教材共五套教材,力图打破原有体系,重新整合划分,构建十七块体系(其第十七为解题方法汇集,可补充相应杂题),原则上简明扼要,努力刻画小学奥数知识的主树干。
概述一、计算1.四则混合运算繁分数⑴运算顺序⑵分数、小数混合运算技巧一般而言:①加减运算中,能化成有限小数的统一以小数形式;②乘除运算中,统一以分数形式。
⑶带分数与假分数的互化⑷繁分数的化简2.简便计算⑴凑整思想⑵基准数思想⑶裂项与拆分⑷提取公因数⑸商不变性质⑹改变运算顺序①运算定律的综合运用②连减的性质③连除的性质④同级运算移项的性质⑤增减括号的性质⑥变式提取公因数形如:3.估算求某式的整数部分:扩缩法4.比较大小①通分a. 通分母b. 通分子②跟“中介”比③利用倒数性质若,则c>b>a.。
形如:,则。
5.定义新运算6.特殊数列求和运用相关公式:①②③④⑤⑥⑦1+2+3+4…(n-1)+n+(n-1)+…4+3+2+1=n二、数论1.奇偶性问题奇奇=偶奇×奇=奇奇偶=奇奇×偶=偶偶偶=偶偶×偶=偶2.位值原则形如: =100a+10b+c3.数的整除特征:整除数特征2 末尾是0、2、4、6、83 各数位上数字的和是3的倍数5 末尾是0或59 各数位上数字的和是9的倍数11 奇数位上数字的和与偶数位上数字的和,两者之差是11的倍数4和25 末两位数是4(或25)的倍数8和125 末三位数是8(或125)的倍数7、11、13 末三位数与前几位数的差是7(或11或13)的倍数4.整除性质①如果c|a、c|b,那么c|(a b)。
二年级学而思秋季数学超常班讲义第五讲
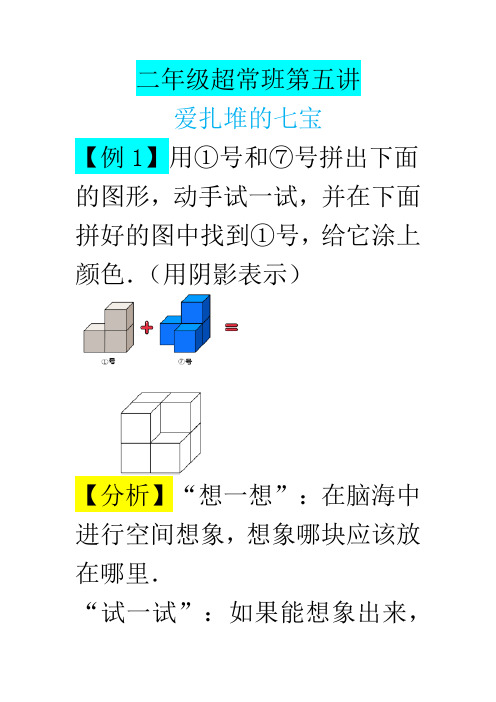
二年级超常班第五讲爱扎堆的七宝【例1】用①号和⑦号拼出下面的图形,动手试一试,并在下面拼好的图中找到①号,给它涂上颜色.(用阴影表示)【分析】“想一想”:在脑海中进行空间想象,想象哪块应该放在哪里.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.我们已经学习了“知道位置两拼”和“知道粘贴面两拼”,本活动是知道拼好的样子去两拼,和前面的方法一样,可以先将其中的一个摆在桌子上,比如先将⑦号放在桌子上,再将①号和⑦号拼在一起,观察拼成的图形是什么样子,是否和题中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和题中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助分析图形,在题目所给的图形中,找到①号,标注出来,如果①号在上面一层,那么剩下的不可能是⑦号;如果①号在下面一层,那么剩下的可能是⑦号;如果①号在左面一层,那么剩下的可能是⑦号;如果①号在右面一层,那么剩下的不可能是⑦号;如果①号在前面一层,那么剩下的不可能是⑦号;如果①号在后面一层,那么剩下的可能是⑦号.再在所有可能的情况里确定①号和⑦号的具体位置,将①号画出来.要求学生至少能找到一种可能,并画出来,程度好的班,可以要求学生找出尽可能多的情况.通过尝试,答案如下:【例2】用①号和⑥号拼出下面的图形,动手试一试,并在下面拼好的图中找到①号,给它涂上颜色.(用阴影表示)【分析】用①号和⑥号拼出下面的图形,动手试一试,并在下面拼好的图中找到①号,给它涂上颜色.(用阴影表示)“想一想”:在脑海中进行空间想象,想象哪块应该放在哪里.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.我们已经学习了“知道位置两拼”和“知道粘贴面两拼”,本例题是知道拼好的样子去两拼,和前面的方法一样,可以先将其中的一个摆在桌子上,比如先将⑥号放在桌子上,再将①号和⑥号拼在一起,观察拼成的图形是什么样子,是否和题中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和题中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助分析图形,在题目所给的图形中,找到①号,标注出来,如果①号在上面一层,那么剩下的不可能是⑥号;如果①号在下面一层,那么剩下的可能是⑥号;如果①号在左面一层,那么剩下的不可能是⑥号;如果①号在右面一层,那么剩下的可能是⑥号;如果①号在前面一层,那么剩下的不可能是⑥号;如果①号在后面一层,那么剩下的可能是⑥号.再在所有可能的情况里确定①号和⑥号的具体位置,将①号画出来.要求学生至少能找到一种可能,并画出来,程度好的班,可以要求学生找出尽可能多的情况.通过尝试,答案如下:(答案不唯一)【例3】①号和③号拼在一起会变成什么样的图形呢?请你动手试一试.下面的A、B、C、D 都是由①号和③号拼成的,请你把它们的①号都涂上颜色.(用阴影表示)【分析】“想一想”:在脑海中进行空间想象,想象①号和③号拼在一起,会变成什么样子.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.和前面的方法一样,可以先将其中的一个摆在桌子上,比如先将③号放在桌子上,再将①号和③号拼在一起,观察拼成的图形是什么样子,是否和选项中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和选项中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助排除选项,在选项中,找到③号,本题可以从和①号相比特殊的③号入手,③号要在能放下3块的地方,那么A选项中,③号可以在右面横着,剩下的部分正好是①号,A选项正确,在选项中画出①号;B选项中,③号可以在下面横着,剩下的部分正好是①号,B选项正确,在选项中画出①号;C选项中,③号可以在前面横着,剩下的部分正好是①号,C选项正确,在选项中画出①号;D选项中,③号可以在后面横着,剩下的部分正好是①号,D选项正确,在选项中画出①号.要求学生至少可以判断出选项是否符合题意,程度好的班,可以要求学生自己动手操作,尽量多的拼出和选项不同的情况.通过尝试,答案如下:(答案不唯一)【例4】④号和⑦号拼在一起会变成什么样的图形呢?请你动手试一试.下面的A、B、C、D都是由④号和⑦号拼成的,请你把它们的④号都涂上颜色.(用阴影表示)【分析】“想一想”:在脑海中进行空间想象,想象⑦号和④号拼在一起,会变成什么样子.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.和前面的方法一样,可以先将其中的一个摆在桌子上,比如先将④号放在桌子上,再将⑦号和④号拼在一起,观察拼成的图形是什么样子,是否和选项中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和选项中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助排除选项,在选项中,找到④号,本题可以从和⑦号相比特殊的④号入手,④号要在能放下3块的地方,那么A选项中,④号可以在后面横着,剩下的部分正好是⑦号,A选项正确,在选项中画出④号;B选项中,④号可以在后面竖着,剩下的部分正好是⑦号,B选项正确,在选项中画出④号;C选项中,④号可以在后面竖着,剩下的部分正好是⑦号,C选项正确,在选项中画出④号;D选项中,④号可以在后面横着,剩下的部分正好是⑦号,D选项正确,在选项中画出④号.要求学生至少可以判断出选项是否符合题意,程度好的班,可以要求学生自己动手操作,尽量多的拼出和选项不同的情况.通过尝试,答案如下:(答案不唯一)【例5】用③号、⑤号和⑦号拼出下面的床,动手试一试,并在下面拼好的床中找到⑦号,给它涂上颜色.(用阴影表示)【分析】“想一想”:在脑海中进行空间想象,想象哪块应该放在哪里.⑤号和⑦号无论从哪个方向都是两层,只有③号可以平铺在一层,而床头是两层,床板是一层,可以推测③号平铺在床板上,⑤号和⑦号拼出床头.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.可以先将其中的一个摆在桌子上,比如先将③号放在桌子上,再将⑤号和⑦号拼在一起,观察拼成的图形是什么样子,是否和题中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和题中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助从结果入手分析图形,在题目所给的图形中,找到⑤号和⑦号,本题中⑤号和⑦号比较特殊,它们不能平铺在一层,总要高出一块,那么可以知道⑤号和⑦号要拼出床头,剩下的用③号补充完整.要求学生一定要动手操作.通过尝试,答案如下:【超常挑战】1.用①号、②号、③号和④号拼出下面的墙角,动手试一试,并在下面拼好的墙角中找到②号,给它涂上颜色.(用阴影表示)2.用②号、④号、⑤号和⑦号拼出下面的楼梯,动手试一试,并在下面拼好的楼梯中找到⑦号,给它涂上颜色.(用阴影表示)3.用①号、②号、④号和⑤号拼出下面的坦克,动手试一试,并在下面拼好的坦克中找到④号,给它涂上颜色.(用阴影表示)4.有3个和图1相同的图形.把3个图形组合到一起,可以组成各种形状.从①到⑥的6个图形中,找出能够用3个图1的图形组合起来构成的图形,并用○表示,不能组成的,请用×表示.(2009年第1届日本算术奥林匹克预赛试题)【分析】1.用①号、②号、③号和④号拼出下面的墙角,动手试一试,并在下面拼好的墙角中找到②号,给它涂上颜色.(用阴影表示)答案如下:(答案不唯一)2.“想一想”:在脑海中进行空间想象,想象哪块应该放在哪里.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.可以先将其中的一个摆在桌子上,比如先将②号放在桌子上,再将④号、⑤号和⑦号拼在一起,观察拼成的图形是什么样子,是否和题中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和题中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助从结果入手分析图形,可以从楼梯的顶端开始拼,能放在顶端的只有④号或⑦号,如果将⑦号放在顶端,那么剩下的三块不能拼出剩下的楼梯.那么顶端就是④号竖着放,剩下的用②号、⑤号和⑦号补充完整.要求学生一定要动手操作.通过尝试,答案如下:3.答案如下:(答案不唯一)4.①○;②○;③○;④×;⑤×;⑥×.显而易见,①、②、③都可以分成3个图1的图形,④、⑤、⑥最多可以分出两个图1的图形.在④中,面前的两个小正方体都只能和中间的小正方体组合,所以不行;在⑤中,高出去的两个小正方体无法组成图①的图形,所以不行;在⑥中,最左和最右的两个小正方体都只有一种组合方法,这样剩下中间一列三个小正方体,所以不行.。
二年级奥数讲义学而思

二年级奥数讲义学而思应用题之移多补少有这样一种问题:哥哥比弟弟多6块糖,哥哥给弟弟几块后,两人的糖同样多呢?显然,哥哥只能给出比弟弟多的一半,也就是 3块糖才能让两人的糖一样多。
像这样的问题我们简称为“移多补少”的问题。
“移多补少”看起来容易,可在解决具体问题时也容易出错误,现在我们就一起来研究移多补少的学问吧!(★★★)二⑴班同学分成两队进行拔河比赛,第一队有31人,如果从第一队中调3人到第二队,这时两队的人数才会一样多。
第二队原来有学生多少人?通过“移多补少”使得两者相等时:如果移动量为n,那么原来两者相差量为2n。
也就是说,相差量是移动量的两倍。
(★★★)农场有两个兔笼,甲兔笼里的兔子比乙兔笼里的兔子多24只,从甲兔笼里放几只兔子到乙兔笼里之后,⑴甲乙两笼兔子的数目相等?⑵甲兔笼里的兔子就比乙兔笼多4只兔子?“移多补少”后两者不相等时:⑴先假设两者相等,不看不等的量。
⑵利用“移多补少”使剩下部分相等(★★★★)学校合唱队原有68人,比鼓乐队人数多.如果合唱队员中的5人参加鼓乐队,合唱队比鼓乐队少2人。
原来鼓乐队有多少人?1解决“不相等”问题的关键:⑴假设相等⑵移多补少⑶将“假设”还原(★★★★)小华有两盒糖果,甲盒有糖78粒,乙盒有糖38粒,每次从甲盒取5粒糖放到乙盒,取几次两盒糖的粒数就同样多?【例4拓展】(★★★★)哥哥和弟弟集邮,原来两人的邮票张数相等,如果哥哥给弟弟9张邮票,则弟弟的邮票张数是哥哥的3倍,哥哥、弟弟原来各有邮票多少张?“移多补少”+差倍问题: 1.差倍问题解题 2.“移多补少”定差(★★★★★)如果从第二个盒子里拿出4颗放到第一个盒子里面,两个盒子里面的糖果就一样多。
如果从第一个盒子里面拿出6颗糖果放到第二个盒子里面,第二个盒子里的糖果是第一个盒子的2倍。
你知道两个盒子里各有多少颗糖果吗?2。
二年级学而思秋季数学超常班讲义

蜗牛爬井第六讲【例题分析】第6天;可以先考虑特殊的最后一天,蚂蚁爬5米刚好爬到井口,不再滑下,那么它在前几天一共向上移动了205-=15米;它每天爬上5米,又滑下2米,相当于每天只移动了52-=3米,之前爬了153÷=5天,所以第51+=6天爬到井口.一只蚂蚁从一口20米深的枯井底部往上爬,它每天往上爬5米后,就会滑下2米,像这样爬,这只蚂蚁第几天刚好爬到井口?【例题分析】第7天;水缸打水和蜗牛爬井一样,可以先考虑最后一天,这天早上工作人员刚好第一次将水缸装满,那么在此之前水缸里一共有水295-=24桶.每天打回5桶水,又用掉1桶水,则相当于每天往缸里增加51-=4桶水,需要244÷=6天,则第61+=7天第一次把水缸装满.有一口空水缸,需要29桶水才能刚好装满.工作人员每天早上会打回5桶水倒入缸中,傍晚又会用掉缸里1桶水,那么工作人员第几天才能第一次让水缸装满水?【例题分析】第6天;先考虑最后一天,水缸刚好第一次装满,那么在此之前水缸里一共有水216-=15桶.每天倒入6桶水,又用掉3桶水,则相当于每天往缸里增加63-=3桶水,需要153÷=5天,则第51+=6天才能第一次将水缸装满.【例题分析】32米;树懒每天向上爬6米,晚上滑下2米,每天树懒只向上移动了62-=4米.树懒第8天才到顶端,那么前7天共移动了47⨯=28米,再加上第8天的4米,树一共高284+=32米.树懒爬树,它从树底端开始,每天白天向上爬6米,晚上睡觉时滑下2米,第8天爬了4米后终于爬到了树顶端.请问这棵树高多少米?一个空水缸装满水需要21桶,婷婷每天早上向缸里倒入6桶水,晚上又用掉缸里3桶水,婷婷第几天才能第一次将水缸装满?【例题分析】31个;洋洋每次装5个桃子,又吃掉1个,相当于每次只装了514-=个桃子,7次后一共装了7428⨯=个桃子,最后又装3个桃子筐就满了.那么这个筐装满能装28331+=个桃子.【例题分析】18米;小猴爬的最高的位置,是第8次往上爬,还没有滑下来时的位置.小猴每次向上爬4米,然后滑下2米,相当于每次只向上移动了422-=米,第7次时爬到了2714⨯=米的位置,第8次时再往上爬4米到了最高位置,即14418+=米.【例题分析】6米;小丑第8天爬了4米爬到了树顶, 说明前817-=天小丑共向上移动了25421-=米,每天移动了2173÷=米.每次滑下3米,那么每次向上爬336+=米.一个小丑从一棵25米高的树底往上爬,每次向上爬若干米,接着又滑下3米,第8次爬了4米爬到树顶,那么小丑每次向上爬了几米呢?小猴爬竹杆,每次先向上爬4米,接着滑下2米.小猴从竹杆底端开始,共爬了8次,那么小猴最高时爬到了多少米高的位置?洋洋往一个空筐里装桃子,她每次往筐里装5个桃子,然后偷吃掉1个,像这样,第8次装了3个就把筐装满了,那么这个筐装满能装多少个桃子?【例题分析】4米;小蜗牛第6天爬了5米到井口,也就说明前5天一共向上移动了1055-=米,每天移动了551÷=米. 每天白天向上爬5米,则每天夜里会滑下514-=米.【例题分析】42桶;梦梦每天白天打回6桶水,晚上又用掉2桶,相当于每天水缸会增加624-=桶水,30624-=桶,2446÷=天,即第7天打6桶水时,水缸刚好第一次装满.此时梦梦一共打了6742⨯=桶水.一个空水缸,装满需要30桶水,梦梦每天白天会打回6桶水倒入水缸,晚上又会用掉水缸里的2桶水,那么到水缸刚好第一次装满时,梦梦一共打了多少桶水呢?一个空水缸,装满需要33桶水,洋洋每天白天会打回7桶水倒入水缸,晚上又会用掉水缸里的几桶水,第七天洋洋打回3桶水后水缸刚好第一次装满,那么洋洋每天晚上用掉了几桶水呢?小蜗牛从10米深的井底往上爬,每天白天向上爬5米,每天夜里又滑下若干米,第6天爬了5米爬到井口,那么小蜗牛每天夜里滑下了几米呢?【例题分析】64步;舞者先前进4步再后退2步,这样跳一次实际只向前移动了422-=步,24420-= 步,20210÷=次,即第11次时前进4步刚好跳到了另一头.前10次每一次跳了426+=步,这个人一共跳了610464⨯+=步.一位舞者沿一条直线前进4步,接着后退2步,像这样从舞台的一头跳到另一头.舞台的两头相距24步,这个人一共跳了多少步?。
小学二年级奥数精品讲义 第四讲 排队问题(学生)

2、 (2011 年全国“春蕾杯”小学二年级(决赛)试题) 二年级小朋友排练团体操,他们排成正方形的队伍。无论从前往后数、从后前数,还是从右 往左数、从左往右数,小亚都排在第 5 个,一共有( 解:每排人数和每列人数相同,都是:5+5-1=9(人) 所用所有的人数为: 9 9 8 (人) 1 81 )人在排练团体操
练习: 1、张老师出了两道思考题给兴趣组的同学做,每人至少做对一道题,其中做对第一题的 有 14 人,做对第 2 题的有 6 人,两题都做对的只有 3 人,求兴趣组共有学生多少人?
杯赛练习: 1、 (2012 年第二届学而思杯小学二年级试题)学而思举办智力运动会,二年级的同学都积 极参加,获奖同学和小何老师排成一排合影时,从左边数小何老师排在第 12 个,从右边数 小何老师排在第 13 个,那么,共有__23___名同学获奖。 解:所用的人数:12+13-1=24(人) 获奖学生人数为:24-1=23(人)
小灵童奥数
二年级春季班讲义
第四讲
排队问题
例 1、朗读小组的同学排成一排表演诗朗诵,从左往右数起,玲玲是第 8 个,从右边数起, 玲玲是第 7 个,有多少个同学报数我报 6,倒着报数我报 9,请你算一算,一共有多少个小朋 友在报数?
2、12 个小朋友排一队跳舞,从左往右数,小红是第 8 个;从右往左数,小红是第几个?
小东
小丽
解:小丽右边共有:12-4-3=5(人) 所以从右往左数,小丽排在第:5+1=6 答:小丽排在第 6 个。 5、 二(2)班同学人人都订报纸,订《语文报》的有 36 人,订《数学报》的 32 人,两种 报纸都订的有 14 人,求二(2)班共有多少人? 6、
订语文报:36 人
都订:14 人
学而思小学奥数知识点梳理(大纲视图)精编版

植 四、 典型应用题
1. 树问题
①开放型与封闭型 ②间隔与株数的关系 阵 2. 方 问题 外层边长数-2=内层边长数 (外层边长数-1)×4=外周长数 外层边长数 2-中空边长数 2=实面积数 车 桥 3. 列 过 问题 ①车长+桥长=速度×时间 ②③列车车车长长与甲甲人++车车或长长骑乙乙车==速速人度度或和差另××一追相列及遇车时时上间间的司机的相遇及追及问题 车长=速度和×相遇时间 车长=速度差×追及时间 龄 4. 年 问题
概述
一、 计算
1. 四则混合运算繁分数 ⑴ 运算顺序 ⑵ 分数、小数混合运算技巧
①一般而言: 加减运算中,能化成有限小数的统一以小数形式;
② 乘除运算中,统一以分数形式。
⑶带分数与假分数的互化 ⑷繁分数的化简 2. 简便计算 ⑴凑整思想 ⑵基准数思想 ⑶裂项与拆分 ⑷提取公因数 ⑸商不变性质 ⑹改变运算顺序
六、 计数问题
类枚举 1. 加法原理:分 排 2. 乘法原理: 列组合 容斥 3. 原理:
① 总 量数 =A+B+C-(AB+AC+BC)+ABC ② 常 总 量 用: 数 =A+B-AB
抽屉 4. 原理:
5. 握手至问多题至少问题
在 广泛 图形计数中应用 ① 角、线段、三角形,
② ③
长正方方形形、梯形、平行四边形
3.
路流程水行差船=速度差×追及时间 顺逆水水速速度度==船船速速+-水水速速
4. 船水多速速次相==((遇顺顺水水速速度度+-逆逆水水速速度度))÷÷22
线环型型路路程程:: 甲甲乙乙共共行行全全程程数数==相相遇遇次次数数×2-1
5. 环其形中跑甲道共行路程=单在单个全程所行路程×共行全程数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用题之移多补少
有这样一种问题:
哥哥比弟弟多6块糖,哥哥给弟弟几块后,两人的糖同样多呢
显然,哥哥只能给出比弟弟多的一半,也就是 3块糖才能让两人的糖一样多。
像这样的问题我们简称为“移多补少”的问题。
“移多补少”看起来容易,可在解决具体问题时也容易出错误,现在我们就一起来研究移多补少的学问吧!
(★★★)
二⑴班同学分成两队进行拔河比赛,第一队有31人,如果从第一队中调3人到第二队,这时两队的人数才会一样多。
第二队原来有学生多少人
通过“移多补少”使得两者相等时:
如果移动量为n,那么原来两者相差量为2n。
也就是说,相差量是移动量的两倍。
(★★★)
农场有两个兔笼,甲兔笼里的兔子比乙兔笼里的兔子多24只,从甲兔笼里放几只兔子到乙兔笼里之后,
⑴甲乙两笼兔子的数目相等
⑵甲兔笼里的兔子就比乙兔笼多4只兔子
“移多补少”后两者不相等时:
⑴先假设两者相等,不看不等的量。
⑵利用“移多补少”使剩下部分相等
(★★★★)
学校合唱队原有68人,比鼓乐队人数多.如果合唱队员中的5人参加鼓乐队,合唱队比鼓乐队少2人。
原来鼓乐队有多少人
解决“不相等”问题的关键:
⑴假设相等
⑵移多补少
⑶将“假设”还原
(★★★★)
小华有两盒糖果,甲盒有糖78粒,乙盒有糖38粒,每次从甲盒取5粒糖放到乙盒,取几次两盒糖的粒数就同样多
【例4拓展】(★★★★)
哥哥和弟弟集邮,原来两人的邮票张数相等,如果哥哥给弟弟9张邮票,则弟弟的邮票张数是哥哥的3倍,哥哥、弟弟原来各有邮票多少张
“移多补少”+差倍问题:
1.差倍问题解题
2.“移多补少”定差
(★★★★★)
如果从第二个盒子里拿出4颗放到第一个盒子里面,两个盒子里面的糖果就一样多。
如果从第一个盒子里面拿出6颗糖果放到第二个盒子里面,第二个盒子里的糖果是第一个盒子的2倍。
你知道两个盒子里各有多少颗糖果吗。
