山西省高考考前适应性训练考试(理科数学)
山西省高考前(3月)适应性测试数学试题(理)含答案

山西省高三下学期适应性考试理科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设复数z 满足12iz i =+,则z 的共轭复数z 的虚部是( ) A .i B .i -C .1-D .1答案:D 解析:12221i i z i i +-===--,则z 的共轭复数z =2i +,虚部为1。
2.已知实数集R ,集合{}2|log 3M x x =<,{}2|450N x x x =-->,则()R M N =( ) A .[1,8)- B .(0,5]C .[1,5)-D .(0,8)答案:B解析:集合{}|08M x x =<<,{}|51N x x x =><-或,R C N ={x|-1≤x ≤5}, 所以,()R MN =(0,5]3.已知函数2,0,()1,0,xe a xf x x a x ⎧+≤⎪=⎨++>⎪⎩a 为实数,若(2)()f x f x -≥,则x 的取值范围为( ) A .(,1]-∞ B .(,1]-∞-C .[1,)-+∞D .[1,)+∞答案:A解析:由题可知,函数()f x 在R 上为单调递增函数,因为(2)()f x f x -≥, 所以,2x x -≥,解得1x ≤4.若双曲线C :22221x y a b-=(0a >,0b >)的中心为O ,过C 的右顶点和右焦点分别作垂直于x 轴的直线,交C 的渐进线于A ,B 和M ,N ,若OAB ∆与OMN ∆的面积比为1:4,则C 的渐进线方程为( )A .y x =±B .3y x =±C .2y x =±D .3y x =±答案:B解析:依题可知△AOB 与△MON 相似,由三角形面积比等于相似比的平方,得:2214a c =,所以,2c a =,即222a b a +=4,所以,3b a=, 所以,C 的渐进线方程为3y x =±5.甲、乙二人争夺一场围棋比赛的冠,若比赛为“三局两胜”制,甲在每局比赛中获胜的概率均为23,且各局比赛结果相互,则在甲获得冠的情况下,比赛进行了3局的概率为( ) A .13 B .25 C .23 D .45答案:B解析:甲获得冠的概率为:,其中比赛进行了3局的概率为:,故所求概率为:820227275÷= 6.已知P 是圆222x y R +=上的一个动点,过点P 作曲线C 的两条互相垂直的切线,切点分别为M ,N ,MN 的中点为E ,若曲线C :22221(0)x y a b a b+=>>,且222R a b =+,则点E 的轨迹方程为22222222x y x y a ba b++=+,若曲线C :22221x y a b -=(0a b >>),且222R a b =-,则点E 的轨迹方程为( )A .22222222x y x y a b a b+-=-B .22222222x y x y a ba b+-=+. 22222222x y x y a b a b++=-D . 22222222x y x y a ba b++=+答案:A解析:由于椭圆与双曲线的定义中运算互为逆运算,所以,猜想双曲线对应的点E 的轨迹方程为:22222222x y x y a ba b+-=-7.72(1)x x+的展开式中3x 的系数为( ) A .1- B .1C .7-D .7答案:D解析:展开式:661371()17C x C x ⨯=,故系数为78.已知椭圆C :22221(0)x y a b a b+=>>与直线3y x =+只有一个公共点,且椭圆的离心率为5C 的方程为( ) A .221169x y += B .22154x y += C .22195x y += D .2212520x y += 答案:B解析:把3y x =+代入椭圆的方程,得:2222222()69a b x a x a a b +++-=0, 由于只有一个公共点,所以,△=0,得22a b +=9,又5c a =2245b a =,解得225,4a b == 9.已知函数()sin()f x A x ωϕ=+(0A >,0ω>,||2πϕ<)的部分图像如图所示,将函数()y f x =的图象向左平移43π个单位,得到函数()y g x =的图象,则函数()y g x =在区间5,22ππ⎡⎤⎢⎥⎣⎦上的最大值是( )A .3B .332C .322D .22答案:C解析:由图可知,函数()f x 的周期为24ππω=,所以,12ω=, 又点3(,0),(0,)32π-在函数图象上,所以,有10.如图,在ABC ∆中,6AB BC ==,90ABC ∠=︒,点D 为AC 的中点,将ABD ∆沿BD 折起到PBD ∆的位置,使PC PD =,连接PC ,得到三棱锥P BCD -,若该三棱锥的所有顶点都在同一球面上,则该球的表面积是( )A.7πB.5πC.3πD.π答案:A解析:依㼵意可得该三棱锥的面PCD是边长为3的正三角形,且BD⊥平面PCD,设三棱锥P-BDC外接球的球心为O,△PCD外接圆的圆心为O1,则OO1⊥平面PCD,所以四边形OO1DB为直角梯形,由BD=3,O1D=1,及OB=OD,可得OB=72,即外接球的半径为72,则其表面积为7π11.运行如图所示的程序框图,输出的数称为“水仙花数”.(算术符号MOD表示取余数,如1121MOD=).下列说法正确的个数是()①“水仙花数”是三位数;②152是“水仙花数”;③407是“水仙花数”.A.0 B.1 C.2 D.3答案:C解析:由程序框图知,a 表示一个数的个数,b 表示其十位数,c 表示其得位数。
2020年山西省高考考前适应性测试理科数学·答案与解析

则
A
′(0,0,
3),设 2
P(52
-
a,
3
a,0),其中 0
<
a
≤
3 2
,则
A′P
=
(
5 2
-
a,
3 a, -
3 2
).
平面 A′BM 的法向量为 n=(0,1,0),设直线 PA′与平面 A′BM 所成角为 θ,
| | 则 sinθ = cos A′P, n =
3a
= 3 10 .
( 5 - a )2 + 3a2 + 3
10
2
4
2a2 - 15a + 21 = 0. 解得 a = 15 ± 57 > 3 ,
4
2
所以不存在 P 满足条件 . ………………………………………………………………………………………… 12 分
19. 解:(1)设点 A( a, 0 )关于直线 y = x - 1 的对称点为 A′( x′, y′ ),
P
满足条件,这时
PB
=
3.
………………………………………………
12 分
(iii)若用条件③A′B= 7 ,在△A′BM 中,由余弦定理得 ∠A′MB = 120°.
过 A′作 A′O⊥BM,垂足为 O,则 A′O⊥平面 BCNM.
同(ii),以 O 为原点,OB, OD, OA′ 分别为 x, y, z 轴建立空间直角坐标系 .
ì y′
则
ïï í ïï î
x′ y′ 2
=
a a
=
+ 2
- 1, x′ -
解得 x′ 1,
=
省适应性考试数学(理)

2019年山西省高考适应性训练高三数学(理科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{|110},{|23,}A x x x B x x x =<->=-<<∈Z 或,则()R C A B ⋂=( ) A. {1,2}-B. {2,2}-C. {0,1,2}D. {1,0,1,2}-2. 下列函数中既不是奇函数,又不是偶函数的是( ) A. 3y x x =-B. ||x y e =C. |ln |y x =D. sin y x =3. 已知复数z 满足121zi z+=-+-(i 为虚数单位),则z =( ) A. 2i +B. 2i -C. 2i -+D. 2i --4. 某人连续投篮6次,其中3次命中,3次未命中,则他第1次、第2次两次均未命中的概率是( ) A.1 B.3 C.1 D.15. 已知直线:4360l x y -+=和抛物线2:4C y x =,P C 为上的一点,且P 到直线l 的距离与P 到C 的焦点距离相等,那么这样的点P 有( )、 A.0个B.1个C.2个D.无数个6. 已知函数()sin 2sin 23f x x x π⎛⎫=++ ⎪⎝⎭,将其图象向左平移()0ϕϕ>个单位长度之后得到的函数为偶函数,则ϕ的最小值是( )A.12π B.6πC.3π D.56π7. 某几何体的三视图如图所示,则该几何体的体积是( )A.113B.133C.143D.1638. 我们知道欧拉数 2.7182818284e =,它的近似值可以通过执行如图所示的程序框图计算。
当输入50i =时,下列各式中用于计算e 的近似值的是( )A.525352⎛⎫⎪⎝⎭B.515251⎛⎫ ⎪⎝⎭C.505150⎛⎫ ⎪⎝⎭D.495049⎛⎫ ⎪⎝⎭9. 在正三角形ABC ∆中,12,,2AB BD DC AE EC ===,且AD 与BE 相交于点O ,则O AO B ⋅=( ) A.45- B. 34- C.23- D. 12-OFB ∆,)1334AB AB AC ⎛⎫-=-⎪⎝⎭.10. ()()*23nx y n N -∈的展开式中倒数第二项与倒数第三项的系数互为相反数,则()()*32nx y n N -∈展开式中各二项式系数之和等于( )A.16B. 32C.64D. 12811. ABC ∆的内角,,A B C的对边分别为,,a b c ,若ABC ∆)222a c b +-,周长为6,则b 的最小值是( )A.2C.32cos ac B12. 设函数())f x a R =∈,若曲线c o s 2y x =+上存在点()00,x y 使得()()00f f y y =,则a 的取值范围是( )A. []ln 36,0- B. []ln36,ln22--C. []2ln 212,0- D. []2ln 212,ln 22--等价于f ln x x x +-二、填空题:本题共4小题,每小题5分,共20分.13. 已知s i n 3c o s 0αα-=,则s i n 2α= .14. 某次考试结束,甲、乙、丙三位同学聚在一起聊天。
2020年山西省高考考前适应性测试理科数学(含解析)

2020年山西省高考考前适应性测试理科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
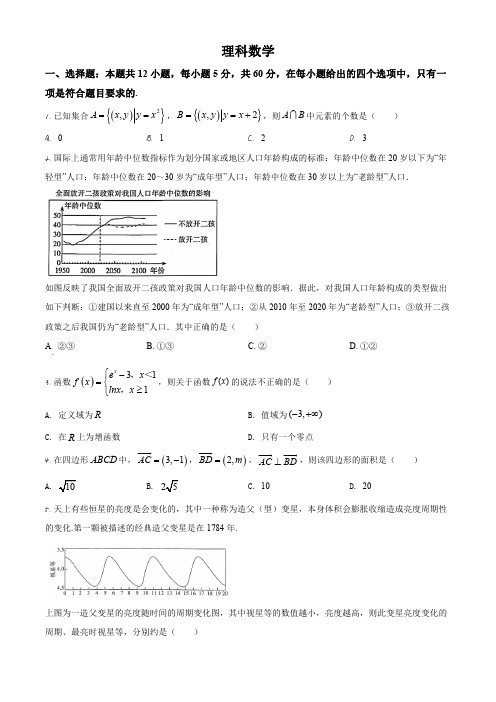
1.已知集合(){}2,A x y y x ==,(){},2B x y y x ==+,则A B I 中元素的个数是( )A.0B.1C.2D.32.国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成类型的标准:年龄中位数在20岁以下为年轻型人口;年龄中位数在20~30岁为成年型人口;年龄中位数在30岁以上为老年型人口. 全面放开二孩政策对我国人口年龄中位数的影响上图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为成年型人口;②从2010年至2020年为老年型人口;③放开二孩政策之后我国仍为老年型人口.其中正确的是( ) A.②③ B.①③ C.② D.①②3.已知函数()e 3,1,ln ,1,x x x f x x -<≥⎧=⎨⎩则关于函数()f x 的说法不正确的是( )A.定义域为RB.值域为()3,-+∞C.在R 上为增函数D.只有一个零点4.在四边形ABCD 中,()3,1AC =-u u u r ,()2,BD m =u u u r,AC BD ⊥u u u r u u u r ,则该四边形的面积是( )B.C.10D.205.天上有些恒星的亮度是会变化的,其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化.第一颗被描述的经典造父变星是在1784年.上图为一造父变星的亮度随时间的周期变化图,其中视星等的数值越小,亮度越高,则此变星亮度变化的周期、最亮时视星等,分别约是( ) A.5.5,3.7 B.5.4,4.4 C.6.5,3.7 D.5.5,4.46.双曲线1C :22221x y a b -=与2C :22221x y b a-=(0a b >>)的离心率之积为4,则1C 的渐近线方程是( )A.y x =±B.2y x =±C.(2y x =±+D.(2y x =±7.某几何体的三视图如图所示,已知网格纸中小正方形的边长为1,则此几何体的体积是( )A.279π+B.2712π+C.33πD.189π+8.已知Rt ABC △中,90A ∠=o ,角A ,B ,C 的对边分别为a ,b ,c ,其内切圆半径为r ,由12ABC S bc =△,又111222ABC S ar br cr =++△,可得bcr a b c=++.类比上述方法可得:三楼锥P ABC -中,若90BAC ∠=o ,PA ⊥平面ABC ,设ABC △的面积为1S ,PAB △的面积为2S ,PAC △的面积为3S ,PBC △的面积为4S ,则该三棱锥内切球的半径是( )12341234123412349.6312x x x ⎛⎫-+ ⎪⎝⎭展开式中,常数项是( )A.220B.220-C.924D.924-10.函数()222sin x x f x =+,若()()123f x f x ⋅=-,则12x x +的最小值是( ) A.6πB.4π C.3π D.23π11.已知长方体1111ABCD A B C D -,2AB AD ==,14AA =,M 是1BB 的中点,点P 在长方体内部或表面上,且//MP 平面11AB D ,则动点P 的轨迹所形成的区域面积是( ) A.6B.C.D.912.数列{}n a 中,156a =,()()1251056515n n n n a a n n a n ++=++++,则99a =( ) A.12019B.20182019C.12020D.20192020二、填空题:本题共4小题,每小题5分,共20分。
2020年山西省高考考前适应性测试理科数学·答案与解析

c sinC
得 sinA
sinC cosA
=
3 sinC.
而行 又因为 sinC ≠ 0,∴tanA =
3 ,∴A =
π 3
.
…………………………………………………………………………
6分
西思 (2)由△ABC 的面积为 3 ,得 bc = 4,
山 司 由余弦定理得 a2 = b2 + c2 - 2bccosA = b2 + c2 - bc ≥ 2bc - bc = bc = 4,
的最小值为
π 6
.
思 公 11. D 【解 析】如 图 所 示 ,E, F, G, H, N 分 别 为 B1C1, C1 D1, DD1, DA, AB 的 中 点 ,则 西 限 EF ∥ B1 D1 ∥ NH,MN ∥ B1 A ∥ FG,所以平面 MEFGHN∥平面 AB1D1,所以动点 P 山 有 的轨 迹 是 六 边 形 MEFGHN 及 其 内 部 . 因 为 AB = AD = 2,AA1 = 4,所 以 EF=HN=
山西 司 棱锥组合而成,圆柱体的体积为 27π,正四棱锥的体积为 12,所以几何体的体积为 27π + 12.
限公 8. B 【解析】设 PA = a,AB = b,AC = c,则
科技有 VP - ABC
=
1 3
·S
△ABC
·PA
=
1 6
abc,又 VP - ABC
=
1 3
S1 R
+
1 3
S2 R
15. 2;y = -
2x 4
【解析】由已知得| AF1 | + | AF2 | = 2a | | ①,AF1 2 | | + AF2 2 = 4c2 ②,
2020届山西省高三高考考前适应性测试数学(理)试题
17.在 ABC 中,内角 A , B , C 的对边分别为 a , b , c ,且 a cos B tan A tan B 3c .
B.
2 S1S 2 S3
S1 S2 S3 S4
C.
3S1S 2 S3
S1 S2 S3 S4
D.
2 S1S2S3
S1 S2 S3 S4
9.
x3
2
x
1 x
6
展开式中,常数项是(
)
A. 220
B. 3 sin 2x 2sin2 x ,若 f (x1) f (x2 ) 3 ,则 x1 x2 的最小值是( )
(1)求 A ; (2)若 ABC 的面积为 3 ,求 a 的最小值. 18.如图 1,已知等边 ABC 的边长为 3,点 M ,N 分别是边 AB ,AC 上的点,且 BM 2MA ,AN 2NC . 如图 2,将 AMN 沿 MN 折起到△AMN 的位置.
(1)求证:平面 ABM 平面 BCNM ; (2)给出三个条件:① AM BC ;②二面角 A MN C 大小为 60 ;③ AB 7 .在这三个条件中任 选一个,补充在下面问题的条件中,并作答:在线段 BC 上是否存在一点 P ,使直线 PA 与平面 ABM 所 成角的正弦值为 3 10 ,若存在,求出 PB 的长;若不存在,请说明理由.注:如果多个条件分别解答,按第
15.设
F1 , F2 分别为椭圆 C
:
x2 4
y2
1 的左、右焦点,
山西省临汾市2020年高考考前适应性训练考试(三)数学(理科)试题答案
所以 BC =3 ................................................................................................12 分
在 ∆ACD 中,由余弦定理的推论可得 cos ∠ACD = AC 2 + CD 2 − AD 2 ............................................................5 分
2AC ⋅ CD = m2 + 9m2 − 8m2 = 1 ..........................................................6 分
33
所以直线 PD 和平面 PAB 所成角的正弦值为 2 ...............................12 分 2
【另解】
(1)因为点 C 是正 ∆PAB 边 PB 的中点, 所以 AC ⊥ BC ,又因为 PA ⊥ BC ,且 AC ∩ PA = A ,
所以 BC ⊥ 平面PAC ................................................................................4 分
6 ) , PA = ( 4
32 ,0,−
6 ) , AB = (−2
3,2,0) .
3
3
3
3
.....................................8 分
山西省临汾市高三考前适应性训练考试(三)数学(理)试题含答案【精选】.doc
临汾市高考考前适应性训练考试(三)理科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}(){}22|log 0,|log 12A x x B x x =≥=-≤,则集合A B =I ( ) A .{}1,2,3 B .{}1,3 C .(]1,3 D .(]1,5 2.已知函数()(),f x g x :x 0 1 23 ()f x20 31则函数y f g x =的零点是( )A .0B .1C .2D .33. 已知命题:1:p 函数()x x f x e e -=-在R 上单调递增;2:p 函数()x xg x e e -=+在R 上单调递减,则在命题()112212312:,:,:q p p q p p q p p ∨∧⌝∨和()412:q p p ∧⌝中,真命题是( )A .13,q qB .23,q qC .14,q qD .24,q q 4. 已知数列{}n a 是等差数列,1010a =,其前10项和1060S =,则其公差d =( ) A .29-B .29 C. 89- D .895.已知平面α,及直线,a b 下列说法正确的是( )A .若直线,a b 与平面 α所成角都是30o ,则这两条直线平行B .若直线,a b 与平面 α所成角都是30o ,则这两条直线不可能垂直 C. 若直线,a b 平行,则这两条直线中至少有一条与平面α平行 D .若直线,a b 垂直,则这两条直线与平面 α不可能都垂直6. 已知等比数列{}n a 的前n 项和413n n S -=,则数列{}na 的前n 项和nT=( )A .21n- B 413n -213n - D .1233n +-7.高考前第二次适应性训练结束后,对全市的英语成绩进行统计,发现英语成绩的频率分x 0 1 23 ()g x213布直方图形状与正态分布()2~95,8N 的密度曲线非常拟和,据此估计在全市随机抽取的4名高三同学中,恰有2 名同学的英语成绩超过95分的概率是( ) A .16 B .13 C.12 D .388. 执行如图所示的程序框图,如果输入的10x =-,则输出的y =( )A .0B .1 C. 8 D .279.已知椭圆()2221025x y m m +=>与双曲线()222107x y n n-=>有相同的焦点,则m n +的取值范围是 ( ) A .(]0,6 B .[]3,6 C. (32,6⎤⎦D .[)6,910. 如图,网格纸上小正方形长为1,图中粗线画出的是某零件的三视图,该零件由一个棱长为4的正方形毛坯切削得到,则切削掉部分的体积与原毛坯体积的比值为( )A .38 B .58C.512 D .71211. 对定义在R 上的连续非常函数()()(),,f x g x h x ,如果()()()2g x f x h x =⋅总成立,则称()()(),,f x g x h x 成等比函数.若()()(),,f x g x h x 成等比函数,则下列说法中正确的个数是( )①若()(),f x h x 都是增函数,则()g x 是增函数;②若()(),f x h x 都是减函数,则()g x 是减函数;③若()(),f x h x 都是偶函数,则()g x 是偶函数;④若()(),f x h x 都是奇函数,则()g x 是奇函数;A .0B .1 C.2 D .312.已知椭圆22:12x C y +=的上、下顶点分别为,M N ,点P 在椭圆C 外,直线PM 交椭圆于点A ,若PN NA ⊥,则点P 的轨迹方程是 ( )A .()210y x x =+≠ B .()230y x x =+≠C.()2210,02x y y x -=>≠ D .()30y x =≠ 第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13.已知函数()()()22x x a f x x-+=为偶函数,则a = . 14.设i 为虚数单位,则(2i 6)x -的展开式中含4x 项的系数为 . 15. 已知函数()ln f x x =,若()()()0f m f n m n =>>,则11m nm n +=++ .16.在ABC ∆中,,,a b c 分别是角,,A B C 的对边,且满足()()sin 12,cos 522C C a b a b +=-=,则c = .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知函数()443sin cos 2cos 2f x x x x x =+. (1)求()f x 的最小正周期; (2)当0,4x π⎡⎤∈⎢⎥⎣⎦时,求()f x 的最值.18. 如图,梯形ABCD 中,90,22BAD ADC CD AD ∠=∠===o,四边形BDEF 为矩形,平面BDEF ⊥平面,ABCD BD CF ⊥. (1)若AF CE ⊥,求证:CE CF ⊥;(2)在棱AE 上是否存在点G ,使得直线//BG 平面EFC ?并说明理由.19.学校的校园活动中有这样一个项目,甲箱子中装有大小相同、质地均匀的4个白球,3个黑球 . 乙箱子中装有大小相同、质地均匀的3个白球,2个黑球 .(1)从两个箱子中分别摸出1个球,如果它们都是白球则获胜,有人认为,这两个箱子里装的白球比黑球多,所以获胜的概率大于0.5,你认为呢?并说明理由;(2)如果从甲箱子中不放回地随机取出4个球,求取到的白球数的分布列和期望; (3)如果从甲箱子中随机取出2个球放入乙箱子中,充分混合后,再从乙箱子中2个球放回甲箱,求甲箱中白球个数没有减少的概率.20. 已知动圆C 与圆()221:21C x y -+=外切,又与直线:1l x =-相切 . (1)求动圆C 的圆心的轨迹方程E ;(2)若动点M 为直线l 上任一点,过点()1,0P 的直线与曲线E 相交,A B 两点.求证:2MA MB MP k k k +=.21. 已知函数()()2xf x x x e =-.(1)求曲线()y f x =在原点处的切线方程;(2)若()0f x ax e -+≥恒成立,求实数a 的取值范围;(3)若方程()(f x m m =∈R)有两个正实数根12,x x ,求证:121mx x m e-<++.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22. 选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1C的参数方程为2cos (3cos 2cos x y αααααα⎧=-⎪⎨=--⎪⎩为参数). 以坐标原点为极点,以x 轴正半轴为极轴建立极坐标系,曲线2C的极坐标方程为sin 4πρθ⎛⎫-= ⎪⎝⎭. (1)求曲线1C 的普通方程和曲线2C 的直角坐标方程; (2)若曲线1C 与曲线2C 有公共点,求实数m 的取值范围.23.选修4-5:不等式选讲已知函数()2,f x x m m =+-∈R ,且()0f x ≤的解集为[]3,1--. (1)求m 的值;(2)设,,a b c 为正数,且a b c m ++=.山西省临汾市2017届高三考前适应性训练考试(三)数学(理)试题参考答案一、选择题1-5DBCDD 6-10ADCCC 11-12:AD 二、填空题13. 2 14.60- 15. 1 16.13 三、解答题17. 解:()44sin cos 2cos 22f x x x x x =++()22222sin cos 2sin cos 4x x x x x =+-+211sin 242x x =-11cos 41422x x -=-⋅+1313sin 4cos 4sin 4444264x x x π⎛⎫=++=++ ⎪⎝⎭. (1)242T ππ==. (2)当0,4x π⎡⎤∈⎢⎥⎣⎦时,714,,sin 4,166662x x ππππ⎡⎤⎛⎫⎡⎤+∈+∈- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭,则当462x ππ+=,即12x π=时,函数()f x 取到最大值54;当7466x ππ+=,即4x π=时,函数()f x 取到最小值12.所以,函数()f x 最大值54,最小值12. 18. 解:(1)容易知:,,DA DC DE 两两垂直.因此,可以以D 为原点,以,,DA DC DE 为x 轴,y 轴,z 轴正半轴建立空间直角坐标系.不妨设,DE m AB y ==,则()()()()()()()()0,0,0,1,,0,1,0,0,0,0,,1,,,0,2,0,1,,0,1,2,D B y A E m F y m C DB y CF y m ==-u u u r u u u r.()()(),0, 1.0,1,,0,2,1,1,BD CF BD CF y AF m CE m DF m ⊥∴⋅=∴=∴==-=u u u r u u u r u u u r u u u r u u u rQ ,,0AF CE AF CE ⊥∴⋅=u u u r u u u rQ ,即220m -+=,又22,0,CE DF m CE DF CE DF ⋅=-+∴⋅=∴⊥u u u r u u u r u u u r u u u r Q .(2)在棱AE 上存在点G ,使得直线//BG 平面EFC ,且12AG GE =,证明如下:由(1)知:()()21,0,,,1,,1,1,0,0,2,3333m m G BG EF EC m ⎛⎫⎛⎫∴=--==- ⎪ ⎪⎝⎭⎝⎭u u ur u u u r u u u r .设平面EFC 的一个法向量为(),,n a b c =r ,则00n EF n EC ⎧⋅=⎪⎨⋅=⎪⎩r u u u rr u u u r,即020a b b mc +=⎧⎨-=⎩,可取()()212121,1,,111103333m n BG n m m ⎛⎫⎛⎫=-⋅=-⨯-+-⨯+⋅=-+= ⎪ ⎪⎝⎭⎝⎭r u u u r r Q ,,//BG n BG ∴⊥∴u u u r r平面EFC .19. 解:(1)我认为“获胜”的概率小于0.5,理由如下:记“获胜”为事件A ,则()43120.57535P A =⨯=<,所以获胜的概率比0.5小.(2)设取出的白球的个数为变量X ,则X 可取的值为1,2,3,4.从而有:()()1322434344774181,23535C C C C P X P X C C ⋅⋅======,()()3140434344771213,43535C C C C P X P X C C ⋅⋅======, 所以X 的发布列为:()16123435353535357E X =⨯+⨯+⨯+⨯==. (3)记“甲箱中白球个数没有减少”为事件B ,则()21121122343443542222277777C C C C C C C C P B C C C C C ⋅+⋅=+⋅+⋅3722011321147147147=++=. 20. 解:(1)依题知,动圆C 的圆心到点()2,0的距离等于到直线2x =-的距离,所以由抛物线的定义可知:动圆C 的圆心轨迹是以()2,0为焦点,2x =-为准线的抛物线,所以动圆圆心C 的轨迹方程为:28y x =.(2)由题知当直线AB 斜率为0时,不符合题意,所以可设直线AB 的方程为1x my =+,联立218x my y x=+⎧⎨=⎩,消去x ,得22880,64320y my m --=∆=+>恒成立,所以可设()()()1122,,,,1,A x y B x y M t -,则2121212128,8,82,1y y m y y x x m x x +=⋅=-+=+⋅=,而2211MP tk t =⋅=---, ()12211212121212122111MA MB y x y x y y t x x ty t y t k k x x x x x x +++-+---+=+=+++++ ()()()2121212122121212848184y y y y y y t x x tt m t x x x x m +++-+--+===-++++,所以2MA MB MP k k k +=成立.21. 解:(1)()()()()2'1,'01,00xf x x x e f f =+-=-=,故曲线()y f x =在原点处的切线方程0x y +=.(2) ①当0x =时,R a ∈;②当0x >时,问题等价为()1x ea x e x≤-+恒成立,设()()()10x e g x x e x x =-+>,则()2'x eg x xe x=-,因为()'y g x =在()0,+∞上单调递增,且()'10g =,所以()g x 在()0,1上单调递减,在()1,+∞上单调递增,所以()y g x =上的最小值为()1g e =,所以a e ≤.③当0x <时,问题等价为()1x ea x e x≥-+恒成立,设()()()10x eh x x e x x =-+<,则()()20,'0x e h x h x xe x<=-<,所以()y h x =在(),0-∞上单调递减,而x →-∞时,()0h x →所以0a ≥即可.综上所述0a e ≤≤.(3)依第(2)问,取a e =,有()2xx x e ex e -≥-,因为()y f x =在0x =处的切线方程为y x =-.设()()()20x x x x e x x ϕ=-+>,则()()()()22'11,''3x xx x x e x x x e ϕϕ=+-+=+,令()''0x ϕ=得3x =-或0x =.容易知道()'y x ϕ=在()(),3,0,-∞-+∞单调递增,在()3,0-单调递减,而()'00ϕ=,所以当0x >时,()()'0,x y x ϕϕ>=单调递增.而()00ϕ=,所以,当0x >时,()0x ϕ>恒成立.所以()2xx x e x -≥-.设y m =分别与y x =-和()1y e x =-的两个交点的横坐标为34,x x ,则3124x x x x <<<,所以12431mx x x x m e-<-=++. 22. 解:(1)曲线1C 的普通方程为2y x =;曲线2C 的直角坐标方程为0x y m -+=.(2)联立2y x x y m ⎧=⎨-+=⎩,消去y 得20x x m --=,因为曲线1C 与曲线2C 有公共点,所以()()2140m ∆=---≥,解得14m ≥-,所以实数m 的取值范围为1|4m m ⎧⎫≥-⎨⎬⎩⎭.23. 解:(1) 由()0f x ≤得2x m +≤,所以022m m x m ≥⎧⎨--≤≤-⎩,又 ()0f x ≤的解集为[]3,1--, 所以2321m m --=-⎧⎨-=-⎩,解得1m =.(2)由(1) 知1a b c ++=,由柯西不等式得:2≤()()2222111⋅++所以()()233318a b c ≤+++=,≤=,即13a b c ===+的最大值为。
【答案】山西省2023届高三适应性考试数学试题
1.【答案】B 【解析】由(1)4x -≥可得2230x x --≥解得1x -≤或3x ≥,所以或3}x ≥,又因为{2,1,0,1,2}B =--,所以1}2,{A B =-- ,故选:B . 2.【答案】A 【解析】设i,,z a b a b =+∈R ,由2z z +=可得i+i 2a b a b +-=,1a ∴=,由1z =得z =,即212b +=,故1b =±,所以1i z =±,故选:A 3.【答案】C 【解析】因为cos 6024cos 604a b a b ⋅=⋅︒=⨯⨯︒=,所以22224241612a b a a b b -=-⋅+=-⨯+= ,所以a b -= ,故选:C .4.【答案】C 【解析】由题意可知222R 1,Q,()(),Q. x x f x x D x x x ⎧-∈=-=⎨∈⎩所以2(1)110f =-=,22f ==,23f ==,而()1f x =无解.故选:C .5.【答案】D 【解析】由题意可知,1122(482521)=-0111102921011011111111111111C 485C 485(1)C 485(1)C 485(1)C (1)log =⨯+⨯⨯-+⨯⨯-++⨯⨯-+⨯- 由此可知2222除以5的余数,即为111111C (1)1⨯-=-除以5的余数,故所求余数为4.故选:D . 6.【答案】D【解析】因为函数π2sin ()sin cos (0)6f x x x x ωωωω⎛⎫=-⎪⎝⎭=->,由()1f x =,得π2sin 16x ω⎛⎫-= ⎪⎝⎭,当(0,π)x ∈时,ππ,666x πωωπ⎛⎫-∈-- ⎪⎝⎭,则2π6663πωππππ-+-<≤,733ω∴<≤.7.【答案】B【解析】设圆锥体积为1V ,底面半径为R ,其内切球体积为2V ,半径为r ,由题意可得21321π231π344R V V r ⨯==,则232R r =①, 又POD PBC △∽△可得OD PO BC PB =,即r R =2222(4)16r r R R-=+②, 将①代入②化简整理得2210r r -+=,则1r =,故选:B8.【答案】A【解析】设直线l 为曲线()ln f x x =在点11(,())x f x 处的切线,11()1f x x '=,所以1111:ln ()l y x x x x -=-,即111:ln 1l y x x x =+-;设直线l 为曲线()(0,0)a g x x x a =>≠在点22(,())x g x 处的切线,1()a g x ax -'=,所以1222:()a a a l y x ax x x --=-,即122:(1)a a l y ax x a x -=+-, 由题意知121121ln 1(1)a aax x x a x -⎧=⎪⎨⎪-=-⎩,因为10x >,20x >,由1211a ax x -=可得12ln ln (1)ln x a a x =---,将其代入12ln 1(1)ax a x -=-可得: 22ln (1)ln 1(1)aa a x a x ----=-,显然1a ≠,整理得221ln ln 1a a x x a +-=-.记()ln (0n h x x x a =->且1)a ≠,则111()aa ax h x ax x x--'=-=,当110,a x a ⎛⎫⎛⎫ ⎪∈ ⎪ ⎪⎝⎭⎝⎭时,()0h x '>;当11,a x a ⎛⎫⎛⎫⎪∈+∞ ⎪ ⎪⎝⎭⎝⎭时,()0h x '<,所以函数()h x 在110,a a ⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭上单调递增,在11,a a ⎛⎫⎛⎫⎪+∞ ⎪ ⎪⎝⎭⎝⎭上单调递减,所以1max 11ln ()a a h x h a a ⎛⎫+⎛⎫⎪==- ⎪ ⎪⎝⎭⎝⎭,则2max ()()h x h x ≤,即1ln 1ln 1a a a a ++--≤,化简得1ln 0(1)a a a +-≤,解得10,(1,)e a ⎛⎤∈+∞ ⎥⎝⎦,故选:A . 9.【答案】ABD【解析】对于A ,函数sin sin ()e e xxf x =+的定义域为R ,且sin sin sin sin ()e e e e ()xxxxf x f x ---=+=+=,所以函数为偶函数,故选项A 正确;对于B ,若命题“R x ∃∈,2210x ax ++<”是假命题,则2210x ax ++≥恒成立, 所以2(2)40a ∆=-≤,解得11a -≤≤,故选项B 正确;对于C ,若1x ≥,且1y ≥,则222x y +≥成立,反之不一定成立,例如:2x =-,3y =-满足222x y +≥,但是0,0x y <<,故“1x ≥,且1y ≥”是“222x y +≥”充分不必要条件,故选C错误;对于D ,若111a b b a -=-,则2230a ab b -+=,当b a =时方程有解,所以0ab ∃>,111a b b a-=-,故选项D 正确;故选:ABD . 10.【答案】BD 【解析】对于A 选项,由平均数公式可知,女生每周锻炼身体的平均时长的平均值等于7.365.1 5.66 6.3 6.5 6.87.27.37.57.78.18.28.48758.69.29.416()h ++++++++++=+++++,A 错;对于B 选项,因为160.812.8⨯=,因此,男生每周锻炼身体的平均时长的80%分位数是9.2h ,B 对; 对于C 选项,男生每周锻炼身体的平均时长大于9h 的有4周,所求概率为40.2516=,C 错; 对于D 选项,男生每周锻炼身体的平均时长分布在区间(8,9)内共有8个,女生有4个, 男生每周锻炼身体的平均时长分布在区间(7,10)内的共14个,女生为10个, 男生每周锻炼身体的平均时长的极差为10.1 6.3 3.8-=,女生为9.4 5.1 4.3-=,据此可知与男生相比,女生每周锻炼身体的平均时长波动性比较大,所以,与男生相比,女生每周锻炼身体的平均时长波动性比较大,D 对.故选:BD . 11.【答案】ABC【解析】当1n ==,112a ∴=,当2n ≥=, 平方可得112n n n n S S S S -+-=-,112n n S S -=-,11(2)2n n S n S -∴=-≥,选项A 正确; 则2n ≥时,111111122n n n n S S S S -----=-=--,所以1112111111n n n n S S S S ----==----, 111111n n S S -∴-=---,故11n S ⎧-⎫⎨⎬⎩⎭是首项为1121S =--,公差为1-的等差数列,选项B 正确; 则12(1)(1)(1)1n n n S =-+-⨯-=-+-,*,1n nS n n ∴=∈+N ,所以221(1)n a n n ⎛==+=,选项D 错误; 记2221321()4n f n nS S S -=⋅⋅⋅,则22221(1)1121(21)111()224(1)4(1)n f n n n n n S f n n n n n n n n ++++++⎛⎫====+> ⎪+++⎝⎭, 故(1)()f n f n +>,()f n 为递增数列,所以21()(1)41f n f a ==≥,即222132114n S S S n- ≥,选项C 正确,故选:ABC12.【答案】BD 【解析】设2F B m = ,27(0)AF m m =>,由双曲线的定义可得:12272AF AF a m a =+=+ ,1222F B F B a m a =+=+,在12AF F △中,由余弦定理可得:222(72)(7)(2)272cos120m a m c m c +=+-⋅⋅⋅︒, 即22214270a am c cm +--=,所以2222714a c cm am -=-,在12BF F △中,由余弦定理可得:222(2)(2)22cos 60m a m c m c +=+-⋅⋅⋅︒, 即222220a am c cm +-+=,所以22222a c cm am -=--, 所以,7142cm am cm am -=--,整理可得32c a =,所以该双曲线的离心率为32e =,A 错; 对于B 选项,1212227AF F BF F S AF S BF ==△△,B 对; 对于C 选项,因为32c a =,代入222220a am c cm +-+=可得2222527c a m a a c -==+,所以,275AF m a == ,1527AF a a a =+=,12AF F △的周长为121275215AF AF F F a a c a ++=++= ,257BF m a == ,1519277a aBF a =+= ,所以,12BF F △的周长为1212195452777a a aBF BF F F c ++=++= , 所以,12AF F △和12BF F △的周长之比为45715:73a a =,C 错; 对于D 选项,设12AF F △和12BF F △的内切圆半径分别为1r 、2r ,则1212121152714527AF F BF F a r S a S r ⨯⨯==⨯⨯△△,解得123r r =,D 对.故选:BD .解法二:直线l倾斜角60θ=︒,则221cos 71cos AF e BF e θθ+==-,解得3cos 4e θ=,而1cos 2θ=,所以离心率32e =,A 错;B 显然正确; 不妨设2a =,则3c =,b =,22101cos b a AF e θ==-,2107BF =,12214AF AF a =+=, 123827BF BF a =+=,1226F F c ==,12AF F △的周长为12121410630AF AF F F ++=++= ,12BF F △的周长为12123810906777BF BF F F ++=++= ,所以,12AF F △和12BF F △的周长之比为73,C 错误;对于D 选项,设12AF F △和12BF F △的内切圆半径分别为1r 、2r ,则1212121302719027AF F BF F r S S r⨯⨯==⨯⨯△△,解得123r r =,D 对.故选:BD . 13.【答案】①.0.4##25②.415【解析】设i H 表示“第i 次摸到红球”,i B 表示“第i 次摸到白球”,i L 表示“第i 次摸到蓝球”,1,2i =,则第一次摸到红球的概率为140.44()33P H ==++; 第一次没有摸到红球第二次摸到红球包括第一次摸到白球第二次摸到红球,和第一次摸到蓝球第二次摸到红球,所以所求概率为21121211344(|)()(|)()(|)210915P H H P B P H B P L P H L =+=⨯⨯=. 14.【答案】(,8]-∞-【解析】由图可知当圆C 位于两直线1l 与2l 之间时,点P 到两直线1l 和2l 的距离之和即为1l 与2l 两平行直线间的距离, 即点P 到直线1l 和2l 的距离之和与点P 的位置无关, 当直线2l=,解得8m =-或2m =(舍去),所以8m -≤,即m 的取值范围是(,8]-∞-.15.【解析】将图1中的1AA B △和1A BC △放置于同一平面内,如图2所示,则PA PC AC +≥.因为直三棱柱111ABC A B C 中,122BC AA ==,AB AC ==,所以1Rt A AB △中,130ABA ∠=︒,12A B =.同理,在1A AC △中,12AC =,所以160A BC ∠=︒, 所以在图2中,1190ABC ABA A BC ∠=∠+∠=︒,所以2227AC AB BC =+=,即AC =.所以PA PC +. 16.【答案】2【解析】由1(1)()()2f x f x g x +=-+,得()(1)()g x f x f x =+①,所以(1)(2)(1)g x f x f x +=++②.将①②代入1(1)()()2g x g x f x +=--,并整理得(2)(1)()f x f x f x +=-+-,所以(3)(2)(1)()f x f x f x f x +=-+-+=,所以()f x 是以3为周期的周期函数. 由①可知,()g x 也是以3为周期的周期函数,所以(2)(365)g g ==.由①(3)(2)(2)f f g +==,又因为()(5)f x f x =-, 所以(3)(53)(2)f f f =-=,解得(3)(2)1f f ==-,所以(1)(4)(3)(2)2f f f f ==--=.所以[]20231()674[(1)(2)(3)](1)6742(1)(1)22k f k f f f f ==⨯+++=⨯+-+-+=∑.故答案为:2.17.【答案】(1)12n n a -=;(2)选①,23()23nn S n =⋅-+;选②,21n nS n =+. 【解析】(1)由等比数列的性质可得14238a a a a ==,由题意可得411414780,0a a a a a a -=⎧⎪=⎨⎪>>⎩,················2分解得11a =,48a =,·································································································4分所以等比数列{}n a的公比为2q,所以1112n n n a a q --==.··································5分 (2)若选①,1(21)(21)2n n n b n a n -=-=-⋅.·······························································6分所以01221123252(23)2(21)2n n n S n n --=⋅+⋅+⋅++-⋅+-⋅ ,①····································7分则12312123252(23)2(21)2n n n S n n -=⋅+⋅+⋅++-⋅+-⋅ ,②-①②,得211212(12)12(222)(21)21(21)212n n nn n S n n ----=++++--⋅=+--⋅-1124(21)2(32)23n n n n n +=+---⋅=-⋅-,································································9分因此,23()23nn S n =⋅-+.······················································································10分若选②,2211111(21)log (21)(21)22121n n b n a n n n n ⎛⎫===- ⎪++--+⎝⎭,·····························7分所以11111112335212121n nS n n n ⎛⎫=-+-++-= ⎪-++⎝⎭ .·············································10分 18.【答案】(1;(2). 【解析】(1)因为sin cos θθ+=,所以27(sin cos )16θθ+=,即92sin cos 016θθ=-<.因为θ为ABD △的内角,所以sin 0θ>,cos 0θ<.·····················································2分又225(sin cos )12sin cos16θθθθ-=-=,所以5sin cos 4θθ-=②,联立①②,得sin θ=cos θ=,···························································4分所以ABD △的面积为11sin 4222ABD S AB AD θ=⋅⋅=⨯=⨯△···················5分 (2)由(1)知cos θ=,sin θ=2222222cos 3024242BC BD AD AB AD AB θ==+-⋅⋅=+=⨯--⨯.········6分设ABD α∠=,由正弦定理,得sin sin AD BD αθ=,即2sin sin BDθα=, 所以π2sin cos cos sin 2ABC BD θαα⎛⎫∠=+=-=- ⎪⎝⎭.·······················································8分在ABC △中,由余弦定理,得2222cos 2sin 16(3024AC AB BC AB BC AB D C BD B θ⎛⎫=+=+-⋅--⨯⨯⨯-⋅ ⎝∠⎪⎭4616sin 461566θ=-+=-+=,·····················································11分所以AC =.····································································································12分19.【答案】(1)16;(2)ˆ310y x =-;(3)是可靠的【解析】(1)从12组数据中任选2组,选法数为212C ;·····················································1分选取的2组数据恰好是相邻的2天,选法数为11;···························································2分所以所求概率为21211111C 666P ===.·············································································3分 (2)设剩下的10组数据分别为11221010(,),(,),,(,)u v u v u v .1012111021102229654302535i ii ii i u v x y ===-⨯-⨯=-=∑∑;················································5分1212111110.8,22.710102043i i i i v y u x ==⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎭-⎝-∑∑,101010.822.72451.6u v ⋅=⨯⨯=;··6分10122221121013942001194i ii i u x===-⨯=-=∑∑,································································7分22101010.81166.4u =⨯=;·······················································································8分所以122110101025352451.63.011941166.4i i i i i u v uvbu nu==--==≈--∑∑ .·····························································10分所以ˆˆ22.7310.89.710a v bu=-=-⨯=-≈-.所以所求回归方程为ˆ310y x =-.···············11分 (3)当10x =时,ˆ3101020y=⨯-=.因为212012-=<;22202-=, 所以根据所给的研究方案,可以判断(2)中所得的线性回归方程是可靠的.·························12分20.【答案】(1)证明见解析;(2)存在点P ,三棱锥C APE -的体积为29. 【解析】(1)连接BD 与CE 交于点Q ,连接PQ ,如图所示.由题意可得//DE BC ,12DE BC =,所以12DQ DE BQ BC ==.又因为2AP PD =,所以12DP DQ PA BQ ==,········································2分 所以//AB PQ .因为PQ ⊂平面PEC ,AB ⊄平面PEC ,所以//AB 平面PEC .·············4分(2)由(1)知,当2AP PD =时,//PQ AB .因为AB AE ⊥,所以AE PQ ⊥.··············5分取BE 的中点为O ,连接AO ,如图所示,由已知得,在矩形ABCD 中,E 为AD 的中点,AB AE =,O 是BE 的中点,所以AO BE ⊥,因为平面ABE ⊥平面BCDE ,平面ABE 平面BCDE BE =,AO ⊂平面ABE ,所以AO ⊥平面BCDE .由已知得,在矩形ABCD 中,O 是BE 的中点,所以2BE ==,所以112AO BE ==. 由已知得,在矩形ABCD 中,E 为AD 的中点,12AB AE AD ==. 所以12DE DC AD ==,所以45AEB DEC ∠=∠=︒,所以90BEC ∠=︒,即CE BE ⊥.····7分 因为平面ABE ⊥平面BCDE ,平面ABE 平面BCDE BE =,CE ⊂平面BCDE ,所以CE ⊥平面ABE .因为AE ⊂平面ABE ,所以CE AE ⊥.········································9分 又因为CE PQ Q = ,CE ⊂平面PEC ,PQ ⊂平面PEC ,所以AE ⊥平面PEC .因为AE ⊂平面AEC ,所以平面AEC ⊥平面PEC ,即当2AP PD =时,平面AEC 与平面PEC 的夹角为90︒.··············································10分此时,222121213333929C APE C ADE A CDE CDE V V V S OA ---⎛⎫===⨯⨯⨯=⨯= ⎪⎝⎭△.········12分21.【答案】(1)()f x 在(0,)+∞上单调递增.(2){1}[)0,1- .【解析】(1)()f x 定义域为(0,)+∞,ln 1ln 1()1x x x f x x x x-+'=-++=,························2分 记()ln 1h x x x =-+,11()1x h x x x-'=-=,当(0,1)x ∈时,()0h x '<;当(1,)x ∈+∞时,()0h x '>,()h x ∴在(0,1)上单调递减,在(1,)+∞上单调递增,·························································4分 故()(1)20h x h =>≥,()0f x '∴>,()f x ∴在(0,)+∞上单调递增.································6分 (2)()g x 定义域为R ,e e ())(x x g x a a x x x '=-=-,①当0a =时,()(1)e x g x x =-有唯一零点1x =,符合题意;············································7分 ②当0a <时,e 0x a ->,当),(0x ∈-∞时,()0g x '<,()g x 在(,0)-∞单调递减; 当,()0x ∈+∞时,()0g x '>,()g x 在(0,)+∞单调递增,故min 2()(0)1g x g a ==-,若1a <-,则0(0)()g g x >>,()g x 无零点,不符题意;若1a =-,()g x 有唯一零点0x =,符合题意;若10a -<<,则2(0)10g a =-<,又21(1)02g a a =->, 1x <-时,(1)e 12x x x x ->->,20a >,2()2(4)22ax x g x x ax ∴>-=-,40g a ⎛⎫∴> ⎪⎝⎭,故()g x 在(0,1),4,0a ⎛⎫⎪⎝⎭内各有一个零点,函数有两个零点,不符题意;·····························9分③当01a <<时,当(ln ),0x a ∈时,()0g x '<,当(,)0,(ln )x a ∈-∞+∞ 时,()0g x '>, 则()g x 在(n ),l a -∞,(0,)+∞上单调递增,在(ln ),0a 上单调递减,又22(ln )(ln )(ln 1)()(1)02a a g a a a a af a af =--+=<=,1x >时,令2()e x m x x =-,()e 2x m x x '∴=-,令()e 2x n x x =-,()e 20x n x '∴=->, 即()e 2x m x x '=-在(1,)+∞单调递增,故()(1)e 20m x m '>=->, 故2()e x m x x =-在(1,)+∞单调递增,则()(1)e 10m x m >=->,所以2e x x >,故222g()(1)122ax a x x x x x ⎛⎫>--=-- ⎪⎝⎭,则102a g ⎛⎫+> ⎪⎝⎭,故()g x 此时在ln ,12a a ⎛⎫+ ⎪⎝⎭上有唯一零点,符合题意;·····················································11分 综上,a 的取值范围为{1}[)0,1- .·············································································12分 22.【答案】(1);(2)1k ,3k ,2k 或2k ,3k ,1k 成等差数列,证明见解析.【解析】(1)设点11(,)M x y ,其中2211214x y b+=,122x -≤≤且11x ≠,则AM ===················2分由1AM ≥,得22222111112(2)10442≥b b b x x b x x ⎡⎤⎛⎫⎛⎫--+=---⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦,···························4分12x ≤,02b <<,120x ∴-≤,2104b ->,2211042b b x ⎛⎫∴-- ⎪⎝⎭≤,21224b x b ∴-≤,只需22224b b-≤,又02b <<2b <≤,所以b 的取值范围是.···················6分 (2)1k ,3k ,2k 或2k ,3k ,1k 成等差数列,证明如下:·················································7分 若1b =,则22:14x C y +=,设点(1,),0E t t ≠.①若直线l 斜率为0,则点(4,0)P ,不妨令点(2,0)M ,(2,0)N -,则1k t =,23t k =,33tk =-,此时1k ,2k ,3k 的任意排列1i k ,2i k ,3i k 均不成等比数列,1k ,3k ,2k 或2k ,3k ,1k 成等差数列.···8分②直线l 斜率不为0,设直线(:10)l x my m =+≠,11(,)M x y ,22(),N x y ,则点34,P m ⎛⎫ ⎪⎝⎭, 由22114x my x y =+⎧⎪⎨+=⎪⎩得22(4)230m y my ++-=,216(3)0m ∆=+>, 故12224m y y m -+=+,12234y y m -=+,··········································································10分因为1111y t k x -=-,2221y t k x -=-,33333tmt m k m--==, 所以1212211212121212121212()()2()11y t y t y t y t y y t y y t y y t y y k k x x my my my y my y -----+--++=+=+==-- 22326262442334mtmtm m k m m m -+-++===-+,所以1k ,3k ,2k 或2k ,3k ,1k 成等差数列,综合上述,1k ,3k ,2k 或2k ,3k ,1k 成等差数列.························································12分。
高三高考考前适应性训练试题数学理
山西省高三年级高考考前适应性训练试题数 学 试 题(理)注意事项:1.本试题分第I 卷(选择题)和第II 卷(非选择题)两部分。
2.回答第I 卷前,考生务必将自己的姓名、准考证号、考试科目涂写在机读卡上。
3.回答第I 卷时,选出每小题答案后,用2B 铅笔把机读卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,写在本试题和答题纸上无效。
4.第II 卷中凡需填空的位置有 ▲ 标记,所填内容请写在答题纸相应位置上;除填空题外的其他题目,也须将答案写在答题纸相应位置上,写在本试题上无效。
5.考试结束后,将本试题、机读卡和答题纸一并交回。
参考公式:样本数据n x x x ,,21的标准差 锥体体积公式])()()[(122221x x x x x x nS n -++-+-= Sh V 31= 其中x 为样本平均数其中S 为底面面积,h 为高 柱体体积公式球的表面积、体积公式 Sh V =3234,4R V R S ππ== 其中S 为底面面积,h 为高 其中R 为球的半径第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合2{|0},{|lg },S x x x T x y x ST =-≥==则= ( )A .{|01}x x x <≥或B .{|1}x x >C .{|01}x x x ≤≥或D .{|1}x x ≥2.若a R ∈,且(1)(2)ai i +-为纯虚数,则a 的值是( ) A .-2 B .12- C .12 D .23.若向量(3,1),(1,1)a b a b +=-=-,则向量a 与b 的夹角是( )A .34πB .3πC .4πD .6π 4.已知函数2()2,[4,6]f x x x x =+-∈-,在函数()f x 的定义域内任取一点0x ,使得0()0f x ≥的概率是( ) A .910B .710C .12D .310 5.执行如图所示的程序框图,输出的结果等于 ( )A .12B .2C .-1D .-2 6.将函数3sin cos y x x =-的图象沿x 轴向右平移a 个单位(0a >),所得图像关于y 轴对称,则a 的最小值是( ) A .3π B .23π C .2π D .6π 7.测得变量x 与y 的一组数据为: x2 4 5 6 8 y 20 30 50 60 70若这两个变量之间的关系符合回归直线方程ˆ8.5yx a =+,则a 的值是 ( ) A .4.5B .3.5C .2.5D .1.5 8.已知下列四个命题:①命题“已知()f x 是R 上的减函数,若0a b +≥,则()()()()f a f b f a f b +≤-+-”的逆否命题为真命题;②若p 为q 的真命题,则p 、q 均为真命题;③若命题22:,10,:,10p x R x x p x R x x ∃∈-+<⌝∀∈-+≥则;④“1sin 2x =”是“6x π=”的充分不必要条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山西省2013年高考考前适应性训练考试
理科数学(试卷类型A )
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数i
2i 2-+的模是( ) A .5 B .2 C .2 D .1
2.若平面向量a ,b 满足1||=+b a ,且b a 2=,则=||b ( )
A .
31 B .3
2 C .1 D .2 3.曲线x y sin =,]2 ,0[π∈x 与x 轴围成的平面图形的面积是( ) A .0 B .2 C .4 D .8
4.若双曲线的焦点到其渐近线的距离等于双曲线的实半轴长,则该双曲线的离心率是( )
A .2
B .2
C .3
D .3
5.一艘轮船从O 点的正东方向10km 处出发,沿直线向O 点的正北方向10km 处的港口航行,某台风中心在点O ,距中心不超过r km 的位置都会受其影响,且r 是区间]10 ,5[内的一个随机数,则轮船在航行途中会遭受台风影响的概率是( )
A .
212- B .2
21- C .12- D .22- 6.执行如图所示的程序框图,输入1173=m ,828=n ,则输出的实数m 的值是( )
A .68
B .69
C .138
D .139
7.已知某几何体的三视图如图所示,正视图和侧视图中各边长均为3,则该几何体的表面积是( )
A .28
B .38
C .328
D .3
38 8.过抛物线)0(
22>=p px y 的焦点作倾斜角为︒30的直线l 与抛物线义于P ,Q 两点,分别过P ,Q 两点
俯视图侧视图正视图222第6题图 第7题图
作1PP ,1QQ 垂直于抛物线的准线于1P ,1Q ,若2||=PQ ,则四边形Q Q PP 11的面积是( )
A .1
B .2
C .3
D .3
9.若α
ααααcos sin cos sin tan -+=
,则α的值可能是( ) A .83π B .85π C .43π D .45π 10.已知数列}{n a 中,11=a ,)1 *,(271
>∈=--n n a a n n n N ,则当n a 取得最小值时n 的值是( ) A .7或8 B .6或7 C .5或6 D .4或5
11.对于实数a ,b ,若2111
b
a H +=,2
b a A +=,22
2b a Q +=,则有Q A H ≤≤.据此推断22⎪⎪⎭
⎫ ⎝⎛+=b a M ,2
1222---⎪⎪⎭⎫ ⎝⎛+=b a N 与H ,A ,Q 的大小关系是( ) A .M Q A N H ≤≤≤≤ B .Q A M N H ≤≤≤≤
C .Q A M H N ≤≤≤≤
D .M Q A H N ≤≤≤≤ 12.函数⎪⎩⎪⎨⎧∞+∈-∈--=) ,2[ ),2(2
1]2 ,0[ |,1|1)(x x f x x x f ,则下列说法中正确的是( ) ①函数)1ln()(+-=x x f y 有3个零点;
②若0>x 时,函数x k x f ≤)(恒成立,则实数k 的取值范围是) ,2
3[∞+; ③函数)(x f 的极大值中一定存在最小值;
④)2(2)(k x f x f k +=,)(N ∈k ,对于一切) ,0[∞+∈x 恒成立.
A .①③
B .②④
C .①④
D .②③ 第Ⅱ卷
本卷包括必考题和选考题两部分,第(13)~(21)题为必考题,每个试题考生都必须作答.第(22)题~(24)题为选考题,考生根据要求作答.
二、填空题:本大题共4小题,每小题5分.
13.等差数列}{n a 中,83=a ,127=a ,则=5a .
14.给出下面几个命题:
①“若2>x ,则3>x ”的否命题;
②“) ,0(∞+∈∀a ,函数x a y =在定义域内单调递增”的否定;
③“π是函数x y sin =的一个周期”或“π2是函数x y 2sin =的一个周期”;
④“022=+y x ”是“0=xy ”的必要条件。
其中,真命题的序号是 .
15.已知变量x ,y 满足约束条件⎪⎩
⎪⎨⎧≤--≥-+≥+-0630202y x y x y x ,若目标函数)0(≥-=a ay x z 恰好在点)6 ,4(处取得最
小值,则a 的取值范围是 .
16.由6根长度均为2米的钢管(钢管的直径忽略不计)焊接成一个三棱锥钢架,并在钢架内嵌一个体积
最大的球体,则这个球的体积是 米3.
三、解答题:解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
ABC ∆中,角A ,B ,C 的对边分别是a ,b ,c ,若2=a ,13-=b ,且b 是c 2与A cos 的等比中项.
(1)求A ,B ,C ;
(2)若函数)4|)(|2sin()(πϕϕ<+=x x f 满足2
)2(c C f =,求函数)(x f 的解析式及单调递减区间. 18.(本小题满分12分)
“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间]10 ,0[内的一个数,该数越接近10表示越满意.为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示:
(1)完成频率分布直方图,并根据频率分布直方图估算该城市
市民幸福感指数的平均值;
(参考数据:6469257305403312=⨯+⨯+⨯+⨯+⨯)
(2)如果市民幸福感指数达到6,则认为他幸福.据此,在该
市随机调查5对夫妇,求他们之中恰好有3对夫妇二人都幸福的概
率.(以样本的频率作为总体的概率)
19.(本小题满分12分)
在直角梯形CDEF 中,CF DC ⊥,EF DC //,22===EF CF CD . 将它绕CD 旋转得到CDBA ,使得面⊥CDBA 面CDEF .
(1)若点M 是ED 的中点,证明://BM 平面AEC ;
(2)求AE 与面BED 所成角的正弦值.
20.(本小题满分12分) 已知椭圆)0(122
22>>=+b a b
y a x ,其左、右焦点分别为1F ,2F ,过1F 作直线交椭圆于P ,Q 两点,PQ F 2∆ M F E D
C B A
的周长为34.
(1)若椭圆离心率2
2=e ,求椭圆的方程; (2)若M 为椭圆上一点,121=⋅MF MF ,求21F MF ∆面积的最大值.
21.(本小题满分12分) 已知函数2211ln )(x
x x a x f ++
=,R ∈a . (1)讨论函数)(x f 的单调性; (2)证明:3
2ln 2)e )(1(<+---x x x x . 请考生在第22、23、24三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分,作答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑.
22.(本小题满分10分)选修4—1:几何证明选讲
如图,半圆O 的直径AB 的长为4,点C 平分弧AE ,过C 作AB 的垂线交AB 于D ,
交AE 于F .
(1)求证:AF AE CE ⋅=2;
(2)若AE 是CAB ∠的角平分线,求CD 的长.
23.(本小题满分10分)选修4——4:坐标系与参数方程 在平面直角坐标系xOy 中,曲线1C 的参数方程为⎩
⎨⎧-=-=,2cos 3,sin 32ααy x (其中α为参数,R ∈α).在极坐标系(以坐标原点O 为极点,以x 轴非负半轴为极轴)中,曲线2C 的极坐标方程为a =-
)4cos(πθρ. (1)把曲线1C 和2C 的方程化为直角坐标方程;
(2)若曲线1C 上恰有三个点到曲线2C 的距离为2
3,求曲线2C 的直角坐标方程. 24.(本小题满分10分)
已知函数||)(a x x f +=.
(1)当1-=a 时,求不等式1|1|)(++≥x x f 的解集;
(2)若不等式2)()(<-+x f x f 存在实数解,求实数a 的取值范围.。
