第七章 虚拟变量
第七章 虚拟变量和随机解释变量 (2)

第七章 虚拟变量和随机解释变量本章将讨论两种不同的模型:虚拟变量模型和随机解释变量模型,以及模型设定的其它问题。
第一节 虚拟变量模型在我们以前考虑的模型中,解释变量都是定量变量(如成本、价格、收入、产出等),但在经济研究中,因变量经常受到一些定性变量的影响(如性别、种族、季节、不同历史时期等),我们把这类定性变量称为虚拟变量。
习惯上用D表示虚拟变量,虚拟变量的取值通常为0和1。
0表示变量具备某种属性,1表示变量不具备某种属性。
一、包含一个虚拟变量的模型如果我们要研究的问题中解释变量只分为两类。
则需引入一个模拟变量。
例9.1建立模型研究中国妇女在工作中是否受到歧视。
令Y=年薪,X=工作年限⎩⎨⎧=,女性,男性101D 可以建立如下模型:i i i i u D B X B B Y +++=210 )1.9( 与一般的回归模型一样,假定0)(=i u E 男性就业者的平均年薪:i i i i X B B D X Y E 10)0,(+== )2.9(女性就业者的平均年薪:210)1,(B X B B D X Y E i i i i ++== )3.9(如果B 2=0则说明不存在性别歧视,如果02<B ,则说明存在性别歧视。
图9.1表明男女就业者的平均年薪对工龄的函数具有相同斜率B 1,即随着工龄的增长男女工资的增长幅度相同;截距不同,说明男女的初始年薪不同。
我们称这种虚拟变量只影响截距不影响斜率的模型为加法模型。
图9.1不同性别就业者的收入(加法模型,B 2<0)如果随着工龄增加,男性与女性的年薪差距也发生变化,则模型(9.1)就变为i i i i i u X D B X B B Y +++=210 )4.9(图9.2描绘了男性年薪增加较快的情况。
我们称虚拟变量只影响斜率而不影响截距的模型为乘法模型如(9.4)如果男性与女性的初始年薪和年薪增加速度都有差异,我们可以将加法模型和乘法模型结合起来,得到如下模型i i i i i i u D B X D B X B B Y ++++=3210 )5.9(模型(9.5)可以用来表示截距和斜率都发生变化的模型。
第7章 虚拟变量与随机解释变量

图7.1.2 虚拟变量对斜率的影响
(3)一般方式 实际应用中,一般是直接以加法和乘法方式引入虚
拟变量,然后再利用t检验判断其系数是否显著的不等
于零,进而确定虚拟变量的具体引入方式。 我们还可以用加法模型与乘法模型相结合的方式建立 模型来拟合经济发展出现转折的情况。
例7.1.6 进口商品消费支出y主要取决于国民生 产总值x的多少。我国改革开放前后,由于国家政策的 变化,及改革开放后外资的大量引入等因素的影响, 1978年前后,y和x
模型结构不稳定。
3.虚拟变量在分段回归中的应用 在实际经济问题的研究中,有些经济关系需要用分段回归加 以描述。假定现在要描绘并比较不同收入水平人群的消费函数, 为简单起见,只取一个解释变量x(收入),设定模型如下:
图7.1.10 分段线性回归模型 现在考虑如何设模型。为满足第一个要求,将所有样本 一起回归,并显示出差异,将模型设定为
第7章 单方程回归模型的几个专门问题
7.1 虚拟变量
7.1.1 虚拟变量的概念及作用
1.虚拟变量的内涵 在计量经济学中,我们把反映定性(或属性)因素变化,取值为0和1的人 工变量称为虚拟变量(Dummy Variable),或称为哑变量、虚设变量、属性变 量、双值变量、类型变量、定性变量、二元型变量、名义变量等,习惯上用 字母D表示。例如
2.虚拟变量在模型结构稳定性检验中的应用
利用不同的样本数据估计同一形式的计量经济模型, 可能会得到不同的估计结果。如果估计的参数之间存在着 显著差异,则称模型结构是不稳定的,反之则认为是稳定 的。
模型结构的稳定性检验主要有两个用途:一是分析模 型结构对样本变化的敏感性,如多重共线性检验;二是比 较两个(或多个)回归模型之间的差异情况,即分析模型结 构是否发生了显著变化。
计量经济学虚拟变量实验报告
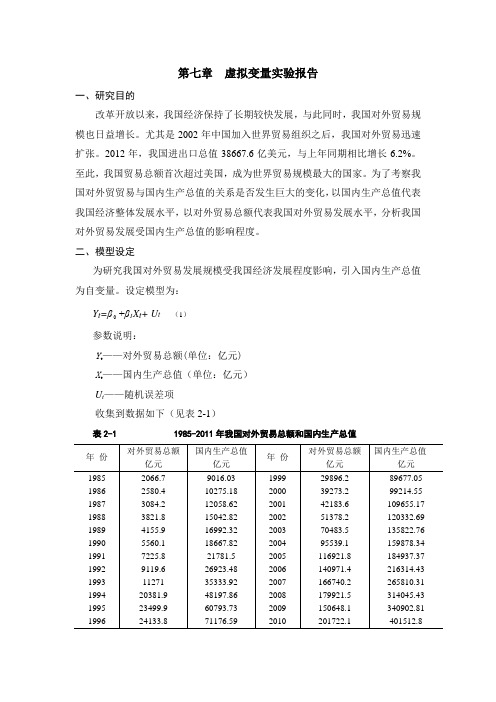
第七章虚拟变量实验报告一、研究目的改革开放以来,我国经济保持了长期较快发展,与此同时,我国对外贸易规模也日益增长。
尤其是2002年中国加入世界贸易组织之后,我国对外贸易迅速扩张。
2012年,我国进出口总值38667.6亿美元,与上年同期相比增长6.2%。
至此,我国贸易总额首次超过美国,成为世界贸易规模最大的国家。
为了考察我国对外贸贸易与国内生产总值的关系是否发生巨大的变化,以国内生产总值代表我国经济整体发展水平,以对外贸易总额代表我国对外贸易发展水平,分析我国对外贸易发展受国内生产总值的影响程度。
二、模型设定为研究我国对外贸易发展规模受我国经济发展程度影响,引入国内生产总值为自变量。
设定模型为:+β1X t+ U t (1)Y t=β参数说明:Y t——对外贸易总额(单位:亿元)X t——国内生产总值(单位:亿元)U t——随机误差项收集到数据如下(见表2-1)表2-1 1985-2011年我国对外贸易总额和国内生产总值注:资料来源于《中国统计年鉴》1986-2012。
为了研究1985-2011年期间我国对外贸易总额随国内生产总值的变化规律是否有显著不同,考证对外贸易与国内生产总值随时间变化情况,如下图所示。
图2.1 对外贸易总额(Y)与国内生产总值(X)随时间变化趋势图从图2.1中,可以看出对外贸易总额明显表现出了阶段特征:在2002年、2007年和2009年有明显的转折点。
为了分析对外贸易总额在2002年前后、2007年前后及2009年前后几个阶段的数量关系,引入虚拟变量D1、D2、D3。
这三个年度对应的GDP分别为120332.69亿元、265810.31亿元和340902.81亿元。
据此,设定以下以加法和乘法两种方式同时引入虚拟变量的模型:Y t=β0+β1Xt+β2(Xt-120332.69)D1+β3(Xt-265810.31)D2+β4(Xt-340902.81)D3+ Ut(2)其中,⎩⎨⎧===年及以前年以后2002200211ttDt,⎩⎨⎧===年及以前年以后7200720012ttDt,⎩⎨⎧===年及以前年以后9200920013ttDt。
第七章虚拟变量

当截距与斜率发生变化时,则需要同时引入加法与乘法形 式的虚拟变量。
例,考察1990年前后的中国居民的总储蓄-收入关 系是否已发生变化。 表中给出了中国1979~2001年以城乡储蓄存 款余额代表的居民储蓄以及以GNP代表的居民收 入的数据。
90年前 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990
1 春季 D1t 0 其他
1 夏季 D2t 0 其他
1 秋季 D3t 0 其他
则冷饮销售量的模型为:
Yt 0 1 X1t k X kt 1D1t 2 D2t 3 D3t t
在上述模型中,若再引入第四个虚拟变量:
1 冬季 D4t 0 其他
则冷饮销售模型变量为:
Yt 0 1 X1t k X kt 1D1t 2 D2t 3 D3t 4 D4t t
可以通过传统的回归检验,对2的统计显著性进 行检验,以判断企业男女职工的平均薪金水平是
否有显著差异。
年薪 Y
2 0
男职工 女职工
工龄 X
又例:在横截面数据基础上,考虑个人保 健支出对个人收入和教育水平的回归。
教育水平考虑三个层次:高中以下, 高中, 大学及其以上。
这时需要引入两个虚拟变量:
1 D1 0
消费模型可建立如下:
Ct 0 1 X t 2 Dt X t t
这里,虚拟变量D以与X相乘的方式引入了模型中, 从而可用来考察消费倾向的变化。
假定E(i)= 0,上述模型所表示的函数可化为:
正常年份:
E(Ct | X t , Dt 1) 0 (1 2 ) X t
反常年份:
E(Ct | X t , Dt 0) 0 1 X t
虚拟变量回归模型_OK

是一样的,但两者的平均薪金水平相差 a。
可以通过传统的回归检验,对 a的统计显著性进行检验,以
判断男女职工的平均薪金水平是否显著差异。
16
例7.1.4 居民家庭的教育费用支出除了受收入水平的影响之外,还与子女 的年龄结构密切相关。如果家庭中有适龄子女(6-21岁),教育费用支出就 多。因此,为了反映“子女年龄结构”这一定性因素,设置虚拟变量:
当tt*=1978年, Dt = 1
ˆyt = bˆ0 aˆxt + bˆ1 + aˆ xt
32
28
例如,进口消费品数量Y主要取决于国民收入 X的多少,中国在改革开放前后,Y对X的回归关 系明显不同。
这时,可以t*=1978年为转折期,以1978年的 国民收入Xt*为临界值,设如下虚拟变量:
1 Dt = 0
t t* t t*
则进口消费品的回归模型可建立如下:
yt = b0 + b1 xt + a xt xt Dt + ut
9
概念:
同时含有一般解释变量与虚拟变量的模型称为 虚 拟 变 量 模 型或 者 方差 分 析 ( analysis-of variance: ANOVA)模型。
一个以性别为虚拟变量考察企业职工薪金的模型:
Yt = b 0 + b1 Xt + b 2Dt + mt
其中:Yt为企业职工的薪金,Xt为工龄, Dt=1,若是男性,Dt=0,若是女性。
D4=
1 喜欢某种商品 0 不喜欢某种商品
5)表示天气变化的虚拟变量可取为
D5=
1 晴天 0 雨天
6
2.引入虚拟变量的作用 引入虚拟变量的作用,在于将定性因素或属性因素对因变量
第七章虚拟变量

14
1 第一季度 D1 ={
0 其他
1 第二季度 D2 ={
0 其他 1 第三季度
D3={ 0 其他
15
年、季度
1990年1-3月 4-6月 7-9月 10-12月
1991年1-3月 4-6月 7-9月 10-12月
1992年 1-3月 4-6月 7-9月 10-12月
0
7-9月
0
10-12月
0
1992年 1-3月
1
4-6月
0
7-9月
0
10-12月 0
1993年1-3月
1
4-6月
0
7-9月
0
10-12月 0
1994年1-3月
1
D2
D3
0
0
1
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
18
估计结果如下:
Y= 9.0681+0.068301X-2.05875D1-1.8009D2-0.76594D3 所有t值都在1%的水平显著
103
208
1990
105
206
1991
96
203
1992
105
209
1993
78
213
1994
120
220
计量经济学课件虚拟变量

通过引入虚拟变量,可以更准确地刻画经济现象的非线性特征,从而提高计量经济学模型 的精度和预测能力。
拓展应用领域
虚拟变量的引入使得计量经济学模型能够应用于更多的领域,如金融、环境、社会等,进 一步拓展了计量经济学的应用范围。
未来研究方向和趋势
深入研究虚拟变量的理论 和方法
未来研究将进一步深入探讨虚 拟变量的理论和方法,包括虚 拟变量的选择、设定和估计方 法等,以更准确地刻画经济现 象。
https://
未来研究将积极推动虚拟变量 在交叉学科领域的应用,如环 境经济学、金融经济学等,以 促进不同学科之间的交流和合 作。
WENKU DESIGN
WENKU DESIGN
2023-2026
END
THANKS
感谢观看
KEEP VIEW
WENKU DESIGN
WENKU DESIGN
WENKU
REPORTING
要点二
虚拟变量的设置原则
在设置虚拟变量时,需要遵循完备性 和互斥性的原则。完备性要求虚拟变 量的取值能够覆盖所有可能的情况, 而互斥性则要求不同虚拟变量之间不 能存在重叠或交叉的情况。
要点三
虚拟变量的回归系数 解释
在线性回归模型中,虚拟变量的回归 系数表示该定性因素对因变量的影响 程度。当虚拟变量取值为1时,其对 应的回归系数表示该水平与参照水平 相比对因变量的影响;当虚拟变量取 值为0时,则表示该水平对因变量没 有影响。
参数估计与假设检验
参数估计
采用最小二乘法等估计方法,对引入虚拟变量后的模型进行参数估计,得到各 解释变量的系数估计值。
假设检验
根据研究问题和假设,构建相应的原假设和备择假设,通过t检验、F检验等方 法对参数进行假设检验,判断虚拟变量对模型的影响是否显著。
第七章 虚拟变量

在E(i)=0 的初始假定下,高中以下、高中、大学 及其以上教育水平下个人保健支出的函数:
高中以下:
E (Yi | X i , D1 0, D2 0) 0 1 X i
• 高中:
E (Yi | X i , D1 1, D2 0) ( 0 2 ) 1 X i
可视为截距项的解释变 量,即α0= α0×1
所以引入4个虚拟变量出现了完全多重共线 性的问题! OLS法不能使用! 这就是虚拟变量陷阱问题!
如果只取六个观测值,其中春季与夏季取了 两次,秋、冬各取到一次观测值,则式中的:
1 1 1 ( X, D) 1 1 1 X 11 X k1 X 12 X k 2 X 13 X k 3 X 14 X k 4 X 15 X k 5 X 16 X k 6 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0
1.定义
虚拟变量是一用以反映质的属性的一个人工 变量,取值为0或1,通常记为D(Dummy Variable),又可称之为哑变量或二进制变量。 对基础类型或肯定类型设 D=1 对比较类型或否定类型设 D=0 虚拟变量示例 注意:虚拟变量D只能取0或1两个值,即属性 之间不能运算!
(-6.11) (22.89) (4.33) (-2.55)
R 2 =0.9836
由3与4的t检验可知:参数显著地不等于0,强 烈示出两个时期的回归是相异的, 储蓄函数分别为:
1990年前: 1990年后:
ˆ 1649.7 0.4116X Y i i
ˆ 15452 0.8881X Y i i
1 D2 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则居民消费函数为:Yt=b0+b1Xt+a1Dt+μt
接前页
城镇居民住房消费模型(即D=1时):
Yt=(b0 +a1)+b1Xt+μt
农村居民住房消费模型(即D=0时):
Yt=b0 +b1Xt+μt
2、多个因素各两种属性
如果有m个定性因素,且每个因素各有两个不同的 属性类型,则引入m个虚拟变量。
例2
研究居民住房消费函数时,考虑到城乡差异和不同 收入层次的影响将消费函数设定为: Yt=b0+b1Xt+a1D1t+ a2D2t+ μt
Yt=居民住房消费支出
Xt=居民可支配收入
1城镇居民 D1t= 0农村居民
1高收入家庭 D2t= 0低收入家庭 μt=随机误差项
该模型反映出不同类型居民家 庭的住房消费情况
通过上例我们可以看出,如果有m个定 性因素,且每个因素各有两个不同的属 性类型,则应该引入 m个虚拟变量。
因此,“多因素各两个属性”的虚拟变 量引入可以推广到一般情况,若有些因 素有多个属性类型,则可参照“一个因 素,多种类型”的设置原则来设置虚拟 变量(即应该引入m-1个虚拟变量)。
课堂练习
某商品需求函数为 Yt=b0+b1Xt+μt,其中,
加法形式引入虚拟解释变量,其作用是改 变了设定模型的截距水平。
例4
居民家庭的教育费用支出除了受收入水平的影响外,还 与子女的年龄结构密切相关。如果一个家庭中有适龄子 女(6—21岁),教育费用支出就多。为了反映“子女 年龄结构”这一定性因素,可设置虚拟变量:
1 有适龄子女
D=
0 无适龄子女
将家庭教育费用支出函数写成:Yt=b0+b1Xt+aDt+μt 即以加法形式引入虚拟变量。
子女年龄结构不同的家庭教育 费用支出函数为:
无适龄子女家庭的教育费用支出函数 (D=0):Yt=b0+b1Xt+μt
有适龄子女家庭的教育费用支出函数 (D=1):Yt=(b0+a)+b1Xt+μt
虚拟变量对截距的影响
y
有适龄子女
b0+a
无适龄子女
a
b0
o
图1 虚拟变量对截距的影响
x
2、乘法方式引入虚拟变量
Y为需求量,X为价格,考虑“地区(农村和城 市)和季节(春夏秋冬)”两个因素的影响, 如何引入虚拟变量建立所需模型。
3、虚拟变量取值应从分析问题
的目的出发予以界定
定性因素的变化通常表现为某种属性或特征是否 存在,所以用1,0两个数值来量化。
一般地,1表示这种属性或特征存在,0表示这种 属性和特征不存在。而且设置虚拟变量时,基础 类型、否定类型通常取值为0,而比较类型、肯定 类型取值为1。如:在引入“政策”这个虚拟变量 时,将“政策不变”设置为0,将“政策变动”设 置为1;又如:引入“自然灾害”变量对产量影响, 可将“受灾年份”设置为0,将“不受灾年份”设 置为1。
第七章 虚拟变量
在回归分析中,被解释变量的影响因素 除了量(或定量)的因素还有质(或定 性)的因素,这些质的因素可能 会使回 归模型中的参数发生变化,为了估计质 的因素产生的影响,在模型中就需要引 入一种特殊的变量—虚拟变量。
本章主要讲授内容
一、虚拟变量的概念及作用 二、虚拟变量的设置 (一)设置规则 (二)引入方式 三、虚拟变量的特殊应用 (一)调整季节波动 (二)检查模型结构的稳定性 (三)分段回归 (四)混合回归
农村低收入家庭(D1=D2=0): Yt=b0+b1Xt+μt
农村高收入家庭(D1=0,D2=1):Yt=(b0+a2)+ b1Xt+μt 城镇低收入家庭(D1=1,D2=0):Yt=(b0+a1)+ b1Xt+μt 城镇高收入家庭(D1=D2=1):
Yt=(b0+a1+ a2)+ b1Xt+μt
总结与推广
4、虚拟变量在单一方程中可以作为解释变量, 也可以作为被解释变量。
(二)虚拟变量的引入方式
1、加法式引入虚拟变量
加法式引入虚拟变量,是在所设定的模型 中,根据所研究问题中数值变量的作用, 按照虚拟变量设置原则,直接在所设定的 计量经济模型中加入适当的虚拟变量,此 时虚拟变量与其他解释变量在设定模型中 是相加关系。
一、虚拟变量的概念和作用
(一)概念
在计量经济学中,把反映定性(或属性)因 素变化,取值为0和1的人工变量称为虚拟变 量(dummy variable) ,或称为亚变量、虚 设变量、定性变量、属性变量、双值变量、 类型变量、二元变量和名义变量等。习惯上 用字母D表示。例如:
1城镇居民
1男性
1就业
D= 0农村居民 D= 0女性 D= 0失业
Yt=b0+b1Xt+aDtXt+μt 该函数形式可以分别写成:
有适龄子女(D=1):Yt=b0+(b1+a)Xt+μt 无适龄子女(D=0):Yt=b0+b1Xt+μt
虚拟变量对斜率的影响
y
有适龄子女
基本思想:以乘法方式引入虚拟解释变量,
是在所设定的计量经济模型中,将虚拟解 释变量与其他解释变量相乘作为新的解 释变量,以达到其调整模型斜率的目的。
该方式引入虚拟变量主要作用:
两个回归模型之间的比较; 因素之间的交互影响分析; 提高模型对现实经济现象的描述精度。
例5
随着收入水平的提高,家庭教育消费支 出的边际消费倾向可能会发生变化。如 下图2。为了反映定性因素对斜率的影响, 可以用乘法方式引入虚拟变量,将家庭 教育费用支出函数写成:
(二)作用
1、可以描述和测量定性(或属性)因素 的影响;
2、能够正确反映经济变量之间的相关关 系,提高模型的估计精度;
3、便于处理异常数据在模型中设置虚拟变量时,应遵循一定的设置规 则,以免使虚拟变量之间产生多重共线性。
1、一个因素多个属性 若定性因素有m个不同属性或相互排斥的类型, 在模型中只能引入m-1个虚拟变量,否则会产生 多重共线性。
例如:一个定性因素“居民”分为“城镇居民”和 “农村居民”两个属性,则在引入虚拟变量时只 能引入1个。
例1
居民消费函数为:
Yt=b0+b1Xt+μt 其中, Yt=第t个居民的住房消费支出
Xt=第t个居民的可支配收入
μt=随机误差项 为了将城镇居民和农村居民这两种不同类型的居民对住房消
费支出的影响反映到上述模型中,需要引入一个虚拟变 量
