数字信号处理第一次大作业
数字信号处理实验课大作业

DSP 实验课大作业设计一 实验目的 在DSP 上实现线性调频信号的脉冲压缩、上实现线性调频信号的脉冲压缩、动目标显示(动目标显示(动目标显示(MTI MTI MTI)和动目标检测)和动目标检测)和动目标检测(MTD)(MTD)(MTD),,并将结果与MATLAB 上的结果进行误差仿真。
上的结果进行误差仿真。
二 实验内容1. MATLAB 仿真仿真设定带宽、脉宽、采样率、脉冲重复频率,用MATLAB 产生16个脉冲的LFM LFM,每个脉冲,每个脉冲有4个目标(静止,低速,高速),依次做:,依次做:1) 脉冲压缩;脉冲压缩;2) 相邻2脉冲做MTI MTI,产生,产生15个脉冲;个脉冲;3) 16个脉冲到齐后,做MTD MTD,输出,输出16个多普勒通道个多普勒通道4) 改变PRF 后,利用两次PRF 下不同的速度结果,求不模糊速度下不同的速度结果,求不模糊速度2. DSP 实现实现将MATLAB 产生的信号,在visual dsp 中做频域脉压、中做频域脉压、MTI MTI MTI、、MTD MTD,将,将MTI 和MTD 结果导入Matlab ,并将其结果与MATLAB 的结果作比较。
三 实验原理1.1. 频域脉冲压缩原理频域脉冲压缩原理一般通过匹配滤波实现脉冲压缩。
在接收机中设置一个与发射信号频率相匹配的压缩网络使经过调制的宽脉冲的发射信号(一般认为也是接受机输入端的回波信号)变成窄脉冲,使之得到良好的距离分辨力,这个过程就称为“脉冲压缩”。
而这个脉冲压缩网络实际上就是一个匹配滤波器网络。
络实际上就是一个匹配滤波器网络。
2.2. MTI 原理原理MTI MTI((Moving Target Indication Indication)即动目标显示是利用运动目标带来的多普勒频)即动目标显示是利用运动目标带来的多普勒频移来消除静止杂波。
当雷达按照一定的周期辐射LFM 信号时,目标与雷达的距离不同会使得回波的相位有所不同。
数字信号处理习题集(附答案解析)

第一章数字信号处理概述简答题:1.在A/D变换之前和D/A变换之后都要让信号通过一个低通滤波器,它们分别起什么作用?答:在A/D变化之前为了限制信号的最高频率,使其满足当采样频率一定时,采样频率应大于等于信号最高频率2倍的条件。
此滤波器亦称为“抗混叠”滤波器。
在D/A变换之后为了滤除高频延拓谱,以便把抽样保持的阶梯形输出波平滑化,故又称之为“平滑”滤波器。
判断说明题:2.模拟信号也可以与数字信号一样在计算机上进行数字信号处理,自己要增加一道采样的工序就可以了。
()答:错。
需要增加采样和量化两道工序。
3.一个模拟信号处理系统总可以转换成功能相同的数字系统,然后基于数字信号处理理论,对信号进行等效的数字处理。
()答:受采样频率、有限字长效应的约束,与模拟信号处理系统完全等效的数字系统未必一定能找到。
因此数字信号处理系统的分析方法是先对抽样信号及系统进行分析,再考虑幅度量化及实现过程中有限字长所造成的影响。
故离散时间信号和系统理论是数字信号处理的理论基础。
第二章 离散时间信号与系统分析基础一、连续时间信号取样与取样定理 计算题:1.过滤限带的模拟数据时,常采用数字滤波器,如图所示,图中T 表示采样周期(假设T 足够小,足以防止混叠效应),把从)()(t y t x 到的整个系统等效为一个模拟滤波器。
(a ) 如果kHz rad n h 101,8)(=π截止于,求整个系统的截止频率。
(b ) 对于kHz T 201=,重复(a )的计算。
解 (a )因为当0)(8=≥ωπωj e H rad 时,在数 — 模变换中)(1)(1)(Tj X Tj X Te Y a a j ωω=Ω=所以)(n h 得截止频率8πω=c 对应于模拟信号的角频率c Ω为8π=ΩT c因此 Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为Tπ,因此对T8π没有影响,故整个系统的截止频率由)(ωj e H 决定,是625Hz 。
武汉理工大学数字信号处理第一次实验报告完整答案

第一部分:例题调试(一)单位抽样序列10()(00n n n δδ =⎧⎧= ⎨⎨ ≠ ≠⎩⎩0001n=n 或n-n )=0n n代码如下:%先建立函数impseq(n1,n2,n0)function [x,n]=impseq(n1,n2,n0)n=[n1:n2];x=[(n-n0)==0];%编写主程序调用该函数[x,n]=impseq(-2,8,2);stem(n,x);title('DSP_example01单位抽样序列——徐樱笑');(二)单位阶跃序列0110()(-)000n n u n u n n n n ≥ ≥⎧⎧= = ⎨⎨ < <⎩⎩00n 或n 代码如下:%先建立函数stepseq(n1,n2,n0)function [x,n]=stepseq(n1,n2,n0)n=[n1:n2];x=[(n-n0)>=0];%编写主程序调用该函数[x,n]=stepseq(-2,8,2);stem(n,x)title('DSP_example01单位阶跃序列——徐樱笑');(三)实数指数序列x(n)=a n (运算符“.^”)代码如下:n=[0:10];x=0.9.^n;stem(n,x);title('DSP_example03实数指数序列——徐樱笑');(四)复数指数序列(0.10.3)()(1010)j n x n e n -+= -≤≤代码如下:n=[-10:10];alpha=-0.1+0.3*j;x=exp(alpha*n);real_x=real(x); image_x=imag(x);mag_x=abs(x); phase_x=angle(x);subplot(2,2,1); stem(n,real_x);subplot(2,2,2); stem(n,image_x);subplot(2,2,3); stem(n,mag_x);subplot(2,2,4); stem(n,phase_x);suptitle('DSP_example04复数指数序列——徐樱笑')(五)正、余弦序列(0()sin()m x n U n ωθ=+)代码如下:n=[0:42];x=2*cos(0.1*pi*n+pi/3);stem(n,x);title('DSP_example05正余弦序列——徐樱笑');第二部分:课后习题(一)利用zeros函数生成单位抽样序列:代码如下:n=-10:10;y=[zeros(1,10),1,zeros(1,10)];stem(n,y)axis([-10,10,0,2]);title('DSP_test01单位抽样序列——徐樱笑'); (二)利用zeros函数和ones函数生成单位阶跃序列代码如下:n=-5:10;y=[zeros(1,5),1,ones(1,10)];stem(n,y)axis([-5,10,0,2]);title('DSP_test02单位阶跃序列——徐樱笑'); (三)已知x1(n)=u(n+1) (-3<n<5); x2(n)=u(n-3) (-4<n<7)。
数字信号处理作业答案(参考版-第一章)

1-2习题1-2图所示为一个理想采样—恢复系统,采样频率Ωs =8π,采样后经过理想低通G jΩ 还原。
解:(1)根据余弦函数傅里叶变换知:)]2()2([)]2[cos(πδπδππ-Ω++Ω=t F ,)]6()6([)]6[cos(πδπδππ-Ω++Ω=t F 。
又根据抽样后频谱公式:∑∞-∞=∧Ω-Ω=Ωk s a a jk j X T j X )(1)(,得到14T= ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]82()82([4)(1ππδππδπ∑∞-∞=∧--Ω+-+Ω=Ωk a k k j X )]86()86([4)(2ππδππδπ所以,)(1t x a ∧频谱如下所示)(2t x a ∧频谱如下所示(2))(1t y a 是由)(1t x a ∧经过理想低通滤波器)(Ωj G 得到,)]2()2([)()()]([11πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a ,故)2cos()(1t t y a π=(4π) (4π) (4π)(4π)(4π) (4π) Ω-6π-10π-2π 2π0 6π10π)(1Ω∧j X a Ω10π-10π -6π-2π 0 2π6π-14π 14π(4π)(4π) (4π)(4π) (4π) (4π)(4π) (4π))(2Ω∧j X a同理,)]2()2([)()()]([22πδπδπ-Ω++Ω=ΩΩ=∧j G j X t y F a a 故)2cos()(2t t y a π=(3)由题(2)可知,无失真,有失真。
原因是根据采样定理,采样频率满足信号)(1t x a 的采样率,而不满足)(2t x a 的,发生了频谱混叠。
1-3判断下列序列是否为周期序列,对周期序列确定其周期。
(1)()5cos 86x n A ππ⎛⎫=+ ⎪⎝⎭(2)()8n j x n eπ⎛⎫- ⎪⎝⎭=(3)()3sin 43x n A ππ⎛⎫=+ ⎪⎝⎭解:(1)85πω=,5162=ωπ为有理数,是周期序列,.16=N (2)πωπω162,81==,为无理数,是非周期序列; (3)382,43==ωππω,为有理数,是周期序列,8=N 。
数字信号处理作业(附答案)1-郑佳春
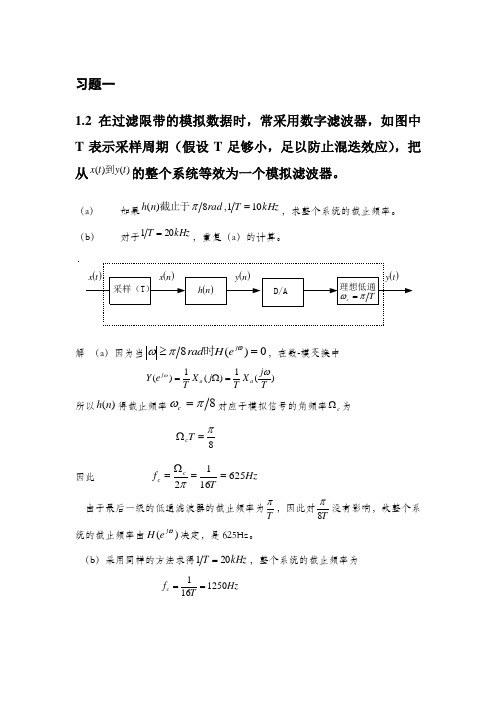
习题一1.2 在过滤限带的模拟数据时,常采用数字滤波器,如图中T 表示采样周期(假设T 足够小,足以防止混迭效应),把从)()(t y t x 到的整个系统等效为一个模拟滤波器。
(a ) 如果kHz rad n h 101,8)(=π截止于,求整个系统的截止频率。
(b )对于kHz T 201=,重复(a )的计算。
解 (a )因为当0)(=≥ωπωj e H rad 时,在数-模变换中)(1)(1)(Tj X T j X T e Y a a j ωω=Ω= 所以)(n h 得截止频率πω=c对应于模拟信号的角频率c Ω为8π=ΩT c因此 Hz Tf c c 6251612==Ω=π 由于最后一级的低通滤波器的截止频率为Tπ,因此对T 8π没有影响,故整个系统的截止频率由)(ωj eH 决定,是625Hz 。
(b )采用同样的方法求得kHz 201=,整个系统的截止频率为 Hz Tf c 1250161==1.3 一模拟信号x(t)具有如图所示的带通型频谱,若对其进行采样,试确定最佳采样频率,并绘制采样信号的频谱。
解:由已知可得:==35,25H L f kHz f kHz ,10k H L B f f Hz =-=,为使无失真的恢复原始信号,采样频率应满足:2f 21c c s B f Bf m m+-≤≤+且220s f B kHz >=、0/12H m f B ≤≤-=⎡⎤⎣⎦ 当m=1时,2501c s f Bf kHz -==,满足: 3550s kHz f kHz ≤≤ 当m=2时,2252c s f Bf kHz -==,满足:23.325s kHz f kHz ≤≤ 故最佳采样频率为25kHz,采样信号的频谱图如下图所示 :1.5 判断下面的序列是否是周期的,若是周期的,确定其周期,并绘制一个周期的序列图(1)16()cos()58x n A n ππ=-,A 是常数 解:2251685N wπππ===,所以x(n)是周期的,且最小正周期为5 1285()cos()40n x n A π-= 绘图:方法一:计算法 当n=0时,1()cos()8x n A π-==0.99A 当n=1时,123()cos()40x n A π==3cos()40A ππ+=0.998A 当n=2时,251()cos()40x n A π==11cos()40A π=0.863A 当n=3时,379()cos()40x n A π==19cos()40A ππ+=0.996A 当n=4时,507()cos()40x n A π==27cos()40A π=0.999A 当n=5时,635()cos()40x n A π==6405cos()40A π-= 方法二:Matlab 法> xn=cos(16*n*pi/5-pi/8); > plot(n,xn) > n=0:4;> xn=cos(16*n*pi/5-pi/8); > plot(n,xn)> plot(n,xn,'.');grid;1.6对如下差分方程所述系统,试分析其线性特性与时变特性(1)()()2(1)y n x n x n =-- (3)2()4()y n x n =解:(1)121212[()()]()()2{(1)(1)}T ax n bx n ax n bx n ax n bx n +=+--+- 121122[()][()]()2(1)()2(1)T ax n T bx n ax n ax n bx n bx n +=--+--故 1212[()()][()][()]T ax n bx n T ax n T bx n +=+所以y(n)为线性又0000[()]()2(1)()T x n n x n n x n n y n n -=----=- 所以y(n)为时不变(3)2222121122[()()]4()8()()4()T ax n bx n a x n abx n x n b x n +=++ 221212[()][()]4()4()T ax n T bx n ax n bx n +=+ 故1212[()()][()][()]T ax n bx n T ax n T bx n +≠+ y(n)为非线性又2000[()]4()()T x n n x n n y n n -=-=- 故y(n)为时不变1.7试判断如下算法是否是因果的?是否是稳定的?并说明理由。
数字信号处理作业第1章

X(Z)= 0.5nZ-n=(1-0.510Z-10)/(1-0.5Z-1)=(Z10-0.510)/[Z9(Z-0.5)],|Z|>0
极点:Z=0 9 阶极点,零点:Zk=0.5ej(2πk/10),k=1,2,…,9 1.10 X(Z)=1/(1-Z-1)(1-2Z-1),1<|Z|<2
解:x(n)=1/(2πj)∮cx(z)zn-1dz 因为 1<|Z|<2
=-u(n)-2n+1u(-n-1)
1.11(3) y(z)= y(n)z-n= y(n)z-n+ y(n)z-n
= y(2r)z-2r+ y(2r+1)z-(2r+1)=x(z)+z-1x(z2)
1.13(1)y(n)=2x(n)+5=T[x(n)] T[ax1(n)+bx2(n)]=2[ax1(n)+bx2(n)]+5≠T[ax1(n)]+T[bx2(n)] 系统非线性 T[x(n-n0)]=2x(n-n0)+5=y(n-n0)时不变 所以系统为非线性时不变系统
Sinφ 0
-0.59 0.95 -0.95 0.59 0 -0.59 0.95
1.3
1.4 解:因为采样频率Ωs=8π 所以采样周期 Ts=2π/Ωs=1/4(S)
采样信号
= xa1(t)δ(t-nTs)=
Cos(2πt)δ(t-1/4n)
=- Cos(6πt)δ(t-1/4n)
= Cos(10πt)δ(t-1/4n)
=an-2u(n-2)
1.22(1)H(Z)=(1-a-1z-1)/(1-a-1)=(z-a-1)/(z-a) |a|<1 系统稳定
课程大作业——数字信号处理实验报告

实验一 信号、系统及系统响应一.实验目的1.熟悉理想采样的性质,了解信号采用前后的频谱变化,加深对采样定理的理解。
2.熟悉离散信号和系统的时域特性。
3.熟悉线性卷积的计算编程方法:利用卷积的方法,观察、分析系统响应的时域特性。
4.掌握序列傅氏变换的计算机实现方法,利用序列的傅氏变换对离散信号、系统及系统响应进行频域分析。
二.实验原理1.连续时间信号的采样采样是从连续时间信号到离散时间信号的过渡桥梁,对采样过程的研究不仅可以了解采样前后信号时域和频域特性发生的变化以及信号内容不丢失的条件,而且有助于加深对拉氏变换、傅氏变换、z 变换和序列傅氏变换之间关系的理解。
对一个连续时间信号进行理想采样的过程可以表示为该信号和个周期冲激脉冲的乘积,即)()()(ˆt M t x t xa a = (1-1) 其中)(ˆt xa 是连续信号)(t x a 的理想采样,)(t M 是周期冲激脉冲 ∑+∞-∞=-=n nT t t M )()(δ (1-2)它也可以用傅立叶级数表示为:∑+∞-∞=Ω=n tjm s e T t M 1)( (1-3)其中T 为采样周期,T s /2π=Ω是采样角频率。
设)(s X a 是连续时间信号)(t x a 的双边拉氏变换,即有:⎰+∞∞--=dt e t xs X st aa )()( (1-4)此时理想采样信号)(ˆt xa 的拉氏变换为 ∑⎰+∞-∞=+∞∞--Ω-===m s a sta a jm s X T dt e t x s X )(1)(ˆ)(ˆ (1-5)作为拉氏变换的一种特例,信号理想采样的傅立叶变换[]∑+∞-∞=Ω-Ω=Ωm s a a m j X T j X )(1)(ˆ (1-6)由式(1-5)和式(1-6)可知,信号理想采样后的频谱是原信号频谱的周期延拓,其延拓周期等于采样频率。
根据Shannon 采样定理,如果原信号是带限信号,且采样频率高于原信号最高频率分量的2倍,则采样以后不会发生频率混淆现象。
《数字信号处理》作业答案

第一章离散时间系统4.判断下列每个序列是否是周期的,若是周期的,试确定其周期。
(1)⎪⎭⎫ ⎝⎛-=873cos )(ππn A n x (2)⎪⎭⎫⎝⎛=n A n x π313sin )( (3))6()(π-=nj e n x解:(1)由⎪⎭⎫ ⎝⎛-=873cos )(ππn A n x 可得31473220==ππωπ,所以)(n x 的周期是14。
(2)由⎪⎭⎫⎝⎛=n A n x π313sin )(可得136313220==ππωπ,所以)(n x 的周期是6。
(3)由⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-==-6sin 6cos 6sin 6cos )()6(n j n n j n e n x nj πππ,所以)(n x 是非周期的。
6.试判断(1)∑-∞==nm m x n y )()(是否是线性系统?解:根据∑-∞==nm m x n y )()(可得 ∑-∞===nm m x n x T n y )()]([)(111,∑-∞===nm m xn x T n y)()]([)(222∑∑∑∑∑-∞=-∞=-∞=-∞=-∞=+=+=++=+nm n m n m nm nm n xb n x a n bx m ax n bx n ax T n x b n x a n by n ay )()()]()([)]()([)()()()(2121212121所以系统是线性的。
9.列出图P1-9系统的差分方程并按初始条件y(n)=0,n<0,求输入为x(n)=u(n)时的输出序列y(n),并画图。
解:x 1(n)=x(n)+x 1(n-1)/4 x 1(n)- x 1(n-1)/4=x(n) x 1(n-1)- x 1(n-2)/4=x(n-1) y(n)=x 1(n)+x 1(n-1) y(n-1)/4=x 1(n-1)/4+x 1(n-2)/4y(n)-y(n-1)/4=x(n)+x(n-1) y(n) =x(n)+x(n-1) +y(n-1)/4y(0)=u(0)=1y(1)=u(1)+u(0)+y(0)/4=2+1/4y(2)=u(2)+u(1)+y(1)/4=2+(2+1/4)/4=2(1+1/4)+(1/4)2 y(3)=u(3)+u(2)+y(2)/4==2(1+1/4+(1/4)2)+(1/4)3y(n)=2(1+1/4+……+(1/4)n-1)+(1/4)ny(n)=2(1-(1/4)n )/(1-1/4)+(1/4)n =[8/3-5/3(1/4)n ]u(n)11.有一理想抽样系统,抽样角频率为π6=Ωs ,抽样后经理想低通滤波器)(ωj H a 还原,其中:⎪⎩⎪⎨⎧≥<=πωπωω30321)(j H a令有两个输入信号)2cos()(1t t x a π=,)5cos()(12t t x a π=输出信号有没有失真?为什么?解:抽样频率大于两倍信号最大频率则无失真,)2cos()(1t t x a π=信号角频率为2π<3π,y a1(n)无失真。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验名称实验1 基于谐波检测的移频闭塞信号数字接收实验目的1.掌握基于FFT 的信号频谱分析技术,认识近似分析中出现的混叠现象、泄露现象和栅栏现象,加深理解这些现象对频谱分析精度的影响。
2.初步掌握噪声中谐波检测算法,了解影响频率估计精度的主要因素。
3.了解铁路移频闭塞系统的信号发送和接收过程。
实验内容1.通过理论分析推导移频闭塞信号s(t)及其等效低通形式s l(t)的傅里叶变换表达式(为离散谱),由此计算f1取不同值时国产18信息和ZPW-2000两类闭塞信号的主谐波分量频率和有效值,并统计其功率最强的几根谱线(国产18信息为6根,ZPW-2000 为3根)的功率之和占信号总功率的百分比。
将计算结果制作成表格。
2.参照实验原理部分提供的波形仿真示例程序,针对国产18信息和ZPW-2000两种制式,产生f1为标准值时移频闭塞信号等效低通信号仿真波形(可根据需要设定生成数据的长度和对采样频率等参数进行调整),由FFT分析该信号频谱并计算其主谐波的频率和有效值,将计算结果与内容1计算结果进行比较。
3.假设移频闭塞信号的参数f c和f1取标准值(即频率偏差为0),设计算法分析接收到的等效低通信号,通过提取移频闭塞信号的主谐波分量,估计调制低频f1的最佳取值。
将编写的程序对10段信号样本进行分析,输出f1的估计结果。
4.假设移频闭塞信号的参数f c和f1的偏差满足|Δf c|<5Hz,|Δf1|<0.1Hz,根据接收到的等效低通信号设计算法估计Δf c和Δf1,并确定调制低频f1对应的最佳标准值。
将编写的程序对10 段信号样本进行分析,输出Δf c、Δf1和f1的估计结果。
实验结果与分析内容1记v=Δff1=TΔf由题可知s(t)=A0∑{c n cosθ0cos[2π(f c+nf1)t]+c n sinθ0sin[2π(f c+nf1)t]} +∞n=−∞其中c n=sinπ(v−n)2π(v−n)+(−1)nsinπ(v+n)2π(v+n)若要求移频信号归一化功率为1,则移频信号的各个谐波分量的归一化值为A̅n=c√∑|c n|2+∞n=−∞=c√|c0|2+2∑|c n|2+∞n=1内容2ZPW-2000制式,仿真结果如下主谐波频率f=1T=1(0.4937−0.009338)/13≈26.8394Hz偏移4Hz。
归一化后,在4Hz±0.5f上进行积分后开方,得有效值0.6458。
国产18信息制式,仿真结果如下f=1T=1(0.4982−0.01508)/8≈16.5590Hz主谐波频率为49.677Hz偏移4Hz。
归一化后,进行数值积分后开方,得有效值0.8177。
将以上结果与理论值相比较,可以看出,由于噪声作用,二者有一定误差,但仍然体现出了一致性。
内容3对于ZPW-2000信息制式,幅频特性类似于下图对于国产18制式,幅频特性类似于下图从文件读入时域波形,用fft函数得到频谱。
取峰值中最大的n个(对于ZPW-2000信息制式,取n=3;对于国产18制式,取n=6),将其对应的频率放在数组f里。
以0.1为步长,不断列举f1的值,记录下使nS=∑|f1−f[i]|i=1最小的f1的值。
然后将f1与标准值相比较,选择最接近的一个。
编写程序如下%初始化close all;clear all;fs=1024;f1=zeros(10,1);type=6;if (type==3)F1Set=10.3+1.1*(0:17);elseF1Set=[7,8,8.5,9.0,9.5,11.0,12.5,13.5,15.0,16.5,17.5,18.5,20.0,21.5,22.5,23.5,24.5,26];End%数据处理部分for step=1:10%读取数据load 2009010990_dat3;x=Data(:,step);%频谱分析X=fftshift(fft(x));%抽取主谐波频率[X_sorted,index_sorted]=sort(X);n=length(index_sorted);k=type;m=0;t=zeros(type,1); while (m<type)a=sort(index_sorted(n-k+1:n));m=1;t(1)=a(1);for i=2:kif (a(i)~=a(i-1)+1)m=m+1;t(m)=a(i);elseif (X(t(m))<X(a(i)))t(m)=a(i);endendendk=k+1;endindex=(t-257)*2;%确定f1b=sort(abs(index));r=zeros(type,1);delta=0;while (delta<100)for i=floor(min(F1Set))*10:b(round(type/2))*10 tmp=0;for j=1:typer(j)=b(j)/(i*0.1);tmp=tmp+abs(r(j)-round(r(j)));endif (tmp<=0.02*delta)f1(step)=i*0.1;endendif (f1(step)<7)delta=delta+1;elsedelta=100;endend%将f1与标准值匹配mindelta=abs(f1(step)-F1Set(1));f1tmp=F1Set(1);for i=2:length(F1Set)if (mindelta>abs(f1(step)-F1Set(i)))mindelta=abs(f1(step)-F1Set(i));f1tmp=F1Set(i);endendf1(step)=f1tmp;end%输出结果disp(f1);分别从2009010990_dat1和2009010990_dat3读取数据,运行程序进行分析,得到结果如下表所示。
与任务3算法原理相似,但需要加入对△f c和△f1的处理,因此程序结构上有所改变。
仍然从文件中读入采样数据,用fft()函数进行频谱分析,并抽取频谱中的n个最大值,将其对应频率放入数组f。
先以0.01为步长,不断列举△f c的值,再以0.01为步长,不断列举△f1的值,并枚举f1为标准值,记录下使nS=∑|f1−f[i]+△f c|i=1最小的△f c,△f1与f1。
编写程序如下。
close all;clear all;fs=1024;type=6;if (type==3)F1Set=10.3+1.1*(0:17);elseF1Set=[7,8,8.5,9.0,9.5,11.0,12.5,13.5,15.0,16.5,17.5,18.5,20.0,21.5,22.5,23.5,24.5,26];endfor step=1:10load 2009010990_dat4;x=Data(:,step);X=fftshift(fft(x));[X_sorted,index_sorted]=sort(X);n=length(index_sorted);k=type;m=0;t=zeros(type,1);while (m<type)a=sort(index_sorted(n-k+1:n));m=1;t(1)=a(1);for i=2:kif (a(i)~=a(i-1)+1)m=m+1;t(m)=a(i);elseif (X(t(m))<X(a(i)))t(m)=a(i);endendendk=k+1;endindex=(t-257)*2;a=sort(abs(index));df1=(-0.1:0.01:0.1)';F1Set0=df1*ones(1,length(F1Set))+ones(length(df1),1)*F1Set;deltamin=100;f1index=0;dffinal=0;for dfc=-5:0.01:5index0=index-dfc;thedelta=100;for i=1:length(F1Set)for j=1:length(df1)delta=sum(abs((index0/F1Set0(j,i))-round(index0/F1Set0(j,i))));if (delta<=thedelta)thedelta=delta;theindex=i;thedf1=df1(j);endendendif (thedelta<=deltamin)deltamin=thedelta;f1index=theindex;dfcfinal=dfc;df1final=thedf1;endenddisp([dfcfinal,df1final,F1Set(f1index)]);end分别从2009010990_dat2和2009010990_dat4读取数据,运行程序进行分析,得到结果电94 胡天骐2009010990其f1应为30左右,远超出了标准值的取值范围,因此程序识别错误,认为f1=15Hz。
我查看了其他同学的一些数据,没有发现类似这样的数据。
事实上在任务3中,制式为国产18信息的第9条数据,同样出现了f1=30Hz,只不过任务3中采用了另一种算法,程序没有出错。
误差分析由于频谱分析后频率最小间隔为2Hz,因此对于单个峰值,误差在1Hz之内。
而谐波分析过程中,采用了多个峰值所对应的频率,造成误差应当在0.1Hz数量级。
需要注意的是,这一误差可以通过增加采样频率来减少。
忽略频谱离散造成的误差,该算法中△f c,△f1,f1的误差都在0.01Hz以内,并可以通过缩减步长而减小。
11。
