光的偏振马吕斯定律汇总.
光的偏振特性 马吕斯定律

出射光强:明 黑 明 黑 明
·10 ·
Chapter 16. 光的偏振 §16. 1 光的偏振特性 马吕斯定律
例 自然光光强 I0,P1⊥P3,现以与P1成 30o角插入P2,
求出射光强。
解
I1
1 2
I0
30o
I0
I1
I2
I3
I2 I1 cos230o
一、线偏振光与非偏振光
振动面:电矢量 E与传播方向构成的面。
称:线偏振光(或平面/完全偏振光)
Fig. 1 振动面平行于屏幕
振
动
面
E
Fig. 2 振动面垂直于屏幕 Fig. 3 振动面不在屏幕内
平面波
·3 ·
Chapter 16. 光的偏振 §16. 1 光的偏振特性 马吕斯定律
自然光:光矢量 E 沿任意方向概率相同 !
立体电影
·8 ·
210
Chapter 16. 光的偏振 §16. 1 光的偏振特性 马吕斯定律
·9 ·
Chapter 16. 光的偏振
三、马吕斯定律
§16. 1 光的偏振特性 马吕斯定律
光强: I A2
I1 I2
A12 A22
A2 A1 cos
I1 A1 A2
I2 ቤተ መጻሕፍቲ ባይዱ1 cos2
I2 ?
属非偏振光!
表示法:
Iy
I0
Ix
Iy
1 2
I0
Ix
·4 ·
Chapter 16. 光的偏振 §16. 1 光的偏振特性 马吕斯定律
部分偏振光:光矢量 E 沿某一方向占优势 !
表示法:
光的偏振实验马吕斯定律

光的偏振实验马吕斯定律光的偏振实验马吕斯定律光的偏振是指光波振动方向的特性。
在物理学中,马吕斯定律是描述光的偏振性质的基本定律之一。
本文将介绍光的偏振实验以及马吕斯定律的原理与应用。
一、光的偏振实验光的偏振实验是通过一系列实验来观察和测量光波在通过偏振器材料时的偏振现象。
常用的偏振实验方法包括偏振片实验、旋光仪实验等。
1. 偏振片实验偏振片是一种特殊的光学材料,可以选择允许特定振动方向的光通过。
在偏振片实验中,我们可以通过两块偏振片的组合来观察光的偏振现象。
通常,将第一块偏振片设置为偏振器,通过旋转它的角度,可以改变光波通过的偏振方向。
随后,将第二块偏振片作为分析器,用于观察通过的光的强度。
根据分析器的角度,我们可以观察到光的透射光强度的变化。
2. 旋光仪实验旋光仪是一种常用的光学仪器,用于测量物质的旋光性质。
旋光性是指物质对偏振光的旋转效应。
在旋光仪实验中,通过旋转样品槽里的物质,可以观察到经过样品后偏振光旋转的现象。
二、马吕斯定律的原理马吕斯定律是法国科学家马吕斯在1808年提出的,该定律描述了光在通过各向同性材料(无论是吸收还是反射)时的偏振性质。
根据马吕斯定律,当一束不偏振光从一个均匀各向同性介质(例如空气、玻璃等)射入时,经过该介质后的光将成为线偏振光。
具体来说,假设光波的振动方向与入射面垂直,那么经过介质后,与入射面垂直的振动方向会被选择性地减弱,而平行于入射面的振动方向则会保持不变。
马吕斯定律的实质是光的振动方向在介质中受到选择性的吸收和减弱,从而导致光的偏振现象。
三、马吕斯定律的应用马吕斯定律在生活和科学研究中有着广泛的应用。
1. 偏振片根据马吕斯定律的原理,偏振片可以选择性地通过特定方向的光波,使其成为偏振光。
这种特性被广泛应用于摄影、光学仪器、偏振显微镜等领域。
2. 偏振光的产生与检测马吕斯定律的原理可以通过适当的实验装置来产生和检测偏振光。
例如,通过透镜和线性偏振片的组合,可以用于研究偏振光与物质的相互作用,有助于了解材料的光学性质。
光学18光的偏振性、马吕斯定律

在一切可能方向上都有光振动且各个方向的光 矢量的若振把幅自又然相光等所的有光方—向—的自光然振光动(都na分tu解re到li相gh互t)。
垂直的两个方向上,在这两个方向上的光振动的 振幅和能量都相等。
表示为
自然光的分解
自然光的简化表示
自然光的光矢量可以用两个振幅相等、振动方向 互相垂直的分振动来表示。
偏器后的光强为I I, 有I:0 cos2
马吕斯定律
马吕斯定律 I I0 cos2 说明了入射到
偏振片上的线偏振光,其透射光强度的变化规律。
自然光
I0
偏振化方向
I1
I0 2
I2
起偏器
检偏器
Note:自然光通过起偏器后强度为原来
的一半!
I0
I1
I0 2
I2
I1 c os2
3、如果光强由亮至暗(尚有光线透过)(I≠0) 待检光是部分偏振光。
这样,根据透射光强度变化的情况,可将线偏振光
和自然光和部分偏振光区别开来。 这充分说明光为横波!
三、马吕斯定律 Law of Malus (important!)
光通过偏振片后光强变化了多少 ?
偏振化方向
I0
I
...
起偏器
检偏器
如图,起偏器与检偏器的偏振化方 向之间的夹角为,通过起偏器后 的偏振光的强度为I0 , 继续通过检
二、 起偏和检偏 (polarization and examine polarization )
狭缝与振动同方向
狭缝与振动 方向垂直
把自然光变为偏振光的过程称为起偏;
检验(观察)偏振光的过程称为检偏。
偏振化方向
第十二讲 光的偏振现象马吕斯定律

机械横波与纵波的区别
机 械 波 穿 过 狭 缝
波动光学
波动光学
二、五种偏振态
(振光 3、部分偏振光 *4、圆偏振光 *5、椭圆偏振光
自然界大多数光源发出的光是自然光。
波动光学
三、自然光与偏振光
1、自然光 (非偏振光 )
在垂直于光传播方向的平面内,沿各个方向都有光 振动,且每个方向光矢量的振幅相等的光。
马吕斯定律的验证实验:
线偏振光有两次消光现象
波动光学
例题 有两个偏振片,一个用作起偏器, 一
个用作检偏器.当它们偏振化方向间的夹角
为 30时 , 一束单色自然光穿过它们, 出射 光强为 I1 ; 当它们偏振化方向间的夹角为60
时,另一束单色自然光穿过它们 , 出射光强
为
I
,
2
且
I1 I2
。求两束单色自然光的强
2、原因 普通光源所发出的光, 波列之间是相互独立的,没 有固定的关联(相位、振动方向、振幅、波列长短 等),按统计原理,无论哪一方向的振动在各方向 上的分布是对称的,振幅也可看成是完全相等的 (统计平均),这种光称为自然光。
波动光学
3、线偏振光和部分偏振光 线偏振光:在垂直于光传播方向的平面内,只包 含单一振动方向的光。 部分偏振光:在垂直于光传播方向的平面内,各 方向都有光振动但振幅不等的光。
波动光学
四、偏振片 起偏和检偏
1、二向色性 : 某些物质能吸收某一方向的光振动 , 而只让与这个方向垂直的光振动通过, 这种性质称 二向色性。
2、偏振片 :能吸收某一方向的光振动,而只让与 之垂直方向上的光振动通过的一种透明薄片。
波动光学
3、偏振化方向 :当自然光照射在偏振片上时,它 只让某一特定方向的光通过,这个方向叫此偏振片 的偏振化方向 .
光的偏振性马吕斯定律

I10
I10/2
I1
••
I1
I10 2
cos2
30
同理:
I2
I20 2
cos2
600
取 I1 = I2
I10 cos2 30 I20 cos2 60
2
2
两束单色自然光的强度 比为:
I10 I20
cos2 cos2
60 30
1 3
§2 反射和折射光的偏振 一. 反射时光的偏振
法线
e光 • • • o光 光轴
二.惠更斯原理对双折射的 解释 1. 晶 体 的 主 折 射 率 , 正 晶
体、负晶体
法线 入射线
光轴
109º 主截面
71º
主平面:
晶体中光的传播方向 与晶体光轴构成的平面.
一般情况下, o主平面 与e主平面是不重合的.
实验表明:
o光是光矢量与o主平面 垂直的线偏振光.
I变,无消光?是什 么光
三. 马吕斯定律
I0
P I
E0
P
I0
E
2 0
,
E=E0cos
IE
2
E
2 0
cos
2
I I0 cos2
马吕斯定律(1809)
0,I Imax I0
,I 0 ——消
2
光
例题1.
有两个偏振片,一个用作 起偏器,一个用作检偏器. 当它们的偏振化方向之 间的夹角为30º时,一束单 色自然光穿过它们,出射 光强为I1;当它们的偏振 化方向之间的夹角为60º 时,另一束单色自然光穿 过它们,出射强度为I2, 且 I 1=I2 . 求两束单色自然 光的强度之比.
10-8光的偏振性 马吕斯定律

光的波动性 光波是横波
机械横波与纵波的区别
光的干涉、衍射 . 光的偏振 .
机 械 波 穿 过 狭 缝
第十章 波动光学
10-8 光的偏振性 马吕斯定律 一、自然光 偏振光 自然光 :在垂直于光的传播方向的平面内的一切 方向上,光矢量的时间平均值都相等。
自然光以两互相垂直的互为 独立的(无确定的相位关系)振幅 相等的光振动表示,并各具有一半 的振动能量。
注意
v
E
两个互相垂直方向是任选的。 各光矢量间无固定的相位关系。
符号表示
第十章 波动光学
10-8 光的偏振性 马吕斯定律
偏振光(线偏振光):如果光矢量在垂直于光的 传播方向的平面内,只沿一个固定的方向振动 。
E v
振动面
符号表示
部分偏振光 :在垂直于光的传播方向的平面内, 如果某一方向的光振动比与之垂直的光振动强 。
符号表示
第十章 波动光学
10-8 光的偏振性 马吕斯定律
二、偏振片 起偏与检偏 二向色性:某些物质(如硫酸碘奎宁或电气石等)能
强烈吸收某个方向的光振动,而对垂直方向的光振动 吸收却很少.
偏振片:涂有二向色性材料的透明薄片.
偏振化方向:当自然光照射在偏振片上时,它只 让某一特定方向的光通过,这个方向叫此偏振片的偏 振化方向.三、马吕斯定律NI0M
EI
起偏器
N
M
E
E0
E0
检偏器
E E0 cos
I I0
E2 E02
马吕斯定律 强度为 I0 的偏振
光通过检偏振器后, 出射光的强度为
I I0 cos2
第十章 波动光学
光的偏振现象与相关计算方法的归纳与总结

光的偏振现象与相关计算方法的归纳与总结一、引言光是一种电磁波,具有传播方向和振动方向。
偏振现象描述了光波的振动方向相对于传播方向的特性。
了解光的偏振现象对于光学应用具有重要意义。
本文将对光的偏振现象进行归纳总结,并介绍相关的计算方法。
二、光的偏振现象1. 偏振现象定义光的偏振现象指的是光波在传播过程中,振动方向在空间中具有一定的规律性。
光波的振动方向可以分为垂直于传播方向的横向振动和平行于传播方向的纵向振动。
2. 偏振方式常见的偏振方式包括线偏振、圆偏振和椭圆偏振。
线偏振光中的电场矢量沿着特定方向振动,圆偏振光中的电场矢量沿着圆周方向振动,椭圆偏振光中的电场矢量沿着椭圆轨迹振动。
3. 偏振器与偏振片偏振器是通过选择特定偏振方向的光而剔除其他方向的光的光学元件。
偏振片则是一种常用的偏振器,它能够将非偏振光转换为偏振光。
三、光的偏振计算方法1. 马吕斯定律马吕斯定律是计算光通过偏振片后的偏振方向的基本方法。
根据马吕斯定律,入射光的偏振方向与偏振片的偏振方向之间的夹角决定了透射光的偏振方向。
2. 光的偏振椭圆参数描述椭圆偏振光的主要参数包括长半轴、短半轴、旋转角和相位差。
这些参数能够完整地描述椭圆偏振光的偏振特性。
3. 光的偏振度偏振度是衡量光偏振程度的物理量,它描述了光波偏离非偏振状态的程度。
偏振度的计算方法可以根据光的电场矢量进行推导。
4. 光的偏振矢量法偏振矢量法是用于计算光经过偏振器等光学元件后的偏振状态的一种常用方法。
通过将光波的振动方向表示为复数形式,并进行相应的运算,可以得到光的最终偏振矢量。
四、光的偏振现象应用1. 光偏振在液晶显示技术中的应用液晶显示器采用了液晶分子在电场作用下的偏振特性,通过控制电场以实现显示效果。
光偏振的理论和计算方法为液晶显示技术的研究提供了基础。
2. 光偏振在光学显微镜中的应用光学显微镜利用了光的偏振现象,通过观察样品处于特定偏振状态下的相位变化,实现对样品细微结构的观察和分析。
马吕斯定律(精)
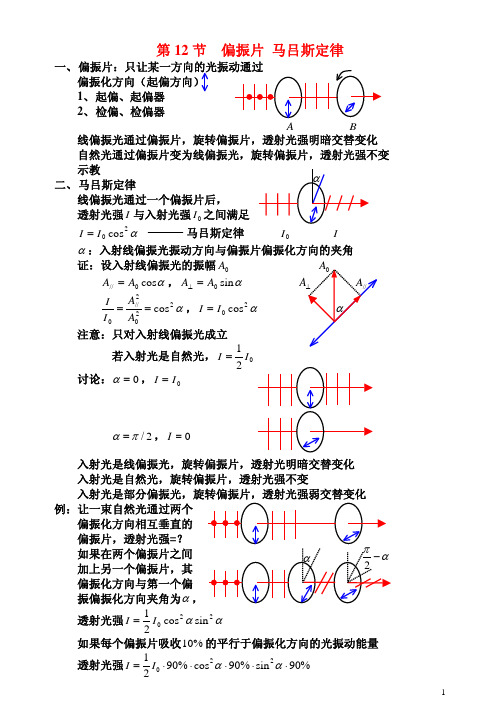
第12节 偏振片 马吕斯定律一、 偏偏振化方向(起偏方向)1、 起偏、起偏器2、 检偏、检偏器A B 线偏振光通过偏振片,旋转偏振片,透射光强明暗交替变化 自然光通过偏振片变为线偏振光,旋转偏振片,透射光强不变 示教二、 马吕斯定律 线偏振光通过一个偏振片后,透射光强I 与入射光强之间满足0I α20cos I I = 马吕斯定律α证:设入射线偏振光的振幅 0A αcos 0//A A =,αsin 0A A =⊥ α2202//0cos ==A A I I,α20cos I I = 注意:只对入射线偏振光成立若入射光是自然光,01I I = 讨论:0=α,0I I =2/πα=,0=I例:让一束自然光通过两个偏振化方向相互垂直的偏振片,透射光强=?如果在两个偏振片之间 加上另一个偏振片,其 偏振化方向与第一个偏振偏振化方向夹角为α,透射光强αα220sin cos 21I I =如果每个偏振片吸收的平行于偏振化方向的光振动能量 %10透射光强%90sin %90cos %9021220⋅⋅⋅⋅⋅=ααI I第13节 反射和折射光的偏振入射面:(入射线,法线)Π反射定律i i =′折射定律γsin sin 21n i n = M ′反射光和折射光都是部分偏振光 反射光中,⊥振动多于//振动折射光中,//振动多于振动⊥120n n arctg i i ==时 反射光为完全偏振光,只包含⊥0i :布儒斯特角(起偏角) 120n n tgi =:布儒斯特定律 注意:(1)0i i =时,只反射部分⊥振动,不反射//振动 折射光中包含其余的⊥振动和全部的//振动折射光仍是部分偏振光(2)0i i =时,反射光线⊥折射光线证明:γsin sin 201n i n =,120n n tgi ==00cos sin i i ,0201cos sin i n i n = γsin 2n =,02cos i n γsin ==0cos i )sin(0i −π,20πγ=+i(3)自然光以布儒斯特角 照射玻璃片堆,可使折射光成为完全偏振光折射光中只剩下//振动例:一束自然光以布儒斯特角从空气照射玻璃片,界面2上的反射光是()自然光A (B )完全偏振光,光矢量振动方向⊥()完全偏振光,光矢量振动方向// C ()部分偏振光D 解:对界面1,是布儒斯特角,对界面2,0i γ是布儒斯特角 120n n tgi =,20πγ=+i ,210n n ctgi tg ==γ 例:第14节 晶体的双折射现象一、晶体的双折射现象用自然光照射某些晶体(方解石)表面 产生两条折射光线 双折射现象,示教特点:(1) 寻常光线(o 光),遵守折射定律非常光线(e 光),不遵守折射定律(2) 两条光线都是线偏振光,振向不同(3) 光轴(光线沿该方向入射不产生双折射)p253,单轴晶体,双轴晶体某条光线与光轴构成的平面:该光线的主平面 (光,光轴):o 光主平面 Πo (光,光轴):e 光主平面Πe (4)光振向o ⊥o 光主平面光振向//光主平面e e 二、 对双折射的解释产生双折射的原因: o 光、光在晶体中的传播速度不同e o 光波面是球面,光波面是旋转椭球面e 沿光轴方向o 光、e 光速度相同垂直光轴方向o 光、e 光速度相差最大o V :e 光速度oo V e Vo V e e o 晶体对光的折射率,o o n V c =/o e e n V c =/晶体对e 光的折射率 、:晶体的主折射率o n e n 1、 平行光斜入射(光轴位于 2、平行光垂直入射(光轴位于 入射面内,光轴与界面斜交) 入射面内,光轴与界面斜交)3、 平行光垂直入射(光轴平行4、平行光垂直入射(光轴位于 界面,光轴位于入射面内) 入射面内,光轴垂直界面)光轴光同传播方向,但速度不同 光同传播方向,速度相同 e o ,e o , 仍属于双折射 不属于双折射5、 平行光斜入射(光轴//界面,光轴垂直入射面)光、光都遵守折射定律,o e e e o o n n i n γγsin sin sin 1==三、 偏振棱镜1、 尼科耳(棱镜)用加拿大树胶粘在一起加拿大树胶对o 2、 渥拉斯顿镜两块方解石直角棱镜构成两者光轴相垂直负晶体,,e e V >o V e n n <垂直板面振动的光线: 对第一块棱镜是o 光对第二块棱镜是e 光平行板面振动的光线: 对第一块棱镜是e 光对第二块棱镜是o 光垂直板面振动的光线由o 光,光密→光疏,折射光偏离法线 →e 平行板面振动的光线由e 光,光疏→光密,折射光靠近法线 →o 两条光线分开,都是线偏振光四、 偏振片某些双折射晶体对o 光和e获得偏振光的方法:(1)偏振片(2)偏振棱镜(3)以布儒斯特角照射玻璃片例:两块偏振片叠放在一起,其偏振化方向夹角,用强度相同的o 30自然光和线偏振光混合而成的光束垂直入射,已知两成分的入 射光透射后强度相等求:(1)入射光中线偏振光振向与第一块偏振片偏振化方向夹角(2)透射光强与入射光强之比(3)若每个偏振片对透射光吸收率为,%5 再求透射光强与入射光强之比解:(1)设入射线偏振光强为I ,入射自然光强为Io o 30cos 2130cos cos 222I I =α,21cos 2=α,o45=α (2)375.083230cos 2130cos cos 222==+=I I I oo α入射光强透射光强(3)=入射光强透射光强=I I I 2%9530cos %9521%9530cos %95cos 222⋅⋅+⋅⋅⋅o o α=338.0%)95(832=×。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注意
二互相垂直方向是任选的 . 符号表示
各光矢量间无固定的相位关系 .
19-13 光的偏振性 马吕斯定律 偏振光(线偏振光)
第十九章 波动光学
光振动只沿某一固定方向的光 .
E
振动面
符号表示
v
部分偏振光 :某一方向的光振动比与之垂直方 向上的光振动占优势的光为部分偏振光 . 符号表示
19-13 光的偏振性 马吕斯定律 二 偏振片 起偏与检偏
I10 I 20 经过起偏器后光强分别为 和 . 2 2
I I 2 2 10 20 经过检偏器后 I1 cos 30 I 2 cos 60 2 2 I10 cos2 30 1 I1 I 2 2 I 20 cos 60 3
19-13 光的偏振性 马吕斯定律
第十九章 波动光学
讨论 在两块正交偏振片 p1 , p 3 之间插入另一块偏 振片 p 2 ,光强为 I 0 的自然光垂直入射于偏振片 p1 , 讨论转动 p 2 透过 p 3 的光强 I 与转角的关系 .
I0
p1
p3
p1
p2
p3
I0
p1
I1
p2
I2
2
p3
I3
1 I1 I 0 2
I0 2 I 2 I1 cos cos 2
19-13 光的偏振性 马吕斯定律
第十九章 波动光学
I0
p1
I1
p2
I2
p3
I3
p1
p2
p3
I0 2 π 2 I 2 cos I 3 I 2 cos ( ) 2 2 1 2 2 2 I 3 I 2 sin I 0 cos sin 2 1 I 3 I 0 sin 2 2
1 I0 2 偏振化方向
19-13 光的偏振性 马吕斯定律
第十九章 波动光学
检 偏
起偏器 检偏器
19-13 光的偏振性 马吕斯定律 三 马吕斯定律(1880 年) N
第十九章 波动光学
I0
E0
M
E
检偏器
I
起偏器 N
M
E
E0
光通过检偏振器后, 出射光的强度为
I E 2 E E0 cos I 0 E0 马吕斯定律 强度为 I 0 的偏振
19-13 光的偏振性 马吕斯定律
第十九章 波动光学
光的波动性 光波是横波
机械横波与纵波的区别
光的干涉、衍射 . 光的偏振 .
机 械 波 穿 过 狭 缝
19-13 光的偏振性 马吕斯定律
第十九章 波动光学
一
自然光 偏振光
自然光 :一般光源发出的光中,包含着各个方 向的光矢量在所有可能的方向上的振幅都相等(轴 对称)这样的光叫自然光 . 自然光以两互相垂直的互 v 为独立的 (无确定的相位关 系)振幅相等的光振动表示 , E 并各具有一半的振动能量 .
第十九章 波动光学
二向色性 : 某些物质能吸收某一方向的光振 动 , 而只让与这个方向垂直的光振动通过, 这种性质 称二向色性 . 偏振片 : 涂有二向色性材料的透明薄片 . 偏振化方向 : 当自然光照射在偏振片上时, 它只让某一特定方向的光通过,这个方向叫此偏振 片的偏振化方向 .
起 偏Hale Waihona Puke I0起偏器2
I I 0 cos 2
19-13 光的偏振性 马吕斯定律
第十九章 波动光学
例1 有两个偏振片,一个用作起偏器, 一个用作检 30 偏器. 当它们偏振化方向间的夹角为 时 , 一束单色 自然光穿过它们, 出射光强为 I1 ; 当它们偏振化方向间 的夹角为 60 时, 另一束单色自然光穿过它们 , 出射光 强为 I 2 , 且 I1 I 2 . 求两束单色自然光的强度之比 . 解 设两束单色自然光的强度分别为 I10 和 I 20 .
8
若
在
0 ~ 2π 间变化, I 3如何变化?
I0 π 3π 5π 7π π 3π 0, ,π , , I 3 0 , , , , I 3 4 4 4 4 8 2 2
