材料力学课件：第六章 弯 曲 应 力
合集下载
材料力学06(第六章 弯曲应力)分析
F / 4 2 103 mm 134 mm
30 MPa 5493104 mm4
F 24.6 kN
因此梁的强度由截面B上的最大拉应力控制
[F] 19.2 kN
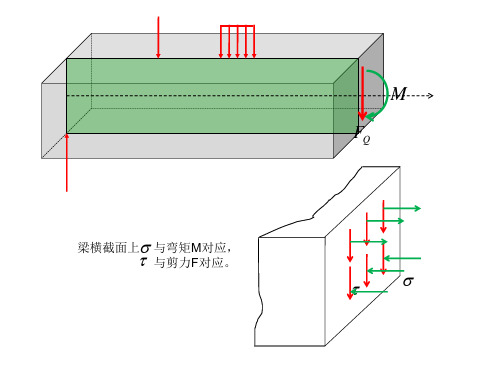
§6-3 梁横截面上的切应力•梁的切应力强度条件
Ⅰ、梁横截面上的切应力
分离体的平衡
横截面上切应力 分布规律的假设
横截面上弯曲切 应力的计算公式
二.工字形截面梁 1、腹板上的切应力
h
d
y
d
O
y b
O
' A*
y dA
FS
S
* z
Izd
S
* z
bd
2
h
d
d 2
h 2
d
2
y2
腹板与翼缘交界处
max
min
FS Izd
bd
h d
max O
中性轴处
max
FS
S
* z,m
ax
Izd
y
min
FS
bd
h
d
d
h
d
2
I z d 2
160 MPa 148 MPa
2
Ⅲ 梁的正应力强度条件
max 材料的许用弯曲正应力
中性轴为横截面对称轴的等直梁
M max
Wz
拉、压强度不相等的铸铁等脆性材料制成的梁
为充分发挥材料的强度，最合理的设计为
t,max
M max yt,max Iz
[
t]
c,max
M max yc,max Iz
Myc,max Iz
典型截面的惯性矩与抗弯截面系数 ( d D)
b
材料力学(理工科课件)第六章 弯曲变形)
§6-1 基本概念及工程实例 （Basic concepts and example problems）
一、工程实例（Example problem）
(Deflection of Beams)
但在另外一些情况下,有时却要求构件具有较大的弹性变 形,以满足特定的工作需要.
例如,车辆上的板弹簧,要求有足够大的变形,以缓解车辆受
M 0 w 0
x
O
M 0 w 0
M
(Deflection of Beams)
w (1 w )
2 3 2
M ( x) EI
2 w 与 1 相比十分微小而可以忽略不计,故上式可近似为
w"
M ( x) EI
(6.5)
此式称为 梁的挠曲线近似微分方程（differential equation of the deflection curve） 近似原因 : （1） 略去了剪力的影响; （2） 略去了 w2项; （3） tan w w( x )
x Cx D
4
(Deflection of Beams)
边界条件x=0 和 x=l时, w 0
梁的转角方程和挠曲线方程 A 分别为 q 2 3 3 (6lx 4 x l ) 24 EI qx 2 3 3 w (2lx x l ) 24 EI 最大转角和最大挠度分别为 在 x=0 和 x=l 处转角的绝对值相等且都是最大值，
A a l D B
b
(Deflection of Beams)
解: 梁的两个支反力为
FRA F FRB F b l a l
x
l x
F FRA
A 1 a D b 2
材料力学课件 第六章弯 曲 内 力(土木专业)
M
A
0
FRA
A
a
F1
C
F2
D
FRB
B
FRB l F1a F2b 0
MB 0
c
E
F
d
FRAl F1 ( l a ) F2 ( l b) 0
FRA F1 ( l a ) F2 ( l b) l
b l
FRB
F1a F2b l
第六章
记 E 截面处的剪力为
FRA
A
弯曲内力
a F1 C F2 D B
FSE 和弯矩 ME ，且假设
FSE 和弯矩ME 的指向和转 向均为正值.取左段为研究
E
c b l
F
d
对象。
Fy 0 , M 0,
E
FRA FS E 0
M E FRA c 0
FRA
A E
FSE
解得 FSE FRA
ME
M E FRA c
第六章
6.1引言
1.弯曲的概念
弯曲内力
工程实例
第六章
工程实例
弯曲内力
第六章
弯曲内力
车刀轴
第六章
弯曲内力
火车轮轴
第六章
弯曲内力
起重机大梁
第六章
弯曲内力
镗刀杆轴
第六章
基本概念
弯曲内力
1.弯曲变形 （1） 受力特征 外力（包括力偶）的作用线垂直于杆轴线. （2） 变形特征 变形前为直线的轴线,变形后成为曲线. 2.梁 以弯曲变形为主的杆件 3.平面弯曲 作用于梁上的所有外力都在纵向对称面内,弯曲变形后的轴 线是一条在该纵向对称面内的平面曲线,这种弯曲称为平面弯曲.
材料力学第6章弯曲应力
图6.5
页 退出
材料力学
出版社 理工分社
例6.1如图6.6所示，矩形截面悬臂梁受集中力和集中力偶作用。试求Ⅰ—Ⅰ 截面和固定端Ⅱ—Ⅱ截面上A，B，C，D ４点处的正应力。
图6.6
页 退出
材料力学
出版社 理工分社
解矩形截面对中性轴的惯性矩为 对于Ⅰ—Ⅰ截面，弯矩MⅠ=20 kN·m，根据式(6.2)，各点正应力分别为
页 退出
材料力学
出版社 理工分社
(1)变形几何关系 弯曲变形前和变形后的梁段分别表示于图6.4(a)和(b)。以梁横截面的对称 轴为y轴且向下为正(见图6.4(c))。以中性轴为z轴，但中性轴的位置尚待确 定。在中性轴尚未确定之前，x轴只能暂时认为是通过原点的横截面的法 线。根据弯曲平面假设，变形前相距为dx的两个横截面，变形后各自绕中性 轴相对旋转了一个角度dθ ，且仍然保持为平面。这就使得距中性层为y的纵 向纤维bb的长度变为
式中积分
是横截面对y轴和z轴的惯性积。由于y轴是横截面的对
称轴，必然有Iyz=0(见附录)。所以式(g)是自然满足的。 将式(b)代入式(e)，得
式中积分∫Ay2dA=Iz是横截面对z轴(中性轴)的惯性矩。于是式(h)改写为 式中 ——梁轴线变形后的曲率。
页 退出
材料力学
出版社 理工分社
式(6.1)表明，EIz越大，则曲率 越小，故EIz称为梁的抗弯刚度。从式 (6.1)和式(b)中消去 ，得
而对于变截面梁，虽然是等截面梁但中性轴不是横截面对称轴的梁，在计算 最大弯曲正应力时不能只注意弯矩数值最大的截面，应综合考虑My/Iz的值 (参看例6.5和例6.8)。
页 退出
材料力学
出版社 理工分社
引用记号
材料力学第六章弯曲应力
但相应的最大弯矩值变为
Fl ql2
M max
4
8
375 kN m 13 kN m 388 kN m
而危险截面上的最大正应力变为
max
388103 N m 2342106 m3
165.7106
Pa
165.7
MPa
显然，梁的自重引起的最大正应力仅为
165.7 160 MPa 5.7 MPa
<2>. 相邻横向线mm和nn，在梁弯曲后仍为直线，只是
相对旋转了一个角度，且与弧线aa和bb保持正交。
根据表面变形情况，并设想梁的侧面上的横向线mm和 nn是梁的横截面与侧表面的交线，可作出如下推论(假设)：
平面假设 梁在纯弯曲时，其原来的横截面仍保持为平面， 只是绕垂直于弯曲平面(纵向平面)的某一轴转动，转动后 的横截面与梁弯曲后的轴线保持正交。
力的值max为
max
M ym a x Iz
M
Iz ymax
M Wz
式中，Wz为截面的几何性质，称为弯曲截面系数（对Z轴）
(section modulus in bending)，其单位为m3。
b
h d
o
z
o
z
y
y
中性轴 z 不是横截面的对称轴时(参见图c)，其横截面 上最大拉应力值和最大压应力值为
A
r
(b)
M z
y d A E
A
r
y2 d A EI z M
A
r
(c)
由于式(a)，(b)中的
E
r
不可能等于零，因而该两式要求：
1. 横截面对于中性轴 z 的静矩等于零，A y d A 0 ；显
第六章弯曲应力
? 中性轴的位置
中性层的曲率半径r
3. 静力学关系
statics relation
M
z
FN
A dFN
σdA
A
O
x
M y
A dM y
zσdA
A
y
M z
A dM z
yσdA
A
凹入一侧的受压应力，凸出的一侧受拉应力
应用公式时，一般将 My 以绝对值代入. 根据梁变形的情况直接
按强度要求设计梁时，主要是依据梁的正应力强度条件
σmax M max [σ] Wz
一、降低梁的最大弯矩值
1.合理地布置梁的荷载
F
F
l
Fl/4
l/4
l/2 l/4
Fl/8
2.合理地设置支座位置
q
q
l
ql2/2
a
a
l
0.0214ql2
当两端支座分别向跨中移动a=0.207l 时，最大弯矩减小.
二、增大Wz
deformation geometric relationship
physical relationship
static relationship
Examine the deformation， 变
then propose the hypothesis 形
几
何
关
Distribution regularity
z
0.8a2 a2
π D12 4
2a22
0.8 1.6a22 ,a2
1.05D1
Wz4 4.57Wz1
工字形截面与框形截面类似.
2.合理的放置
W1 h W2 b
材料力学弯曲应力课件
材料力学弯曲应力课件曲在工程中的应用。
这是一个厂房，这是一个大梁，这个吊车可以在这个大梁上运动。
对于这样一个问题，我们可以把它简化成一个简支梁，这个吊车的移动呢可以处理成一个移动荷载。
那么对于这个移动荷载而言，它所导致的应力如何计算行车移动时，它的应力如何变化这就是本章的内容之一。
我们再看看这个图片，这是我们拍摄的汽车的下部分，大家注意一些这个部分，这是就是汽车的板簧，它的模型就是这个样子，可以看成好几个钢板的组合，那么，为什么要设计成这个样子呢它有什么优点呢这也是本章要解决的问题。
这是一个运动员，撑杆跳，对吧。
大家常常见到，利用这个杆的助力，人可以跳的更高。
我们可以处理成这样一个模型。
她在跳高的过程中，杆就发生了弯曲。
那么，这个时候，跳杆横截面上的应力和杆曲率半径有什么关系这个杆在什么情况下才满足强度要求大家看看这个场面，对于这个场面，我们截面几何性质那章提到过，都是薄壁杆件，那么薄壁杆件有弯曲正应力和弯曲切应力，专门有一小节来讲解它的弯曲切应力，看看这些切应力有什么特点如何避免薄壁杆件的强度失效这也是本章的问题这个大家都熟悉，著名的比萨斜塔。
对于这个结构，初步计算，我们可以简化成这样一个均质圆筒，那么它有哪些变形效应它的危险截面、危险点在哪儿如何计算其应力这也是本章可以解决的问题。
因此，本章所涉及的问题是比较广的。
基本内容那么本章到底需要同学们掌握哪些内容呢1、熟练张博横截面上弯曲正应力和弯曲切应力的分布规律，并能正确熟练的进行梁的强度分析。
2、熟悉提高梁强度的主要措施。
、正确理解薄壁杆件横截面上弯曲切应力的分布规律，了解弯曲中心的概念。
4、熟悉掌握梁在组合变形中的应力的计算方法。
第一、第四条是很重要的。
这是以后大家经常需要处理的问题。
基本概念平面弯曲首先我们来看弯曲正应力。
在这章具体内容介绍之前呢，我们先介绍一些概念。
关于梁弯曲的基本概念。
梁的平面弯曲。
什么是梁的平面弯曲呢这是一个悬臂梁，截面是矩形截面，那么这个横截面就有一个中心对称轴，整个梁就存在一个对称面，如果我们的所有的外荷载都作用在这个平面之内，比如外荷载是这样的，那么发生变形后，梁的轴线仍然在这个平面内，像这样的弯曲，我们就叫做平面弯曲。
第六章 - 弯曲应力
查表 N0 12.6工字钢
WZ=77.5cm3
kN
15
28.1
13.16
kNm
3.75
例题
F 25kN
铸铁梁受荷载情况如图示。已知截面对形心轴
的惯性矩Iz=403×10－7m4，铸铁抗拉强度［σ ＋］ =50MPa，抗压强度［σ －］=125MPa。试按正应力强
度条件校核梁的强度。
200
q 12kN m
最大截面上的最大拉应力和最大压应力。
y
F
150
A
L 2
B
L 2
M max
FL 4
16kNm
y max
200 50 96.4 153.6mm
y max
96.4mm
50
96.4
z
200
C
50
max
My
max
IZ
24.09MPa
max
My max IZ
对梁的某一截面： 对全梁（等截面）：
max
Mymax Iz
M
WZ
max
M max ymax Iz
M max Wz
max
M max Wz
例题
长为L的矩形截面悬臂梁，在自由端作用一集中力
F，已知b＝120mm，h＝180mm、L＝2m，F＝1.6kN， 试求B截面上a、b、c各点的正应力。
1 M Z (b)
EIZ
由(a)(b)式得
Mzy
Iz
y
M
m
Mz
n
中性轴
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2. 设计截面形状
相同材料重量下，提高W ；
3. 设计载荷分布形式
减小最大M
4. 等强设计(全局优化)
全局应力接近许用值
23
一、梁的合理截面形状
第六章 弯曲应力
dA
R0
C
z
y
1. 让材料远离中性轴 2. 腹板壁厚较小，但不能太小(承受剪切)。
Hale Waihona Puke 24第六章 弯曲应力•截面上下不对称的脆性材料梁
C ,max
第六章 弯曲应力
上一讲回顾
梁的弯曲切应力分析 对象：对称弯曲的矩形截面直梁 条件：应力方向假设＋应力分布假设
( y) FS Sz ( )
Iz b
对称薄壁梁的弯曲切应力 梁的强度校核－危险截面，危险点，强度条件
外伸梁＋非对称截面＋脆性材料＋载荷移动＋支持移动
1
第六章 弯曲应力
第六章 弯 曲 应 力
20
第六章 弯曲应力
其它截面内不同方向的最大弯曲切应力之比
21
课后思考问题
c,max
第六章 弯曲应力
t,max
o
y
判断题：最大切应力位于中性轴处（× or √）
22
第六章 弯曲应力
§6-5 梁的合理强度设计
依据 M , My
W
Iz
1. 提高材料利用率
FS Sz ( ) Iz
对同一截面，使大部分材料承受基本相同的较高应力；
29
第六章 弯曲应力
30
第六章 弯曲应力
Q 合理安排加载方式—尽量分散载荷
F
F
l2
l2
M
Fl 4
l3 l6 l6 l3
M Fl 6
x
x
qF l
l
Fl 8
M
x
31
第六章 弯曲应力 在成都132厂11K车间里，技术员和工人正面临着一个问 题，如何用现有的起吊重量只有5T的吊车吊起10T的重物？ 经过大家的认真思考和努力，改进了装置，结果就吊起了 10T的重物。
高度/宽度＝10/1～1/1
8
第六章 弯曲应力
弯曲切应力的沿宽度方向的分布
高度/宽度＝1/1～1/10
9
第六章 弯曲应力
ratiomtopax 1.0120 ratiommiadx 1.0015
ratiomtopax 1.2589 ratiommiadx 1.1524
10
第六章 弯曲应力
附加：梁弯曲切应力的进一步讨论 §6-5 梁的合理强度设计 §6-6 弯拉(压)组合与截面核心
2
第六章 弯曲应力
梁弯曲切应力的进一步讨论 弯曲切应力的回顾
F1 ( y) b dx F2
( y) F2 F1
b dx
3
第六章 弯曲应力
o
y
F1 ( y) b dx F2
F1
c > t
•截面等强设计
yc c yt t
yC
C
z
yt y
t ,max
脆性材料梁
25
第六章 弯曲应力
•Iz与Wz的区别
Iz
a4 12
(1 r)3(1 3r)
Wz
2 12
a3(1 r)2 (1 3r)
在区间(0,1),
I
无极值
z
当r
1 9
,
Wz有极大值
ar
a
(1 r)a z
r为截取的比例系数
5
第六章 弯曲应力
o
y
中性轴处(y=0)，剪应变最大 截面边缘(y=h/2)，剪应变最小
有剪力存在的区域，有翘 曲存在。
无分布载荷 q 0
沿轴向剪力不变，翘曲程度相同
则 ab ab 剪力不影响纵向应变
正应力公式适用
分布载荷 q 0
沿轴向剪力变化，翘曲程度不同
正应力公式不适用
但当L>5h 时，纯弯正应力公式仍然
————Timoshenko （mechanics of materials）
17
第六章 弯曲应力
总结与思考
严密推导
工程实用
主要矛盾与次要矛盾
不仅仅是工程方法，各学科的分析方法。
量变与质变—— 适用条件
18
第六章 弯曲应力
其它截面沿剪力方向的弯曲切应力分布
19
第六章 弯曲应力
其它截面垂直于剪力方向的弯曲切应力分布
W
z
(
1 9
)
1.053497, 可 提 高 5.35%
W z (1)
26
二、梁的合理受力
Q 合理安排约束
q
l
ql 2 8
M
x
a
F
a
l
第六章 弯曲应力
q
l 5 3l 5 l 5
M
ql 2 40
ql 2 50
ql 2 50 x
a = ? [ F ] 最大.
27
第六章 弯曲应力
28
第六章 弯曲应力
弯曲切应力的方向
假设：横截面上各点处的切应力，均平行于剪力或截面侧边， 并沿截面宽度均匀分布。
问题：是否存在垂直于剪力方向的切应力？
M
如何分布？合力效果？ 对称分布，相互抵消
FS
弯曲正应力
弯曲切应力
11
第六章 弯曲应力
垂直于剪力方向的弯曲切应力分布
高度/宽度＝10/1～1/1
12
第六章 弯曲应力
相当精确
6
第六章 弯曲应力
假设弯曲切应力的分布
F1 ( y) b dx F2
假设：横截面上各点处的切应力，均平行于 剪力或截面侧边，并沿截面宽度均匀分布。
基础： 截面是窄而高的
Q (y)
y
yz
问题：横截面窄而高的具体比例？ 问题：不满足窄而高条件，切应力的分布形态？
7
第六章 弯曲应力
弯曲切应力的沿宽度方向的分布
15
第六章 弯曲应力
总结与思考
材料力学中弯曲切应力的推导基于某 些假设基础之上。尽管该推导在严密 性方面有一定瑕疵，但对于细长的、 高度大于宽度的大多数工程梁问题， 材料力学解答具有较高的精度。
16
第六章 弯曲应力
总结与思考
D.J Jourawski (1821－1891)是俄国桥梁与铁路工程 师，发展了现在广泛应用的梁的剪切近似理论，尽管 Saint－Venant已经提出梁中剪应力的精确理论，但其 仅用于很少几种实际情况。因此看来，Todhunter与 Pearson在第642页中对Jourawski提出极其苛刻的评语 是不公平的。
垂直于剪力方向的弯曲切应力分布
高度/宽度＝1/1～1/10
13
第六章 弯曲应力
问题：为什么出现垂直于剪力方向的切应力？
剪力存在
沿轴向弯矩变化
沿轴向正应力变化
泊松效应
沿轴向横向变形变化
沿轴向正应变变化
剪切变形
出现垂直于剪力方向的切应力
相对于沿剪力方向的切应力，该切应力的量级如何？
14
第六章 弯曲应力 矩形截面内不同方向的最大弯曲切应力之比
dA
M ydA MSz ( )
Iz
Iz
F2
(M
dM )Sz ( )
Iz
( y) F2 F1
b dx
( y) FS Sz ( )
Iz b
弯曲切应力的推导是否严密？
4
第六章 弯曲应力
横截面上的正应力采用了纯弯正应力公式：
F dA
My
Iz
M
M
平面假设：变形后，横截面仍为平面，且仍与纵线正交
相同材料重量下，提高W ；
3. 设计载荷分布形式
减小最大M
4. 等强设计(全局优化)
全局应力接近许用值
23
一、梁的合理截面形状
第六章 弯曲应力
dA
R0
C
z
y
1. 让材料远离中性轴 2. 腹板壁厚较小，但不能太小(承受剪切)。
Hale Waihona Puke 24第六章 弯曲应力•截面上下不对称的脆性材料梁
C ,max
第六章 弯曲应力
上一讲回顾
梁的弯曲切应力分析 对象：对称弯曲的矩形截面直梁 条件：应力方向假设＋应力分布假设
( y) FS Sz ( )
Iz b
对称薄壁梁的弯曲切应力 梁的强度校核－危险截面，危险点，强度条件
外伸梁＋非对称截面＋脆性材料＋载荷移动＋支持移动
1
第六章 弯曲应力
第六章 弯 曲 应 力
20
第六章 弯曲应力
其它截面内不同方向的最大弯曲切应力之比
21
课后思考问题
c,max
第六章 弯曲应力
t,max
o
y
判断题：最大切应力位于中性轴处（× or √）
22
第六章 弯曲应力
§6-5 梁的合理强度设计
依据 M , My
W
Iz
1. 提高材料利用率
FS Sz ( ) Iz
对同一截面，使大部分材料承受基本相同的较高应力；
29
第六章 弯曲应力
30
第六章 弯曲应力
Q 合理安排加载方式—尽量分散载荷
F
F
l2
l2
M
Fl 4
l3 l6 l6 l3
M Fl 6
x
x
qF l
l
Fl 8
M
x
31
第六章 弯曲应力 在成都132厂11K车间里，技术员和工人正面临着一个问 题，如何用现有的起吊重量只有5T的吊车吊起10T的重物？ 经过大家的认真思考和努力，改进了装置，结果就吊起了 10T的重物。
高度/宽度＝10/1～1/1
8
第六章 弯曲应力
弯曲切应力的沿宽度方向的分布
高度/宽度＝1/1～1/10
9
第六章 弯曲应力
ratiomtopax 1.0120 ratiommiadx 1.0015
ratiomtopax 1.2589 ratiommiadx 1.1524
10
第六章 弯曲应力
附加：梁弯曲切应力的进一步讨论 §6-5 梁的合理强度设计 §6-6 弯拉(压)组合与截面核心
2
第六章 弯曲应力
梁弯曲切应力的进一步讨论 弯曲切应力的回顾
F1 ( y) b dx F2
( y) F2 F1
b dx
3
第六章 弯曲应力
o
y
F1 ( y) b dx F2
F1
c > t
•截面等强设计
yc c yt t
yC
C
z
yt y
t ,max
脆性材料梁
25
第六章 弯曲应力
•Iz与Wz的区别
Iz
a4 12
(1 r)3(1 3r)
Wz
2 12
a3(1 r)2 (1 3r)
在区间(0,1),
I
无极值
z
当r
1 9
,
Wz有极大值
ar
a
(1 r)a z
r为截取的比例系数
5
第六章 弯曲应力
o
y
中性轴处(y=0)，剪应变最大 截面边缘(y=h/2)，剪应变最小
有剪力存在的区域，有翘 曲存在。
无分布载荷 q 0
沿轴向剪力不变，翘曲程度相同
则 ab ab 剪力不影响纵向应变
正应力公式适用
分布载荷 q 0
沿轴向剪力变化，翘曲程度不同
正应力公式不适用
但当L>5h 时，纯弯正应力公式仍然
————Timoshenko （mechanics of materials）
17
第六章 弯曲应力
总结与思考
严密推导
工程实用
主要矛盾与次要矛盾
不仅仅是工程方法，各学科的分析方法。
量变与质变—— 适用条件
18
第六章 弯曲应力
其它截面沿剪力方向的弯曲切应力分布
19
第六章 弯曲应力
其它截面垂直于剪力方向的弯曲切应力分布
W
z
(
1 9
)
1.053497, 可 提 高 5.35%
W z (1)
26
二、梁的合理受力
Q 合理安排约束
q
l
ql 2 8
M
x
a
F
a
l
第六章 弯曲应力
q
l 5 3l 5 l 5
M
ql 2 40
ql 2 50
ql 2 50 x
a = ? [ F ] 最大.
27
第六章 弯曲应力
28
第六章 弯曲应力
弯曲切应力的方向
假设：横截面上各点处的切应力，均平行于剪力或截面侧边， 并沿截面宽度均匀分布。
问题：是否存在垂直于剪力方向的切应力？
M
如何分布？合力效果？ 对称分布，相互抵消
FS
弯曲正应力
弯曲切应力
11
第六章 弯曲应力
垂直于剪力方向的弯曲切应力分布
高度/宽度＝10/1～1/1
12
第六章 弯曲应力
相当精确
6
第六章 弯曲应力
假设弯曲切应力的分布
F1 ( y) b dx F2
假设：横截面上各点处的切应力，均平行于 剪力或截面侧边，并沿截面宽度均匀分布。
基础： 截面是窄而高的
Q (y)
y
yz
问题：横截面窄而高的具体比例？ 问题：不满足窄而高条件，切应力的分布形态？
7
第六章 弯曲应力
弯曲切应力的沿宽度方向的分布
15
第六章 弯曲应力
总结与思考
材料力学中弯曲切应力的推导基于某 些假设基础之上。尽管该推导在严密 性方面有一定瑕疵，但对于细长的、 高度大于宽度的大多数工程梁问题， 材料力学解答具有较高的精度。
16
第六章 弯曲应力
总结与思考
D.J Jourawski (1821－1891)是俄国桥梁与铁路工程 师，发展了现在广泛应用的梁的剪切近似理论，尽管 Saint－Venant已经提出梁中剪应力的精确理论，但其 仅用于很少几种实际情况。因此看来，Todhunter与 Pearson在第642页中对Jourawski提出极其苛刻的评语 是不公平的。
垂直于剪力方向的弯曲切应力分布
高度/宽度＝1/1～1/10
13
第六章 弯曲应力
问题：为什么出现垂直于剪力方向的切应力？
剪力存在
沿轴向弯矩变化
沿轴向正应力变化
泊松效应
沿轴向横向变形变化
沿轴向正应变变化
剪切变形
出现垂直于剪力方向的切应力
相对于沿剪力方向的切应力，该切应力的量级如何？
14
第六章 弯曲应力 矩形截面内不同方向的最大弯曲切应力之比
dA
M ydA MSz ( )
Iz
Iz
F2
(M
dM )Sz ( )
Iz
( y) F2 F1
b dx
( y) FS Sz ( )
Iz b
弯曲切应力的推导是否严密？
4
第六章 弯曲应力
横截面上的正应力采用了纯弯正应力公式：
F dA
My
Iz
M
M
平面假设：变形后，横截面仍为平面，且仍与纵线正交