信号处理原理作业2答案
信息检测与信号处理习题2含答案

第二章习题一、选择题2.非线性度是表示定度曲线( )的程度。
A.接近真值B.偏离其拟合直线C.正反行程的不重合3.测试装置的频响函数H (j ω)是装置动态特性在( )中的描述。
A .幅值域 B.时域 C.频率域 D.复数域5.下列微分方程中( )是线性系统的数学模型。
A.225d y dy dx t y x dt dt dt ++=+ B. 22d y dx y dt dt+= C.22105d y dy y x dt dt -=+ 6.线性系统的叠加原理表明( )。
A.加于线性系统的各个输入量所产生的响应过程互不影响B.系统的输出响应频率等于输入激励的频率C.一定倍数的原信号作用于系统所产生的响应,等于原信号的响应乘以该倍数7.测试装置能检测输入信号的最小变化能力,称为( )。
A.精度B.灵敏度C.精密度D.分辨率8.一般来说,测试系统的灵敏度越高,其测量范围( )。
A.越宽B. 越窄C.不变10.线性装置的灵敏度是( )。
A.随机变量B.常数C.时间的线性函数12.输出信号与输入信号的相位差随频率变化的关系就是系统的( )。
A.幅频特性B.相频特性C.传递函数D.频率响应函数13.时间常数为τ的一阶装置,输入频率为 1ωτ=的正弦信号,则其输出与输入间的相位差是( )。
A.-45° B-90° C-180°14.测试装置的脉冲响应函数与它的频率响应函数间的关系是( )。
A.卷积B.傅氏变换对C.拉氏变换对D.微分16.对某二阶系统输入周期信号 000()sin()x t A t ωϕ=+,则其输出信号将保持()。
A.幅值不变,频率、相位改变B.相位不变,幅值、频率改变C.频率不变,幅值、相位可能改变18.二阶系统的阻尼率ξ越大,则其对阶越输入的时的响应曲线超调量()。
A.越大B.越小C.不存在D.无关19.二阶装置引入合适阻尼的目的是()。
A.是系统不发生共振B.使得读数稳定C.获得较好的幅频、相频特性20.不失真测试条件中,要求幅频特性为(),而相频特性为()。
信息检测与信号处理习题2含答案

第二章习题一、选择题2.非线性度是表示定度曲线( )的程度。
A.接近真值B.偏离其拟合直线C.正反行程的不重合3.测试装置的频响函数H (j ω)是装置动态特性在( )中的描述。
A .幅值域 B.时域 C.频率域 D.复数域5.下列微分方程中( )是线性系统的数学模型。
A.225d y dy dx t y x dt dt dt ++=+ B. 22d y dx y dt dt+= C.22105d y dy y x dt dt -=+ 6.线性系统的叠加原理表明( )。
A.加于线性系统的各个输入量所产生的响应过程互不影响B.系统的输出响应频率等于输入激励的频率C.一定倍数的原信号作用于系统所产生的响应,等于原信号的响应乘以该倍数7.测试装置能检测输入信号的最小变化能力,称为( )。
A.精度B.灵敏度C.精密度D.分辨率8.一般来说,测试系统的灵敏度越高,其测量范围( )。
A.越宽B. 越窄C.不变10.线性装置的灵敏度是( )。
A.随机变量B.常数C.时间的线性函数12.输出信号与输入信号的相位差随频率变化的关系就是系统的( )。
A.幅频特性B.相频特性C.传递函数D.频率响应函数13.时间常数为τ的一阶装置,输入频率为 1ωτ=的正弦信号,则其输出与输入间的相位差是( )。
A.-45° B-90° C-180°14.测试装置的脉冲响应函数与它的频率响应函数间的关系是( )。
A.卷积B.傅氏变换对C.拉氏变换对D.微分16.对某二阶系统输入周期信号 000()sin()x t A t ωϕ=+,则其输出信号将保持()。
A.幅值不变,频率、相位改变B.相位不变,幅值、频率改变C.频率不变,幅值、相位可能改变18.二阶系统的阻尼率ξ越大,则其对阶越输入的时的响应曲线超调量()。
A.越大B.越小C.不存在D.无关19.二阶装置引入合适阻尼的目的是()。
A.是系统不发生共振B.使得读数稳定C.获得较好的幅频、相频特性20.不失真测试条件中,要求幅频特性为(),而相频特性为()。
信号处理-习题(答案)

数字信号处理习题解答 第二章 数据采集技术基础2。
1 有一个理想采样系统,其采样角频率Ωs =6π,采样后经理想低通滤波器H a (j Ω)还原,其中⎪⎩⎪⎨⎧≥Ω<Ω=Ωππ30321)(,,j H a 现有两个输入,x 1(t )=cos2πt ,x 2(t )=cos5πt 。
试问输出信号y 1(t ),y 2(t )有无失真?为什么?分析:要想时域采样后能不失真地还原出原信号,则采样角频率Ωs 必须大于等于信号谱最高角频率Ωh 的2倍,即满足Ωs ≥2Ωh 。
解:已知采样角频率Ωs =6π,则由香农采样定理,可得 因为x 1(t )=cos2πt ,而频谱中最高角频率πππ32621=<=Ωh ,所以y 1(t )无失真;因为x 2(t )=cos5πt ,而频谱中最高角频率πππ32652=>=Ωh ,所以y 2(t )失真。
2.2 设模拟信号x (t )=3cos2000πt +5sin6000πt +10cos12000πt ,求:(1) 该信号的最小采样频率;(2) 若采样频率f s =5000Hz ,其采样后的输出信号; 分析:利用信号的采样定理及采样公式来求解.错误!采样定理采样后信号不失真的条件为:信号的采样频率f s 不小于其最高频率f m 的两倍,即f s ≥2f m○,2采样公式)()()(s nT t nT x t x n x s===解:(1)在模拟信号中含有的频率成分是f 1=1000Hz ,f 2=3000Hz,f 3=6000Hz∴信号的最高频率f m =6000Hz由采样定理f s ≥2f m ,得信号的最小采样频率f s =2f m =12kHz (2)由于采样频率f s =5kHz,则采样后的输出信号⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛====n n n n n n n n n n n f n x nT x t x n x s s nT t s522sin 5512cos 13512cos 10522sin 5512cos 35112cos 105212sin 5512cos 3562cos 10532sin 5512cos 3)()()(πππππππππππ 说明:由上式可见,采样后的信号中只出现1kHz 和2kHz 的频率成分,即kHzf f f kHzf f f ss 25000200052150001000512211======,,若由理想内插函数将此采样信号恢复成模拟信号,则恢复后的模拟信号()()t t t f t f t y ππππ4000sin 52000cos 132sin 52cos 13)(21-=-=可见,恢复后的模拟信号y (t ) 不同于原模拟信号x (t ),存在失真,这是由于采样频率不满足采样定理的要求,而产生混叠的结果.第三章 傅里叶分析I. 傅里叶变换概述3。
东大14秋学期《数字信号处理器原理及应用》在线作业2答案

?
正确答案:C
3. CAN总线只用了7层模型中的
A.物理层、数据链路层
B.物理层、数据链路层和应用层
C.网络层、数据链路层
D.物理层、数据链路层和网络层
?
正确答案:B
4.事件管理器的捕获单元用来对外部硬件信号的
A.输入响应
B.
时间测量
C.模数转换
D. PWM控制
?
正确答案:B
5. TMS320F2812的ADC模块最高采样带宽
A.高电平
B.低电平
C.高阻
D.悬空
?
正确答案:B
二,判断题
1.当采用双电源器件芯片设计系统时,需要考虑系统上电或掉电操作过程中内核和IO供电的相对电压和上电次序。
A.错误
B.正确
?
正确答案:B
2.在许多运动/电机和功率电子应用中,常将功率器件上下臂串联起来控制。上下被控的臂可以短时同时导通。
A.错误
B.正确
?
正确答案:A
3.复位程序引导(boot)完成后,系统自动重新初始化PIE中断向量表,应用程序使能PIE中断向量表,中断将从PIE向量表中获取向量。
A.错误
B.正确
?
正确答案:B
4.事件管理器的捕获单元用来对外部硬件信号的时间测量,利用边沿检测单元测量外部信号的时间差,从而可以确定电机转子的转速。
A.错误
B.正确
?
正确答案:A
9. SCI的接收和发送数据都采用归零的数据格式。
A.错误
B.正确
?
Hale Waihona Puke 正确答案:A10. 28xx有4级带有流水线存储器访问的流水线保护机制,流水线使得28xx高速运行时不需要大容量的快速存储器。
电子科技大学14秋《数字信号处理》在线作业2答案

14秋《数字信号处理》在线作业2
一,单选题
1. 要处理一个连续时间信号,对其进行采样的频率为6kHz,要无失真的恢复该连续信号,则该连续信号的最高频率可能是()。
A. 12kHz
B. 6kHz
C. 4kHz
D. 3kHz
?
正确答案:D
2. 数字信号的特征是()。
A. 时间连续、幅值量化
B. 时间离散、幅值量化
C. 时间离散、幅值连续
D. 时间连续、幅值连续
?
正确答案:B
3. 对连续时间周期信号的谱分析工具是()。
A. 傅里叶变换
B. 傅里叶级数
C. 离散傅里叶变换
D. 离散傅里叶级数
?
正确答案:B
4. 题目及选项如下图所示
A.
B.
C.
D.
?
正确答案:C
5. 两有限长序列的长度分别是12和15,要利用DFT计算两者的线性卷积,则DFT的点数至少应取()。
A. 15
B. 26
C. 27
D. 28。
(完整word版)数字信号处理答案第二章

第二章2.1 判断下列序列是否是周期序列。
若是,请确定它的最小周期.(1)x (n )=Acos(685ππ+n ) (2)x (n)=)8(π-ne j(3)x (n)=Asin(343ππ+n ) 解 (1)对照正弦型序列的一般公式x (n )=Acos (ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x (n )=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x (n)=Acos(ϕω+n ),又x (n)=Asin (343ππ+n )=Acos (-2π343ππ-n )=Acos(6143-n π),得出=ω43π.因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =2.2在图2.2中,x (n )和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x (n )和h (n)的线性卷积以得到系统的输出y(n ),并画出y(n)的图形。
(a)1111(b)(c)111110 0-1-1-1-1-1-1-1-1222222 33333444………nnn nnnx(n)x(n)x(n)h(n)h(n)h(n)21u(n)u(n)u(n)a n ===22解 利用线性卷积公式y(n )=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a ) y (0)=x (O)h (0)=1y (l )=x (O )h(1)+x (1)h (O)=3y (n)=x(O)h (n )+x (1)h(n-1)+x(2)h (n —2)=4,n ≥2 (b) x(n )=2δ(n )-δ(n-1)h(n)=-δ(n)+2δ(n —1)+ δ(n —2)y(n )=-2δ(n)+5δ(n —1)= δ(n-3) (c ) y (n )=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u (n )2。
(完整word版)数字信号处理第二章习题解答
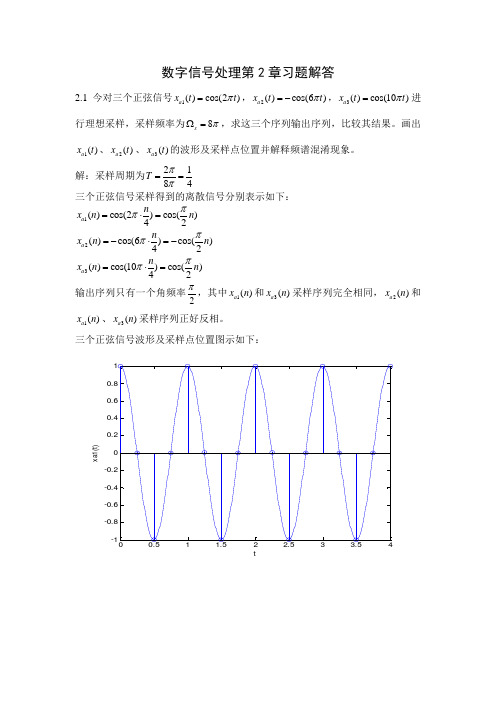
数字信号处理第2章习题解答2.1 今对三个正弦信号1()cos(2)a x t t π=,2()cos(6)a x t t π=-,3()cos(10)a x t t π=进行理想采样,采样频率为8s πΩ=,求这三个序列输出序列,比较其结果。
画出1()a x t 、2()a x t 、3()a x t 的波形及采样点位置并解释频谱混淆现象。
解:采样周期为2184T ππ== 三个正弦信号采样得到的离散信号分别表示如下:1()cos(2)cos()42a n x n n ππ=⋅=2()cos(6)cos()42a n x n n ππ=-⋅=-3()cos(10)cos()42a n x n n ππ=⋅=输出序列只有一个角频率2π,其中1()a x n 和3()a x n 采样序列完全相同,2()a x n 和1()a x n 、3()a x n 采样序列正好反相。
三个正弦信号波形及采样点位置图示如下:tx a 1(t )tx a 2(t )tx a 3(t )三个正弦信号的频率分别为1Hz 、3Hz 和5Hz ,而采样频率为4Hz ,采样频率大于第一个正弦信号频率的两倍,但是小于后两个正弦信号频率的两倍,因而由第一个信号的采样能够正确恢复模拟信号,而后两个信号的采样不能准确原始的模拟信号,产生频谱混叠现象。
2.3 给定一连续带限信号()a x t 其频谱当f B >时,()a X f 。
求以下信号的最低采样频率。
(1)2()a x t (2)(2)a x t (3)()cos(7)a x t Bt π解:设()a x t 的傅里叶变换为()a X j Ω(1)2()a x t 的傅里叶变换为22()[()]Ba a BX j X j d ππωωω-⋅Ω-⎰因为22,22B B B B πωππωπ-≤≤-≤Ω-≤ 所以44B B ππ-≤Ω≤即2()a x t 带限于2B ,最低采样频率为4B 。
数字信号处理 课后习题答案 第2章.docx

习题1.设X(e"。
)和r(e JC0)分别是印7)和)仞的傅里叶变换,试求下面序列的傅里叶变换:(1) x("-"o) (3) x(-n) (5) x(")y(")(7) x(2n)⑵ x*(〃)(4) x(") * v(«) (6) nx(n) (8) /(〃)解:⑴00 FT[X(/7-Z70)] = £x(〃一〃o)e—S令n r = n-n0,即〃=n' + n Q,贝!J00FT[x(n-n o y\=工》(〃')以"''*""="初。
乂(烈)00 00(2)FT[x («)] = £ x* (n)e*= [ £ 戏〃)攻以]* = X* (e「W=—00 w=—00(3)00FT[x(—")]= 〃)e*"令=一〃,则00FT[x(—”)]= Zx(〃')e" =X(e—〃")”'=—00(4)00 x(〃) *'(〃)= ^\x(jrT)y(n -m)W=-0000 00FT[x(n) * v(w)] = Z【Z x("y("-初)]e""' n=-<x> w=-oo k = n-m,贝U00 00FT[x(ri)*y(ri)]= £[ £x(初) k=—CD W=-0000 00k=-<x> m=—cc= X(e5(em)_00 00 1时[x(M)贝〃)]= Z》(〃)贝〃)e「9 = Zx(〃)[-Lf/(em'"'"d 渺]e-加""=—00 〃=—00 2l "1 00=—£ Y(e j0)')2l " n=—<x>1 伙=一L "口")*?®"、技或者FT[x{n)y{ny\ = —「171 »兀oo(6)因为X(e,")= »("初,对该式两边口求导,得到叫、)=-J £仗"如=-jFT[nx(n)]因此矶孙(〃)]=j至@3)dco00⑺ FT\x(2ri)\=加n=-(x)令n' = 2n ,则FT[X(2W)]= £x(z/)e 7 %W--00,且取偶数00 1 r r・l 八1°0 . 1 00 . 1£?kO + (T)“x(")厂=| 广伽+£ef ("广伽〃=—oo 匕匕〃=—oo 〃=—00=L「xa*+x(/*E)F7[x(2z?)] = | X(e‘2") + X(—e'尸)(8) F7[X2(»)]= J X2(77)6^»=-OO利用(5)题结果,令x{n) = y{n),则F巾2(”)] = _£x(em)*X(eS) = —「X®。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.两个函数的傅立叶变换与逆傅立叶变换都是相等的,这两个函数----------是相等的。
(一定)
4.信号的傅立叶变换存在的充分条件是信号f(t)-----------,用数学表示就是--------------。
(绝对可积)
5)符号函数不满足绝对可积条件但是却存在--------------------。
FT 6)用数学表达式描述信号f (t)的FT 的线性性和叠加性,线性性的描述为
[k f (t)]=------------------.。
叠加性的描述为 [f (t)+g (t)]=--------------------.。
( k [f (t)], [f(t)]+ [g (t)] )
7)若信号在时域被压缩,则其频谱会--------------------。
(扩展)
8)单位冲击信号的特性有对称性,时域压扩性,其时域压扩性的数学表达式是 ------------------------。
9.关于FT 的反褶与共轭的描述是:信号反褶的FT 等于-------------------的反褶,信号共扼的FT 等于--------------------的共轭。
(信号的FT , 信号FT 的反褶)
10)傅立叶变换以及傅立叶逆变换的定义中分别引入了核函数,这两个核函数是---------------------------的。
(共轭对称)
11)傅立叶正变换的变换核函数为----------------------------( t j e ω-)
12)傅立叶变换与傅立叶逆变换的本质是一致的,但是在数学形式上有着某中关系,这种关系称为------------,数学表示为-------------------。
(对偶性, )(f 2)]t (F [F ω-π=) 13)FT 的尺度变换特性又称为-------------------,压扩特性
对它的数学描述是------------------------------------------------------。
14)信号的时域平移不影响信号的FT 的-----------------,但是会影响到-----------------------。
(幅度谱 相位谱)
15)所谓频谱搬移特性是指时间域信号乘一个复指数信号后的频谱相当于原来的频谱搬移到复指数信号的 处。
(频率位置) 16)如果一个信号是偶函数那么它的反褶 它本身,如果一个信号是奇函数那么至少经过 次反褶后才能还原为原始信号。
(是 2)
17)要保证信号抽样后的离散时间信号没有失真的恢复原始时间连续信号,或者说要保证信号的抽样不导致任何信号丢失,必须满足两个条件: 1.信号必须是 的。
2.采样频率至少是信号 的2倍。
18)偶周期信号的傅立叶级数中只有直流项和-------------(余弦项) 19)奇周期信号的傅立叶级数中只有 正弦项 。
20)若信号f(t)的傅立叶变换为 )(F ω=1,则F (t )的傅立叶变换为---------------。
)(2ωπδ 一、一、 证明题
1、若 [f(t)]= )(ωF ,则 0
)()]([0t j e F t t f F ωω-=-
证明:
因为
[f( 0t t -)]=
⎰
∞
∞
--)
t t (f 0t j e ω-dt
令
[
[f (t)]=2 /(
[f (t)]=2 /[ (j /2 )f ( t )]=1 /
(
[
[
[[
=
[
[]+ [
[
=
[
[-[ [f (t)
[f (t)
-1
--
=
--
)]
[G (t) ]= [f (t) [G (t)
2. 2. 画出矩形信号 τG (t)及其FT 的波形
解答教材P52。
