《三角形的证明》单元测试1(含答案)

合集下载

(完整版)三角形的证明测试题(最新版含答案)

第一章三角形的证明检测题（本试卷满分：100分，时间：90分钟）一、选择题（每小题3分，共30分）1.下列命题：①等腰三角形的角平分线、中线和高重合；②等腰三角形两腰上的高相等；③等腰三角形的最短边是底边；④等边三角形的高、中线、角平分线都相等；⑤等腰三角形都是锐角三角形.其中正确的有（）A.1个B.2个C.3个D.4个2.如图，在△ABC中，∠BAC=90°，AB=3，AC=4．AD平分∠BAC交BC于点D，则BD 的长为（）A.157B.125C.207D.2153. 如图，在△ABC中，，点D在AC边上，且，则△A的度数为（）A. 30°B. 36°C. 45°D. 70°4.（2015•湖北荆门中考）已知一个等腰三角形的两边长分别是2和4，则该等腰三角形的周长为（）A.8或10B.8C.10D.6或125.如图，已知，，，下列结论：①；②；③；④△≌△．其中正确的有（）A.1个B.2个C.3个D.4个6. 在△ABC中，△A△△B△△C=1△2△3，最短边cm，则最长边AB的长是（）A.5 cmB.6 cmC.5cmD.8 cm7.如图，已知，，下列条件能使△≌△的是（）A. B.C. D.三个答案都是8.（2015·陕西中考）如图，在△ABC中，∠A=36°，AB＝AC，BD是△ABC的角平分线，若在边AB上截取BE＝BC，连接DE，则图中等腰三角形共有（）A.2个 B.3个 C.4个 D.5个9.已知一个直角三角形的周长是26，斜边上的中线长为2，则这个三角形的面积为（） A.5 B.2C.45D.110.如图，在△ABC 中，AB 的垂直平分线交AC 于点D ，交AB 于点E ，如果cm ，那么△的周长是（）A.6 cmB.7 cmC.8 cmD.9 cm二、填空题（每小题3分，共24分） 11.如图所示，在等腰△ABC 中，AB =AC , ∠BAC =50°, ∠BAC 的平分线与AB 的垂直平分线交于点O ，点 C 沿EF 折叠后与点O 重合，则∠OEC 的度数是 .12.若一个三角形的三条高线交点恰好是此三角形的一个顶点，则此三角形是________三角形.13.（2015•四川乐山中考）如图，在等腰三角形ABC 中，AB ＝AC ，DE 垂直平分AB ，已知∠ADE ＝40°，则∠DBC ＝________°. 14.如图，在△ABC 中，，AM 平分△，cm ，则点M 到AB 的距离是_________.15.如图，在等边△ABC 中，F 是AB 的中点， FE △AC 于E ，若△ABC 的边长为10，则_________，_________.16.(2015•江苏连云港中考)在△ABC 中，AB ＝4,AC ＝3，AD 是△ABC 的角平分线，则△ABD 与△ACD 的面积之比是 . 17.如图，已知的垂直平分线交于点，则.18.一副三角板叠在一起如图所示放置,最小锐角的顶点D 恰好放在等腰直角三角板的斜边AB 上,BC 与DE 交于点M ,如果∠ADF =100°,那么∠BMD 为度.三、解答题（共46分）19.（6分）如图，在△ABC中，，是上任意一点（M与A不重合），MD⊥BC，且交∠的平分线于点D，求证：.20.（6分）联想三角形外心的概念，我们可引入如下概念.定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心.举例：如图（1），若P A＝PB，则点P为△ABC的准外心.应用：如图（2），CD为等边三角形ABC的高，准外心P在高CD上，且PD＝AB，求∠APB的度数.探究：已知△ABC为直角三角形，斜边BC＝5，AB＝3，准外心P在AC边上，试探P A 的长.21.（6分）如图所示，在四边形中，平分∠.求证：.22.（6分）如图所示，以等腰直角三角形ABC的斜边AB为边作等边△ABD，连接DC，以DC为边作等边△DCE，B，E在C，D的同侧，若2，求BE的长.23.（6分）如图所示，在Rt△ABC中，，点D是AC的中点，将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A，D重合，连接BE，EC．试猜想线段BE和EC的数量及位置关系，并证明你的猜想．24.（8分）（2015·陕西中考）如图，在△ABC中，AB＝AC，作AD⊥AB交BC的延长线于点D，作AE∥BD，CE⊥AC，且AE，CE相交于点E.求证：AD＝CE.第24题图25.（8分）已知：如图，，是上一点，于点，的延长线交的延长线于点.求证：△是等腰三角形．第一章三角形的证明检测题参考答案1.B 解析：只有②②正确.2.A 解析：②②BAC =90°，AB =3，AC =4，②5BC ===， ② BC 边上的高=123455⨯÷=. ② AD 平分②BAC ，②点D 到AB ，AC 的距离相等，设为h ，则111123452225ABC S h h ∆=⨯+⨯=⨯⨯，解得127h =，1121123 2725ABD S BD ∆=⨯⨯=⨯，解得157BD =．故选A ． 3.B 解析：因为，所以.因为，所以.又因为，所以，所以所以4.C 解析：当等腰三角形的腰长是2，底边长是4时，等腰三角形的三边长是2，2，4，根据三角形的三边关系，不能构成三角形，所以不合题意，舍去；当等腰三角形的腰长是4，底边长是2时，等腰三角形的三边长是4，4，2，根据三角形的三边关系，能构成三角形，所以该三角形的周长为4＋4＋2=10.5.C 解析：因为，所以②②②（），所以，所以，即故②正确.又因为，所以②②②（ASA ），所以，故②正确. 由②②②，知，又因为，所以②②②，故②正确.由于条件不足，无法证得②故正确的结论有：②②②.6.D 解析：因为②A ②②B ②②C =1②2②3，所以②ABC 为直角三角形，且②C 为直角. 又因为最短边cm ，则最长边cm.7.D 解析：添加A 选项中条件可用“AAS”判定两个三角形全等；添加B 选项中条件可用“SAS”判定两个三角形全等；添加C 选项中条件可用“HL”判定两个三角形全等.故选D ． 8.D 解析：在②ABC 中，② ②A =36°，AB =AC ， ② ②ABC 是等腰三角形，②ABC =②C =72°. ② BD 平分②ABC ，② ②ABD =②CBD =36°， ② ②A =②ABD ，②CDB =②A +②ABD ＝36°+36°=72°， ② ②C ＝②CDB ，② ②ABD ，②CBD 都是等腰三角形. ② BC =BD .② BE =BC ，② BD =BE ， ② ②EBD 是等腰三角形， ② ②BED ＝=＝72°.在②AED 中，② ②A =36°，②BED ＝②A +②ADE ，② ②ADE ＝②BED -②A ＝72°-36°＝36°，② ②ADE =②A =36°，② ②AED 是等腰三角形. ② 图中共有5个等腰三角形.9.B 解析：设此直角三角形为②ABC ，其中因为直角三角形斜边的长等于斜边上中线长的2倍，所以又因为直角三角形的周长是624+，所以62=+b a . 两边平方，得24)(2=+b a ，即24222=++ab b a . 由勾股定理知16222==+c b a ，所以4=ab ，所以221=ab . 10.D 解析：因为垂直平分，所以.所以②的周长（cm ）.11.100° 解析:如图所示，由AB =AC ，AO 平分∠BAC ，得AO 所在直线是线段BC 的垂直平分线，连接OB ，则OB=OA=OC ，所以②OAB =②OBA =×50°=25°，得②BOA=②COA=1802525130,︒-︒-︒=︒②BOC=360°-②BOA -②COA =100°. 所以②OBC=②OCB=1801002︒-︒=40°.由于EO=EC ，故②OEC =180°-2×40°=100°.12.直角解析:直角三角形的三条高线交点恰好是此三角形的一个顶点；锐角三角形的三条高线交点在此三角形的内部；钝角三角形的三条高线交点在三角形的外部.13.15 解析：在Rt②AED 中，②ADE ＝40°，所以②A ＝50°. 因为AB ＝AC ，所以②ABC ＝（180°－50°）÷2＝65°. 因为DE 垂直平分AB ，所以DA ＝DB ，所以②DBE ＝②A ＝50°. 所以②DBC ＝65°－50°＝15°.14.20 cm 解析:根据角平分线的性质：角平分线上的点到角两边的距离相等可得答案. 15.251②3 解析：因为，F 是AB 的中点，所以.在Rt②中，因为，所以.又，所.16.4②3 解析：如图所示，过点D 作DM ②AB ，DN ②AC ，垂足分别为点M 和点N . ② AD 平分②BAC ，② DM ＝DN . ②AB ×DM ，AC ×DN ，② . 第16题答图17.60︒ 解析:② ②BAC=120︒，AB=AC ， ② ②B=②C=180********.22BAC ︒-∠︒-︒==︒② AC 的垂直平分线交BC 于点D ，② AD=CD . ② 30,C DAC ∠=∠=︒② 303060.ADB C DAC ∠=∠+∠=︒+︒=︒18. 85 解析:② ②BDM =180°-②ADF -②FDE =180°-100°-30°=50°，② ②BMD=180°-②BDM-②B =180°-50°-45°=85°.19.证明：②，② ②，② .又② 为②的平分线，② ，② ，② .20. 解：应用：若PB＝PC，连接PB，则②PCB＝②PBC.② CD为等边三角形的高，② AD＝BD，②PCB＝30°，② ②PBD＝②PBC＝30°，②②②与已知PD＝AB矛盾，② PB≠PC.若P A＝PC，连接P A，同理，可得P A≠PC.若P A＝PB，由PD＝AB，得PD＝BD，② ②BPD＝45°，②②APB＝90°.探究：若PB＝PC，设P A＝x，则x2+32=(4-x)2，② x ＝，即P A＝.若P A＝PC，则P A＝2.若P A＝PB，由图（2）知，在Rt②P AB中，这种情况不可能.故P A＝2或.21.证明：如图，过点D作DE②AB交BA的延长线于点E，过点D作于点F.因为BD平分②ABC，所以.在Rt②EAD和Rt②FCD中，所以Rt②EAD②Rt②FCD（HL）.所以②=②.因为②②80°，所以②.22.解：因为②ABD和②CDE都是等边三角形，所以，②②60°.所以②②②②，即②②.在②和②中，因为所以②②②，所以.又，所以.在等腰直角②中，2，故.23.解：，BE②EC.证明：② ，点D是AC的中点，② .② ②②45°，② ②②135°.② ，② ②EAB②②EDC.② ②②.② ②②90°.② ②.24.证明：② AE②BD，② ②EAC＝②ACB.② AB＝AC，② ②B＝②ACB.② ②EAC＝②B.又② ②BAD＝②ACE＝90°，② ②ABD②②CAE（ASA）.② AD＝CE.25.证明：② ，② ②②．②于点，② ②②．② ②②②②．② ②②．② ②②，② ②②．② ②是等腰三角形.。

北师大版2020八年级数学下册第一章三角形的证明单元基础达标测试题1(附答案)

北师大版2020八年级数学下册第一章三角形的证明单元基础达标测试题1（附答案） 1．如图，平行四边形ABCD 中，E 是AB 上一点，DE 、CE 分别是∠ADC 、∠BCD 的平分线，若AD=5，DE=6，则平行四边形的面积为（）A ．96B ．48C ．60D ．302．如图，△ABC 中，AB ＝AC ，AD 是∠BAC 的平分线．已知AB ＝5，AD ＝3，则BC 的长为（）A ．5B ．6C ．8D ．103．如图，在△ABC 中，P 、Q 分别是BC 、AC 上的点，作PR ⊥AB ，PS ⊥AC ，垂足分别为R 、S ，若AQ ＝PQ ，PR ＝PS ，①PA 平分∠BAC ；②AS ＝AR ；③QP ∥AR ；④△BRP ≌△CSP ．则这四个结论中正确的有( )A ．4个B ．3个C ．2个D ．1个4．如图，在□ABCD 中，CM ⊥AD 于点M ，CN ⊥AB 于点N ，若∠B=40°，则∠MCN=（）A ．40°B ．50°C ．60°D ．70°5．已知等腰△ABC 中，AD ⊥BC 于点D ，且AD=12BC ，则△ABC 底角的度数为（） A ．45° B ．75° C ．60°D ．45°或75° 6．如图所示，在平面直角坐标系中，直线OM 是正比例函数3y x =的图象，点A 的坐标为(1，0)，在直线OM 上找一点N ，使△ONA 是等腰三角形，则符合条件的点N有( )A．2个B．3个C．4个D．5个7．已知∠AOB的大小为α，P是∠AOB内部的一个定点，且OP＝2，点E、F分别是OA、OB上的动点，若△PEF周长的最小值等于2，则α＝（）A．30°B．45°C．60°D．90°8．如图，已知等腰三角形，若以点为圆心，长为半径画弧，交腰于点，则下列结论一定正确的是（）A ．B．C．D．9．下列各组数不是．．勾股数的是（）A．2、3、4 B．3、4、5 C．6、8、10 D．5、12、1310．如图，将△ABC沿着直线DE折叠，使点C与点A重合，已知AB=7，BC=9，则△BAD的周长为______________。

(典型题)初中数学八年级数学下册第一单元《三角形的证明》检测题(含答案解析)

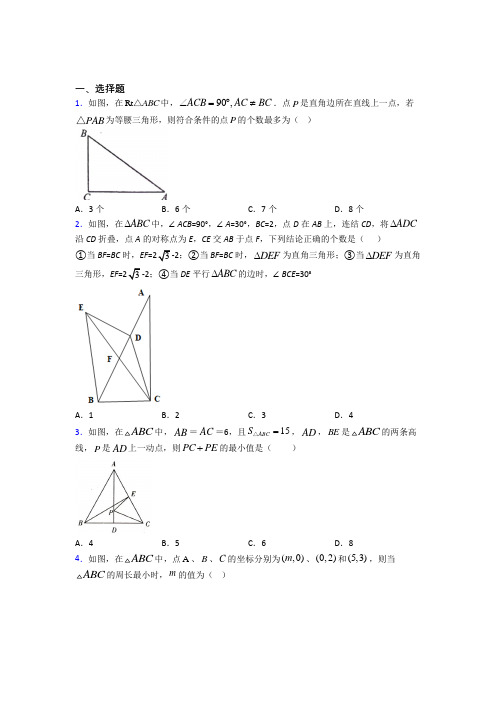
一、选择题1．如图，在Rt ABC △中，90,ACB AC BC ∠=︒≠．点P 是直角边所在直线上一点，若PAB △为等腰三角形，则符合条件的点P 的个数最多为（）A ．3个B ．6个C ．7个D ．8个2．如图，在ABC ∆中，∠ACB =90°，∠A =30°，BC =2，点D 在AB 上，连结CD ，将ADC ∆沿CD 折叠，点A 的对称点为E ，CE 交AB 于点F ，下列结论正确的个数是（） ①当BF =BC 时，EF =23-2；②当BF =BC 时，DEF ∆为直角三角形；③当DEF ∆为直角三角形，EF =23-2；④当DE 平行ABC ∆的边时，∠BCE =30°A ．1B ．2C ．3D ．43．如图，在ABC 中，AB ＝AC ＝6，且15ABC S =△，AD ，BE 是ABC 的两条高线，P 是AD 上一动点，则PC PE +的最小值是（）A ．4B ．5C ．6D ．84．如图，在ABC 中，点A 、B 、C 的坐标分别为(,0)m 、(0,2)和(5,3)，则当ABC 的周长最小时，m 的值为（）A．0 B．1 C．2 D．35．下列各组线段a、b、c中不能组成直角三角形的是（）A．a＝7，b＝24，c＝25 B．a＝4，b＝5，c＝6C．a＝3，b＝4，c＝5 D．a＝9，b＝12，c＝156．如图，△ABC中，DC=2BD=2，连接AD，∠ADC=60°．E为AD上一点，若△BDE和△BEC都是等腰三角形，且AD=31，则∠ACB=（）A．60°B．70°C．55°D．75°7．如图，直线AB，CD交于点O，若AB，CD是等边△MNP的两条对称轴，且点P在直线CD上（不与点O重合），则点M，N中必有一个在（）A．∠AOD的内部B．∠BOD的内部C．∠BOC的内部D．直线AB上8．如图，在平面直角坐标系中，点A1在x轴的正半轴上，B1在第一象限，且△OA1B1是等边三角形．在射线OB1上取点B2，B3，…，分别以B1B2，B2B3，…为边作等边三角形△B1A2B2，△B2A3B3，…使得A1，A2，A3，…在同一直线上，该直线交y轴于点C．若OA1＝1，∠OA1C＝30°，则点B9的横坐标是（）A ．2552B ．5112C ．256D ．51329．如图，点B 是线段AC 上任意一点（点B 与点A ，C 不重合），分别以AB 、BC 为边在直线AC 的同侧作等边三角形ABD 和等边三角形BCE ，AE 与BD 相交于点G 、CD 与BE 相交于点F ，AE 与CD 相交于点H ，连HB ，则下列结论：①AE CD =；②120AHC ∠=︒；③HB 平分AHC ∠；④CH EH BH =+．其中正确的结论有（）A ．4个B ．3个C ．2个D ．1个10．如图所示，在ABC 中，90BAC ∠=︒，30ACB ∠=︒，AD BC ⊥于D ，BE 是ABC ∠的平分线，且交AD 于P ，如果1AP =，则AC 的长为（）A ．1B ．2C ．3D ．411．如图，在平面直角坐标系中，点A 的坐标为()1,0，以线段OA 为边在第四象限内作等边ABO ，点C 为x 轴正半轴上一动点（1OC >），设点C 的坐标为(),0x ，连结BC ，以线段BC 为边的第四象限内作等边CBD ，直线DA 交y 轴于点E ，点E 的坐标是（）A ．()0,3B ．0,2x ⎛⎫ ⎪⎝⎭C ．()0,3D ．30,x ⎛⎫ ⎪ ⎪⎝⎭ 12．等腰三角形一腰的垂直平分线与另一腰所在直线的夹角是40°，则这一等腰三角形的底角为（）A ．65°B ．25°C ．50°D ．65°或25°二、填空题13．如图，在△ABC 中，∠C ＝90°，以A 为圆心，任意长为半径画弧，分别交AC ，AB 于点M ，N ，再分别以M ，N 为圆心，大于12MN 长为半径画弧，两弧交于点O ，作射线AO ，交BC 于点E ．已知CB ＝8，BE ＝5，则点E 到AB 的距离为_____．14．如图，等腰三角形ABC 的面积为80，底边10BC =，腰AC 的垂直平分线EF 交,AC AB 于点E ，F ，若D 为BC 边中点，M 为线段EF 上一动点，则CDM 的周长最小值为________．15．如图，DE ∥BC ，AE ＝DE ＝1，BC ＝3，则线段CE 的长为_____．16．如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝BC ＝6，D 为BC 上一点，连接AD ，过点A作AE ⊥AD ，取AE ＝AD ，连接BE 交AC 于F ．当△AEF 为等腰三角形时，CD ＝_____．17．如图，D 是等边三角形ABC 外一点，3AD =，2CD =，则BD 的最大值是________________．18．如图，80AOB ∠=︒，OC 平分AOB ∠，如果射线OA 上的点E 满足OCE △是等腰三角形，那么OEC ∠的度数为________．19．如图，在ABC 中，AB BC =，30C ∠=︒，过点B 作BD BC ⊥，交AC 于点D ，若2CD =，则AD 的长为__________．20．如图，△ABC 中，∠ABC 与∠ACB 的平分线交于点D ，过点D 作EF ∥BC ，分别交AB 、AC 于点E 、F ．那么下列结论：①BD=DC ；②△BED 和△CFD 都是等腰三角形；③点D 是EF 的中点；④△AEF 的周长等于AB 与AC 的和．其中正确的有______．（只填序号）三、解答题21．如图1，直线AB ：y=43x ＋4分别与x 轴、y 轴交于A 、B 两点，过点B 的直线交x 轴负半轴于点C ，将△BOC 沿BC 折叠，使点O 落在BA 上的点M 处．（1）求A 、B 两点的坐标；（2）求线段BC 的长；（3）点P 为x 轴上的动点，当∠PBA=45°时，求点P 的坐标．22．如图，在ABC 中，AB BC =，90ABC ∠=︒，点E 在BC 上，点F 在AB 的延长线上，且AE CF =．（1）求证：ABE CBF △≌△；（2）若75ACF ∠=︒，求EAC ∠的度数．23．阅读下列材料，完成相应任务．三角形中边与角之间的不等关系学习了等腰三角形，我们知道：在一个三角形中，等边所对的角相等；反过来，等角所对的边也相等．那么，不相等的边所对的角之间的大小关系怎样呢？大边所对的角也大吗？下面是奋进小组的证明过程．如图1，在△ABC中，已知AB＞AC＞BC．求证：∠C＞∠B＞∠A．证明：如图2，将△ABC折叠，使边AC落在AB上，点C落在AB上的点C′处，折痕AD交BC于点D．则∠A C′D=∠C．∵∠A C′D=∠B+∠BDC′（依据1）∴∠A C′D＞∠B∴∠C＞∠B（依据2）如图3，将△ABC折叠，使边CB落在CA上，点B落在CA上的点B′处，折痕CE交AB于点E．则∠CB′E=∠B．∵∠CB′E=∠A+∠AEB′∴∠CB′E＞∠A∴∠B＞∠A∴∠C＞∠B＞∠A．归纳总结：利用轴对称的性质可以把研究边与角之间的不等问题，转化为较大量的一部分与较小量相等的问题，这是几何中研究不等问题是常用的方法．类似地，应用这种方法可以证明“在一个三角形中，大角对大边，小角对小边”的问题．如图1，已知△ABC中，∠C＞∠B＞∠A．求证：AB＞AC＞BC．下面是智慧小组的证明过程（不完整）．证明：如图2，在∠BCA的内部，作∠BCF=∠B，CF交AB于点F．则CF=BF（依据3）在△ACF中，AF+CF＞AC，∴AF+BF＞AC，∴AB＞AC；…任务一：①上述材料中依据1，依据2，依据3分别指什么？依据1：；依据2：；依据3：．②上述材料中不论是由边的不等关系，推出角的不等关系，还是由角的不等关系推出边的不等关系，都是转化为较大量的一部分与较小量相等的问题，再用三角形外角的性质或三边关系进而解决，这里主要体现的数学思想是_____________；（填正确选项的代码） A ．转化思想 B ．方程思想 C ．数形结合思想任务二：请将智慧小组的证明过程补充完整，并在备用图中作出辅助线．任务三：根据上述材料得出的结论，判断下列说法，正确的有__________（将正确的代码填在横线处）．①在△ABC 中，AB ＞BC ，则∠A ＞∠B ；②在△ABC 中，AB ＞BC ＞AC ，∠C =89°，则△ABC 是锐角三角形；③Rt △ABC 中，∠B =90°，则最长边是AC ；④在△ABC 中，∠A =55°，∠B =70°，则AB =BC ．24．如图，已知点D 、E 是△ABC 内两点，且∠BAE ＝∠CAD ，AB ＝AC ，AD ＝AE ．（1）求证：ABD ACE △≌△．（2）延长BD 、CE 交于点F ，若86BAC ∠=︒，20ABD ∠=︒，求BFC ∠的度数． 25．如图，在ABC 中，AB AC =，100BAC ∠=︒，AD 是BC 边上的中线，且BD BE =，CD 的垂直平分线FM 交AC 于点F ，交BC 于点M ．（1）求ADE ∠的度数；（2）ADF 是什么三角形？说明理由．（3）若将题目中“100BAC ∠=︒”改为“∠BAC =120°”，且FM =4，其他条件不变，求AB 的长．26．如图，射线,ON OE OS OW ､､分别表示从点O 出发北､东､南､西四个方向，将直角三角尺的直角顶点与点O 重合．（1）图中与∠BOE 互余的角是____________或____________；（2）①用直尺和量角器作AOE ∠的平分线OP ；②在①所做的图形中，如果132AOE ∠=︒，那么点P 在点O 北偏东____________°的方向上（请说明理由）．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】分为三种情况：①BP=AB，②AP=AB，③AP=BP，再求出答案即可．【详解】解：作BC、AC所在直线，然后分别以B、A点为圆心，以AB为半径作圆分别交BC、AC 所在直线于6点，再作AB的垂直平分线与BC所在直线交于2点，总共符合条件的点P的个数最多有8个，故选：B．【点睛】本题考查了等腰三角形的判定，线段垂直平分线的性质．能求出符合的所有情况是解此题的关键．2．C解析：C【分析】由勾股定理可求A C 的长，利用折叠的性质和等腰三角形的性质依次计算可得①②正确．利用直角三角形分类讨论可知EF 有两种情况，③不正确，由平行内错角角相等可知④正确；【详解】解：①∵BF =BC ，且∠ABC =60°，∴BCF ∆为等边三角形，BF =CF =BC =2，ACAB =4，∵ADC ∆沿CD 折叠，∴CE =ACEF =CE -CF ，故①正确；②当BF =BC 时，∠EFD =∠BFC =60°，∴∠DEF =∠A =30°，∠EDF =90°，∴EDF ∆为直角三角形，故②正确；③当DEF ∆为直角三角形时，此处要分情况讨论，当∠EDF =90°时，∵∠DEF =∠A =30°，∴∠EFD =60°=∠BFC ，EF =EC -CF-2，当∠EFD =90°时，∵∠ABC =60°，∠BCF =30°，∴FCEF =EC -FC ，综上所述，EF ，故③错误；④当DE 平行于ABC ∆的边时，∵DE ∥BC ，∴∠EDF =∠ABC =60°，∵∠DEC =30°，∴∠BCF =∠DEC =30°，故④正确，故选C【点睛】本题考查了翻折变换，等腰三角形的判定和性质，勾股定理等知识；熟练掌握翻折变换的性质，由直角三角形的性质和勾股定理求出CA ，学会运用分类讨论是解题的关键． 3．B解析：B【分析】连接PB ，根据等腰三角形的性质和垂直平分线的性质计算即可；【详解】连接PB ，∵AB AC =，BD CD =，∴AD 是等腰△ABC 底边BC 边的中垂线，∴PB PC =，∴PC PE PB PE +=+，又PB PE BE +≥，∴B ，P ，E 三点共线时，PB PE +最小，即等于BE 的长，又∵△1152ABC S AC BE ==，6AC =， ∴5BE =；故答案选B ．【点睛】本题主要考查了等腰三角形的性质、垂直平分线的性质，结合轴对称的性质计算是解题的关键． 4．C解析：C【分析】做出B 关于x 轴对称点为B′，连接B′C ，交x 轴于点A'，此时ABC 的周长最小，由等腰直角三角形的性质可求∠OB'A'=∠OA'B'=45°，可求OB'=OA'=1，即可求解．【详解】解：如图所示，做出B 关于x 轴对称点为B′，连接B′C ，交x 轴于点A'，此时△ABC 周长最小过点C作CH⊥x轴，过点B'作B'H⊥y轴，交CH于H，∵B（0，2），∴B′（0，-2），∵C（5，3），∴CH= B′H=5，∴∠CB'H=45°，∴∠BB' A'=45°，∴∠OB'A'=∠OA'B'=45°，∴OB'=OA'=2，则此时A'坐标为（2，0）．m的值为2．故选：C．【点睛】此题考查了轴对称-最短路径问题，考查了轴对称的性质，等腰直角三角形的性质等知识，根据已知得出A点位置是解题关键．5．B解析：B【分析】根据判断三条线段是否能构成直角三角形的三边，需验证两小边的和的平方是否等于最长边的平方，分别对每一项进行分析，即可得出答案；【详解】A、222724=25+，能构成直角三角形；B、222+≠，不能构成直角三角形；45=416C、222+，能构成直角三角形；34=5D、222912=225=15+，能构成直角三角形；故选：B．【点睛】本题考查了勾股定理的逆定理，用到的知识点是已知△ABC 的三边满足222+=a b c ，则△ABC 是直角三角形；6．D解析：D【分析】根据等腰三角形的性质求解即可；【详解】∵60EDC ∠=︒，∴60EBD BED ∠+∠=︒，∵△BDE 是等腰三角形，∴30EBD BED ∠=∠=︒，1BD DE ==，∵△BEC 是等腰三角形，∴30EBD ECD ∠=∠=︒，∵60EDC ∠=︒，∴90DEC ∠=︒，在Rt △DEC 中，∵30ECD ∠=︒，1DE =，∴tan 30DEEC ==︒又∵AD 1， ∴AE AD DE EC =-==，∴△AEC 为等腰三角形，又∵90DEC AEC ∠=∠=︒，∴45ECA EAC ∠=∠=︒，∴453075ACB ACE ECD ∠=∠+∠=︒+︒=︒；故答案选D ．【点睛】本题主要考查了等腰三角形的性质应用，准确计算是解题的关键．7．D解析：D【分析】根据等边三角形是轴对称图形，利用轴对称图形的性质解决问题即可．【详解】解：如图，∵△PMN 是等边三角形，等边三角形的对称轴一定经过三角形的顶点，又∵直线CD ，AB 是△PMN 的对称轴，直线CD 经过点P ，∴直线AB 一定经过点M 或N ，故选：D ．【点睛】本题考查轴对称，等边三角形的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．8．B解析：B【分析】利用待定系数法求得两条直线的解析式，根据等边三角形的性质，点的坐标规律，即可求解．【详解】解：∵OA 1=1，∠OA 1C=30︒，∴3 ∴点C 的坐标为(0，33-)， ∵A 1、A 2、A 3所在直线过点A 1(1，0)，C (0，33-，设直线A 1A 2的解析式为3y kx =-∴30k =， ∴3k = ∴直线A 1A 2的解析式为3333y x =-， ∵△OA 1B 1为等边三角形，∴点B 1的坐标为(123， ∵B 1、B 2、B 3所在直线过点O(0，0)，B 1 (12，32)，同理可求得直线O B 1的解析式为y =，∵△OA 1B 1和△B 1A 2B 2为等边三角形，∴∠B 1OA 1=∠B 2 B 1A 2=60︒，∴B 1A 2∥OA 1，∵B 1 (12，∴A 2的纵坐标为2x = 解得：52x =，∴点A 2的坐标为(52， ∴B 1A 2=2，同理点B 2的坐标为(32，点B 3的坐标为(72，点B 4的坐标为(152，，总结规律： B 1的横坐标为12， B 2的横坐标为13122+=， B 3的横坐标为171222++=， B 4的横坐标为11512422+++=，，∴B 9的横坐标为1511124816326422+++++++=，故选：B【点睛】本题考查了待定系数法求一次函数的解析式，点的坐标规律，等边三角形的性质，解决本题的关键是寻找点的坐标规律． 9．A解析：A【分析】利用等边三角形,ABD BCE 的性质，证明 ,ABE DBC ≌ 从而可判断①，由,ABE DBC ≌可得,EAB CDB ∠=∠ 再利用三角形的内角和定理可判断②，如图，过B 作BM AE ⊥交AE 于,M 过B 作BN DC ⊥交DC 于,N 利用全等三角形的对于高相等证明,BM BN = 从而可判断③，如图，在CH 上截取,HK HE = 连接,EK 证明EHK 为等边三角形，再证明,EHB EKC ≌ 可得,HB KC = 从而可判断④．【详解】解：,ABD BCE 为等边三角形， ,60,60BA BD ABD BC BE CE CBE ∴=∠=︒==∠=︒，，,ABD DBE CBE DBE ∴∠+∠=∠+∠ 即,ABE DBC ∠=∠(),ABE DBC SAS ∴≌,AE DC ∴= 故①符合题意；,ABE DBC ≌,EAB CDB ∴∠=∠,DGH AGB ∠=∠180,180,DHG CDB DGH ABD EAB AGB ∠=︒-∠-∠∠=︒-∠-∠60DHG ABD ∴∠=∠=︒，120AHC ∴∠=︒，故②符合题意；如图，过B 作BM AE ⊥交AE 于,M 过B 作BN DC ⊥交DC 于,N,ABE DBC ≌,AE DC 为对应边，,BM BN ∴=HB ∴平分,AHC ∠ 故③符合题意；如图，在CH 上截取,HK HE = 连接,EK60,EHK AHD ∠=∠=︒EHK ∴为等边三角形，,60,EK EH HEK ∴=∠=︒60,60,HEK HEB FEK BEC FEK KEC ∠=︒=∠+∠∠=︒=∠+∠,HEB KEC ∴∠=∠,BE CE =(),EHB EKC SAS ∴≌,HB KC ∴=.CH CK HK BH EH ∴=+=+ 故④符合题意；综上：①②③④都符合题意，故选：.A【点睛】本题考查的是三角形的内角和定理的应用，全等三角形的判定与性质，等边三角形的判定与性质，角平分线的判定，掌握以上知识是解题的关键．10．C解析：C【分析】由三角形的内角和定理和等腰三角形的性质，得到AP=BP=AE=PE=1，CE=BE=2，即可求出AC 的长度．【详解】解：∵在ABC 中，90BAC ∠=︒，30ACB ∠=︒，∴60ABC ∠=︒，∵AD BC ⊥于D ，BE 是ABC ∠的角平分线，∴30ABP DBP BAP ∠=∠=∠=︒，∴1AP BP ==，∵90BAC ∠=︒，30ACB ∠=︒，∴60EAP AEP ∠=∠=︒，∴△APE 是等边三角形，∴AP=BP=AE=PE=1，∵30DBP C ∠=∠=︒，∴CE=BE=1+1=2，∴213AC CE AE =+=+=；故选：C ．【点睛】本题考查了等边三角形的判定和性质，等腰三角形的性质，三角形的内角和定理，解题的关键是熟练掌握所学的知识，正确的进行解题．11．A解析：A【分析】由等边三角形的性质可得AO ＝OB ＝AB ＝1，BC ＝BD ＝CD ，∠OBA ＝∠CBD ＝60°，可证△OBC ≌△ABD ，可得∠BAD ＝∠BOC ＝60°，可求∠EAO ＝60°，即可求OE 3点E 坐标．【详解】解：∵△AOB ，△BCD 是等边三角形，∴AO ＝OB ＝AB ＝1，BC ＝BD ＝CD ，∠OBA ＝∠CBD ＝60°，∴∠OBC ＝∠ABD ，且OB ＝AB ，BC ＝BD ，∴△OBC ≌△ABD （SAS ），∴∠BAD ＝∠BOC ＝60°，∴∠EAO ＝180°−∠OAB−∠BAD ＝60°，在Rt △AOE 中，AO ＝1，∠EAO ＝60°，∠OEA=30°，∴AE=2 AO=2，∴OE=2221-＝3，∴点E 坐标(0，3)，故选A ．【点睛】本题考查了全等三角形的判定和性质，等边三角形的性质，坐标与图形性质，灵活运用全等三角形的判定和性质是本题的关键．12．D解析：D【分析】由题意可知其为锐角等腰三角形或钝角等腰三角形，不可能是等腰直角三角形，所以应分开来讨论．【详解】解：①当为锐角等腰三角形时，如图：∵∠ADE ＝40°，∠AED ＝90°，∴∠A ＝50°，∴∠B=∠C=180502︒-︒ =65°； ②当为钝角等腰三角形时，如图：∵∠ADE ＝40°，∠AED ＝90°，∴∠BAC ＝∠ADE+∠AED ＝40°+90°＝130°，∴∠B=∠C=1801302︒-︒ =25°．故选：D ．【点睛】本题考查了等腰三角形的性质、三角形内角和定理以及三角形外角性质，分类讨论是正确解答本题的关键．二、填空题13．【分析】根据作图过程可知AE 平分∠CAB 根据角平分线的性质即可得出结论【详解】解：根据作图过程可知：AE 平分∠CAB ∵CB ＝8BE ＝5∴CE ＝BC ﹣BE ＝8﹣5＝3∵∠C ＝90°∴EC ⊥AC ∴点E 到解析：【分析】根据作图过程可知AE 平分∠CAB ，根据角平分线的性质即可得出结论．【详解】解：根据作图过程可知：AE 平分∠CAB ，∵CB ＝8，BE ＝5，∴CE ＝BC ﹣BE ＝8﹣5＝3，∵∠C ＝90°，∴EC ⊥AC ，∴点E 到AB 的距离为3．故答案为：3．【点睛】本题考查了作图-基本做图，解决本题的关键是掌握基本的作图方法和理解角平分线的性质．14．21【分析】连接ADAM 由于△ABC 是等腰三角形点D 是BC 边的中点故AD ⊥BC 再根据三角形的面积公式求出AD 的长再根据EF 是线段AC 的垂直平分线可知点A 关于直线EF 的对称点为点CMA ＝MC 推出MC ＋解析：21【分析】连接AD ，AM ，由于△ABC 是等腰三角形，点D 是BC 边的中点，故AD ⊥BC ，再根据三角形的面积公式求出AD 的长，再根据EF 是线段AC 的垂直平分线可知，点A 关于直线EF 的对称点为点C ，MA ＝MC ，推出MC ＋DM ＝MA ＋DM≥AD ，故AD 的长为BM ＋MD 的最小值，由此即可得出结论．【详解】解：连接AD ，MA ．∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，∴S△ABC＝12BC•AD＝12×10×AD＝80，解得：AD＝16，∵EF是线段AC的垂直平分线，∴点A关于直线EF的对称点为点C，MA＝MC，∴MC＋DM＝MA＋DM≥AD，∴AD的长为CM＋MD的最小值，∴△CDM的周长最短＝（CM＋MD）＋CD＝AD＋12BC＝16＋12×10＝21．故答案是：21．【点睛】本题考查的是轴对称−最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．15．【分析】由平行线的性质可得∠ADE=∠B由AE=DE=1可得∠ADE=∠DAE易得∠DAE=∠B可得AC=BC易得结果【详解】解：∵DE∥BC∴∠ADE＝∠B∵AE ＝DE＝1∴∠ADE＝∠DAE∴∠解析：【分析】由平行线的性质可得∠ADE=∠B，由AE=DE=1，可得∠ADE=∠DAE，易得∠DAE=∠B，可得AC=BC，易得结果．【详解】解：∵DE∥BC，∴∠ADE＝∠B，∵AE＝DE＝1，∴∠ADE＝∠DAE，∴∠DAE＝∠B，BC＝3，∴AC＝BC＝3，∴CE＝AC﹣AE＝3﹣1＝2，故答案为：2．【点睛】本题主要考查了平行线的性质和等腰三角形的性质等，关键是运用性质定理得出AC=BC=3．16．2或6【分析】分两种情形：当AE=AF时如图1中过点E作EH⊥AC于H证明AH＝FH＝CF＝CD可得结论如图2中当AF＝EF时点D与D重合此时CD＝BC ＝6【详解】解：①当AE=EF时如图1中过点E解析：2或6【分析】分两种情形：当AE=AF 时，如图1中，过点E 作EH ⊥AC 于H ．证明AH ＝FH ＝CF ＝CD ，可得结论，如图2中，当AF ＝EF 时，点D 与D 重合，此时CD ＝BC ＝6【详解】解：①当AE=EF 时，如图1中，过点E 作EH ⊥AC 于H ．∵EA ＝EF ，EH ⊥AF ，∴AH ＝HF ，∵EA ⊥AD ，∴∠EAD ＝∠EHA ＝∠C ＝90°，∴∠EAH ＋∠CAD ＝90°，∠CAD ＋∠ADC ＝90°，∴∠EAH ＝∠ADC ，在△EHA 和△ACD ，EAH ADC EHA C AE DA ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△EHA ≌△ACD （AAS ），∴AH ＝CD ，EH ＝AC ＝CB ．在△EHF 和△BCF 中，EFH BFC EHF C EH BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△EHF ≌△BCF （AAS ），∴FH ＝CF ，∴AH ＝FH ＝CF ＝CD ，∴CD ＝13AC ＝2， ②如图2中，当AF ＝EF 时，点B 与点D 重合，此时CD ＝BC ＝6综上所述，满足条件的CD的长度为2或6故答案为：2或6【点睛】本题考查等腰直角三角形的性质，全等三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．17．5【分析】将AD顺时针旋转60°得连结可得AD=DD′=AD′可证△ABD′≌△ACD（SAS）可得BD′=CD由BD′+DD′≥BD当BD′D三点在一线时BD最大BD最大=BD′+DD′=5【详解解析：5【分析】将AD顺时针旋转60°，得AD'，连结BD'，可得AD=DD′=AD′，可证△ABD′≌△ACD （SAS），可得BD′=CD，由BD′+DD′≥BD，当B、D′、D三点在一线时，BD最大，BD最大=BD′+DD′=5．【详解】解：∵将AD顺时针旋转60°，得AD'，连结BD'，则AD=DD′=AD′，∴△ADD′是等边三角形，又∵等边三角形ABC，∴∠BAC=∠D AD'，∴∠BAD′+∠D′AC=∠CAD+∠D′AC=60°，∴AB=AC，AD′=AD，∴△ABD′≌△ACD（SAS），∴BD′=CD，∴BD′+DD′≥BD，当B、D′、D三点在一线时，BD最大，BD最大=BD′+DD′=CD+AD=2+3=5．故答案为：5．．【点睛】本题考查三角形旋转变换，等边三角形判定与性质，掌握三角形旋转变换的性质，等边三角形判定与性质，用三角形三边关系确定B、D′、D共线是解题关键．18．40°或70°或100°【分析】求出∠AOC根据等腰得出三种情况OE＝CEOC＝OEOC＝CE根据等腰三角形性质和三角形内角和定理求出即可【详解】解：∵∠AOB＝80°OC平分∠AOB∴∠AOC＝4解析：40°或70°或100°【分析】求出∠AOC，根据等腰得出三种情况，OE＝CE，OC＝OE，OC＝CE，根据等腰三角形性质和三角形内角和定理求出即可．【详解】解：∵∠AOB＝80°，OC平分∠AOB，∴∠AOC＝40°，①当E在E1时，OE＝CE，∵∠AOC＝∠OCE＝40°，∴∠OEC＝180°﹣40°﹣40°＝100°；②当E在E2点时，OC＝OE，则∠OCE＝∠OEC＝12（180°﹣40°）＝70°；③当E在E3时，OC＝CE，则∠OEC＝∠AOC＝40°；故答案为：100°或70°或40°．【点睛】本题考查了角平分线定义，等腰三角形性质，三角形的内角和定理的应用，用了分类讨论思想．19．【分析】利用等腰三角形的性质判定证明BD=AD 利用直角三角形中30°角的性质计算BD 即可得解【详解】∵∴∠A=30°∠ABC=120°∵∴∠CBD=90°BD=1∴∠DBA=30°∴∠DBA=∠A ∴ 解析：1.【分析】利用等腰三角形的性质，判定，证明BD=AD ，利用直角三角形中30°角的性质计算BD 即可得解.【详解】∵AB BC =，30C ∠=︒，∴∠A=30°，∠ABC=120°，∵BD BC ⊥，2CD =，∴∠CBD=90°，BD=1，∴∠DBA=30°，∴∠DBA=∠A ，∴BD=AD ，∴AD=1.【点睛】本题考查了等腰三角形的判定和性质，直角三角形的性质，熟练掌握性质，并灵活运用性质是解题的关键.20．②④【分析】由平行线得到角相等由角平分线得角相等根据平行线的性质及等腰三角形的判定和性质逐一判断即得答案【详解】解：∵EF ∥BC ∴∠EDB=∠DBC ∠FDC=∠DCB ∵∠ABC 与∠ACB 的平分线交于解析：②④【分析】由平行线得到角相等，由角平分线得角相等，根据平行线的性质及等腰三角形的判定和性质逐一判断即得答案．【详解】解：∵EF ∥BC ，∴∠EDB=∠DBC ，∠FDC=∠DCB ，∵∠ABC 与∠ACB 的平分线交于点D ，∴∠EBD=∠DBC ，∠FCD=∠DCB ，∴∠EDB =∠EBD ，∠FCD=∠FDC ，∴ED=EB ，FD=FC ，即△BED 和△CFD 都是等腰三角形；故②正确；∴△AEF 的周长为：AE+EF+AF=AE+ED+DF+AF=AB+AC ；故④正确；∵∠ABC 不一定等于∠ACB ，∴∠DBC 不一定等于∠DCB ，∴BD 与CD 不一定相等，故①错误．∵BE 与CF 无法判定相等，∴ED 与DF 无法判定相等，故③错误；综上，正确的有②④．故答案为：②④．【点睛】本题考查了等腰三角形的性质及角平分线的性质及平行线的性质；题目利用了两直线平行，内错角相等，及等角对等边来判定等腰三角形；等量代换的利用是解答本题的关键．三、解答题21．（1）A （-3，0），B （0，4）；（2）BC ；（3）P （-28，0）或（47，0）【分析】（1）令0x =，求得y ，令0y =，求得x ，即可求解；（2）设OC=a ，在Rt △ACM 中，利用勾股定理列式计算可求得43a =，即可求解；（3）分点P 在点A 的右边和左边两种情况讨论，分别作出辅助线，构造直角三角形，利用勾股定理求解即可．【详解】（1）令0x =，4443y x =+=，令0y =，4043x =+，则3x =-， ∴点A 的坐标为（-3，0），点B 的坐标为（0，4）；（2）设OC=a ，由折叠的性质可知：CM ⊥AB ，OC=CM=a ，OB=BM=4，由勾股定理得：5==，∴AM=1，在Rt △ACM 中，222AM MC AC +=，∴2221(3)a a +=-， ∴43a =， ∴222244()03341BC BO CO =+=+=；（3）如图，点P 在点A 的右边时，过P 作PG ⊥AB 于G ， ∵点A 的坐标为（-3，0），点B 的坐标为（0，4），∴OA<OB ，∴点P 在点O 的右边，设PO= m ，则AP=3m +，∵APB 1122S AB PG AP OB =⨯=⨯， ∴()435PG m =+， ()()()22224333355AG AP PG m m m ⎡⎤=-=+-+=+⎢⎥⎣⎦， ∵∠PBA=45°，∴△BPG 是等腰直角三角形，∴()435BG PG m ==+， ∵ AG BG AB +=，∴()()3433555m m +++=，解得：47m =，此时点P 的坐标为(47，0)；如图，点P 在点A 的左边时，过P 作PH ⊥AB 于H ，设PO= n ，则AP=n 3-， ∵APB 1122S AB PH AP OB =⨯=⨯， ∴()4n 35PH =-， ()()()22224333355AH AP PH n n n ⎡⎤=-=---=-⎢⎥⎣⎦， ∵∠PBA=45°，∴△BPH 是等腰直角三角形，∴()435BH PH n ==-， ∵BH AH AB -=， ∴()()4333555n n ---=，解得：28n =，此时点P 的坐标为(28-，0)；综上，点P 的坐标为(28-，0)或(47，0) ．【点睛】本题考查了坐标与图形，一次函数的性质，以及等腰直角三角形的判定和性质，解题的关键是作出合适的辅助线，构造直角三角形，利用勾股定理求解．22．（1）见详解；（2）15°【分析】（1）由AB ＝CB ，∠ABC ＝90°，AE ＝CF ，即可利用HL 证得Rt △ABE ≌Rt △CBF ；（2）由AB ＝CB ，∠ABC ＝90°，即可求得∠CAB 与∠ACB 的度数，即可得∠FCB 的度数，又由Rt △ABE ≌Rt △CBF ，即可求得∠EAB 的度数，再得出∠EAC 的度数即可．【详解】（1）证明：∵∠ABC ＝90°，∴△ABE 与△CBF 为直角三角形．∵在Rt △ABE 与Rt △BCF 中，AB BC AE CF⎧⎨⎩＝＝， ∴Rt △ABE ≌Rt △CBF （HL ）；（2）∵AB ＝BC ，∠ABC ＝90°，∴∠BAC ＝∠ACB ＝45°，∵∠ACF ＝75°，∴∠FCB ＝30°，∵Rt △ABE ≌Rt △CBF ，∴∠EAB ＝∠FCB ＝30°，∴∠EAC ＝45°-30°=15°．【点睛】此题考查了直角三角形全等的判定与性质，等腰直角三角形的性质，解题的关键是正确寻找全等三角形全等的条件，属于中考常考题型．23．任务一：①依据1：三角形的外角等于与它不相邻的两个内角的和；依据2：等量代换；依据3：如果一个三角形有两个角相等，那么这两个角所对的边也相等（或等角对等边）； ②A ；任务二：见解析；任务三：②③④【分析】任务一：①根据三角形的外角性质、等量代换以及三角形中等角对等边性质即可写出依据；②根据分析过程渗透的思想为转化的思想方法；任务二：仿照推导AB ＞AC 的方法证明AC ＞BC 即可证明结论正确；任务三：根据结论“在一个三角形中，大角对大边，小角对小边，等边对等角”进行判断即可解答．【详解】解：任务一：①根据推导过程可知：依据1：三角形的外角等于与它不相邻的两个内角的和；依据2：等量代换；依据3：如果一个三角形有两个角相等，那么这两个角所对的边也相等（或等角对等边）；故答案为：三角形的外角等于与它不相邻的两个内角的和；等量代换；如果一个三角形有两个角相等，那么这两个角所对的边也相等（或等角对等边）；②根据推导过程体现了转化的数学思想方法，故选：A ；任务二：智慧小组的证明过程补充如下：证明：如图2，在∠BCA 的内部，作∠BCF=∠B ，CF 交AB 于点F ．则CF=BF ，（等边对等角）在△ACF 中，AF+CF ＞AC ，∴AF+BF ＞AC ，∴AB ＞AC ；同理，如图，在∠ABC 的内部，作∠ABG=∠A ，BG 交AC 于点G ，如图，则AG=BG在△BCG 中，BG+CG ＞BC ，∴BG+CG ＞BC ，∴AC ＞BC∴AB ＞AC ＞BC ．任务三：①∵AB ＞BC ，∴∠C ＞∠A ，错误；②∵在△ABC 中，AB ＞BC ＞AC ，∠C=89°，∴∠C ＞∠A ＞∠B ，又∠C=89°＜90°，∴△ABC 是锐角三角形，正确；③∵Rt △ABC 中，∠B=90°，则最长边是斜边AC ，正确；④∵在△ABC 中，∠A=55°，∠B=70°，∴∠C=180°﹣∠A ﹣∠B=180°﹣55°﹣70°=55°，∴∠A=∠C∴AB=BC ，正确，故答案为：②③④．【点睛】本题考查三角形的边与角之间的不关系的推导及其应用，涉及三角形的外角性质、等腰三角形的等角对等边性质、三角形的内角和定理、判断三角形的形状、命题的证明等知识，掌握在一个三角形中，大角对大边，小角对小边这一性质的推导过程，会利用转化的思想进行命题的证明是解答的关键．24．（1）见解析；（2）126BFC ∠=︒．【分析】（1）由SAS 证明ABD ACE △≌△即可；（2）先由全等三角形的性质的20ACE ABD ∠=∠=︒再由等腰三角形的性质和三角形内角和定理得47ABC ACB ∠=∠=︒，则27FBC FCB ∠=∠=︒，即可得出答案．【详解】（1）证明∵BAE CAD ∠=∠∴BAD CAE ∠=∠，在ABD △和ACE △中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴ABD ACE SAS △≌△()；（2）解：∵ABD ACE △≌△，∴20ACE ABD ∠=∠=︒，∵AB ＝AC ， ∴1(18086)472ABC ACB ∠=∠=︒-︒=︒， ∴472027FBC FCB ∠=∠=︒-︒=︒，∴1802727126BFC ∠=︒-︒-︒=︒．【点睛】本题主要考查全等三角形的性质及判定、等腰三角形的性质，熟练掌握全等三角形的判定和性质是解题的关键．25．（1）∠ADE =20°；（2）△ADF 是等腰三角形，证明见解析；（3）AB=16．【分析】（1）根据等腰三角形的性质和三角形内角和定理求出∠B 和∠C ，求出∠BDE ，即可求出答案；（2）根据垂直平分线的性质定理和等边对等角可求得∠FDC ，再根据三线合一和直角三角形两锐角互余可求得∠DAF 和∠ADF 得出它们相等即可得出△ADF 为等腰三角形；（3）可求得∠C=30°根据30°角所对直角边是斜边的一般可得FC ，可证明△ADF 为等边三角形即可求得AF ，从而求得AC ，继而求得AB ．【详解】解：（1）∵在△ABC 中，AB=AC ，∠BAC=100°，∴∠B=∠C=12×（180°-∠BAC ）=40°， ∵BD=BE ，∴∠BDE=∠BED=12×（180°-∠B ）=70°， ∵在△ABC 中，AB=AC ，AD 是BC 边上的中线，∴AD ⊥BC ，∴∠ADB=90°，∴∠ADE=∠ADB-∠BDE=20°；（2）△ADF 是等腰三角形，理由是：∵CD 的垂直平分线MF 交AC 于F ，交BC 于M ，∴DF=CF ，∵∠C=40°，∴∠FDC=∠C=40°，∵AD ⊥BC ，∴∠ADC=90°，∴∠DAF=90°-∠C=50°，∴∠ADF=50°，∴∠DAF=∠ADF ，∴AF=DF ，∴△ADF 是等腰三角形；（3）∵∠BAC =120°，AB=AC ，∴∠B=∠C=12×（180°-∠BAC ）=30°，又∵AD 是BC 边上的中线，∴AD ⊥BC ，∴∠DAC=90°-∠C=60°，∵CD 的垂直平分线MF ，∴∠FMC=90°，DF=FC ，∴∠FDC=∠C=30°，∴∠ADF=∠ADC-∠FDC=60°，∠AFD=∠C+∠FDC=60°，∴△ADF 为等边三角形，AF=DF=FC ，∵MF=4，∴FC=2MF=8，∴AF= 8，∵AC=AF+CF=8+8=16，∵AB=AC ，∴AB=16．【点睛】本题考查了线段垂直平分线性质，等边三角形的性质和判定，含30°角的直角三角形的性质，等腰三角形的性质等知识点，能综合运用定理进行推理是解此题的关键．26．（1）BON ∠；AOW ∠；（2）①见解析；②24︒，见解析【分析】（1）根据互余，平角的定义判断即可；（2）①作出角平分线即可；②利用角平分线的定义求出∠POE ，再求出∠NOP 即可解决问题；【详解】（1）90180AOB WOE ︒∠=∠=︒，，90AOW BOE ∴∠+∠=︒，90NOB BOE ∠+∠=︒， ∴图中与∠BOE 互余的角是BON ∠和AOW ∠；故答案为：BON ∠和AOW ∠；（2）①如图所示：②132AOE ∠=︒，OP 平分AOE ∠，1132662POE ∴∠=⨯︒=︒， 90NOE ∠=︒，906624NOB ∴∠=︒-︒=︒，∴点P 在点O 北偏东24︒的方向上；【点睛】本题考查了作图-应用与设计，角平分线的定义，方向角等知识解题的关键是理解题意，灵活运用所学知识解决问题；。

北师大版八下数学《三角形的证明》单元测试1(含答案)

第一章三角形的证明单元测试一、填空题1.一个等腰三角形有一角是70°，则其余两角分别为_________.2.一个等腰三角形的两边长为5和8，则此三角形的周长为_________.3.如图1，△ABC中，∠C=90°，AM平分∠CAB，CM=20 cm，则点M到AB 的距离是_________.图1 图24.如图2，等边△ABC中，F是AB中点，EF⊥AC于E，若△ABC的边长为10，则AE=_________，AE∶EC=_________.5.如图3，△ABC中，DE垂直平分BC，垂足为E，交AB于D，若AB=10 cm，AC=6 cm，则△ACD的周长为_________.图3 图46.如图4，∠C=90°，∠ABC=75°，∠CDB=30°，若BC=3 cm，则AD=___ cm.7.如图5，B在AC上，D在CE上，AD=BD=BC，∠ACE=25°，∠ADE=_________.图5图68.等腰直角三角形一条边长是1 cm ，那么它斜边上的高是_________ cm. 9.如图6，在∠AOB 的两边OA 、OB 上分别取OQ =OP ，OT =OS ，PT 和QS 相交于点C ，则图中共有_________对全等三角形.10.等腰三角形两腰上的高相等，这个命题的逆命题是________________，这个逆命题是_________命题.11.三角形三边分别为a 、b 、c ，且a 2－bc =a (b －c )，则这个三角形（按边分类）一定是_________三角形.二、选择题12.等边三角形的高为23，则它的边长为（） A.4B.3C.2D.513.等腰三角形的顶角是n °，那么它的一腰上的高与底边的夹角等于（）A.290 nB.90－2nC.2n D.90°－n °14.下列由线段a 、b 、c 组成的三角形，不是直角三角形的是（） A.a =3，b =4，c =5 B.a =1，b =34，c =35 C.a =9，b =12，c =15D.a =3，b =2，c =515.直角三角形的三边长为连续自然数，则它的面积为（） A.6B.7.5C.10D.1216.△ABC 中，∠A ∶∠B ∶∠C =1∶2∶3，最小边BC =4 cm ，最长边AB 的长是（）A.5 cmB.6 cmC.5 cmD.8 cm17.如图7，△ABC 中，AB =AC ，BC =BD ，AD =DE =EB ，则∠A 的度数为（）图7A.55°B.45°C.36°D.30°18.等腰△ABC 中，AC =2BC ，周长为60，则BC 的长为（） A.15B.12C.15或12D.以上都不正确19.直角三角形两直角边分别是5 cm 、12 cm ，其斜边上的高是（） A.13 cmB.1330cmC.1360cmD.9 cm20.直角三角形中，以直角边为边长的两个正方形的面积分别为30和20，则以斜边为边长的正方形的面积为（）A.25B.50C.100D.6021.等腰三角形的底边为a ，顶角是底角的4倍，则腰上的高是（） A.23a B.33 a C.63a D.21a 22.若一个三角形的三条高线交点恰好是此三角形的一个顶点，则此三角形一定是（）A.等腰三角形B.等边三角形C.等腰直角三角形D.直角三角形23.等腰三角形ABC 中，∠A =120°，BC 中点为D ，过D 作DE ⊥AB 于E ，AE =4cm，则AD等于（）A.8 cmB.7 cmC.6 cmD.4 cm24.下列说法中，正确的是（）A.两边及一对角对应相等的两个三角形全等B.有一边对应相等的两个等腰三角形全等C.两边及其中一边上的中线对应相等的两个三角形全等D.两边及其中一边上的高对应相等的两个三角形全等25.如图8，AB⊥CD，△ABD、△BCE都是等腰三角形，如果CD=8，BE=3，那么AC长为（）图8A.8B.5C.3D.3426.将两个全等的有一个角为30°的直角三角形拼成下图9，其中两条长直角边在同一直线上，则图中等腰三角形的个数是（）图9A.4B.3C.2D.127.下列定理中逆定理不存在的是（）A.角平分线上的点到这个角的两边距离相等B.在一个三角形中，如果两边相等，那么它们所对的角也相等C.同位角相等，两直线平行D.全等三角形的对应角相等*28.已知一个直角三角形的周长是4+26，斜边上中线长为2，则这个三角形的面积为（）A.5B.2C.45D.1三、解答题29.已知：如图10，AB =AC ，DE ∥AC ，求证：△DBE 是等腰三角形.图1030.已知：如图11，在Rt △ABC 中，∠C =90°，∠BAD =21∠BAC ，过点D 作DE ⊥AB ，DE 恰好是∠ADB 的平分线，求证：CD =21DB .图1131.已知三角形的三边分别是n 2+n ，n +21和n 2+n +21(n ＞0)，求证：这个三角形是直角三角形.32.如图12，△ABC 中，AB =AC ，∠1=∠2，求证：AD 平分∠BA C.图1233.如图13，以等腰直角三角形ABC的斜边AB与边面内作等边△ABD，连结DC，以DC当边作等边△DCE，B、E在C、D的同侧，若AB=2，求BE的长.图13*34.①在△ABC中，AB=AC，AB的垂直平分线交AC于N，交BC的延长线于M，∠A=30°，求∠NMB的大小.②如果将①中的∠A的度数改为70°，其余条件不变，再求∠NMB的大小.③你感到存在什么样的规律性？试证明.（请同学们自己画图）④将①中的∠A改为钝角，对这个问题规律性的认识是否需要加以修改？参考答案一、1.55°，55°或70°，40° 2.18或21 3.20 cm 4.251∶3 5.16 cm 6.6 7.75° 8.22或219.4 10.如果一个三角形两边上的高相等，那么这个三角形是等腰三角形真 11.等腰二、12.A 13.C 14.D 15.A 16.D 17.B 18.B 19.C 20.B 21.D 22.D 23.A 24.C 25.D 26.B 27.D 28.B三、29.略 30.略 31.略 32.略 33.134.①15° ②35° ③AB 的垂直平分线与底边BC 所夹的锐角等于∠A 的一半 ④不需要修改。

(必考题)初中数学八年级数学下册第一单元《三角形的证明》检测卷(有答案解析)

一、选择题1．如图，在Rt ABC △中，90,ACB AC BC ∠=︒≠．点P 是直角边所在直线上一点，若PAB △为等腰三角形，则符合条件的点P 的个数最多为（）A ．3个B ．6个C ．7个D ．8个2．如图，在△ABC 中，AB =AC ，∠BAC =64°，∠BAC 的平分线与AB 的垂直平分线交于点O ，点E 、F 分别在BC 、AC 上，点C 沿EF 折叠后与点O 重合，则∠BEO 的度数是（）A ．26°B ．32°C ．52°D ．58°3．如图，在ABC ∆中，AB AC =，120BAC ∠=︒，AD 是ABC ∆的中线，且6AD =，AE 是BAD ∠的角平分线，//DF AB 交AE 的延长线于点F ，则DF 的长为（）A ．3B ．4C ．5D ．6 4．如图，在△ABC 中，∠ACB ＝90°，CD ⊥AB ，垂足为D ，若∠A ＝30°，BD ＝1，则AD 的长为（）A ．3B ．2C ．3D ．235．如图，在平面直角坐标系中，点A 1在x 轴的正半轴上，B 1在第一象限，且△OA 1B 1是等边三角形．在射线OB 1上取点B 2，B 3，…，分别以B 1B 2，B 2B 3，…为边作等边三角形△B 1A 2B 2，△B 2A 3B 3，…使得A 1，A 2，A 3，…在同一直线上，该直线交y 轴于点C ．若OA 1＝1，∠OA 1C ＝30°，则点B 9的横坐标是（）A ．2552B ．5112C ．256D ．51326．在下列命题中，真命题是（）A ．同位角相等B ．到线段距离相等的点在线段垂直平分线上C ．三角形的外角和是360°D ．角平分线上的点到角的两边相等7．如图，在ABC 中，以点A 为圆心，AC 的长为半径作弧，与BC 交于点E ，分别以点E 和点C 为圆心、大于12EC 的长为半径作弧，两弧相交于点P ，作射线AP 交BC 于点D ．若45B ∠=︒，2C CAD ∠=∠，则BAE ∠的度数为（）A ．15︒B ．25︒C ．30D ．35︒ 8．如图，ABC 为等边三角形，BO 为中线，延长BA 至D ，使AD AO =，则DOB ∠的度数为（）A ．105︒B ．120︒C ．135︒D ．150︒ 9．如图AD 是ABC 的角平分线，DE AB ⊥于E ，点F ，G 分别是AB ，AC 上的点，且DF DG =，ADG 与DEF 的面积分别是10和3，则ADF 的面积是（）A ．4B ．5C ．6D ．710．如图，ABC ∆中，AB AC =，3BC =，6ABC S ∆=，AD BC ⊥于点D ，EF 是AB 的垂直平分线，交AB 于点E ，交AC 于点F ，在EF 上确定一点P ，使PB PD +最小，则这个最小值为（）A ．3.5B ．4C ．4.5D ．511．如图，每个小正方形的边长都相等，A，B，C是小正方形的顶点，则ABC∠的度数为（）A．45︒B．50︒C．55︒D．60︒12．如图，以△ABC的边AB、AC为边向外作等边△ABD与等边△ACE，连接BE交DC于点F，下列结论：①CD=BE；②FA平分∠DFE；③∠BFC=120°；④AFEEFCS AFS FC∆∆=．其中正确的有（）A．4个B．3个C．2个D．1个二、填空题13．在平面直角坐标系中，一块等腰直角三角板如图放置，其中(2,0)A，(0,1)B，则点C的坐标为_______．14．如图，己知等边△ABC的边长为8cm，∠A＝∠B＝60°，点D为边BC上一点，且BD＝3cm．若点M在线段CA上以2cm/s的速度由点C向点A运动，同时，点N在线段AB上由点A向点B运动，△CDM与△AMN全等，则点N的运动速度是______15．如图，在△ABC中，∠ACB＝90°，AC＝6，AB＝10，点O是AB边的中点，点P是射线AC上的一个动点，BQ∥CA交PO的延长线于点Q，OM⊥PQ交BC边于点M．当CP＝1时，BM 的长为_____．16．已知C ，D 两点在线段AB 的垂直平分线上，且∠ACB ＝50°，∠ADB ＝86°，则∠CAD 的度数是_____．17．如图，∠MON =33°，点P 在∠MON 的边ON 上，以点P 为圆心，PO 为半径画弧，角OM 于点A ，连接AP ，则∠APN =____．18．如图，在ABC ∆中，AB AC =，36BAC ∠=︒，BD 是ABC ∠的平分线，交AC 于点D ，E 是AB 的中点．连接ED 并延长，交BC 的延长线于点F ，连接AF ．写出图中三角形中所有的等腰三角形______．19．如图，已知∠MON=30°，点123,,A A A ...在射线ON 上，点123,,B B B ...在射线OM 上，112233334,,A B A A B A A B A ∆∆∆..均为等边三角形，若11OA =，则202020202021A B A ∆的边长为_______．20．如图，点M 是等边△ABC 的边BC 的中点，AB =4，射线CD BC ⊥于点C ，点P 是射线CD 上一动点，点N 是线段AB 上一动点，当MP +NP 的值最小时，则AN 长为____．三、解答题21．如图，在ABC 中，AB BC =，90ABC ∠=︒，点E 在BC 上，点F 在AB 的延长线上，且AE CF =．（1）求证：ABE CBF △≌△；（2）若75ACF ∠=︒，求EAC ∠的度数．22．如图，在△ABC 中，∠BAC ＝62°，∠B ＝78°，AC 的垂直平分线交BC 于点D ．（1）求∠BAD 的度数；（2）若AB ＝8，BC ＝11，求△ABD 的周长．23．问题提出（1）如图1，在直角△ABC 中，∠BAC =90°，AC =12，AB =5，若P 是BC 边上一动点，连接AP ，则AP 的最小值为______．问题探究（2）如图2，在等腰直角△ABC 中，∠ABC =90°，AC =m ，求边AB 的长度（用含m 的代数式表示）．问题解决（3）在图3中，若AC =8，点D 是BC 边的中点，若P 是AB 边上一动点，试求PD 2AP 的最小值．24．如图，在△ABC中，AC=BC，∠ACB=90°，延长CA至点D，延长CB至点E，使AD=BE，连接AE，BD，交点为O．（1）求证：OB=OA；（2）连接OC，若AC=OC，则∠D的度数是度．25．如图1，将三角形纸片ABC，沿AE折叠，使点B落在BC上的F点处；展开后，再沿BD折叠，使点A恰好仍落在BC上的F点处（如图2），连接DF．（1）求∠ABC的度数；（2）若△CDF为直角三角形，且∠CFD=90°，求∠C的度数；（3）若△CDF为等腰三角形，求∠C的度数．26．如图，点D是△ABC内部的一点，BD＝CD，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F，且BE＝CF．（1）求证：∠DBE＝∠DCF；（2）求证：△ABC为等腰三角形．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】分为三种情况：①BP=AB，②AP=AB，③AP=BP，再求出答案即可．【详解】解：作BC、AC所在直线，然后分别以B、A点为圆心，以AB为半径作圆分别交BC、AC 所在直线于6点，再作AB的垂直平分线与BC所在直线交于2点，总共符合条件的点P的个数最多有8个，故选：B．【点睛】本题考查了等腰三角形的判定，线段垂直平分线的性质．能求出符合的所有情况是解此题的关键．2．C解析：C【分析】连结OB，根据角平分线定义得到∠OAB=32°，再根据等腰三角形的性质得到∠ABC=∠ACB，再根据线段垂直平分线的性质得到OA=OB，则∠OBA=∠OAB，所以得出∠1，由于AB=AC，OA平分∠BAC，根据等腰三角形的性质得OA垂直平分BC，则BO=OC，所以得出∠1=∠2，然后根据折叠的性质得到EO=EC，于是∠2=∠3，再根据三角形内角和定理计算∠OEC，解答即可．【详解】解：连结OB、OC，∵∠BAC=64°，∠BAC的平分线与AB的中垂线交于点O，∴∠OAB=32°，∵AB=AC，∠BAC=64°，∴∠ABC=∠ACB=58°，∵OD垂直平分AB，∴OA=OB，∴∠OBA=∠OAB=32°，∴∠1=58°-32°=26°，∵AB=AC，OA平分∠BAC，∴OA垂直平分BC，∴BO=OC，∴∠1=∠2=26°，∵点C沿EF折叠后与点O重合，∴EO=EC，∴∠2=∠3=26°，∴∠BEO=∠2+∠3=52°，故选择:C．【点睛】本题考查了线段的垂直平分线的性质和等腰三角形的性质,折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．3．D解析：D【分析】根据等腰三角形三线合一的性质可得AD⊥BC，∠BAD=∠CAD，求出∠DAE=∠EAB=30°，根据平行线的性质求出∠F=∠BAE=30°，从而得到∠DAE=∠F，根据等角对等边求出AD=DF，即可求解.【详解】∵AB= AC，AD是△ABC的中线，∴AD⊥BC，∠BAD=∠CAD=12∠BAC=12×120°= 60°，∵AE是∠BAD的角平分线，∴∠DAE=∠EAB=12∠BAD=1260°= 30°，∵DF// AB∴∠F=∠BAE= 30°，∴∠DAE=∠F= 30°，∴AD= DF=6；故答案为:D.【点睛】本题考查的是直角三角形的性质，等腰三角形的性质，平行线的性质，掌握等腰三角形的性质是解题的关键.4．C解析：C【分析】求出∠BCD=30°，根据含30°角的直角三角形的性质求出BC=2，求出AB=4，即可得出答案．【详解】解：∵△ABC中，∠ACB=90°，∠A=30°，∴∠B=60°，∵CD是高，∴∠CDB=90°，∴∠BCD=30°，∵BD=1，∴BC=2BD=2，∵在△ACB中，∠ACB=90°，∠A=30°，∴AB=2BC=4，∴AD=AB-BD=4-1=3，故选：C．【点睛】本题考查了三角形的内角和定理，含30度角的直角三角形的性质的应用，解题的关键是得出BC=2BD和AB=2BC，难度适中．5．B解析：B【分析】利用待定系数法求得两条直线的解析式，根据等边三角形的性质，点的坐标规律，即可求解．【详解】解：∵OA 1=1，∠OA 1C=30︒，∴OC=3，∴点C 的坐标为(0，-，∵A 1、A 2、A 3所在直线过点A 1(1，0)，C (0，，设直线A 1A 2的解析式为y kx =-∴03k =-，∴k =∴直线A 1A 2的解析式为33y x =-， ∵△OA 1B 1为等边三角形，∴点B 1的坐标为(12，∵B 1、B 2、B 3所在直线过点O(0，0)，B 1 (12，2)，同理可求得直线O B 1的解析式为y =，∵△OA 1B 1和△B 1A 2B 2为等边三角形，∴∠B 1OA 1=∠B 2 B 1A 2=60︒，∴B 1A 2∥OA 1，∵B 1 (12，∴A 2的纵坐标为2，则233x =-，解得：52x =，∴点A 2的坐标为(52， ∴B 1A 2=2，同理点B 2的坐标为(32，点B 3的坐标为(72，点B 4的坐标为(152，，总结规律： B 1的横坐标为12， B 2的横坐标为13122+=， B 3的横坐标为171222++=， B 4的横坐标为11512422+++=，，∴B 9的横坐标为1511124816326422+++++++=，故选：B【点睛】本题考查了待定系数法求一次函数的解析式，点的坐标规律，等边三角形的性质，解决本题的关键是寻找点的坐标规律． 6．C解析：C【分析】直接利用同位角的定义及线段垂直平分线的判定、多边形的外角和、角平分线的性质等知识分别判断得出答案．【详解】解：A.同位角相等，错误，是假命题；B.不是到线段距离相等的点在线段垂直平分线上，而是到线段两端点距离相等的点在这条线段的垂直平分线上，是假命题；C.三角形的外角和是360°，是真命题；D.角平分线上的点到角的两边的距离相等，不是角平分线上的点到角的两边相等，是假命题．故选：C ．【点睛】本题主要考查了命题与定理，正确掌握相关定义是解题关键．7．A解析：A【分析】根据作图过程可得，AP是EC的垂直平分线，可得AE＝AC，∠ADB＝∠ADC＝90°，再根据∠B＝45°，∠C＝2∠CAD，即可求出∠CAD的度数，进而即可求解．【详解】解：由作图过程可知：AP是EC的垂直平分线，也是∠CAE的角平分线，∴AE＝AC，∠ADB＝∠ADC＝90°，∵∠B＝45°，∴∠BAD＝45°，∵∠C＝2∠CAD，∴3∠CAD＝90°，∴∠CAD＝30°，∴∠EAD＝30°，=45°-30°=15°．∴BAE故选：A．【点睛】本题考查了作图−基本作图，直角三角形的性质，解决本题的关键是掌握基本作图方法．8．B解析：B【分析】由△ABC为等边三角形，可求出∠BOA=90°，由△ADO是等腰三角形求出∠ADO=∠AOD=30°，即可求出∠BOD的度数．【详解】解：∵△ABC为等边三角形，BO为中线，∴∠BOA＝90°，∠BAC＝60°∴∠CAD＝180°﹣∠BAC＝180°﹣60°＝120°，∵AD＝AO，∴∠ADO=∠AOD=30°，∴∠BOD＝∠BOA+∠AOD＝90°+30°＝120°，故选：B．【点睛】本题主要考查了等边三角形的性质及等腰三角形的性质，解题的关键是熟记等边三角形的性质及等腰三角形的性质．9．A解析：A【分析】过点D作DH⊥AC于H，根据角平分线上的点到角的两边距离相等可得DF=DH，然后利用“HL”证明Rt△DEF和Rt△DGH全等，根据全等三角形的面积相等可得S△EDF=S△GDH，然后根据S △ADF =S △ADH 列出方程求解即可．【详解】解：如图，过点D 作DH ⊥AC 于H ，∵AD 是△ABC 的角平分线，DF ⊥AB ，DH ⊥AC∴DF=DH ，在Rt △DEF 和Rt △DGH 中，DE DG DF DH ⎧⎨⎩＝＝， ∴Rt △DEF ≌Rt △DGH （HL ），∴S △EDF =S △GDH =3，同理Rt △ADF ≌Rt △ADH ，∴S △ADF =S △ADH =ADG GDH △△S -S =10-3=7∴S △AED = =7-3=4ADF EDF SS -，故选：A ．【点睛】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，作辅助线构造出全等三角形并利用角平分线的性质是解题的关键． 10．B解析：B【分析】根据三角形的面积公式得到AD=4，由EF 垂直平分AB ，得到点A ，B 关于直线EF 对称，于是得到AD=PB+PD 的最小值，即可得到结论．【详解】解：∵AB=AC ，BC=3，S △ABC =6，AD ⊥BC 于点D ，∴AD=4，∵EF 垂直平分AB ，∴点A ，B 关于直线EF 对称，∴EF 与AD 的交点P 即为所求，如图，连接PB ，此时PA=PB ，PB+PD=PA+PD=AD ，AD=PB+PD 的最小值，即PB+PD 的最小值为4，故选：B ．【点睛】本题考查了轴对称-最短路线问题，线段的垂直平分线的性质，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．11．A解析：A【分析】由勾股定理及其逆定理可得三角形ABC是等腰直角三角形，从而得到∠ABC 的度数．【详解】解：如图，连结AC，由题意可得：222222+==+==+=AB AC BC1310,125,125,∴AC=BC，222=+，AB AC BC∴△ABC是等腰直角三角形，∴∠ABC=∠BAC=45°，故选A ．【点睛】本题考查勾股定理的应用，熟练掌握勾股定理及其逆定理、等腰直角三角形的性质是解题关键．12．A解析：A【分析】过点A作AM⊥CD于M，AN⊥BE于N，过点C作CH⊥BE于H，证明△ADC≌△ABE，可判断①，再证明AM=AN，结合AM⊥CD于M，AN⊥BE于N，可判断②，证明∠ACF+∠BEC+∠ACE=120°，结合三角形的外角的性质可判断③，证明∠FAN=∠FCH=30°，利用含30的直角三角形的性质与勾股定理可得： 33,,22AN AF HC FC == 再利用三角形的面积公式可判断④．【详解】解：过点A 作AM ⊥CD 于M ，AN ⊥BE 于N ，过点C 作CH ⊥BE 于H ，∵△ABD ，△ACE 都是等边三角形，∴AD =AB ，AE =AC ，∠DAB =∠EAC =60°，∴∠DAC =∠BAE ．在△ADC 和△ABE 中，AD AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩，∴△ADC ≌△ABE （SAS ），∴CD =BE ，∠AEB =∠ACD ，故①正确∵△ADC ≌△ABE ，∴AM =AN ．∵AM ⊥CD 于M ，AN ⊥BE 于N ，∴AF 平分∠DFE ，故②正确．∵∠AEB =∠ACD ，∴∠AEC +∠ACE =120°=∠AEB +∠BEC +∠ACE ，∴∠ACF +∠BEC +∠ACE =120°，∴∠BFC =∠ACF +∠BEC +∠ACE =120°，故③正确，∴∠DFE =120°， ∴∠DFA =∠EFA =60°=∠CFE ．∵AN ⊥BE ，CH ⊥EF ，∴∠FAN =∠FCH =30°， ∴22222,3,2,3,AF FN AN AF FN FN FC FH HC FC FH FH ==-===-= ∴33,,22AN AF HC FC ==∴13 22.132AEFEFCEF AN AFS AN AFS CH FCEF CH FC⨯⨯====⨯⨯故④正确．故选：A．【点睛】本题考查的是全等三角形的判定与性质，等边三角形的性质，角平分线的判定与性质，勾股定理的应用，掌握以上知识是解题的关键．二、填空题13．【分析】如图过点C作CH⊥x轴于H证明△AHC≌△BOA（AAS）可得结论【详解】解：如图过点C作CH⊥x轴于H∵∠AHC=∠CAB=∠AOB=90°∴∠BAO+∠CAH=90°∠CAH+∠ACH=解析：(3,2)【分析】如图，过点C作CH⊥x轴于H．证明△AHC≌△BOA（AAS），可得结论．【详解】解：如图，过点C作CH⊥x轴于H．∵∠AHC=∠CAB=∠AOB=90°，∴∠BAO+∠CAH=90°，∠CAH+∠ACH=90°，∴∠ACH=∠BAO，在△AHC和△BOA中，AHC AOBACH OABAC AB∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AHC≌△BOA（AAS），∴AH=OB，CH=OA，∵A（2，0），B（0，1），∴OA=CH=2，OB=AH=1，∴OH=OA+AH=3，∴C（3，2）．故答案为：（3，2）．【点睛】本题考查等腰直角三角形的性质，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．14．cm/s或cm/s【分析】由于∠C=∠A所以当△CDM与△AMN全等时分两种情况：①△CDM≌△AMN；②△CDM≌△ANM根据全等三角形的对应边相等求出AN再根据速度=路程÷时间求解即可【详解】解解析：cm/s或52cm/s【分析】由于∠C=∠A，所以当△CDM与△AMN全等时，分两种情况：①△CDM≌△AMN；②△CDM≌△ANM．根据全等三角形的对应边相等求出AN，再根据速度=路程÷时间求解即可．【详解】解：设点M、N的运动时间为ts，则CM=2tcm．∵三角形ABC是等边三角形，∴∠C=∠A=60°，∴当△CDM与△AMN全等时，分两种情况：①如果△CDM≌△AMN，那么AN=CM=2tcm，∴点N的运动速度是2tt=2（cm/s）；②如果△CDM≌△ANM，那么CM=AM=12AC=4cm，AN=CD=BC-BD=5cm，∴点M的运动时间为：42=2（s），∴点N的运动速度是52cm/s．综上可知，点N的运动速度是2或52cm/s．故答案为：2 cm/s或52cm/s．【点睛】本题考查了全等三角形的对应边相等的性质，等边三角形的性质，路程、速度与时间之间的关系，进行分类讨论是解题的关键．15．5或1【分析】如图设BM=x首先证明BQ=AP分两种情形利用勾股定理构建方程求解即可【详解】解：如图设BM＝x在Rt△ABC中AB＝10AC＝6∴BC＝＝＝8∵QB∥AP∴∠A＝∠OBQ∵O是AB的解析：5或1【分析】如图，设BM=x，首先证明BQ=AP，分两种情形，利用勾股定理，构建方程求解即可．【详解】解：如图，设BM ＝x ，在Rt △ABC 中，AB ＝10，AC ＝6，∴BC ＝22AB AC -＝22106-＝8，∵QB ∥AP ，∴∠A ＝∠OBQ ，∵O 是AB 的中点，∴OA ＝OB ，在△OAP 和△OBQ 中，A OBQ OA OBAOP BOQ ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△OAP ≌△OBQ （ASA ），∴PA ＝BQ ＝6﹣1＝5，OQ ＝OP ，∵OM ⊥PQ，∴MQ ＝MP ，∴52+x 2＝12+（8﹣x ）2，解得x ＝2.5．当点P 在AC 的延长线上时，同法可得72+x 2＝12+（8﹣x ）2，解得x ＝1，综上所述，满足条件的BM 的值为2.5或1．故答案为：2.5或1．【点睛】本题考查勾股定理，全等三角形的判定和性质，线段的垂直平分线的性质等知识，解题的关键是学会利用参数构建方程解决问题，学会用分类讨论的思想思考问题． 16．18°或112°【分析】分点C 与点D 在线段AB 两侧点C 与点D 在线段AB 同侧两种情况根据线段垂直平分线的性质等腰三角形的性质解答【详解】解：如图∵CD 两点在线段AB 的中垂线上∴CA ＝CBDA ＝DB ∵C解析：18°或112°【分析】分点C 与点D 在线段AB 两侧、点C 与点D 在线段AB 同侧两种情况，根据线段垂直平分线的性质、等腰三角形的性质解答．【详解】解：如图，∵C、D两点在线段AB的中垂线上，∴CA＝CB，DA＝DB，∵CD⊥AB，∴∠ACD＝12∠ACB＝12×50°＝25°，∠ADC＝12∠ADB＝12×86°＝43°，当点C与点D在线段AB两侧时，∠CAD＝180°﹣∠ACD﹣∠ADC＝180°﹣25°﹣43°＝112°，当点C与点D′在线段AB同侧时，∠CAD′＝∠AD′C﹣∠ACD′＝43°﹣25°＝18°，故答案为：18°或112°．【点睛】本题考查的是线段垂直平分线的性质、等腰三角形的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．17．66°【分析】根据等腰三角形的性质可知∠MON=∠PAO再用外角的性质求解即可【详解】解：由作图可知PO=PA∴∠MON=∠PAO=33°∠APN=∠MON+∠PAO=66°故答案为：66°【点睛】解析：66°【分析】根据等腰三角形的性质可知∠MON=∠PAO，再用外角的性质求解即可．【详解】解：由作图可知，PO=PA，∴∠MON=∠PAO=33°，∠APN=∠MON+∠PAO=66°，故答案为：66°．【点睛】本题考查了等腰三角形的性质和外角的性质，解题关键是通过作图得到等腰三角形，依据等腰三角形的性质熟练计算．18．△ABD△BCD△ABC△ACF△ABF【分析】分别求出所有的角度即可求解【详解】解：∵AB=AC∠BAC=36°∴∠ABC=∠ACB=72°△ABC是等腰三角形∵BD是∠ABC 的平分线∴∠ABD=解析：△ABD ，△BCD ，△ABC ，△ACF ，△ABF【分析】分别求出所有的角度，即可求解．【详解】解：∵AB=AC ，∠BAC=36°，∴∠ABC=∠ACB=72°，△ABC 是等腰三角形，∵BD 是∠ABC 的平分线，∴∠ABD=∠CBD=36°=∠BAC ，∴AD=BD ，∠BDC=∠BAC+∠ABD=72°=∠ACB ，∴△ABD 是等腰三角形，BD=BC ，∴△BDC 是等腰三角形，∵AD=BD ，E 是AB 的中点，∴DE 是AB 的中垂线，∴AF=BF ，∴∠ABF=∠BAF=72°，△ABF 是等腰三角形，∴∠CAF=36°=∠AFB ，∴AC=CF ，∴△ACF 是等腰三角形，故答案为：△ABD ，△BCD ，△ABC ，△ACF ，△ABF ．【点睛】本题考查了等腰三角形的判定和性质，掌握等腰三角形的性质是本题的关键． 19．【分析】根据等边三角形的性质等腰三角形的性质以及含角的直角三角形得出得出以此类推进而得到答案【详解】∵是等边三角形∴∴∵∴∴∵∴∴∵是等边三角形同理可得：∴∴以此类推∴的边长故答案为：【点睛】本题考解析：20192【分析】根据等边三角形的性质、等腰三角形的性质以及含30角的直角三角形得出22122A B B A =，得出331244A B B A ==，441288A B B A ==，551216A B B A =，以此类推，进而得到答案．【详解】∵112A B A ∆是等边三角形，∴1121A B A B =，11211212160A B A B A A A A B ∠=∠=∠=︒，∴11120OA B ∠=︒，∵30MON ∠=︒，∴11111801801203030OB A OA B MON ∠=︒-∠-∠=︒-︒-︒=︒，∴1211112306090OB A OB A A B A ∠=∠+∠=︒+︒=︒，∵1130MON OB A ∠=∠=︒，∴1111OA A B ==，∴211A B =，∵233A B A ∆、334A B A ∆是等边三角形，同理可得：∴22122A B B A =，33232A B B A =，∴3123312242A B B A -===，4134412282A B B A -===，51455122162A B B A -===，以此类推，∴202020202021A B A ∆的边长20192=，故答案为：20192．【点睛】本题考查了规律性-图形的变化类，等边三角形的性质、等腰三角形的性质，30角的锐角三角函数，解答本题的关键是通过观察图形的变化寻找出规律．20．1【分析】作点M 关于直线CD 的对称点G 过G 作于N 交CD 与P 再根据等边三角形的性质计算即可；【详解】作点M 关于直线CD 的对称点G 过G 作于N 交CD 与P ∵△ABC 是等边三角形AB=4∴AB=BC=AC=4解析：1【分析】作点M 关于直线CD 的对称点G ，过G 作GN AB ⊥于N ，交CD 与P ，再根据等边三角形的性质计算即可；【详解】作点M 关于直线CD 的对称点G ，过G 作GN AB ⊥于N ，交CD 与P ，∵△ABC 是等边三角形，AB =4，∴AB=BC=AC=4，30G ∠=︒，∵M 是BC 的中点，∴2BM CM CG ===，∴6BG =，在Rt △BNG 中，30G ∠=︒，6BG =，∴3BN =，∴431AN =-=；故答案是1．【点睛】本题主要考查了轴对称最短路径问题，准确计算是解题的关键．三、解答题21．（1）见详解；（2）15°【分析】（1）由AB ＝CB ，∠ABC ＝90°，AE ＝CF ，即可利用HL 证得Rt △ABE ≌Rt △CBF ；（2）由AB ＝CB ，∠ABC ＝90°，即可求得∠CAB 与∠ACB 的度数，即可得∠FCB 的度数，又由Rt △ABE ≌Rt △CBF ，即可求得∠EAB 的度数，再得出∠EAC 的度数即可．【详解】（1）证明：∵∠ABC ＝90°，∴△ABE 与△CBF 为直角三角形．∵在Rt △ABE 与Rt △BCF 中，AB BC AE CF⎧⎨⎩＝＝， ∴Rt △ABE ≌Rt △CBF （HL ）；（2）∵AB ＝BC ，∠ABC ＝90°，∴∠BAC ＝∠ACB ＝45°，∵∠ACF ＝75°，∴∠FCB ＝30°，∵Rt △ABE ≌Rt △CBF ，∴∠EAB ＝∠FCB ＝30°，∴∠EAC ＝45°-30°=15°．【点睛】此题考查了直角三角形全等的判定与性质，等腰直角三角形的性质，解题的关键是正确寻找全等三角形全等的条件，属于中考常考题型．22．（1）22°；（2）19．【分析】（1）利用三角形内角和求得∠C ＝40°，利用垂直平分线的性质，求得∠DAC ＝40°，最后计算∠BAD 的度数即可；（2）利用周长的定义，垂直平分线的性质计算即可．【详解】解：（1）∵∠BAC ＝62°，∠B ＝78°，∴∠C ＝180°﹣∠BAC ﹣∠B ＝180°﹣62°﹣78°＝40°，∵DE 垂直平分AC ，∴AD ＝CD ，∴∠CAD ＝∠C ＝40°，∴∠BAD ＝∠BAC ﹣∠CAD ＝62°﹣40°＝22°；（2）∵AD ＝CD ，AB ＝8，BC ＝11，∴△ABD 的周长＝AB+AD+BD ＝AB+CD+BD ＝AB+BC ＝8+11＝19．【点睛】本题考查了三角形的内角和定理，线段垂直平分线的性质，熟练运用定理和性质是解题的关键．23．（1）6013；（2）AB =22m ；（3）DP +22PA 的最小值为6 【分析】（1）过A 作AE ⊥CB 于E ，根据点到直线的距离垂线段最短，则AE 即为所求，根据勾股定理求出BC ，再利用等积面积法即可求出AE ，即可解答（2）利用等腰三角形性质，再利用勾股定理即可解答（3）连接PD ，作PE ⊥AC 于点E ，作点D 关于AB 的对称点D ，连接PD ’，则PD PD '=．作D F '⊥AC 于点F ，PD +PE =PD '+PE ≥D F '，当且仅当D 、P 、F 三点共线时，PD +PE 最短，即PF 的长，利用勾股定理求出BC 的长，即可得到D C '的长，再利用勾股定理即可求得D F '的长，即可解答【详解】解：（1）如图1，过A 作AE ⊥CB 于E ，在Rt △ABC 中，∵∠BAC =90°，AB =5，AC =12，∴BC 2212513+=∵1111512132222ABC S AB AC BC AE AE =⋅=⋅=⨯⨯=⨯⨯△， ∴AE =6013（2）∵∠ABC =90°，∴AB 2+BC 2=AC 2，∵AB =AC ，AC =m∴2AB 2=m 2，∴AB 2 （3）如图3，连接PD ，作PE ⊥AC 于点E ，由（2）得PE =22AP ∴PD +22PA =PD +PE 作点D 关于AB 的对称点D ，连接PD '，则PD =PD '．作D F '⊥AC 于点F ， PD +PE =PD ' +PE ≥D F '，当且仅当D 、P 、F 三点共线时，PD +PE 最短，∵AC =8，∠A =∠C =45°∴BC =28422= ∵D 是BC 中点，∴BD =DC =22∵点D 与点D 关于直线AB 对称，∴D B '=22即CD '=62又∵D F '⊥AC ，∠C =45°，∴D F FC '=222CD D F FC D F '''=+=∴D F '226= 22PD AP +的最小值为6．【点睛】本题考查了勾股定理，等腰三角形的性质，以及垂线段最短求线段和最小值，知道线段最短是点的位置并能确定出最小值时点的位置是解题关键．24．（1）见解析；（2）22.5【分析】（1）根据全等三角形的判定和性质得出△ABD ≌△BAE ，进而得出OB=OA ；（2）根据全等三角形的判定和性质以及三角形内角和解答．【详解】证明：（1）∵AC=BC ，∠ACB=90°，∴∠ABC=∠BAC=45°．∴∠EBA=∠DAB=135°．在△ABD 与△BAE 中，135BE AD EBA DAB AB AB =⎧⎪∠=∠=︒⎨⎪=⎩，∴△ABD ≌△BAE （SAS ），∴∠DBA=∠EAB ，∴OB=OA ；（2）由（1）得：OB=OA ，在△OBC 与△OAC 中，OB OA OC OC BC AC =⎧⎪=⎨⎪=⎩，∴△OBC ≌△OAC （SSS ），∴∠OCB=∠OCA=12∠ACB=12×90°=45°， ∵AC=BC ，AC=OC ，∴OC=BC ， ∴∠CBO=∠COB 1801804567.522OCB ︒︒︒︒-∠-===，在Rt △BCD 中，∠D=180°-90°-∠CBO=22.5°．故答案为：22.5．【点睛】本题考查了全等三角形的判定和性质，等腰三角形的判定和性质，关键是根据全等三角形的判定和性质解答．25．（1）60°；（2）30°；（3）20°或40°．【分析】（1）由折叠的性质可知△ABF 是等边三角形，即可得出结论；（2）根据折叠的性质及三角形内角和定理即可得出结论；（3）根据折叠的性质、三角形外角的性质及等腰三角形的性质表示出∠AFD ，根据平角的定义表示出∠DFC ，然后分三种情况讨论即可得出结论．【详解】解：（1）由折叠的性质可知：AB=AF，BA=BF，∴AB=BF=AF，∴△ABF是等边三角形，∴∠ABC=∠AFB=60°；（2）∵∠CFD=90°，∴∠BFD=90°．由折叠的性质可知：∠BAD=∠BFD，∴∠BAC=∠BAD=90°，∴∠C=180°-∠BAC-∠ABC=180°-90°-60°=30°；（3）设∠C=x°．由折叠的性质可知，AD=DF，∴∠FAD=∠AFD．∵∠AFB=∠FAD+∠C，∴∠FAD=∠AFB-∠C=60°-x，∴∠AFD=60°-x，∴∠DFC=180°-∠AFB-∠AFD=180°-60°-（60°-x）=60°+x．∵△CDF为等腰三角形，∴分三种情况讨论：①若CF=CD，则∠CFD=∠CDF，∴60°+x+60°+x+x=180°，解得：x=20°；②若DF=DC，则∠DFC=∠C，∴60°+x=x，无解，∴此种情况不成立；③若DF=FC，则∠FDC=∠C=x，∴60°+x+x+x=180°，解得：x=40°．综上所述：∠C的度数为20°或40°．【点睛】本题考查了等边三角形的判定与性质，等腰三角形的判定与性质，折叠的性质．分三种情况讨论是解答本题的关键．26．(1)见解析(2)见解析【分析】（1）根据HL可证明Rt△DBE≌Rt△DCF；（2）由全等三角形的性质得出∠EBD＝∠FCD，由等腰三角形的性质得出∠DBC＝∠DCB，则可得出结论．【详解】证明：（1）∵DE⊥AB，DF⊥AC，∴∠BED＝∠CFD＝90°．在Rt△BDE和Rt△CDF中，BE CF BD CD =⎧⎨=⎩， ∴Rt △BDE ≌Rt △CDF （HL ）；（2）∵Rt △DBE ≌Rt △DCF ，∴∠EBD ＝∠FCD ，∵BD ＝CD ，∴∠DBC ＝∠DCB ，∴∠DBC ＋∠EBD ＝∠DCB ＋∠FCD ，即∠ABC ＝∠ACB ，∴AB ＝AC ．【点睛】本题考查全等三角形的判定和性质，等腰三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．。

2020-2021学年北师大版八年级下册数学第一章三角形的证明单元测试(含解析)

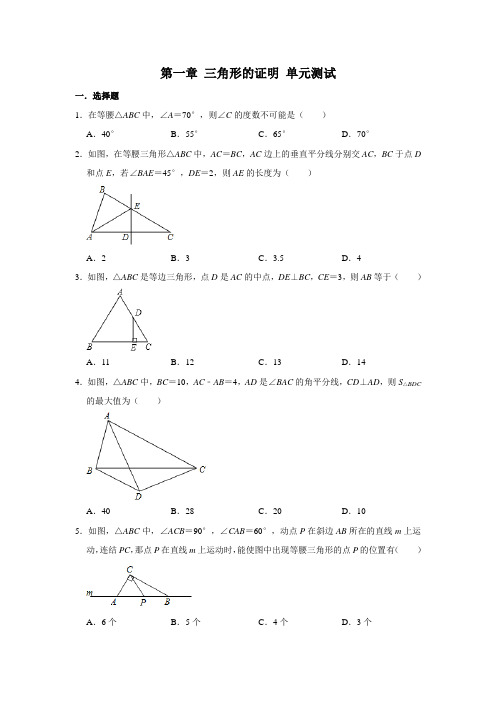
第一章三角形的证明单元测试一．选择题1．在等腰△ABC中，∠A＝70°，则∠C的度数不可能是（）A．40°B．55°C．65°D．70°2．如图，在等腰三角形△ABC中，AC＝BC，AC边上的垂直平分线分别交AC，BC于点D 和点E，若∠BAE＝45°，DE＝2，则AE的长度为（）A．2B．3C．3.5D．43．如图，△ABC是等边三角形，点D是AC的中点，DE⊥BC，CE＝3，则AB等于（）A．11B．12C．13D．144．如图，△ABC中，BC＝10，AC﹣AB＝4，AD是∠BAC的角平分线，CD⊥AD，则S△BDC 的最大值为（）A．40B．28C．20D．105．如图，△ABC中，∠ACB＝90°，∠CAB＝60°，动点P在斜边AB所在的直线m上运动，连结PC，那点P在直线m上运动时，能使图中出现等腰三角形的点P的位置有（）A．6个B．5个C．4个D．3个6．如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝2，则AB等于（）A．2B．3C．4D．67．如图，在Rt△ABC中，∠BAC＝90°，点D在BC上，过D作DF⊥BC交BA的延长线于F，连接AD，CF，若∠CFE＝32°，∠ADB＝45°，则∠B的大小是（）A．32°B．64°C．77°D．87°8．如图，DE是△ABC中AC边的垂直平分线，若BC＝4cm，AB＝5cm，则△EBC的周长为（）A．8cm B．9cm C．10cm D．11cm9．如图，在△ABC中，∠B＝15o，∠C＝30o，MN是AB的中垂线，PQ是AC的中垂线，已知BC的长为，则阴影部分的面积为（）A．B．C．3D．10．如图，在△ABC中，∠BAC＝90°，AD是BC边上的高，BE是AC边的中线，CF是∠ACB的角平分线，CF交AD于点G，交BE于点H，下面说法正确的是（）①△ABE的面积＝△BCE的面积；②∠F AG＝∠FCB；③AF＝AG；④BH＝CH．A．①②③④B．①②③C．②④D．①③二．填空题11．如图，已知△ABC中，AB＝AC，BD⊥AC于D，∠A＝50°，则∠DBC的度数是．12．等腰三角形ABC中，∠A＝4∠B．若∠A为底角，则∠C＝°．13．如图，在△ABC中，AB＝AC．AD是BC边上的中线，点E在边AB上，且BD＝BE．若∠BAC＝100°，则∠ADE的大小为度．14．如图，在Rt△ABC中，∠ABC＝90°，CD⊥AB，垂足为点D，∠DCB＝30°，BD＝1，则AB的长为．15．如图，在Rt△ABC中，∠A＝90°，∠B＝30°，CM平分∠ACB交AB于点M，过点M作MN∥BC交AC于点N，且MN平分∠AMC，若AN＝1，则BC的长为．16．如图，AD⊥BC，BD＝DC，点C在AE的垂直平分线上．若AB＝5cm，BC＝6cm，则AC＝，DE＝．17．如图所示，在△ABC中，DE、MN是边AB、AC的垂直平分线，其垂足分别为D、M，分别交BC于E、N，且DE和MN交于点F．（1）若∠B＝20°，则∠BAE＝；（2）若∠EAN＝40°，则∠F＝；（3）若AB＝8，AC＝9，设△AEN周长为m，则m的取值范围为．18．如图，在△ABC中AB的垂直平分线交AB于点D，交线段BC于点E．BC＝6，AC＝5，则△ACE的周长是．19．如图，AD垂直平分BC于点D，EF垂直平分AB于点F，点E在AC上，BE+CE＝20cm，则AB＝．20．如图，Rt△ABC中，∠C＝90°，∠BAC的角平分线AE与AC的中线BD交于点F，P 为CE中点，连结PF，若CP＝2，S△BFP＝15，则AB的长度为．三．解答题21．如图，在△ABC中，AB＝AC，D是BC边上的中点，∠B＝40°．求：（1）∠ADC的大小；（2）∠BAD的大小．22．如图，△ABC中，∠ABC＝∠ACB，点D、E分别在AB、AC上，DE∥BC，BE，CD 交于点F．（1）求证：DC＝EB；（2）在不添加任何辅助线的情况下，请直接写出图中所有的等腰三角形．23．如图，已知Rt△ABC中，∠ACB＝90°，∠A＝30°，AC边上的垂直平分线DE交AB 于点D，交AC于E．求：（1）∠BCD的度数；（2）若DE＝3，求AB的长．24．如图，在Rt△ABC中，∠ACB＝90°，∠CAB＝2∠B，AD平分∠CAB．（1）求∠CAD的度数；（2）延长AC至E，使CE＝AC，求证：DB＝DE．25．如图，在△ABC中，∠ACB为直角，AB上的高CD及中线CE恰好把∠ACB三等分，若AC＝20，求△ABC的两锐角及AD、DE、EB各为多少？26．（1）如图1，求证：三角形的三条角平分线相交于一点，并且这一点到三边的距离相等；（2）如图2，若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P，连接AP，若∠BAC＝62°，则∠P AC是度．27．如图，已知四边形ABCD中，∠ABC与∠BCD的平分线交于点O，作OE⊥AB于点E，OF⊥CD于点F．求证：OE＝OF．28．如图（1）将三角板ABC与∠DAE摆放在一起，射线AE与AC重合，射线AD在三角形ABC外部，其中∠ACB＝30°，∠B＝60°，∠BAC＝90°，∠DAE＝45°．固定三角板ABC，将∠DAE绕点A按顺时针方向旋转，如图（2），记旋转角∠CAE＝α．（1）当α为60°时，在备用图（1）中画出图形，并判断AE与BC的位置关系，并说明理由；（2）在旋转过程中，当0°＜α＜180°，∠DAE的一边与BC平行时，求旋转角α的值；（3）在旋转过程中，当0°＜α≤90°时，探究∠CAD与∠BAE之间的关系．（温馨提示：对于任意△ABC，都有∠A+∠B+∠C＝180°）参考答案一．选择题1．解：当∠A＝∠C时，∠C＝70°；当∠A＝∠B＝70°时，∠C＝180°﹣∠A﹣∠B＝40°；当∠B＝∠C时，∠C＝∠B＝（180°﹣∠A）＝55°；即∠C的度数可以是70°或40°或55°，故选：C．2．解：设∠C＝x．∵DE垂直平分线段AC，∴EA＝EC，∴∠EAC＝∠C＝x，∴∠AEB＝∠EAC+∠C＝2x，∵CA＝CB，∴∠B＝∠CAB＝45°+x，在△ABE中，∵∠BAE+∠B+∠AEB＝180°，∴45°+45°+x+2x＝180°，∴x＝30°，∵∠EDC＝90°，DE＝2，∴AE＝EC＝2DE＝4，故选：D．3．解：∵△ABC是等边三角形，∴AB＝AC，∠C＝60°，∵DE⊥BC，∴∠DEC＝90°，∴CD＝2CE＝6，∵点D是AC的中点，∴AC＝2CD＝12，∴AB＝AC＝12，故选：B．4．解：如图：延长AB，CD交于点E，∵AD平分∠BAC，∴∠CAD＝∠EAD，∵CD⊥AD，∴∠ADC＝∠ADE＝90°，在△ADE和△ADC中，，∴△ADE≌△ADC（ASA），∴AC＝AE，DE＝CD；∵AC﹣AB＝4，∴AE﹣AB＝4，即BE＝4；∵DE＝DC，∴S△BDC＝S△BEC，∴当BE⊥BC时，S△BDC最大，即S△BDC最大＝××10×4＝10．故选：D．5．解：如图所示：以B为圆心，BC长为半径画弧，交直线m于点P4，P2，以A为圆心，AC长为半径画弧，交直线m于点P1，P3，边AC和BC的垂直平分线都交于点P3位置，因此出现等腰三角形的点P的位置有4个，故选：C．6．解：∵在Rt△ABC中，∠A＝30°，BC＝2，∴AB＝2CB＝4，故选：C．7．解：如图，取CF的中点T，连接DT，AT．∵∠BAC＝90°，FD⊥BC，∴∠CAF＝∠CDF＝90°，∴AT＝DT＝CF，∴TD＝TC＝TA，∴∠TDA＝∠TAD，∠TDC＝∠TCD，∵∠ADB＝45°，∴∠ADT+∠TDC＝135°，∴∠ATC＝360°﹣2×135°＝90°，∴AT⊥CF，∵CT＝TF，∴AC＝AF，∴∠AFC＝45°，∴∠BFD＝45°﹣32°＝13°，∵∠BDF＝90°，∴∠B＝90°﹣∠BFD＝77°，故选：C．8．解：∵DE是△ABC中AC边的垂直平分线，∴AE＝CE，∴AE+BE＝CE+BE＝AB＝5cm，∴△EBC的周长＝BC+BE+CE＝5+4＝9（cm）．故选：B．9．解：∵MN是AB的中垂线，PQ是AC的中垂线，AN＝BN，AQ＝CQ，∴∠BAN＝∠B＝15°，∠CAQ＝∠C＝30°，∴∠ANQ＝∠B+∠BAN＝30°，∠AQN＝∠C+∠CAQ＝60°，∴∠NAQ＝90°，∴BN＝AN＝NQ，AQ＝CQ＝NQ，∵BC＝，∴NQ+NQ+NQ＝3+，∴NQ＝2，∴AN＝，AQ＝1，∴阴影部分的面积＝AN•AQ＝＝，故选：B．10．解：∵BE是AC边的中线，∴AE＝CE，∵△ABE的面积＝，△BCE的面积＝AB，∴△ABE的面积＝△BCE的面积，故①正确；∵AD是BC边上的高，∴∠ADC＝90°，∵∠BAC＝90°，∴∠DAC+∠ACB＝90°，∠F AG+∠DAC＝90°，∴∠F AG＝∠ACB，∵CF是∠ACB的角平分线，∴∠ACF＝∠FCB，∠ACB＝2∠FCB，∴∠F AG＝2∠FCB，故②错误；∵在△ACF和△DGC中，∠BAC＝∠ADC＝90°，∠ACF＝∠FCB，∴∠AFG＝180°﹣∠BAC﹣∠ACF，∠AGF＝∠DGC＝180°﹣∠ADC﹣∠FCB，∴∠AFG＝∠AGF，∴AF＝AG，故③正确；根据已知不能推出∠HBC＝∠HCB，即不能推出HB＝HC，故④错误；即正确的为①③，故选：D．二．填空题11．解：∵AB＝AC，∴∠C＝∠ABC，∵∠A＝50°．∴∠C＝∠ABC＝＝＝65°，∵BD⊥AC，∴∠BDC＝90°，∴∠DBC＝90°﹣∠C＝90°﹣65°＝25°．故答案为：25°．12．解：设∠B＝x°，当∠A是底角时，∠A＝∠C＝4∠B＝4x°，∵∠A+∠B+∠C＝180°，∴4x+x+4x＝180，解得x＝20，∴∠C＝80°故答案为：80．13．解：∵AB＝AC，∠BAC＝100°，∴∠B＝∠C＝（180°﹣∠BAC）＝40°，∵BD＝BE，∴∠BDE＝∠BED＝（180°﹣∠B）＝70°，∵AB＝AC，AD⊥BC，∴∠ADB＝90°，∴∠ADE＝∠ADB﹣∠BDE＝90°﹣70°＝20°，故答案为：20．14．解：在Rt△ABC中，∠ABC＝90°，∠DCB＝30°，∴2BD＝BC，∵CD⊥AB，∴∠A＝∠DCB＝30°，∴2BC＝AB，∴AB＝4BD，∵BD＝1，∴AB＝4．故答案为：4．15．解：在Rt△ABC中，∠A＝90°，∠B＝30°，∴∠ACB＝60°，∵MN∥BC，∴∠AMN＝∠B＝30°，∵∠A＝90°，AN＝1，∴MN＝2AN＝2，∵MN平分∠AMC，∠AMN＝30°，∴∠AMC＝∠NMC＝60°，∵CM平分∠ACB，∠ACB＝60°，∴∠ACM＝ACB＝30°，∴∠ACM＝∠NMC，∴MNCN＝2，∴AC＝AN+CN＝1+2＝3，∵在Rt△ABC中，∠A＝90°，∠B＝30°，∴BC＝2AC＝2×3＝6，16．解：∵BC＝6cm，∴BD＝DC＝3（cm），∵AD⊥BC，BD＝DC，AB＝5cm，∴AC＝AB＝5（cm），∵点C在AE的垂直平分线上，∴EC＝AC＝5（cm），∴DE＝DC+EC＝8（cm），故答案为：5cm；8cm．17．解：（1）∵DE是线段AB的垂直平分线，∴EA＝EB，∴∠BAE＝∠B＝20°；（2））∵DE、MN是边AB、AC的垂直平分线，∴AE＝BE，AN＝CN，∴∠BAE＝∠B，∠CAN＝∠C，∵∠EAN＝40°，∠B+∠BAE+∠EAN+∠CAN+∠C＝180°，∴∠BAE+∠CAN＝70°，∴∠BAC＝∠BAE+∠CAN+∠EAN＝110°，∵∠ADF＝∠AMF＝90°，∴∠F＝360°﹣∠ADF﹣∠AMF﹣∠BAC＝360°﹣90°﹣90°﹣110°＝70°；（3）∵DE、MN是边AB、AC的垂直平分线，∴AE＝BE，AN＝CN，∴△AEN的周长＝AE+EN+AN＝BE+EN+CN＝BC，在△ABC中，AB＝8，AC＝9，∴9﹣8＜BC＜9+8，∴1＜m＜17．故答案为：（1）20°；（2）70°；（3）1＜m＜17．18．解：∵DE是AB的垂直平分线，∴EA＝EB，∴△ACE的周长＝AC+CE+EA＝AC+CE+EB＝AC+CB＝11，19．解：∵EF垂直平分AB于点F，∴AE＝BE，∵BE+CE＝20cm，∴AE+CE＝20cm，即AC＝20cm，∵AD垂直平分BC于点D，∴AB＝AC＝20cm，故答案为：20cm．20．解：过E作EG⊥AB于G，连接CF，∵P为CE中点，∵S△EFP＝S△CFP，设S△EFP＝S△CFP＝y，∵BD是AC边上的中线，∴设S△CDF＝S△AFD＝z，∵S△BFP＝15，∴S△BCD＝15+y+z，∴S△ABC＝2S△BCD＝30+2y+2z，∵S△ACE＝S△ACF+S△CEF＝2y+2z，∴S△ABE＝S△ABC﹣S△ACE＝30+2y+2z﹣（2y+2z）＝30，∵AE是∠CAB的角平分线，∴EG＝CE＝2CP＝4，∴S△ABE＝AB•EG＝30，∴AB＝15，故答案为：15．三．解答题21．解：（1）∵AB＝AC，D是BC边上的中点，∴AD⊥BC，即∠ADC＝90°；（2）∵∠B＝40°，∴∠BAD＝50°．22．（1）证明：∵∠ABC＝∠ACB，∴AB＝AC，∵DE∥BC，∴∠ADE＝∠ABC，∠AED＝∠ACB，∴∠ADE＝∠AED，∴AD＝AE，∴AB＝AD＝AC＝AE，即BD＝CE，在△DBC和△ECB中，，∴△DBC≌△ECB（SAS），∴DC＝EB；（2）解：图中所有的等腰三角形为△ABC、△ADE、△DEF、△BCF，理由如下：由（1）得：AB＝AC，AD＝AE，△DBC≌△ECB，∴△ABC、△ADE是等腰三角形，∠BCD＝∠CBE，∴△BCF是等腰三角形，BF＝CF，∵DE∥BC，∴∠FDE＝∠BCD，∠FED＝∠CBE，∴∠FDE＝∠FED，∴△DEF是等腰三角形，FE＝FD．23．解：（1）∵AC边上的垂直平分线是DE，∴CD＝AD，DE⊥AC，∴∠A＝∠DCA＝30°，∵∠ACB＝90°，∴∠BCD＝∠ACB﹣∠DCA＝90°﹣30°＝60°，（2）∵∠B＝60°∴∠BCD＝∠B＝60°∴BD＝CD，∴BD＝CD＝AD＝AB，∵DE＝3，DE⊥AC，∠A＝30°，∴AD＝2DE＝6，∴AB＝2AD＝12．24．证明：（1）∵∠ACB＝90°，∴∠CAB+∠B＝90°，又∵∠CAB＝2∠B，∴∠B＝30°，∠CAB＝60°，∵AD平分∠CAB，∴∠CAD＝∠DAB＝30°；（2）∵∠DAB＝30°＝∠B，∴AD＝DB，∵AC＝EC，∠ACB＝90°，∴AD＝DE，∴DE＝DB．25．解：∵△ABC中，∠C为直角，AB上的高CD及中线CE恰好把∠ACB三等分，∴∠ACD＝∠DCE＝∠ECB＝30°，又∵CD⊥AB，AC＝20，∴∠A＝60°，AD＝10，∵∠ACB为直角，∴∠B＝30°∵AC＝20，∴AB＝40，∵CE是△ABC中线，∴AE＝BE＝20，∴DE＝10．26．解：（1）已知：△ABC．求证：∠ABC、∠BCA、∠ACB三个角的平分线相交于点F，且点F到三边的距离相等．证明：如图，作∠ABC的角平分线FB，作∠BCA的角平分线FC，两条线相交于点F，作FG⊥AB于点G，FD⊥BC边于点D，FE⊥AC于点E，∵点F是∠ABC平分线上的一点，∴FG＝FD，同理可得，FD＝FE，∴FG＝FD＝FE（等量代换），∴点F在∠BAC的平分线上，∴三角形的三条角平分线相交于一点，并且这一点到三边的距离相等；（2）解：延长BA，作PN⊥BD于N，PF⊥BA于F，PM⊥AC于M，∵CP平分∠ACD，∴∠ACP＝∠PCD，PM＝PN，∵BP平分∠ABC，∴∠ABP＝∠PBC，PF＝PN，∴PF＝PM，∴∠F AP＝∠P AC，∴∠F AC＝2∠P AC，∵∠F AC+∠BAC＝180°，∴2∠P AC+∠BAC＝180°，∴∠P AC＝（180°﹣∠BAC）＝（180°﹣62°）＝59°．故答案为：59．27．证明：作OG⊥BC，∵∠ABC的平分线，OE⊥AB，OG⊥BC，∴OE＝OG，∵∠BCD的平分线，OF⊥CD，OG⊥BC，∴OF＝OG，∴OE＝OF．28．解：（1）当α为60°时，AE⊥BC，如图（1），设AE与BC交于点F，∵∠CAE＝α＝60°，∠ACB＝30°，∴∠AFC＝90°，∴AE⊥BC；（2）当AD∥BC时，如图（2），∠DAC＝∠C＝30°，∵∠DAE＝45°，∴∠CAE＝α＝15°；当AE∥BC时，如图（3），∠B＝∠EAB＝60°，∴∠CAE＝α＝∠BAC+∠EAB＝150°，故旋转角α的值为15°或150°；（3）①如（2），当α≤45°时，α+∠BAE＝90°，α+∠CAD＝45°，∴∠BAE﹣∠CAD＝45°；②如图（1），当45°＜α＜90°时，∵∠DAE+∠CAD+∠BAE＝90°，∠DAE＝45°，∴∠CAD+∠BAE＝45°．。

(典型题)初中数学八年级数学下册第一单元《三角形的证明》测试(含答案解析)(1)

一、选择题1．下列命题中，是假命题的是（）A ．两条直角边对应相等的两个直角三角形全等；B ．每个命题都有逆命题；C ．每个定理都有逆定理；D ．在一个角的内部（包括顶点）且到角的两边距离相等的点，在这个角的平分线上． 2．在ABC 中，已知::5:12:13AC BC AB =，AD 是ABC 的角平分线，DE AB ⊥于点E ．若ABC 的面积为S ，则ACD △的面积为（）A ．14SB ．518SC ．625SD ．725S 3．如图，在ABC 中，PD ，PE 分别是AC ，BC 边的垂直平分线，且分别与AB 交于点M ，N 连接CM ，CN ．有下列四个结论：①P A B ∠=∠+∠；②ACB MCN P ∠=∠+∠；③ACB ∠与P ∠是互为补角；④MCN △的周长与AB 边长相等其中正确结论的个数是（）A ．1B ．2C ．3D ．44．下列说法中，不正确的有（）①不在角的平分线上的点到这个角的两边的距离不相等；②三角形两内角的平分线的交点到各边的距离相等；③到三角形三边距离相等的点有1个④线段中垂线上的点到线段两端点的距离相等，⑤到三角形三个顶点距离相等的点有1个A ．0个B ．1个C ．2个D ．3个5．如图，平面直角坐标系中，O 是坐标原点，点A （3，2），点P （m ，0），若△POA 是等腰三角形，则m 可取的值最多有（）A ．2个B ．3个C ．4个D ．5个6．下列各组数分别为一个三角形三边的长，其中不能构成直角三角形的一组是（）A ．8，10，12B ．3，4，5C ．5，12，13D ．7，24，25 7．下列命题中真命题的个数（）（1）面积相等的两个三角形全等（2）无理数包含正无理数、零和负无理数（3）在直角三角形中，两条直角边长为n 2﹣1和2n ，则斜边长为n 2＋1；（4）等腰三角形面积为12，底边上的高为4，则腰长为5．A ．1个B ．2个C ．3个D ．4个8．下列说法错误的是（）A ．有两边相等的三角形是等腰三角形B ．直角三角形不可能是等腰三角形C ．有两个角为60°的三角形是等边三角形D ．有一个角为60°的等腰三角形是等边三角形9．如图，ABC 中，BAC 60∠=︒，BAC ∠的平分线AD 与边BC 的垂直平分线MD 相交于点D ，DE AB ⊥交AB 的延长线于点E ，DF AC ⊥于点F ，现有下列结论：①DE DF =；②DE DF AD +=；③DM 平分ADF ∠；④2AB AC AE +=．其中正确的有（）A ．①②B ．①②③④C ．①②④D ．②④ 10．如图，ABC 为等边三角形，BO 为中线，延长BA 至D ，使AD AO =，则DOB∠的度数为（）A ．105︒B ．120︒C ．135︒D ．150︒ 11．等腰三角形一腰的垂直平分线与另一腰所在直线的夹角是40°，则这一等腰三角形的底角为（）A ．65°B ．25°C ．50°D ．65°或25°12．如图，直线a，b相交形成的夹角中，锐角为52°，交点为O，点A在直线a上，直线b上存在点B，使以点O，A，B为顶点的三角形是等腰三角形，这样的点B有（）A．1个B．2个C．3个D．4个二、填空题13．如图，在△ABC中，∠ABC的平分线与AC的垂直平分线相交于点D，过点D作DF⊥BC，DG⊥AB，垂足分别为 F、G．若BG＝5，AC＝6，则△ABC 的周长是_____．14．如图，已知一次函数y＝﹣x+1的图象与x轴、y轴分别交于点A，B，点M在y轴上（M不与原点重合），并且使以点A，B，M为顶点的三角形是等腰三角形，则M的坐标为_____．15．上午9时，一条船从海岛A出发，以12海里/时的速度向正北航行，11时到达海岛B 处，如图，海岛A在灯塔C的南偏西32°方向，灯塔C在海岛B的北偏东64°方向，则灯塔C到海岛B的距离是______海里．16．如图，∠AOB =30°，点P 在∠AOB 的内部，OP =6cm ，点E 、F 分别为OA 、OB 上的动点，则△PEF 周长的最小值为________cm ．17．已知：如图，在ABC 中，AB AC =，30C ∠=︒，AB AD ⊥，4cm AD =，则BC 的长为__________cm ．18．如图，在等腰直角三角形ABC 中，90,A AC AB ∠=︒=．BD 为ABC ∠的平分线，交AC 于点D ，若BCD △的面积为2，则ABD △的面积为____________．19．等腰三角形腰上的高与另一腰的夹角为30°，则底角度数是_________．20．如图，50AOB ∠=︒，OC 平分AOB ∠，如果射线OA 上的点E 满足OCE △是等腰三角形，那么OEC ∠的度数为________．三、解答题21．在平面直角坐标系中，坐标轴上的三个点(),0A a ，()0,B b ，(),0C c ()0,0a b <>满足()210c a b -++=，F 为射线BC 上的一个动点．（1）c 的值为______，ABO ∠的度数为______．（2）如图()a ，若AF BC ⊥，且交OB 于点E ，求证：OE OC =．（3）如图()b ，若点F 运动到BC 的延长线上，且2FBO FAO ∠=∠，O 在AF 的垂直平分线上，求ABF 的面积．22．如图，△ABC 的三个顶点都在方格纸的格点上，其中点A 的坐标是（-1，0），B 点坐标是（-3，1），C 点坐标是（-2，3）．（1）作△ABC 关于y 轴对称的图形△DEF ，其中A 、B 、C 的对应点分别为D 、E 、F ；（2）动点P 的坐标为（0，t ），当t 为何值时，PA ＋PC 的值最小，并写出PA ＋PC 的最小值；（3）在（1）的条件下，点Q 为x 轴上的动点，当△QDE 为等腰三角形，请直接写出Q 点的坐标．23．已知等边ABC ，点D 为BC 上一点，连接AD ．（1）若点E 是AC 上一点，且CE BD =，连接BE ，BE 与AD 的交点为点P ，在图（1）中根据题意补全图形，求出APE ∠的大小；（2）将AD 绕点A 逆时针旋转120︒，得到AF ，连接BF 交AC 于点Q ，在图（2）中根据题意补全图形，用等式表示线段AQ 和CD 的数量关系，并证明．（记得充分利用（1）的解题思路和结论）24．如图，ABE △是等腰三角形，AB AE =，45BAE ∠=︒，过点B 作BC AE ⊥于点C ，在BC 上截取CD CE =，连接AD 、DE 并延长AD 交BE 于点P（1）求证：AD BE =；（2）试说明AD 平分BAE ∠．25．已知，如图，在△ABC 中，AD 是BC 边上的高线，CE 是AB 边上的中线（1）若∠B=30°，∠ACD=45°，AB=2，求BC 的长．（2）若点G 是线段CE 的中点，连接DG ，当DG ⊥EC 时，求证: AB=2CD ．（3）在（2）的条件下，试判断∠AEC 与∠B 之间的数量关系，并说明理由．26．已知：任意一个三角形的三条角平分线都交于一点．如图，在ABC 中，BD 、CD 分别平分ABC ∠、ACB ∠，过点D 作直线分别交AB 、AC 于点E 、F ，若AE AF =，解答下列问题：（1）证明：DE DF =；（2）若60A ∠=︒，8AB =，7BC =，5AC =，求EF 的长．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据全等三角形的判定，命题与定理及角平分线的判定等知识一一判断即可．【详解】解：A ．两条直角边对应相等的两个直角三角形，符合两三角形的判定定理“SAS”；故本选项是正确；B 、每个命题都有逆命题，所以B 选项正确；C 、每个定理不一定有逆定理，所以C 选项错误；D 、在一个角的内部（包括顶点）且到角的两边距离相等的点，在这个角的平分线上，正确．故选C ．【点睛】本题考查了全等三角形的判定，命题与定理以及角平分线的判定方法，熟练利用这些判定定理是解题关键．2．B解析：B【分析】根据勾股定理的逆定理可得ABC 为直角三角形，再根据AAS 得出ACD AED ≅，从而得出ACD △的面积=AED 的面积和BE 的长，继而得出AED 的面积和BED 的面积比，即可得出答案【详解】解：∵::5:12:13AC BC AB =，设AC=5k ，BC=12k ，AB=13k ，∴AC 2+BC 2=AB 2∴ABC 为直角三角形，∠C=90°，∵AD 是ABC 的角平分线，DE AB ⊥，∴∠CAD=∠BAD ，∠C=∠AED =90°，∵AD=AD ，∴ACD AED ≅， ∴△△S S =ACD AED ，AE=AC=5k ，∴BE=13k-5k=8k ，∵AED 和BED 同高， ∴8:5△BE △S :S =D AED ，∵ABC 的面积为S ， ∴518△S =ACD S ．故选：B【点睛】本题考查了勾股定理的逆定理、全等三角形的性质与判定，根据同高得出8:5△BE △S :S =D AED 是解题的关键．3．D解析：D【分析】根据四边形内角和等于360°，即可得出③正确，再根据三角形内角和定理、等腰三角形的性质可得结论①②正确；根据线段的垂直平分线的性质得到MA MC =，NB NC =，即可判定④正确．【详解】解：∵PD ，PE 分别是AC ，BC 边的垂直平分线，∴90CDP ∠=︒，90CEP ∠=︒，又∵360P AC DP B C CE P ∠∠+∠=∠++︒，∴180P ACB ∠=︒∠+，故结论③正确；又∵180AC A B B ∠+︒∠+∠=， ∴P A B ∠=∠+∠，故结论①正确；直线PD 是AC 的垂直平分线，AM CM ∴=，∴A ACM ∠=∠同理，NB NC =，B BCN ∠=∠，∵AC MC ACB M N N BC ∠∠+∠∠=+，∴M ACB N A C B ∠∠∠=+∠+，∴ACB MCN P ∠=∠+∠，故结论②正确； AMN △的周长为MC MN NC =++，∴AMN 的周长=AM MN NB AB ++=，故结论④正确；综上所述，①②③④正确，共4个．故选D ．【点睛】本题主要考查了线段的垂直平分线的性质、三角形内角和定理，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．4．C解析：C【分析】根据角平分线的性质和线段垂直平分线的性质逐一进行判断即可．【详解】①根据角平分线的判定可知①正确；②根据角平分线的性质可知②正确；③缺乏前提条件：在三角形内部，若不限制条件，到三角形三边距离相等的点有4个，故③错误；④根据垂直平分线的性质可知④正确；⑤缺乏前提条件：在平面内，若不在平面内到三角形三个顶点距离相等的点有无数个，故⑤错误，∴错误的有2个，故选：C ．【点睛】本题主要考查角平分线的性质和判定及垂直平分线的性质，掌握角平分线的性质和垂直平分线的性质是解题的关键．5．C解析：C【分析】分两种情况分析：①以点OP 为底，②OP 为腰，讨论点P 的个数，再求出m 的值即可.【详解】解：由点P （m ，0）知点P 在x 轴上，分两种情况：当OP 为底时，以A 点为圆心OA 为半径画圆，交x 轴于点P ，以OA=AP 为腰，点P 的坐标为m=2×3=6，当OP 为腰时，以O 为圆心，OA 长为半径，画圆交x 轴于两点P ，点P 在y 轴左侧或右侧，OP=OA=222313+=，∴m=13±，点P 在y 轴右侧，以OA 为底，作AO 的垂直平分线交x 轴与P ，过A 作AB ⊥x 轴，OP=AP=()2223m +-，则m=()2223m +-，解得m=136，综上，共有4个点P ，即m 有4个值，故选择：C.【点睛】本题考察等腰三角形的性质，解题时分两种情况进行讨论，注意以点A 、O 为顶角顶点时应以点为圆心画弧线，避免有遗漏．6．A解析：A【分析】利用勾股定理的逆定理：如果三角形两条边的平方和等于第三边的平方，那么这个三角形就是直角三角形，最长边所对的角为直角来判定即可．【详解】解：A 、∵82＋102≠122，∴三条线段不能组成直角三角形，故A 选项符合题意； B 、∵32＋42＝52，∴三条线段能组成直角三角形，故B 选项不符合题意；C 、∵52＋122＝132，∴三条线段能组成直角三角形，故C 选项不符合题意；D 、∵72＋242＝252，∴三条线段能组成直角三角形，故D 选项不符合题意；故选：A ．【点睛】本题考查的是勾股定理逆定理，解题的关键是掌握勾股定理逆定理以及准确计算． 7．B解析：B【分析】根据三角形全等的性质、无理数的定义、勾股定理进行判断即可；【详解】面积相等的三角形不一定全等，故（1）是假命题；零不是无理数，故（2）是假命题；()()222242214211n n n n n -+=++=+，故（3）是真命题；根据题意可得，底边长为12246⨯÷=，则底边长的一半为623÷=，腰长为5=，故（4）是真命题；综上所述，真命题有2个；故答案选B ．【点睛】本题主要考查了命题的真假判断，结合全等三角形的定义、无理数定义、勾股定理判断是解题的关键．8．B解析：B【分析】利用等腰三角形和等边三角形的判定解答即可．【详解】A.有两边相等的三角形是等腰三角形，所以A选项正确；B.等腰直角三角形就是等腰三角形，故B选项错误；C.有两个角为60°的三角形是等边三角形，正确；D.有一个角为60°的等腰三角形是等边三角形，正确．故选B．【点睛】本题考查了等腰三角形和等边三角形的判定，解题的关键是熟练掌握有关性质．9．C解析：C【分析】①由角平分线的性质可知①正确；②由题意可知∠EAD=∠FAD=30°，故此可知ED=12AD，DF=12AD，从而可证明②正确；③若DM平分∠EDF，则∠EDM=60°，从而得到∠ABC为等边三角形，条件不足，不能确定，故③错误；④连接BD、DC，然后证明△EBD≌△DFC，从而得到BE=FC，从而可证明④．【详解】解：如图所示：连接BD、DC．①∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴ED=DF．∴①正确．②∵∠EAC=60°，AD平分∠BAC，∴∠EAD=∠FAD=30°．∵DE⊥AB，∴∠AED=90°．∵∠AED=90°，∠EAD=30°，∴ED=12AD．同理：DF=12 AD．∴DE+DF=AD．∴②正确．③由题意可知：∠EDA=∠ADF=60°．假设MD 平分∠EDF ，则∠ADM=30°．则∠EDM=60°，又∵∠E=∠BMD=90°，∴∠EBM=120°．∴∠ABC=60°．∵∠ABC 是否等于60°不知道，∴不能判定MD 平分∠EDF ，故③错误．④∵DM 是BC 的垂直平分线，∴DB=DC ．在Rt △BED 和Rt △CFD 中DE DF BD DC ⎧⎨⎩＝＝， ∴Rt △BED ≌Rt △CFD ．∴BE=FC ．∴AB+AC=AE-BE+AF+FC又∵AE=AF ，BE=FC ，∴AB+AC=2AE ．故④正确．故选：C ．【点睛】本题主要考查的是全等三角形的性质和判定、角平分线的性质、线段垂直平分线的性质，掌握本题的辅助线的作法是解题的关键．10．B解析：B【分析】由△ABC 为等边三角形，可求出∠BOA =90°，由△ADO 是等腰三角形求出∠ADO =∠AOD =30°，即可求出∠BOD 的度数．【详解】解：∵△ABC 为等边三角形，BO 为中线，∴∠BOA ＝90°，∠BAC ＝60°∴∠CAD ＝180°﹣∠BAC ＝180°﹣60°＝120°，∵AD ＝AO ，∴∠ADO =∠AOD =30°，∴∠BOD ＝∠BOA +∠AOD ＝90°+30°＝120°，故选：B ．【点睛】本题主要考查了等边三角形的性质及等腰三角形的性质，解题的关键是熟记等边三角形的性质及等腰三角形的性质．11．D解析：D【分析】由题意可知其为锐角等腰三角形或钝角等腰三角形，不可能是等腰直角三角形，所以应分开来讨论．【详解】解：①当为锐角等腰三角形时，如图：∵∠ADE ＝40°，∠AED ＝90°，∴∠A ＝50°，∴∠B=∠C=180502︒-︒ =65°； ②当为钝角等腰三角形时，如图：∵∠ADE ＝40°，∠AED ＝90°，∴∠BAC ＝∠ADE+∠AED ＝40°+90°＝130°，∴∠B=∠C=1801302︒-︒ =25°．故选：D ．【点睛】本题考查了等腰三角形的性质、三角形内角和定理以及三角形外角性质，分类讨论是正确解答本题的关键． 12．D解析：D【分析】以点O 、A 、B 为顶点的等腰三角形有3种情况，分别为OA OB =，OA AB =，OB AB =，从这三方面考虑点B 的位置即可．【详解】解：如图所示，=时，以点O为圆心，OA为半径作圆，与直线b在O点两侧各有一个交①当OA OB点，此时B点有2个；=时，以点A为圆心，OA为半径作圆，与直线b有另外一个交点，此时B点②当OA AB有1个；=时，作OA的垂直平分线，与直线b有一个交点，此时B点有1个，③当OB AB综上，B点总共有4个，故选：D．【点睛】本题考查了等腰三角形的判定，两条边相等的三角形为等腰三角形，因此要注意分类讨论，由每种情况的特点选择合适的方法确定点B是解题的关键．二、填空题13．16【分析】连接ADDC证明Rt△DGA≌Rt△DFC（HL）可得出AG＝CF再证明Rt△BDG≌Rt△BDF（HL）得出BG＝BF则可求出答案【详解】解：连接ADDC∵BD平分∠ABCDG⊥ABD解析：16【分析】连接AD、DC．证明Rt△DGA≌Rt△DFC（HL）可得出AG＝CF，再证明Rt△BDG≌Rt△BDF （HL），得出BG＝BF，则可求出答案【详解】解：连接AD、DC．∵BD平分∠ABC，DG⊥AB，DF⊥BC，∴DG＝DF．∵D在AC的中垂线上，∴DA＝DC．在Rt△DGA与Rt△DFC中，∵DG＝DF，DA＝DC，∴Rt△DGA≌Rt△DFC（HL）．∴AG＝CF．又∵BD＝BD，DG＝DF．∴Rt△BDG≌Rt△BDF（HL）．∴BG＝BF．又∵AG＝CF，∴△ABC的周长＝AB+BC+AC＝BG﹣AG+BF+FC+AC＝2BG+AC＝2×5+6＝16．故答案为：16．【点睛】此题考查了线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质，属于中考常考题型．14．（01+）（01-）（0-1）【分析】分别以点AB为圆心以AB的长为半径画圆两圆与y轴的交点即为M点再由OA=OB可知原点也符合题意【详解】解：分别以点AB为圆心以AB的长为半径画圆如图共有4个点对解析：（0，1+2），（0，1-2），（0，-1）．【分析】分别以点A、B为圆心，以AB的长为半径画圆，两圆与y轴的交点即为M点，再由OA=OB可知原点也符合题意．【详解】解：分别以点A、B为圆心，以AB的长为半径画圆，如图，共有4个点对于y=-x+1，当x=0时，y=1，当y=0时，x=1∴A（1，0），B（0，1）∴OA=OB=1∴2∴当AB 为腰时，BM1∴OM1∴点M1的坐标为（0，），∵OA=1，∴OM 3=1∴点M 3的坐标为（0，-1）∵BM2∴OM2∴点M2的坐标为（0，+1）∵OA=OB∴点M 4的坐标为（0，0）（舍去）综上，点M 的坐标为：（0，0，），（0，-1）．故答案为：（0，），（0，），（0，-1）．【点睛】此题考查了等腰三角形的性质，勾股定理，以及一次函数与坐标轴的交点，利用了数形结合及分类讨论的思想，在分类讨论分情况解决数学问题时，必须认真审题，全面考虑，做到不重不漏，一次分类必须按同标准进行，分出的每一部分必需都是相互独立的．本题要求学生求出相应线段后，注意根据点在坐标轴上的位置选择合适的符号，进而写出坐标． 15．24【分析】作点C 垂直AB 于点DBE 垂直CE 于点E 由题意可求出AB 的长继而根据方位角可求出∠ACE=∠CAB=∠BCA 即可求解；【详解】解：如图作点C 垂直AB 于点DBE 垂直CE 于点E 由题意知：船的速解析：24【分析】作点C 垂直AB 于点D ，BE 垂直CE 于点E ，由题意可求出AB 的长，继而根据方位角可求出∠ACE=∠CAB=∠BCA ，即可求解；【详解】解：如图，作点C 垂直AB 于点D ，BE 垂直CE 于点E ，由题意知：船的速度为12海里，时间为2小时，∴ ()1211924AB =⨯-=，∵∠CBD=64°，∴∠BCD=90°-64°=26°，∵∠ACE=32°，∴∠BCA=90°-26°-32°=32°，∴∠ACE=∠CAB=∠BCA=32°，∴AB=BC=24，故答案为：24．【点睛】本题考查了平行线的性质，方位角以及等腰三角形的性质，正确掌握知识点是解题的关键．16．6【分析】作点P 关于OA 对称的点作点P 关于OB 对称的点连接与OA 交于点E 与OB 交于点F 此时△PEF 的周长最小然后根据∠AOB=30°结合轴对称的性质证明△是等边三角形从而可得答案【详解】解：如图作点解析：6【分析】作点P 关于OA 对称的点1P ，作点P 关于OB 对称的点2P ，连接1122,,,OP PP OP 12PP 与OA 交于点E ，与OB 交于点F ，此时△PEF 的周长最小，然后根据∠AOB=30°，结合轴对称的性质证明△12OPP 是等边三角形，从而可得答案．【详解】解：如图，作点P 关于OA 对称的点1P ，作点P 关于OB 对称的点2P ，连接1122,,,OP PP OP 12PP 与OA 交于点E ，与OB 交于点F ，此时△PEF 的周长最小．此时△PEF 的周长就是12PP 的长，由轴对称的性质可得：12,,POE POE P OF POF ∠=∠∠=∠12OP OP OP ==()122222,POP POE POF POE POF AOB ∴∠=∠+∠=∠+∠=∠∵∠AOB=30°，∴1260POP ∠=︒，∴△12OPP 是等边三角形．6OP =，∴121 6.PP OP OP ===∴△PEF 周长的最小值是6．故答案为：6．【点睛】本题考查轴对称最短路径问题，关键是确定E ，F 的位置，本题的突破点是证明△12OPP 是等边三角形．17．【分析】已知AB=AC 根据等腰三角形的性质可得∠B 的度数再求出∠DAC 的度数然后根据30°角直角三角形的性质求得BD 的长再根据等角对等边可得到CD 的长即可求得BC 的长【详解】∵AB=AC ∠C=30°解析：12【分析】已知AB=AC ，根据等腰三角形的性质可得∠B 的度数，再求出∠DAC 的度数，然后根据30°角直角三角形的性质求得BD 的长，再根据等角对等边可得到CD 的长，即可求得BC 的长．【详解】∵AB=AC ，∠C=30°，∴∠B=∠C=30°，∴∠BAC=120°，∵AB ⊥AD ，AD=4，∴∠BAD=90°，BD=2AD=8，∴∠DAC=120°-90°=30°，∴∠DAC =∠C=30°，∴AD=CD=4，∴CB=DB+CD=12故答案为：12【点睛】本题考查了等腰三角形的判定与性质及30°角直角三角形的性质，熟练运用等腰三角形的性质及30°角直角三角形的性质是解决问题的关键.18．【分析】由等腰直角三角形的性质得到然后利用三角形的面积公式即可求出答案【详解】解：作DE ⊥BC 垂足为E 如图：∵为的平分线∴∵∴△ABC 是等腰直角三角形∴∵的面积为2∴∴∴∴的面积为：；故答案为：【点解析：2【分析】由等腰直角三角形的性质，得到2BCAB ，然后利用三角形的面积公式，即可求出答案．【详解】解：作DE ⊥BC ，垂足为E ，如图：∵BD 为ABC ∠的平分线，∴AD DE =，∵90,A AC AB ∠=︒=，∴△ABC 是等腰直角三角形， ∴2BC AB ，∵BCD △的面积为2， ∴122BC DE •=， ∴1222DE •=， ∴122AB DE •= ∴ABD △的面积为：122AB DE •= 2【点睛】本题考查了角平分线的性质，等腰直角三角形的性质，以及三角形的面积公式，解题的关键是熟练掌握角平分线的性质定理和等腰直角三角形的性质，正确得到2BC AB ． 19．60°或30°【分析】由于此高不能确定是在三角形的内部还是在三角形的外部所以要分锐角三角形和钝角三角形两种情况求解【详解】解：分两种情况：①在左图中AB=ACBD ⊥AC ∠ABD=30°∴∠A=60° 解析：60°或30°【分析】由于此高不能确定是在三角形的内部，还是在三角形的外部，所以要分锐角三角形和钝角三角形两种情况求解．【详解】解：分两种情况：①在左图中，AB=AC ，BD ⊥AC ，∠ABD=30°，∴∠A=60°，∴∠C=∠ABC=180602A ︒-∠=︒； ②在右图中，AB=AC ，BD ⊥AC ，∠ABD=30°，∴∠DAB=60°，∠BAC=120°，∴∠C=∠ABC=180302BAC ︒-∠=︒．故答案为：30°或60°．【点睛】本题考查了等腰三角形的定义、直角三角形两锐角互余．由于题中没有图，要根据已知画出图形并注意要分类讨论．20．或【分析】求出∠AOC 根据等腰得出三种情况OE=CEOC=OEOC=CE 根据等腰三角形性质和三角形内角和定理求出即可【详解】解：∵∠AOB=50°OC 平分∠AOB ∴∠AOC=25°①当E 在E1时OE解析：25︒，130︒或775︒.【分析】求出∠AOC ，根据等腰得出三种情况，OE=CE ，OC=OE ，OC=CE ，根据等腰三角形性质和三角形内角和定理求出即可．【详解】解：∵∠AOB=50°，OC 平分∠AOB ，∴∠AOC=25°，①当E 在E 1时，OE=CE ，∵∠AOC=∠OCE=25°，∴∠OEC=180°-25°-25°=130°；②当E 在E 2点时，OC=OE ，则∠OCE=∠OEC=12（180°-25°）=77.5°； ③当E 在E 3时，OC=CE ，则∠OEC=∠AOC=25°；故答案为：130°或77.5°或25°．【点睛】本题考查了角平分线定义，等腰三角形性质，三角形的内角和定理的应用，解题的关键是掌握所学的知识，运用分类讨论思想进行分析．三、解答题21．（1）1； 45°；（2）见解析；（3）93344【分析】（1）根据非负数的性质可求得c 的值，得到OA=OB ，即可求得∠ABO 的度数；（2）证明△AOE ≅△BOC 即可证明OE OC =；（3）连结OF ，过点F 作FG x ⊥轴，垂足为点G ，根据线段垂直平分线的性质得到OA=OF ，证明∠OBC=30°，根据直角三角形的性质、三角形的面积公式计算，得到答案．【详解】（1）∵()210c a b -++=，∴10c -=，0a b +=，∴1c =，∵A(a ，0)， B(0，b)，∴OA=OB ，∵∠AOB=90°，∴△AOB 是等腰直角三角形，∴∠ABO=45°，故答案为：1；45°；（2）∵AF BC ⊥，∴90AOE BFE ∠=∠=︒，∵AEO BEF ∠=∠，∴OBC OAE ∠=∠，由（1）得：OA=OB ，在AOE △和BOC 中，AO BO AOE BOC OBC OAE =⎧⎪∠=∠⎨⎪∠=∠⎩，∴AOE BOC ≅△△(AAS)，∴OE OC =；（3）连结OF ，过点F 作FG x ⊥轴，垂足为点G ，∵O 在AF 的垂直平分线上∴AO OF =，∴OAF OFA x ∠=∠=，∴2GOF OAF OFA x ∠=∠+∠=∵22FBO FAO x ∠=∠=，OB OA OF ==，∴2OFC OBF x ∠=∠=，∴4BCO COF OFB x ∠=∠+∠=，∵90OBC OCB ∠+∠=︒，∴690x =，解得15x =，∴230OBC GOF x ∠=∠==︒，∵1c =，∴C(1，0)，1OC =，∵90BOC ∠=°，30OBC ∠=︒，∴22BC OC ==，22OB BC OC 3=-= ∴3OA OF OB === 同理可得：32FG =， ∴31AC AO OC =+=∴()11119331333222244ABF ACB ACF S S S AC FG AC OB ⎛⎫=+=⋅+⋅=++=+ ⎪⎝⎭△△△．【点睛】本题考查了全等三角形的判定和性质、线段垂直平分线的性质、等腰直角三角形的性质、含30度角的直角三角形的性质、三角形的面积计算，掌握全等三角形的判定定理和性质定理是解题的关键．22．（1）见解析；（2）t=1，最小值为32；（3）Q （51-+，0）或（51+，0）或（5，0）或（94，0）【分析】（1）分别作出A ，B ，C 的对应点D ，E ，F 即可．（2）连接CD 交y 轴于点P ，连接PC ，点P 即为所求作．（3）根据等腰三角形的判定画出图形分类求解即可．【详解】解：（1）如图，△DEF 即为所求作；（2）如图，点P 即为所求作，点P 的坐标为（0，1），∴当1t =时，PA ＋PC 的值最小，最小值为CD=223332+=；（3）DE 22215=+=，如图，当5Q 的坐标为：Q 1（51，0），Q 251，0）；当5Q 的坐标为：Q 3（5，0）；当DQ=EQ 时，设Q （m ，0），∵D （1，0），E （3，1），2DQ =2EQ ，∴()()222131m m -=-+，解得：94m =． ∴Q4（94，0）；综上，满足条件的点Q 的坐标为：（51-+，0）或（51+，0）或（5，0）或（94，0）．【点睛】本题考查了作图-轴对称变换，等腰三角形的性质，轴对称最短问题等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．23．（1）图见解析，60°；（2）图见解析，12AQ CD =，理由见解析【分析】（1）根据题意补充图形，通过证明ABD BCE △≌△得到BAD CBE ∠=∠，利用三角形外角的性质可得APE BAD ABP ∠=∠+∠CBE ABP ABC =∠+∠=∠即可求解；（2）根据题意补全图形，通过证明BEQ FAQ ≌得到1122AQ QE AE CD ===，即可得证．【详解】解：（1）补全图形证明：在ABD △和BCE 中，60AB BC ABD C BC CE =⎧⎪∠=∠=︒⎨⎪=⎩()ABD BCE SAS ∴≌BAD CBE ∴∠=∠．APE ∠是ABP △的一个外角，APE BAD ABP ∠=∠+∠∴60CBE ABP ABC =∠+∠=∠=︒；（2）补全图形图2，12AQ CD =，证明：根据（1）ABD BCE △≌△可知BD EC =，即DC AE =．再证明BEQ FAQ ≌．得到1122AQ QE AE CD ===．【点睛】本题考查全等三角形的判定与性质、等边三角形的性质，掌握上述性质定理是解题的关键．24．（1）见解析；（2）见解析【分析】（1）利用SAS 证明△BCE ≌△ACD ，根据全等三角形的对应边相等得到AD=BE ．（2）根据△BCE ≌△ACD ，得到∠EBC=∠DAC ，由∠BDP=∠ADC ，得到∠BPD=∠DCA=90°，利用等腰三角形的三线合一，即可得到AD 平分∠BAE ．【详解】证明：（1）∵BC ⊥AE ，∠BAE=45°，∴∠CBA=∠CAB ，∴BC=CA ，在△BCE 和△ACD 中， 90BC AC BCE ACD CE CD ︒=⎧⎪∠=∠=⎨⎪=⎩，∴△BCE ≌△ACD （SAS ），∴AD=BE ．（2）∵△BCE ≌△ACD ，∴∠EBC=∠DAC ，∵∠BDP=∠ADC ，∴∠BPD=∠DCA=90°，∵AB=AE ，∴AD 平分∠BAE ．【点睛】本题考查了全等三角形的性质定理与判定定理，解决本题的关键是证明△BCE ≌△ACD ．也考查了等腰三角形三线合一的性质．25．（11；（2）见解析；（3）32AEC B =∠∠，理由见解析. 【分析】（1）由直角三角形中，30°角所对的直角边等于斜边的一半解得AD=DC=1，再结合勾股定理解题即可；（2）由三线合一性质证明DC=DE ，由直角三角形斜边中线等于斜边的一半得到12DE AB =，据此利用等量代换解题即可；（3）由直角三角形斜边中线性质可证BE=ED ，再结合等边对等角解得∠DEC=∠DCE ，最后根据角的和差解题即可.【详解】解：（1）∵AD 是BC 边上的高线∴∠ADC=∠ADB=90°∵∠ACD=45°，∠B=30°∴∠ACD=∠CAD=45°，∠BAD=60°∴AD=DC ，12AD AB =又∵AB=2∴AD=DC=1在Rt △ABD 中，BD =∴1；（2）证明：∵G 是线段CE 的中点，DG ⊥EC∴DC=DE∵CE 是AB 边上的中线，AD ⊥BC ∴12DE AB =∴12DC AB =即AB=2CD ；（3）32AEC B =∠∠，理由如下， ∵12DE AB =,AE=BE ∴BE=ED ∴∠B=∠EDB∵DE=DC∴∠DEC=∠DCE∴∠B=∠EDB=2∠DCE又∵∠AEC=∠B+∠DCE∴∠AEC=3∠DCE ∴32AEC B =∠∠. 【点睛】本题考查含30°的直角三角形的性质、直角三角形斜边的中线、三线合一性质、勾股定理、等边对等角等知识，是重要考点，难度一般，掌握相关知识是解题关键. 26．（1）见解析；（2）4【分析】（1）连接AD 由AE AF =可得AEF 是等腰三角形，由三条角平分线交于一点可证AD 平分BAC ∠即可；（2）在BC 上取点M N 、，使得BE BM CF CN ==，，设2EF x =，则DE DF x ==，易证AEF 为等边三角形，可得2AE AF EF x ===，60AEF ∠=︒，可证BED ≌BMD （SAS ）可得DM DE =，82BM BE x ==-，BED BMD ∠=∠60DMN AEF ∠=∠=︒，再证NCD ≌FCD （SAS ）可得,52DN DF CN CF x ===-，可证DMN 为等边三角形，由BC BM MN NC =++构造方程解之即可．【详解】（1）证明：连接AD ，AE AF =，∴AEF 是等腰三角形，BD 、CD 分别平分ABC ∠、ACB ∠，∴AD 平分BAC ∠，∴DE DF =；（2）解：在BC 上取点M N 、，使得BE BM CF CN ==，，设2EF x =，则DE DF x==，60A AE AF∠=︒=，，∴AEF为等边三角形，∴2AE AF EF x===，60AEF∠=︒，在BED和BMD中，BE BMEBD MBDBD BD=⎧⎪∠=∠⎨⎪=⎩，∴BED≌BMD（SAS），∴DM DE=，82BM BE x==-，BED BMD∠=∠，60DMN AEF∴∠=∠=︒，在CND△和CFD△中，CN CFBMNCD FCDCD CD=⎧⎪∠=∠⎨⎪=⎩，∴NCD≌FCD（SAS），∴,52DN DF CN CF x===-，又DE DF=，∴DM DN DE x===，又60DMN∠=︒，∴DMN为等边三角形，∴MN DM x==，∴(82)(52)7BC BM MN NC x x x=++=-++-=，即2x=，∴24EF x==．【点睛】本题考查等腰三角形性质，角平分线性质，等边三角形判定与性质，三角形全等判定与性质，利用BC BM MN NC=++构造方程是解题关键．。

北师大版八年级数学下册第1章三角形的证明单元测试卷(含答案)

北师大版八年级数学下册第1章三角形的证明单元测试卷(时间：120分钟满分：150分)一、选择题(本大题共15个小题，每小题3分，共45分.在每小题的四个选项中，只有一个选项正确，请把你认为正确的选项填在相应的答题框内)1.如图，若∠B＝30°，∠C＝90°，AC＝20，则AB＝( )A.25B.30C.20 3D.402.如图，已知DE∥BC，AB＝AC，∠1＝55°，则∠C的度数是( )A.55°B.45°C.35°D.65°3.在△ABC中，其两个内角如下，则能判定△ABC为等腰三角形的是( )A.∠A＝40°，∠B＝50°B.∠A＝40°，∠B＝60°C.∠A＝20°，∠B＝80°D.∠A＝40°，∠B＝80°4.以下各组数为三角形的三条边长，其中是直角三角形的三条边长的是( )A.2，3，4B.1，2， 3C.4，5，6D.2，2，45.如图，∠A＝∠D＝90°，AC＝DB，则△ABC≌△DCB的理由是( )A.HLB.ASAC.AASD.SAS6.如图，在△ABC中，AB＝AC，D为BC的中点，∠BAD＝35°，则∠CAD的度数为( )A.35°B.45°C.55°D.60°7.等边△ABC的两条角平分线BD和CE相交所夹锐角的度数为( )A.30°B.45°C.60°D.75°8.如图，D是Rt△ABC的斜边BC上一点，AB＝AD，记∠CAD＝α，∠ABC＝β，若α＝10°，则β的度数是( )A.40°B.50°C.60°D.不能确定9.如图，在Rt△ABC中，∠C＝90°，∠CAB＝60°，AD平分∠CAB，DE⊥AB，CD＝3，则BD的长为( )A.1.5B.3C.6D.910.用反证法证明“直角三角形中的两个锐角不能都大于45°”，第一步应假设这个直角三角形中( )A.每一个锐角都小于45°B.有一个锐角大于45°C.有一个锐角小于45°D.每一个锐角都大于45°11.如图，在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，那么下列各条件中，不能使Rt△ABC≌Rt△A′B′C′的是( )A.AB＝A′B′＝5，BC＝B′C′＝3B.AB＝B′C′＝5，∠A＝∠B′＝40°C.AC＝A′C′＝5，BC＝B′C′＝3D.AC＝A′C′＝5，∠A＝∠A′＝40°12.观察下列命题的逆命题：①有两边相等的三角形是等腰三角形；②到角的两边的距离相等的点在这个角的平分线上；③直角三角形的两个锐角互余；④全等三角形的面积相等.其中逆命题为假命题的个数是( )A.1B.2C.3D.413.如图，在△ABC中，BC的垂直平分线EF交∠ABC的平分线BD于E.如果∠BAC＝60°，∠ACE＝24°，那么∠BCE 的大小是( )A.24°B.30°C.32°D.36°14.如图，直角三角形纸片的两直角边长分别为6，8，按如图那样折叠，使点A与点B重合，折痕为DE，则S△BCE∶S△BDE ＝( )A.2∶5B.14∶25C.16∶25D.4∶2115.如图，P是等边三角形ABC内的一点，且PA＝3，PB＝4，PC＝5，以BC为边在△ABC外作△BQC≌△BPA，连接PQ，则以下结论错误的是( )A.△BPQ是等边三角形B.△PCQ是直角三角形C.∠APB＝150°D.∠APC＝135°二、填空题(本大题共5个小题，每小题5分，共25分)16.在直角三角形中，其中一个锐角是22°，则另外一个锐角是.17.如图，某失联客机从A地起飞，飞行1 000 km到达B地，再折返飞行1 000 km到达C地后在雷达上消失，已知∠ABC＝60°，则失联客机消失时离起飞地A地的距离为km.18.如图，O为数轴原点，A，B两点分别对应－3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴于点M，则点M对应的实数为.19.如图，已知△ABC的周长是22，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD＝3，△ABC的面积是.20.如图，在等腰△ABC中，AB＝AC，∠BAC＝54°，∠BAC的平分线与AB的垂直平分线交于点O，点C沿EF 折叠后与点O重合，则∠OEC的度数是.三、解答题(本大题共7个小题，各题分值见题号后，共80分)21.(本题8分)一个机器零件的形状如图所示，在Rt△ABC中，∠BAC＝30°，BC＝2.5 cm，BD＝13 cm，AD＝12 cm，求△ABD的面积.22.(本题8分)在加快城镇建设中，有两条公路OA和OB交会于O点，在∠AOB的内部有蔬菜基地C和D，现要修建一个蔬菜转运站P，使转运站P到两条公路OA，OB的距离相等，且到两个蔬菜基地C，D的距离也相等，用尺规作出蔬菜转运站P的位置.(要求：不写作法，保留作图痕迹.)23.(本题10分)如图，点P为△ABC的BC边上一点，且PC＝2PB，∠ABC＝45°，∠APC＝60°，CD⊥AP，连接BD，求∠ABD的度数.24.(本题12分)如图，∠AOB＝60°，OC平分∠AOB，C为角平分线上一点，过点C作CD⊥OC，垂足为C，交OB于点D，CE∥OA交OB于点E.(1)判断△CED的形状，并说明理由；(2)若OC＝3，求CD的长.25.(本题12分)如图，△ABC的外角∠DAC的平分线交BC边的垂直平分线于点P，PD⊥AB于D，PE⊥AC于E.(1)求证：BD＝CE；(2)若AB＝6 cm，AC＝10 cm，求AD的长.26.(本题14分)如图，在△ABC中，MP，NO分别垂直平分AB，AC.(1)若BC＝10 cm，试求出△PAO的周长；(2)若AB＝AC，∠BAC＝110°，试求∠PAO的度数；(3)在(2)中，若无AB＝AC的条件，你能求出∠PAO的度数吗？若能，请求出来；若不能，请说明理由.27.(本题16分)如图，△ABC中，AB＝BC＝AC＝12 cm，现有两点M，N分别从点A，B同时出发，沿三角形的边运动，已知点M的速度为1 cm/s，点N的速度为2 cm/s.当点N第一次到达点B时，M，N同时停止运动.(1)点M，N运动几秒后，M，N两点重合？(2)点M，N运动几秒后，可得到等边三角形△AMN?(3)当点M，N在BC边上运动时，能否得到以MN为底边的等腰三角形AMN？如存在，请求出此时M，N运动的时间.参考答案一、选择题(本大题共15个小题，每小题3分，共45分.在每小题的四个选项中，只有一个选项正确，请把你认为正确的选项填在相应的答题框内)1.如图，若∠B＝30°，∠C＝90°，AC＝20，则AB＝(D)A.25B.30C.20 3D.402.如图，已知DE∥BC，AB＝AC，∠1＝55°，则∠C的度数是(A)A.55°B.45°C.35°D.65°3.在△ABC中，其两个内角如下，则能判定△ABC为等腰三角形的是(C)A.∠A＝40°，∠B＝50°B.∠A＝40°，∠B＝60°C.∠A＝20°，∠B＝80°D.∠A＝40°，∠B＝80°4.以下各组数为三角形的三条边长，其中是直角三角形的三条边长的是(B)A.2，3，4B.1，2， 3C.4，5，6D.2，2，45.如图，∠A＝∠D＝90°，AC＝DB，则△ABC≌△DCB的理由是(A)A.HLB.ASAC.AASD.SAS6.如图，在△ABC中，AB＝AC，D为BC的中点，∠BAD＝35°，则∠CAD的度数为(A)A.35°B.45°C.55°D.60°7.等边△ABC的两条角平分线BD和CE相交所夹锐角的度数为(C)A.30°B.45°C.60°D.75°8.如图，D是Rt△ABC的斜边BC上一点，AB＝AD，记∠CAD＝α，∠ABC＝β，若α＝10°，则β的度数是(B)A.40°B.50°C.60°D.不能确定9.如图，在Rt△ABC中，∠C＝90°，∠CAB＝60°，AD平分∠CAB，DE⊥AB，CD＝3，则BD的长为(C)A.1.5B.3C.6D.910.用反证法证明“直角三角形中的两个锐角不能都大于45°”，第一步应假设这个直角三角形中(D)A.每一个锐角都小于45°B.有一个锐角大于45°C.有一个锐角小于45°D.每一个锐角都大于45°11.如图，在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，那么下列各条件中，不能使Rt△ABC≌Rt△A′B′C′的是(B)A.AB＝A′B′＝5，BC＝B′C′＝3B.AB＝B′C′＝5，∠A＝∠B′＝40°C.AC＝A′C′＝5，BC＝B′C′＝3D.AC＝A′C′＝5，∠A＝∠A′＝40°12.观察下列命题的逆命题：①有两边相等的三角形是等腰三角形；②到角的两边的距离相等的点在这个角的平分线上；③直角三角形的两个锐角互余；④全等三角形的面积相等.其中逆命题为假命题的个数是(A)A.1B.2C.3D.413.如图，在△ABC中，BC的垂直平分线EF交∠ABC的平分线BD于E.如果∠BAC＝60°，∠ACE＝24°，那么∠BCE 的大小是(C)A.24°B.30°C.32°D.36°14.如图，直角三角形纸片的两直角边长分别为6，8，按如图那样折叠，使点A与点B重合，折痕为DE，则S△BCE∶S△BDE ＝(B)A.2∶5B.14∶25C.16∶25D.4∶2115.如图，P是等边三角形ABC内的一点，且PA＝3，PB＝4，PC＝5，以BC为边在△ABC外作△BQC≌△BPA，连接PQ，则以下结论错误的是(D)A.△BPQ是等边三角形B.△PCQ是直角三角形C.∠APB＝150°D.∠APC＝135°二、填空题(本大题共5个小题，每小题5分，共25分)16.在直角三角形中，其中一个锐角是22°，则另外一个锐角是68__°.17.如图，某失联客机从A地起飞，飞行1 000 km到达B地，再折返飞行1 000 km到达C地后在雷达上消失，已知∠ABC＝60°，则失联客机消失时离起飞地A地的距离为1__000km.18.如图，O 为数轴原点，A ，B 两点分别对应－3，3，作腰长为4的等腰△ABC ，连接OC ，以O 为圆心，CO 长为半径画弧交数轴于点M ，则点M19.如图，已知△ABC 的周长是22，OB ，OC 分别平分∠ABC 和∠ACB ，OD ⊥BC 于点D ，且OD ＝3，△ABC 的面积是33.20.如图，在等腰△ABC 中，AB ＝AC ，∠BAC ＝54°，∠BAC 的平分线与AB 的垂直平分线交于点O ，点C 沿EF 折叠后与点O 重合，则∠OEC 的度数是108__°.三、解答题(本大题共7个小题，各题分值见题号后，共80分)21.(本题8分)一个机器零件的形状如图所示，在Rt △ABC 中，∠BAC ＝30°，BC ＝2.5 cm ，BD ＝13 cm ，AD ＝12 cm ，求△ABD 的面积.解：∵Rt △ABC 中，∠BAC ＝30°，BC ＝2.5 cm ， ∴AB ＝2BC ＝5 cm.∵52＋122＝132，即AB 2＋AD 2＝BD 2， ∴△ABD 是直角三角形.∴S △ABD ＝12AB·AD ＝12×5×12＝30(cm 2).22.(本题8分)在加快城镇建设中，有两条公路OA 和OB 交会于O 点，在图中∠AOB 的内部有蔬菜基地C 和D ，现要修建一个蔬菜转运站P ，使转运站P 到两条公路OA ，OB 的距离相等，且到两个蔬菜基地C ，D 的距离也相等，用尺规作出蔬菜转运站P 的位置.(要求：不写作法，保留作图痕迹.)解：如图所示.23.(本题10分)如图，点P 为△ABC 的BC 边上一点，且PC ＝2PB ，∠ABC ＝45°，∠APC ＝60°，CD ⊥AP ，连接BD ，求∠ABD 的度数.解：∵∠APC ＝60 °，CD ⊥AP ， ∴∠PCD ＝90 °－∠APC ＝90 °－60 °＝30 °. ∴PC ＝2PD.∵PC ＝2PB ，∴PB ＝PD. ∴∠PBD ＝∠PDB.又∵∠APC ＝∠PBD ＋∠PDB ，∴∠PBD ＝12∠APC ＝12×60 °＝30 °.∵∠ABC ＝45 °，∴∠ABD ＝∠ABC －∠PBD ＝45 °－30 °＝15 °.24.(本题12分)如图，∠AOB ＝60°，OC 平分∠AOB ，C 为角平分线上一点，过点C 作CD ⊥OC ，垂足为C ，交OB 于点D ，CE ∥OA 交OB 于点E.(1)判断△CED 的形状，并说明理由； (2)若OC ＝3，求CD 的长.解：(1)△CED 是等边三角形.理由如下： ∵OC 平分∠AOB ，∠AOB ＝60 °，∴∠AOC ＝∠COE ＝30 °. ∵CE ∥OA ，∴∠AOC ＝∠COE ＝∠OCE ＝30 °，∠CED ＝60 °. ∵CD ⊥OC ，∴∠OCD ＝90 °. ∴∠EDC ＝60 °.∴△CED 是等边三角形.(2)∵△CED 是等边三角形，∴CD ＝CE ＝ED. 又∵∠COE ＝∠OCE ，∴OE ＝EC. ∴CD ＝ED ＝OE.设CD ＝x ，则OD ＝2x.在Rt △OCD 中，根据勾股定理得：x 2＋9＝4x 2，解得x ＝ 3. 则CD ＝ 3.25.(本题12分)如图，△ABC 的外角∠DAC 的平分线交BC 边的垂直平分线于点P ，PD ⊥AB 于D ，PE ⊥AC 于E. (1)求证：BD ＝CE ；(2)若AB ＝6 cm ，AC ＝10 cm ，求AD 的长.解：(1)证明：连接BP ，CP.∵点P 在BC 的垂直平分线上，∴BP ＝CP. ∵AP 是∠DAC 的平分线，∴DP ＝EP ，在Rt △BDP 和Rt △CEP 中，⎩⎪⎨⎪⎧BP ＝CP ，DP ＝EP ，∴Rt △BDP ≌Rt △CEP (HL )，∴BD ＝CE.(2)在Rt △ADP 和Rt △AEP 中，⎩⎪⎨⎪⎧AP ＝AP ，DP ＝EP ，∴Rt △ADP ≌Rt △AEP (HL )，∴AD ＝AE.∵AB ＝6 cm ，AC ＝10 cm ，∴6＋AD ＝10－AE ，即6＋AD ＝10－AD.解得AD ＝2 cm.26.(本题14分)如图，在△ABC 中，MP ，NO 分别垂直平分AB ，AC.(1)若BC ＝10 cm ，试求出△PAO 的周长； (2)若AB ＝AC ，∠BAC ＝110°，试求∠PAO 的度数；(3)在(2)中，若无AB ＝AC 的条件，你能求出∠PAO 的度数吗？若能，请求出来；若不能，请说明理由.解：(1)∵MP ，NO 分别垂直平分AB ，AC ， ∴AP ＝BP ，AO ＝CO.∴△PAO 的周长为AP ＋PO ＋AO ＝BO ＋PO ＋OC ＝BC. ∵BC ＝10 cm ，∴△PAO 的周长为10 cm.(2)∵AB ＝AC ，∠BAC ＝110 °，∴∠B ＝∠C ＝12×(180 °－110 °)＝35 °.由(1)知AP ＝BP ，AO ＝CO. ∴∠BAP ＝∠B ＝35 °，∠CAO ＝∠C ＝35 °. ∴∠PAO ＝∠BAC －∠BAP －∠CAO ＝110 °－35 °－35 °＝40 °. (3)能.理由如下： ∵∠BAC ＝110 °，∴∠B ＋∠C ＝180 °－110 °＝70 °.由(1)知AP ＝BP ，AO ＝CO.∴∠BAP ＝∠B ，∠CAO ＝∠C.∴∠PAO ＝∠BAC －∠BAP －∠CAO ＝∠BAC －(∠B ＋∠C )＝110 °－70 °＝40 °.27.(本题16分)如图，△ABC 中，AB ＝BC ＝AC ＝12 cm ，现有两点M ，N 分别从点A ，B 同时出发，沿三角形的边运动，已知点M 的速度为1 cm /s ，点N 的速度为2 cm /s .当点N 第一次到达点B 时，M ，N 同时停止运动.(1)点M ，N 运动几秒后，M ，N 两点重合？(2)点M ，N 运动几秒后，可得到等边三角形△AMN?(3)当点M ，N 在BC 边上运动时，能否得到以MN 为底边的等腰三角形AMN ？如存在，请求出此时M ，N 运动的时间.解：(1)设点M ，N 运动x 秒后，M ，N 两点重合，x ×1＋12＝2x ，解得x ＝12.(2)设点M ，N 运动t 秒后，可得到等边三角形△AMN ，如图1，AM ＝t ×1＝t ，AN ＝AB －BN ＝12－2t.∵三角形△AMN 是等边三角形，∴t ＝12－2t ，解得t ＝4.∴点M ，N 运动4秒后，可得到等边三角形△AMN.(3)当点M ，N 在BC 边上运动时，可以得到以MN 为底边的等腰三角形.由(1)知，12秒时M ，N 两点重合，恰好在C 处.如图2，假设△AMN 是以MN 为底边的等腰三角形，∴AN ＝AM.∴∠AMN ＝∠ANM.∴∠AMC ＝∠ANB.∵AB ＝BC ＝AC ，∴△ACB 是等边三角形.∴∠C ＝∠B.在△ACM 和△ABN 中，⎩⎪⎨⎪⎧∠C ＝∠B ，∠AMC ＝∠ANB ，AC ＝AB ， ∴△ACM ≌△ABN (AAS ).∴CM ＝BN.设当点M ，N 在BC 边上运动时，M ，N 运动的时间y 秒时，△AMN 是等腰三角形.∴CM ＝y －12，NB ＝36－2y ，由CM ＝NB ，得y －12＝36－2y ，解得y ＝16.故假设成立.∴当点M ，N 在BC 边上运动时，能得到以MN 为底边的等腰三角形AMN ，此时M ，N 运动的时间为16秒.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第一章三角形的证明
一、选择题(每题3分,共30分)
1、△ABC 中，AB = AC ，BD 平分∠ABC 交AC 边于点D ，∠BDC = 75°，则∠A 的度数为（） A 35° B 40° C 70° D 110°
2、适合条件∠A =∠B =
3
1
∠C 的三角形一定是（） A 锐角三角形 B 钝角三角形 C 直角三角形 D 任意三角形
3、用两个全等的直角三角形拼下列图形：①平行四边形（不包含菱形、矩形、正方形）；②矩形；③正方形；④等腰三角形，一定可以拼成的图形是（） A ①②④ B ②④ C ①④ D ②③④
4、已知△ABC 中，AB ＝AC ，AB 的垂直平分线交AC 于D ，△ABC 和△DBC 的周长分别是60 cm 和38 cm ，则△ABC 的腰和底边长分别为 ( ) A 24 cm 和12 cm B 16 cm 和22 cm C 20 cm 和16 cm D 22 cm 和16 cm
5、如图，△ABC 中，AC ＝BC ，直线l 经过点C ，则 ( )
A l 垂直A
B B l 平分AB
C l 垂直平分AB
D 不能确定 6、三角形中，若一个角等于其他两个角的差，则这个三角形是 ( ) A 钝角三角形 B 直角三角形 C 锐角三角形 D 等腰三角形 7、已知等腰三角形的两边长分别为6㎝、3㎝，则该等腰三角形的周长是( ) A 9㎝
B 12㎝
C 12㎝或者15㎝
D 15㎝
8、如图，已知在△ＡＢＣ中，ＡＢ＝ＡＣ，Ｄ为ＢＣ上一点，ＢＥ＝ＣＤ，ＣＦ＝ＢＤ，那么∠ＥＤＦ等于（）Ａ 90°－∠ＡＢ 90°－2
1
∠ＡＣ 45°－
2
1
∠ＡＤ 180°－∠Ａ 9、一个正方形和一个等腰三角形有相等的周长，已知等腰三角形有两边长分别为 5.6 cm 和13.2 cm ，则这个正方形的面积为（）Ａ 64 cm ２
Ｂ 48 cm ２
Ｃ 36 cm ２
Ｄ 24 cm ２
10、如图，等边△ABC 中，BD=CE ，AD 与BE 相交于点P ，
则∠APE的度数是（）
A 45°
B 55°
C 60°
D 75°
二、填空题（每小题3分，共30分）
1、“直角三角形两条直角边的平方和等于斜边的平”的方逆定理是
2、等腰三角形的腰长为2cm，面积等于1cm2，则它的顶角的度数
为 .
3、如图，在Rt△ABC中，∠B=90°，∠A=40°，AC的垂直平分线MN
与AB相交于D点，则∠BCD的度数是 .
4、等腰三角形一腰上的高与另一腰的夹角为30°，腰长为a，则其底边上的高是 .
5、正三角形的边长为a，则它的面积为．
6、在△ABC中，AB=AC，∠A＝58°，AB的垂直平分线交AC于N，则∠NBC
= .
7、在直角三角形中，如果一个锐角为30°，而斜边与较小直角边的和
为12，那么斜边长为．
8、已知：如图，AB＝AC，FD⊥BC于D，DE⊥AB于E，若∠AFD＝145°，则∠EDF＝．
9、在等腰三角形ABC中，AB=AC=5，BC=6，D是BC上一点，作DE⊥AB，DF⊥AC，则DE+DF= ．
10、如图，一张直角三角形的纸片，象图中那样折叠，使A与B重合，
∠B=30°，AC=3，则折痕DE等于．
三、解答题(本题共8个小题，共60分)
1、（7分）已知：如图，等腰三角形ABC中，AC＝BC，∠ACB＝90°，直线l经过点C(点A、B都在直线l的同侧)，AD⊥l，BE⊥l，垂足分别为D、E．求证：△ADC≌△CEB.
2、（7分）用反证法证明一个三角形中不能有两个角是直角．
3、（8分）如图，在△ABC 中，AD 是高，CE 是中线，DC=BE ，DG⊥CE 于G ．
求证：①G 是CE 的中点． ②∠B=2∠BCE．
4、（7分）在四边形ABCD 中，AC 平分∠BAD，过C 作CE⊥AB 于E ，且AE ＝2
1
（AB ＋AD ），求∠ABC＋∠ADC 的度数．
5、（7分）如图，△ABC 中，E 是BC 边上的中点，DE⊥BC 于E ，交∠BAC 的平分线AD 于D ，过D 作DM⊥AB 于M ，作DN⊥AC 于N ，试证明：BM ＝CN ．
6、（7分）已知：如图，在Rt△ABC 中，∠ACB=90°，AC=BC ，点D 是BC 的中点，CE⊥AD，垂足为点E ，BF//AC 交CE 的延长线于点F ．求证：AC=2BF ．
A
B
C
D
E
G
A
B
C
E D
A
B
C D
M
N
E
B
F
7、（7分）在△ABC中，AB＝AC，D是AB上一点，E是AC延长线上一点，且BD＝CE．
求证：DM＝EM．
A
D
B C
E
8、（10分）已知：如图，在Rt△ABC中，∠C＝90°，沿过B点的一条直线BE折叠这个三角形，使C点与AB边上的一点D重合．
(1)当∠A满足什么条件时，点D恰为AB的中点?写出一个你认为适当的条件，并利用此条件证明D为AB的中点；
(2)在(1)的条件下，若DE＝1，求△ABC的面积．
参考答案一、选择题
1、B
2、B
3、A
4、D
5、D
6、B
7、D
8、B
9、A 10、C 二、填空题
1、如果三角形的两边的平方和等于第三边的平方，那么这个三角形是直角三角形
2、30°或150°
3、10° 4 52 6、3° 7、 6 8、55° 9、
24
5
10、1 三、解答题(本题共8个小题，共60分) 1、略 2、略
3、提示：连结DE ，由直角三角形斜边中线等于斜边的一半易证．
4、提示：过C 点作AD 的延长线的垂线，垂足为F ．利用角平分线的性质和AE=2
1
（AB+AD ）可知BE=DF ，CF=CE ，再由△CDF≌CBE 即得．
5、提示：连结BD 、CD 利用角平分线和中垂线的性质证△BDM≌CDN．
6、提示：证△ACD≌CBF．
7、提示：过D 点作AC 的平行线（或者过E 点作AB 的平行线）利用三角形全等可证． 8、（1）∠A = 30°；证明略
（2）△ABC 的面积为2
．。