复利终值系数表
复利终值系数表

复利终值系数表复利终值系数是金融学中的一个重要概念,用于计算一笔本金在经过一定期限后,按一定的利率进行复利计算后的终值。
本文将为您介绍复利终值系数的定义、计算方法以及如何使用复利终值系数表。
定义复利终值系数是指在一定期限(通常以年为单位)内,按一定的利率进行复利计算后的终值与本金之间的比率。
复利终值系数可以帮助我们快速准确地计算未来某一时间点的资金终值。
计算方法复利终值系数可以通过以下公式来计算:FV = PV * (1 + r)^n其中,FV是终值,PV是本金,r是利率,n是期数。
利率r通常以年利率的形式给出,需要注意的是,如果期数n不是整数年,那么需要将年利率除以期数n,得到每期的利率。
使用方法为了方便计算复利终值,可以使用复利终值系数表。
下面是一个示例的复利终值系数表:期数5%6%7%8%9%10%1 1.050 1.060 1.070 1.080 1.090 1.1002 1.102 1.124 1.144 1.166 1.188 1.2103 1.157 1.191 1.225 1.260 1.295 1.3314 1.216 1.262 1.311 1.464 1.487 1.4645 1.281 1.340 1.407 1.469 1.540 1.610使用复利终值系数表的步骤如下:1.找到对应期数的行;2.找到对应利率的列;3.交叉得到的数值就是该期数下利率对应的复利终值系数。
举个例子,假设我们有1000元资金,想计算在5年后以6%利率复利计算后的终值。
我们可以在表格中找到对应的行和列,交叉点得到的数值是1.340。
那么终值就是1000 * 1.340 = 1340元。
复利终值系数表可以大大简化计算过程,特别是在需要频繁计算不同期数和不同利率下的终值时,更加方便快捷。
结论复利终值系数是金融学中的重要工具,用于计算本金在经过一定期限后按一定利率复利计算后的终值。
通过使用复利终值系数表,我们可以快速准确地计算未来某一时间点的资金终值,从而对资金的增长和投资决策进行科学的评估和决策。
复利终值系数表

复利终值系数表说明复利终值系数是金融学中用于计算一笔资金在经过一定期间后的终值的系数。
通过复利终值系数,可以帮助投资者在理财中做出更准确的决策。
本文档将提供一份复利终值系数表,以方便读者在进行理财计算时使用。
复利终值系数定义复利终值系数(Compound Factor)是指一笔资金经过一定周期,按照一定的利率计算,最终的终值与最初的本金之间的比值。
复利终值系数可以用公式表示为:复利终值系数 = (1 + 利率)^周期数复利终值系数表利率(%)1年2年3年4年5年1 1.01 1.02 1.03 1.04 1.052 1.02 1.04 1.08 1.16 1.103 1.03 1.06 1.09 1.14 1.164 1.04 1.08 1.13 1.16 1.215 1.05 1.10 1.15 1.21 1.28使用方法为了使用表格中的复利终值系数计算终值,您需要按照以下步骤操作:1.找到表格中的对应利率,并找到所需的周期数;2.将所需的利率和周期数代入复利终值系数的公式中,进行计算。
举个例子:假设您有一笔本金为1000元,希望在3年后计算终值,利率为2%。
根据表格,使用3年和2%对应的复利终值系数为1.08。
通过公式计算:终值 = 本金 * 复利终值系数 = 1000 * 1.08 = 1080因此,在本金为1000元,利率为2%,周期为3年的情况下,最终的终值为1080元。
注意事项在使用复利终值系数表时,需要注意以下几点:1.表格中的利率单位为百分比,需要将百分比转化为小数使用;2.表格中的周期数可以是任意整数,但需要与实际情况相符;3.复利终值系数表可用于计算一次投资的终值,但不能应用于连续投资的情况;4.复利终值系数表中的数值仅供参考,实际计算中应根据实际情况进行调整。
结论本文档提供了一份复利终值系数表,通过该表格可以方便地计算资金在不同利率和周期下的终值。
表格提供了1到5年的时间范围以及不同利率水平的复利终值系数。
(完整版)复利系数表

2.0400
0.4902
0.5302
1.8861
3
1.1249
0.8890
3.1216
0.3203
0.3603
2.7751
4
1.1699
0.8548
4.2465
0.2355
0.2755
3.6299
5
1.2167
0.8219
5.4163
0.1846
0.2246
4.4518
6
1.2653
0.7903
0.1081
9.2526
12
1.4258
0.7014
14.1920
0.0705
0.1005
9.9540
13
1.4685
0.6810
15.6178
0.0640
0.0940
10.6350
14
1.5126
0.6611
17.0863
0.0585
0.0885
11.2961
15
1.5580
0.6419
18.5989
0.5067
32.4529
0.0308
0.0608
16.4436
24
2.0328
0.4919
34.4265
0.0290
0.0590
16.9355
25
2.0938
0.4776
36.4593
0.0274
0.0574
17.4131
26
2.1566
0.4637
38.5530
0.0259
0.0559
17.8768
(完整版)年金现值、终值、复利现值、终值系数表

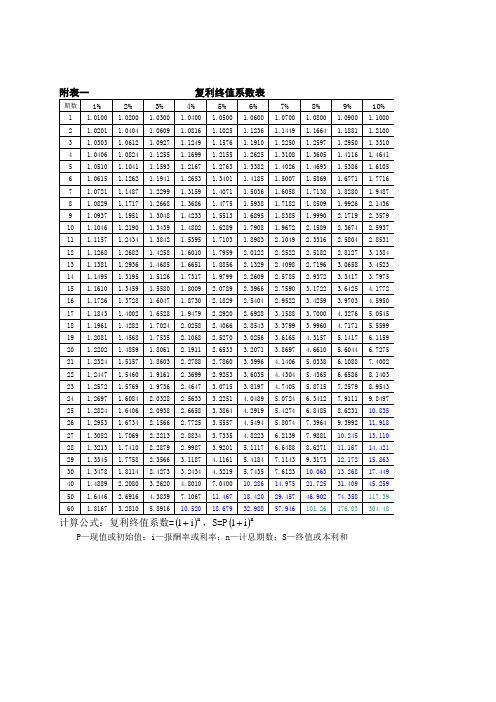
附表一 复利终值系数表计算公式:复利终值系数=()n i 1+,S=P ()ni 1+P —现值或初始值;i —报酬率或利率;n —计息期数;S —终值或本利和附表一 复利终值系数表 续表注:*〉99 999计算公式:复利终值系数=()n i 1+,S=P ()ni 1+P —现值或初始值 i —报酬率或利率 n —计息期数 S —终值或本利和附表二 复利现值系数表注:计算公式:复利现值系数=()-ni 1+,P=()ni 1S+=S ()-ni 1+P —现值或初始值;i —报酬率或利率;n —计息期数;S —终值或本利和附表二 复利现值系数表 续表注:*<0.0001计算公式:复利现值系数=()-ni 1+,P=()ni 1S+=S ()-ni 1+P —现值或初始值;i —报酬率或利率;n —计息期数;S —终值或本利和附表三年金终值系数表注:计算公式:年金终值系数=()i1i1n-+,S=A()i1i1n-+A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;S—年金终值或本利和附表三年金终值系数表续表注:*>999 999.99计算公式:年金终值系数=()i1i1n-+,S=A()i1i1n-+A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;S—年金终值或本利和附表四年金现值系数表计算公式:年金现值系数=()ii11n-+-,P=A()ii11n-+-A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;P—年金现值或本利和附表四年金现值系数表续表注:计算公式:年金现值系数=()ii11n-+-,P=A()ii11n-+-A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;P—年金现值或本利和。
4%复利20年终值系数表

4%复利20年终值系数表
摘要:
1.复利的概念和计算方法
2.复利20 年的终值系数表
3.复利20 年对投资收益的影响
4.如何利用复利20 年终值系数表进行投资规划
正文:
一、复利的概念和计算方法
复利是指在每个计息周期结束时,将上期所得利息加入本金,作为下一期的本金来计算复利。
复利的计算方法采用复利公式:A=P(1+r)^n,其中A 表示未来的投资价值,P 表示本金,r 表示年利率,n 表示投资年限。
二、复利20 年的终值系数表
复利20 年的终值系数表是一个数据表格,用于查找在给定年利率和投资年限下,本金经过20 年后的未来价值与本金的倍数关系。
例如,如果年利率为5%,投资年限为20 年,则可以通过查找复利20 年终值系数表,得知
20 年后的本金倍数为2.653。
三、复利20 年对投资收益的影响
复利20 年对投资收益的影响是显著的。
由于每个计息周期结束时,都将上期所得利息加入本金作为下一期的本金来计算复利,因此随着时间的推移,复利效应使得投资收益不断累积,最终实现财富的快速增长。
四、如何利用复利20 年终值系数表进行投资规划
在进行投资规划时,可以利用复利20 年终值系数表进行以下方面的分析:
1.确定投资目标:根据期望的未来收益,查找相应的终值系数,从而确定需要的本金投入。
2.选择投资产品:比较不同投资产品的年利率和投资年限,选择适合自己风险承受能力和收益期望的投资产品。
3.风险控制:根据投资年限和年利率,预测投资过程中可能出现的风险,并制定相应的风险控制措施。
总之,复利20 年终值系数表对于投资者进行投资规划具有重要的参考价值。
财务管理系数表、年金现值、终值、复利现值、终值
计算公式:复利终值系数=i 1+,S=P i 1+P —现值或初始值;i —报酬率或利率;n —计息期数;S —终值或本利和计算公式:复利终值系数=()n i 1+,S=P ()ni 1+P —现值或初始值 i —报酬率或利率 n —计息期数 S —终值或本利和附表二 复利现值系数表注:计算公式:复利现值系数=()-ni 1+,P=()ni 1S+=S ()-ni 1+P —现值或初始值;i —报酬率或利率;n —计息期数;S —终值或本利和附表二 复利现值系数表 续表注:*<0.0001计算公式:复利现值系数=()-ni 1+,P=()ni 1S+=S ()-ni 1+P —现值或初始值;i —报酬率或利率;n —计息期数;S —终值或本利和计算公式:年金终值系数=()i1i1n-+,S=A()i1i1n-+A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;S—年金终值或本利和计算公式:年金终值系数=()i1i1n-+,S=A()i1i1n-+A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;S—年金终值或本利和附表四年金现值系数表注:计算公式:年金现值系数=()ii11n-+-,P=A()ii11n-+-A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;P—年金现值或本利和附表四年金现值系数表续表注:计算公式:年金现值系数=()ii11n-+-,P=A()ii11n-+-A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;P—年金现值或本利和计算公式:自然对数值=lnN。
表示以自然数e为底,N的对数值。
如N=5.83,则查纵列5.8横列3对应的数值,即ln(5.83)=1.7630。
附表五自然对数表续表注:计算公式:自然对数值=lnN。
表示以自然数e为底,N的对数值。
如N=9.83,则查纵列9.8横列3对应的数值,即ln(9.83)=2.2854。
用excel生成复利终值系数表

用excel生成复利终值系数表复利是一种常见的投资方式,它可以使投资者的财富得到长期稳定的增长。
对于投资者来说,了解复利的计算方式和终值系数是非常重要的。
本文将介绍如何使用Excel生成复利终值系数表。
首先,我们需要确定复利的利率和投资的期数。
假设我们的投资方案是每年投入1000元,年利率为5%,持续投资10年。
接下来,我们需要使用Excel中的复利计算公式来计算每年的终值系数。
Excel中的复利计算公式为:=FV(rate, nper, pmt, pv, type)其中,rate是年利率,nper是投资期数,pmt是每期投入的金额,pv是初始投入的金额,type是投资类型,0表示期末付款,1表示期初付款。
在本例中,我们可以使用以下公式来计算第一年的终值系数: =FV(0.05, 1, -1000, 0, 0)其中,年利率为0.05,投资期数为1年,每期投入-1000元,初始投入为0元,投资类型为期末付款。
计算结果为1050元,即第一年的终值系数为1.05。
接下来,我们可以使用Excel的填充功能来自动填充剩余的终值系数。
首先,我们需要将第一年的终值系数放入第一行的第一列。
接着,我们需要选中这个单元格,然后将鼠标放在右下角的黑色小方块上,当鼠标变成黑色十字时,我们就可以按住鼠标左键,向下拖动,自动填充剩余的终值系数。
完成上述步骤后,我们就可以得到完整的复利终值系数表。
该表显示了每年的终值系数及其累计值,可以帮助我们快速了解复利投资的长期效果。
在使用Excel生成复利终值系数表的过程中,需要注意使用正确的公式和填充方式,才能得到准确可靠的结果。
同时,我们还需要对投资方案进行合理的规划和管理,才能最大化地利用复利效应,实现财富的增值和保值。
财务管理系数表、年金现值、终值、复利现值、终值

附表一复利终值系数表计算公式:复利终值系数=,S=PP—现值或初始值;i—报酬率或利率;n—计息期数;S—终值或本利和附表一复利终值系数表续表注:*〉99 999计算公式:复利终值系数=,S=PP—现值或初始值i—报酬率或利率n—计息期数S—终值或本利和附表二复利现值系数表注:计算公式:复利现值系数=,P==SP—现值或初始值;i—报酬率或利率;n—计息期数;S—终值或本利和附表二复利现值系数表续表注:*<0.0001计算公式:复利现值系数=,P==SP—现值或初始值;i—报酬率或利率;n—计息期数;S—终值或本利和附表三年金终值系数表注:计算公式:年金终值系数=,S=AA—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;S—年金终值或本利和附表三年金终值系数表续表注:*>999 999.99计算公式:年金终值系数=,S=AA—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;S—年金终值或本利和附表四年金现值系数表注:计算公式:年金现值系数=,P=AA—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;P—年金现值或本利和附表四年金现值系数表续表注:计算公式:年金现值系数=,P=AA—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;P—年金现值或本利和附表五自然对数表注:计算公式:自然对数值=lnN。
表示以自然数e为底,N的对数值。
如N=5.83,则查纵列5.8横列3对应的数值,即ln(5.83)=1.7630。
附表五自然对数表续表注:计算公式:自然对数值=lnN。
表示以自然数e为底,N的对数值。
如N=9.83,则查纵列9.8横列3对应的数值,即ln(9.83)=2.2854。
附表六正态分布下的累积概率[N(d)](即变量取值小于其均值与d个标准差之和的概率)注:例如,d=0.22,则N(d)=0.5871,即正态分布变量有0.5871的可能取值小于其均值与0.22个标准差之和。
