(整理)电路理论基础(梁贵书)第11章答案
华北电力大学电路理论基础(梁贵书)第10章答案

第十章习题答案10-1设有三个电压源,它们的电压相量分别为.0V ab s U U ︒=∠,.60V cd s U U ︒=∠,.60V ef s U U ︒=∠-,问这些电源应如何联结以组成(1)Y 联结对称三相电源;(2)Δ联结对称三相电源。
解:三个电压源分别表示为:-+60s U ︒∠0Vs U ︒∠60V s ︒∠-abcdef三个电压源的相量图分别为:.U -∴(1)Y 联结对称三相电源 (2)Δ联结对称三相电源A B Ce10-2对称Y 联结的三相电源,已知相电压为220V ,试求其线电压;并写出以A 相相电压为参考相量时的 .AB U ,.BC U ,.CA U 解:∵220V P U =,∴380V l P U ==若以A 相相电压为参考相量,即:.2200V A U ︒=∠∴..3038030V AB A U ︒︒=∠=∠..12038090V BC AB U U ︒︒=∠-=∠-...120120380150V CA BC AB U U U ︒︒︒=∠-=∠=∠10-5有一三相四线制三相电路,电源是对称的 ,相电压为220V ,中线阻抗为零,48.4A B Z Z ==Ω,242C Z =Ω,试 (a)求线电流...,,A B C I I I 和中线电流.N I .(b )若中线断开,其它条件不变,求负载相电压。
.CI解:....0A B C I I I I =++∵中线阻抗为零,∴'.000U =,∴可以将三相电路转化为三个单相分别计算.A I ,.B I ,.C I.U.A.BU .B.CU .C若以A 相相电压为基准,即:.2200V A U ︒=∠,∴.220120V B U ︒=∠-,.220120V C U ︒=∠∴..2200 4.550A 48.4A A A U I Z ︒︒∠===∠,..220120 4.55120A 48.4B B B U I Z ︒︒∠-===∠-..2201200.91120A 242C C C U I Z ︒︒∠===∠∴....0 4.55 4.551200.91120 1.82 3.152 3.6460A A B C I I I I j ︒︒︒=++=+∠-+∠=-=∠- (b )中线断开情况如图解:若以A 相相电压为参考相量,即:.2200V A U ︒=∠ ∴..120220120V B A U U ︒︒=∠-=∠-,..120220120V C A U U ︒︒=∠=∠.'....00111()A B CA B C A B CU U U U Z Z Z Z Z Z ++=++ 代入数值:'.001112200220120220120()48.448.424248.448.4242U ︒︒︒∠∠-∠++=++ '.0011 3.6460242U ︒=∠- ∴'.00242 3.646080.860V 11U ︒︒⨯∠-==∠-∴''...00022080.860179.670192.7621.3V A A U U U j ︒︒=-=-∠-=+=∠ ''...00022012080.860192.73141.3V B B U U U ︒︒︒=-=∠--∠-=∠-''...00022012080.860300.8120V C C U U U ︒︒︒=-=∠-∠-=∠10-6图示电路中,对称三相电源的 线电压为380V ,100L C R R X ==-=Ω,0200R =Ω,Y 300R =Ω ,求电阻0R 两端的电压。
潘双来第二版电路理论基础习题答案(完整版)

3-2. 155V. 3-3. 190mA. 3-4. 1.8 倍. 3-5. 左供 52W, 右供 78W. 3-6. 1 ; 1A; 0.75A. 3-7. 3A; 1.33mA; 1.5mA; 2/3A; 2A. 3-8. 20V, –75.38V. 3-9. –1A; 2A; 1A. 3-10. 5V, 20 ; –2V, 4 . 3-12. 4.6 . 3-13. 2V; 0.5A. 3-14. 10V, 5k . 3-15. 3-16.22.5V 3-17. 4/3 , 75W; 4/3 , 4.69W. 3-18. 3 , 529/12W.; 1 , 2.25W. 3-19 3-20. 50 . 3-21. 0.2A. 3-22. 1A. 3-23. 1.6V. 3-24. 4A; 3-25. 23.6V; 5A,10V. 3-26. 3-27 4V 3-28. ※ 第四章 o o o 4-1. 141.1V, 100V, 50Hz, 0.02s,0 , –120 ; 120 . o o o 4-2. 7.07/0 A, 1/–45 A, 18.75/–40.9 A. 4-3. U m 3 , 7.75mA . o o o 4-4. 10/53.13 A, 10/126.87 A, 10/–126.87 A, o 10/–53.13 A;各瞬时表达式略。 4-5. 67.08V, 30V, 25V; 12V, 0, 12V, 0; 0, 0, 12V. 4-6. 7.07A; 10A, 50A. 4-7. 173.2 . 4-8. 4 , 1.5H. 4-9.11V 4-10. 5 , 0.1F. o o 4-11. 5A; 20/–53.13 , 0.05/53.13 S. 4-12 4-13. 5 , 0.0577F; 3 , 29.33H; 3 ,0.125F; 0 ,0.02F 4-14.-Z 4-15. 4-16. 10A, 141V.
《新编基础物理学答案》-第11章

第11章 恒定电流与真空中的恒定磁场11-1 电源中的非静电力与静电力有什么不同?答:在电路中,电源中非静电力的作用是,迫使正电荷经过电源内部由低电位的电源负极移动到高电位的电源正极,使两极间维持一定的电位差。
而静电场的作用是在外电路中把正电荷由高电位的地方移动到低电位的地方,起到推动电流的作用;在电源内部正好相反,静电场起的是抵制电流的作用。
电源中存在的电场有两种:1、非静电起源的场;2、稳恒场。
把这两种电场与静电场比较,静电场由静止电荷所激发,它不随时间的变化而变化。
非静电场不由静止电荷产生,它的大小决定于单位正电荷所受的非静电力,kF E q=。
当然电源种类不同,k F 的起因也不同。
11-2静电场与恒定电场有什么相同处和不同处?为什么恒定电场中仍可应用电势概念? 答:稳恒电场与静电场有相同之处,即是它们都不随时间的变化而变化,基本规律相同,并且都是位场。
但稳恒电场由分布不随时间变化的电荷产生,电荷本身却在移动。
正因为建立稳恒电场的电荷分布不随时间变化,因此静电场的两条基本定理,即高斯定理和环路定理仍然适用,所以仍可引入电势的概念。
11-3一根铜导线表面涂以银层,当两端加上电压后,在铜线和银层中,电场强度是否相同?电流密度是否相同?电流强度是否相同?为什么? 答:此题涉及知识点:电流强度d sI =⋅⎰j s ,电流密度概念,电场强度概念,欧姆定律的微分形式j E σ=。
设铜线材料横截面均匀,银层的材料和厚度也均匀。
由于加在两者上的电压相同,两者的长度又相等,故铜线和银层的场强E 相同。
由于铜线和银层的电导率σ不同,根据j E σ=知,它们中的电流密度j 不相同。
电流强度d sI =⋅⎰j s ,铜线和银层的j 不同但相差不太大,而它们的横截面积一般相差较大,所以通过两者的电流强度,一般说来是不相同的。
11-4一束质子发生侧向偏转,造成这个偏转的原因可否是: (1)电场? (2)磁场?(3)若是电场或者是磁场在起作用,如何判断是哪一种场?答:造成这个偏转的原因可以是电场或磁场。
(完整版)电子线路-梁明理第五版全答案

第1章 半导体器件的特性1.1知识点归纳1.杂质半导体与PN 结在本征半导体中掺入不同杂质就形成N 型和P 型半导体。
半导体中有两种载流子,自由电子和空穴,载流子因浓度而产生的运动成为扩散运动,因电位差而产生的运动成为漂移运动。
在同一种本征半导体基片上制作两种杂质半导体,在它们的交界面上,上述两种运动达到动态平衡,就形成了PN 结。
其基本特性是单向导电性。
2.半导体二极管一个PN 结引出电极后就构成了二极管,加上正向偏压时形成扩散电流,电流与电压呈指数关系,加反向电压时,产生漂移电流,其数值很小。
体现出单向导电性。
3晶体管晶体管具有电流放大作用,对发射极正向偏置集电极反向偏置时,从射区流到基区的非平衡少子中仅有很少部分与基区的多子复合,形成基极电流B I ,而大部分在集电结外电场作用下形成漂移电流C I ,体现出B I 对C I 的控制,可将C I 视为B I 控制的电流源。
晶体管有放大、饱和、截止三个工作区域。
4.场效应管场效应管是电压控制器件,它通过栅-源电压的电场效应去控制漏极电流,因输入回路的PN 结处于反向偏置或输入端处于绝缘状态因此输入电阻远大于晶体管。
场效应管局又夹断区(即截止区)、横流区(即线性区)和可比阿安电阻区三个工作区域。
学完本章后应掌握:1.熟悉下列定义、概念和原理:自由电子与空穴,扩散与漂移,复合,空间电荷区,PN 结,耗尽层,导电沟道,二极管单向导电性,晶体管和场效应管的放大作用及三个工作区域。
2.掌握二极管、稳压管、晶体管,场效应管的外特性,主要参数的物理意义。
1.2习题与思考题详解1-1试简述PN 结的形成过程。
空间电荷压,阻挡层,耗尽层和势垒压等名称是根据什么特性提出来的。
答:PN 结的形成过程:当两块半导体结合在一起时,P 区的空穴浓度高于N 区,于是空穴将越过交界面由P 区向N 区扩散;同理,N 区的电子浓度高于P 区,电子越过交界面由N 区向P 区扩散。
多子由一区扩散到另一区时,形成另一区的少子并与该区的多子复合,因此,在交界面的一侧留下带负电荷的受主离子,另一侧留下带正电荷的施主离子。
电路理论课后答案,带步骤
解:(1)该电路有三个网孔。设网孔电流分别为 、 ,
参考方向如图3-4所示。并设受控源两端电压为U。
(2)列写网孔方程:
辅助方程为:
联立求解得:
U= V
所以: mW
3-5电路如题图3-5所示,试用网孔分析法求电流 和电压 。
题图3-5题图3-5(b)
解:(1)将原图中20A电流源与2 电阻并联部分等效为40V电压源与2 电阻串联,如图3-5(b)所示。
(2)列写节点方程:
整理得:
求解得: V
V
所以: V
3-7电路如题图3-7所示,①试用节点分析法列写电路的节点方程;②该电路能否用网孔分析法分析?为什么?
题图3-7题图3-7(b)
①解:
(1)将原图中的 电压源与 串联部分等效为 电流源与 并联。
且 。如图3-7(b)所示。
(2)该电路有5个节点,以节点5为参考点,节点电压分别设为: 、 、 ,
Ua=10-3I=4V
Ub=2I=4V
Uab=Ua–Ub=0V
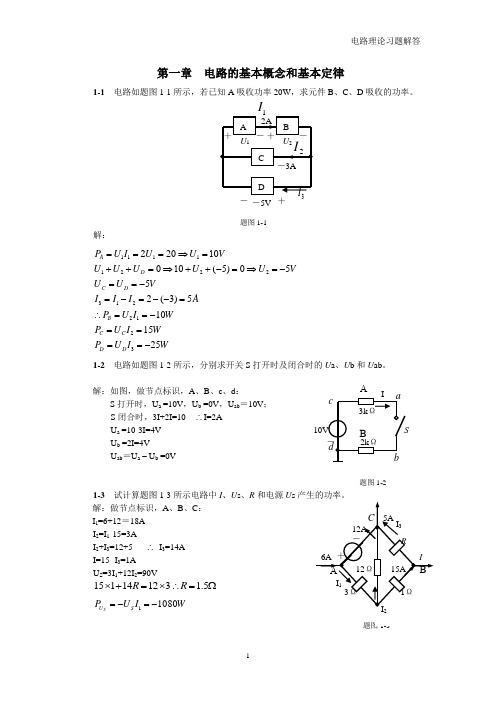
题图1-2
1-3试计算题图1-3所示电路中I、Us、R和电源Us产生的功率。
解:做节点标识,A、B、C:
I1=6+12=18A
I2=I1-15=3A
I2+I3=12+5 I3=14A
I=15- I3=1A
US=3I1+12I2=90V
题图1-3
2-15题图2-15所示电路,试问当电阻R等于何值时,可获得最大功率,最大功率等于多少?
题图2-15图2-15(b)
解:先将a,b与R断开,则
得:
所以:共戴维南等效电路为图(a)所示
所以:当 时,获得最大功率
电路基础-贺洪江-课后习题答案集

第一章 电路的根本概念和根本定律习题解答1-1 题1-1图所示电路,求各段电路的电压U ab 及各元件的功率,并说明元件是消耗功率还是对外提供功率?解 根据功率计算公式及题给条件,得〔a 〕U ab =6V, P =6×2= 12W 消耗功率〔b 〕U ab =-8V ,P =1×(-8)=-8W 提供功率〔c 〕U ab =-10V , P =-(-8)⨯(-10)=-80W 提供功率〔d 〕U ab =-8V , P =-(-2)⨯(-8)=-16W 提供功率〔e 〕U ab =-(-6)=6V ,P =-(-1)⨯(-6)=-6W 提供功率〔f 〕U ab =-16V , P =(-2)⨯16=-32W 提供功率1-2 在题1-2图所示各元件中,:元件A 吸收66W 功率,元件B 发出25W 功率;元件C 吸收负68W 功率,求i A 、u B 和i C 。
解 根据题意,对元件A ,有P A =6i A =66, i A =666=11A 对元件B ,有P B =-5u B =-25, u B =525--=5V 对元件C ,有P C =-4i C =-68, i C =468--=17A (a) (b) (d) (e) (f) 6V b -8V b -10V b (c) -8V b 16V b -6V b 题1-1图 题1-2图6V B -4V1-3 题1-3图所示电路中,5个元件代表电源或负载。
通过实验测量得知:I 1=-2A ,I 2=3A ,I 3=5A ,U 1=70V ,U 2=-45V ,U 3=30V ,U 4=-40V ,U 5=-15V 。
〔1〕试指出各电流的实际方向和各电压的实际极性?〔2〕判断那些元件是电源;那些元件是负载?〔3〕计算各元件的功率,验证功率平衡?解〔1〕图中虚线箭头为各支路电流的实际方向。
⊕极性为各元件电压的实际极性。
〔2〕按实际方向判断元件的状态:U 、I 关联者为负载,U 、I 非关联者为电源。
高中物理第十一章 电路及其应用第十一章 电路及其应用精选试卷综合测试(Word版 含答案)

高中物理第十一章电路及其应用第十一章电路及其应用精选试卷综合测试(Word版含答案)一、第十一章电路及其应用选择题易错题培优(难)1.如图所示,三个定值电阻R1、R2、R3的电阻值均不相等,在A、B之间接一个电源,在C、D之间接一个电流表,电流表的示数为I.现将电源、电流表的位置互调,则电流表的示数()A.可能增大B.可能减小C.一定不变D.由于R1、R2、R3大小关系不知,故无法判定【答案】C【解析】两种情况下的电路连接如图所示:设电源电压为U=6V,R1=3Ω,R2=2Ω,R3=6Ω,在甲图中2323= 1.5R RRR R⋅=Ω+甲并,112==1U RU R甲并甲并,1=6V2V33UU=⨯=甲并,电流表的示数为32V1=A63UIR==Ω甲并甲,在乙图中1212= 1.2R RRR R⋅=Ω+乙并,335==1U RU R乙并乙并,1=6V1V66UU=⨯=乙并,电流表的示数为11V1=A33UIR乙并乙==Ω,故两次示数相同,则选C.【点睛】在A、B之间接一个电源,假设A端为正极,在C、D之间接一个电流表时,通过电流表的电流通路是:A----R1----电流表----R3----B 电路中的电阻是R1+R3;将电源、电流表的地位互调,假设D端为正极,通过电流表的电流通路是:D----R1----电流表----R3----C 电路中的电阻是R1+R3.电路的电源不变,电阻不变,故电流一定不变.2.一根长为L、横截面积为S的金属棒,其材料的电阻率为ρ,棒内单位体积自由电子数为n,电荷量为e。
在棒两端加上恒定的电压时,棒内产生电流,自由电子定向运动的平均速率为v,则金属棒内的电场强度大小为A.ρnev B.ρnSev C.ρnLev D.ρnSLev【答案】A【解析】【详解】根据题意可知,流过导体的电流和导体的电阻分别为I nSev =,L R Sρ= 所以可得,加在导体两端的电压为 L U IR nSev nev L Sρρ=== 又因为此时导体内的电场为恒定电场,可得 U E nev Lρ== 故选A3.如图所示的部分电路中,已知I =3 A ,I 1=2 A ,R 1=10 Ω,R 2=5 Ω,R 3=30 Ω,则通过电流表的电流大小和方向是( )A .0.5 A ,向右B .0.5 A ,向左C .1 A ,向右D .1 A ,向左【答案】A【解析】【详解】 对于稳恒电路中的某一节点,流入的电流总和一定等于流出的电流总和.对于节点c ,已知流入的电流I =3 A ,流出的电流I 1=2 A ,则还有1 A 的电流要流出节点c ,由此可知经过R 2的电流I 2=1 A 向右.根据欧姆定律,U 1=I 1R 1=20 VU 2=I 2R 2=5 V电压等于电势之差U 1=φc -φaU 2=φc -φb两式相减可得φb -φa =15 V即b 点电势比a 点高15 V ,则通过R 3的电流330.5A b a φφI R -==方向向上,对于节点b ,流入的电流I 2=1 A ,流出的电流I 3=0.5 A ,则还有0.5 A 的电流流出b 点,因此可判断流过电流表的电流为0.5 A ,向右,故A 正确.故选A 。
电路基础课后习题答案专科教材汇总

最新资料整理推荐第1章章后习题解析1. 1 一只“100 Q、:L00W”的电阻与120 V电源相串联,至少要串入多大的电阻水才能使该电阻正常工作?电阻丘上消耗的功率又为多少?解:电阻允许通过的最大电流为所以应有100 + /?=耳,由此可解得:/? = ¥_100 = 20。
电阻水上消耗的功率为P=l2 X 20=20W1.2 图1. 27 (a)、(b)电路中,若让F0. 6A,於?图1. 27 (c)、聞刁題(d)电路中,若让庐0.6V,解:(Q图电路中,3Q电阻中通过的电流为r =2 -0. 6=1. 4A 水与3Q电阻相并联,端电压相同且为A1.4X 3=4. 2V所以斥4・2*0・6=7Q(b)图电路中,3 Q电阻中通过的电流为《T=3十3=1A水与3Q电阻相并联,端电压相同,因此用34-0. 6=5 Q(c)图电路中,2?与3Q电阻相串联,通过的电流相同,因此用0.6宁2=0・3Q(d)图电路中,3Q电阻两端的电压为U,=3 —0. 6=2. 4VR与3Q电阻相串联,通过的电流相同且为^2.44-3=0. 8A所以启0・6+0・8=0・75QUOV, 100W”1. 3两个额定值分别是“110V, 40W” “的灯泡,能否串联后接到220V的电源上使用?如果两只灯泡的额定功率相同时又如何?解:两个额定电压值相同、额定功率不等的灯泡,其灯丝电阻是不同的,“ 110V, 40W”灯泡的灯丝电阻为:R^~U - 11()~ -302.5Q ;"110V, 100W”灯泡的灯丝电阻为:P 40心严与=磐=加,若串联后接在220V的电源上时,其通r 100过两灯泡的电流相同,且为:心丽%"52A,因此40W灯泡两端实际所加电压为:“和=0.52x302.5 = 157.3 V,显然这个电压超过了灯泡的额定值,而100 W灯泡两端实际所加电压为:«oo=0. 52X121=62. 92V,其实际电压低于额定值而不能正常工作,因此,这两个功率不相等的灯泡是不能串联后接到220V电源上使用的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章习题解答11-1周期性矩形脉冲如图所示,试求其傅立叶级数展开形式。
t解:02212w T πππ=== 00011()22T m m U a f t dt U dt T πππ===⎰⎰ 00002211()cos 2cos sin 0Tm k m U a f t kw tdt U ktdt ktT kππππ=⋅===⎰⎰0002()sin 12sin 2211()cos ()(cos 1)21cos 41,3,5,00,2,4,Tk m mm m mb f t kw tdtT U ktdt U U kt k k k U k k U k k k πππππππππ=⋅===⋅⋅----=⎧=⎪=⎨⎪=⎩⎰⎰ ∴14mU b π=,343m U b π=,54,5mU b π=0135()sin sin 3sin 5444sin sin 3sin 5354111(sin sin 3sin 5sin 7)357mmm m m m f t a b t b t b t U U U Ut t t U U t t t t ππππππ=++++=++++=+++++11-3在图示电路中,无源一端口网络N 的 端口电压和端口电流分别为()100cos31450cos(94230)V u t t t ︒=+- 3()10cos314 1.75cos(942)A i t t t θ=++若把N 看作为RLC 串连电路,试求:(1)R,L,C 之值;(2)3θ之值;(3)电路消耗的功率。
解:(1)13()100cos31450cos(94230)()()u t t t u t u t ︒=+-=+313()10cos314 1.75cos(942)()()i t t t i t i t θ=++=+∵1()100cos314u t t =,∴.10V U ︒=∵1()10cos314i t t =,∴.10A I ︒=∵.1U 与.1I 同相,∴LC 串连分支对基波而言发生 串连谐振,∴.1.1100U R I ︒===Ω21314314C L =⇒= ∵3()50cos(94230)V u t t ︒=-,∴.330U ︒=-,3U = 33() 1.75cos(942)i t t θ=+,∴.33A I θ=∴333501.75U Z I ==== ∴22110(942)816.33942L C+-= 21(942)716.33942L C -= 194226.76942L C -=(∵w 时谐振,∴3w 时呈感性)∵21314C L =∴2194226.761942314L L -= 31494226.763LL -=∴31.9mH L =231317.94F 31431.910C μ-==⨯⨯(2)∵.330V U ︒=-,.33I θ= 33611(942)10(94231.910)942942317.941010(30 3.34)28.4769.44Z R j L j C j --︒=+-=+⨯⨯-⨯⨯=+-=∠Ω .3333.333028.4769.44U U Z I I θ︒︒==∠--≈∠ ∴33069.44θ︒︒--=∴33069.4499.44θ︒︒︒=--=-(3)1︒1()100cos314V u t t =单独作用时,1()10cos314A i t t =∴221110500W P I R =⨯=⨯= 2︒ 3()50cos(94230)V u t t ︒=-单独作用时,3() 1.75cos(94299.44)A i t t ︒=-2233101015.31W P I =⨯=⨯=1350015.31515.31W P P P =+=+=11-10图示电路为滤波电路,要求14w 的谐波电流传至负载,而使基波电流无法达到负载。
如电容1F C μ=,11000rad s w =,试求1L 和2L 。
负载解:根据题意,该电路对14w 的谐波分量发生串连谐振,对基波分量发生并联谐振,即:144000w =11000w == ∵1F C μ=, ∴126111H 1000100010L w C -===⨯⨯ 22111212121211616w w CL L L L L L C L L =⇒=+⋅+ 21121(161)w CL L L ⇒-=,∴1221110.067H 67mH 16115L L w CL ====-11-11图示电路中,()s u t 为非正弦波,其中含有13w 和17w 的 谐波分量。
若要求在输出电压()u t 中不含这两个谐波分量,问L C 和应为多少?()s u t )t解:方法一对3次谐波发生并联谐振,对7次谐波发生串连谐振。
121139w L w =⇒= 1211749w C w =⇒=方法二对7次谐波发生并联谐振,对3次谐波发生串连谐振。
1211749w L w =⇒=121139w C w =⇒= 11-12在图示的 对称三相电路中,电源电压()100sin 40sin 3V A u t wt wt =+,负载的基波阻抗68Z R jwL j =+=+。
试求(1)k 闭合时负载相电压,线电压,相电流及中线电流的有效值。
(2)k 打开时负载相电压,线电压,相电流及两中点间电压的有效值。
Au 解 :k 闭合13()100sin 40sin 3()()A A A u t wt wt u tu t =+=+1︒ 基波分量1()A u t 单独作用1Au .Z∵1()100sin A u t wt =,∴.10V A U ︒=681053.1Z R jwL j ︒=+=+=∠Ω..1153.1A A AU I Z ︒===- 2︒ 三次谐波分量3()A u t 单独作用∵3()40sin 3A u t wt =,∴.30V A U ︒= 相量模型为3B I 3CI 624j +624j +...33374.96AA B CI I I ︒=====- ..033 4.8674.96A A I I ︒==∠- ∴负载相电压的有效值为76.16V p U == 负载线电压的有效值为 122.5V l U == 相电流的有效值为 7.16A p I ==中线电流的有效值为 0 4.86A I = (1) k 打开1︒基波分量1()Au t 单独作用..1153.1A A AU I Z ︒===- 2︒ 三次谐波分量3()A u t 单独作用时.30A I =∴k 打开时,负载相电压的有效值为 70.7V p U ==负载线电压的有效值为 122.5V l p U U ==相电流的有效值为17.07A p A I I ===两中点间电压的有效值为'30028.28V A U U ===12-11在图示稳态电路中,100R =Ω,1200wL wC==Ω ()20200cos 68.5cos(230)V s u t wt wt ︒=+++,求0()u t 。
R0()u t s u解:∵012()20200cos 68.5cos(230)()()s s s s u t wt wt U u t u t ︒=+++=++1︒ 直流分量0s U 单独作用∵电感对直流而言,相当于短路,∴00U =2︒ 基波分量1s u 单独作用∵21200cos 200sin()s u wt wt π==+ ∴.190V s U ︒=相量模型为100Ω-+.01U s u∵1200wL wC==Ω,∴对基波而言LC 并联分支发生并联谐振。
∴..01190V s U U ︒==∴01()200sin(90)200cos V u t wt wt ︒=+=3︒ 二次谐波分量2()s u t 单独作用∵2()68.5cos(230)68.5sin(2120)s u t wt wt ︒︒=+=+∴.2120V s U ︒=相量模型为100Ω-+.02U100400400400'100//40040010033j j Z j j j j j j-⨯=-===-Ω-.02400'4003120120120400100'300400100340012083.1350053.1jZ j U Z j j j ︒︒︒︒︒︒--===+---==∠- ∴02()54.8sin(283.13)u t wt ︒=+∴000102()()()200sin(90)54.8sin(283.13)V u t U u t u t wt wt ︒︒=++=+++另:一部分谐波分析法1.一个RLC 串连电路,其中11R =Ω,0.015L H =,70C F μ=,外加电压()11141.4cos100035.4sin 2000V u t t t =+-,试求电路中的电流()i t 和电路消耗的功率。
RC-+()u t解:∵012()11141.4cos100035.4sin 2000V ()()u t t t u u t u t =+-=++ (1)直流分量单独作用,即011V u =单独作用∵电容具有隔直作用,∴00I = (2)1()u t 单独作用∵.21()141.4cos1000141.4sin(1000)V u t t t π==+ ∴.110090V U ︒=∠110000.01515L X wL ==⨯=Ω1611110014.29100070107C X w C --=-==-=-Ω⨯⨯ 相量模型为:-+11Ω15j Ω14.29j -Ω.1U11(1514.29)110.6911.02 3.6Z j j ︒=+-=+=∠Ω..11100909.0786.4A 11.02 3.6U I Z ︒︒︒∠===∠∠ ∴1()12.83sin(100086.4)A i t t ︒=+ (3)2()u t 单独作用∵2()35.4sin 200035.4sin(2000180)V u t t t ︒=-=+∴.218025180V U ︒︒==∠ 21221530L L X X ==⨯=Ω,127.1452C C X X ==-Ω 相量模型为-+11Ω30j Ω7.145j -Ω.2U11(307.145)1122.8525.3664.3Z j j ︒=+-=+=∠Ω..12251800.986115.7A 25.3664.3U I Z ︒︒︒∠===∠∠ 2() 1.39sin(2000115.7)A i t t ︒=+∴012()()()12.83sin(100086.4) 1.39sin(2000115.7)A i t I i t i t t t ︒︒=++=+++9.12A I ==≈229.1211915.6W P I R =⋅=⨯=2.在图示的电路中,12R =Ω,2wL =Ω,118wC=Ω, ()1030)3V u t wt wt ︒=+++,求电磁式电流表,电动式电压表及电动式瓦特表的读数。
