《圆的对称性》综合练习
《圆的对称性》综合练习

《圆的对称性》综合练习◆随堂检测1下列说法中,不成立的是A.弦的垂直平分线必过圆心B.弧的中点与圆心的连线垂直平分这条弧所对的弦C.垂直于弦的直线经过圆心,且平分这条弦所对的弧D.垂直于弦的直径平分这条弦2如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为点E,则图中不大于半圆的相等的弧有A.1对B.2对C.3对D.4对3如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,如果AB=10,CD=8,那么AE的长为A.2B.3C.4D.54如图,AB为⊙O的直径,弦CD⊥AB,垂足为点8cm3cm,∴AE=4cm.又∵OE=3cm,在Rt△AOE中,所以⊙O的半径为5cm.点评:从例中可以知道作“弦心距”是很重要的一条辅助线,弦心距的作用就是平分弦,平分弦所对的弧,它和直径一样.求圆的半径问题,要和弦心距,弦的一半和半径构造出一个直角三角形,和勾股定理联系起来.◆课下作业●拓展提高1.下列四个命题中,叙述正确的是A.平分一条直径的弦必垂直于这条直径B.平分一条弧的直径垂直于这条弧所对的弦C.弦的垂线必经过这条弦所在圆的圆心D.平分一条弦的直线必经过这个圆的圆心2.如图,⊙O的半径为4cm,点C是AB的中点,半径OC交弦AB于点D,OD=23cm,则弦AB的长为A.2cmB.3cmC.23cmD.4cm3.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,那么下列结论错误的是A.CE=DEB.BC BDC.∠BAC=∠BADD.AC>AD为24.若小唐同学掷出的铅球在场地上砸出一个直径约为10cm 、深约cm 的小坑,则该铅球的直径约为A .10cmB .C .19.5 cmD .20cm5.如图,⊙O 的半径为5,弦AB=8,OC⊥AB 于C ,则OC 的长等于_______.6.如图,⊙O 的直径AB 和弦CD 相交于点E ,AE=1cm ,EB=5cm ,∠DEB=60o,求CD 的长.7.已知:如图,∠,DB=10cm ,以DB 为直径作⊙O,交射线A AE BE =O ⊙AB CD P P OB 6cm CD =AB 23cm 32cm 42cm 43cm 3 16m10m .参考答案◆随堂检测1、C2、B3、A 提示:连接OC ,利用勾股定理求解4、10提示:连接OC ,设AP=,BP=4,则半径为,OP=,由垂径定理知CP=4,有勾股定理知=2,AB=5=105、100提示:垂径定理得AC=AD◆课下作业●拓展提高1、C2、D 提示:连接OA ,由勾股定理知AD=2,则AB=43、D 提示:垂径定理4、8提示:过O 点做OD 垂直AB 于D ,连接OA ,有OD=3,OA=5,AD=4,所以AB=85、3提示:连接OA6、00O OF CD D ODAE=1,BE=5,3sin ,sin 2OF OEF OF OE OE ODF CD DF ⊥∴====∴==解:过点作于,连接半径为,在直角三角形中,6060在直角三角形中7、0OM AP M,OFDB=10,5AO=8Rt OAM OM=AOsin 4O AP 4.,2Rt OFM 3,6O OM AP EF MFEF ⊥∴∴=∴⊥∴==∴=解:过作于连接半径为,在中,30圆心到的距离为在中, ●体验中考1、D2、A3、A 提示:35OM ≤≤4、4提示:6OD ==。
数学随堂小练北师大版(2012)九年级下册:3.2圆的对称性(有答案)

数学随堂小练北师大版(2012)九年级下册:3.2圆的对称性一、单选题1.如图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )A.60°B.90°C.120°D.180°2.下列说法正确的是()A.每一条直径都是圆的对称轴B.圆的对称轴是唯一的C.圆的对称轴一定经过圆心D.圆的对称轴与对称中心重合3.下列说法正确的是( )A.直径是圆的对称轴B.经过圆心的直线是圆的对称轴C.与圆相交的直线是圆的对称轴D.与半径垂直的直线是圆的对称轴4.下列说法中,错误的是()A.半圆是弧B.半径相等的圆是等圆C.过圆心的线段是直径D.直径是弦5.下列说法:①圆心相同的圆是同圆;②圆心不同,半径相等的圆是等圆;③长度相等的弧是等弧;④在同圆或等圆中,长度相等的弧是等弧;⑤大于半圆的弧叫做优弧;⑥小于半圆的弧叫做劣弧.其中正确的有( )A.1个B.2个C.3个D.4个6.已知,如图,AOB COD∠=∠,下列结论不一定成立的是( )A.AB CD =B. AB CD =C.AOB COD ≅△△D.,AOB COD △△都是等边三角形7.如图,A B C D ,,,是O 上的点,则图中与A ∠相等的角是( )A.B ∠B.C ∠C.DEB ∠D.D ∠8.如图,,AB CD 是O 的直径,AE BD =,若32AOE ∠=︒,则COE ∠的度数是()A.32︒B.60︒C.68︒D.64︒9.如图所示,在O 中,AB CD =,则在①AB CD =;②AB CD =;③AOC BOD ∠=∠;④AB CD =中,正确的个数是( )A.1B.2C.3D.4 二、填空题10.如图,AB CD EF ,,都是O 的直径,且123∠=∠=∠,则O 的弦AC BE DF ,,的大小关系是 .11.如图,在O 中,30AB AC A =∠=︒,,则B ∠= .12.如图,AB 是半圆O 的直径,E 是半圆上一点,且OE AB ⊥,点C 为BE 的中点,则A ∠= °.13.如图,AB 是O 的直径,BC CD DE ==,32COD ∠=︒,则AEO ∠的度数为 .三、解答题14.如图,,,A B C 为O 上的三等分点.(1)求BOC ∠的度数;(2)若3AB =,求O 的半径长及ABC S △.参考答案1.答案:C由题意可知ABC △为正三角形,O 为圆心,连接圆心和三角形的三个顶点,即可得到120AOB BOC AOC ∠=∠=∠=°,所以旋转120°后,能使旋转后的图形与原图形重合.故选C.2.答案:C对称轴是直线,不是线段,故A 不正确;圆的对称轴有无数条,故B 不正确;不能说点和线重合,故D 不正确.只有C 正确,故选C.3.答案:B利用直径所在的直线是圆的对称轴对各选项进行判断,故选B.4.答案:C过圆心的弦为直径.所以C 选项的说法错误;选项A 、B 、D 说法都正确.故选C.5.答案:D能够重合的两个圆叫做等圆.与此意思相同的是“圆心不同,半径相等的圆是等圆”,故①错误,②正确;等弧不仅考虑长度要相等,还要考虑是否能够互相重合,即必须是“在同圆或等圆中,能够互相重合的弧叫做等弧”,与此意思相同的是“在同圆或等圆中,长度相等的弧是等弧”故③错误,④正确;⑤⑥是优弧、劣弧的定义,正确.所以正确的共有4个.6.答案:DAOB COD ∠=∠,AB CD ∴=,AB CD =.OA OB OC OD ===,OB COD ∴≅△△,∴选项A 、B 、C 成立;只有当60AOB COD ∠=∠=︒时,,AOB COD △△才是等边三角形,所以选项D 不一定成立故选D7.答案:DD ∠与A ∠都是BC 所对的圆周角,D A ∴∠=∠.8.答案:DAE BD =,32BOD AOE ∴∠=∠=︒,BOD AOC ∠=∠,32AOC ∴∠=︒,COE AOE AOC ∴∠=∠+∠323264=︒+︒=︒ .9.答案:D 在O 中,AB CD AB CD AB BC CD BC =∴=-=-,,, AC BD AC BD AOC BOD ∴=∴=∠=∠,,,∴①②③④都正确10.答案:AC BE DF ==123123AOC BOE DOF ∠=∠∠=∠∠=∠∠=∠=∠,,,且, AOC BOE DOF AC BE DF ∴∠=∠=∠∴==.11.答案:75在O 中,AB AC =,AB AC ∴=,ABC ∴△是等腰三角形,B C ∴∠=∠12.答案:22.5如图,连接OC . ,90.OE AB EOB ⊥∴∠=° ∵点C 为BE 的中点,45BOC ∴∠=°.114522.522A BOC ∴∠=∠=⨯=°° .13.答案:48°BC CD DE ==,32COD ∠=︒,32BOC EOD COD ∴∠=∠=∠=︒,18084AOE EOD COD BOC ∠=︒-∠-∠-∠=︒. 又OA OE =,AEO OAE ∴∠=∠,118(08)4482AEO ∴∠=⨯︒-︒=︒ 14.答案:(1),,A B C 为O 上的三等分点AB BC AC ∴== BOC ∴∠的度数为:13601203⨯︒=︒. (2)过点O 作OD AB ⊥于点D,,A B C 为O 上的三等分点3AB AC BC ∴===即ABC △是等边三角形,且30BAO OBA ∠=∠=︒则32AD =,3cos302AO =÷︒=故2DO =132ABC S DO AB =⨯⨯⨯=△。
3.2 圆的对称性(练习)(解析版)

第三章圆第二节圆的对称性精选练习一、单选题1.(2021·全国九年级课时练习)下列说法中,正确的是()A.等弦所对的弧相等B.等弧所对的弦相等C.圆心角相等,所对的弦相等D.弦相等所对的圆心角相等【答案】B【分析】根据圆心角,弦,弧之间的关系判断,注意条件.【详解】A中,等弦所对应的弧可以相等也可以互补构成新圆;B中,等弧所对应的弦相等,故选BC中,圆心角相等所对应的弦可能互补;D中,弦相等,圆心角可能互补;故选B【点睛】本题考查了圆心角,弧,弦之间的观,此类试题属于难度较大的试题,其中,弦和圆心角等一些基本知识容易混淆,从而很难把握.2.(2021·全国九年级课时练习)下列说法中,不正确的是()A.圆是轴对称图形B.圆的任意一条直径所在的直线都是圆的对称轴C.圆的任意一条直径都是圆的对称轴D.经过圆心的任意直线都是圆的对称轴【答案】C【分析】根据轴对称图形的概念并结合圆的特点判断各选项,然后求解即可.【详解】A 、圆是轴对称图形,正确;B 、圆的任意一条直径所在得直线都是圆的对称轴,正确;C 、圆的任一直径所在的直线都是圆的对称轴,错误;D 、经过圆心的任意直线都是圆的对称轴,正确,故选:C .【点睛】本题主要是考查圆的特征、轴对称图形的特征,注意,语言要严密,不能说成圆的直径就是圆的对称轴,因为对称轴是一条直线,直径是线段.3.(2021·全国九年级课时练习)下列说法:①直径是弦;②长度相等的两条弧是等弧;③圆是中心对称图形;④任何一条直径都是圆的对称轴,其中说法正确的有( )个A .1个B .2个C .3个D .4个【答案】B【分析】根据圆的性质依次判断即可得到答案.【详解】①直径是圆中最长的弦,故正确;②在同圆或等圆中,能够完全重合的两条弧是等弧,故②错误;③圆是中心对称图形,故正确;④任何一条直径所在的直线都是圆的对称轴,故④错误,正确的有2个,故选:B.【点睛】此题考查圆的性质,正确掌握弦、等弧的定义,圆的对称性是解题的关键.4.(2020·杭州市建兰中学九年级月考)如图,AB 是圆O 的直径,点C 是半圆O 上不同于,A B 的一点,点D 为弧AC 的中点,连结,,OD BD AC ,设,CAB BDO b a Ð=Ð=,则( ).A .a b=B .290a b °+=C .290a b °+=D .45a b °+=【答案】C利用等腰三角形边角关系表示出∠AOD ,再根据同圆中平分弧平分弦垂直弦求出关系即可.【详解】解析 如图,设AC 与DO 交点为E ,连接BC ,OD OB = ,OBD BDO a \Ð=Ð=,2DOA OBD BDO a \Ð=Ð+Ð=,又D Q 为 AC 中点,AB 为O e 直径,,OD AC BC AC \^^,90AED ACB °\Ð=Ð=,90EAO EOA °\Ð+Ð=,即:290a b °+=.故选C .【点睛】此题考查了垂径定理中同圆中平分弧平分弦垂直弦,等边对等角等有关知识点,难度一般.5.(2020·西安益新中学九年级期末)如图,AB 是O e 的直径,弧BC 、弧CD 与弧DE 相等,36COD Ð=°,则AOE Ð的度数是( )A .30°B .36°C .54°D .72°【答案】D【分析】由弧BC 、弧CD 与弧DE 相等,得36COB COD EOD Ð=Ð=Ð=°,即可求AOE Ð.解:∵弧BC 、弧CD 与弧DE 相等,∴36COB COD EOD Ð=Ð=Ð=°,18036372AOE Ð=°-°´=°,故选:D .【点睛】本题考查了圆心角和弧的关系,解题关键是熟知在同圆和等圆中,相等的弧所对的圆心角相等.6.(2021·全国九年级课时练习)如图,已知:AB 是O e 的直径,C 、D 是 BE上的三等分点,60AOE Ð=o ,则COE Ð是( )A .40oB .60oC .80oD .120o【答案】C【分析】先求出∠BOE=120°,再运用“等弧对等角”即可解.【详解】∵∠AOE=60°,∴∠BOE=180°-∠AOE=120°,∴»BE的度数是120°,∵C 、D 是»BE上的三等分点,∴弧CD 与弧ED 的度数都是40度,∴∠COE=80°,故选C.【点睛】本题主要考查圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.熟练掌握圆周角定理是解题关键.7.(2021·全国九年级课时练习)如图,⊙O 中,弦AB ⊥CD ,垂足为E ,F 为 CBD的中点,连接AF 、BF 、AC ,A F 交CD 于M ,过F 作FH ⊥AC ,垂足为G ,以下结论:① CFDF =;②HC =BF :③MF =FC :④ DF AH BF AF +=+,其中成立的个数是( )A.1个B.2个C.3个D.4个【答案】C【分析】根据弧,弦,圆心角之间的关系,圆周角定理以及三角形内角和定理一一判断即可.【详解】解:∵F为CBD的中点,∴CF DF=,故①正确,∴∠FCM=∠FAC,∵∠FCG=∠ACM+∠FCM,∠AME=∠FMC=∠ACM+∠FAC,∴∠AME=∠FMC=∠FCG>∠FCM,∴FC>FM,故③错误,∵AB⊥CD,FH⊥AC,∴∠AEM=∠CGF=90°,∴∠CFH+∠FCG=90°,∠BAF+∠AME=90°,∴∠CFH=∠BAF,∴=,CF BF∴HC=BF,故②正确,∵∠AGF=90°,∴∠CAF+∠AFH=90°,∴+=180°,AH CF∴+=180°,CH AF∴+=+=+=+,故④正确,AH CF AH DF CH AF AF BF故选:C.【点评】本题考查圆心角,弧,弦之间的关系,三角形内角和定理等知识,解题的关键是熟练掌握基本知识,属于中考选择题中的压轴题.8.(2019·武汉市梅苑学校九年级月考)如图AB 为⊙O 的定直径,过圆上一点C 作弦CD AB ^,OCD Ð的平分线交⊙O 于点P ,当点C (不包括A ,B 两点)在⊙O 上移动时,点P ( )A .到CD 的距离保持不变B .位置不变C .等分弧DBD .随C 点移动而移动【答案】B【分析】连OP ,由CP 平分∠OCD ,得到∠1=∠2,而∠1=∠3,可得2=3,ÐÐ所以有//OP CD ,则OP ⊥AB ,即可得到OP 平分半圆APB .从而可得答案.【详解】解:连OP ,如图,∵CP 平分∠OCD ,∴∠1=∠2,OC=OP ,\ ∠1=∠3,∴∠2=∠3,∴//OP CD ,又∵弦CD ⊥AB ,∴OP ⊥AB ,∴OP 平分半圆APB ,即点P 是半圆的中点.故选:B .【点睛】本题考查了角平分线的定义,平行线的判定,等腰三角形的性质,圆的对称性,掌握以上知识是解题的关键.二、填空题9.(2021·全国九年级课时练习)半径为5的⊙O是锐角三角形ABC的外接圆,AB=BC,连结OB、OC,延长CO 交弦AB于D,若△OBD是直角三角形,则弦BC的长为______________.【答案】【分析】如图1,当∠DOB=90°时,推出△BOC是等腰直角三角形,于是得到=;如图2,当∠ODB=90°时,推出△ABC是等边三角形,解直角三角形得到BC=AB=.【详解】如图1,当∠DOB =90°时,∴∠BOC=90°∴△BOC是等腰直角三角形∴=^如图2,当∠ODB=90°时,即CD AB∴ AD=BD∴ AC=BC∵ AB=BC∴△ABC是等边三角形∴∠DBO=30°∵ OB=5∴BD==∴ BC=AB=.综上所述:若△OBD是直角三角形,则弦BC的长为.故答案为:.【点睛】本题考查了三角形的外接圆与外心,等边三角形的判定和性质,等腰直角三角形的性质,正确的作出图形是解题的关键.10.(2021·全国九年级课时练习)如图,AB是⊙O的直径,AD DE=,AB=5,BD=4,则cos∠ECB=__.【答案】3 5【分析】连接AD,BE,根据直径所对的圆周角是直角,构建两个直角三角形,再利用等弧所对的圆周角相等得:∠ABD=∠CBE,根据等角的余角相等得:∠ECB=∠DAB,最后利用等角的三角函数得出结论.【详解】解:连接AD, BE,AD DE=,∴EBC DBAÐ=Ð,∵AB是⊙O的直径,∴∠AEB=∠ADB=90°,∴∠ECB+∠EBC=90°,∠DBA+∠DAB=90°,∴∠ECB =∠DAB .AB =5,BD =4 ,3AD \==, ∴3cos cos 5ECB DAB Ð=Ð=.【点睛】本题考查了圆周角定理,解直角三角形,余角的性质,以及勾股定理等知识.掌握圆周角的两个定理:①在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.②半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.这两个性质在圆的证明题中经常运用,要熟练掌握.11.(2021·全国九年级课时练习)如图,A 、D 是⊙O 上的两点,BC 是直径,若∠D =32°,则∠OAC =_______度.【答案】58【分析】根据∠D 的度数,可以得到∠ABC 的度数,然后根据BC 是直径,从而可以得到∠BAC 的度数,然后可以得到∠OCA 的度数,再根据OA=OC ,从而可以得到∠OAC 的度数.【详解】解:∵∠D=32°,∠D=∠ABC∴∠ABC=32°∵BC 是直径∴∠BAC=90°∴∠BCA=90°-∠ABC=90°-32°=58°∴∠OCA=58°∵OA=OC∴∠OAC=∠OCA∴∠OAC=58°故答案为58.【点睛】本题考查了圆周角定理,圆心角、弧、弦的关系.解题的关键是明确题意,利用数形结合的思想解答.12.(2021·上海九年级专题练习)一根横截面为圆形的下水管的直径为1米,管内污水的水面宽为0.8米,那么管内污水深度为__________米.【答案】0.8或0.2.【分析】构造垂径定理,分两种情形求得弦心距,从而得到水深.【详解】如图所示,作AB 的垂直平分线,垂足为E ,根据题意,得 AO=0.5,AE=0.4,根据勾股定理,得,∴水深ED=OD-OE=0.5-03=0.2(米)或水深ED=OD+OE=0.5+03=0.8(米),∴水深为0.2米或0.8米.故答案为:0.2米或0.8.【点睛】本题考查了垂径定理,勾股定理,解答时,构造垂径定理,活用分类思想是解题的关键.三、解答题13.(2021·全国九年级课时练习)如图,⊙O的弦AB、CD的延长线相交于点P,且PA=PC.求证:AB CD=.【答案】证明见解析【分析】连接AC、OA、OB、OC、OD,根据等腰三角形的性质得到∠PAC=∠PCA,根据圆周角定理得到∠BOC=∠AOD,根据圆心角、弧、弦的关系定理证明结论.【详解】证明:连接AC、OA、OB、OC、OD,∵PA=PC,∴∠PAC=∠PCA,∵∠PAC12=∠BOC,∠PCA12=∠AOD,∴∠BOC=∠AOD,∴AD BC=n n,∴AD BD BC BD-=-,即AB CD=.【点睛】本题考查的是圆心角、弧、弦的关系定理、圆周角定理,在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.14.(2021·全国九年级课时练习)如图,在⊙O中,弦AD与BC交于点E,且AD=BC,连接AB、CD.求证:(1)AB=CD;(2)AE =CE .【答案】(1)证明见解析;(2)证明见解析.【分析】(1)欲证明AB=CD ,只需证得 AB = CD ;(2)连接AC ,由 AB = CD得出∠ACB=∠CAD ,再由等角对等边即可证的AE =CE.【详解】证明:(1)∵AD =BC∴ AD = BC∴ AD -AC = BC - AC 即 AB = CD∴AB =CD(2)连接AC∵ AB = CD∴∠ACB =∠DAC∴AE =CE【点睛】本题考查了圆周角、弧、弦间的关系,注意(2)中辅助线的作法是求解(2)的关键.15.(2020·江苏苏州市·苏州草桥中学九年级期中)如图,在O e 中, AC CB=,CD OA ^于点D ,CE OB ^于点E .(1)求证:CD CE =;(2)若120AOB Ð=°,2OA =,求四边形DOEC 的面积.【答案】(1)证明见解析;(2【分析】(1)如图,连接OC ,先证明,AOC BOC Ð=Ð再证明:,CDO CEO V V ≌从而可得结论;(2)由120AOB Ð=°,2OA =,求解60AOC Ð=°,再利用三角函数求解,OD CD , 利用,CDO CEO V V ≌从而可得四边形的面积.【详解】(1)证明:如图,连接OC ,AC BC= , ,AOC BOC \Ð=Ð,,CD OA CE OB ^^90CDO CEO \Ð=Ð=°,,OC OC =(),CDO CEO AAS \V V ≌.CD CE \=(2)120,AOB Ð=60AOC BOC \Ð=Ð=°,2OA OC == ,1cos 6021,sin 6022OD OC CD OC \=°=´==°==g g ,CDO CEO V V ≌12212CDO CDOE S S \==´´=V 四边形【点睛】本题考查的是三角形全等的判定与性质,圆的基本性质,两条弧,两个圆心角,两条弦之间的关系定理,解直角三角形的应用,四边形的面积,掌握以上知识是解题的关键.。
圆的对称性练习题

知识点一、 圆的对称性1:已知在O ⊙中,半径5r =,AB CD ,是两条平行弦,且86AB CD ==,,则弦AC 和BD 之间的距离为__________.2、下列命题是真命题的是( )A .同弧或等弧所对的圆周角相等 B .平分弦的直径垂直于弦 C .若两条弦所夹的弧相等,则着两条弦互相平行 D .相等的圆周角所对的弧相等3、如图,在Rt △ABC 中,∠ACB=90°,AC=3,BC=4,以点C 为圆心,CA 为半径的圆与AB 交于点D ,则AD 的长为( )A .59 B .521 C .518 D .254、(古题今解)“今有圆材,埋在壁中,不知大小,以锯锯之,深-寸,锯道长一尺,问径几何”.这是《九章算术》中的问题,用数学语言可表述为:如图,CD 为⊙O 的直径,弦AB ⊥CD 于点E ,CE=1寸,AB=10寸,则直径CD 的长为( )A .12.5寸B .13寸C .25寸D .26寸5、如图.Rt △ABC 内接于⊙O ,BC 为直径,AB=4,AC=3,D 是弧 AB 的中点,CD 与AB 的交点为E ,则DECE 等于( )A .4 B .3.5 C .3 D .2.8 6、如图,MN 是⊙O 的直径,MN=2,点A 在⊙O 上,∠AMN=30°,B 为 弧AN 的中点,P 是直径MN 上一动点,则PA+PB 的最小值为( )A .22 B .2 C .1 D .2 7、已知 弧AB 、弧CD 是同圆的两段弧,且 弧AB =2CD ,则弦AB 与2CD 之间的关系为( )A .AB=2CDB .AB <2CDC .AB >2CD D .不能确定8、如图,AB 是⊙O 的弦,AB 长为8,P 是⊙O 上一个动点(不与A 、B 重合),过点O 作OC ⊥AP 于点C ,OD ⊥PB 于点D ,则CD 的长为 .9、如图,AB 、CD 是半径为5的⊙O 的两条弦,AB=8,CD=6,MN 是直径,AB ⊥MN 于点E ,CD ⊥MN 于点F ,P 为EF 上的任意一点,则PA+PC 的最小值为 .10、如图,AB 是⊙O 的直径,弦BC=4cm ,F 是弦BC 的中点,∠ABC=60°.若动点E 以1cm/s 的速度从A 点出发在AB 上沿着A →B →A 运动,设运动时间为t (s )(0≤t <16),连接EF ,当△BEF是直角三角形时,t(s)的值为(填出一个正确的即可)11、如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.(1)如果⊙O的半径为4,CD=4 3,求∠BAC的度数;(2)若点E为弧ADB 的中点,连接OE,CE.求证:CE平分∠OCD;(3)在(1)的条件下,圆周上到直线AC距离为3的点有多少个?并说明理由.12、如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在圆的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,求小桥所在圆的半径.。
2021-2022学年北师大版九年级数学下册《3-2圆的对称性》同步达标测试题(附答案)
2021-2022学年北师大版九年级数学下册《3-2圆的对称性》同步达标测试题(附答案)一.选择题(共10小题,满分50分)1.下列说法正确的是()A.等弧所对的弦相等B.平分弦的直径垂直弦并平分弦所对的弧C.相等的弦所对的圆心角相等D.相等的圆心角所对的弧相等2.下列命题是真命题的是()A.相等的弦所对的弧相等B.圆心角相等,其所对的弦相等C.在同圆或等圆中,圆心角不等,所对的弦不相等D.弦相等,它所对的圆心角相等3.如图,AB,CD是⊙O的直径,=,若∠AOE=32°,则∠COE的度数是()A.32°B.60°C.68°D.64°4.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为()A.5πcm B.6πcm C.9πcm D.8πcm5.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是()A.AB=AD B.BC=CD C.D.∠BCA=∠DCA6.如图,AB是圆O的直径,BC、CD、DA是圆O的弦,且BC=CD=DA,则∠BCD等于()A.100°B.110°C.120°D.135°7.如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连接AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是()A.50°B.65°C.100°D.130°8.如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是()A.51°B.56°C.68°D.78°9.如图,四边形ABCD内接于半圆O,AB为直径,AB=4,AD=DC=1,则弦BC的长为()A.3.5B.2C.D.10.如图D、A、C、B为⊙O上的点,DC=AB,则AD与BC的大小关系是()A.AD>BC B.AD=BC C.AD<BC D.不能确定二.填空题(共5小题,满分30分)11.如图所示,四边形AB∥CD,AD=DC=DB=p,BC=q,则AC=(用p、q表示).12.弦AB分圆为1:3两部分,则劣弧所对圆心角为.13.一条弦把圆分成1:3两部分,则弦所对的圆心角为度.14.如图,在⊙O中,,∠A=40°,则∠B=度.15.在半径为9cm的圆中,60°的圆心角所对的弦长为cm.三.解答题(共5小题,满分40分)16.已知锐角∠POQ,如图,在射线OP上取一点A,以点O为圆心,OA长为半径作,交射线OQ于点B,连接AB,分别以点A,B为圆心,AB长为半径作弧,交于点E,F,连接OE,EF.(1)证明:∠EAO=∠BAO;(2)若OE=EF.求∠POQ的度数.17.如图,MB,MD是⊙O的两条弦,点A,C分别在,上,且AB=CD,M是的中点.(1)求证:MB=MD;(2)过O作OE⊥MB于点E,当OE=1,MD=4时,求⊙O的半径.18.已知:如图,C,D是以AB为直径的⊙O上的两点,且OD∥BC.求证:AD=DC.19.如图所示,⊙O的直径AB和弦CD相交于点E,且点B是劣弧DF的中点.(1)求证:△EBD≌△EBF;(2)已知AE=1,EB=5,∠DEB=30°,求CD的长.20.如图,已知AB、CD为⊙O的两条弦,,求证:AB=CD.参考答案一.选择题(共10小题,满分50分)1.解:A、正确.本选项符合题意.B、错误.应该是平分弦(此弦非直径)的直径垂直弦并平分弦所对的弧,本选项不符合题意.C、错误,必须在同圆或等圆中,本选项不符合题意.D、错误.必须在同圆或等圆中,本选项不符合题意.故选:A.2.解:A、B、D结论若成立,都必须以“在同圆或等圆中”为前提条件,所以A、B、D 错误;故选:C.3.解:∵=,∴∠BOD=∠AOE=32°,∵∠BOD=∠AOC,∴∠AOC=32°∴∠COE=32°+32°=64°.故选:D.4.解:如图,连接OD、OC.∵AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,∴==,∴∠AOD=∠DOC=∠BOC=60°.又OA=OD,∴△AOD是等边三角形,∴OA=AD=4cm,∴⊙O的周长=2×4π=8π(cm).故选:D.5.解:A、∵∠ACB与∠ACD的大小关系不确定,∴AB与AD不一定相等,故本选项错误;B、∵AC平分∠BAD,∴∠BAC=∠DAC,∴=,∴BC=CD,故本选项正确;C、∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等,故本选项错误;D、∠BCA与∠DCA的大小关系不确定,故本选项错误.故选:B.6.解:连接OC、OD,∵BC=CD=DA,∴∠COB=∠COD=∠DOA,∵∠COB+∠COD+∠DOA=180°,∴∠COB=∠COD=∠DOA=60°,∴∠BCD=×2(180°﹣60°)=120°.故选:C.7.解:由题意可得:AB=AC,∵∠ABC=65°,∴∠ACB=65°,∴∠A=50°,∴∠BOC=100°,故选:C.8.解:如图,∵==,∠COD=34°,∴∠BOC=∠EOD=∠COD=34°,∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=78°.又∵OA=OE,∴∠AEO=∠OAE,∴∠AEO=×(180°﹣78°)=51°.故选:A.9.解:如图,连AC、BD,过D作DE⊥AC于E.∴∠ADB=∠ACB=90°,∠ABD=∠CAD.∵BD==.∵AD=DC=1,∴∠DAC=∠DCA,∵∠DCA=∠ABD,cos∠CAD=cos∠ABD==.∴AE=AD•cos∠CAD=,∴AC=2AE=,∴BC==.故选:A.10.解:∵DC=AB,∴=,∴=,∴AD=BD.故选:B.二.填空题(共5小题,满分30分)11.解:延长CD交半径为p的⊙D于E点,连接AE.显然A、B、C在⊙D上.∵AB∥CD∴=,∴BC=AE=q.在△ACE中,∠CAE=90°,CE=2p,AE=q,故AC==.故答案为:.12.解:设弦AB分圆的两部分别为x,3x,∴x+3x=360°,解得:x=90,则劣弧所对圆心角为90°.故答案为:90°13.解:∵一条弦把圆分成1:3两部分,∴整个圆分为四等分,则劣弧的度数为360°÷4=90°,∴弦所对的圆心角为90°.14.解:∵,∴AB=AC,∵∠A=40°,∴∠B=∠C=(180°﹣∠A)÷2=70°.15.解:由题意知,设圆心为O,60°的圆心角的两边与圆的交点分别为A,B,则△AOB 是等边三角形,∴AO=AB=OB=9cm.三.解答题(共5小题,满分40分)16.(1)证明:连接AE、OE、OF,如图所示,由题意得:OB=OE=OA,AE=AB,∴∠EAO=∠AEO,∠BAO=∠ABO,,∴∠AOE=∠AOB,∴∠EAO=∠BAO;(2)解:∵OE=OF,OE=EF,∴OE=OF=EF,∴∠EOF=60°,∵AE=BF=AB,∴,∴∠AOE=∠BOF=∠AOB,∴∠POQ=∠EOF=20°.17.(1)证明:∵AB=CD,∴=,∵M是的中点,∴=,∴=,∴BM=DM.(2)解:如图,连接OM.∵DM=BM=4,OE⊥BM,∴EM=BE=2,∵OE=1,∠OEM=90°,∴OM===,∴⊙O的半径为.18.证明:连接OC,如图,∵OD∥BC,∴∠1=∠B,∠2=∠3,又∵OB=OC,∴∠B=∠3,∴∠1=∠2,∴AD=DC.19.解:(1)连接OD、OF,∵B是劣弧DF的中点.∴,∴,∴BD=BF,∠DBE=∠EBF,在△EBD和△EBF中,∵,∴△EBD≌△EBF(SAS);(2)∵AE=1,EB=5,∴AB=6,∵AB是⊙O的直径,∴OD=OA=3,OE=3﹣1=2,过O作OG⊥CD于G,则CD=2DG,∵∠DEB=30°,∠EGO=90°,∴OG=OE=1,由勾股定理得:DG===2,∴CD=2DG=4.20.解:∵,∴,即:,∴AB=CD.。
《圆的对称性能力提升 》同步练习(附答案) 2022年北师大版

圆的对称性能力提升1.是同圆的两段弧,且=2,那么弦AB与CD之间的关系为()A.AB=2CDB.AB<2CDC.AB>2CD2.如图,AB是☉O的直径,C是☉O上的一点,OD∥AC,那么的大小关系是()A.B.=2C.23.同圆中,弧长分别为m,n的两段劣弧所对弦的弦长分别为a,b,如果a>b,那么()A.m>nB.m=nC.m<nD.m≤n4.如图,D,E分别是☉O的半径OA,OB上的点,CD⊥OA,CE⊥OB,CD=CE,那么弧长的大小关系是.5.如图,AB,CD,EF都是☉O的直径,且∠1=∠2=∠3,那么☉O的弦AC,BE,DF的大小关系是.(第4题图)(第5题图)6.如图,AB,DE是☉O的直径,C是☉O上的一点,且.(1)求证:BE=CE;(2)假设∠B=50°,求∠AOC的度数.7.如图,AB是☉O的直径,M,N分别是OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N.求证:.创新应用8.如图,P是☉O外一点,PA,PC分别与☉O相交于点A,B和C,D,OF⊥AB,OE⊥CD,∠BPO=∠DPO,求证:.参考答案1.B如图,设的中点为E,连接AE,BE.∵=2,∴,∴AE=BE=CD.在△ABE中,∵AE+BE>AB,∴2CD>AB,应选B.2.A如图,连接OC.∵OA=OC,∴∠A=∠ACO.∵OD∥AC,∴∠A=∠DOB,∠ACO=∠COD,∴∠DOB=∠COD,∴.3.A4.相等5.AC=BE=DF6.(1)证明:∵∠AOD=∠BOE,∴.∵,∴,∴BE=CE.(2)解:∵OB=OE,∴∠OEB=∠B=50°,∴∠BOE=80°,∠AOE=100°.∵,∴∠COE=∠BOE=80°,∴∠AOC=100°-80°=20°.7.证明:如图,连接OC,OD,那么OC=OD.∵OA=OB,且OM=OA,ON=OB,∴OM=ON.∴Rt△CMO≌Rt△DNO.∴∠1=∠2.∴.8.证明:∵∠BPO=∠DPO,∠PEO=∠PFO=90°,OP=OP,∴△PFO≌△PEO.∴OF=OE.如图,连接OB,OD,在Rt△BOF和Rt△DOE中.∵OF=OE,OB=OD,∴Rt△BOF≌Rt△DOE.∴∠B=∠D.连接OA,OC,那么∠OAB=∠OCD=∠B=∠D.又OB=OD,∴△OAB≌△OCD,∴AB=CD,∴.能力提升1.以下各式能用完全平方公式进行因式分解的是()A.x2+1B.x2+2x-1C.x2+x+1D.x2+4x+42.假设x为任意实数,那么多项式x-1-x2的值()3.以下多项式中,不能用公式法因式分解的是()A.-x2+16y2B.81(a2+b2-2ab)-(a+b)2C.m2-mn+n2D.-x2-y24.因式分解:(a+b)(a+b+6)+9=.5.因式分解:4+12(x-y)+9(x-y)2=.6.当x=时,多项式-x2+2x-1有最大值.7.利用因式分解计算:1012+101×198+992的值.8.先因式分解,再求值:(a2+b2)2-4a2b2,其中a=3.5,b=1.5.9.a,b,c为△ABC的三条边长,且b2+2ab=c2+2ac,试判断△ABC的形状.创新应用10.观察思考:1×2×3×4+1=25=52,2×3×4×5+1=121=112,3×4×5×6+1=361=192,4×5×6×7+1=841=292,…………从以上几个等式中,你能得出什么结论?能证明吗?答案:能力提升1.D2.B3.D4.(a+b+3)25.(3x-3y+2)26.107.解:原式=1012+2×101×99+992=(101+99)2=2021年=40 000.8.解:(a2+b2)2-4a2b2=(a2+b2+2ab)(a2+b2-2ab)=(a+b)2(a-b)2,当a=3.5,b=1.5时,原式=(3.5+1.5)2×(3.5-1.5)2=25×4=100.9.解法一:∵b2+2ab=c2+2ac,∴b2-c2+2ab-2ac=0,∴(b+c)(b-c)+2a(b-c)=0,(b-c)(b+c+2a)=0.∵a,b,c为三角形的三边长,∴b+c+2a>0.∴b-c=0,即b=c.∴△ABC为等腰三角形.解法二:∵b2+2ab=c2+2ac,∴b2+2ab+a2=c2+2ac+a2,∴(a+b)2=(a+c)2.∵a,b,c为三角形的三边长,∴a+b=a+c.∴b=c.∴△ABC为等腰三角形.创新应用10.分析:仔细观察,寻找规律是关键.等式左边是四个连续自然数的积与1的和,等式右边是一个完全平方数,因此结论是四个连续自然数的积与1的和是一个完全平方数.解:结论:四个连续自然数的积与1的和是一个整数的完全平方数.证明:设最小的自然数是n,那么这四个自然数的积与1的和可以表示为n(n+1)(n+2)(n+3)+1=n(n+3)(n+1)·(n+2)+1=(n2+3n)(n2+3n+2)+1=(n2+3n)2+2(n2+3n)+1=(n2+3 n+1)2.。
(完整版)圆的对称性习题(有答案)

2 圆的对称性一、选择题(共10小题)1.(2012•江宁区二模)形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为()A.(﹣1,)B.(0,)C.(,0)D.(1,)2.已知⊙O中,弦AB长为,OD⊥AB于点D,交劣弧AB于点C,CD=1,则⊙O的半径是()A.1B.2C.3D.43.下列说法:①若∠1与∠2是同位角,则∠1=∠2②等腰三角形的高,中线,角平分线互相重合③对角线互相垂直且相等的四边形是正方形④等腰梯形是轴对称图形,但不是中心对称图形⑤平分弦的直径垂直于弦,并且平分弦所对的两条弧,其中正确的个数是()A.0B.1C.2D.34.(2013•邵东县模拟)⊙O的半径为R,若∠AOB=α,则弦AB的长为()A.B.2RsinαC.D.R sinα5.已知矩形ABCD的边AB=3,AD=4,如果以点A为圆心作⊙A,使B,C,D三点中在圆内和在圆外都至少有一个点,那么⊙A的半径r的取值范围是()A.3<r<5 B.3<r≤4 C.4<r≤5 D.无法确定6.已知圆的半径为5cm,圆心到弦的距离为4cm,那么这条弦长是()A.3cm B.6cm C.8cm D.10cm7.半径为5的⊙O,圆心在原点O,点P(﹣3,4)与⊙O的位置关系是()A.在⊙O内B.在⊙O上C.在⊙O外D.不能确定8.一个点到圆周的最小距离为4cm,最大距离为9cm,则该圆的半径是()A.2.5 cm或6.5 cm B.2.5 cm C.6.5 cm D.5 cm或13cm9.(2010•昌平区一模)如图,在半径为1的⊙O中,直径AB把⊙O分成上、下两个半圆,点C是上半圆上一个动点(C与点A、B不重合),过点C作弦CD⊥AB,垂足为E,∠OCD的平分线交⊙O于点P,设CE=x,AP=y,下列图象中,最能刻画y与x的函数关系的图象是()A.B.C.D.10.(2013•合肥模拟)如图,是半径为1的圆弧,△AOC为等边三角形,D 是上的一动点,则四边形AODC 的面积s的取值范围是()A.≤s ≤B.<s ≤C.≤s ≤D.<s <二、填空题(共10小题)(除非特别说明,请填准确值)11.牛牛和壮壮在沙滩上玩游戏,需要画一个圆,而他们手中没有任何工具,请你帮他们想一个办法,怎样可以得到一个圆?12.一条弦AB分圆的直径为3cm和7cm两部分,弦和直径相交成60°角,则AB=_________cm.13.若⊙O的半径为13cm,圆心O到弦AB的距离为5cm,则弦AB的长为_________cm.14.已知点P是半径为5的⊙O内一定点,且PO=4,则过点P的所有弦中,弦长可取到的整数值共有的条数是_________.15.若⊙A的半径为5,圆心A的坐标为(3,4),点P的坐标是(5,8),则点P在⊙A_________.16.在下图所列的图形中选出轴对称图形:_________.17.作圆,使这些圆都经过线段AB的两个端点A和B,这些圆的圆心所组成的图形是_________.18.以已知点O为圆心,可以画_________个圆.19.如图,AB为⊙O的直径,AD∥OC,∠AOD=84°,则∠BOC=_________.20.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D=_________度.三、解答题(共10小题)(选答题,不自动判卷)21.已知:AB交⊙O于C、D,且AC=BD.请证明:OA=OB.22.如图,AB是⊙O的直径,CD是弦,CE⊥CD交AB于E,DF⊥CD交AB于F,求证:AE=BF.23.如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE∥AB,求证:=2.24.已知⊙O的半径为12cm,弦AB=16cm.(1)求圆心O到弦AB的距离;(2)如果弦AB的长度保持不变,两个端点在圆周上滑动,那么弦AB的中点形成什么样的图形?25.如图,△ABC的三个顶点在⊙0上,AD⊥BC,D为垂足,E是的中点,求证:∠OAE=∠EAD.(写出两种以上的证明方法)26.如图,⊙O的直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=60°,(1)求CD的长;(2)若直线CD绕点E顺时针旋转15°,交⊙O于C、D,直接写出弦CD的长.27.已知:如图,在⊙O中,∠A=∠C,求证:AB=CD(利用三角函数证明).28.如图,CD是⊙O的直径,弦AB⊥CD于点H,若∠D=30°,CH=1cm,求弦AB的长.29.已知:等腰△ABC内接于半径为6cm的⊙O,AB=AC,点O到BC的距离OD的长等于2cm.求AB的长.30.如图,在⊙O内有折线OABC,其中OA=7,AB=12,∠A=∠B=60°,求BC的长.参考答案与试题解析一、选择题(共10小题)1.(2012•江宁区二模)形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的一个端点P、Q,线段PQ交y轴于点A,则点A的坐标为()A.(﹣1,)B.(0,)C.(,0)D.(1,)考点:圆心角、弧、弦的关系;坐标与图形性质;解直角三角形.分析:连接OQ、OP,求出∠POQ的度数,得出等边三角形POQ,得出PQ=OQ=OP=2,∠OPQ=∠OQP=60°,求出∠AOQ度数,根据三角形的内角和定理求出∠QAO,求出AQ、OA,即可得出答案.解答:解:连接OQ、PO,则∠POQ=120°﹣60°=60,∵PO=OQ,∴△POQ是等边三角形,∴PQ=OP=OQ=×4cm=2cm,∠OPQ=∠OQP=60°,∵∠AOQ=90°﹣60°=30°,∴∠QAO=180°﹣60°﹣30°=90°,∴AQ=OQ=2cm,∵在Rt△AOQ中,由勾股定理得:OA==,∴A的坐标是(0,),故选B.点评:本题考查了圆心角、弧、弦之间的关系,三角形的内角和定理,勾股定理,等边三角形的性质和判定等知识点,解此题的关键是构造三角形后求出OA的长,主要考查学生分析问题和解决问题的能力.2.已知⊙O中,弦AB长为,OD⊥AB于点D,交劣弧AB于点C,CD=1,则⊙O的半径是()A.1B.2C.3D.4考点:垂径定理;勾股定理.分析:连接OA,根据垂径定理求出AD,设⊙O的半径是R,则OA=R,OD=R﹣1,在Rt△OAD中,由勾股定理得出方程R2=(R﹣1)2+()2,求出R即可.解答:解:连接OA,∵OC是半径,OC⊥AB,∴AD=BD=AB=,设⊙O的半径是R,则OA=R,OD=R﹣1,在Rt△OAD中,由勾股定理得:OA2=OD2+AD2,即R2=(R﹣1)2+()2,R=2,故选B.点评:本题考查了垂径定理和勾股定理,关键是构造直角三角形,用了方程思想.3.下列说法:①若∠1与∠2是同位角,则∠1=∠2②等腰三角形的高,中线,角平分线互相重合③对角线互相垂直且相等的四边形是正方形④等腰梯形是轴对称图形,但不是中心对称图形⑤平分弦的直径垂直于弦,并且平分弦所对的两条弧,其中正确的个数是()A.0B.1C.2D.3考点:垂径定理;同位角、内错角、同旁内角;等腰三角形的性质;正方形的判定;等腰梯形的性质.分析:根据只有在平行线中,同位角才相等,等腰三角形的顶角的平分线,底边上的高,底边上的中线互相重合,对角线互相平分、垂直、相等的四边形才是正方形,等腰梯形是轴对称图形,但不是中心对称图形,即可判断①②③④;画出反例图形即可判断⑤.解答:解:∵只有在平行线中,同位角才相等,∴①错误;∵等腰三角形的顶角的平分线,底边上的高,底边上的中线互相重合,∴②错误;∵对角线互相平分、垂直、相等的四边形才是正方形,∴③错误;∵等腰梯形是轴对称图形,但不是中心对称图形,∴④正确;如图AB是⊙O直径,CD是⊙O弦,AB平分CD,但AB和CD不垂直,∴⑤错误;故选B.点评:本题考查了等腰三角形性质,平行线的性质,同位角,等腰梯形性质,正方形的判定等知识点的应用,主要考查学生的辨析能力.4.(2013•邵东县模拟)⊙O的半径为R,若∠AOB=α,则弦AB的长为()A.B.2RsinαC.D.R sinα考点:垂径定理;解直角三角形.分析:过O作OC⊥AB于C,由垂径定理得出AB=2AC,根据等腰三角形性质求出∠AOC=∠BOC=∠AOB=,根据sin∠AOC=求出AC=Rsin,即可求出AB.解答:解:过O作OC⊥AB于C,则由垂径定理得:AB=2AC=2BC,∵OA=OB,∴∠AOC=∠BOC=∠AOB=,在△AOC中,sin∠AOC=,∴AC=Rsin,∴AB=2AC=2Rsin,故选A.点评:本题考查了垂径定理,等腰三角形性质,解直角三角形等知识点,关键是求出AC的长和得出AB=2AC.5.已知矩形ABCD的边AB=3,AD=4,如果以点A为圆心作⊙A,使B,C,D三点中在圆内和在圆外都至少有一个点,那么⊙A的半径r的取值范围是()A.3<r<5 B.3<r≤4 C.4<r≤5 D.无法确定考点:点与圆的位置关系.分析:四边形ABCD是矩形,则△ABC是直角三角形.根据勾股定理得到:AC=5,B,C,D三点中在圆内和在圆外都至少有一个点,由题意可知一定是B在圆内,则半径r>3,一定是点C在圆外,则半径r<5,所以3<r<5.解答:解:∵AB=3,AD=4,∴AC=5,∴点C一定在圆外,点B一定在圆内,∴⊙A的半径r的取值范围是:3<r<5.故选A.点评:本题主要考查了勾股定理,以及点和圆的位置关系,可以通过点到圆心的距离与圆的半径比较大小,判定点和圆的位置关系.6.已知圆的半径为5cm,圆心到弦的距离为4cm,那么这条弦长是()A.3cm B.6cm C.8cm D.10cm考点:垂径定理;勾股定理.专题:计算题.分析:连接OA,根据垂径定理求出AC=BC,根据勾股定理求出AC即可.解答:解:连接OA,∵OC⊥AB,OC过圆心O,∴AC=BC,由勾股定理得:AC===3(cm),∴AB=2AC=6(cm).故选B.点评:本题主要考查对勾股定理,垂径定理等知识点的理解和掌握,能求出AC=BC和AC的长是解此题的关键.7.半径为5的⊙O,圆心在原点O,点P(﹣3,4)与⊙O的位置关系是()A.在⊙O内B.在⊙O上C.在⊙O外D.不能确定考点:点与圆的位置关系;勾股定理.专题:计算题.分析:连接OP,根据勾股定理求出OP,把OP和圆的半径比较即可.解答:解:连接OP.∵P(﹣3,4),由勾股定理得:OP==5,∵圆的半径5,∴P在圆O上.故选B.点评:本题主要考查对勾股定理,直线与圆的位置关系等知识点的理解和掌握,能求出OP长和能根据直线与圆的位置关系性质进行判断是解此题的关键.8.一个点到圆周的最小距离为4cm,最大距离为9cm,则该圆的半径是()A.2.5 cm或6.5 cm B.2.5 cm C.6.5 cm D.5 cm或13cm考点:点与圆的位置关系.分析:点P应分为位于圆的内部位于外部两种情况讨论.当点P在圆内时,点到圆的最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.解答:解:当点P在圆内时,最近点的距离为4cm,最远点的距离为9cm,则直径是13cm,因而半径是6.5cm;当点P在圆外时,最近点的距离为4cm,最远点的距离为9cm,则直径是5cm,因而半径是2.5cm.故选A.点评:本题考查了点与圆的位置关系,注意分两种情况进行讨论是解决本题的关键.9.(2010•昌平区一模)如图,在半径为1的⊙O中,直径AB把⊙O分成上、下两个半圆,点C是上半圆上一个动点(C与点A、B不重合),过点C作弦CD⊥AB,垂足为E,∠OCD的平分线交⊙O于点P,设CE=x,AP=y,下列图象中,最能刻画y与x的函数关系的图象是()A.B.C.D.考点:动点问题的函数图象;垂径定理.专题:压轴题;动点型.分析:连接OP,根据条件可判断出PO⊥AB,即AP是定值,与x的大小无关,所以是平行于x轴的线段.要注意CE的长度是小于1而大于0的.解答:解:连接OP,∵OC=OP,∴∠OCP=∠OPC.∵∠OCP=∠DCP,CD⊥AB,∴∠OPC=∠DCP.∴OP∥CD.∴PO⊥AB.∵OA=OP=1,∴AP=y=(0<x<1).故选A.点评:解决有关动点问题的函数图象类习题时,关键是要根据条件找到所给的两个变量之间的函数关系,尤其是在几何问题中,更要注意基本性质的掌握和灵活运用.10.(2013•合肥模拟)如图,是半径为1的圆弧,△AOC为等边三角形,D 是上的一动点,则四边形AODC的面积s的取值范围是()A.≤s≤B.<s≤C.≤s≤D.<s<考点:等边三角形的性质;垂径定理.专题:压轴题;动点型.分析:根据题意,得四边形AODC的最小面积即是三角形AOC的面积,最大面积即是当OD⊥OC时四边形的面积.要求三角形AOC的面积,作CD⊥AO于D.根据等边三角形的性质以及直角三角形的性质,求得CD=,得其面积是;要求最大面积,只需再进一步求得三角形DOC的面积,即是,则最大面积是.解答:解:根据题意,得四边形AODC的面积最小即是三角形AOC的面积,最大面积即是当OD⊥OC 时四边形的面积.作CH⊥AO于H,∵△AOC为等边三角形∴CH=∴S△AOC=;当OD⊥OC时面积最大,∴S△OCD=,则最大面积是+=∴四边形AODC的面积s的取值范围是<s≤.故选B.点评:此题首先要能够正确分析出要求的四边形的最小面积和最大面积,然后根据等边三角形的性质以及三角形的面积公式进行计算.二、填空题(共10小题)(除非特别说明,请填准确值)11.牛牛和壮壮在沙滩上玩游戏,需要画一个圆,而他们手中没有任何工具,请你帮他们想一个办法,怎样可以得到一个圆?考点:圆的认识.分析:根据圆的定义:到定点的距离等于定长的点的集合可以得到答案.解答:解:可让牛牛站在原地旋转,壮壮拉直牛牛的手臂,绕牛牛走一圈,用脚在沙滩上画出一条曲线,就是一个圆.点评:本题考查了圆的认识,了解圆的定义是解决本题的关键.12.一条弦AB分圆的直径为3cm和7cm两部分,弦和直径相交成60°角,则AB=2cm.考点:垂径定理.分析:根据题意画出图形,作弦的弦心距,根据题意可知,半径OA=5cm,ND=3cm,ON=2cm,利用勾股定理易求得NM=1cm,OM=cm,进一步可求出AM,进而求出AB.解答:解:根据题意画出图形,如图示,作OM⊥AB于M,连接OA,∴AM=BM,CD=10cm,ND=3cm,∴ON=2cm,∵∠ONM=60°,OM⊥AB,∴MN=1cm,∴OM=,在Rt△OMA中,AM===,∴AB=2AM=2.点评:本题主要考查了垂径定理,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,设法确定其中两边,进而利用勾股定理确定第三边.13.若⊙O的半径为13cm,圆心O到弦AB的距离为5cm,则弦AB的长为24cm.考点:垂径定理;勾股定理.专题:计算题.分析:在△OBD中,利用勾股定理即可求得BD的长,然后根据垂径定理可得:AB=2BD,即可求解.解答:解:连接OB,∵在Rt△ODB中,OD=4cm,OB=5cm.由勾股定理得:BD2=OB2﹣OD2=132﹣52=144,∴BD=12,又OD⊥AB,∴AB=2BD=2×12=24cm.故答案是24.点评:本题主要考查垂径定理,圆中有关半径、弦长以及弦心距的计算一般是利用垂径定理转化成解直角三角形.14.已知点P是半径为5的⊙O内一定点,且PO=4,则过点P的所有弦中,弦长可取到的整数值共有的条数是8条.考点:垂径定理;勾股定理.专题:推理填空题.分析:求出最长弦(直径)和最短弦(垂直于OP的弦),再求出之间的数,得出符合条件的弦,相加即可求出答案.解答:解:过P点最长的弦是直径,等于10,最短的弦是垂直于PO的弦,根据勾股定理和垂径定理求出是6,10和6之间有7,8,9,每个都有两条弦,关于OP对称,共6条,1+1+6=8,故答案为:8条.点评:本题考查了勾股定理和垂径定理的应用,此题是一道比较容易出错的题目,考虑一定要全面,争取做到不重不漏.15.若⊙A的半径为5,圆心A的坐标为(3,4),点P的坐标是(5,8),则点P在⊙A内部.考点:点与圆的位置关系;坐标与图形性质.分析:首先根据两点的坐标求得两点之间的距离,然后利用两点之间的距离和圆A的半径求得点与圆的位置关系.解答:解:∵A的坐标为(3,4),点P的坐标是(5,8),∴AP==2∵⊙A的半径为5,∴5>2∴点P在⊙A的内部故答案为:内部.点评:本题考查了点与圆的位置关系,解题得到关键是根据两点的坐标求得两点之间的距离.16.在下图所列的图形中选出轴对称图形:②③④⑥.考点:圆的认识;轴对称图形.分析:根据轴对称图形的概念:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形进行判断.解答:解:①⑤都不是轴对称图形,②③④⑥是轴对称图形,故答案为:②③④⑥.点评:本题主要考查轴对称的知识点,轴对称图形的判断方法:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.17.作圆,使这些圆都经过线段AB的两个端点A和B,这些圆的圆心所组成的图形是线段AB的垂直平分线.考点:圆的认识;线段垂直平分线的性质.分析:利用圆的性质可以得到圆上的所有点到圆心的距离相等,从而得到所有圆心到A、B两点的距离相等,从而得到结论.解答:解:∵圆上的所有点到圆心的距离相等,∴无论圆心O在哪里,总有OA=OB,即:所有圆心到A、B两点的距离相等,∵到A、B两点的距离相等的点在线段AB的垂直平分线上,故答案为:线段AB的垂直平分线.点评:本题考查的是线段垂直平分线的性质,即线段的垂直平分线上的点到线段的两个端点的距离相等.18.以已知点O为圆心,可以画无数个圆.考点:圆的认识.分析:圆心固定,半径不确定,可以画出无数个圆,由此选择答案解决问题.解答:解:以一点为圆心,以任意长为半径可以画无数个同心圆,故答案为:无数.点评:此题考查:圆心确定圆的位置,半径确定圆的大小这一知识.19.如图,AB为⊙O的直径,AD∥OC,∠AOD=84°,则∠BOC=48°.考点:圆的认识;平行线的性质.分析:根据半径相等和等腰三角形的性质得到∠D=∠A,利用三角形内角和定理可计算出∠A,然后根据平行线的性质即可得到∠BOC的度数.解答:解:∵OD=OC,∴∠D=∠A,∵∠AOD=84°,∴∠A=(180°﹣84°)=48°,又∵AD∥OC,∴∠BOC=∠A=48°.故答案为:48°.点评:本题考查了有关圆的知识:圆的半径都相等.也考查了等腰三角形的性质和平行线的性质.20.如图,⊙O的弦AB、半径OC延长交于点D,BD=OA,若∠AOC=105°,则∠D=25度.考点:圆的认识;三角形内角和定理;三角形的外角性质.分析:解答此题要作辅助线OB,根据OA=OB=BD=半径,构造出两个等腰三角形,结合三角形外角和内角的关系解决.解答:解:连接OB,∵BD=OA,OA=OB所以△AOB和△BOD为等腰三角形,设∠D=x度,则∠OBA=2x°,因为OB=OA,所以∠A=2x°,在△AOB中,2x+2x+(105﹣x)=180,解得x=25,即∠D=25°.点评:此题主要考查了等腰三角形的基本性质,以及三角形内角和定理,难易程度适中.三、解答题(共10小题)(选答题,不自动判卷)21.已知:AB交⊙O于C、D,且AC=BD.请证明:OA=OB.考点:垂径定理;线段垂直平分线的性质.专题:证明题.分析:过O作OE⊥AB于E,根据垂径定理求出CE=DE,求出AE=BE,根据线段的垂直平分线定理求出即可.解答:证明:过O作OE⊥AB于E,∵OE过圆心O,∴CE=DE,∵AC=BD,∴AE=BE,∵OE⊥AB,∴OA=OB.点评:本题考查了线段的垂直平分线定理和垂径定理的应用,主要培养学生运用定理进行推理的能力,题目比较典型,难度适中.22.如图,AB是⊙O的直径,CD是弦,CE⊥CD交AB于E,DF⊥CD交AB于F,求证:AE=BF.考点:垂径定理.专题:证明题.分析:过O作OG⊥CD,由垂径定理可知OG垂直平分CD,再由平行线分线段成比例定理即可求解.解答:证明:过O作OG⊥CD,由垂径定理可知OG垂直平分CD,则CG=DG,∵CE⊥CD,DF⊥CD,OG⊥CD,∴CE∥OG∥DF,∵CG=DG,∴OE=OF,∵OA=OB,∴AE=BF.点评:本题综合考查了垂径定理和平行线分线段成比例定理,解答此题的关键是作出辅助线,构造出平行线,再利用平行线的性质解答.23.如图,⊙O中,AB是直径,半径CO⊥AB,D是CO的中点,DE∥AB,求证:=2.考点:圆心角、弧、弦的关系;平行线的判定与性质;三角形内角和定理;含30度角的直角三角形.专题:证明题.分析:连接OE,推出DE⊥OC,求出∠EDO=90°,根据OD=OC=OE,求出∠DEO=30°,求出∠EOC,根据OC⊥AB,求出∠AOC=90°,求出∠AOE=30°,即可求出答案.解答:证明:连接OE,∵AB⊥OC,DE∥AB,∴DE⊥OC,∴∠EDO=90°,∵D为OC中点,∴OD=OC=OE,∴∠DEO=30°,∴∠EOC=90°﹣30°=60°,∵OC⊥AB,∴∠AOC=90°,∴∠AOE=90°﹣60°=30°,即∠AOE=30°,∠COE=60°,∴=2(圆心角的度数等于它所对的弧的度数).点评:本题考查了三角形的内角和定理,平行线的性质和判定,圆心角、弧、弦之间的关系,和30度角的直角三角形,主要考查学生运用定理进行推理的能力,题目比较好,综合性比较强.24.已知⊙O的半径为12cm,弦AB=16cm.(1)求圆心O到弦AB的距离;(2)如果弦AB的长度保持不变,两个端点在圆周上滑动,那么弦AB的中点形成什么样的图形?考点:垂径定理;勾股定理.专题:计算题.分析:(1)连接OB,过O作OC⊥AB于C,则线段OC的长就是圆心O到弦AB的距离,求出BC,再根据勾股定理求出OC即可;(2)弦AB的中点形成一个以O为圆心,以4cm为半径的圆周.解答:(1)解:连接OB,过O作OC⊥AB于C,则线段OC的长就是圆心O到弦AB的距离,∵OC⊥AB,OC过圆心O,∴AC=BC=AB=8cm,在Rt△OCB中,由勾股定理得:OC===4(cm),答:圆心O到弦AB的距离是4cm.(2)解:如果弦AB的长度保持不变,两个端点在圆周上滑动,那么弦AB的中点到圆心O的距离都是4cm,∴如果弦AB的长度保持不变,两个端点在圆周上滑动,那么弦AB的中点形成一个以O为圆心,以4cm为半径的圆周.点评:本题考查了勾股定理和垂径定理的应用,主要培养学生运用定理进行推理和计算的能力,题型较好,难度适中.25.如图,△ABC的三个顶点在⊙0上,AD⊥BC,D为垂足,E是的中点,求证:∠OAE=∠EAD.(写出两种以上的证明方法)考点:圆心角、弧、弦的关系;三角形内角和定理.专题:证明题.分析:方法一:连接OB,利用同弧所对的圆周角是它所对圆心角的一半,三角形内角和定理,同弧所对的圆周角相等即可证明此题.方法二:连接OE,利用垂径定理可得OE⊥BC,再利用AD⊥BC,可得OE∥AD,然后即可证明.解答:证明:(1)连接OB,则∠AOB=2∠ACB,∠OAB=∠OBA,∵AD⊥BC,∴∠OAB=(180°﹣∠AOB),=90°﹣∠AOB=90°﹣∠ACB=∠DAC,∵E是弧BC的中点,∴∠EAB=∠EAC,∴∠EAO=∠EAB﹣∠OAB=∠EAC﹣∠DAC=∠EAD.(2)连接OE,∵E是的中点,∴弧BE=弧EC,∴OE⊥BC,∵AD⊥BC,∴OE∥AD,∴∠OEA=∠EAD,∵OE=OA,∴∠OAE=∠OEA,∴∠OAE=∠EAD.点评:此题主要考查学生对三角形内角和定理和圆心角、弧、弦的关系等知识点的理解和掌握,此题难度不大,关键是作好辅助线,方法一:连接OB,方法二:连接OE,属于中档题.26.如图,⊙O的直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=60°,(1)求CD的长;(2)若直线CD绕点E顺时针旋转15°,交⊙O于C、D,直接写出弦CD的长.考点:垂径定理;勾股定理.分析:(1)作OH⊥CD于H,连接OD,求出AB=6cm,半径OD=3cm,在Rt△OHE中,OE=2cm,∠OEH=60°,由勾股定理求出OH=cm,在Rt△OHD中,由勾股定理得求出HD=cm,由垂径定理得出DC=2DH,代入即可;(2)求出OE,∠OEH=45°,根据勾股定理求出OH,在Rt△OHD中,由勾股定理得求出HD,由垂径定理得出DC=2DH,代入即可.解答:解:(1)作OH⊥CD于H,连接OD,∵AE=1cm,BE=5cm,E在直径AB上,∴AB=1cm+5cm=6cm,半径OD=3cm,∵在Rt△OHE中,OE=3cm﹣1cm=2cm,∠OEH=60°,∴OH=cm,在Rt△OHD中,由勾股定理得:HD=cm,∵OH⊥CD,∴由垂径定理得:DC=2DH=2cm;(2)作OH⊥CD于H,连接OD,∵AE=1cm,BE=5cm,E在直径AB上,∴AB=1cm+5cm=cm6,半径OD=3cm,∵若直线CD绕点E顺时针旋转15°,∴∠OEH=60°﹣15°=45°,在Rt△OHE中,OE=3cm﹣1cm=2cm,∠OEH=45°,∴OH=cm,在Rt△OHD中,由勾股定理得:HD==(cm),∵OH⊥CD,∴由垂径定理得:DC=2DH=2cm;即CD=2cm.点评:本题考查了垂径定理,勾股定理,含30度角的直角三角形性质,等腰直角三角形性质等知识点的应用,主要考查学生运用性质进行推理和计算的能力,题目比较典型,是一道比较好的题目.27.已知:如图,在⊙O中,∠A=∠C,求证:AB=CD(利用三角函数证明).考点:垂径定理;解直角三角形.专题:证明题.分析:作OE⊥AB于E,OF⊥CD于F,设⊙O半径为R,根据sinA=,、inC=和∠A=∠C求出OE=OF,由勾股定理求出AE=CF,由垂径定理得出DC=2DF,AB=2AE,即可求出答案.解答:证明:作OE⊥AB于E,OF⊥CD于F设⊙O半径为R,sinA=,sinC=,∴OE=RsinA,OF=RsinC,∵∠A=∠C,∴sinA=sinC,∴OE=OF,由勾股定理得:CF2=OC2﹣OF2,AE2=OA2﹣OE2,∴AE=CF,由垂径定理得:DC=2DF,AB=2AE,∴AB=CD.点评:本题考查了勾股定理,垂径定理,解直角三角形等知识点,主要培养学生运用定理进行推理的能力.28.如图,CD是⊙O的直径,弦AB⊥CD于点H,若∠D=30°,CH=1cm,求弦AB的长.考点:垂径定理;含30度角的直角三角形;勾股定理.分析:连接OA,根据等腰三角形性质求出∠D=∠OAD=30°,求出∠AOH=60°,根据垂径定理求出AB=2AH=2BH,求出∠HAO=30°,推出AO=2OH=C0,求出OH=CH=1cm,AO=2cm,在Rt△AHO 中,由勾股定理求出AH即可.解答:解:连接OA,∵OA=OD,∴∠D=∠OAD=30°,∴∠AOH=30°+30°=60°,∵AB⊥DH,∴∠AHO=90°,AB=2AH=2BH,∴∠HAO=30°,∴AO=2OH=C0,∴OH=CH=1cm,∴AO=2cm,在Rt△AHO中,由勾股定理得:AH==cm,∴AB=2cm.点评:本题考查了三角形的内角和定理,含30度角的直角三角形的性质,勾股定理,垂径定理,等腰三角形的性质等知识点的应用,主要考查学生综合运用性质进行计算和推理的能力,题目具有一定的代表性,是一道比较好的题目.29.已知:等腰△ABC内接于半径为6cm的⊙O,AB=AC,点O到BC的距离OD的长等于2cm.求AB 的长.考点:垂径定理;等腰三角形的性质;勾股定理.专题:计算题.分析:①连接AD、OB,根据三线合一得出AO过D,在Rt△OBD中,根据勾股定理求出BD,在Rt△ADB 中,根据勾股定理求出AB即可.②求出BD、AD,根据勾股定理求出AB即可.解答:解:①如图,连接AD,连接OB,∵△ABC是等腰三角形,∴根据等腰三角形的性质(三线合一定理)得出,AO⊥BC,AO平分BC,∵OD⊥BC,∴根据垂直定理得:OD平分BC,即A、O、D三点共线,∴AO过D,∵等腰△ABC内接于半径为6cm的⊙O,∴OA=6cm,BD=DC,AD⊥BC,在Rt△OBD中,由勾股定理得:BD===4(cm),在Rt△ADB中,由勾股定理得:AB===4(cm),②如图:同法求出BD=4cm,AD=6cm﹣2cm=4cm,由勾股定理得:AB===4(cm),答:AB的长是4cm或4cm.点评:本题考查了垂径定理,等腰三角形性质,勾股定理等知识点的应用,关键是正确作辅助线后求出BD的长,题目具有一定的代表性,难度也适中,是一道比较好的题目.注意:分类讨论.30.如图,在⊙O内有折线OABC,其中OA=7,AB=12,∠A=∠B=60°,求BC的长.考点:垂径定理;等边三角形的判定与性质;含30度角的直角三角形.专题:计算题.分析:延长AO交BC于D,过O作OE⊥BC于E,根据垂径定理求出BC=2BE,根据等边三角形的性质和判定求出AD=BD=AB=12,求出OD的长,根据含30度角的直角三角形性质求出DE即可解答:解:延长AO交BC于D,过O作OE⊥BC于E,∵OE过圆心O,OE⊥BC,∴BC=2CE=2BE(垂径定理),∵∠A=∠B=60°,∴DA=DB,∴△DAB是等边三角形(有一个角等于60°的等腰三角形是等边三角形),∴AD=BD=AB=12,∠ADB=60°,∴OD=AD﹣OA=12﹣7=5,∵∠OED=90°,∠ODE=60°,∴∠DOE=30°,∴DE=OD=(在直角三角形中,如果有一个角是30°,那么它所对的直角边等于斜边的一半),∴BE=12﹣=,∴BC=2BE=19(根据垂径定理已推出,在第三行).点评:本题考查了垂径定理,等边三角形的性质和判定,含30度角的直角三角形的性质等知识点的理解和掌握,关键是正确作辅助线后求出BE的长,题目比较典型,难度适中.。
圆的对称性练习题
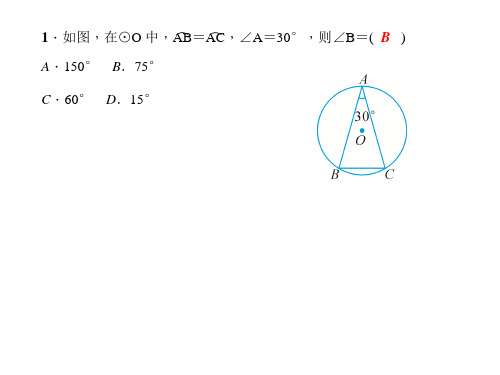
OA2+OB′2= 2,即 PA+PB 的最小值为 2.
A.到 CD 的距离保持不变 B.位置不变 C.平分B︵D D,半径为 5 的⊙A 中,弦 BC,ED 所对的圆心角分别是
∠BAC,∠EAD.已知 DE=6,∠BAC+∠EAD=180°,则弦 BC 的弦心
距等于( D )
A.
41 2
B.
34 2
C.4
D.3
9.如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,BG=8 cm, AG=1 cm,DE=2 cm,则EF=__6__c_m___.
1.如图,在⊙O 中,A︵B=A︵C,∠A=30°,则∠B=( B ) A.150° B.75° C.60° D.15°
2.下列判断正确的是( C ) A.平分弦的直径垂直于弦 B.平分弦的直径必平分弦所对的两条弧 C.弦的垂直平分线必平分弦所对的两条弧 D.平分一条弧的直线必平分这条弧所对的弦
3.如图,在⊙O 中,A,C,D,B 是⊙O 上四点,OC,OD 交 AB 于 点 E,F,且 AE=FB,下列结论中不正确的是( C )
(2)设他在不弯腰的情况下向 CD 左侧活动时他的头顶与A︵C的接触点 为点 E,向 CD 右侧活动时他的头顶与B︵C的接触点为点 F,连结 EF,则 EF⊥OC.设垂足为点 G,连结 OE.由题意,得 OG=3-2.3+1.7=2.4(m).在 Rt△OEG 中,EG= OE2-OG2= 32-2.42=1.8(m),∵OC⊥EF,∴EF= 2EG=3.6 m,∴该菜农在不弯腰的情况下,横向活动的范围有 3.6 m.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1 圆的对称性
◆随堂检测
1.下列说法中,不成立的是( )
A.弦的垂直平分线必过圆心
B.弧的中点与圆心的连线垂直平分这条弧所对的弦
C.垂直于弦的直线经过圆心,且平分这条弦所对的弧
D.垂直于弦的直径平分这条弦
2.如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为点
E,则图中不大于半圆的相等的弧有( )
A.1对B.2对C.3对D.4对
3.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,如果AB=10,CD=8,那么AE的长为( )
A.2 B.3 C.4 D.5
4.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,若AP:PB=1:4,CD=8,则AB=_________.
5.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,∠CAD=80o,则
∠OCE=_________.
◆典例分析
如图,已知在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O 的半径.
解:连结OA,作OE⊥AB,垂足为E.
∵OE⊥AB,∴AE=EB.
∵AB=8cm,∴AE=4cm.
又∵OE=3cm,
在Rt△AOE中,
∵⊙O的半径为5cm.
点评:从例中可以知道作“弦心距”是很重要的一条辅助线,弦心距的作用就是平分弦,平分弦所对的弧,它和直径一样.求圆的半径问题,要和弦心距,弦的一半和半径构造出一个直角三角形,和勾股定理联系起来.
◆课下作业
●拓展提高
1.下列四个命题中,叙述正确的是( )
A.平分一条直径的弦必垂直于这条直径
B.平分一条弧的直径垂直于这条弧所对的弦
C.弦的垂线必经过这条弦所在圆的圆心
D.平分一条弦的直线必经过这个圆的圆心
2.如图,⊙O的半径为4 cm,点C是»AB的中点,半径OC交弦AB于点D,OD=23cm,则弦AB的长为( )
A.2 cm B.3 cm
C.23cm D.4 cm
3.如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,那么下列结论错误的是( )
A .CE=DE
B .»»BC
BD = C .∠BAC=∠BAD D .AC>AD 为2
4.若小唐同学掷出的铅球在场地上砸出一个直径约为10 cm 、深约cm 的小坑,则该铅球的直径约为( )
A .10 cm
B .14.5 cm
C . 19.5 cm
D .20 cm
5.如图,⊙O 的半径为5,弦AB=8,OC ⊥AB 于C ,则OC 的长等于_______.
6.如图,⊙O 的直径AB 和弦CD 相交于点E ,AE=1 cm ,EB=5 cm ,∠DEB=60o ,求CD 的长.
7.已知:如图,∠PAC=30o ,在射线AC 上顺次截取AD=3 cm ,DB=10 cm ,以DB 为直径作⊙O ,交射线AP 于E 、F 两点,求圆心O 到AP 的距离及EF 的长.
●体验中考
1.(2009年娄底)如图,AB 是⊙O 的弦,OD ⊥AB 于D 交⊙O 于E ,则下列说法错误..
的是( ) A .AD=BD B .∠ACB=∠AOE
C .¼¼AE BE =
D .OD=DE
⊙的直径AB垂直弦CD于P,且P是半径OB的中2.(2009年恩施市)如图,O
CD ,则直径AB的长是( )
点,6cm
A.23cm B.32cm
C.42cm D.43cm
3.(2009年甘肃庆阳)如图,⊙O的半径为5,弦AB=8,M是弦AB上的动点,则OM不可能为( )
A.2 B.3 C.4 D.5
4.(2009年广西梧州)某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为m.
参考答案
◆随堂检测
1、C
2、B
3、A(提示:连接OC ,利用勾股定理求解)
4、10(提示:连接OC ,设AP=k ,BP=4k ,则半径为2.5k ,OP=1.5k ,由垂径定理知CP=4,有勾股定理知k=2,AB=5k=10)
5、100(提示:垂径定理得AC=AD)
◆课下作业
●拓展提高
1、C
2、D(提示:连接OA ,由勾股定理知AD=2,则AB=4)
3、D(提示:垂径定理)
4、8(提示:过O 点做OD 垂直AB 于D ,连接OA ,有OD=3,OA=5,AD=4,所以AB=8)
5、3(提示:连接OA)
6
、00O OF CD D OD
AE=1,BE=5,3sin ,sin 2OF OEF OF OE OE ODF CD DF ⊥∴=
===∴==Q 解:过点作于,连接半径为,
在直角三角形中,6060在直角三角形中 7
、0OM AP M,OF
DB=10,5AO=8
Rt OAM OM=AOsin 4O AP 4.,2Rt OFM 3,6
O OM AP EF MF
EF ⊥∴∴=∴⊥∴==∴=Q V Q V 解:过作于连接半径为,在中,30圆心到的距离为在中,
●体验中考
1、D
2、A
3、A(提示:35OM ≤≤)
4、4(
提示:6OD ==)。
