广义表的定义与实现.
数据结构第5章 串和广义表

5.1 串的定义和基本运算
• (4)串的连接StrCat(S,T)。 • 初始条件:串S和T存在。 • 操作结果:将串T的值连接在串S的后面。 • (5)求子串SubString(Sub,S,pos,len)。 • 初始条件:串S存在,1≤pos≤StrLength(S)且
1≤len≤StrLength(S)-pos+1。 • 操作结果:用Sub返回串S的第pos个字符起长度为len的
1≤len≤StrLength(S)-pos+1。 • 操作结果:从串S中删除第pos个字符起长度为len的子串。 • (9)串的替换StrReplace(S,T,V)。 • 初始条件:串S,T和V存在,且T是非空串。 • 操作结果:用V替换串S中出现的所有与T相等的不重叠子
串。 • (10)判断串空StrEmpty(S)。 • 初始条件:串S存在。 • 操作结果:若串S为空串,则返回1;否则返回0。
• (1)非紧凑存储。设串S="Hello boy",计算机字长为32 位(4个Byte),用非紧凑格式一个地址只能存一个字符, 如图5-2所示。其优点是运算处理简单,但缺点是存储空 间十分浪费。
• (2)紧凑存储。同样存储S="Hello boy",用紧凑格式一 个地址能存四个字符,如图5-3所示。紧凑存储的优点是 空间利用率高,缺点是对串中字符处理的效率低。
•}
5.3 串的基本运算的实现
• (3)求子串操作。求串S从第pos位置开始,长度为len的 子串,并将其存入到串Sub中。操作成功返回1,不成功 返回0。其算法描述如下:
• int SubString(String *S,String *Sub,int pos,int len)
第5章 广义表
12
例:求下列广义表操作的结果(严题集5.10②) (k, p, h) ; 1. GetTail【(b, k, p, h)】=
2. GetHead【( (a,b), (c,d) )】= 3. GetTail【( (a,b), (c,d) )】=
(c,d)
((c,d)) ;
;
4. GetTail【 GetHead【((a,b),(c,d))】】=(b) ; 5. GetTail【(e)】= 6. GetHead 【 ( ( ) )】= 7. GetTail【 ( ( ) ) 】= () ; . .
讨论:广义表与线性表的区别和联系? 广义表中元素既可以是原子类型,也可以是列表; 当每个元素都为原子且类型相同时,就是线性表。
3
广义表是递归定义的线性结构,
LS = ( 1, 2, , n ) 其中:i 或为原子 或为广义表
例如: A = ( ) F = (d, (e)) D = ((a,(b,c)), F) C = (A, D, F) B = (a, B) = (a, (a, (a, , ) ) )
13
(a,b)
()
()
5.5 广义表的存储结构
由于广义表的元素可以是不同结构(原子或列表),难以用 顺序存储结构表示 ,通常用链式结构,每个元素用一个结 点表示。 注意:列表的“元素”还可以是列表,所以结点可能有两种形 式 1.原子结点:表示原子,可设2个域或3个域,依习惯而选。 法1:标志域,数值域 tag=0 标志域 value 数值域 法2:标志域、值域、表尾指针 tag=0 atom
} ADT Glist
10
基 结构的创建和销毁 InitGList(&L); DestroyGList(&L); 本 CreateGList(&L, S); CopyGList(&T, L); 操 作 状态函数
3.4 广义表

((b,c,d)) C → 1 a 0 a 1
((b,c,d)) C → 1 a 0 a 1 (b,c,d)
((b,c,d)) C → 1 a 0 a 1 () (b,c,d)
((b,c,d)) C → 1 a 0 a 1 ^ () (b,c,d)
((b,c,d)) C → 1 a 0 a 1 1 ^ () (b,c,d)
3.4.2 广义表的存储结构
1. 头尾表示法
表结点 tag=1 hp tp
指向表尾的指针
原子结点 tag=0 data
指向表头的指针
class GLNode{ private: int tag; tag=0 data union { ptr tag=1 DataType data; hp tp struct { GLNode *hp,*tp; }ptr; }; };//GLNode
2. 孩子兄弟表示法 有孩子结点 tag=1 hp tp
指向第一个孩子的指针 指向兄弟的指针
无孩子结点 tag=0 data tp
class GLNode{ private: int tag; union { DataType data; GLNode *hp; }; GLNode * tp; };//GLNode
例1
参赛队清单的表示。 参赛队清单的表示。
参赛队清单=(俄罗斯,巴西,东道主,古巴,美国,韩国,日本 参赛队清单 俄罗斯,巴西,东道主,古巴,美国,韩国,日本) 俄罗斯 东道主= 国家队 香港队,澳门队) 国家队, 东道主 (国家队,香港队,澳门队 韩国= 韩国 ( ) (俄罗斯,巴西,(国家队,香港队,澳门队 ,古巴,美国,( ),日本 俄罗斯,巴西, 国家队 香港队,澳门队),古巴,美国, ,日本) 国家队, 俄罗斯
广义表的应用课程设计

广义表的应用课程设计一、课程目标知识目标:1. 理解广义表的定义和基本概念;2. 学会使用广义表表示复杂的线性结构;3. 掌握广义表的基本操作,如创建、插入、删除、查找等;4. 能够运用广义表解决实际问题。
技能目标:1. 能够运用广义表的基本操作,实现线性结构的存储和运算;2. 能够分析实际问题,选择合适的广义表结构进行建模;3. 能够编写简单的程序,利用广义表解决具体问题;4. 培养学生的逻辑思维能力和编程实践能力。
情感态度价值观目标:1. 培养学生对数据结构和算法的兴趣,激发学习热情;2. 培养学生的团队协作意识和解决问题的能力;3. 培养学生面对复杂问题,勇于尝试、积极探究的精神;4. 增强学生的自信心和成就感,鼓励他们发挥创新精神。
课程性质:本课程为计算机科学领域的数据结构与算法课程,旨在帮助学生掌握广义表这一数据结构,并运用其解决实际问题。
学生特点:学生具备一定的编程基础,对数据结构有一定了解,但可能对广义表的认识较为陌生。
教学要求:结合学生特点,注重理论与实践相结合,通过实例讲解、课堂互动、上机实践等环节,使学生掌握广义表的应用。
同时,关注学生的情感态度,激发学习兴趣,培养其解决问题的能力和团队协作精神。
在教学过程中,将课程目标分解为具体的学习成果,以便于教学设计和评估。
二、教学内容1. 广义表的定义与基本概念:- 线性表、广义表的概念与区别;- 广义表的元素、表头、表尾及表长等基本概念。
2. 广义表的存储结构:- 顺序存储结构;- 链式存储结构。
3. 广义表的基本操作:- 创建广义表;- 插入、删除、查找等操作;- 广义表的遍历。
4. 广义表的应用:- 利用广义表解决实际问题,如多项式的表示与运算;- 广义表在数据压缩中的应用;- 广义表在计算机图形学中的应用。
5. 教学案例与上机实践:- 结合实际案例,分析广义表的应用场景;- 上机实践,编写程序实现广义表的基本操作;- 团队协作,共同探讨广义表在解决复杂问题中的应用。
数据结构广义表

结点结构是无论什么结点都有三个域:
第一个域是结点类型标志tag; 第二个域是指向一个列表的指针(当tag=1时) 或一个原子(当tag=0时); 第三个域是指向下一个结点的指针tp。
3 广义表的存储结构
形式描述为:
typedef enum{ ATOM, LIST }ElemTag typedef struct GLNode { //定义广义表结点 ElemTage tag; //公共部分,用以区分 原子结点和表结点 Unin{ //原子结点和表结点的联合部分 AtomType atom;//原子类型结点域, // AtomType由用户定义 struct GLNode *hp,; //表结点的表头指针域 }; struct GLNode *tp; //指向下一个结点的指针 }*Glist; //广义表类型
5. E=(a,E)
这是一个递归列表,其元素中有自己。
广义表也可以用图形表示,例如前述的广义表D和E可表示为:
广义表D
D
广义表E
E
C
A
B
a
e
a b c d
2 广义表的基本运算
广义表的基本运算 ⑴ 取表头 HEAD(LS); ⑵ 取表尾 TAIL(LS)。
3 广义表的存储结构
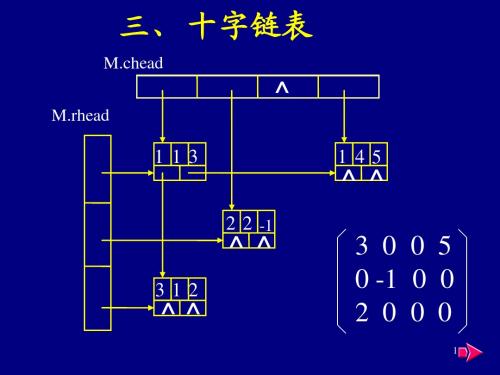
广义表中的数据元素可以是单元素,或是广义表, •很难用顺序存储结构表示,常采用链式存储结构。 1.表头表尾链存储结构 有两类结点:表结点和单元素结点。
P 1 3 1 1
A=y((c,3),(D,2)) C=x((1,10),(2,6))
^
1 2
A
z y 1 1 1 3
C
x 0 0 15 ^
B
1 2
1 2
^
广义表及本章小结

2 .广义表的同层结点链存储结构 在这种结构中,无论是单元素结点还是子表结点均由三个域构成。其结点结 构如下图所示。
tag=1 hp tp
表结点
tag=0 atom tp
原子结点
广义表的同层结点链结点结构
广义表 A、 B、 C、 D 的扩展线性链表存储结构如下图所示。
D 1 ∧∧
A
1
∧
0a
1
∧
B
1
第 5 讲 广义表及本章小结——教学讲义 广义表,也是线性表的一种推广。它被广泛的应用于人工智能等领域的表处 理语言 LISP 语言中。在 LISP 语言中,广义表是一种最基本的数据结构,LISP 语言 编写的程序也表示为一系列的广义表。
一、 广义表的概念
在第 2 章中,线性表被定义为一个有限的序列( a1 ,a2 ,a3 ,…, an),其中 ai 被限定 为是单个数据元素。广义表也是 n 个数据元素( d1 ,d2 ,d3 ,…, dn)的有限序列,但不 同的是,广义表中的 di 既可以是单个元素,还可以是一个广义表,通常记做: GL =( d1 ,d2 ,d3 ,…, dn)。 GL 是广义表的名字,通常广义表的名字用大写字母表示。 n 是广义表长度。若其中 di 是一个广义表,则称 di 是广义表 GL 的子表。在广义表 GL 中,d1 是广义表表头,而广义表 GL 其余部分组成的表( d2 ,d3 ,…, dn)称为广义表 表尾。由此可见广义表的定义是递归定义的,因为在定义广义表时又使用了广义 表的概念。下面给出一些广义表的例子,以加深对广义表概念的理解。 D=() 空表;其长度为零。 A=(a,(b,c)) 表长度为 2 的广义表,其中第一个元素是单个数据 a,
A[i][j] f B[K]
广义表总结

5.4 稀疏矩阵
在特殊矩阵中,元素的分布呈现某种规律,故一定能找 到一种合适的方法,将它们进行压缩存放。但是,在实 际应用中,我们还经常会遇到一类矩阵:其矩阵阶数很 大,非零元个数较少,零元很多,但非零元的排列没有 一定规律,我们称这一类矩阵为稀疏矩阵。(非零元不 足5%的矩阵) 按照压缩存储的概念,要存放稀疏矩阵的元素,由于没 有某种规律,除存放非零元的值外,还必须存储适当的 辅助信息,才能迅速确定一个非零元是矩阵中的哪一个 位置上的元素。下面将介绍稀疏矩阵的几种存储方法及 一些算法的实现。
(b )
(2)下三角矩阵 即矩阵的下三角部分元素是随机的,而上三角 部分元素全部相同(为某常数C)或全为0,具 体形式见下图(b)。
3.对角矩阵
若矩阵中所有非零元素都集中在以主对角线为中心的带 状区域中,区域外的值全为 0 ,则称为对角矩阵。常见 的有三对角矩阵、五对角矩阵、七对角矩阵等。 例如,下图为7×7的三对角矩阵(即有三条对角线上元 素非0)。
a00 a10 a20 ...
a11 a21 ... a22 ... ... ... ... an1n1
an10 a n11 a n12
一个下三角矩阵
下三角矩阵的压缩存储形式
思考:只存放上三角部分
以行序为主序存储上三角部分。
对于对称矩阵,除了用下三角存入外,还可用上三角形式 存放。这时数组a[0][0]存入sa[0],a[0][1]存入sa[1], a[0][2]存入sa[2]…,如下图。则sa[k]和a[i][j]之间的 对应关系为:
5.1 5.3
数组的基本概念 5.2 数组的存储结构
特殊矩阵及其压缩存储 5.4 稀疏矩阵 5.5 广义表 5.6 小结 5.7 练习
广义表知识点总结

广义表知识点总结一、广义表的概念和基本操作1.1 概念广义表是一种递归定义的数据结构,它可以包含原子元素和其他广义表,类似于树的结构。
广义表在计算机科学中广泛应用,常用于表示复杂的数据结构和递归算法。
1.2 基本操作广义表的基本操作包括创建、插入、删除、查找等,通过这些操作可以对广义表进行灵活的操作和管理。
在实际应用中,需要根据具体的需求对广义表进行不同的操作。
二、广义表的存储结构2.1 顺序存储结构顺序存储结构是将广义表中的元素按照顺序存储在内存中的一片连续空间中,可以通过下标访问元素,适合于对广义表进行随机访问的场景。
2.2 链式存储结构链式存储结构是通过指针将广义表中的元素连接起来,每个元素包含指向下一个元素的指针,适合于对广义表进行插入和删除操作的场景。
2.3 各种存储结构的比较在选择广义表的存储结构时,需要根据实际应用场景和需求来进行选择,顺序存储结构适合于对广义表进行随机访问,链式存储结构适合于对广义表进行插入和删除操作。
三、广义表的操作和应用3.1 创建广义表创建广义表可以通过递归的方式来实现,对于包含原子元素和子表的广义表,需要递归地创建子表并将它们链接起来。
3.2 插入和删除元素对于顺序存储结构的广义表,可以通过数组的插入和删除操作来实现元素的插入和删除;对于链式存储结构的广义表,可以通过修改指针来实现元素的插入和删除。
3.3 查找元素查找元素可以通过顺序遍历的方式来实现,对于包含子表的广义表,需要递归地进行遍历。
3.4 应用场景广义表在计算机科学中具有广泛的应用场景,包括对树的表示和操作、对图的表示和操作、对复杂数据结构的表示和操作等。
四、广义表的递归算法4.1 递归算法概念递归算法是指在解决问题的过程中,通过调用自身来处理子问题,直到子问题为空或者达到终止条件为止。
广义表的表示和操作通常涉及到递归算法。
4.2 广义表的递归遍历对于包含子表的广义表,需要通过递归算法来实现遍历操作,递归地对子表进行遍历,直到遍历到最底层的子表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.2.3 操作的实现
glist.cpp
#include "glist.h" ⑴ 初始化 void initGList(GList& L) { L=NULL; }
5.1.2 举例
分别用圆圈和方框表示表(表元素)和单元素 ①A=() 空表,其长度为零。
②B=(e) B中只有一个单元素,长度为1,表头为'e',表尾为 空。
③C=(a,(b,c,d)) 长度为2,表头为‘a’,表尾为子表((b,c, d))。
④D=(A,B,C) 长度为3,表头为A, 表尾为(B,C)。
void initGList(GList& L); // 创建空的广义表L int getLength(GList L); int getDepth(GList L); void creatGList(GList& L,string s); void printGList(GList& L,int k=0);
③有深度: 广义表的深度(多少层)定义为广义表书写 形式中括弧的最大重数,因此空表的深度为1, 因为一个"单原子"不是广义表,所以没有"深 度"可言,但可以认为它的深度为0。 如:A,B:1;C:2;D:3; E:无穷大。 ④可递归: 如E。 ⑤可共享: 子表可共享。
5.1.4 广义表的存储结构
⑤E=(a,E) 长度为2,表头为a,表尾为(E)--表头为E,表尾为 ()。E相当于无穷表(a,(a,(a,(…))))。
5.1.3广义表的几个性质
①有次序性: 广义表中的数据元素有固定的相对次序。 线性排列 --线性表的推广 层次结构 --树的推广 ②有长度: 广义表的长度定义为最外层括弧中包含的数 据元素个数。 表元素个数一定,不能无限,可以是空表。
enum ElemTag {ATOM,LIST}; typedef char AtomType;
struct GLNode{ ElemTag tag; union { //匿名共用体 AtomType atom; struct { GLNode *hp,*tp; } ptr; }; }; typedef GLNode* GList;
何谓"递归函数"?
一个含直接或间接调用本函数语句的函数被 称之为递归函数,它必须满足以下两个条件: ①在每一次调用自己时,必须是(在某种意义 上)更接近于解; ②函数中必须有一个终止处理或计算的准则。
5.2.2 广义表的头尾链表存储表示
glist.h #include <iostream> #include <string> using namespace std;
tag=0 atom
原子结点
tag=1
ptr---表结点的指针域 hp tp
表结点
广义表的头尾链表存储表示:
enum ElemTag {ATOM,LIST}; typedef char AtomType;
struct GLNode{ ElemTag tag; union { AtomType atom; struct { GLNode *hp,*tp; } ptr; }; };
④((x,y),((z)))的表头为列表(x,y)
其余分析同上。
5.2 广义表操作的实现
基于广义表是递归定义的结构,因此实现广 义表操作的算法均为递归函数。
5.2.1 分治法与递归求解
分治法是进行算法设计的一种方法,其严格定义为: 对于一个输入规模为 n 的函数或问题,用某种 方法把输入分割成 k(1<k≤n) 个子集,从而产生m个 子问题,分别求解这m个问题,得出m个问题的子 解,再用某种方法把它们组合成原来问题的解。若 子问题还相当大,则可以反复使用分治法,直至最 后所分得的子问题足够小,以至可以直接求解为止。 在利用分治法求解时,若所得子问题的性质和原问 题相同,则可递归求解。
由于广义表中的数据元素可以是原子,也可 以是广义表,显然难以用顺序存储结构表示。 由于列表中的数据元素可能为原子或列表, 由此需要两种结构的结点:一种是表结点, 用以表示列表;一种是原子结点,用以表示 原子。
为了在存储结构中便于分辩原子和子表,令表示广 义表的链表中的结点为"异构"结点,如图所示, 结 点中设有一个"标志域tag", 并约定 tag=0 表示原 子结点,tag=1 表示表结点。原子结点中的 data 域 存储原子,表结点中指针域的两个值分别指向表头 和表尾。
typedef GLNode* GList;
例:广义表 L=(a,(x,y),((z))) 的存储结构。
可由对L进行表头和表尾的分析得到--若列表不空, 则可分解成表头和表尾(采用头尾链表存储结构)。 分析: ①L为一非空列表
②L的表头为原子a③L的表尾为列表((x,y),((z)))
设ai为广义表的第i个元素,广义表LS可表示为: LS=(a1,a2,…, an) 其中: ①LS——广义表的名字; ②n——广义表的长度; 或者是单元素 (小写) ③ ai--表中的元素 ; 或者是表元素 (大写) ④n=0 空表; ⑤当广义表非空时,称a1为表头(head),其余元素组 成的表(a2,a3, …, an)为表尾(tail); 广义表的抽象数据类型:P107
第5章 广义表
5.1 广义表的定义 5.2 广义表操作的实现
5.1 广义表的定义
5.1.1 定义
广义表(Lists)简称表,它是线性表的推广。 一个广义表是n(n≥0)个元素的序列,当 n=0时称为空表。在一个非空的广义表中,其 元素可以是某一确定类型的对象(这种元素 被称作单元素),也可以是由单元素构成的 表(这种元素可相对地被称作子表或表元 素)。显然,广义表的定义是递归的,广义 表是一种递归的数据结构。
