初三数学视图与投影练习题
(典型题)初中数学九年级数学上册第五单元《投影与视图》测试题(含答案解析)
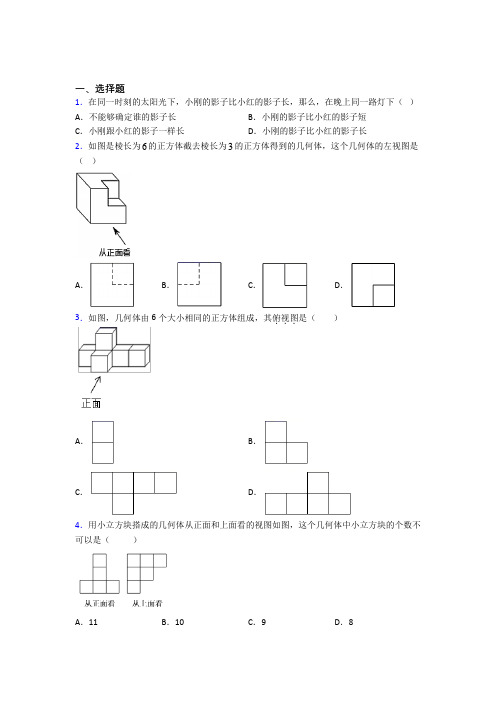
一、选择题1.在同一时刻的太阳光下,小刚的影子比小红的影子长,那么,在晚上同一路灯下()A.不能够确定谁的影子长B.小刚的影子比小红的影子短C.小刚跟小红的影子一样长D.小刚的影子比小红的影子长2.如图是棱长为6的正方体截去棱长为3的正方体得到的几何体,这个几何体的左视图是()A.B.C.D.3.如图,几何体由6个大小相同的正方体组成,其俯视图...是()A.B.C.D.4.用小立方块搭成的几何体从正面和上面看的视图如图,这个几何体中小立方块的个数不可以是()A.11 B.10 C.9 D.85.下列哪个图形,主视图、左视图和俯视图相同的是()A.圆锥B.圆柱C.三棱柱D.正方体6.如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同7.下列几何体是由4个相同的小正方体搭成的,其中左视图与主视图相同的是()A.B.C.D.8.在皮影戏的表演中,要使银幕上的投影放大,下列做法中正确的是()A.把投影灯向银幕的相反方向移动B.把剪影向投影灯方向移动C.把剪影向银幕方向移动D.把银幕向投影灯方向移动9.小明在太阳光下观察矩形木板的影子,不可能是()A.平行四边形B.矩形C.线段D.梯形10.如图是由七个相同的小正方体堆成的物体,从上面看这个物体的图是()A.B.C.D.11.如图是一个由多个相同小正方体堆积而成的几何体从上面看到的形状图,图中所示数字为该位置小正方体的个数,则这个几何体从正面看到的形状图是( )A.B.C.D.12.某立体图形如图,其主视图是()A.B.C.D.二、填空题13.如图,一个 5 ⨯ 5 ⨯ 5 的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则凿掉部分的体积为_____.14.一个物体的三视图如图所示,其中主视图和左视图是全等的等边三角形,俯视图是圆,根据图中所示数据,可求这个物体的表面积是______15.一个长方体从正面和左面看到的图形如图所示(单位cm),则从其上面看到的图形的面积是_____.16.如图()1表示一个正五棱柱形状的建筑物,如图()2是它的俯视图,小明站在地面上观察该建筑物,当只能看到建筑物的一个侧面时,他的活动区域有________个.17.写出图中圆锥的主视图名称________.18.长方体从正面看和从上面看所得到的图形如图所示,则这个长方体的体积是________.19.一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为,则a的值为__________.20.如图,电灯P在横杆AB的上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是3m,则P到AB的距离是__________m.三、解答题21.如图所示是由几个小立方体所组成的几何体的从上面看的形状图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的从正面看、从左面看的图形.【答案】答案见解析【分析】直接利用俯视图结合小正方体个数得出左视图和左视图.【详解】解:由题意可得:.【点睛】此题考查几何体的三视图,熟练掌握几何体三视图的视角和图形构成是解题的关键.22.如图是由四个大小相同的小正方体搭成的一个立体图形,画出从正面,从上面,从左面三个方向看到的立体图形的形状图.【答案】见解析【分析】观察图形可知,从正面看到的图形是两层:下层3个正方形,上层1个靠中间;从左面看到的图形是2层:下层2个正方形,上层1个靠左边;从上面看到的图形是两行:后面一行3个正方形,前面一行1个正方形靠左边,据此即可画图【详解】解:如图【点睛】此题考查了从不同方向观察几何体,锻炼了学生的空间想象力和抽象思维能力.23.如图是由若干个大小相同的小正方体搭成的几何体,请画出从正面、左面、上面看到的这个几何体的形状图.【答案】图见解析.【分析】根据几何体的三视图(主视图、左视图、俯视图)的定义即可得.【详解】画图如下:【点睛】本题考查了三视图,熟练掌握三视图的画法是解题关键.24.如图是某几何体的三种形状图.(1)说出这个几何体的名称;(2)若从正面看到的形状图的长为15cm,宽为4cm;从左面看到的形状图的宽为3cm,从上面看到的形状图的最长边长为5cm,求这个几何体的所有棱长的和为多少?它的侧面积为多少?它的体积为多少?【答案】(1)直三棱柱;(2)所有棱长的和69cm,侧面积180cm2,体积90cm3【分析】(1)只有棱柱的主视图和左视图才能出现长方形,根据俯视图是三角形,可得到此几何体为三棱柱;(2)这个几何体的所有棱长的和为2个3cm、2个4cm、2个5cm,3个15cm的和;三个长为15cm,宽分别为3cm、4cm、5cm的长方形的面积即是几何体的侧面积;先求出俯视图的面积,再乘高15cm,即为体积.【详解】解:(1)直三棱柱;(2)这个几何体所有棱长的和:153345269cm⨯+++⨯=.它的侧面积:(3+4+5)15⨯=180cm2;它的体积:12×3×4×15=90cm3故这个几何体的所有棱长的和为69cm,它的侧面积为180cm2,它的体积为90cm3.【点睛】此题考查从三视图判断几何体,掌握棱柱的侧面都是长方形,上下底面是几边形就是几棱柱是解决问题的关键.25.如图是一些棱长为1cm的小立方块组成的几何体.请你画出从正面看,从左面看,从上面看到的这个几何体的形状图.【答案】见解析【分析】根据三视图的定义画出图形即可.【详解】解:三视图如图所示:【点睛】本题考查作图-三视图,解题的关键是理解三视图的定义,属于中考常考题型.26.一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方体的个数.(1)请在方格纸中分别画出从正面、从左面看到的这个几何体的形状图;(2)若每个小立方体的边长为1cm,根据从三个方向看到的形状图,直接写出这个几何体的表面积为______2cm.【答案】(1)见解析;(2)24【分析】(1)由已知条件可知,从正面看有2列,每列小正方数形数目分别为2,3,从左面看有2列,每列小正方形数目分别为3,1.据此可画出图形.(2)首先确定该几何体的六个面上裸露的正方形的个数,然后确定面积即可.【详解】解:(1)如图所示.(2)该几何体的表面积为2×(3+4+5)=24;故答案为:24.【点睛】本题考查从不同方向看几何体,重点考查学生的空间想象能力,要弄清楚每个方向有几列,每列有多少个正方体.【参考答案】***试卷处理标记,请不要删除一、选择题1.A解析:A【分析】在同一路灯下由于两人所在位置不同,因此影长也不同,所以无法判断谁的影子长.【详解】在同一路灯下由于位置不同,影长也不同,所以无法判断谁的影子长.故选:A.【点睛】本题综合考查了平行投影和中心投影的特点及规律,正确理解平行投影和中心投影的特点和规律是解题的关键.2.A解析:A【分析】根据几何体三视图解答.【详解】该几何体的三视图如下:主视图:左视图:俯视图:故选:A.【点睛】此题考查几何体的三视图,正确掌握几何体三视图的画法是解题的关键.3.C解析:C【分析】细心观察图中几何体中正方体摆放的位置,根据俯视图是从上面看到的图形判定则可.【详解】解:从物体上面看,底层是1个小正方形,上层是并排放4个小正方形.故选:C.【点评】本题考查了三视图的知识,俯视图是从物体上面看所得到的图形,解答时学生易将三种视图混淆而错误的选其它选项.4.A解析:A【分析】首先从正视图易得这个几何体共有3层,由俯视图可得第一层正方体的个数;然后再根据主视图可得第二层和第三层最少或最多的正方体的个数,相加即可.【详解】从正面看这个几何体共有3层,由俯视图可得第一层正方体的个数是6个;由主视图可得第二层最多有正方体2个,最少有1个,第三层最多的正方体的个数是2个,最少有1个,∴这个几何体中小立方块的个数最多有:6+2+2=10个,最少有:6+1+1=8个,故选:A.【点睛】本题主要考查的是三视图判断几何体,熟练掌握几何体的三视图画法是解题的关键.5.D解析:D【分析】分别得出圆锥体、圆柱体、三棱柱、正方体的三视图的形状,再判断即可.【详解】解:圆锥的主视图、左视图都是等腰三角形,而俯视图是圆,因此选项A不符合题意;圆柱体的主视图、左视图都是矩形,而俯视图是圆形,因此选项B不符合题意;三棱柱主视图、左视图都是矩形,而俯视图是三角形,因此选项C不符合题意;正方体的三视图都是形状、大小相同的正方形,因此选项D符合题意;故选:D.【点睛】本题考查简单几何体的三视图,明确圆锥、圆柱、三棱柱、正方体的三视图的形状和大小是正确判断的前提.6.D解析:D【分析】分别画出所给两个几何体的三视图,然后比较即可得答案.【详解】第一个几何体的三视图如图所示:第二个几何体的三视图如图所示:观察可知这两个几何体的主视图、左视图和俯视图都相同,故选D.【点睛】本题考查了几何体的三视图,正确得出各几何体的三视图是解题的关键.7.B解析:B【分析】分别画出四个选项中简单组合体的三视图即可.【详解】A、左视图为,主视图为,左视图与主视图不同,故此选项不合题意;B、左视图为,主视图为,左视图与主视图相同,故此选项符合题意;C、左视图为,主视图为,左视图与主视图不同,故此选项不合题意;D、左视图为,主视图为,左视图与主视图不同,故此选项不合题意;故选B.【点睛】此题主要考查了简单组合体的三视图,关键是掌握左视图和主视图的画法.8.B解析:B【分析】根据中心投影的特点可知:在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,据此分析判断即可.【详解】解:根据中心投影的特点可知,如图,当投影灯接近银幕时,投影会越来越大;相反当投影灯远离银幕时,投影会越来越小,故A错误;当剪影越接近银幕时,投影会越来越小;相反当剪影远离银幕时,投影会越来越大,故B 正确,C错误;当银幕接近投影灯时,投影会越来越小;当银幕远离投影灯时,投影会越来越大,故D错误.故选:B.【点睛】此题主要考查了中心投影的特点,熟练掌握中心投影的原理和特点是解题的关键.9.D解析:D【分析】根据平行投影的特点可确定矩形木板与地面平行且与光线垂直时所成的投影为矩形;当矩形木板与光线方向平行且与地面垂直时所成的投影为一条线段;除以上两种情况矩形在地面上所形成的投影均为平行四边形,据此逐一判断即可得答案.【详解】A.将木框倾斜放置形成的影子为平行四边形,故该选项不符合题意,B.将矩形木框与地面平行放置时,形成的影子为矩形,故该选项不符合题意,C.将矩形木框立起与地面垂直放置时,形成的影子为线段,D.∵由物体同一时刻物高与影长成比例,且矩形对边相等,梯形两底不相等,∴得到投影不可能是梯形,故该选项符合题意,故选:D.【点睛】本题考查了平行投影特点:在同一时刻,不同物体的物高和影长成比例,平行物体的影子仍旧平行或重合.灵活运用平行投影的性质是解题的关键.10.C解析:C【分析】根据从上面看这个物体的方法,确定各排的数量可得答案.【详解】从上面看这个物体,可得后排三个,前排一个在左边,故选:C.【点睛】本题考查了三视图,注意俯视图后排画在上边,前排画在下边.11.C解析:C【解析】【分析】根据俯视图可判断主视图有3列,根据数字可判断每列最多的小正方体的个数,即可得答案.【详解】由俯视图中的数字可得:主视图有3列,从左到右的最大数字分别是:3,3,2.故选C.【点睛】本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方体数目为俯视图中该列小正方体数字中的最大数字.12.B解析:B【解析】【分析】找到从正面看所得到的图形即可.【详解】从物体正面看,左边1个正方形,中间2个正方形,右边2个正方形.故选B.【点睛】本题考查了三视图的知识,主视图是从物体的正面看得到的视图,解答时学生易将三种视图混淆而错误的选其它选项.二、填空题13.49【分析】分别计算前后上下左右方向凿掉的体积然后求和即可【详解】前后方向凿掉部分的体积为5525上下方向又凿掉了522214左右方向又凿掉了5210凿掉部分的总体积为2514解析:49【分析】分别计算前后、上下、左右方向凿掉的体积,然后求和即可.【详解】前后方向凿掉部分的体积为 5 ⨯ 5 = 25 ,上下方向又凿掉了 5 ⨯ 2 + 2 ⨯ 2 = 14 ,左右方向又凿掉了5 ⨯ 2 = 10 ,∴凿掉部分的总体积为 25 + 14 + 10 = 49【点睛】本题考查不规则图形的几何体的体积,关键是找到凿掉小正方形的个数.14.3π【分析】由三视图可知:该几何体是一个圆锥其轴截面是一个高为的正三角形可计算边长为2据此即可得出表面积【详解】由三视图可知:该几何体是一个圆锥其轴截面是一个高为的正三角形∴正三角形的边长==2∴圆解析:3π【分析】3为2,据此即可得出表面积.【详解】3∴正三角形的边长=3=2.60sin︒∴圆锥的底面圆半径是1,母线长是2,∴底面周长为2π∴侧面积为1×2π×2=2π,∵底面积为πr2=π,2∴全面积是3π.故填:3π.【点睛】本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.15.6cm2【分析】先根据从左面从正面看到的形状图的相关数据可得从上面看到的形状图是长为3宽为2的长方形再根据长方形的面积公式计算即可【详解】根据从左面从正面看到的形状图的相关数据可得:从上面看到的形状解析:6cm2【分析】先根据从左面、从正面看到的形状图的相关数据可得,从上面看到的形状图是长为3宽为2的长方形,再根据长方形的面积公式计算即可.【详解】根据从左面、从正面看到的形状图的相关数据可得:从上面看到的形状图是长为3宽为2的长方形,则从上面看到的形状图的面积是2×3=6cm2;故答案为6cm2.【点睛】此题考查了由三视图判断几何体,关键是根据从左面、从正面看到的形状图的相关数据得出从上面看到的形状图是长为3宽为2的长方形.16.【分析】根据正五棱柱形状的建筑物它的俯视图可知当只能看到建筑物的一个侧面时正好是以正五边形其中一条边的正三角形即可得出符合要求的活动区域【详解】根据正五棱柱形状的建筑物它的俯视图可知当只能看到建筑物解析:5【分析】根据正五棱柱形状的建筑物,它的俯视图,可知当只能看到建筑物的一个侧面时,正好是以正五边形其中一条边的正三角形,即可得出符合要求的活动区域.【详解】根据正五棱柱形状的建筑物,它的俯视图,可知,当只能看到建筑物的一个侧面时,他的活动区域是以每一条正五边形的边长为以其中一条边的正三角形,∴当只能看到建筑物的一个侧面时,他的活动区域有 5个,是以每一条边构成的等边三角形.故答案为5.【点睛】此题主要考查了视点、视角与盲区,根据题意得出当只能看到建筑物的一个侧面时的盲区是以正五边形其中一条边的正三角形是解决问题的关键.17.等腰三角形【解析】主视图是指从正面看圆锥体从正面看是等腰三角形故答案为:等腰三角形解析:等腰三角形【解析】主视图是指从正面看,圆锥体从正面看是等腰三角形,故答案为:等腰三角形.18.36【解析】由图可知这个长方体的长为4宽为3高为3∴长方体的体积V=4×3×3=36故答案为36解析:36【解析】由图可知,这个长方体的长为4,宽为3,高为3,∴长方体的体积V=4×3×3=36,故答案为36.19.【解析】试题分析:本题考查三视图的有关知识解题关键是理解左视图中的a就是俯视图等边三角形的高学会用方程的思想解决问题属于中考常考题型根据左视图中的a就是俯视图等边三角形的高由此根据侧面积列出方程即可【解析】试题分析:本题考查三视图的有关知识,解题关键是理解左视图中的a就是俯视图等边三角形的高,学会用方程的思想解决问题,属于中考常考题型.根据左视图中的a就是俯视图等边三角形的高,由此根据侧面积列出方程即可解决.由题意:解得考点:由三视图判断几何体.20.1【解析】试题分析:根据AB∥CD易得△PAB∽△PCD根据相似三角形对应高之比等于对应边之比列出方程求解即可考点:1相似三角形的应用2中心投影解析:1【解析】试题分析:根据AB∥CD,易得,△PAB∽△PCD,根据相似三角形对应高之比等于对应边之比,列出方程求解即可.考点:1.相似三角形的应用.2.中心投影.三、解答题21.无22.无23.无24.无25.无26.无。
初三数学投影与视图试题答案及解析

初三数学投影与视图试题答案及解析1.由一些大小相同的小正方体搭成的几何体的主视图和左视图如图,则搭成该几何体的小正方体的个数最少是()A.3B.4C.5D.6【答案】B【解析】根据左视图和主视图,这个几何体的底层最少有1+1+1=3个小正方体,第二层最少有1个小正方体,因此组成这个几何体的小正方体最少有3+1=4个.故选B.【考点】三视图2.如图,该几何体的左视图是()A.B.C.D.【答案】D【解析】左视图有2列,从左往右依次有2,1个正方形,其左视图为:.【考点】简单组合体的三视图.3.如下左图是由五个小正方体搭成的几何体,它的左视图是()【答案】A.【解析】从左面可看到从左往右2列小正方形的个数为:2,1,故选A.【考点】简单组合体的三视图.4.如图是由四个小正方体叠成的一个立体图形,那么它的左视图是()【答案】D.【解析】从左面可看到第一列有2个正方形,第一列有一个正方形.故选D.【考点】简单组合体的三视图.5.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的高和底面边长分别为()A.3,2B.2,2C.3,2D.2,3【答案】C【解析】设底面边长为x,则x2+x2=(2)2,解得x=2,即底面边长为2,根据图形,这个长方体的高是3,根据求出的底面边长是2.【考点】1.由三视图判断几何体;2.简单几何体的三视图.6.如图所示的几何体中,俯视图形状相同的是()A.①④B.②④C.①②④D.②③④【答案】B.【解析】找到从上面看所得到的图形比较即可:①的俯视图是圆加中间一点;②的俯视图是一个圆;③的俯视图是一个圆环;④的俯视图是一个圆. 因此,俯视图形状相同的是②④. 故选B.【考点】简单几何体的三视图.7.如图是由相同的小正方体组成的几何体,它的俯视图为()【答案】B【解析】根据几何体的三视图可知,主视图是从正面看到的图形,左视图是从左面看到的图形,俯视图是从上面看到的图形,由图可得它的为俯视图第二个,故选B【考点】几何体的三视图.8.如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是()【答案】A【解析】从几何体上面看,是左边2个,右边1个正方形.故选A.【考点】简单组合体的三视图.9.一个几何体的三视图如图所示,则这个几何体是()【答案】D.【解析】如图,俯视图为三角形,故可排除A、B.主视图以及左视图都是矩形,可排除C,故选D.【考点】由三视图判断几何体.10.下列四个水平放置的几何体中,三视图如右图所示的是()【答案】D【解析】三视图是指分别从物体的前面、左面、上面看到的平面图形.故选D.11.一个几何体的三视图如图所示,则这个几何体是()A.四棱锥B.四棱柱C.三棱锥D.三棱柱【答案】D【解析】根据主视图和左视图可以确定该物体是棱柱,根据俯视图可以确定该物体的底面是三角形,满足上述条件的只有三棱柱,故选D.12.如图所示零件的左视图是()A. B. C. D.【答案】D.【解析】:零件的左视图是两个竖叠的矩形.中间有2条横着的虚线.故选D.【考点】三视图.13.如图是由五个相同的小正方体组成的几何体,则下列说法正确的是( )A.左视图面积最大B.左视图面积和主视图面积相等C.俯视图面积最小D.俯视图面积和主视图面积相等【答案】D.【解析】观察图形可知,几何体的主视图由4个正方形组成,俯视图由4个正方形组成,左视图由3个正方形组成,所以左视图的面积最小,俯视图面积和正视图面积相等.故选D.考点: 简单组合体的三视图.14.某几何体的三视图如下图所示,则该几何体可能为()【答案】D.【解析】试题分析:由主视图和左视图可以得到该几何体是圆柱和小圆锥的复合体,由俯视图可以得到小圆锥位于圆柱的正中间.故选D.考点:三视图判断几何体.15.如图是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是()A.4个B.5个C.6个D.7个【答案】A.【解析】根据给出的几何体,通过动手操作,观察可得答案为4,也可以根据画三视图的方法,发挥空间想象能力,直接想象出每个位置正方体的数目,再加上来.故选A.【考点】三视图.16.如图所示是小红在某天四个时刻看到一个棒及其影子的情况,那么她看到的先后顺序是.【答案】④③①②.【解析】根据平行投影中影子的变化规律:就北半球而言,从早晨到傍晚物体的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长.可知先后顺序是④③①②.故答案是④③①②.【考点】平行投影.17.如图下面几何体的左视图是A.B.C.D.【答案】B【解析】左视图即从物体左面看到的图形,从左面看易得三个竖直排列的长方形,且上下两个长方形的长大于高,比较小,中间的长方形的高大于长,比较大。
(必考题)初中数学九年级数学上册第五单元《投影与视图》测试(含答案解析)
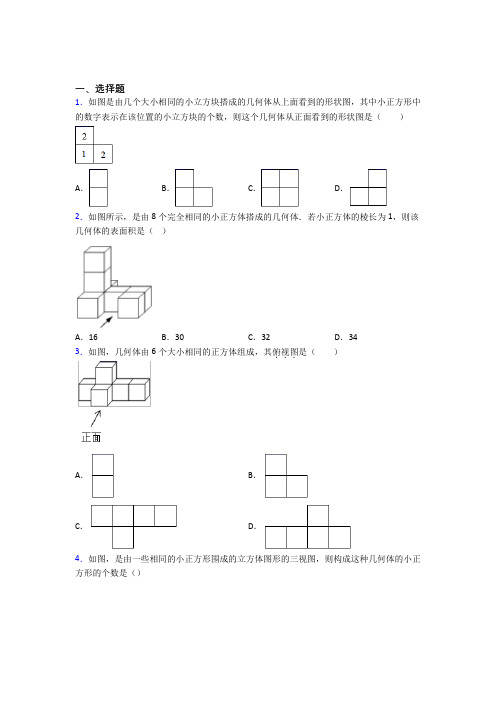
一、选择题1.如图是由几个大小相同的小立方块搭成的几何体从上面看到的形状图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体从正面看到的形状图是()A.B.C.D.2.如图所示,是由8个完全相同的小正方体搭成的几何体.若小正方体的棱长为1,则该几何体的表面积是()A.16 B.30 C.32 D.343.如图,几何体由6个大小相同的正方体组成,其俯视图...是()A.B.C.D.4.如图,是由一些相同的小正方形围成的立方体图形的三视图,则构成这种几何体的小正方形的个数是()A .4B .6C .9D .125.如图,一个几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )A .4π B .2π C .32π D .π6.如图是由五个棱长为2的小立方块搭建而成的几何体,则它的左视图的面积是( )A .3B .4C .12D .167.如下图所示是由一些大小相同的小正方体构成的三种视图,那么构成这个立体图的小正方体的个数是 ( )A .6B .7C .8D .98.如图的几何体的俯视图是( )A.B.C.D.9.一个密封的圆柱体容器中装了一半的水,如果将该容器水平放置如图,那么稳定后的水面形状为().A.B.C.D.10.下列四个几何体中,从正面看得到的平面图形是三角形的是()A.B.C.D.11.下图是从不同的方向看一个物体得到的平面图形,则该物体的形状是()A.圆锥B.圆柱C.三棱锥D.三棱柱12.如右图所示的是由几个相同小立方体组成的几何体从上面所看到的图形,正方形中的数字表示在该位览的小立方体的个数,则从左面乔这个几何体所得到的图形是()A.B.C.D.二、填空题13.写出图中圆锥的主视图名称________.14.由若干个相同的小立方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小立方体的个数,则x=______,y=________.15.如图,直角坐标平面内,小明站在点A(﹣10,0)处观察y轴,眼睛距地面1.5米,他的前方5米处有一堵墙DC,若墙高DC=2米,则小明在y轴上的盲区(即OE的长度)为_____米.16.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是_______.17.一个立体图形的三视图如图所示,这个立体图形的名称是__.18.如图1所示的是由8个相同的小方块组成的几何体,它的三个视图都是22的正方形若拿掉若干个小方块后,从正面和左面看到的图形如图2所示,则可以拿掉小方块的个数为_____.19.如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图,若组成这个几何体的小正方体的块数为n,则n的最小值与最大值的和为______.20.一个几何体,从不同方向看到的图形如图所示.拼成这个几何体的小正方体的个数为______.三、解答题21.如图,在阳光下,小玲同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时小强同学在测量树的高度时,发现树的影子有一部分(0.2 米)落在教学楼的第一级台阶上,落在地面上的影长为4.42米,每级台阶高为0.3米.小玲说:“要是没有台阶遮挡的话,树的影子长度应该是 4.62米.”小强说:“要是没有台阶遮挡的话,树的影子长度肯定比 4.62米要长.”(1)你认为谁的说法对?并说明理由;(2)请根据小玲和小强的测量数据计算树的高度.【答案】(1)小强的说法对,理由见解析;(2)8米.【分析】(1)画出解题示意图,利用同一时刻,物高与影长成正比,计算判断即可;(2)利用同一时刻,物高与影长成正比,计算判断即可;【详解】解:(1)小强的说法对;根据题意画出图形,如图所示,根据题意,得10.6DE EH =, ∵DE=0.3米,∴0.30.60.18EH =⨯=(米).∵GD ∥FH ,FG ∥DH , ∴四边形DGFH 是平行四边形, ∴0.2FH DG ==米. ∵AE=4.42米,∴AF=AE+EH+FH=4.42+0.18+0.2=4.8(米), 即要是没有台阶遮挡的话,树的影子长度是4.8米, ∴小强的说法对;(2)由(1)可知:AF=4.8米.∵10.6AB AF =, ∴8AB =米.答:树的高度为8米. 【点睛】本题考查了太阳光下的平行投影问题,准确理解影长的意义,灵活运用同一时刻,物高与影长成正比是解题的关键.22.请你画出下面几何体的主视图,左视图,俯视图.【答案】见解析. 【分析】根据三视图的概念作图即可.【详解】解:如图所示:【点睛】此题主要考查了三视图,用到的知识点为:三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看所得到的图形.23.作图题(1)如图所示的几何体是由5个相同的正方体搭成的,请画出它的三视图.(涂阴影)(2)如图是一些小正方块所搭几何体的俯视图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体的主视图和左视图:(涂阴影)【答案】(1)见解析;(2)见解析.【分析】(1)根据三视图的定义画图即可;(2)根三视图的定义再结合题意画图即可.【详解】解:(1)该立体图形的三视图如图:(2)该几何体的主视图和左视图如图:【点睛】本题考查了根据立体图形画三视图,较好的空间想象能力是解答本题的关键.24.在阳光下,小玲同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时小强同学测量树的高度时,发现树的影子有一部分0.2米落在教学楼的第一级台阶上,落在地面上的影长为4.42米,每级台阶高为0.3米.小玲说:“要是没有台阶遮挡的话,树的影子长度应该是4.62米”;小强说:“要是没有台阶遮挡的话,树的影子长度肯定比4.62米要长”.(1)你认为小玲和小强的说法对吗?(2)请根据小玲和小强的测量数据计算树的高度;(3)要是没有台阶遮挡的话,树的影子长度是多少?【答案】(1)小玲的说法不对,小强的说法对;(2)树的高度为8米;(3)树的影子长度是4.8米.【分析】(1)根据题意可得小玲的说法不对,小强的说法对;(2)根据题意可得DEEH=10.6,DE=0.3,EH=0.18,进而可求大树的影长AF,所以可求大树的高度;(3)结合(2)即可得树的影长.【详解】(1)小玲的说法不对,小强的说法对,理由如下(2)可得;(2)根据题意画出图形,如图所示,根据平行投影可知:DEEH=10.6,DE=0.3,∴EH=0.3×0.6=0.18,∵四边形DGFH是平行四边形,∴FH=DG=0.2,∵AE=4.42,∴AF=AE+EH+FH=4.42+0.18+0.2=4.8,∵ABAF =10.6,∴AB=4.80.6=8(米).答:树的高度为8米.(3)由(2)可知:AF=4.8(米),答:树的影子长度是4.8米.【点睛】考查了相似三角形的应用、平行投影,解题关键是掌握并运用平行投影.25.如图,某一广告墙PQ旁有两根直立的木杆AB和CD,某一时刻在太阳光下,木杆CD 的影子刚好不落在广告墙PQ上.(1)画出太阳光线CE和AB的影子BF;(2)若AB=10米,CD=6米,CD到PQ的距离DQ的长为8米,求此时木杆AB的影子BF的长.【答案】(1)如图所示,见解析;(2)木杆AB 的影长BF 是403米. 【分析】(1)连结CQ ,即为太阳光线CE ,过A 点作CE 的平行线与BQ 交于点F ,即可得到AB 的影子BF ;(2)根据在同一时刻的太阳光线下,物体高度与影子长度对应成比例可列出关系式,代入数值计算即可求得BF 的长. 【详解】解:(1)如图所示,CE 和BF 即为所求;(2)设木杆AB 的影长BF 为x 米, 由题意,得:CD DQ AB BF =,即6810x=, 解得:403x =. 答:木杆AB 的影子BF 的长为403米. 【点睛】本题考查了相似三角形的应用,理解题意并熟练运用相似三角形的性质是解题的关键.26.如图,甲、乙两个几何体是由一些棱长是1的正方体粘连在一起所构成的,这两个几何体从上面看到的形状图相同是“”请回答下列问题:(1)请分别写出粘连甲、乙两个几何体的正方体的个数.(2)甲、乙两个几何体从正面、左面、上面三个方向所看到的形状图中哪个不相同?请画出这个不同的形状图.(3)请分别求出甲、乙两个几何体的表面积.【答案】(1)见解析,甲的正方体有8个;乙的正方体有7个;(2)见解析;(3)甲几何体的表面积为:28;乙几何体的表面积为:28【分析】(1)分别利用几何的形状得出组成的个数;(2)甲的左视图从左往右3列正方形的个数依次为2,2,2;乙的左视图从左往右3列正方形的个数依次为2,1,2;(3)直接利用几何体的形状进而得出表面积.【详解】解:(1)如图所示:甲的正方体有4+4=8个;乙的正方体有4+3=7个;(2)甲、乙两个几何体的主视图相同,俯视图也相同,只有左视图不同;甲、乙两个几何体的左视图不同,如图所示:;(3)甲几何体的表面积为:14+14=28;乙几何体的表面积为:14+1+5+8=28.【点睛】本题考查了视图的相关知识;用到的知识点是:三视图分别是从物体的正面、左面、上面看得到的平面图形.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据主视图的定义判断即可.【详解】解:这个几何体从正面看到的图形是C,故选:C.【点睛】本题考查三视图的应用,熟练掌握三视图的意义及观察方法是解题关键.2.D解析:D【分析】首先要数清这个组合体的表面是由几个正方形组成的,再乘以1个正方形的面积即可得到表面积.【详解】+6×2+2)×21=34解:这个组合几何体的表面积为:(5×2+52故选:D.【点睛】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.3.C解析:C【分析】细心观察图中几何体中正方体摆放的位置,根据俯视图是从上面看到的图形判定则可.【详解】解:从物体上面看,底层是1个小正方形,上层是并排放4个小正方形.故选:C.【点评】本题考查了三视图的知识,俯视图是从物体上面看所得到的图形,解答时学生易将三种视图混淆而错误的选其它选项.4.D解析:D【分析】根据三视图,得出立体图形,从而得出小正方形的个数.【详解】根据三视图,可得立体图形如下,我们用俯视图添加数字的形式表示,数字表示该图形俯视图下有几个小正方形则共有:1+1+1+2+2+2+1+1+1=12故选:D【点睛】本题考查三视图,解题关键是在脑海中构建出立体图形,建议可以如本题,通过在俯视图上标数字的形式表示立体图形帮助分析.5.D解析:D【分析】这个几何体的侧面是以底面圆周长为长、圆柱体的高为宽的矩形,根据矩形的面积公式计算即可.【详解】根据三视图可得几何体为圆柱,圆柱体的侧面积=底面圆的周长⨯圆柱体的高=11ππ⨯⨯= 故答案为:D .【点睛】本题考查了圆柱体的侧面积问题,掌握矩形的面积公式是解题的关键.6.C解析:C【分析】先确定几何体的左视图的形状,再根据图形求面积.【详解】由图知该几何体的左视图由两列构成,第一列是两个小正方块,第二列是一个小正方块,共三个小正方块,∴它的左视图的面积是23212,故选:C.【点睛】此题考查几何体的三视图,根据几何体得到三视图的图形形状是解题的关键. 7.B解析:B【解析】【分析】根据三视图,将每一层的小正方体的个数求出来相加,即可得到答案.【详解】根据三视图得:该几何体由两层小正方体构成,最底层有6个,顶层由1个,共有7个,故选:B.【点睛】此题考察正方体的构成,能够理解图形的位置关系是解题的关键.8.C解析:C【分析】安装几何体三视图进行判断即可;【详解】解:本几何体的俯视图是后排有三个,前排有两个,即答案为C.【点睛】本题主要考查了简单几何体的三视图,掌握是从物体正面、左面和上面看物体以及较好的空间思维能力是解答本题的关键.9.A解析:A【分析】根据垂直于圆柱底面的截面是矩形,可得答案.【详解】由水平面与圆柱的底面垂直,得水面的形状是长方形.故选:A.【点睛】本题考查了截几何体和认识立体图形.解题的关键是能够正确认识立体图形,明确垂直于圆柱底面的截面是长方形,平行圆柱底面的截面是圆形.10.B解析:B【分析】依次分析每个几何体的主视图,即可得到答案.【详解】A.主视图为矩形,不符合题意;B.主视图为三角形,符合题意;C.主视图为矩形,不符合题意;D.主视图为矩形,不符合题意.故选:B.【点睛】此题考查几何体的三视图,掌握每一个几何体的三视图的图形是解题关键.11.A解析:A【解析】【分析】根据图形的三视图特点,进行选择.【详解】由题意图形的三视图可判断图形为圆锥.故答案选A.【点睛】本题主要考查的是三视图的性质特征,熟练掌握三视图的性质特征是本题的解题关键. 12.D解析:D【分析】从正面看,得到从左往右2列正方形的个数依次为3, 3;从左面看得到从左往右2列正方形的个数依次为5,1,依此画出图形即可.【详解】解:由题意知:该几何体为:故从左面看为:故选D.【点睛】本题考查三视图,解题关键是得到每列正方形的具体的数目为这列正方体的最多数目.二、填空题13.等腰三角形【解析】主视图是指从正面看圆锥体从正面看是等腰三角形故答案为:等腰三角形解析:等腰三角形【解析】主视图是指从正面看,圆锥体从正面看是等腰三角形,故答案为:等腰三角形.14.1或23【分析】由俯视图可知该组合体有两行两列左边一列前一行有两个正方体结合主视图可知左边一列叠有2个正方体从而求解【详解】解:由俯视图可知该组合体有两行两列左边一列前一行有两个正方体结合主视图可知解析:1或2 3【分析】由俯视图可知,该组合体有两行两列,左边一列前一行有两个正方体,结合主视图可知左边一列叠有2个正方体,从而求解【详解】解:由俯视图可知,该组合体有两行两列,左边一列前一行有两个正方体,结合主视图可知左边一列叠有2个正方体,故x=1或2;由主视图右边一列可知,右边一列最高可以叠3个正方体,故y=3.故答案为1或2;3.15.5【详解】首先作出BM⊥EO得出△BND∽△BME即可得出再利用已知得出BNBMDN的长即可求出EM进而求出EO即可解:过点B作BM⊥EO交CD于点N∵CD∥EO∴△BND∽△BME∴∵点A(﹣10解析:5【详解】首先作出BM⊥EO,得出△BND∽△BME,即可得出BN DNBM EM=,再利用已知得出BN,BM,DN的长,即可求出EM,进而求出EO即可.解:过点B作BM⊥EO,交CD于点N,∵CD∥EO,∴△BND∽△BME,∴BN DNBM EM=,∵点A(﹣10,0),∴BM=10米,∵眼睛距地面1.5米,∴AB=CN=MO=1.5米,∵DC=2米,∴DN=2﹣1.5=0.5米,∵他的前方5米处有一堵墙DC,∴BN=5米,∴50.510EM=,∴EM=1米,∴EO=1+1.5=2.5米.故答案为2.5.16.72【解析】分析:∵由主视图得出长方体的长是6宽是2这个几何体的体积是36∴设高为h则6×2×h=36解得:h=3∴它的表面积是:2×3×2+2×6×2+3×6×2=72解析:72【解析】分析:∵由主视图得出长方体的长是6,宽是2,这个几何体的体积是36,∴设高为h,则6×2×h=36,解得:h=3.∴它的表面积是:2×3×2+2×6×2+3×6×2=72.17.正四棱柱【分析】由主视图和左视图可确定是柱体再由俯视图可确定具体形状【详解】解:由主视图和左视图可确定是柱体再由俯视图可确定是正四棱柱故答案为:正四棱柱【点睛】本题考查了由三视图还原立体图形掌握立体解析:正四棱柱.【分析】由主视图和左视图可确定是柱体,再由俯视图可确定具体形状.【详解】解:由主视图和左视图可确定是柱体,再由俯视图可确定是正四棱柱.故答案为:正四棱柱.【点睛】本题考查了由三视图还原立体图形,掌握立体图形的三视图的形状,注意解题所用的方法.18.4或5【分析】根据正面和左面看到的图形可知上面一层必须保留左后面的正方体上层其它的正方体拿掉下层已经拿掉正方体的对应位置的正方体保留右前面的正方体其它两个可有可无或者去掉右前方的正方体另外两个保留据解析:4或5【分析】根据正面和左面看到的图形可知,上面一层必须保留左后面的正方体,上层其它的正方体拿掉,下层已经拿掉正方体的对应位置的正方体保留右前面的正方体其它两个可有可无或者去掉右前方的正方体,另外两个保留,据此作答即可.【详解】解:根据题意,拿掉若干个小立方块后,从正面和左面看到的图形如图2所示,所以可拿掉的小方块的个数可为5个或4个.故答案为:4或5.【点睛】本题考查了简单组合体的三视图.主要考查学生的空间想象能力.19.26【分析】从俯视图中可以看出最底层小正方体的个数及形状由主视图可以看出每一列的最大层数和个数从而算出总的个数【详解】解:根据主视图和俯视图可知该几何体中小正方体最少分别情况如下:故n的最小值为1+解析:26【分析】从俯视图中可以看出最底层小正方体的个数及形状,由主视图可以看出每一列的最大层数和个数,从而算出总的个数【详解】解:根据主视图和俯视图可知,该几何体中小正方体最少分别情况如下:故n的最小值为1+1+1+1+3+2+1=10,该几何体中小正方体最多分别情况如下:该几何体中小正方体最大值为3+3+3+2+2+2+1=16,故最大值与最小值得和为10+16=26故答案为:26【点睛】本题主要考查了由三视图判断几何体中小正方体的个数问题,可从主视图上分清物体的上下和左右的层数,从俯视图上分清物体的左右和前后位置,综合上述分析数出小立方块的可能个数.20.6【分析】根据从不同方位看到的图形的形状可知该几何体有2列2行底面有4个小正方体摆成大正方体上面至少2个小正方体放在靠前面的2个小正方体上面由此解答【详解】由题图可知该几何体第一层有4个小正方体第二解析:6【分析】根据从不同方位看到的图形的形状可知,该几何体有2列2行,底面有4个小正方体摆成大正方体,上面至少2个小正方体,放在靠前面的2个小正方体上面.由此解答.【详解】由题图可知,该几何体第一层有4个小正方体,第二层有2个小正方体,所以拼成这个几何体的小正方体的个数为6.故答案为:6.【点睛】本题主要考查从不同方向观察物体和几何体,关键注重培养学生的空间想象能力.三、解答题21.无22.无23.无24.无25.无26.无。
九年级数学投影与视图测试题(后附答案)
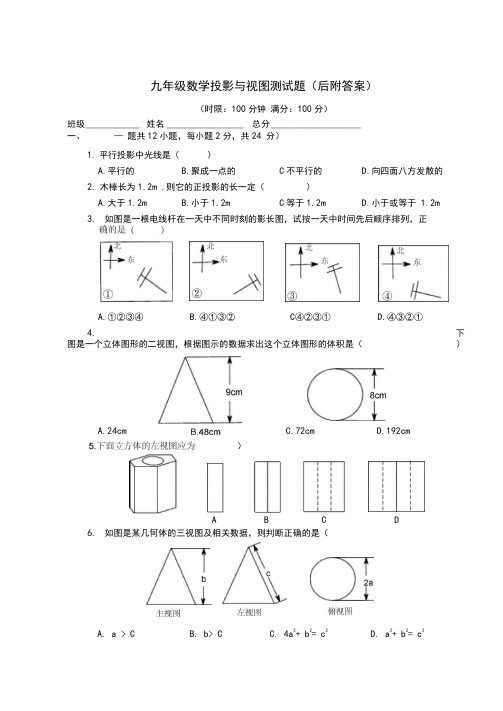
九年级数学投影与视图测试题(后附答案)(时限:100分钟 满分:100分)班级 ____________ 姓名 _________________ 总分 ____________________ 一、 — 题共12小题,每小题2分,共24 分)1. 平行投影中光线是( )A.平行的B.聚成一点的 C 不平行的D.向四面八方发散的 2. 木棒长为1.2m ,则它的正投影的长一定()A.大于1.2mB.小于1.2mC 等于1.2mD.小于或等于 1.2m3. 如图是一根电线杆在一天中不同时刻的影长图,试按一天中时间先后顺序排列,正A.①②③④B.④①③② C ④②③① D.④③②①4.下图是一个立体图形的二视图,根据图示的数据求出这个立体图形的体积是()6. 如图是某几何体的三视图及相关数据,则判断正确的是(C.72cmD.192cmA. a >C B. b >C C. 4a 2+ b 2= c 2D. a 2+ b 2= c 2)A.24cmAB C D7. 如图是由一些相同的小正方体构成的几何体的三视图,则这个几何体的小正方体的 个数是(9•一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的高和底边长10.下列投影一定不会改变厶 ABC 的形状和大小的是( )A.中心投影B.平行投影 C 正投影。
.当厶ABC 平行投影面时的平行投影主视图 B. 5左视图 C. 6A. 4个8.将一个几何体放在桌子上,它的三视图如下,这个几何体是(俯视图D. 7个主视图A.三棱体B ∙长方体C 正方体D 球体A. 3,2√B. 2,2√C. 3, 2D. 2,311.已知一个物体由X 个相同的正方体堆成,值是()它的主视图和左视图如图, 那么X 的最大A. 13B. 12C. 11D.1012.下面左图表示一个由相同小立方块搭成的几何体的俯视图,位置上小立方块的个数,则该几何体的主视图为(小正方形中的数字表示 )俯视图 分别为(主视图左视图俯视图A B C D2420.如图,水平放置的长方体的底面是边长为则长方体的体积等于 __________ .2和4的矩形,它的左视图的面积为 6,、填空题:(本大题共8小题,每小题3分,共24分)13. 在①长方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中,其主视图、左视图、俯视图都完全相同的是 _________.(填序号)14. 由一些大小相同的小正方体组成的几何体三视图如图所示,那么,组成这个几何体的小正方体有 ____________ 块•主视图左视图 俯视图15. 正方形ABCD 的边长为3,以直线AB 为轴旋转一周,所得几何体的左视图的周长 是 ___________ .16. 如图是一个几何体的三视图,其中主视图、左视图、都是腰为13cm ,底为IOcm的等腰三角形,则这个几何体的表面积为 ____________ .17. 一个圆锥的轴截面平行于投影面, 已知圆锥的正投影是边长为a 的等边三角形,则圆锥的体积是 __________ .18. 某一时刻,身高为165cm 的小丽影长是55cm ,此时,小玲在同一地点测得旗杆的 影长为5m ,则该旗杆的高度为 ____________ m. 19. 如图是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是 ________________ (把下图中正确和立体图形的序号都填在横线上)③ ④三、解答题:(本大题共52分)21. ( 7分)圆形餐桌正上方有一个灯泡 A ,灯泡A 照射到餐桌后在地面上形成阴影已知餐桌的半径为 0∙4m 、高为1m ,灯泡距地面2.5m,求地面上阴影部分的面积A22. ( 7分)一个几何体的三视图如图所示,它的俯视图为菱形,请写出该几何体的形状,并根据图中所给的数据求出它的侧面积∙23. (8分)某班一位学生要过生日了,为了筹备生日聚会,班主任准备让学生自己动 手制作生日礼帽.如图所示,是礼帽的三视图,请计算制作一个这样的生日礼帽需 要纸板的面积为多少?30cm4 20cm *一24. ( 8分)求证:一个人在两个高度相同的路灯之间行走,他前后的两个影子的长度 之和是一个定值.俯视图25. (8分)如图,花丛中有一路灯杆 AB ,在灯光下,小丽在D 点处的影长DE = 3米, 沿BD 方向行走到达 G 点,DG = 5米,这时小丽的影长 GH = 5米.如果小丽的身高 为1.7米,求路灯杆 AB 的高度(精确到0.1米)26. ( 7分)八年级美术老师在课堂上进行立体模型素描教学时,把14个棱长为10的正方体摆成如图所示的形式,然后他把露出的表面都涂上不同的颜色,求被他涂 上颜色部分的面积.27. ( 7分)观察下列由棱长为 1的小立方体摆成的图形•寻找规律,如图①中共有 1个小立方体,其中1个看得见,0个看不见;如图②共有 8个立方体,其中7个看 得见,1个看不见;如图③中,共有 27个小立方体,其中19个看得见,8个看不照此规律,请你判断第⑥个图中有多少个小立方块,有多少个看不见?③a同理BN = b -^FB.a• MB + BN = (DB + FB)=常数(定值) b-a、选择题:参考答案:1.A ;2.D ;3.B ;4.B ;5.B ;6.D ;7.B ;8.A ;9.C ; 二、填空题:10.D ; 11.C ; 12.C ;13.②;14.5; 15.18 π; 16.90 ∏cm2; 17. n ;18.15 ; 19.①、②、 ④;20.24 ;三、解答题:21.解:如图所示, DE// BC 设底面半径为 可得22.解: 23.解:0.4 =1.5=解得•••底面面积为:该几何体的形状是直四棱柱 .由三视图可知:棱柱底面菱形的对角线长分别为5•菱形的边长为-Cm5•棱柱的测面积=2× 8× 4 = 80 (cm 2)由三视图可知,该几何体是圆锥体 其中,底面直径是 20cm ,高为 30cm. 则圆锥的母线长为 圆锥的表面积为1S=1× 20 π× 4cm 、3cm ,=100 π√10 ( cm 2)•制作生日礼帽需要纸板 100 ∏√0 (cm 2).24.解:如图所示,CD EF 为路灯高度,BM 、BN 为该人前后的两个影子 AB 为该人高度,∙∙∙ AB // CDMB a DM = bMB _ a DB b-aa即MB=b-TDB.F√102+ 302= 10√∣0cm25. 解:如图所示,∙∙∙ CD// AB26. 解:从前、后、左、右看该物体均为 6个正方形,从上面看有9个正方形,所以被涂上颜色部分的面积为6 × 100 × 4+ 900= 3300.27. 解:照此规律,第⑥个图形中有 216个小立方块,有125个小立方块看不见CD 3 X BE1.7 3 x-1.7BD 1.75 x-1.7BG ②得3BD1.7 3—C C 1.7—3—2 1∙75E G15∙∙∙.∙. X ≈ 6.①5 同理BD + 55 BD + 5x-1.72。
人教版数学九年级下学期第29章《投影与视图》测试题含答案
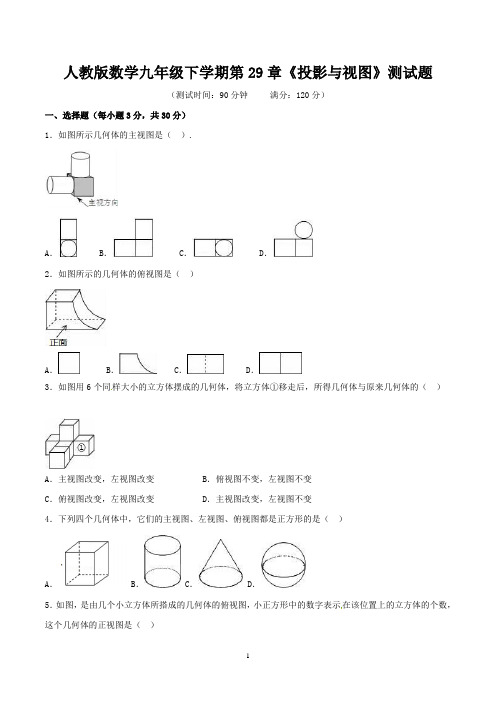
人教版数学九年级下学期第29章《投影与视图》测试题(测试时间:90分钟满分:120分)一、选择题(每小题3分,共30分)1.如图所示几何体的主视图是().A. B. C. D.2.如图所示的几何体的俯视图是()A. B. C. D.3.如图用6个同样大小的立方体摆成的几何体,将立方体①移走后,所得几何体与原来几何体的()A.主视图改变,左视图改变 B.俯视图不变,左视图不变C.俯视图改变,左视图改变 D.主视图改变,左视图不变4.下列四个几何体中,它们的主视图、左视图、俯视图都是正方形的是()A. B. C. D.5.如图,是由几个小立方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置上的立方体的个数,这个几何体的正视图是()A. B. C. D.6.如图所示是由六个相同的小立方块搭成的几何体,这个几何体的俯视图是().A. B. C. D.7.下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( ) 8.如图,按照三视图确定该几何体的全面积为(图中尺寸单位:cm)()A.128πcm2 B.160πcm2 C.176πcm2 D.192πcm29.如图所示的几何体的左视图是()A. B. C. D.10.如图,在房子屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区是()A.△ACE B.△ADF C.△ABD D.四边形BCED二、填空题(每小题3分,共30分)11.苏轼的诗句“横看成岭侧成峰,远近高低各不同”把此诗句用在视图上,说明的现象是________.12.如图,请写出图,图,图是从哪个方向可到的:图________;图________;图________.13.图是一个几何体的主视图、左视图和俯视图,则这个几何体是________.(填序号)14.如图,②是①中图形的________视图.②15.下列投影:①阳光下遮阳伞的影子;②灯光下小明读书的影子;③阳光下大树的影子;④阳光下农民锄地的影子;⑤路灯下木杆的影子.其中属于平行投影的是_______,属于中心投影的是_____.(填序号) 16.图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是_________.17.有两根大小、形状完全相同的铁丝,甲铁丝与投影面的夹角是45°,乙铁丝与投影面的夹角是30°,那么两根铁丝在投影面的正投影的长度的大小关系是:甲____乙(填“>”“<”或“=”).18.如图,Rt△ABC中,∠ACB=90°,CD⊥AB,那么线段AC在AB上的正投影是___,线段CD在AB上的正投影是___,线段BC在AB上的正投影是___.19.如图,是一个包装盒的三视图,则这个包装盒的表面积是(结果保留π)20.如图,小明同学在非洲旅游期间想自己测出金字塔的高度,首先小明在阳光下测量出了长1 m的木杆CD的影子CE长1.5m;其次测出金字塔中心O到影子的顶部A的距离为201m。
初三数学投影与视图试题答案及解析

初三数学投影与视图试题答案及解析1.如图所示的几何体,其主视图是()A.B.C.D.【答案】A.【解析】找到从正面看所得到的图形即可:从正面看有两层,上层右边有一小矩形,下边一个大矩形. 故选A.【考点】简单组合体的三视图.2.用4个完全相同的小正方体组成如图所示的立方体图形,它的俯视图是()A.B.C.D.【答案】A【解析】从上面看可得到一个有2个小正方形组成的长方形.故选A.【考点】三视图3.一个几何体的三视图如图所示,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱【答案】B【解析】从主视图和左视图看这个几何体是个柱体,从俯视图看是个三角形,因此可以确定是三棱柱,故选B【考点】三视图4.如图,贤贤同学用手工纸制作一个台灯灯罩,做好后发现上口太小了,于是他把纸灯罩对齐压扁,剪去上面一截后,正好合适,以下裁剪示意图中,正确的是()A.B.C.D.【答案】A【解析】压扁后圆锥的主视图是梯形,故该圆台压扁后的主视图是A选项中所示的图形.故选:A.【考点】三视图5.如图,所给三视图的几何体是()A.球B.圆柱C.圆锥D.三棱锥【答案】C【解析】主视图和左视图看到的是一个三角形,可确定为锥体,俯视图看到的是带有圆心的圆,因此可以确定是圆锥故选C.【考点】三视图6.写出一个三视图中主视图与俯视图完全相同的几何体的名称 .【答案】正方体(答案不唯一).【解析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.因此,∵球的三视图都为圆;正方体的三视图为正方形,∴应填球或正方体(答案不唯一).【考点】1.开放型;2.由三视图判断几何体.7.如图所示的几何体的主视图是()A.B.C.D.【答案】D【解析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.从正面看易得第一层有3个正方形,第二层最右边有一个正方形.故选D.【考点】简单组合体的三视图.8.下图是由7个完全相同的小立方块搭成的几何体,那么这个几何体的左视图是【解析】从左面看得到从左往右2列正方形的个数依次为3,1;故选A.考点: 简单组合体的三视图.9.如图所示,几何体的主视图是 ()【答案】B【解析】主视图反映的是物体的长和高,是从物体的正面看到的图形,故应选B.10.如图为主视图方向的几何体,它的俯视图是()【答案】D.【解析】从上面看可得到三个左右相邻的长方形,D符合.故选D.【考点】简单组合体的三视图.11.下图是由几个相同的小立方块组成的几何体的三视图,小立方块的个数是 .【答案】4个.【解析】根据三视图的知识,可判断该几何体有两列两行,底面有3个正方形,第二层有1个.试题解析:综合三视图可看出,底面有3个小立方体,第二层应该有1个小立方体,因此小立方体的个数应该是3+1=4个.考点: 由三视图判断几何体.12.如图,空心圆柱的左视图是()A.B.C.D.【解析】空心圆柱的左视图是两个长方形,其中里面的是看不见的,应该用虚线表示. 故选C.【考点】几何体的三视图.13.下面几何体的左视图是A.B.C.D.【答案】A【解析】左视图是从图形的左面看到的图形,从左面看,是一个等腰三角形。
初三数学投影与视图练习题

一.选择题1.下面四个几何体中,从上往下看,其正投影不是圆的几何体是()。
A.$B.$C.$D.$2.下列投影一定不会改变△ABC的形状和大小的是()。
A.中心投影B.平行投影C.正投影D.当△ABC平行投影面时的正投影3.木棒长为 3.5m,则它的正投影的长一定()。
A.等于 3.5mB.小于 3.5mC.大于 3.5mD.小于或等于 3.5m4.一根电线杆的接线柱部分AB在阳光下的投影CD的长为 1.2,太阳光线与地面的夹角,则AB的长为()。
A.12B.0.6C.D.5.图中的八边形是一个正八棱柱的俯视图,如果要想恰好看到这个正八棱柱的三个侧面,在图中标注的4个区域中,应该选择站在()。
A.①B.②C.③D.④6.如图,几个完全相同的小正方体组成一个几何体,这个几何体的三视图中面积最大的是()。
A.主视图B.左视图C.俯视图D.主视图和左视图7.如图是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体是()。
A.主视图改变,左视图改变B.俯视图不变,左视图不变C.俯视图改变,左视图改变D.主视图改变,左视图不变8.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的表面积为()。
A.66B.48C.482+36D.579.如图所示的几何体的俯视图是()。
A.$B.$C.$D.$10.某商品的外包装盒的三视图如图所示,则这个包装盒的体积是()。
A.200π(cm3)B.500π(cm3)C.1000π(cm3)D.2000π(cm3)二.填空题11.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为 1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为_____米。
12.如图,是某一个几何体的俯视图,主视图、左视图,则这个几何体是_____。
13.如果一个圆锥的主视图是等边三角形,俯视图是面积为4π的圆,那么它的左视图的高是_____。
初三数学投影与视图试题

初三数学投影与视图试题1.由5个相同的立方体搭成的几何体如图,则它的主视图是()A.B.C.D.【答案】B.【解析】找到从正面看所得到的图形即可,从正面看第一层是三个正方形,第二层是左边一个正方形,故选B.【考点】简单组合体的三视图.2.如图的几何体是由4个完全相同的正方体组成的,这个几何体的左视图是()A B C D【答案】C.【解析】由几何体可知左视图由两列组成,从左至右小正方形的个数分别为2个、1个,故选C.【考点】三视图.3.如图是由5个大小相同的正方体组成的几何体,它的俯视图为()A.B.C.D.【答案】A.【解析】此几何体的俯视图有2列,从左往右小正方形的个数分别是2,2.故选A.考点: 简单组合体的三视图.4.下列四个几何体中,俯视图为四边形的是().【答案】D.【解析】A、五棱柱的俯视图是五边形,故此选项错误;B、三棱锥的俯视图是,故此选项错误;C、球的俯视图是圆,故此选项错误;D、正方体俯视图是正方形,故此选项正确;故选:D.【考点】简单几何体的三视图.5.如图,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是A.①②B.②③C.②④D.③④【答案】B【解析】正方体主视图、左视图、俯视图都是正方形;圆柱主视图和左视图是长方形,俯视图是圆;圆锥主视图和左视图是三角形、俯视图是带圆心的圆;球主视图、左视图、俯视图都是圆,故选:B.【考点】简单几何体的三视图.6.下列几何体中,俯视图为四边形的是()【答案】D.【解析】A、五棱柱的俯视图是五边形,故此选项错误;B、三棱锥的俯视图是,故此选项错误;C、球的俯视图是圆,故此选项错误;D、正方体俯视图是正方形,故此选项正确.故选D.【考点】三视图.7.一个几何体是由一些大小相同的小正方体摆成的,其主视图与左视图如右图所示,则组成这个几何体的小正方体最少有个.【答案】5.【解析】综合左视图和主视图,这个几何体的底层最少有2+1=3个小正方体,第二层最少有2个小正方体,因此组成这个几何体的小正方体最少有3+2=5个.故答案为:5.考点: 三视图.8.如图,由三个小立方体搭成的几何体的俯视图是【】A.B.C.D.【答案】A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九上数学第四章视图与投影
一、知识梳理
1.三视图之间要保持长,高,宽
2. 在画视图时,看得见的部分的轮廓线通常画成线,看不见的部分轮廓线通常画成线。
3.太阳光线可以看成平行的光线,像这样的光线所形成的投影称为投影;探照灯、手电筒、路灯的光线可以看成是从一点出发的,像这样的光线所形成的投影称为投影。
※区分平行投影和中心投影:①观察光源;②观察影子。
4.眼睛的位置称为视点;由视点发出的线称为视线;眼睛看不到的地方称为。
二、例题赏析
1.如果某物体的三视图是如图所示的
三个图形,那么该物体的形状是( )
A、正方体
B、长方体
C、三棱柱
D、圆锥
2、如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触
路灯B的底部,这时他离路灯 A 25米,离路灯 B 5米,如果小亮的身高为 1.6米,那么路灯高度为( )
A.6.4米
B. 8米
C.9.6米
D. 11.2米
A B
3、如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的
是()
A.①②③④
B.④①③②
C.④②③①
D.④③②①
4.电影院呈阶梯或下坡形状的主要原因是( ).
A.为了美观
B.盲区不变
C.增大盲区
D.减小盲区
5、如图5,某学习小组选一名身高为 1.6m的同学直立于旗杆影子的顶端
处,其他人分为两部分,一部分同学测量该同学的影长为 1.2m,另一部
分同学测量同一时刻旗杆影长为9m,那么旗杆的高度是______m。
6.画出下图所示的三视图
7、下面是一个四棱柱的俯视图,请你画出它的主视图和左视图。
