材料的许用应力和安全系数计算三角
螺栓的材料和许用应力
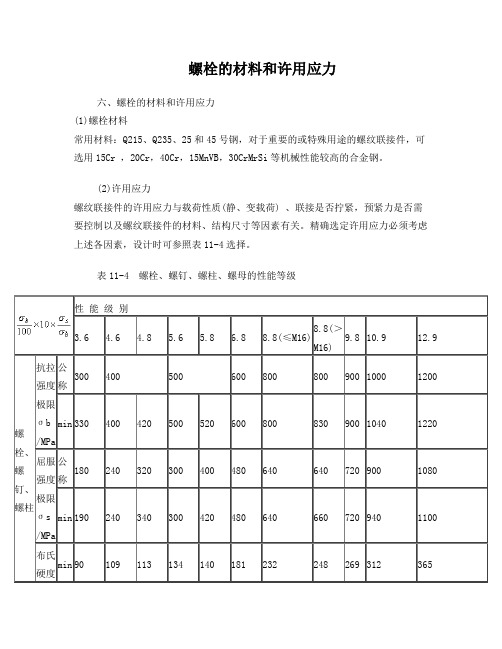
螺栓的材料和许用应力六、螺栓的材料和许用应力(1)螺栓材料常用材料:Q215、Q235、25和45号钢,对于重要的或特殊用途的螺纹联接件,可选用15Cr ,20Cr,40Cr,15MnVB,30CrMrSi等机械性能较高的合金钢。
(2)许用应力螺纹联接件的许用应力与载荷性质(静、变载荷) 、联接是否拧紧,预紧力是否需要控制以及螺纹联接件的材料、结构尺寸等因素有关。
精确选定许用应力必须考虑上述各因素,设计时可参照表11-4选择。
表11-4 螺栓、螺钉、螺柱、螺母的性能等级性能级别3.64.6 4.85.6 5.86.8 8.8(≤M16)8.8(>M16)9.8 10.9 12.9螺栓、螺钉、螺柱抗拉强度极限σb/MPa公称300 400 500 600 800 800 900 1000 1200 min 330 400 420 500 520 600 800 830 900 1040 1220屈服强度极限σs/MPa公称180 240 320 300 400 480 640 640 720 900 1080 min 190 240 340 300 420 480 640 660 720 940 1100布氏硬度min 90 109 113 134 140 181 232 248 269 312 365注:9.8级仅适用于螺纹公称直径≤16mm 的螺栓、螺钉和螺柱。
表11-5紧螺栓联接的许用应力及安全系数注:松螺栓联接时,取:[σ]=σs/S,S=1.2~1.7。
表11-6 许用剪切和挤压应力及安全系数例11-1 如例图11-1所示,一铸铁吊架用两个螺栓固紧在混凝土梁上。
吊架所承受的静载荷为P=6000 N,吊架底面尺寸及其它有关尺寸如图所示。
试求受力最大的螺栓所受的拉力。
解:该螺栓联接属受轴向载荷的普通螺栓联接(受拉螺栓联接),螺栓受拉力和螺纹间的摩擦力矩的作用。
若将增加30%以考虑的影响,则可认为螺栓所受的当量拉力为=1.31、计算受力最大的螺栓所受的轴向工作载荷:F=P/2+PL/500=6000/2+6000×350/500=7200N2、预紧力F' 的大小应能满足下面两个条件:受弯矩M=PL作用后,联接的右端不出现间隙;受弯矩M=PL作用后,联接的左端不被压溃。
玻璃钢材料许用应力计算公式

玻璃钢材料许用应力计算公式全文共四篇示例,供读者参考第一篇示例:玻璃钢是一种由玻璃纤维及树脂组成的复合材料,具有优良的物理和化学性能,广泛应用于船舶、化工、建筑等领域。
在使用玻璃钢材料时,需要考虑其许用应力,以确保其安全可靠地工作。
本文将介绍玻璃钢材料许用应力的计算公式及相关知识。
一、玻璃钢材料许用应力的定义玻璃钢材料许用应力是指在一定的工作条件下,材料内部所能承受的最大应力值。
超过这个应力值,材料可能会发生破裂或变形,影响整个结构的安全性。
玻璃钢材料的许用应力受多种因素影响,如材料本身的性能、工作环境、结构设计等。
在进行许用应力计算时,需要考虑这些因素,并选取合适的计算方法和公式。
玻璃钢材料的许用应力通常采用静态方法进行计算,常用的计算方法包括极限状态设计方法和允许状态设计方法。
1. 极限状态设计方法极限状态设计方法是指在结构承受最大荷载时,结构内部任意部位的应力均已达到或接近许用应力的设计方法。
在进行极限状态设计时,需要考虑结构在最不利荷载作用下的应力分布,并根据结构强度、刚度等特性来确定许用应力。
玻璃钢材料许用应力的计算公式可以根据材料的断裂性能、强度性能等来确定。
通常情况下,玻璃钢材料的许用应力计算公式主要包括拉伸强度、压缩强度、弯曲强度等方面的公式。
1. 拉伸强度计算公式拉伸强度是指材料在受拉力作用下的最大应力值,通常用σt表示。
玻璃钢材料的拉伸强度计算公式可表示为:σt = P/AP为拉力大小,A为受力截面积。
M为弯矩大小,S为截面惯性矩。
在进行玻璃钢材料许用应力计算时,需要注意以下几个方面:1. 要充分了解玻璃钢材料的性能特点,选择合适的计算方法和公式。
2. 考虑结构在不同工作条件下的应力状态,避免出现许用应力突然破坏的情况。
3. 结构设计时要考虑结构的强度、刚度等特性,确保结构安全可靠地工作。
4. 及时对结构进行监测和检测,发现结构存在安全隐患时要及时修复或更换。
玻璃钢材料许用应力的计算是保证结构安全可靠的重要步骤。
盲板厚度计算公式

盲板厚度计算公式是工程设计中非常重要的一个环节,因为盲板的厚度直接影响到设备的安全性能和使用寿命。
盲板厚度的计算需要根据不同的情境和需求进行,因此盲板厚度计算公式并不是唯一的。
在设计过程中,我们需要根据实际情况进行选择和调整。
在已知设计压力P、盲板直径D、材料许用应力和安全系数S的情况下,我们可以通过以下两个公式来计算盲板壁厚:
盲板壁厚= (PD)/(2σ*S )
或
盲板壁厚= (PD)/(2(σ-P)S)
其中,P为设计压力,D为盲板直径,σ为材料的许用应力,S为当地的安全系数。
这两个公式都是基于力学原理和材料力学的知识推导出来的,具有较高的准确性和可靠性。
另外,如果已知水压试验的压力P、盲板的最大直径D、盲板材料的抗拉强度标准值S,我们可以通过以下公式来计算盲板的最小厚度t:
t = PD/2S
这个公式是在特定的水压试验情境下使用的,适用于需要承受水压的盲板设计。
需要注意的是,以上内容仅供参考,在实际生产过程中,我们需要根据实际情况进行选择并计算,以确保结果准确。
同时,还需要考虑其他因素,如盲板的材质、工作环境等。
不同的材质和工作环境可能会对盲板的厚度产生影响,因此在设计过程中需要充分考虑这些因素。
总之,盲板厚度计算公式的选择和使用需要根据实际情况进行判断和调整,以确保设备的安全性能和使用寿命。
在实际应用中,我们需要综合考虑各种因素,并进行充分的实验和验证,以确保设计的可靠性和准确性。
z许用应力和安全系数

FN 2 FN 1
30
y
C
x
G
解 (1)计算BC杆的轴力 当电动葫芦处于AC梁的C 端时,杆 BC受力最大。此时取铰链C为研究对 象,其受力如图所示,其中FN1、FN2 分别为AC、BC杆的轴力。由平衡方 程
§3-3 拉伸与压缩时的强度计算
å
Fy = 0, F
N 2
?sin 30
G=0
FN 2 =
第三章 杆件的基本变形
许用应力和安全系数
§3-3 直杆轴向拉伸和压缩时的强度计算
一、材料失效与构件失效
材料发生屈服或断裂而丧失正常功能,称为材料失效。 对于脆性材料,其失效形式为断裂;对于塑性材料,因为工 程中一般不允许出现明显的塑性变形,因此塑性材料的失效 形式为屈服。
结构构件或机器零件在外力作用下丧失正常工作能力,称为 构件失效。构件的失效主要有强度失效、刚度失效、稳定失 效和疲劳失效等形式。
§3-3 拉伸与压缩时的强度计算
例3-4 图示支架中,杆①的许用应力[]1=100MPa,杆②的 许用应力[]2=160MPa,两杆的面积均为A=200mm2,求结构 的许可载荷[F]。
B
解 (1)计算AC杆和BC杆的轴力
取C铰为研究对象,受力如图所示。列平衡 方程
A
①
② 45 30
C
å å
45 30
G = 40kN sin 30
(2)设计截面
FN 2 A? [s ]
40´ 103 N = 400mm2 100MPa
由于BC杆由两根角钢组成,每根角钢的面积记为A1,则
A A1 = ? 200mm 2 2
查型钢表,3.6号角钢中,b=36mm,d=3mm,r =4.5mm,面积为 210.9mm2>A1,可满足要求。故选用3.6号等边角钢。
许用应力等于屈服强度除以安全系数

许用应力等于屈服强度除以安全系数【导言】在工程设计和材料选择过程中,许用应力是一个至关重要的概念。
它不仅涉及到材料的性能和抗力能力,还与设计的安全性密切相关。
在本文中,我们将从许用应力的概念出发,深入探讨它与屈服强度、安全系数的关系,以及如何有效地应用于工程实践中。
【定义】许用应力,顾名思义,即允许材料在工作时所能承受的最大应力值。
它是根据材料的屈服强度和安全系数来确定的,通常表示为σ_allow。
许用应力的概念是为了保证材料在长期工作加载下不发生塑性变形和失效,同时保证结构和构件的安全运行。
【屈服强度】屈服强度是指材料在受到一定应力作用下开始产生塑性变形的应力值。
用σ_yield表示。
在材料的应力应变曲线中,屈服强度对应着材料从线性弹性阶段进入塑性变形阶段的临界点。
对于金属材料来说,屈服强度是一个重要的材料性能参数,直接关系到材料的可塑性和抗拉性能。
【安全系数】安全系数是指设计中为了保证结构的安全性和可靠性,在许用应力和材料屈服强度之间设置的一个比值。
常用符号为N_safety。
通过在设计中设置适当的安全系数,可以有效地避免结构或构件因过载或其它外部因素而发生塑性变形、破坏甚至垮塌。
【许用应力与屈服强度、安全系数的关系】根据许用应力的定义,我们可以得到以下等式:许用应力σ_allow = 屈服强度σ_yield / 安全系数N_safety即,许用应力是由材料的屈服强度除以安全系数得到的。
这种关系体现了对材料性能和结构安全的综合考虑,能够有效地指导工程设计和材料选择。
【应用实例】以一根直径为10mm、长度为1m的钢材为例,其屈服强度为250MPa,安全系数为2.5。
根据许用应力的计算公式,可得到该钢材的许用应力为100MPa。
这意味着在工程设计中,我们可以将该钢材在工作时的应力控制在100MPa以下,从而保证其安全可靠地运行。
【结论】许用应力的概念是工程设计中的重要内容,它不仅关乎材料的性能和抗力能力,还直接关系到结构和构件的安全性。
钢板许用应力计算公式

钢板许用应力计算公式钢板许用应力的计算公式在工程领域中可是相当重要的哦!先来说说啥是许用应力。
简单来讲,许用应力就是材料在工作时允许承受的最大应力值。
就好比我们人干活儿,不能一直拼命,得有个限度,不然就累垮啦。
钢板也是一样,超过了它能承受的应力,就可能出问题。
那钢板许用应力的计算公式是咋来的呢?这可不是拍拍脑袋想出来的。
它是通过大量的实验和研究,综合考虑了钢板的材料特性、工作环境、安全系数等等因素得出来的。
咱们来具体看看这个公式:[σ] = σs / n 。
这里的[σ]就是许用应力,σs 呢,代表的是屈服强度,n 就是安全系数。
比如说,有一块钢板,它的屈服强度是 300MPa,我们设定的安全系数是 1.5。
那它的许用应力就是 300÷1.5 = 200MPa 。
这就意味着在实际使用中,这块钢板所承受的应力不能超过 200MPa ,超过了可就危险喽。
我记得有一次,在一个工厂里,工人们正在安装一批新的机器设备。
其中有一个关键的部件就是用钢板制作的。
负责这个项目的工程师在计算钢板的许用应力时,不小心把安全系数给算错了。
结果在设备运行的时候,那块钢板承受的应力超过了它的许用应力,出现了裂缝。
这可把大家急坏了,整个生产线都不得不停下来,进行紧急维修。
不仅耽误了生产进度,还造成了不小的经济损失。
从那以后,大家对钢板许用应力的计算可不敢马虎了。
在实际应用中,钢板的工作环境也会对许用应力产生影响。
比如说,如果钢板长期处于高温或者腐蚀性的环境中,它的性能就会下降,许用应力也得相应降低。
另外,不同类型的钢板,它的屈服强度也不一样。
比如说,普通碳素钢和合金钢的屈服强度就有很大差别,所以在计算许用应力的时候,一定要先搞清楚钢板的材质。
总之,钢板许用应力的计算公式虽然看起来简单,但是要准确地运用它,需要我们对钢板的各种特性有深入的了解,还得小心谨慎,不能出一点差错。
不然,就可能像我刚才说的那个工厂一样,出现大问题。
机械设计中的安全系数选择问题

工程中的材料强度、刚度、稳定性。
ﻫ强度-构件在确定的外力作用下,不发生破坏或过量塑性变形的能力。
杆-拉杆与压杆。
工程中承受拉伸的杆件统称为拉杆,受压的杆件成为杆或柱,承受扭转的杆件称为轴,承受弯曲的杆件统称为梁。
在工程力学中,把一些杆轴交汇于一点的工程结构称为桁架结构,这种结构受力特征是内力只有轴力,没有弯矩和剪力。
如:井架的主体桁架、建筑脚手架、三角形屋架梁等。
许用应力与安全系数ﻫ最近听到对于建井结构安全的一些言论,有的说安全凭经验即可,我原来怎样用的,现在怎样用是没有问题的;有的说,计算是什么结果,应该遵守。
ﻫ用伟人毛泽东的哲学思想是“实践—理论—实践”,ﻫ我们正常工作中选用的钢丝绳安全系数、钢材安全系数许用应力和安全系数都是比较成熟的,是规范推荐值或强制值。
ﻫ在非标准或特殊情况下,安全应由自己评估。
许用应力与安全系数常常应由自己选取决策。
ﻫ强度—在确定的外力作用下,不发生破坏的能力。
刚度—在确定的外力作用下,变形或位移在工程允许的范围内。
稳定性—在可能的外力作用下不会发生突然转变的能力。
例如:建筑施工脚手架,强度、刚度能满足,但由于局部结构不稳定,使整个脚手架倾覆或塌陷。
材料名称屈服点σs抗拉强度σb抗剪强度τ单位材料使用地点ﻫQ235 235 375 MPa或N/mm^2 普通结构ﻫ355 600轴类件4530CrMnTi 147060Si2CrVA 1678 1865 钢丝安全系数S应该综合荷载确定的准程度、材料性能数据的可靠性、所有计算方法的合理性、加工装配精度以及所设计的零件的重要性来确定。
各行各业都有一些经验的安全系数,目前均偏于保守。
目前,流行的安全系数法是部分系数法,他将各个对安全系数有影响的因素分别用一个分系数如:S1、S2、……标示,这些系数的乘积即即为安全系数:S=S1•S2•S3。
在实际应用中,取大取小带有一定主观性,即一般取大值或中间值,考虑的因素越多,系数值越大。
第二章 强度条件、安全系数与许用应力

120kN 220kN 260kN
①
B
FN / kN 120
②
C
③
160
160kN
A
D
BC段: 100 3 FN 2 100 10 N 160 106 Pa 160MPa(压应力) 2 A2 625 106 m2 CD段: FN 3 160 103 N (拉应力) 177.8 106 Pa 177.8MPa 3 6 2 A3 900 10 m
FN ,max A
考虑到许用应力是概率统计的数值,为了经济起见,最大工作 正应力也可略大于材料的许用应力,一般认为以不超过许用应 力的5%为宜。
2.选择杆件的横截面尺寸 已知结构承受的荷载和材料的许用应力,即可算出杆件的最大 轴力,并由此确定杆件的横截面面积。
A
3.确定结构的许用载荷
③ 由强度条件求直径
0.4m
FAy
FN 4 FN 由 得 2 A d
d
4 FN
170 10 Pa
6
4 26.5 103 N
0.0141m 14.1mm
为了经济起见,选用钢拉杆的直径为14mm。其值略小于计算 结果,但是其工作正应力超过许用应力不到5%。
V2 A1 A2 A3 l1 1741m 1.31m 1.49m 5m 19. . m
Ⅱ拉(压)杆的强度计算/三 拉压杆的强度条件/例题
gA( x)dx
采用等强度石柱
F
F x x N Ax
Ax dAx Ax gAxdx
FN 2,max A2 [ ]2 a 2 4.5 106 45KN
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四节 许用应力·安全系数·强度条件. 强度计算。
三角函数
由脆性材料制成的构件,在拉力作用下,当变形很小时就会突然断裂,脆性材料断裂时的应力即强度极限σb ;塑性材料制成的构件,在拉断之前已出现塑性变形,在不考虑塑性变形力学设计方法的情况下,考虑到构件不能保持原有的形状和尺寸,故认为它已不能正常工作,塑性材料到达屈服时的应力即屈服极限σs 。
脆性材料的强度极限σb 、塑性材料屈服极限σs 称为构件失效的极限应力。
为保证构件具有足够的强度,构件在外力作用下的最大工作应力必须小于材料的极限应力。
在强度计算中,把材料的极限应力除以一个大于1的系数n (称为安全系数),作为构件工作时所允许的最大应力,称为材料的许用应力,以[σ]表示。
对于脆性材料,许用应力
(5-8)
对于塑性材料,许用应力
(5-9)
其中、分别为脆性材料、塑性材料对应的安全系数。
安全系数的确定除了要考虑载荷变化,构件加工精度不同,计算差异,工作环境的变化等因素外,还要考虑材料的性能差异(塑性材料或脆性材料)及材质的均匀性,以及构件在设备中的重要性,损坏后造成后果的严重程度。
安全系数的选取,必须体现既安全又经济的设计思想,通常由国家有关部门制订,公布在有关的规范中供设计时参考,一般在静载下,对塑性材料可取;脆性材料均匀性差,且断裂突然发生,有更大的危险性,所以取,甚至取到5~9。
为了保证构件在外力作用下安全可靠地工作,必须使构件的最大工作应力小于材料的许用应力,即
(5-10)
上式就是杆件受轴向拉伸或压缩时的强度条件。
根据这一强度条件,可以进行杆件如下三方
面的计算。
1.强度校核 已知杆件的尺寸、所受载荷和材料的许用应力,直接应用(5-10)式,验算杆件是否满足强度条件。
2.截面设计 已知杆件所受载荷和材料的许用应力,将公式(5-10)改成
,
由强度条件确定杆件所需的横截面面积。
3.许用载荷的确定 已知杆件的横截面尺寸和材料的许用应力,由强度条件
确定杆件所能承受的最大轴力,最后通过静力学平衡方程算出杆件所能承担的
最大许可载荷。
例5-4 一结构包括钢杆1和铜杆2,如图5-21a 所示,A 、B 、C 处为铰链连接。
在
b
b
n σσ=
][s
s
n σσ=
][b n s n 0.2~5.1=s n 0.5~0.2=b n ][max
max σσ≤=
A N ][σN A ≥
][max σA N ≤
节点A 悬挂一个G=20kN 的重物。
钢杆AB 的横截面面积为A 1=75mm 2,铜杆的横截面面积为A 2=150mm 2。
材料的许用应力分别为=160MPa ,=100MPa ,试校核此结构的强度。
图5-21
解:(1)求各杆的轴力
取节点A 为研究对象,作出其受力图(图5-21b ),图中假定两杆均为拉力。
由平衡方程
解得
两杆横截面上的应力分别为
由于,故此结构的强度足够。
例5-5 如图5-22a 所示,三角架受载荷Q=50kN 作用,AC 杆是圆钢杆,其许用应力=160MP a ;BC 杆的材料是木材,圆形横截面,其许用应力=8MP a ,试设计两杆的直径。
][1σ][2
σ045sin 30sin ,
012=︒-︒=∑X N N 030cos 45cos ,021=-+=∑Y G N N kN 4.101=N kN 6.142=N a
a A N MP =P ⨯⨯==-1391075104.106
3
111σa
A N MP =⨯⨯==-6.9710150106.146
3
222σa a M P =<M P =<100][,160][2211σσσσ]
[1σ][2σ
图5—22
解: 由于、已知,故首先求出AC 杆和BC 杆的轴力N 1和N 2,然后由
,
求解。
(1) 求两杆的轴力
取节点C 研究,受力分析如图5-22b ,列平衡方程
解得
解得
N AC =Q=50kN (拉)
N BC = - N AC = -50kN (压)
(2) 求截面直径
分别求得两杆的横截面面积为
直径
例5-6 图5-23所示某冷镦机的曲柄滑块机构,镦压时,截面为矩形的连杆AB 处于
水平位置,高宽比h/b=1.2,材料为45钢,许用应力[σ]=90MPa 。
若不考虑杆的自重,已知
镦压力P=4500kN ,试按照强度条件确定h 、b 的大小。
][1σ][2σ]
[111σN ≥
A ]
[222σN ≥
A 030cos 30cos ,0=--=∑X ︒︒BC AC N N AC BC N N -=030sin 30sin ,0=--=∑Y ︒︒Q N N BC AC 2
242
6
32222
242
6
311
1cm 5.62m 105.62m 1081050][cm 13.3m 1013.3m 10
1601050][=⨯=⨯⨯=≥A =⨯=⨯⨯=≥A --σσN N cm
9.84,
cm 0.242
21
1≥=
≥=
π
π
A d A d
图5-23
解:如图5-23b 所示,AB 杆为轴向压缩,由截面法可得连杆的轴力数值大小为
N=P=4500kN
将强度条件改写为
,由于,所以
即
h=1.2b 0.245m
例5-7 图5-24a 所示的三角架由钢杆AC 和木杆BC 在A 、B 、C 处铰接而成,钢杆
AC 的横截面面积为A AC =12cm 2,许用应力[σ1]=160MP a ,木杆BC 的横截面面积A BC =200cm 2,许用应力[σ2]=8MP a ,求C 点允许起吊的最大载荷P 为多少?
图5-24
解: (1)求AC 杆和BC 杆的轴力
取节点C 研究,受力分析如图5-24b 所示,列平衡方程
-N AC cos300-N BC =0 N AC sin300 - P=0
解得
(2)求许可的最大载荷
P
][σN
A ≥
22.1b bh A ==2
2.1b ][σN ≥
m
204.0m 10902.1104500][2.16
3
=⨯⨯⨯=≥σN b
≥,0=∑X ,0=∑Y )(3)
(2压拉P N P N BC AC -==
由公式(5-10)得到N AC ≤A AC [σ1],即
2P ≤12⨯10-4⨯160⨯106N , P 1≤96kN
同样,由公式(5-10)得到 N BC ≤A BC [σ2],即
, P 2≤92.4kN
为了保证整个结构的安全,C 点允许起吊的最大载荷应选取所求得的P 1、P 2中的较小值,即。
N 1081000236-4⨯⨯⨯≤P 92.4kN ][max =P。
