第三章-微波传输线复习过程
合集下载
第三章传输线理论
第三章传输线理论本章的目的是概述由集总电路向分布电路表示法过度的物理前提。
在此过程中，推导出一个最有用的公式：一般的射频传输线结构的空间相关阻抗表示公式。
正如我们知道的，频率的提高意味着波长的减小，该结论用于射频电路，就是当波长可与分立的电路元件的几何尺寸相比拟时，电压和电流不再保持空间不变，必须把它们看做是传输的波。
因为基尔霍夫电压和电流定律都没有考虑到这些空间的变化，我们必须对普通的集总电路分析进行重大的修改。
本章重点介绍传输线理论，首先介绍传输线理论的实质，再介绍常用的几种传输线，其中重点介绍微带传输线，以及一般的传输线方程及阻抗的一般定义公式。
3.1传输线的基本知识传输微波能量和信号的线路称为微波传输线。
本节主要介绍传输线理论的实质以及理论基础3.1.1传输线理论的实质传输线理论是分布参数电路理论，它在场分析和基本电路理论之间架起了桥梁。
随着工作频率的升高，波长不断减小，当波长可以与电路的几何尺寸相比拟时，传输线上的电压和电流将随着空间位置而变化，使电压和电流呈现波动性，这一点与低频电路完全不同。
传输线理论用来分析传输线上电压和电流的分布，以及传输线上阻抗的变化规律。
在射频阶段，基尔霍夫定律不再成立，因而必须使用传输线理论取代低频电路理论。
现在举例说明：分析一个简单的电路，该电路由内阻为R1的正弦电压源V1通过1.6cm的铜导线与负载电阻R2组成。
电路图如下：图3.1 简单电路并且我们假设导线的方向与z轴方向一致，且它们的电阻可以忽略。
我们假设振荡器的频率是1MHz，由公式(3.1)10m/s, rε=10, rμ=1 因此可以得到波长其中是相速度，=9.49×7λ=94.86m.连接源和负载的1.6cm长的导线，在如此小的尺度内感受的电压空间变化是不明显的。
但是当频率提高到10GHz时情况就明显的不同了，此时波长降低到λ=p v/1010=0.949cm，近似为导线长度的2/3，如果沿着1.6cm的导线测量电压，确定信号的相位参考点所在的位置是十分重要的。
(四川理工学院)微波技术与天线-第3章 TEM波传输线
第3章 TEM波传输线理论
电压反射系数与电流反射系数间差一个负号Γ u=-Γ i 。 通常将电压反射系数简称为反射系数, 并记作Γ(z)。
对于无耗传输线 j
Ae jz Zl Z 0 j 2 z ( z ) e jz Be Zl Z0
反射系数与终端位置有关，而且是位置的函数，在终端
d 2 I ( z) 2 I ( z) 0 dz2
第3章 TEM波传输线理论
电压、电流的通解为
U Aez Bez 1 I ( Aez Bez ) Z0
式中，Z0 (R1 jL1 ) /(G1 jC1 )称为传输线的特性阻抗 。
解中的待定常数由边界条件决定 传输线的边界条件通常有以下三种: ① 已知终端电压Ul和终端电流Il ② 已知始端电压Ui和始端电流Ii ③ 已知信源电动势Eg和内阻Zg以及负载阻抗Zl。 在实际工程中，通常选择1类边界条件，因此
vp与频率ω有关,这就称为色散特性。
在微波工程中,特性阻抗Z0对分析TEM传输线的传输特性 具有重要意义，它是表征传输线与前级匹配和后级匹配的重 要参量。
第3章 TEM波传输线理论
3.2 传输线阻抗与反射
传输线与前级源的匹配主要取决于传输线在入端的输入阻 抗，传输线与后级的匹配不仅取决于传输线终端接收机的输入 阻抗，还与传输线本身的特性阻抗有关。它们的这些关系用特
对于时谐电压和电流, 可用复振幅表示为
u(z, t)=Re［U(z)e jωt］ i(z, t)=Re［I(z)e jωt］ 可得传输线方程在频域的表示为：
dU R1 jL1 I Z1 I dz dI G1 jC1 U Y1U dz
这里Z1 R1 jL1和Y1 G1 jC1分别是传输线单位长度 的串联阻抗和并联导纳 。
第三章微波传输线教材
线单位长度分布电容为C1, 则
空气微带线传播相速： vp0 c
1 LC0
介质微带线传播相速：vp1
c
r
1 LC1
14:00
电子科技大学电子工程学院
微波技术与天线
第三章 微波传输线
引入微带线等效介电常数 c
2
c
vp0 vp1
C1 C0
设空气微带线特性阻抗为
Z
，则实际微带线特性阻抗为
00
Z0
Z00
cr
只要求得空气微带线的特性阻抗
Z
00
及有效介电常数
,
c
就
可求得介质微带线的特性阻抗。
14:00
电子科技大学电子工程学院
微波技术与天线
第三章 微波传输线
工程上常用的一组实用经验公式:
(1) 导带厚度为零时
59.952ln(8h w ) w 4h
( w 1) 4h
微波技术与天线
第三章 微波传输线
第三章 微波传输线
导波系统中的电磁波按纵向场分量的有无，可分为 以下三种波型(或模)：
(1) 横磁波(TM波)，又称电波(E波)：Hz 0, Ez 0
(2) 横电波(TE波)，又称磁波(H波)：Ez 0, Hz 0
(3) 横电磁波(TEM波)：
Ez 0, Hz 0
Z00
119.904
w 2.42 0.44 h (1 12h)2
h
w
w
( w 1) w：导带宽度 h h：基片厚度
e
r 1
2
r 1 (1
2
12
第三章 微波传输线
图
H11模
图
E11模
Z
Ez
Eψ
Er
O Ψ
Y
r
X
圆柱坐标系
1 ∂H z ∂H ϕ = jωεE r − ∂z r ∂ϕ ∂H r ∂H z − = jωεEϕ ∂z ∂r 1 ∂ 1 ∂H r (rH ϕ ) − = jωεE z r ∂r r ∂ϕ 1 ∂E z ∂Eϕ = − jωµH r − ∂z r ∂ϕ ∂E r ∂E z − = − jωµH ϕ ∂z ∂r 1 ∂ 1 ∂E r (rEϕ ) − = − jωµH z r ∂r r ∂ϕ
（2）常用低次模的截止波长： 例1：矩形波导尺寸为a=8cm，b=4cm；试求工作频率在 3GHz时该波导能传输的模式。
3、波导尺寸的选取 （1）目的：只传输H10模，抑制H20模和H01模，即只传输主 模。因为这样可以使信号能量集中，减小损耗，且避免模式 间干扰和多模式传输引起的附加色散。 （2）选取原则：
一、直角坐标系中电磁场关系 1、基本方程 对于无损耗的媒质来说，电磁场中的基本方程，即麦克思韦方程变为
r r ∂H ∇ × E = −µ ∂t r r ∂E ∇× H = ε ∂t
（1）
为了求解方便，设场量按正弦规律变换，则
r r jwt −γz E = Em e r r jwt −γz H = H me
可以得到磁场的直角分量为
∂E z + γE y = − jwµH x （书P33，3－6式） ∂y ∂E z − γE x − = − jwµH y ∂x ∂E y ∂E x + = − jwµH z ∂x ∂y
用Ez和Hz表示其它场分量，由上述两个式子可以得到：
Ex = −
第三章微波传输线平行双线与同轴线
• 对微波集成传输元件的基本要求之一就是 它必须具有平面型结构, 这样可以通过调 整单一平面尺寸来控制其传输特性, 从而 实现微波电路的集成化。
各种微波集成传输线
① 准TEM波传输线, 主要包括微带传输线和共 面波导等(a)-(c);
② 非TEM波传输线, 主要包括槽线、 鳍线等 (d);
③开放式介质波导传输线, 主要包括介质波导、 镜像波导(e-f);
2 从同轴线到金属波导管
• 金属波导：和同轴线比较，波导管除去内 导体，不仅降低了内导体的损耗而且提高 了传输线的功率容量；
• 其缺点是比较笨重、高频下批量成本高、 频带较窄等。
3 微波集成传输线
• 随着航空、航天事业发展的需要, 对微波 设备提出了体积要小、重量要轻、 可靠性 要高、性能要优越、一致性要好、 成本要 低等要求, 这就促成了微波技术与半导体 器件及集成电路的结合, 产生了微波集成 电路。
1
1
c
vp
L0C0
r r
p
2
vp f
0 r r
当同轴线的截面尺寸与工作波长可比 拟时，同轴线内将出现高次模式。 要使同 轴线工作于TEM模式，则同轴线的内外半径 应满足以下条件：
min
1
2
D
d
3 损耗特性
通常同轴线介质损耗很小，其传输 损耗基本上决定于导体的欧姆损失。 同轴线的衰减常数仍可按下式估算
通频带：0~nGHz，语音信号
在实际中,广泛使用不同型号的电缆连 接接头（Cable Connector）以实现电缆的 连接， 尽管其功能相似， 但结构不同。 它们的共同点都是将电缆的内导体和外导 体分别连接起来， 使用时要注意连接头电 气和机械很好的匹配。
各种微波集成传输线
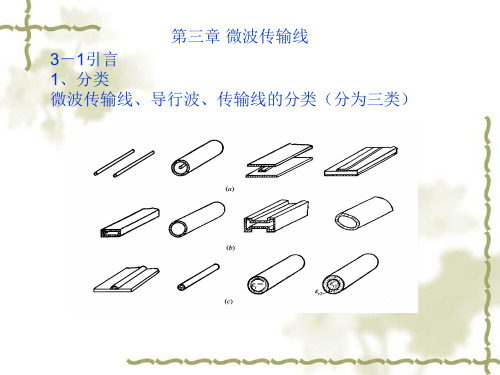
① 准TEM波传输线, 主要包括微带传输线和共 面波导等(a)-(c);
② 非TEM波传输线, 主要包括槽线、 鳍线等 (d);
③开放式介质波导传输线, 主要包括介质波导、 镜像波导(e-f);
2 从同轴线到金属波导管
• 金属波导：和同轴线比较，波导管除去内 导体，不仅降低了内导体的损耗而且提高 了传输线的功率容量；
• 其缺点是比较笨重、高频下批量成本高、 频带较窄等。
3 微波集成传输线
• 随着航空、航天事业发展的需要, 对微波 设备提出了体积要小、重量要轻、 可靠性 要高、性能要优越、一致性要好、 成本要 低等要求, 这就促成了微波技术与半导体 器件及集成电路的结合, 产生了微波集成 电路。
1
1
c
vp
L0C0
r r
p
2
vp f
0 r r
当同轴线的截面尺寸与工作波长可比 拟时，同轴线内将出现高次模式。 要使同 轴线工作于TEM模式，则同轴线的内外半径 应满足以下条件：
min
1
2
D
d
3 损耗特性
通常同轴线介质损耗很小，其传输 损耗基本上决定于导体的欧姆损失。 同轴线的衰减常数仍可按下式估算
通频带：0~nGHz，语音信号
在实际中,广泛使用不同型号的电缆连 接接头（Cable Connector）以实现电缆的 连接， 尽管其功能相似， 但结构不同。 它们的共同点都是将电缆的内导体和外导 体分别连接起来， 使用时要注意连接头电 气和机械很好的匹配。
微波技术_第三章_传输线和波导
3.1.1 TEM波
TEM波的特点
Ez 0 H z 0
必然有
kc 0
E0
2 t
k
H 0
2 t
横向场满足的场方程
TEM波横向场与静场一样都满足二维拉普拉斯方程,可用
势函数来表示
0(3.14)
2 t
E t
电流
I H dl (3.16)
假设时谐场沿z轴传播
j z E( x, y, z ) [et ( x, y) ez ( x, y)]e j z H ( x, y, z ) [ht ( x, y) hz ( x, y)]e
假定传输线或波导区域内是无源的，则Maxwell方程可写为：
场积分（利用安培环路定律）求出电流
6、根据定义求出传播常数、特征阻抗等
3.1.2 TE波
TE波的特征 Ez=0，Hz≠0，即磁场有纵向分量，电场无纵向分量，只 有横向分量。 直角坐标系下横向场与纵向场的关系
j H z Hx 2 kc x j H z Ex 2 k c y j H z Hy 2 kc y j H z Ey 2 k c x
H z j H x j E y x
直角坐标下横向场和纵向场的关系
E z H z j H x 2 (3.5a ) kc y x E z H z j H y 2 (3.5b ) kc x y H z j E z Ex 2 k c x y E z H z j Ey 2 kc y x (3.5c ) (3.5d )
均匀波导的理想化假设
第三章 微波传输线 1
A+为待定常数, 对无耗波导γ=jβ, 而β为相移常数。 现设Eoz(x, y)=A+Ez(x, y), 则纵向电场可表达为 Ez(x, y, z)=Eoz(x, y)e-jβz 同理, 纵向磁场也可表达为: Hz(x, y, z)=Hoz(x, y)e -jβz
而Eoz(x, y), Hoz(x, y)满足以下方程:
微波传输线 第3章 微波传输线
∇t2 Eoz ( x, y ) + kc2 EOZ ( x, y ) = 0 ∇t2 H oz ( x, y ) + kc2 H OZ ( x, y ) = 0
式中, k2c=k2-β2为传输系统的本征值。 由麦克斯韦方程, 无源区电场和磁场应满足的方程为
k
2 c ＜0
这时β= k 2 − kc2 > k 而相速vp= ω / β < c ur ε r , 即相速比 无界媒质空间中的速度要慢, 故又称之为慢波。
微波传输线 第3章 微波传输线 3.2 矩形波导 通常将由金属材料制成的、矩形截面的、内充空气的规 则金属波导称为矩形波导, 它是微波技术中最常用的传输系 统之一。 设矩形波导的宽边尺寸为a, 窄边尺寸为b, 并建立如图 2 2 所示的坐标。 1. 矩形波导中的场 矩形波导中的场 由上节分析可知, 矩形金属波导中只能存在TE波和TM 波。下面分别来讨论这两种情况下场的分布。 1)TE波
微波传输线 第3章 微波传输线
图 3 – 1 金属波导管结构图
微波传输线 第3章 微波传输线 ③ 波导管内的场是时谐场。 由电磁场理论, 对无源自由空间电场E和磁场H满足以下矢 量亥姆霍茨方程:
∇2 E + K 2 E = 0
式中, k2=ω2µε。
微波技术基础第3章
8h w 59 .952 ln w 4h a Z0 119 .904 6 w w h 2.42 0.44 1 h h w
w 1 h w 1 h
（3-1-26）
1. 带状线 带状线又称三板线, 它由两块相距为b的接地板与中间宽度 为w、厚度为t的矩形截面导体构成, 接地板之间填充均匀介质 或空气, 如图 3 - 2（c）所示。
由前面分析可知, 由于带状线由同轴线演化而来, 因此与同
轴线具有相似的特性, 这主要体现在其传输主模也为TEM, 也存
在高次TE和TM模。带状线的传输特性参量主要有:
α=αc+αd
(3-1-5)
式中, α为带状线总的衰减常数；αc为导体衰减常数； αd 为介质衰减常数。
第3章 微波集成传输线
介质衰减常数由以下公式给出:
27 .3 r 1 ad GZ 0 tan dB/m 2 0
(3-1-5)
式中, G为带状线单位长漏电导，tanδ为介质材料的损耗 角正切。
第3章 微波集成传输线
1 2 2 r 1 r 1 1 12 h 0.0411 w w/ h 1 2 2 w h e 1 r 1 r 1 1 12 h 2 w/ h 1 2 2 w （3-1-27）
vp
c
e
(3-1-22)
这样, 有效介电常数εe的取值就在1与εr之间, 具体数值由 相对介电常数εr和边界条件决定。现设空气微带线的分布电容 为C0, 介质微带线的分布电容为C1, 于是有
c
vp
1 LC0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 微波传输线
三、TEM波
1. 场分量基本关系式
T2 0
d
2Uz
dz2
2Uz
0
d 2 Iz
dz2
2
Iz
0
式中 kc2 k2 为传播常数。
其通解形式为
式中相移常数为 波阻抗为
U z A1ejz
I
z
1 ZTEM
A1ejz
k
ZTEM k
第三章 微波传输线
TEM波的全部场分量表达式。
ZTM j
第三章 微波传输线
四、传输功率及损耗
导波系统所传输的电磁波平均功率
P R e S2 1E H d S 2 1 ZSE T2 d SZ 2SH T2 d S
实际中，由于导波系统的电导率是有限的，且所填充的介 质也是非理想的，所以实际的导波系统都存在着导体损耗和介 质损耗。因而电磁波在传输过程中，其振幅会逐渐减小，也就 是说存在功率损耗，这种损耗应根据具体情况来计算。
Tzz ETEzjH T Tzz H TjE TE z
可得到TM波各场分量的基本关系式为
ET UzT HT IzTz
Ez
Iz
j
T2
IzjUzdz
第三章 微波传输线
整理 得
T 2kc20
d
2Uz
dz2
2Uz
0
d 2 Iz
dz2
2
Iz
0
式中 kc2 k2 为 传播常数。
第三章 微波传输线
3-5 矩形波导
矩形波导是横截面为矩形的 空心金属管，如图所示。图中a 和b分别为矩形波导的宽壁和窄 壁尺寸。由于矩形波导不仅具 有结构简单、机械强度大的优 点，而且由于它是封闭结构， 可以避免外界干扰和辐射损耗； 因为它无内导体，所以导体损 耗低，而功率容量大。在目前 大中功率的微波系统中常采用 矩形波导作为传输线和构成微 波元器件。
第三章 微波传输线
2. 群速
这些多种频率成分构成一个“波群”，又称 为波的包络，其传播速度称为群速。
群速的关系式
dz vg dt
群速的定义式为
d vg d
v g d d1
2 k c 2 v1 k ck 2 v1
2
c
群速、相速和光速三者的关系为：vp vg v2
对于TEM波 vg vp v
通解为
Uz A1ejz A2ejz
I z 1 ZTE
A1ejz A2ejz
ZTE 2kc2
第三章 微波传输线
TE波的全部场 分量表达式
HTIzT ETUzTz
Hz UjzT2
UzjIzdz
2. 边界条件
同理可得，TE波用横向分布函数表示的边界条件为
0 n C
式中C为理想波导横截面的边界闭合曲线，n为曲线C 的内法线矢量。
第三章-微波传输线
第三章 微波传输线
二、边界条件
1. 两种媒质界面的边界条件
n E2 E1 0 n H2 H1 Js n D2 D1 s
n B2 B1 0
2. 理想导体表面的边界条件
n E 2 0 n H 2 J s n D 2 s
n B2 0
三、交变电磁场的能量关系
H z 0,Ez 0
Ez 0,H z 0 Ez 0,H z 0
其中横电磁波只存在于多导体系统中，而横磁波和 横电波一般存在于单导体系统中，它们是色散波。
第三章 微波传输线
一、TM波
1. 场分量基本关系式 将TM波的场量：E E T E z,H H T u1u1u2u2zz 代入式(3-3)中的两个旋度方程得
通解为
Uz A1ejz A2ejz
I z
1 ZTM
A1ejz A2ejz
ZTM
2kc2
2. 边界条件 TM波电场纵向分量
Ez
Iz
j
kc2
当 kc2 0 时
0 C
第三章 微波传输线
二、TE波
1. 场分量基本关系式
T 2kc20
d
2Uz
dz2
2Uz
0
d 2 Iz
dz2
2
Iz
0
对于一封闭曲面S，电磁场的能量关系满足复功率 定理，即
S2 1E H n d S P Lj2W m W e
第三章 微波传输线
3-3 理想导波系统的一般理论
导波系统中的电磁波按纵向场分量的有无，可分为 以下三种波型(或模)：
(1) 横磁波(TM波)，又称电波(E波)： (2) 横电波(TE波)，又称磁波(H波)： (3) 横电磁波(TEM波)：
ET UzT HT IzTz
2. 边界条件 TEM波的边界条件可用横向分布函数表示
0 C
式中C为理想波导横截面的边界闭合曲线，为曲线 C的切线矢量。
第三章 微波传输线
3-4 导波系统的传输特性 一、传播常数和截止波长
导波系统中的传播常数为
kc 2k2kc 22
当 kc k ， 0 时，系统处于传输和截止状态 之间的临界状态。此时对应的频率称为临界频率或
相速是指导波系统中传输电磁波的等相位面沿轴向
移动的速度。
vp
dz dt
若将等相位面在一个周期T内移动的距离定义为相 波长，则有
p vpTT2
第三章 微波传输线
对于TEM波，相速为
vp
1 v
其相波长为
p
2
v f
对于TE波和TM波，
相速为
v
vp 1 c 2
相波长为
p
1 c 2
1 c2称为波型因子。
第三章 微波传输线
三、波阻抗
波阻抗定义为相互正交的横向电场与横向磁场之比，
Z Eu1 Eu2
Hu2
Hu1
对于TEM波，ZTEM
k
对于TE波和TM波， ckkc传输状态
ckkc截止状态
1
Z T Ek
1kck2 1c2
Z T M k 1 k ck 2 1 c 2
ZTE j
截止频率，记为
fc
kc
2
kc v
2
相应的临界波长或截止波长为
c
v fc
2
kc
第三章 微波传输线
导波系统传输TM波和TE波的条件可记为：
f fc或 c
而截止条件可记为：
f fc或 c
TEM波在任何频率下都能满足传输条
件 f fc或 c ，因此均处于传输状态。
第三章 微波传输线
二、波的传播速度和色散 1. 相速和相波长
第三章 微波传输线
3. 色散
TE波和TM波的相速和群速都随波长而变化，即是 频率的函数，这种现象称为“色散”。因此，TE波和 TM波统称为“色散波”；而TEM波的相速和群速相同， 且与频率无关，没有色散现象，故称为“非色散波”。
这里所说的波导色散现象与基于媒质特性产生的色散 现象不同，由于我们已假定波导中媒质是线性的，即不 随频率而变化，所以波导中电磁波产生色散的原因是由 波导系统本身的特性(即边界条件)所引起的。