地球重力场的表达方式
合集下载
第六章——地球重力场模型
第六章 地球重力场模型随着空间技术的进步和发展，现在不但有可能根据卫星轨道根数的变化精确地确定地球动力形状因子2J ，而且有可能结合卫星测高仪、卫星追踪卫星技术、卫星重力梯度仪等空间技术的测量结果以及地面重力测量结果计算出地球大地位球函数展开的高阶项系数。
以一组数值球函数展开系数表示的地球大地位称为地球重力场模型，地球重力场模型一方面支持卫星轨道的精确计算，另一方面可以给出地面上的长波重力异常场，为研究地球内部结构及其动力学过程提供重要的地面约束条件。
6.1 大地位的球函数展开现将第二章已经讨论过的大地位球函数展开中的有关公式汇总如下。
用r 表示地球外部空间任一点P 的径矢，则根据（2.2.18）式，地球在P 点的大地位球函数展开表示为其中kM 为地球的地心引力常数，a 为地球的赤道半径，θ、λ分别为P 点的地心余纬和经度，(cos )mn P θ为cos θ的n 阶m 次伴随勒让德多项式，(cos )cos mn P m θλ、(cos )sin mn P m θλ为归一化的n 阶m 次球面函数，根据（2.2-1.3）式、（2.2-1.6）式和（2.2-1.8）式，()n P x 、()n P x 、()mn P x 、()mn P x 分别为m n c 、m n s 和mn c 、mn s 分别为大地位球函数展开系数和规一化的大地位球函数展开系数，根据（2.2.20）式，有根据（2.3.4）式、（2.3.5）式，大地位二阶球函数展开系数等于其中A 、B 、C 分别为地球绕1Ox 、2Ox 和其旋转轴3Ox 轴的转动惯量，12I 、23I 、13I 分别为地球绕相应轴的惯性积，大地位球函数展开有时写成下面的形式nm J 、nm K 与大地位球函数展开系数m n c 、m n s 之间的关系为2J 称为地球的动力形状因子。
当3n 时，()n P x 、()mn P x 的表达式如表6.1.1所示。
地球重力场
在重力勘探和大地测量学中，一般把大地水准面的形状作为地球 的基本形状。
测量结果表明，大地水准面的形状不规则，它在南北两半球并 不对称，北极略为突出，南极略平，呈“梨”型，见下图。
1、计算正常重力值的基本公式：
g0 ge (1 sin2 1 sin2 2)
式中 g p ge ,
ge
1
（1）重力观测是在地球的自然表面上而不是在大地 水准面上进行的（自然表面与大地水准面间的 物质及测点与大地水准面间的高差会引起重力 的变化）
（2）地壳内物质密度的不均匀分布；
（3）重力日变化
3、重力异常的物理意义
A
大地水准面
σ0
△F
σ V
g0 △g
△F
g观
△σ =σ–σ0 △m=Δσ×V
g观 g0 F
（例如，△m=50万吨的球形矿体，当中心埋深为100米， 可产生355μGal 的异常，当中心埋深为1000米； 则只能 产生3.4μGal的异常，该强度的异常仪器不能观测到。）
（5）干扰场不能太强或具有明显的特征。
第二节 岩矿石密度、重力仪
三大岩类物质循环
三大岩类物质循环
一、岩（矿）石的密度及地球密度分布
（2）成岩过程中的冷凝、结晶分异作用也会造成 同一岩体不同岩相带，由边缘相到中心相， 密度逐渐增大；
C=mr ，方向垂直自转轴向外。
（二）重力场
1、重力场强度
单位质量的物体在重力场中所受的力，称为重力 场强度
P = mg
g=P/m
上式左边为重力场强度，右边为重力加速度
由上式可见：重力场强度，无论在数值上，还是 量纲上都等于重力加速度，而且两者的方向也一致。 在重力勘探中，凡是提到重力都是指重力加速度（或 重力场强度）。
第二章地球重力场
f 1 /( 298.257 0.001 )
a ( 9.78033 0.00001)m / s2
U0 ( 6.263686 0.000003) 107 m 2 / s2
GRS80系统正常重力在椭球面上的公式
( 0 ,) 978.0327(1 5.279041103 sin 2 2.32718105 sin 4 0.01262105 sin6 )Gal
Wzz
描述了重力随高程的变化， 称为垂直重力梯度，与水 准面曲率有关。
2-5 地球引力位的球谐函数展开
从重力位W的(2-5)式可以看出，在地球重力位中，离心力位是 简单的解析函数，而引力位由于不知道边界面以及密度，不能 直接计算。对于地球外部空间，可用球谐函数展开式近似表示。 引力位可用基本公式(1-11)表示
故在椭球面S0 上的全部重力以γ 表示时，则有
(2-69)
再引入下列简化符号 第二偏心率
(2-72)
(2-72)
上式是一个重要的近似公式，1738年由克莱劳提出，所以称为 克莱劳理论。比较一下(2-73)式的 γa 和(2-74)式的γb ，以及 (2-72)式中括弧号的量，可以看出 γ 有如下的对称的公式
正常重力场：一个假想的、由形状和质量分布都很规则的物体 所产生的重力场。
此物体称为 正常地球旋转椭球
正常重力场的等位面称为 正常水准面。由于正常位可以根据 正常地球的参数求得，因此正常水准面的形状也是已知的。
如果设定了正常地球的长半径 a、扁率 f、旋转角速度ω 以 及总质量 M，并要求椭球表面就是它本身重力场的水准面。 根据司托克斯定理，这个正常地球唯一地确定其外部空间的 重力场。这时，我们称正常地球为水准椭球。进一步地，采
a 6378137 2m GM ( 398600.5 0.05 ) 109 m 3 / s2 其中包括大气质量 GMa ( 0.35 0.003 ) 109 m 3 / s2 J 2 ( 1082.63 0.005 ) 106
a ( 9.78033 0.00001)m / s2
U0 ( 6.263686 0.000003) 107 m 2 / s2
GRS80系统正常重力在椭球面上的公式
( 0 ,) 978.0327(1 5.279041103 sin 2 2.32718105 sin 4 0.01262105 sin6 )Gal
Wzz
描述了重力随高程的变化， 称为垂直重力梯度，与水 准面曲率有关。
2-5 地球引力位的球谐函数展开
从重力位W的(2-5)式可以看出，在地球重力位中，离心力位是 简单的解析函数，而引力位由于不知道边界面以及密度，不能 直接计算。对于地球外部空间，可用球谐函数展开式近似表示。 引力位可用基本公式(1-11)表示
故在椭球面S0 上的全部重力以γ 表示时，则有
(2-69)
再引入下列简化符号 第二偏心率
(2-72)
(2-72)
上式是一个重要的近似公式，1738年由克莱劳提出，所以称为 克莱劳理论。比较一下(2-73)式的 γa 和(2-74)式的γb ，以及 (2-72)式中括弧号的量，可以看出 γ 有如下的对称的公式
正常重力场：一个假想的、由形状和质量分布都很规则的物体 所产生的重力场。
此物体称为 正常地球旋转椭球
正常重力场的等位面称为 正常水准面。由于正常位可以根据 正常地球的参数求得，因此正常水准面的形状也是已知的。
如果设定了正常地球的长半径 a、扁率 f、旋转角速度ω 以 及总质量 M，并要求椭球表面就是它本身重力场的水准面。 根据司托克斯定理，这个正常地球唯一地确定其外部空间的 重力场。这时，我们称正常地球为水准椭球。进一步地，采
a 6378137 2m GM ( 398600.5 0.05 ) 109 m 3 / s2 其中包括大气质量 GMa ( 0.35 0.003 ) 109 m 3 / s2 J 2 ( 1082.63 0.005 ) 106
第二讲 地球重力场
《应用重力学》第二讲地球重力场一、重力(Gravity)重力 = 地球引力惯性离心力微弱,可忽略=吸引力FF GM E R 3惯性离心力Cm RC = m ⎤ 2r重力GG=F+C地球重力场：在地球内部及其附近存在重力作用的空间。
④重力场强度:单位质量的物体在重力场中所受的重力 ( =G/m )④重力加速度g=G/m④重力加速度在数值上(包括方向)等于单位质量所受的重力，也就是等于重力场强度。
重力加速度重力重力场强度④重力勘探所提的重力都是指重力加速度或重力场强度。
重力(重力加速度)单位④在CGS单位制(克、厘米、秒)：“cm/s2 ”，“伽”或“Gal”1 cm/s2 = 1 Gal④在SI单位制(千克、米、秒)：“m/s2”，“g.u.”1 m/s2 = 106 g.u.1 Gal = 1 cm/s21 g.u. = 10-6m/s21 Gal = ? g.u.1 Gal (伽) = 1 cm/s2 = 10-2 m/s2 = 104 g.u.1 mGal (毫伽) = 10-5 m/s2 = 10 g.u.1 uGal (微伽) = 10-8 m/s2 = 10-2 g.u.重力的变化④包括随不同测点位置的空间变化以及同一测点的重力随时间的变化。
④空间上:地球形状、地形：引起约 6万 g.u. 的变化；地球自转：重力有 3.4万 g.u. 的变化;地下物质密度分布不均匀：能达到几千 g.u.变化人类的历史活动遗迹和建筑物等北赤南极道极在地球表面上，全球重力平均值约为9.8m/s2，赤道重力平均值为9.780m/s2，两极平均值为9.832 m/s2，从赤道到两极重力变化大约为0.05m/s2。
④时间上：潮汐变化：太阳、月亮等天体引力引起的重力的周期性变化，其大小可达 3 g.u.非潮汐变化：地球形状的变化和地下物质运动等引起的非周期性变化，其变化大小一般不超过 1 g.u.④海水每天有两次涨落运动，其中早晨出现的潮涨称为潮，晚上出现的潮落称为汐，总称潮汐。
第二章 地球重力场及地球形状的基本理论
3.2.4源自地球的正常重力位和正常重力
要精确计算出地球重力位，必须知道地球表面的形状及内部物质密度， 但前者正是我们要研究的，后者分布极其不规则，目前也无法知道，故根据 上式不能精确地求得地球的重力位，为此引进一个与其近似的地球重力位— —正常重力位。
dm 2 W f ( x2 y 2 ) r 2 M
3.2.1
引力与离心力
引力：
离心力： 重力：
M m Ff 2 r
P m 2
g FP
其它作用力（太阳、月亮）大多数情况下可忽略。
3.2.2
引力位和离心力位
由理论力学可知，如果某一空间（有限或无限）的任意一点都有一 定力的作用，而力的大小与方向只与该点的位置有关，则这一空间 称为力场。就力场而言，具有共同的特性，即力场所做的功与路径 无关，只与起点与终点有关。这样的力称为保守力。引力与离心力 都是保守力。 1. 定义：单位质点受物质M的引力作用产生的位能称为引力位，或者 说将单位质点从无穷远处移动到该点引力所做的功。 公式推导原理： 任意两质点M和m相互吸引的引力 ：
因此，引力位梯度的负值，在数值上等于单位质点受 r 处的质 体 M 吸引而形成的加速度值。
dm 地球整体的位函数：V dV f r (M ) (M )
3.2.2
引力位和离心力位
续3
引力位对被吸引点各坐标轴的偏导数等于相应坐标轴 上的加速度(或引力)向量的负值。用公式表达为：
V V V az ay ax ， ， z y x
v3
R 3 5 3 3 ( ) ( cos cos )dm r 2 2 M
3.2.4
地球的正常重力位和正常重力
f fM 零阶项V0 :由于 v0 dm r r
要精确计算出地球重力位，必须知道地球表面的形状及内部物质密度， 但前者正是我们要研究的，后者分布极其不规则，目前也无法知道，故根据 上式不能精确地求得地球的重力位，为此引进一个与其近似的地球重力位— —正常重力位。
dm 2 W f ( x2 y 2 ) r 2 M
3.2.1
引力与离心力
引力：
离心力： 重力：
M m Ff 2 r
P m 2
g FP
其它作用力（太阳、月亮）大多数情况下可忽略。
3.2.2
引力位和离心力位
由理论力学可知，如果某一空间（有限或无限）的任意一点都有一 定力的作用，而力的大小与方向只与该点的位置有关，则这一空间 称为力场。就力场而言，具有共同的特性，即力场所做的功与路径 无关，只与起点与终点有关。这样的力称为保守力。引力与离心力 都是保守力。 1. 定义：单位质点受物质M的引力作用产生的位能称为引力位，或者 说将单位质点从无穷远处移动到该点引力所做的功。 公式推导原理： 任意两质点M和m相互吸引的引力 ：
因此，引力位梯度的负值，在数值上等于单位质点受 r 处的质 体 M 吸引而形成的加速度值。
dm 地球整体的位函数：V dV f r (M ) (M )
3.2.2
引力位和离心力位
续3
引力位对被吸引点各坐标轴的偏导数等于相应坐标轴 上的加速度(或引力)向量的负值。用公式表达为：
V V V az ay ax ， ， z y x
v3
R 3 5 3 3 ( ) ( cos cos )dm r 2 2 M
3.2.4
地球的正常重力位和正常重力
f fM 零阶项V0 :由于 v0 dm r r
第二章地球重力场1
椭球和球坐标之间的关系式
（2-84） 采用间接推导方法 （1）
将它们代入(2-83)式，并经符号代换，得
（2-87）
（2）再把位 V 展开为球谐函数的级数 分析：由于旋转对称，它只有带谐项。而且，由于对赤道面 对称，它只有偶阶的带谐项。奇阶的带谐项对负纬度将变号， 所以就不出现，据此，级数的形式将会是 （2-88）
而（2-88）式则为
上述两式右边应当相等，因此得 （2-88）
将正常引力位的球谐函数展开写成一般常见形式
J2n为与正常椭球参数有关的常系数。
（2-92） 引进第一偏心率 e=E/a，在 n＝1 时，则得出重要公式 （292‘）
正常重力场的实用公式（正常重力公式）
a ( 1 sin2 1 sin2 2 )
( 0 , ) 978.0327(1 5.279041 103 sin 2 2.32718105 sin 4
0.01262105 sin 6 )Gal
精品课件！
精品课件！
(2-4)
图 2-1
离心力
为离心力位
总的力，即引力和离心力的合力称为重力。引力位 V 和离心力位 Φ 两者之和称为重力位 W：
（2-5）
式中是对整个地球的积分。 对离心力位微分，得 与布阿桑方程式(1—13)的V合 并，则得出广义的布阿桑重力 位方程式： （2-6）
重力位 W的矢量梯度
其分量为：
2-11
国际椭球的参数
在1979年堪培拉召开的第17届IUGG大会上，推荐了下列的1980 年大地测量参考系统，并建议用它代替1967年系统： a 6378137 2m
GM ( 398600 .5 0.05 ) 109 m 3 / s 2 其中包括大气质量 GM a ( 0.35 0.003) 109 m 3 / s 2 J 2 ( 1082 .63 0.005 ) 106
4-地球重力场(二)
2
k
2
Cnk
0.24396 D 05 0.20319 D 05 0.90666 D 06 0.71770 D 06 0.59665D 08
Snk
0.13980 D 05 0.25086 D 06 0.62102 D 06 0.14152 D 06 0.79801D 08
水准面和铅垂线
3. 水准面与大地水准面
Level Surface and Geoid
① 以平均海水面定义的大地水准面
大地水准面：与平均海水面重合并伸
展到大陆内部形成的水准面，它是一个
形状不规则的物理曲面
大地体：大地水准面包围的形体
3. 水准面与大地水准面
Level Surface and Geoid
N 1
2
G A B 1 3 B A 3 2 3 C cos cos 2 sin 2 2 2 4 2 3 1 n 2 F sin sin 2 n 1 ank cos k bnk sin k Pnk cos 2 n 3 k 0
an 0 G
M
1n Pn cos 1 dm
n k ! ank 2 G 1n Pnk cos 1 cos k 1dm n k ! ank n k ! M J nk n GMa 2 2n 1 n k ! n k ! bnk 2 G 1n Pnk cos 1 sin k 1dm n k ! M n k ! b
定，而与物质的质量分布无关。
推论：σ也可由物体的外表面S代替，但S面
上任一点相对于面上一固定点的重力位差
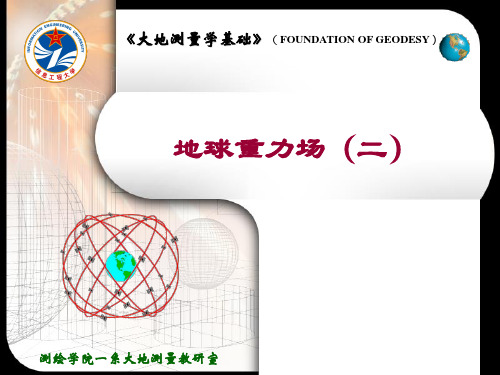
k
2
Cnk
0.24396 D 05 0.20319 D 05 0.90666 D 06 0.71770 D 06 0.59665D 08
Snk
0.13980 D 05 0.25086 D 06 0.62102 D 06 0.14152 D 06 0.79801D 08
水准面和铅垂线
3. 水准面与大地水准面
Level Surface and Geoid
① 以平均海水面定义的大地水准面
大地水准面：与平均海水面重合并伸
展到大陆内部形成的水准面，它是一个
形状不规则的物理曲面
大地体：大地水准面包围的形体
3. 水准面与大地水准面
Level Surface and Geoid
N 1
2
G A B 1 3 B A 3 2 3 C cos cos 2 sin 2 2 2 4 2 3 1 n 2 F sin sin 2 n 1 ank cos k bnk sin k Pnk cos 2 n 3 k 0
an 0 G
M
1n Pn cos 1 dm
n k ! ank 2 G 1n Pnk cos 1 cos k 1dm n k ! ank n k ! M J nk n GMa 2 2n 1 n k ! n k ! bnk 2 G 1n Pnk cos 1 sin k 1dm n k ! M n k ! b
定，而与物质的质量分布无关。
推论：σ也可由物体的外表面S代替，但S面
上任一点相对于面上一固定点的重力位差
长安大学地球物理学原理-第5章 地球的形状及重力场
第五章 地球的形状及重力场
卫星重力探测技术的发展，突破了人们过去获 取重力场信息的局限性，使得物理大地测量的研 究从局部或区域性扩展到全球，从测定静态地球 重力场发展到测定时变重力场。
第五章 地球的形状及重力场
在基础理论方面，重力学的研究内容包括 地球重力场的空间分布特征与规律，重力场 变化所反映的物质质量分布、密度分布的状 态、性质、特征与规律，以及重力场因天体 运动和地球内部物质运动引起的周期性变化 规律与非周期变化的性质、机理。 在应用方面，重力学的研究内容主要为重 力测量技术和观测数据解译技术以及相关的 理论，即“重力勘探”。 重力变化与地震预测。
20世纪初，由于厄特沃什（R. von Eötvös）研制成 适用于野外作业的扭秤，在匈牙利进行了持续的扭秤 观测，结果表明扭秤可以反映地下区域的密度变化。 在应用地球物理方法勘探石油之初就是使用扭秤。 1934 年 拉 科 斯 特 研 制 出 了 高 精度的金属弹簧重力 仪，沃登研制了石英弹簧重力仪，这类仪器的测量精 度约达0.05-0.2mGal，到1939年，这类重力仪完全取 代了扭秤。 从此，重力测量迅速发展，应用于大地测量、地球 内部构造、地球动力学、资源勘探、工程建设、灾害 预防等基础性科学和应用基础性科学的各个方面。
第五章 地球的形状及重力场
地球深部结构及海洋洋流变化 固体地球均衡响应及冰后回弹 地幔和岩石圈密度变化 地球物理勘探 地球重力场与国防、军事
大地测量学
重力测量学
重力测量仪
重力（位场）数据计算与分析处理
计算地球物理学
地球重力学 固体潮与地壳形变 重力勘探 卫星重力学
地球动力学 引力波 微重力测量学 行星重力学
第五章第五章地球的形状及重力场地球的形状及重力场1957年第一颗人造地球卫星发射成功开创了卫星重力探测时代根据卫星轨道摄动理论观测卫星轨道摄动确定低阶位系数利用卫星海洋雷达测高确定高精度高分辨率海洋重力场模型和大地水准面模型gps技术结合水准测量直接测定大陆大地水准面本世纪初利用卫星跟踪卫星和卫星重力梯度测量技术可以确定全球更高精度和分辨率的静态重力场模型和时变重力场模型第五章第五章地球的形状及重力场地球的形状及重力场卫星重力探测技术的发展突破了人们过去获取重力场信息的局限性使得物理大地测量的研究从局部或区域性扩展到全球从测定静态地球重力场发展到测定时变重力场
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
TP
+
1
4p R
òò
s
K
(r,y
)(T
-
TP
)ds
( ) K
(r,y
)
=
-
R2 l5
5R2r - r3 - Rr2 cosy - 3R3 cosy
2R2r 2R4 R2 - l3 + l3r + r2
K
(
R,y
)
=
-
4
1 sin3
y
+1
2
1 地球重力场的表达方法
Vening-Meinesz公式
ò ò ( ) x jP,lP
s
-
cscy
y
csc 2
-
y
tg 2
ö ø÷
¶N ¶y
ds
1 ¶N = x cosa + hsina R ¶y
sina = - cosj sin(lP - l)
siny
cosa = cosjP sinj - sinjP cosj cos(lP - l)
siny
1 地球重力场的表达方法
垂线偏差计算大地水准面
[
1 2
(j
P
+
j
)]
-
sin
2
é ëê
1 2
(j
P
- j )ùûúüýþ
y
s = sin 2
1 地球重力场的表达方法
扰动位径向梯度→扰动位
òò J
T (y )
=
=
R2
4p
6 sin
s
y
2
Trr J(y )ds
+ 2(1 - 3sin2
y
2
)
ln
y
sin + 2
sin y
1
-
4
+
sin2
y
2
2
以上的重力场积分都是在球面上进行，一般采用数值积分 的方法进行计算。计算任何一点的重力场参量往往需要对 全球积分。若要建立一个高分辨率的全球模型，其计算量 势必非常巨大。因此需要采取快速计算方法。
2
N (jP , lP )
ò ò = R
4pg
2p l=0
p
2 j =- p
Dg
(j,
l
)
S
(y
)
cosj
dj
dl
2
P(φP, λP)
r=R
y
yl
2
dσ R
2
R2dσ
单位球 r=1
地球表面 r=R
1 地球重力场的表达方法
逆Vening-Meinesz公式计算重力异常
Dg
=
g 4p R
òò
æ èç
3cscy
2p l=0
p
2 j=
-
p
Dg
(j
,
l
)
S
(
r,y
)
cos
j
dj
dl
2
核函数Biblioteka S (r,y ) =2R l
-
3Rl r2
+
R r
-
R2 r2
cosy (5
+
ln
l
+
r
- R cosy
2r
)
S(r = R,y ) = 1 - 6s - 4 + 10s2
( ) ( ) s
y
- 3 1 - 2s2 ln s + s2 , s = sin
第八章 物理大地测量学的 计算方法
1 地球重力场的表达方法 2 Fourier级数与Fourier变换 3 积分卷积表达式的快速计算 4 级数表达式的快速计算
5 全球重力场模型
1 地球重力场的表达方法
积分
重力场参量之间、球谐分析等
例 ：
ò ò ( ) T
rP ,jP , lP
R =
4p
2p l=0
p
2 j=
-
p
Dg
(j
,
l
)
S
(
r,y
)
cos
j
dj
dl
2
(rP, φP, λP)为计算点球坐标，(r, φ, λ)为积分点球坐标。
级数 例：
主要是重力场参量的球谐展开
å å ( ) ( ) T (rP,JP,lP )
=
GM r
¥ næ n=2 m=0 èç
a ö n+1 r ø÷
C
* nm
cos
ml
V
=
-
1
4p
ò
s
ò
cot
y
2
¶N ¶y
ds
1 ¶N = x cosa + hsina R ¶y
sina = - cosj sin(lP - l)
siny
cosa = cosjP sinj - sinjP cosj cos(lP - l)
siny
1 地球重力场的表达方法
逆Stokes公式
Dg
=
-
R r2
=- 1
4pg
( ) 2p
l=0
p 2 j=
-
p 2
Dg
(j
,
l
)
cos
j
¶S y ¶jP
dj dl
ò ò ( ) h jP,lP
1 =-
4pg cosjP
( ) 2p
l=0
p 2 j=-
p 2
Dg
(j,
l)
cosj
¶S y ¶lP
dj dl
( ) ( ) ¶S(y ) 1 ¶s = - s2 - 6 + 20s -
3- 6s2
1+ 2s s + s2 + 12s ln
s + s2
-
¶s
¶j P
=
1 4s
ì ísin
[j
P
î
+ j ]sin2
é ëê
1 2
(
lP
-
l ) ùûú
- sin(jP
- j )cos2
é ëê
1 2
(
lP
-
l ) ùûú üýþ
¶s -
¶lP
=
1 4s
sin
(
lP
-
l
)
ìícos2 î
+
S n*m
sin
ml
Pnm
cosJ
1 地球重力场的表达方法
重力场参量及其关系
重力扰 动
Hotine
重力异 常
Stokes 逆Stokes
大地水 准面
V-M 逆V-M
垂线偏 差
重力梯 度
1 地球重力场的表达方法
重力异常求解扰动位和大地水准面的公式
ò ò ( ) T
rP ,jP , lP
R =
4p
考虑到上述积分形式均可以用卷积形式表达，而Fourier变 换可快速有效的计算卷积，因此以下将介绍Fourier级数及 快速Fourier变换的知识。