实验阻尼振动与受迫振动
阻尼振动与受迫振动

【实验目的】1.观测阻尼振动,学习测量振动系统基本参数的方法。
2.研究受迫振动的幅频特性和相频特性,观察共振现象。
3.观察不同阻尼对受迫振动的影响。
【实验原理】当摆轮受到周期性强迫外力矩t M M ωcos 0=的作用,并在有空气阻尼的媒质中运动时(阻尼力矩为 ),其运动方程为t M dt d b k dtd J ωθθθcos 022+--= (1)其中,J 为摆轮的转动惯量,θk -为弹性力矩,0M 为强迫力矩的幅值,ω为强迫力的圆频率。
令J k =20ω,J b=β2,JM m 0=,则(1)式变为 t m dt d dtd ωθωθβθcos 22022=++ (2) 其中,β为阻尼系数,0ω为系统的固有频率,m 为强迫力矩。
当0cos =t m ω时,(2)式即为阻尼振动方程,当0=β,即在无阻尼情况时,(2)式变为简谐振动方程。
方程(2)的通解为()()0201cos cos ϕωθαωθθβ+++=-t t e t (3)由(3)式可见,受迫振动可分为两部分:第一部分,()αωθβ+-t e t 01cos 表示阻尼振动,经过一定时间后衰减消失。
第二部分,说明强迫力矩对摆轮作功,向振动体传递能量,最后达到一个稳定的振动状态,其振幅为()22222024ωβωωθ+-=m(4)它与强迫力矩之间的相位差ϕ为()2022022012T T T T tg -=-=-πβωωβωϕ (5) 由(4)式和(5)式可看出,振幅2θ与相位差ϕ的数值取决于强迫力矩m 、频率ω、固有频率0ω和阻尼系数β四个因素,而与振动起始状态无关。
由()[]04222220=+-∂∂ωβωωω极值条件可得出,当受迫力的圆频率2202βωω-= 时产生共振,θ有极大值。
若共振时的圆频率和振幅分别用r ω 、r θ表示,则dtd b θ-2202βωω-=r (6)2222βωβθ-=m r (7)(6)式和(7)式表示,阻尼系数β越小,共振时圆频率越接近于系统固有频率,振幅也越大。
大学物理学-阻尼振动与受迫振动
v
弹性力
粘滞阻力: f r v
粘滞阻力
x
dx
d 2x
kx
m 2
dt
dt
令k / m 0 , / m 2
2
d2x
dx
2
2
0 x 0
2
dt
dt
大学物理学
k (固有频率)
0
m
(阻尼系数)
2m
章目录
节目录
上一页
下一页
4.3 阻尼振动与受迫振动
4.3 阻尼振动与受迫振动
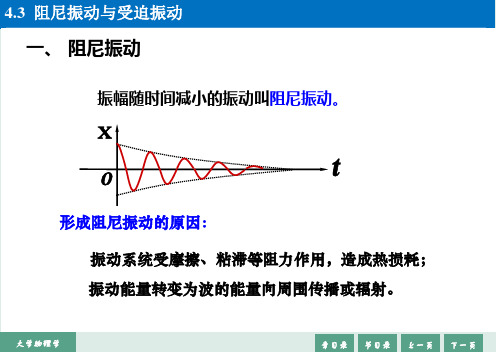
一、 阻尼振动
振幅随时间减小的振动叫阻尼振动。
形成阻尼振动的原因:
振动系统受摩擦、粘滞等阻力作用,造成热损耗;
振动能量转变为波的能量向周围传播或辐射。
大学物理学
章目录
节目录
上一页
下一页
4.3 阻尼振动与受迫振动
1. 阻尼振动的微分方程
弹性力:
F kx
(以液体中的水平弹簧振子为例)
阻尼=0
阻尼较小
pr 02 2 2
阻尼较大
共振振幅 :
Ar
大学物理学
f0
2 02 2
O
p
0
共振曲线
章目录
节目录
上一页
下一页
4.3 阻尼振动与受迫振动
2. 速度共振
受迫振动的速度的振幅出现极大值的现象
v pA sin( pt )
大学物理学
章目录
节目录
r
d2x
k
x0
2
2
dt
m J r
阻尼振动与强迫振动的区别与联系

阻尼振动与强迫振动的区别与联系引言:振动现象广泛存在于自然界和工程领域中。
阻尼振动和强迫振动作为振动现象的两种基本形式,它们在物理特性、引起原因和动力学特征等方面存在一定的区别和联系。
本文将着重讨论阻尼振动与强迫振动的区别与联系,以深入了解这两种振动形式的本质。
一、阻尼振动的定义与特点阻尼振动是指受到阻尼力作用下的振动现象。
在阻尼振动中,振动系统受到阻尼力的耗散作用,会导致振幅的逐渐减小,直至 eventually下降为零。
阻尼振动的物理特性主要包括振动频率的减小、振幅的衰减和振动系统能量的损失。
二、强迫振动的定义与特点强迫振动是指在外界作用下,振动系统受到周期性或非周期性的外力驱动,并由此产生的振动现象。
与阻尼振动不同,强迫振动在无外力驱动时不会自发发生。
强迫振动的物理特性主要包括受迫振动频率与外力频率的一致性、振幅的稳定性和外界驱动力对振动系统的影响。
三、阻尼振动与强迫振动的区别1. 物理特性:阻尼振动主要表现为能量的衰减和振幅的逐渐减小,而强迫振动的振幅较为稳定,受迫振动频率与外力频率一致。
2. 引起原因:阻尼振动产生的主要原因是振动系统与环境介质之间的相互作用,而强迫振动则是由外界施加的外力引起的。
3. 频率依赖性:阻尼振动的频率与外界没有直接的关系,而强迫振动的频率受外界驱动力的影响,与外力频率保持一定的一致性。
4. 能量耗散:阻尼振动会因阻尼力的作用逐渐损失能量,而强迫振动的振动系统能量主要来自外界驱动力。
四、阻尼振动与强迫振动的联系1. 泛化关系:强迫振动可以看作是阻尼振动的一种特殊情况,当外界驱动力的频率趋近于阻尼振动系统的固有频率时,强迫振动会逐渐趋近于稳定状态。
2. 共存关系:在实际物理系统中,阻尼振动与强迫振动可以同时存在。
外界施加的强迫力可能使阻尼振动系统产生共振现象,引起系统的不稳定性。
3. 相互影响:阻尼振动和强迫振动之间存在着相互影响关系。
阻尼振动的存在会导致强迫振动的振幅逐渐减小,而强迫振动的存在也会影响阻尼振动系统的能量耗散。
阻尼振动、受迫振动和共振

v F γ
O x
v v F = −kx
x
dx 动力学方程 m 2 = −kx − γ dt dt k γ 2 令 ω0 = ,2β = m m 2 dx dx 2 + 2β + ω0 x = 0 dt 2 dt
ω0
d2 x
:无阻尼时振子的固有频率
β :阻尼因子
方程解: 方程解:
x = Ae
−β t
f0 dA d 求极值: 求极值: = =0 dω dω ω2 −ω2 2 + 4β 2ω2 0
(
)
共振频率: 共振频率: 共振振幅: 共振振幅:
2 ωr = ω0 − 2β 2
ω0为固有频率
Ar =
f0
2 2β ω0 − β 2
结论: 阻尼系数 β 越 小,共振角频率ωr 越接近于系统的固 有频率 ω0 ,同时 共振振幅A 也越大。 共振振幅 r也越大。
cos( ω − β
2 0
2
t +ϕ
)
x = Ae
−β t
cos(ωt +ϕ)
2π
A
2
x
周期: 周期: T =
ω −β
2 0
O
t
2 β 2 < ω0
角频率: 角频率: ω =
ω −β
2 0
2
A
x = Ae
讨论: 讨论:
−β t
cos ω − β t +ϕ
2 0 2
(
)
2 β 2 < ω2 阻尼较小时( ),振动为减幅振动 振动为减幅振动, 1. 阻尼较小时(β 2 < ω0 ),振动为减幅振动,振幅
阻尼振动与受迫振动

,可以推出������0 =
2������ ������������ 1−������
2
= ,是阻尼振动振幅衰减到原来 ������−1 需要
,是系统共振锐度或频率选择性的量度。
������������ ������
6. 对数缩减率Λ =
=
2������������ 1−������ 2
,定义为衰减阻尼振动中相邻两
������ ������ 0 ������ 、 ������
=
������ 2 ������������ 2������
2 ������2 0 −������
3. 阻尼振动周期������������ = 4. 时间常数������ = 的时间。 5. 品质因素������ ≡
1 2������ 2������ ������ 1 ������
2 小阻尼(������ 2 − ������0 < 0)时,阻尼振动运动方程的解为 2
������ ������ = ������������ exp −������������ cos
2 ������0 − ������ 2 ������ + ������������ 2
由 上 式 可 知 , 阻 尼 振 动 角 频 率 ������������ = ������2 0 − ������ , 而 周 期 为 ������������ =
[2]
即 ������ 2 ������ ������������ ������ 2 + ������ + ������������ = ������������������ cos ������������ ������������ ������������ 它和弹簧支座固定、摆轮受周期外力矩������������������ cos ������������作用时运动 方程在形式上完全一致,等效外激励力矩的振幅为������������������ ,则对 应的稳态解振幅和相位差分别为 ������������ = ������������ ������2 0
利用波尔共振仪研究受迫振动实验报告

利用波尔共振仪研究受迫振动实验报告一、实验目的1、观察摆轮的自由振动、阻尼振动和受迫振动现象。
2、研究不同阻尼力矩对受迫振动的影响,并测定阻尼系数。
3、研究受迫振动的幅频特性和相频特性,观察共振现象,测定受迫振动的共振频率和共振振幅。
二、实验仪器波尔共振仪,包括振动系统、电磁阻尼系统、电机驱动系统、光电计数系统和智能控制仪等部分。
三、实验原理1、自由振动无阻尼的自由振动方程为:$m\frac{d^2\theta}{dt^2}=k\theta$,其中$m$为摆轮的转动惯量,$k$为扭转弹性系数,$\theta$为角位移。
其解为:$\theta = A\cos(\omega_0 t +\varphi)$,其中$\omega_0 =\sqrt{\frac{k}{m}}$为固有角频率,$A$和$\varphi$为初始条件决定的常数。
2、阻尼振动考虑阻尼时,振动方程为:$m\frac{d^2\theta}{dt^2} +b\frac{d\theta}{dt} + k\theta = 0$,其中$b$为阻尼系数。
根据阻尼的大小,可分为三种情况:小阻尼:$\omega =\sqrt{\omega_0^2 \frac{b^2}{4m^2}}$,振动逐渐衰减。
临界阻尼:振动较快地回到平衡位置。
大阻尼:不产生振动。
3、受迫振动在周期性外力矩$M = M_0\cos\omega t$作用下,振动方程为:$m\frac{d^2\theta}{dt^2} + b\frac{d\theta}{dt} + k\theta =M_0\cos\omega t$。
稳定时,振动的角位移为:$\theta = A\cos(\omega t +\varphi)$,其中振幅$A =\frac{M_0}{\sqrt{(k m\omega^2)^2 +(b\omega)^2}}$,相位差$\varphi =\arctan\frac{b\omega}{k m\omega^2}$。
§14阻尼振动受迫振动
课堂练习
2.如图所示演示装置,一根张紧的水平
绳上挂着四个单摆,让b摆摆动,其余各
摆也摆动起来,可以发现( CD )
A. a 摆摆动周期最短
B. c 摆摆动周期最长
C.各摆摆动的周期均与b摆相同
D. d 摆振幅最大
3.两个弹簧振子,甲的固有频率为f,乙的 固有频率为4f,当它们均在频率为2f的驱 动力作用下做受迫振动时,则 ( )C A、甲的振幅较大,振动频率为f B、乙的振幅较大,振动频率为4f C、甲的振幅较大,振动频率为2f D、乙的振幅较大,振动频率为2f
二、受迫振动
1.驱动力: 周期性 的外力. 2.受迫振动:系统在 驱动力 作用下的振动. 思考: 弹簧振子做自由振动的频率是怎样的? 弹簧振子在驱动力作用下做受迫振动,稳定后弹簧
振子的振动频率又怎样?
3.振动稳定后受迫振动的频率 总等于 驱动力 的频率,受迫 振动稳定后的频率与物体的固有 频率 无 关系.
§1.4阻尼振动 受迫振动
问题设计
在研究弹簧振子和单摆振动时,我们强调忽略阻力 的影响,它们做的振动都属于简谐运动.在实验室中让一 个弹簧振子振动起来,经过一段时间它将停止振动,你 知道是什么原因造成的吗? 答案 阻力阻碍了振子的运动,使机械能转化为内能.
阻尼振动实例 同学荡秋千,由于受到空气的阻尼作用,
课堂练习
1. 如图所示,是用来测量各种发动机转速的转 速计原理图。在同一铁支架NM上焊有固有频率 依次为80Hz、60Hz、40Hz、20Hz的四个钢片a、 b、c、d。将M端与正在转动的电动机接触,发 现b钢片振幅最大,则a、b、c、d此时振动频率
约为6__0_H__z____ , 电动机转速3为6_0_0_____r/min 。
阻尼振动__受迫振动
实验表明:
物体在外力驱动下振动时,振动稳定后的频率等于外力 驱动的频率,跟物体的固有频率没有关系.
受迫振动物体
T T驱 f f驱
受迫振动实例:
①跳板在人走过时发生的振动 ②机器底座在机器运转时发生的振动 ③听到声音时耳膜的振动 ④电磁打点计时器的振针所做的振动
1.下列振动中属于受迫振动的是(
D.后一时刻的机械能一定小于前一时刻的机械能
【解题指导】在阻尼振动中,振动系统的动能和势能之 和减小.但在一段较短的时间内,动能和势能不一定都减小,关 键要分析动能与势能之间是如何转化的.
思考: 用什么方法才能得到持续的振动呢?
1,驱动力:作用到振动系统周期性的外力 2,受迫振动:物体在外界驱动力作用下的振动 3、受迫振动的特点:受迫振动的频率总等于驱动力 的频率,与系统的固有频率无关
o
t
阻尼振动图象
注意:阻尼振动的振幅是逐渐减小的,但是它的频率是不发生
变化的,频率与振幅是无关的。
2.系统不受外力作用,也不受任何阻力,只在自身 回复力作用下的振动,称为自由振动 又叫做无阻尼振动。
或无阻尼振动图象
自由振动的频率,叫做系统的固有频率
[要点提炼 ] 1.对阻尼振动的理解 (1)同一简谐运动能量的大小表现为 振幅 的大小.
2.阻尼振动和无阻尼振动的比较 振动类型 阻尼振动 比较项目 产生条件 振幅 受到阻力作用 如果没有能量补充,物 体的振幅会 越来越小
无阻尼振动 不受阻力作用或受到 阻力作用,但外界补 充能量 振幅 不变
振动图像 用锤敲锣,由于锣的振 动,发出响亮的锣声, 弹簧振子的振动,单 但锣声越来越弱,振幅 摆的振动 越来越小,属阻尼振动
实例
1.下列说法中正确的是 [ ACD
机械振动中的阻尼振动与受迫振动
机械振动中的阻尼振动与受迫振动在机械系统中,振动是一种普遍存在的现象,它包含着阻尼振动和受迫振动两种类型。
阻尼振动是指系统在一定的阻尼作用下运动的周期性减弱振动,而受迫振动是指系统受到外部力的作用而发生周期性振动。
本文将探讨机械振动中的阻尼振动和受迫振动的特点及其应用。
一、阻尼振动阻尼振动是指振动系统在受到阻力的作用下产生的振动。
阻尼力可以分为粘性阻尼、干摩擦阻尼和液体摩擦阻尼等不同形式。
阻尼振动的特点是振幅逐渐减小,振动频率也逐渐减小。
阻尼振动的主要原因是能量的损失。
当机械系统受到阻尼力的作用时,振动系统的机械能会逐渐转化为热能而损失。
这导致振动幅度逐渐减小,最终停止振动。
例如,摆钟在受到空气阻力的影响下,其摆动幅度会逐渐减小,最终停止。
阻尼振动的应用广泛。
在机械工程中,阻尼振动常常被用于减震和能量吸收的装置设计。
例如,在车辆的悬挂系统中使用减震器,可以有效地缓解车辆行驶中的颠簸感。
同时,阻尼振动还常用于物体的减振和抗震设计,例如建筑物中的隔震装置。
二、受迫振动受迫振动是指振动系统在外部力的作用下产生的振动。
外力可以是周期性的,也可以是非周期性的。
受迫振动的特点是振幅和频率与外力的频率相关。
外力对振动系统的影响可以分为共振和强迫两种情况。
共振是指外力的频率接近或等于振动系统的固有频率时,振动幅度会显著增大。
强迫是指外力的频率与振动系统的固有频率有一定的差别,但仍然能引起系统振动。
受迫振动在实际生活中有许多应用。
例如,在音乐中,乐器的共振现象使得乐器能够产生特定的音调。
另外,受迫振动还在工程领域中有着广泛的应用,如振动筛、振动输送机等。
它们利用外力作用产生振动,以完成特定的分选和输送任务。
三、阻尼振动与受迫振动的关系阻尼振动与受迫振动是机械振动中两种常见的振动类型,它们在某些情况下可以相互转化。
当受迫振动系统存在阻尼时,会产生阻尼振动。
此时,外力的频率与振动系统的固有频率相同或接近时,阻尼振动的幅度会受到外力的影响,产生共振效应。
《阻尼振动与受迫振动》实验报告
《阻尼振动与受迫振动》实验报告工程物理系核41 崔迎欢 2014011787一.实验名称:阻尼振动与受迫振动二.实验目的1.观测阻尼振动,学习测量振动系统基本参数的方法;2.研究受迫振动的幅频特性和相频特性,观察共振现象;3.观测不同阻尼对受迫振动的影响。
三..实验原理1.有粘滞阻尼的阻尼振动弹簧和摆轮组成一振动系统,设摆轮转动惯量为J,粘滞阻尼的阻尼力矩大小定义为角速度dθ/dt与阻尼力矩系数γ的乘积,弹簧劲度系数为k,弹簧的反抗力矩为-kθ。
忽略弹簧的等效转动惯量,可得转角θ的运动方程为记ω0为无阻尼时自由振动的固有角频率,其值为ω0=,定义阻尼系数β=γ/(2J),则上式可以化为:小阻尼即时,阻尼振动运动方程的解为(*)由上式可知,阻尼振动角频率为,阻尼振动周期为2.周期外力矩作用下受迫振动的解在周期外力矩Mcosωt激励下的运动方程和方程的通解分别为这可以看作是状态(*)式的阻尼振动和频率同激励源频率的简谐振动的叠加。
一般t>>τ后,就有稳态解稳态解的振幅和相位差分别为其中,φ的取值范围为(0,π),反映摆轮振动总是滞后于激励源支座的振动。
3.电机运动时的受迫振动运动方程和解弹簧支座的偏转角的一阶近似式可以写成式中αm是摇杆摆幅。
由于弹簧的支座在运动,运动支座是激励源。
弹簧总转角为。
于是在固定坐标系中摆轮转角θ的运动方程为也可以写成于是得到由θm的极大值条件可知,当外激励角频率时,系统发生共振,θm有极大值。
引入参数,称为阻尼比。
于是,我们得到四.实验仪器:波耳振动仪五.实验步骤。
1.打开电源开关,关断电机和闪光灯开关,阻尼开关置于“0”档,光电门H、I可以手动微调,避免和摆轮或者相位差盘接触。
手动调整电机偏心轮使有机玻璃转盘F上的0位标志线指示0度,亦即通过连杆E和摇杆M使摆轮处于平衡位置。
染货拨动摆轮使偏离平衡位置150至200度,松开手后,检查摆轮的自由摆动情况。
正常情况下,振动衰减应该很慢。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验内容:
1.本实验中振动系统所受的阻力是怎样实现的?如何调节?
2.在阻尼系数β的测量中直接测ห้องสมุดไป่ตู้的量有哪些?与阻尼系数存在什么样的关系?
3.本实验中振动系统所受的策动力是怎样实现的?如何调节?
4.改变受迫振动中电机的电压,改变了策动力的什么参量?此参量与振子振动的幅度和频率有什么样的关系?
4.受迫振动中振动系统的合外力由哪些力组成?各有什么样的变化规律?大小取决于什么因素?
5.策动力不变,受迫振动(稳态)的振动周期是否恒定?
6.策动力振幅初相不变的情况下,改变策动力的振动频率,受迫振动(稳态)的振幅是否变化?会有什么现象发生?若策动力不变,改变阻尼,是否也有类似的变化呢?
7.策动力振幅初相不变的情况下,改变策动力的振动频率,受迫振动(稳态)与策动力之间的相位差是否变化?若策动力不变,改变阻尼,是否也有类似的变化呢?
大学物理实验预习报告
姓名
实验班号
实验号
实验四阻尼振动与受迫振动
实验目的:
实验原理及仪器介绍:
1.阻尼振动中振动系统的合外力由哪些力组成?各有什么样的变化规律?大小取决于什么因素?
2.阻尼不变,阻尼振动的振动周期是否恒定?且周期与忽略阻尼的理想简谐振动是否相同?有什么样的关系?
3.阻尼不变,阻尼振动的振幅如何衰减?与阻尼系数具有什么样的关系?
数据表格:
1.记录所用测量仪器的仪器误差:
2.列出数据记录表格:
教师签字:
月日
