阻尼振动和受迫振动
合集下载
大学物理学-阻尼振动与受迫振动
v
弹性力
粘滞阻力: f r v
粘滞阻力
x
dx
d 2x
kx
m 2
dt
dt
令k / m 0 , / m 2
2
d2x
dx
2
2
0 x 0
2
dt
dt
大学物理学
k (固有频率)
0
m
(阻尼系数)
2m
章目录
节目录
上一页
下一页
4.3 阻尼振动与受迫振动
4.3 阻尼振动与受迫振动
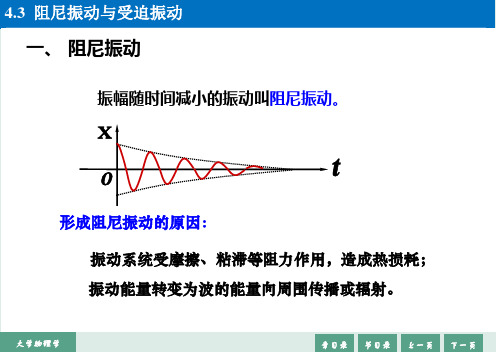
一、 阻尼振动
振幅随时间减小的振动叫阻尼振动。
形成阻尼振动的原因:
振动系统受摩擦、粘滞等阻力作用,造成热损耗;
振动能量转变为波的能量向周围传播或辐射。
大学物理学
章目录
节目录
上一页
下一页
4.3 阻尼振动与受迫振动
1. 阻尼振动的微分方程
弹性力:
F kx
(以液体中的水平弹簧振子为例)
阻尼=0
阻尼较小
pr 02 2 2
阻尼较大
共振振幅 :
Ar
大学物理学
f0
2 02 2
O
p
0
共振曲线
章目录
节目录
上一页
下一页
4.3 阻尼振动与受迫振动
2. 速度共振
受迫振动的速度的振幅出现极大值的现象
v pA sin( pt )
大学物理学
章目录
节目录
r
d2x
k
x0
2
2
dt
m J r
5.4阻尼振动和受迫振动

2 p
2 2 0 p
稳态时振动物体速度:
dx A p cos( p t ) dt 2
式中
m A p
f p
2 2 2 2 (0 p ) 4 2 p
在受迫振动中,周期性的驱动力对振动系统提供 能量,另一方面系统又因阻尼而消耗能量,若二者相 等,则系统达到稳定振动状态。
在小阻尼条件下 ( 0 ) ,微分方程的解为:
2
x Ae
t
cos(t )
2 2 其中 0
x Ae
其中 A 和
t
cos(t )
t
为积分常数,由初始条件决定。上式中的
余弦项表征了在弹性力和阻力作用下的周期运动;e 反映了阻尼对振幅的影响。
对于阻尼较小的情形,运动方程之解表为:
x A0e
衰减项
t
cos(t ) A cos( pt )
Hale Waihona Puke 稳态项经过一段时间后,衰减项忽略不计,仅考虑稳态项。
x A cos( pt )
f ( ) 4
2 0 2 2 p 2 2 p
A
tg
共振的应用和防止 应用
共振筛 防止
共鸣箱
1.队或火车过桥时要放慢速度或便步走 2.在振动物体底座加防振垫 3.装修剧场、房屋时使用吸声材料等
2、共
振
对于受迫振动,当外力幅值恒定时,稳定态 振幅随驱动力的频率而变化。当驱动力的角频率 等于某个特定值时,位移振幅达到最大值的现象 称为位移共振。
A
f
2 2 2 2 (0 p ) 4 2 p
dA 0 dp
共振频率
阻尼振动受迫振动

汇报人:
感谢观看
阻尼系数:影响阻尼振动的衰减速度
质量:影响阻尼振动的频率和振幅
刚度:影响阻尼振动的频率和振幅
外力:影响阻尼振动的频率和振幅
阻尼振动的应用场景
汽车悬挂系统:减少振动提高舒适性
建筑结构:提高抗震性能保护建筑物
机械设备:减少振动提高设备寿命和精度
航空航天:提高飞行稳定性减少振动对设备的影响
03
受迫振动
受迫振动的产生条件
存在外力作用
外力频率与系统固有频率接近或相等
系统具有足够的阻尼
系统处于临界状态或临界附近
受迫振动的应用场景
航空航天:用于控制飞机、火箭等飞行器的振动提高飞行器的稳定性和安全性
机械工程:用于控制机械设备的振动提高设备的稳定性和可靠性
建筑工程:用于控制建筑物的振动提高建筑物的抗震性能和舒适性
在实际应用中阻尼振动和受迫振动都可以用来分析振动系统的稳定性、响应特性等。
区别
阻尼振动:物体在受到外力作用下由于阻尼作用振动逐渐减小直至停止的过程。
受迫振动:物体在受到周期性外力作用下产生与外力频率相同的振动。
阻尼振动的特点:振动逐渐减小直至停止振动频率与外力频率无关。
受迫振动的特点:振动频率与外力频率相同振动幅度与外力大小有关。
受迫振动的定义
受迫振动的振幅和相位取决于系统的固有频率和阻尼。
受迫振动可以分为谐振和非谐振两种情况。
受迫振动是指系统在外部周期性力的作用下产生的振动。
受迫振动的频率等于外部力的频率。
受迫振动的特点
振幅:与驱动力的振幅成正比
频率:与驱动力的频率相同
相位:与驱动力的相位相同
阻尼:受迫振动的阻尼与驱动力的阻尼无关
,
感谢观看
阻尼系数:影响阻尼振动的衰减速度
质量:影响阻尼振动的频率和振幅
刚度:影响阻尼振动的频率和振幅
外力:影响阻尼振动的频率和振幅
阻尼振动的应用场景
汽车悬挂系统:减少振动提高舒适性
建筑结构:提高抗震性能保护建筑物
机械设备:减少振动提高设备寿命和精度
航空航天:提高飞行稳定性减少振动对设备的影响
03
受迫振动
受迫振动的产生条件
存在外力作用
外力频率与系统固有频率接近或相等
系统具有足够的阻尼
系统处于临界状态或临界附近
受迫振动的应用场景
航空航天:用于控制飞机、火箭等飞行器的振动提高飞行器的稳定性和安全性
机械工程:用于控制机械设备的振动提高设备的稳定性和可靠性
建筑工程:用于控制建筑物的振动提高建筑物的抗震性能和舒适性
在实际应用中阻尼振动和受迫振动都可以用来分析振动系统的稳定性、响应特性等。
区别
阻尼振动:物体在受到外力作用下由于阻尼作用振动逐渐减小直至停止的过程。
受迫振动:物体在受到周期性外力作用下产生与外力频率相同的振动。
阻尼振动的特点:振动逐渐减小直至停止振动频率与外力频率无关。
受迫振动的特点:振动频率与外力频率相同振动幅度与外力大小有关。
受迫振动的定义
受迫振动的振幅和相位取决于系统的固有频率和阻尼。
受迫振动可以分为谐振和非谐振两种情况。
受迫振动是指系统在外部周期性力的作用下产生的振动。
受迫振动的频率等于外部力的频率。
受迫振动的特点
振幅:与驱动力的振幅成正比
频率:与驱动力的频率相同
相位:与驱动力的相位相同
阻尼:受迫振动的阻尼与驱动力的阻尼无关
,
阻尼振动与受迫振动

,可以推出������0 =
2������ ������������ 1−������
2
= ,是阻尼振动振幅衰减到原来 ������−1 需要
,是系统共振锐度或频率选择性的量度。
������������ ������
6. 对数缩减率Λ =
=
2������������ 1−������ 2
,定义为衰减阻尼振动中相邻两
������ ������ 0 ������ 、 ������
=
������ 2 ������������ 2������
2 ������2 0 −������
3. 阻尼振动周期������������ = 4. 时间常数������ = 的时间。 5. 品质因素������ ≡
1 2������ 2������ ������ 1 ������
2 小阻尼(������ 2 − ������0 < 0)时,阻尼振动运动方程的解为 2
������ ������ = ������������ exp −������������ cos
2 ������0 − ������ 2 ������ + ������������ 2
由 上 式 可 知 , 阻 尼 振 动 角 频 率 ������������ = ������2 0 − ������ , 而 周 期 为 ������������ =
[2]
即 ������ 2 ������ ������������ ������ 2 + ������ + ������������ = ������������������ cos ������������ ������������ ������������ 它和弹簧支座固定、摆轮受周期外力矩������������������ cos ������������作用时运动 方程在形式上完全一致,等效外激励力矩的振幅为������������������ ,则对 应的稳态解振幅和相位差分别为 ������������ = ������������ ������2 0
§14阻尼振动受迫振动

课堂练习
2.如图所示演示装置,一根张紧的水平
绳上挂着四个单摆,让b摆摆动,其余各
摆也摆动起来,可以发现( CD )
A. a 摆摆动周期最短
B. c 摆摆动周期最长
C.各摆摆动的周期均与b摆相同
D. d 摆振幅最大
3.两个弹簧振子,甲的固有频率为f,乙的 固有频率为4f,当它们均在频率为2f的驱 动力作用下做受迫振动时,则 ( )C A、甲的振幅较大,振动频率为f B、乙的振幅较大,振动频率为4f C、甲的振幅较大,振动频率为2f D、乙的振幅较大,振动频率为2f
二、受迫振动
1.驱动力: 周期性 的外力. 2.受迫振动:系统在 驱动力 作用下的振动. 思考: 弹簧振子做自由振动的频率是怎样的? 弹簧振子在驱动力作用下做受迫振动,稳定后弹簧
振子的振动频率又怎样?
3.振动稳定后受迫振动的频率 总等于 驱动力 的频率,受迫 振动稳定后的频率与物体的固有 频率 无 关系.
§1.4阻尼振动 受迫振动
问题设计
在研究弹簧振子和单摆振动时,我们强调忽略阻力 的影响,它们做的振动都属于简谐运动.在实验室中让一 个弹簧振子振动起来,经过一段时间它将停止振动,你 知道是什么原因造成的吗? 答案 阻力阻碍了振子的运动,使机械能转化为内能.
阻尼振动实例 同学荡秋千,由于受到空气的阻尼作用,
课堂练习
1. 如图所示,是用来测量各种发动机转速的转 速计原理图。在同一铁支架NM上焊有固有频率 依次为80Hz、60Hz、40Hz、20Hz的四个钢片a、 b、c、d。将M端与正在转动的电动机接触,发 现b钢片振幅最大,则a、b、c、d此时振动频率
约为6__0_H__z____ , 电动机转速3为6_0_0_____r/min 。
阻尼振动与阻尼受迫振动.

2
dx dt
02 x
Байду номын сангаас
h cost
则上述方程的解为:
x(t) A0e t cos t 0 阻尼振动(暂态解) B cos t 受迫振动(定态解)
3. 稳定状态的振动表达式
x
受迫振动系统达到稳定时 应做与驱动力频率相同的谐振 动。其表达式为:
x Acos(t )
t
用旋矢法可求出上式的A和
讨论
求极限: dA 0
d
(1)位移共振(振幅取极值)
0
0
0
0
共振频率 : 共振振幅 :
r
Ar
02
h
2 02
2
2
2
共振相位 :
arctan
02 2 2
(振幅共振曲线)
10
第17章 振 动
(2)速度共振 (速度振幅A取极值)
vm
h ( 2 02 )2 4 2 2
共振频率 : 0
6
第17章 振 动
x Acos(t )
d2x dt 2
2
dx dt
02 x
h cost
x Acos(t )
d2x dt 2
A 2
cos(t
dx
dt π)
A
cos(t
π) 2
A 2 cos(t π) 2 A cos(t π )
2
02 A cos(t ) h cost
7
第17章 振 动
台北101大厦定楼神球
18
第17章 振 动
上海环球金融中心风阻尼器
19
第17章 振 动
阻尼越小,越接近谐振动,阻尼越大,“周期”越长。 2) 过阻尼运动
1.4阻尼振动受迫振动

四、振动图象的实际运用
心电图仪
地震仪
AC
二、简谐运动的表达式
由图像知道振动物体离开平衡位置的位移可以 用 X=Asin(ωt+φ)来表示 因为 ω=2π/T f=1/T 所以
物体从不同的位置振动,φ值不同。 ωt+φ叫相位,φ叫初相位。
怎样结合图像写表达式
观察三角函数的正弦值的大小在四个象限中随着 夹角大小变化的关系,和四个象限中正弦值的正 负。
三、简谐运动的相位与相位差的物理意义
用单摆演示当两个摆长与振幅都一样的单摆 在振动步调总一致时,我们就说它们的相位相同, 振动相同;当它们的位移总相反时,我们可以从 振动表达式推知它们的相位一定相差π;两个单 摆的振动步调不相同就是因为它们具有相位差。 所以用来描述简谐运动的物理量有:周期、 频率、相位与相位差。
2 、导入:那么如果用位移图象来表示简谐运动 位移与时间的关系,形状又如何呢?
方案一:在水平弹簧振子的小球上安
置一支记录用的笔,在下面放一条白 纸带,当小球振动时,沿垂直于振动 方向匀速拉动纸带,笔就在带上画出 一条振动图线。
实验演示
点击下图观看实验演示
一、由实验可了解到情况:
1、振动图象(如图)
x/m
x/cm
0
t/s
O
t/s
二. 受迫振动
周期性作用于系统的外力, 叫做驱动力。 物体在周期性外力作用下的振动,叫做受迫振 动。 受迫振动的特点: 受迫振动的频率由驱动力的频率决定,与物体 自由振动时的固有频率无关.
请观察下列运动是受迫振动吗?
三. 共振
1. 定义: 驱动力的频率接近物体的固有频率 时,受迫振动的振幅增大,等于固有频 率时,振幅最大, 这种现象叫做共振.
阻尼和受迫振动

T0
T0 :固有周期
四、阻尼振动的分类
1、欠阻尼 0
2、过阻尼 0 3、临界阻尼 0
x
o
: 固有频率 0 t
例、有一单摆在空气(室温20oC)中摆动,其摆线长1.0m,摆锤是 一半径为5.0mm的铅球。求: (1)摆动周期 (2)振幅减小10%所需时间 (3)能量减小10%所需时间 (已知铅球密度为2.65 g/ml,20oC时空气粘度1.78 x 10-5Pa s)
0
0
阻尼摆动时的周期 :T 2 2 2s
0
(2)在欠阻尼情况下,
由:xt A et cost 0
A A e 单摆的振幅
t
0
设振幅减小10%所需时间为t1,则有:
0.9 A A e t1
0
0
ln 1
t 0.9 174s 3min
1
(3)因为能量与振幅的二次方成正比
E ( A )2 e2t (2)共振振幅 :
r 02 2 2
Ar
2
h
2 0
2
共振现象的危害 1940 年7月1日美国 Tocama 悬索桥因共振而坍塌
气流经过圆柱体时产生的作用相间的涡旋 卡尔曼涡旋
0
0
0
随时间很快衰减为零
等幅振动
3、稳态解: x=Acos( t+)
在达到稳定态时,系统振动频率等于策驱动力的频率
共振
受迫振动的振幅:
h A
[(02 2 )2 4 2 2 ]1/ 2
共振频率
A
小阻尼
阻尼 0
大阻尼
o
0
P
受迫振动在一定条件下, 振幅出现 极大值, 振动剧烈的现象被称为共振。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
共振的防止和应用 1、防止
使驱动力的频率与物体的固有频率不同, 而且相差越大越好。
2、应用 使驱动力的频率接近或等于振动物体的
固有频率。
为什么:登山运动员登山时严禁大声喊叫??
因为喊叫声中某一频率若正好与山上积雪的固有频率 相吻合,就会因共振而引起雪崩,其后果十分严重。
振动类型项 目
自由振动
受力情况 回复力
振动
共振筛、声音 的共鸣等
小结
1、阻尼振动:振幅(能量)逐渐减小的振动。
2、受迫振动:物体在周期性驱动力作用下的振动。
物体做受迫振动时,振动稳定后的频率等于驱动力 的频率,跟物体的固有频率无关。
3、共振: 当驱动力的频率跟物体的固有频率相等时, 受迫振动的振幅最大,这种现象叫共振。
A、利用共振时:应使驱动力的频率f接近或等于振动
生活中的共振现象 1831年,一队骑兵通过曼彻斯特附近的一座便桥 时,由于马蹄节奏整齐,桥梁发生共振而断裂。
军队过桥便步走,火车过桥慢行
生活中的共振现象
1940 年11月7日美国的全长860米的Tocama 悬索桥因 在建成后的4个月就因风共振而坍塌 。
生活中的共振现象
美国有一农场农妇,习惯于用吹笛的方式 招呼丈夫回家吃饭,可当她有一次吹笛时,居 然发现树上的毛毛虫纷纷坠地而死,惊讶之余, 她到自己的果园吹了几个小时,一下子将果树 上的毛毛虫收拾的一干二净,究其原因,还是 笛子发出的声音引起毛毛虫内脏发生剧烈共振 而死亡。
生活中的共振现象 微波炉加热原理: 食物中水分子的振动频率约为2500MHz ,具有 大致相同频率的电磁波称为 “微波” 。微波 炉加热食品时,炉内产生很强的振荡电磁场, 使食物中的水分子作受迫振动,发生共振,将 电磁辐射能转化为内能,从而使食物的温度迅 速升高。微波加热是对物体内部的整体加热, 极大地提高了加热效率。
③发生共振时,一个周期内,外界提供的能量等于系统
克服阻力做功而消耗的能量。
受迫振动实例:
①跳板在人走过时发生的振动 ②机器底座在机器运转时发生的振动 ③听到声音时耳膜的振动 ④电磁打点计时器的振针所做的振动 ⑤ 轮船航行时要看波浪的撞击方向而改变速度和大小 ⑥洗衣机正常工作时的振动。
生活中的共振现象
“龙洗”是我国著名文物之一, 现代工艺制作的仿品,在许 多旅游景点均可见到, “龙洗”也称“金盆洗手”、“聚宝盆”, 用青铜铸成。盆沿图案由回纹和龙纹构成,盆底有四条龙,盆 沿有两只盆耳,倒了些清水到“龙洗”中,用手掌慢慢地去摩 擦盆边的提耳,霎时间,铜盆便可以发出嗡嗡之声,其中盛的 水便会起雾、震荡、溅起层层浪花,随着摩擦越来越快,水花 也越冲越高,
龙 洗 盆
龙洗盆
古代用以盛水盥洗的器皿。传说是明朝开国皇帝朱元璋为 不爱洗脸的独生子,召集全国的能工巧匠打制而成,为皇子的 专用洗盆。后成为皇亲国戚、才子佳人赏玩之物(中央电视台 《中国一绝》栏目曾介绍过),宫中奇宝,后来流落民间。若 以手摩擦两耳得法,产生共振,即可泛起水花,景象十分别致, 后成为一种民间娱乐用品。经现代振动与波的理论分析和实验 研究,这是薄壳圆柱体自激振荡时的不同振型所致。
教材P14
观看视频
四、共振
1.定义:当驱动力的频率跟物体的固有频率相等时,受迫 振动的振幅最大,这种现象叫共振。 2.条件:f驱 = f固 3.共振曲线:横轴:表示驱动力的频率
纵轴:表示受迫振动的振幅
①当f驱=f固时,振幅由最大值。
②f驱与f固越接近,受迫振动的振幅越大, f驱与f固相差越远,受迫振动的振幅越小
受迫振动
周期性驱 动力作用
共振
周期性驱 动力作用
振动周期 或频率
振动能量
由系统本身 固或f驱
即固有周期 决定,即T=
=f固
或固有频率 T驱或f=f驱
振动物体的 机械能不变
由产生驱动 力的物体提
供
振动物体获得 的能量最大
常见例子
弹簧振子或 单摆
(θ≤5°)
机械工作时 底座发生的
振幅不变,而一直振动下去呢?
用周期性的外力作用于振动系统,通过外 力对系统做正功,补偿系统机械能的损耗, 使系统持续地振动下去。
三、受迫振动
1、驱动力: 作用于振动系统 ,使系统能持续振动下 去的周期性外力叫做驱动力
2、受迫振动:物体在周期性驱动力作用下所做的振 动叫受迫振动。
3、规律:
①物体做受迫振动时,振动稳定后的频率等于驱动力的频 率,跟物体的固有频率无关。 ②物体做受迫振动的振幅由驱动力频率和物体的固有频 率共同决定:两者越接近,受迫振动的振幅越大,两者 相差越大受迫振动的振幅越小。
生活中的共振现象
唐朝时候洛阳某寺一僧人房中挂着的一件乐 器,经常莫名其妙地自动鸣响,僧人因此惊恐 成疾,四处求治无效。他有一个朋友是朝中管 音乐的官员,闻讯特去看望他。这时正好听见 寺里敲钟声,那件乐器又随之作响。于是朋友 说:你的病我可以治好,因为我找到你的病根 了。只见朋友找到一把铁锉,在乐器上锉磨几 下,乐器便再也不会自动作响了。
二、阻尼振动及其图象:
1、阻尼振动:系统振动过程中受到阻力作用,振
动逐渐消失,振动能量逐步转变为其他能量。这种振 动叫做阻尼振动。
2、振动系统受到的阻尼越
大,振幅减小得越快,阻 尼过大时,系统将不能发 生振动。
3、阻尼振动过程中:周期和频率不变。
4、实际的振动一定是阻尼振动
思考: 怎样才能使受阻力的振动的物体的
物体的固有频率f0
B、防止共振时:应使驱动力的频率f与物体的固有频
率f0不同,而且相差越大越好
例1:如图,A球振动后,通过水平细绳迫使B、C振
动,下面说法中正确的是( CD
)
A、只有A、C振动周期相等
B、A、B、C的振幅一样大
C、C的振幅比B的振幅大
D、A、B、C的振动周期相等
A 2m C 2m
B 4m
一.自由振动及其图象:
1、自由振动(无阻尼振动):系统不受外力作用,
也不受任何阻力,只在自身回复力作用下的振动称为自 由振动。 2、自由振动的频率,叫做系 统的固有频率。自由振动的周 期叫做系统的固有周期。
弹簧振子:T 2 m
k
单 摆: T 2 l
g
固有周期和固有频率:由系统本身的特征决定,与振幅无关。
例2:支持列车车厢的弹簧固有频率为2Hz,若列车 行驶在每根长为12.5m的铁轨连成的铁道上,则当列 车运行速度多大时,车厢振动的剧烈程度最大?
