立体几何 大题理科
高考大题之立体几何(理科)

1.如图,在三棱柱ABCA1B1C1中,A1A=AB,∠ABC=90°,侧面A1ABB1⊥底面ABC. (1)求证:AB1⊥平面A1BC; (2)若AC=5,BC=3,∠A1AB=60°,求二面角BA1CC1的余弦值. 2.如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2. (1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE; (2)求二面角EBCF的正弦值; (3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长. 3.等边三角形ABC的边长为3,点D,E分别是边AB,AC上的点,且满足ADDB
=CEEA=12,如图1.将△ADE沿DE折起到△A1DE的位置,使二面角A1DEB为直二面角,连接A1B,A1C,如图2.
图1 图2 (1)求证:A1D⊥平面BCED; (2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60°?若存在,求出PB的长;若不存在,请说明理由. 4. 如图,在多面体ABCDEF中,四边形ABCD是正方形,BF⊥平面ABCD,DE⊥平面ABCD,BF=DE,M为棱AE的中点. (1)求证:平面BDM∥平面EFC; (2)若DE=2AB,求直线AE与平面BDM所成角的正弦值. 5.如图,在正三棱柱ABCA1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点. (1)求异面直线BP与AC1所成角的余弦值; (2)求直线CC1与平面AQC1所成角的正弦值. 6.如图1,等腰直角三角形ABC的底边AB=2,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图2).
图1 图2 (1)求证:PB⊥DE; (2)若PE⊥BE,直线PD与平面PBC所成的角为30°,求平面PDE与平面PBC所成的锐二面角的正弦值. 7.如图1,等腰直角三角形ABC的底边AB=2,点D在线段AC上,DE⊥AB于点E,现将△ADE沿DE折起到△PDE的位置(如图2).
立体几何大题理科

立体几何大题理科编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(立体几何大题理科)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为立体几何大题理科的全部内容。
立体几何大题(17Ι)18.如图,在四棱锥P-ABCD中,AB//CD,且。
(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,,求二面角A—PB-C的余弦值。
(17П)19。
如图,四棱锥P—ABCD中,侧面PAD为等比三角形且垂直于底面ABCD,E是PD的中点.(1)证明:直线平面PAB(2)点M在棱PC 上,且直线BM与底面ABCD所成锐角为,求二面角M—AB—D的余弦值(17Ш)19.如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.(16Ι)(18)如图,在已A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,,且二面角D—AF-E与二面角C—BE—F都是.9BAPCDP∠=∠=90A P D∠=o1,90,2AB BC AD BADABC==∠=∠=//CEo4590A F D∠=60(I)证明;平面ABEF 平面EFDC ;(II )求二面角E —BC —A 的余弦值.(16П)(19)如图,菱形ABCD 的对角线AC 与BD 交于点O ,AB =5,AC =6,点E ,F 分别在AD ,CD 上,AE =CF =,EF 交BD 于点H .将△DEF 沿EF 折到△的位置,.(I )证明:平面ABCD ; (II)求二面角的正弦值.(19)如图,四棱锥P —ABCD 中,PA ⊥地面ABCD ,AD∥BC ,AB=AD=AC =3,PA=BC =4,M 为线段AD 上一点,AM=2MD ,N 为PC 的中点.(I )证明MN∥平面PAB ;(II)求直线AN 与平面PMN 所成角的正弦值。
高一数学立体几何计算题(理科)含解析

理科立体几何计算题一.解答题(共30小题)1.如图,在四棱锥P﹣ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.(Ⅰ)求异面直线AP与BC所成角的余弦值;(Ⅱ)求证:PD⊥平面PBC;(Ⅲ)求直线AB与平面PBC所成角的正弦值.2.如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC ∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.(Ⅰ)证明:CE∥平面PAB;(Ⅱ)求直线CE与平面PBC所成角的正弦值.3.如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.(1)证明:直线CE∥平面PAB;(2)点M在棱PC 上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.4.如图,在平行六面体ABCD﹣A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=,∠BAD=120°.(1)求异面直线A1B与AC1所成角的余弦值;(2)求二面角B﹣A1D﹣A的正弦值.5.如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D﹣AE﹣C的余弦值.6.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4.(1)求证:M为PB的中点;(2)求二面角B﹣PD﹣A的大小;(3)求直线MC与平面BDP所成角的正弦值.7.如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是的中点.(Ⅰ)设P是上的一点,且AP⊥BE,求∠CBP的大小;(Ⅱ)当AB=3,AD=2时,求二面角E﹣AG﹣C的大小.8.如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.9.如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.(Ⅰ)求证:MN∥平面BDE;(Ⅱ)求二面角C﹣EM﹣N的正弦值;(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为,求线段AH的长.10.如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE,设PA=1,AD=2.(1)求平面BPC的法向量;(2)求二面角B﹣PC﹣A的正切值.11.在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.(1)证明:CD⊥AB1;(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.12.如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.(Ⅰ)证明:AB⊥A1C;(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.13.如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.(1)求证:PA⊥平面ABCD;(2)求直线BF与平面AFD所成角的正弦值.14.如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.(Ⅰ)求证:EF⊥平面PAC;(Ⅱ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求的值.15.如图,在四棱锥中P﹣ABCD,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2,BC=4,PA=2.(1)求证:AB⊥PC;(2)在线段PD上,是否存在一点M,使得二面角M﹣AC﹣D的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.16.如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD.(Ⅰ)求证:CD⊥AM;(Ⅱ)若AM=BC=2,求直线AM与平面BDM所成角的正弦值.17.如图,四棱锥P﹣ABCD中,底面ABCD为菱形,PD=AD,∠DAB=60°,PD⊥底面ABCD.(1)求证AC⊥PB;(2)求PA与平面PBC所成角的正弦值.18.如图所示,已知斜三棱柱ABC﹣A1B1C1的各棱长均为2,侧棱与底面所成角为,且侧面ABB1A1垂直于底面.(1)判断B1C与C1A是否垂直,并证明你的结论;(2)求四棱锥B﹣ACC1A1的体积.19.在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AA1、A1B1上,且AE=,A1F=,CE⊥EF.(Ⅰ)证明:平面ABB1A1⊥平面ABC;(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.20.如图,四棱锥E﹣ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA ⊥ED,且AB=4,BC=CD=EA=ED=2.(1)求证:BD⊥平面ADE;(2)求直线BE和平面CDE所成角的正弦值.21.如图,在以A,B,C,D,E,F为顶点的多面体中,AF⊥平面ABCD,DE⊥平面ABCD,AD∥BC,AB=CD,∠ABC=60°,BC=AF=2AD=4DE=4.(Ⅰ)请在图中作出平面α,使得DE⊂α,且BF∥α,并说明理由;(Ⅱ)求直线EF与平面BCE所成角的正弦值.22.如图,在四棱锥中S﹣ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=,SE⊥AD.(1)证明:平面SBE⊥平面SEC(2)若SE=1,求直线CE与平面SBC所成角的正弦值.23.如图,在四棱锥A﹣BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.(1)若F是AD的中点,求证:EF∥平面ABC;(2)若AD=DE,求BE与平面ACE所成角的正弦值.24.在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3.将△BCD沿BD折到△BED的位置,使得二面角E﹣BD﹣A的大小为90°(如图).已知Q为EO的中点,点P在线段AB上,且.(Ⅰ)证明:直线PQ∥平面ADE;(Ⅱ)求直线BD与平面ADE所成角θ的正弦值.25.如图所示,在三棱柱ABC﹣A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1C ⊥AC1.(Ⅰ)求证:平面AA1B1B⊥平面BB1C1C;(Ⅱ)若D是CC1中点,∠ADB是二面角A﹣CC1﹣B的平面角,求直线AC1与平面ABC所成角的余弦值.26.等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P﹣AE﹣C为120°,设点P在面ABE上的射影为H.(1)证明:点H为EB的中点;(2))若,求直线BE与平面ABP所成角的正弦值.27.圆O上两点C,D在直径AB的两侧(如图甲),沿直径AB将圆O折起形成一个二面角(如图乙),若∠DOB的平分线交弧于点G,交弦BD于点E,F为线段BC的中点.(Ⅰ)证明:平面OGF∥平面CAD;(Ⅱ)若二面角C﹣AB﹣D为直二面角,且AB=2,∠CAB=45°,∠DAB=60°,求直线FG与平面BCD所成角的正弦值.28.如图,在四棱锥P﹣ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2.(Ⅰ)证明:平面BAP⊥平面DAP;(Ⅱ)点M为线段AB(含端点)上一点,设直线MP与平面DCP所成角为α,求sinα的取值范围.29.如图所示,四棱锥P﹣ABCD的底面是梯形,且AB∥CD,AB⊥平面PAD,E 是PB中点,CD=PD=AD=AB.(Ⅰ)求证:CE⊥平面PAB;(Ⅱ)若CE=,AB=4,求直线CE与平面PDC所成角的大小.30.如图,多面体ABCDE中,AB⊥面ACD,DE⊥面ACD;三角形ACD是正三角形,且AD=DE=2,AB=1(1)求直线AE和面CDE所成角的正切值;(2)求多面体ABCDE的体积;(3)判断直线CB和AE能否垂直,证明你的结论.理科立体几何计算题参考答案与试题解析一.解答题(共30小题)1.(2017•天津)如图,在四棱锥P﹣ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.(Ⅰ)求异面直线AP与BC所成角的余弦值;(Ⅱ)求证:PD⊥平面PBC;(Ⅲ)求直线AB与平面PBC所成角的正弦值.【解答】解:(Ⅰ)如图,由已知AD∥BC,故∠DAP或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC,所以AD⊥PD.在Rt△PDA中,由已知,得,故.所以,异面直线AP与BC所成角的余弦值为.证明:(Ⅱ)因为AD⊥平面PDC,直线PD⊂平面PDC,所以AD⊥PD.又因为BC∥AD,所以PD⊥BC,又PD⊥PB,所以PD⊥平面PBC.解:(Ⅲ)过点D作AB的平行线交BC于点F,连结PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角.因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,所以∠DFP为直线DF和平面PBC所成的角.由于AD∥BC,DF∥AB,故BF=AD=1,由已知,得CF=BC﹣BF=2.又AD⊥DC,故BC⊥DC,在Rt△DCF中,可得.所以,直线AB与平面PBC所成角的正弦值为.2.(2017•浙江)如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.(Ⅰ)证明:CE∥平面PAB;(Ⅱ)求直线CE与平面PBC所成角的正弦值.【解答】证明:(Ⅰ)取AD的中点F,连结EF,CF,∵E为PD的中点,∴EF∥PA,在四边形ABCD中,BC∥AD,AD=2DC=2CB,F为中点,∴CF∥AB,∴平面EFC∥平面ABP,∵EC⊂平面EFC,∴EC∥平面PAB.解:(Ⅱ)连结BF,过F作FM⊥PB于M,连结PF,∵PA=PD,∴PF⊥AD,推导出四边形BCDF为矩形,∴BF⊥AD,∴AD⊥平面PBF,又AD∥BC,∴BC⊥平面PBF,∴BC⊥PB,设DC=CB=1,则AD=PC=2,∴PB=,BF=PF=1,∴MF=,又BC⊥平面PBF,∴BC⊥MF,∴MF⊥平面PBC,即点F到平面PBC的距离为,∵MF=,D到平面PBC的距离应该和MF平行且相等,为,E为PD中点,E到平面PBC的垂足也为垂足所在线段的中点,即中位线,∴E到平面PBC的距离为,在,由余弦定理得CE=,设直线CE与平面PBC所成角为θ,则sinθ==.3.(2017•新课标Ⅱ)如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°,E是PD的中点.(1)证明:直线CE∥平面PAB;(2)点M在棱PC 上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.【解答】(1)证明:取PA的中点F,连接EF,BF,因为E是PD的中点,所以EF AD,AB=BC=AD,∠BAD=∠ABC=90°,∴BC∥AD,∴BCEF是平行四边形,可得CE∥BF,BF⊂平面PAB,CE⊄平面PAB,∴直线CE∥平面PAB;(2)解:四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°,E是PD的中点.取AD的中点O,M在底面ABCD上的射影N在OC上,设AD=2,则AB=BC=1,OP=,∴∠PCO=60°,直线BM与底面ABCD所成角为45°,可得:BN=MN,CN=MN,BC=1,可得:1+BN2=BN2,BN=,MN=,作NQ⊥AB于Q,连接MQ,所以∠MQN就是二面角M﹣AB﹣D的平面角,MQ==,二面角M﹣AB﹣D的余弦值为:=.4.(2017•江苏)如图,在平行六面体ABCD﹣A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=,∠BAD=120°.(1)求异面直线A1B与AC1所成角的余弦值;(2)求二面角B﹣A1D﹣A的正弦值.【解答】解:在平面ABCD内,过A作Ax⊥AD,∵AA1⊥平面ABCD,AD、Ax⊂平面ABCD,∴AA1⊥Ax,AA1⊥AD,以A为坐标原点,分别以Ax、AD、AA1所在直线为x、y、z轴建立空间直角坐标系.∵AB=AD=2,AA1=,∠BAD=120°,∴A(0,0,0),B(),C(,1,0),D(0,2,0),A1(0,0,),C1().=(),=(),,.(1)∵cos<>==.∴异面直线A1B与AC1所成角的余弦值为;(2)设平面BA1D的一个法向量为,由,得,取x=,得;取平面A1AD的一个法向量为.∴cos<>==.∴二面角B﹣A1D﹣A的正弦值为,则二面角B﹣A1D﹣A的正弦值为.5.(2017•新课标Ⅲ)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D﹣AE﹣C的余弦值.【解答】(1)证明:如图所示,取AC的中点O,连接BO,OD.∵△ABC是等边三角形,∴OB⊥AC.△ABD与△CBD中,AB=BD=BC,∠ABD=∠CBD,∴△ABD≌△CBD,∴AD=CD.∵△ACD是直角三角形,∴AC是斜边,∴∠ADC=90°.∴DO=AC.∴DO2+BO2=AB2=BD2.∴∠BOD=90°.∴OB⊥OD.又DO∩AC=O,∴OB⊥平面ACD.又OB⊂平面ABC,∴平面ACD⊥平面ABC.(2)解:设点D,B到平面ACE的距离分别为h D,h E.则=.∵平面AEC把四面体ABCD分成体积相等的两部分,∴===1.∴点E是BD的中点.建立如图所示的空间直角坐标系.不妨取AB=2.则O(0,0,0),A(1,0,0),C(﹣1,0,0),D(0,0,1),B(0,,0),E.=(﹣1,0,1),=,=(﹣2,0,0).设平面ADE的法向量为=(x,y,z),则,即,取=.同理可得:平面ACE的法向量为=(0,1,).∴cos===﹣.∴二面角D﹣AE﹣C的余弦值为.6.(2017•北京)如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD ⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4.(1)求证:M为PB的中点;(2)求二面角B﹣PD﹣A的大小;(3)求直线MC与平面BDP所成角的正弦值.【解答】(1)证明:如图,设AC∩BD=O,∵ABCD为正方形,∴O为BD的中点,连接OM,∵PD∥平面MAC,PD⊂平面PBD,平面PBD∩平面AMC=OM,∴PD∥OM,则,即M为PB的中点;(2)解:取AD中点G,∵PA=PD,∴PG⊥AD,∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PG⊥平面ABCD,则PG⊥AD,连接OG,则PG⊥OG,由G是AD的中点,O是AC的中点,可得OG∥DC,则OG⊥AD.以G为坐标原点,分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系,由PA=PD=,AB=4,得D(2,0,0),A(﹣2,0,0),P(0,0,),C(2,4,0),B(﹣2,4,0),M(﹣1,2,),,.设平面PBD的一个法向量为,则由,得,取z=,得.取平面PAD的一个法向量为.∴cos<>==.∴二面角B﹣PD﹣A的大小为60°;(3)解:,平面PAD的一个法向量为.∴直线MC与平面BDP所成角的正弦值为|cos<>|=||=| |=.7.(2017•山东)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是的中点.(Ⅰ)设P是上的一点,且AP⊥BE,求∠CBP的大小;(Ⅱ)当AB=3,AD=2时,求二面角E﹣AG﹣C的大小.【解答】解:(Ⅰ)∵AP⊥BE,AB⊥BE,且AB,AP⊂平面ABP,AB∩AP=A,∴BE⊥平面ABP,又BP⊂平面ABP,∴BE⊥BP,又∠EBC=120°,因此∠CBP=30°;(Ⅱ)解法一、取的中点H,连接EH,GH,CH,∵∠EBC=120°,∴四边形BECH为菱形,∴AE=GE=AC=GC=.取AG中点M,连接EM,CM,EC,则EM⊥AG,CM⊥AG,∴∠EMC为所求二面角的平面角.又AM=1,∴EM=CM=.在△BEC中,由于∠EBC=120°,由余弦定理得:EC2=22+22﹣2×2×2×cos120°=12,∴,因此△EMC为等边三角形,故所求的角为60°.解法二、以B为坐标原点,分别以BE,BP,BA所在直线为x,y,z轴建立空间直角坐标系.由题意得:A(0,0,3),E(2,0,0),G(1,,3),C(﹣1,,0),故,,.设为平面AEG的一个法向量,由,得,取z1=2,得;设为平面ACG的一个法向量,由,可得,取z 2=﹣2,得.∴cos<>=.∴二面角E﹣AG﹣C的大小为60°.8.(2017•新课标Ⅰ)如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.【解答】(1)证明:∵∠BAP=∠CDP=90°,∴PA⊥AB,PD⊥CD,∵AB∥CD,∴AB⊥PD,又∵PA∩PD=P,且PA⊂平面PAD,PD⊂平面PAD,∴AB⊥平面PAD,又AB⊂平面PAB,∴平面PAB⊥平面PAD;(2)解:∵AB∥CD,AB=CD,∴四边形ABCD为平行四边形,由(1)知AB⊥平面PAD,∴AB⊥AD,则四边形ABCD为矩形,在△APD中,由PA=PD,∠APD=90°,可得△PAD为等腰直角三角形,设PA=AB=2a,则AD=.取AD中点O,BC中点E,连接PO、OE,以O为坐标原点,分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系,则:D(),B(),P(0,0,),C().,,.设平面PBC的一个法向量为,由,得,取y=1,得.∵AB⊥平面PAD,AD⊂平面PAD,∴AB⊥PD,又PD⊥PA,PA∩AB=A,∴PD⊥平面PAB,则为平面PAB的一个法向量,.∴cos<>==.由图可知,二面角A﹣PB﹣C为钝角,∴二面角A﹣PB﹣C的余弦值为.9.(2017•天津)如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.(Ⅰ)求证:MN∥平面BDE;(Ⅱ)求二面角C﹣EM﹣N的正弦值;(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为,求线段AH的长.【解答】(Ⅰ)证明:取AB中点F,连接MF、NF,∵M为AD中点,∴MF∥BD,∵BD⊂平面BDE,MF⊄平面BDE,∴MF∥平面BDE.∵N为BC中点,∴NF∥AC,又D、E分别为AP、PC的中点,∴DE∥AC,则NF∥DE.∵DE⊂平面BDE,NF⊄平面BDE,∴NF∥平面BDE.又MF∩NF=F.∴平面MFN∥平面BDE,则MN∥平面BDE;(Ⅱ)解:∵PA⊥底面ABC,∠BAC=90°.∴以A为原点,分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系.∵PA=AC=4,AB=2,∴A(0,0,0),B(2,0,0),C(0,4,0),M(0,0,1),N(1,2,0),E (0,2,2),则,,设平面MEN的一个法向量为,由,得,取z=2,得.由图可得平面CME的一个法向量为.∴cos<>=.∴二面角C﹣EM﹣N的余弦值为,则正弦值为;(Ⅲ)解:设AH=t,则H(0,0,t),,.∵直线NH与直线BE所成角的余弦值为,∴|cos<>|=||=||=.解得:t=或t=.∴当H与P重合时直线NH与直线BE所成角的余弦值为,此时线段AH的长为或.10.(2017•吴江区三模)如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE,设PA=1,AD=2.(1)求平面BPC的法向量;(2)求二面角B﹣PC﹣A的正切值.【解答】解:(1)∵PA⊥平面ABCD,BD⊂平面ABCD,∴PA⊥BD.∵PC⊥平面BDE,BD⊂平面BDE,∴PC⊥BD.又PA∩PC=P,∴BD⊥平面PAC,AC⊂平面PAC,∴BD⊥AC.又底面ABCD为矩形,∴ABCD为正方形.建立如图所示的空间直角坐标系.A(0,0,0),B(2,0,0),C(2,2,0),P(0,0,1),D(0,2,0).=(0,2,0),=(﹣2,0,1),设平面BPC的法向量为=(x,y,z),∴,∴,取=(1,0,2.).∴平面BPC的一个法向量为=(1,0,2.).(2)平面PAC的法向量为:=(﹣2,2,0).设二面角B﹣PC﹣A=θ,由图可知:θ为锐角.则cos===﹣.∴cosθ=.∴sinθ=.∴tanθ==3.即二面角B﹣PC﹣A的正切值为3.11.(2017•虎林市模拟)在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=,AA1=2,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1.(1)证明:CD⊥AB1;(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.【解答】证明:(1)由题意可知,在Rt△ABD中,tan∠ABD==,在Rt△ABB1中,tan∠AB1B==.又因为0<∠ABD,∠AB1B,所以∠ABD=∠AB1B,所以∠ABD+∠BAB1=∠AB1B+∠BAB1=,所以AB1⊥BD.又CO⊥侧面ABB1A1,且AB1⊂侧面ABB1A1,∴AB1⊥CO.又BD与CO交于点O,所以AB1⊥平面CBD.又因为BC⊂平面CBD,所以BC⊥AB1.(6分)解:(2)如图所示,以O为原点,分别以OD,OB1,OC所在的直线为x轴,y 轴,z轴,建立空间直角坐标系,则A(0,﹣,0),B(﹣,0,0),C(0,0,),B1(0,,0),D(,0,0).又因为=2,所以C1(,,).所以=(﹣,,0),=(0,,),=(,,).设平面ABC的法向量为=(x,y,z),则由,得令y=,则z=﹣,x=1,=(1,,﹣)是平面ABC的一个法向量.设直线C1D与平面ABC所成的角为α,则sin α==.故直线C1D与平面ABC所成角的正弦值为.(12分)12.(2017•广西一模)如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.(Ⅰ)证明:AB⊥A1C;(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.【解答】(Ⅰ)证明:取AB中点,连接OC,OA1,∵CA=CB,AB=A1A,∠BAA1=60°∴OC⊥AB,OA1⊥AB,∵OC∩OA1=O,∴AB⊥平面OCA1,∵CA1⊂平面OCA1,∴AB⊥A1C;(Ⅱ)解:由(Ⅰ)知OC⊥AB,OA1⊥AB,又平面ABC⊥平面AA1B1B,交线为AB,所以OC⊥平面AA1B1B,故OA,OA1,OC两两垂直.以O为坐标原点,的方向为x轴的正向,建立如图所示的坐标系,可得A(1,0,0),A1(0,,0),C(0,0,),B(﹣1,0,0),则=(1,0,),==(﹣1,,0),=(0,﹣,),设=(x,y,z)为平面BB1C1C的法向量,则,可取y=1,可得=(,1,﹣1),故cos<,>=﹣,又因为直线与法向量的余弦值的绝对值等于直线与平面的正弦值,故直线A1C与平面BB1C1C所成角的正弦值为:.13.(2017•徐水县模拟)如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.(1)求证:PA⊥平面ABCD;(2)求直线BF与平面AFD所成角的正弦值.【解答】解:(1)连接AE,∵AF⊥平面PED,ED⊂平面PED,∴AF⊥ED,在平行四边形ABCD中,BC=2AB=4,∠ABC=60°,∴AE=2,,∴AE2+ED2=AD2,∴AE⊥ED,又∵AF∩AE=A,AF⊂平面PAE,PA⊂平面PAE,∴ED⊥平面PAE,∵PA⊂平面PAE,∴ED⊥PA,又PA⊥AD,AD∩ED=D,AE⊂平面ABCD,AD⊂平面ABCD,∴PA⊥平面ABCD.(2)以E为坐标原点,以EA,ED为x轴,y轴建立如图所示的空间直角坐标系,则A(0,2,0),,,∵AF⊥平面PED,所以AF⊥PE,又F为PE中点,∴PA=AE=2,∴P(0,2,2),F(0,1,1),∴,,,设平面AFD的法向量为,由,得,,令x=1,得.设直线BF与平面AFD所成的角为θ,则:,即直线BF与平面AFD所成角的正弦值为.14.(2017•葫芦岛模拟)如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.(Ⅰ)求证:EF⊥平面PAC;(Ⅱ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求的值.【解答】(Ⅰ)证明:∵在平行四边形ABCD中,∠BCD=135°,∴∠ABC=45°,∵AB=AC,∴AB⊥AC.∵E,F分别为BC,AD的中点,∴EF∥AB,∴EF⊥AC.∵侧面PAB⊥底面ABCD,且∠BAP=90°,∴PA⊥底面ABCD.又EF⊂底面ABCD,∴PA⊥EF.又∵PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,∴EF⊥平面PAC.(Ⅱ)解:∵PA⊥底面ABCD,AB⊥AC,∴AP,AB,AC两两垂直,以A为原点,分别以AB,AC,AP为x轴、y轴和z轴建立空间直角坐标系如图:则A(0,0,0),B(2,0,0),C(0,2,0),P(0,0,2),D(﹣2,2,0),E(1,1,0),∴=(2,0,﹣2),=(﹣2,2,﹣2),,=(1,1,﹣2).设=λ(0≤λ≤1),则=(﹣2λ,2λ,﹣2λ),∴==(1+2λ,1﹣2λ,2λ﹣2),显然平面ABCD的一个法向量为=(0,0,1).设平面PBC的法向量为=(x,y,z),则,即令x=1,得=(1,1,1).∴cos<,>==,cos<>==.∵直线ME与平面PBC所成的角和此直线与平面ABCD所成的角相等,∴||=||,即,解得,或(舍).∴.15.(2017•腾冲县校级一模)如图,在四棱锥中P﹣ABCD,PA⊥平面ABCD,AD ∥BC,AD⊥CD,且AD=CD=2,BC=4,PA=2.(1)求证:AB⊥PC;(2)在线段PD上,是否存在一点M,使得二面角M﹣AC﹣D的大小为45°,如果存在,求BM与平面MAC所成角的正弦值,如果不存在,请说明理由.【解答】解:(1)证明:∵四边形ABCD是直角梯形,AD=CD=2,BC=4,∴AC=4,AB===4,∴△ABC是等腰直角三角形,即AB⊥AC,∵PA⊥平面ABCD,AB⊂平面ABCD,∴PA⊥AB,∴AB⊥平面PAC,又PC⊂平面PAC,∴AB⊥PC.(2)假设存在符合条件的点M,过点M作MN⊥AD于N,则MN∥PA,∴MN⊥平面ABCD,∴MN⊥AC.过点M作MG⊥AC于G,连接NG,则AC⊥平面MNG,∴AC⊥NG,即∠MGN是二面角M﹣AC﹣D的平面角.若∠MGN=45°,则NG=MN,又AN=NG=MN,∴MN=1,即M是线段PD的中点.∴存在点M使得二面角M﹣AC﹣D的大小为45°.=S△ABC•MN==,在三棱锥M﹣ABC中,V M﹣ABC=,设点B到平面MAC的距离是h,则V B﹣MAC===2,∵MG=MN=,∴S△MAC∴=,解得h=2.在△ABN中,AB=4,AN=,∠BAN=135°,∴BN==,∴BM==3,∴BM与平面MAC所成角的正弦值为=.16.(2017•五模拟)如图,在多面体ABCDM中,△BCD是等边三角形,△CMD 是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD.(Ⅰ)求证:CD⊥AM;(Ⅱ)若AM=BC=2,求直线AM与平面BDM所成角的正弦值.【解答】(Ⅰ)证明:取CD的中点O,连接OB,OM.∵△BCD是等边三角形,∴OB⊥CD.∵△CMD是等腰直角三角形,∠CMD=90°,∴OM⊥CD.∵平面CMD⊥平面BCD,平面CMD∩平面BCD=CD,OM⊂平面CMD,∴OM⊥平面BCD.又∵AB⊥平面BCD,∴OM∥AB.∴O,M,A,B四点共面.∵OB∩OM=O,OB⊂平面OMAB,OM⊂平面OMAB,∴CD⊥平面OMAB.∵AM⊂平面OMAB,∴CD⊥AM.(Ⅱ)作MN⊥AB,垂足为N,则MN=OB.∵△BCD是等边三角形,BC=2,∴,CD=2.在Rt△ANM中,.∵△CMD是等腰直角三角形,∠CMD=90°,∴.∴AB=AN+NB=AN+OM=2.以点O为坐标原点,以OC,BO,OM为坐标轴轴建立空间直角坐标系O﹣xyz,则M(0,0,1),,D(﹣1,0,0),.∴,,.设平面BDM的法向量为=(x,y,z),由n•,n•,∴,令y=1,得=.设直线AM与平面BDM所成角为θ,则==.∴直线AM与平面BDM所成角的正弦值为.17.(2017•香坊区校级二模)如图,四棱锥P﹣ABCD中,底面ABCD为菱形,PD=AD,∠DAB=60°,PD⊥底面ABCD.(1)求证AC⊥PB;(2)求PA与平面PBC所成角的正弦值.【解答】(1)证明∵底面ABCD为菱形,∴AC⊥BD,∵PD⊥底面ABCD,∴AC⊥PD,∵BD∩PD=D,∴AC⊥面PDB,∵PB⊂面PDB∴AC⊥PB.(2)解:设PD=AD=1,设A到平面PBC的距离为h,==则由题意PA=PB=PC=,S△ABC在等腰△PBC中,可求S==△PBC=V P﹣ABC,=,h=∴V A﹣PBC∴sinθ===18.(2017•徐汇区校级模拟)如图所示,已知斜三棱柱ABC﹣A1B1C1的各棱长均为2,侧棱与底面所成角为,且侧面ABB1A1垂直于底面.(1)判断B1C与C1A是否垂直,并证明你的结论;(2)求四棱锥B﹣ACC1A1的体积.【解答】解:(1)B1C⊥C1A证明如下:在平面BA1内,过B1作B1D⊥AB于D,∵侧面BA1⊥平面ABC,∴B1D⊥平面ABC,∠B1BA是BB1与平面ABC所成的角,∴∠B1BA=π﹣=,连接BC1,∵BB1CC1是菱形,∴BC1⊥B1C,CD⊥平面A1B,B1D⊥AB,∴B1C⊥AB,∴B1C⊥平面ABC1,∴B1C⊥C1A.(2)解:由题意及图,答:四棱锥B﹣ACC1A1的体积为219.(2017•焦作二模)在三棱柱ABC﹣A1B1C1中,CA=CB,侧面ABB1A1是边长为2的正方形,点E,F分别在线段AA1、A1B1上,且AE=,A1F=,CE⊥EF.(Ⅰ)证明:平面ABB1A1⊥平面ABC;(Ⅱ)若CA⊥CB,求直线AC1与平面CEF所成角的正弦值.【解答】证明:(I)取AB的中点D,连结CD,DF,DE.∵AC=BC,D是AB的中点,∴CD⊥AB.∵侧面ABB1A1是边长为2的正方形,AE=,A1F=.∴A1E=,EF==,DE==,DF==,∴EF2+DE2=DF2,∴DE⊥EF,又CE⊥EF,CE∩DE=E,CE⊂平面CDE,DE⊂平面CDE,∴EF⊥平面CDE,又CD⊂平面CDE,∴CD⊥EF,又CD⊥AB,AB⊂平面ABB1A1,EF⊂平面ABB1A1,AB,EF为相交直线,∴CD⊥平面ABB1A1,又CD⊂ABC,∴平面ABB1A1⊥平面ABC.(II)∵平面ABB1A1⊥平面ABC,∴三棱柱ABC﹣A1B1C1是直三棱柱,∴CC1⊥平面ABC.∵CA⊥CB,AB=2,∴AC=BC=.以C为原点,以CA,CB,CC1为坐标轴建立空间直角坐标系,如图所示:则A(,0,0),C(0,0,0),C1(0,0,2),E(,0,),F(,,2).∴=(﹣,0,2),=(,0,),=(,,2).设平面CEF的法向量为=(x,y,z),则,∴,令z=4,得=(﹣,﹣9,4).∴=10,||=6,||=.∴sin<>==.∴直线AC1与平面CEF所成角的正弦值为.20.(2017•秦州区校级模拟)如图,四棱锥E﹣ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.(1)求证:BD⊥平面ADE;(2)求直线BE和平面CDE所成角的正弦值.【解答】解:(1)∵EA=ED=2,EA⊥ED,∴AD=2.∵BC=CD=2,BC⊥CD,∴BD=2又AB=4,∴AD2+BD2=AB2,∴AD⊥BD.又平面EAD⊥平面ABCD,平面EAD∩平面ABCD=AD,BD⊂平面ABCD,∴BD⊥平面ADE.(2)取AD的中点F,连接EF,则EF⊥平面ABCD,EF=.过D点作直线Oz∥EF,则Oz⊥平面ABCD.以D为坐标原点,以DA,DB,Dz为坐标轴建立空间直角坐标系D﹣xyz,∴D(0,0,0),C(﹣,,0),B(0,2,0),E(,0,),∴=(,﹣2,),=(,0,),=(﹣,,0).设平面CDE的一个法向量为=(x,y,z),则,∴,设x=1得=(1,1,﹣1).∴cos<>===﹣.∴直线BE和平面CDE所成角的正弦值为.21.(2017•泉州一模)如图,在以A,B,C,D,E,F为顶点的多面体中,AF⊥平面ABCD,DE⊥平面ABCD,AD∥BC,AB=CD,∠ABC=60°,BC=AF=2AD=4DE=4.(Ⅰ)请在图中作出平面α,使得DE⊂α,且BF∥α,并说明理由;(Ⅱ)求直线EF与平面BCE所成角的正弦值.【解答】解:(Ⅰ)取BC的中点G,连接EG,DG,则平面EDG为所求.∵AD=2,BG=2,AD∥BC,∴四边形ADGB是平行四边形,∴AB∥DG,∵AB⊄平面EDG,DG⊂平面EDG,∴AB∥平面EDG.同理AF∥平面EDG,∵AB∩AF=A,∴平面ABF∥平面EDG,∵FB⊂平面ABF,∴BF∥平面EDG;(Ⅱ)以点A为坐标原点,AD为y轴,AF为z轴,过A垂直于AD的直线为x 轴,建立如图所示的坐标系,则F(0,0,4),E(0,2,1),B(,﹣1,0),C(,3,0),∴=(0,﹣2,3),=(0,4,0),=(﹣,3,1),设平面BCE的法向量为=(x,y,z),则,取=(,0,3),则直线EF与平面BCE所成角的正弦值==.22.(2017•乃东县校级三模)如图,在四棱锥中S﹣ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=,SE⊥AD.(1)证明:平面SBE⊥平面SEC(2)若SE=1,求直线CE与平面SBC所成角的正弦值.【解答】解:(1)证明:∵平面SAD⊥平面ABCD,平面SAD∩平面ABCD=AD,SE⊂平面SAD,SE⊥AD,∴SE⊥平面ABCD,…(2分)∵BE⊂平面ABCD,∴SE⊥BE.∵CD=3AB=3,AE=ED=,∴∠AEB=30°,∠CED=60°.所以∠BEC=90°即BE⊥CE.…(4分)结合SE∩CE=E得BE⊥平面SEC,∵BE⊂平面SBE,∴平面SBE⊥平面SEC.…(6分)(2)由(1)知,直线ES,EB,EC两两垂直.如图,以EB为x轴,以EC为y轴,以ES为z轴,建立空间直角坐标系.则,∴.设平面SBC的法向量为,则解得一个法向量,…(9分)设直线CE与平面SBC所成角为θ,又,则.所以直线CE与平面SBC所成角的正弦值.…(12分)23.(2017•邯郸二模)如图,在四棱锥A﹣BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.(1)若F是AD的中点,求证:EF∥平面ABC;(2)若AD=DE,求BE与平面ACE所成角的正弦值.【解答】证明:(1)取DB中点G,连结EG、FG.∵F是AD的中点,∴FG∥AB.∵BD=2CE,∴BG=CE.∵∠DBC=∠BCE∴E、G到直线BC的距离相等,则BG∥CB,∵EG∩FG=G∴面EGF∥平面ABC,则EF∥平面ABC.解:(2)以点D为原点,建立如图所示的直角坐标系D﹣xyz,设EC=1,则DB=2,取BC中点C,则EG∥BC,∴BC=3,∵AD=DE,则A(0,0,),E(0,,0),B(2,0,0),C(,,0).,.设平面ACE的法向量,=x+y=0令y=1,则,|cos|=.∴BE与平面ACE所成角的正弦值为:24.(2017•湘潭三模)在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3.将△BCD沿BD折到△BED的位置,使得二面角E﹣BD﹣A的大小为90°(如图).已知Q为EO的中点,点P在线段AB上,且.(Ⅰ)证明:直线PQ∥平面ADE;(Ⅱ)求直线BD与平面ADE所成角θ的正弦值.【解答】(Ⅰ)证明:如图,取OD的中点R,连接PR,QR,则DE∥RQ,由题知,又,故AB:AP=4:1=DB:DR,因此AD∥PR,因为PR,RQ⊄平面ADE,且AD,DE⊂平面ADE,故PR∥平面ADE,RQ∥平面ADE,又PR∩RQ=R,故平面PQR∥平面ADE,从而PQ∥平面ADE.…6分(Ⅱ)解:由题EA=ED=5,,设点O到平面ADE的距离为d,则由等体积法可得,故,因此.…12分.25.(2017•城厢区校级模拟)如图所示,在三棱柱ABC﹣A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1C⊥AC1.(Ⅰ)求证:平面AA1B1B⊥平面BB1C1C;(Ⅱ)若D是CC1中点,∠ADB是二面角A﹣CC1﹣B的平面角,求直线AC1与平面ABC所成角的余弦值.【解答】解:(Ⅰ)证明:连接BC1,因为BB1C1C为菱形,所以B1C⊥BC1,又B1C⊥AC1,AC1∩BC1=C1,所以B1C⊥面ABC1.故B1C⊥AB.因为AB⊥BB1,且BB1∩BC1,所以AB⊥面BB1C1C.而AB⊂平面ABB1A1,所以平面AA1B1B⊥平面BB1C1C;(Ⅱ)因为∠ADB是二面角A﹣CC1﹣B的平面角,所以BD⊥CC1,又D是CC1中点,所以BD=BC1,所以△C1BC为等边三角形.如图所示,分别以BA,BB1,BD为x,y,z轴建立空间直角坐标系,不妨设AB=2,则A(2,0,0),,,).设是平面ABC的一个法向量,则,即,取z=1得.所以=,所以直线AC1与平面ABC所成的余弦值为.26.(2017•湖北模拟)等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P﹣AE﹣C为120°,设点P在面ABE上的射影为H.(1)证明:点H为EB的中点;(2))若,求直线BE与平面ABP所成角的正弦值.【解答】(1)证明:依题意,AE⊥BC,则AE⊥EB,AE⊥EP,EB∩EP=E.∴AE⊥面EPB.故∠CEP为二面角C﹣AE﹣P的平面角,则点P在面ABE上的射影H在EB上.由∠CEP=120°得∠PEB=60°.…(3分)∴EH=EP=.∴H为EB的中点.…(6分)(2)解:过H作HM⊥AB于M,连PM,过H作HN⊥PM于N,连BN,则有三垂线定理得AB⊥面PHM.即面PHM⊥面PAB,∴HN⊥面PAB.故HB在面PAB上的射影为NB.∴∠HBN为直线BE与面ABP所成的角.…(9分)依题意,BE=BC=2,BH=BE=1.在△HMB中,HM=,在△EPB中,PH=,∴在Rt△PHM中,HN=.∴sin∠HBN=.…(12分)27.(2017•山东二模)圆O上两点C,D在直径AB的两侧(如图甲),沿直径AB将圆O折起形成一个二面角(如图乙),若∠DOB的平分线交弧于点G,交弦BD于点E,F为线段BC的中点.(Ⅰ)证明:平面OGF∥平面CAD;(Ⅱ)若二面角C﹣AB﹣D为直二面角,且AB=2,∠CAB=45°,∠DAB=60°,求直线FG与平面BCD所成角的正弦值.【解答】证明:(Ⅰ)∵OF为△ABC的一条中位线∴OF∥AC,又OF⊄平面ACD,AC⊂平面ACD,∴OF∥平面ACD.又∵OG为∠DOB的平分线,∴OG⊥BD,∵AB是⊙O的直径,∴AD⊥BD,∴OG∥AD,又OG⊄平面ACD,AD⊂平面ACD,∴OG∥平面ACD,又∵OG,OF为平面OGF内的两条相交直线,∴平面OGF∥平面CAD(Ⅱ)∵O为AB的中点,∴CO⊥AB,∵平面CAB⊥平面DAB,平面CAB∩平面DAB=AB,OC⊂平面ABC,∴CO⊥平面DAB,又Rt△DAB中,AB=2,∠DAB=60°,∴AD=1,又OG∥AD,OG=1,OA=1,∴四边形ADGO为菱形,∠AOG=120°,设DG中点为M,则∠AOM=90°,即OM⊥OB,∴直线OM,OB,OC两两垂直,以O为原点,以OM,OB,OC为坐标轴建立如图所示的空间直角坐标系O﹣xyz.则B(0,1,0),C(0,0,1),D(,,G(,,F(0,,).∴=(,,=(0,﹣1,1),=(,﹣,0).设平面BCD的法向量为=(x,y,z),则,∴,令y=1,=(,1,1).∴=1,||=1,=.∴=.∴直线FG与平面BCD所成角的正弦值为.28.(2017•上饶县模拟)如图,在四棱锥P﹣ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2.(Ⅰ)证明:平面BAP⊥平面DAP;(Ⅱ)点M为线段AB(含端点)上一点,设直线MP与平面DCP所成角为α,求sinα的取值范围.【解答】证明:(I)取PA的中点E,PB的中点O,连接DE,OE,OC.∵OE是△PAB的中位线,∴OE,∵CD∥平面PAB,CD⊂平面ABCD,平面ABCD∩平面PAB=AB,∴CD∥AB,又CD=,∴OE OE,∴四边形CDEO是平行四边形,∴DE∥OC.∵AB⊥平面PBC,OC⊂平面PBC,∴AB⊥OC,∵BC=PC,∴OC⊥PB,又PB⊂平面PAB,AB⊂平面PAB,AB∩PB=B,∴OC⊥平面PAB,又OC∥DE,∴DE⊥平面PAB,∵DE⊂平面PAD,∴平面PAD⊥平面PAB.(II)∵OE∥AB,AB⊥平面PBC,∴OE⊥平面PBC.以O为原点,以OC,OB,OE为坐标轴建立空间直角坐标系,如图所示:则P(0,﹣1,0),C(,0,0),D(,0,1),设M(0,1,a)(0≤a≤2),则=(0,2,a),=(0,0,1),=(,1,0).设平面PCD的法向量为=(x,y,z),则,∴,令x=1得=(1,﹣,0).∴cos<>==.∴sinα=.∴当a=0时,sinα取得最大值,当a=2时,sinα取得最小值.∴sinα的取值范围是[,].。
高三精选立体几何大题30题(含详细解答)
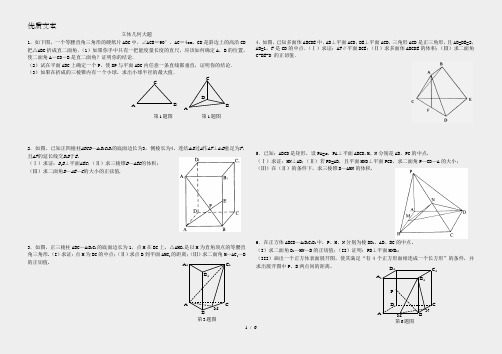
A BC第1题图ABCD第1题图立体几何大题1.如下图,一个等腰直角三角形的硬纸片ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高沿CD 把△ABC折成直二面角.(1)如果你手中只有一把能度量长度的直尺,应该如何确定A,B的位置,使二面角A-CD-B是直二面角?证明你的结论.(2)试在平面ABC上确定一个P,使DP与平面ABC内任意一条直线都垂直,证明你的结论.(3)如果在折成的三棱锥内有一个小球,求出小球半径的最大值.2.如图,已知正四棱柱ABCD—A1B1C1D1的底面边长为3,侧棱长为4,连结A1B过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E。
(Ⅰ)求证:D1B⊥平面AEC;(Ⅱ)求三棱锥B—AEC的体积;(Ⅲ)求二面角B—AE—C的大小的正弦值.3.如图,正三棱柱ABC—A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.(I)求证:点M为BC的中点;(Ⅱ)求点B到平面AMC1的距离;(Ⅲ)求二面角M—AC1—B 的正切值. 4.如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1,F是CD的中点.(Ⅰ)求证:AF∥平面BCE;(Ⅱ)求多面体ABCDE的体积;(Ⅲ)求二面角C-BE-D 的正切值.5.已知:ABCD是矩形,设PA=a,PA⊥平面ABCD.M、N分别是AB、PC的中点.(Ⅰ)求证:MN⊥AB;(Ⅱ)若PD=AB,且平面MND⊥平面PCD,求二面角P—CD—A的大小;(Ⅲ)在(Ⅱ)的条件下,求三棱锥D—AMN的体积.6.在正方体ABCD—A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点。
(I)求二面角B1—MN—B的正切值;(II)证明:PB⊥平面MNB1;(III)画出一个正方体表面展开图,使其满足“有4个正方形面相连成一个长方形”的条件,并求出展开图中P、B两点间的距离。
高三精选立体几何大题30题(含详细解答)

A BC第1题图ABCD第1题图立体几何大题1.如下图,一个等腰直角三角形的硬纸片ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高沿CD 把△ABC折成直二面角.(1)如果你手中只有一把能度量长度的直尺,应该如何确定A,B的位置,使二面角A-CD-B是直二面角?证明你的结论.(2)试在平面ABC上确定一个P,使DP与平面ABC内任意一条直线都垂直,证明你的结论.(3)如果在折成的三棱锥内有一个小球,求出小球半径的最大值.2.如图,已知正四棱柱ABCD—A1B1C1D1的底面边长为3,侧棱长为4,连结A1B过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E。
(Ⅰ)求证:D1B⊥平面AEC;(Ⅱ)求三棱锥B—AEC的体积;(Ⅲ)求二面角B—AE—C的大小的正弦值.3.如图,正三棱柱ABC—A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.(I)求证:点M为BC的中点;(Ⅱ)求点B到平面AMC1的距离;(Ⅲ)求二面角M—AC1—B 的正切值. 4.如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1,F是CD的中点.(Ⅰ)求证:AF∥平面BCE;(Ⅱ)求多面体ABCDE的体积;(Ⅲ)求二面角C-BE-D 的正切值.5.已知:ABCD是矩形,设PA=a,PA⊥平面ABCD.M、N分别是AB、PC的中点.(Ⅰ)求证:MN⊥AB;(Ⅱ)若PD=AB,且平面MND⊥平面PCD,求二面角P—CD—A的大小;(Ⅲ)在(Ⅱ)的条件下,求三棱锥D—AMN的体积.6.在正方体ABCD—A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点。
(I)求二面角B1—MN—B的正切值;(II)证明:PB⊥平面MNB1;(III)画出一个正方体表面展开图,使其满足“有4个正方形面相连成一个长方形”的条件,并求出展开图中P、B两点间的距离。
理科数学高考立体几何大题精选

理科数学高考立体几何大题精选不建系求解1. 本小题总分值12分〕〔注意:在试题卷上作答无效.........〕如图,四棱锥S-ABCD中,SD底面ABCD,AB//DC,AD DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC平面SBC .〔Ⅰ〕证明:SE=2EB;〔Ⅱ〕求二面角A-DE-C的大小 .2.〔本小题总分值12分〕〔注意:在试题......卷上作答无效〕.......如图,四棱锥中,底面为矩形,底面,,,点M在侧棱上,=60°〔I〕证明:M在侧棱的中点〔II〕求二面角的大小。
3.〔2021年普通高等学校招生统一考试辽宁数学〔理〕试题〔WORD版〕〕如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.(I)求证:(II)4.〔2021年普通高等学校招生统一考试重庆数学〔理〕试题〔含答案〕〕如图,四棱锥中,,,为的中点,.(1)求的长; (2)求二面角的正弦值. 5.〔2021年普通高等学校招生统一考试浙江数学〔理〕试题〔纯WORD 版〕〕如图,在四面体中,平面,.是的中点,是的中点,点在线段上,且.(1)证明:平面;(2)假设二面角的大小为,求的大小.6.〔2021年普通高等学校招生统一考试广东省数学〔理〕卷〔纯WORD 版〕〕如图1,在等腰直角三角形中,,,分别是上的点,,为沿折起,得到如图2所示的四棱锥,其中.(Ⅰ) 证明:平面; (Ⅱ) 求二面角的平面角的余弦值.7.〔2021年高考陕西卷〔理〕〕如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD, .(Ⅰ) 证明: A1C⊥平面BB1D1D;(Ⅱ) 求平面OCB 1与平面BB1D1D的夹角的大小.8.〔2021年高考四川卷〔理〕〕如图,在三棱柱中,侧棱底面,,,分别是线段的中点,是线段的中点.(Ⅰ)在平面内,试作出过点与平面平行的直线,说明理由,并证明直线平面;(Ⅱ)设(Ⅰ)中的直线交于点,交于点,求二面角的余弦值.9.〔2021年普通高等学校招生全国统一招生考试江苏卷〔数学〕〔已校对纯WORD版含附加题〕〕本小题总分值10分.如图,在直三棱柱中,,,,点是的中点(1)求异面直线与所成角的余弦值(2)求平面与所成二面角的正弦值.10.〔2021年普通高等学校招生统一考试大纲版数学〔理〕WORD版含答案〔已校对〕〕如图,四棱锥中,与都是等边三角形.(I)证明: (II)求二面角的大小. 11.〔2021年普通高等学校招生统一考试山东数学〔理〕试题〔含答案〕〕如下图,在三棱锥中,平面,,分别是的中点, ,与交于点,与交于点,连接.(Ⅰ)求证:; (Ⅱ)求二面角的余弦值. 12.〔2021年普通高等学校招生统一考试新课标Ⅱ卷数学〔理〕〔纯WORD版含答案〕〕如图,直棱柱中,分别是的中点,.(Ⅰ)证明:平面; (Ⅱ)求二面角的正弦值. 13.〔2021年高考北京卷〔理〕〕如图,在三棱柱ABC-A1B1C1中,AA1C1C 是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.(Ⅰ)求证:AA1⊥平面ABC;(Ⅱ)求二面角A1-BC1-B1的余弦值;(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求的值.。
2020高考理科数学大题专项练习:立体几何综合问题
大题专项:立体几何综合问题一、解答题1.如图,已知四棱台ABCD-A 1B 1C 1D 1的上、下底面分别是边长为3和6的正方形.A 1A=6,且A 1A ⊥底面ABCD.点P ,Q 分别在棱DD 1,BC 上.(1)若P 是DD 1的中点,证明:AB 1⊥PQ ;(2)若PQ ∥平面ABB 1A 1,二面角P-QD-A 的余弦值为37,求四面体ADPQ 的体积.解:由题设知,AA 1,AB ,AD 两两垂直,以A 为坐标原点,AB ,AD ,AA 1所在直线分别为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系,则相关各点的坐标为A (0,0,0),B 1(3,0,6),D (0,6,0),D 1(0,3,6),Q (6,m ,0),其中m=BQ ,0≤m ≤6.(1)证明:若P 是DD 1的中点,则P (0,92,3),PQ ⃗⃗⃗⃗⃗ =(6,m -92,-3).又AB 1⃗⃗⃗⃗⃗⃗⃗ =(3,0,6),于是AB 1⃗⃗⃗⃗⃗⃗⃗ ·PQ ⃗⃗⃗⃗⃗ =18-18=0, 所以AB 1⃗⃗⃗⃗⃗⃗⃗ ⊥PQ ⃗⃗⃗⃗⃗ ,即AB 1⊥PQ.(2)由题设知,DQ ⃗⃗⃗⃗⃗⃗ =(6,m-6,0),DD 1⃗⃗⃗⃗⃗⃗⃗⃗ =(0,-3,6)是平面PQD 内的两个不共线向量.设n 1=(x ,y ,z )是平面PQD 的一个法向量,则{n 1·DQ ⃗⃗⃗⃗⃗⃗ =0,n 1·DD 1⃗⃗⃗⃗⃗⃗⃗⃗ =0,即{6x +(m -6)y =0,-3y +6z =0. 取y=6,得n 1=(6-m ,6,3).又平面AQD 的一个法向量是n 2=(0,0,1), 所以cos <n 1,n 2>=n 1·n 2|n 1|·|n 2|=1·√(6-m )+62+32=√(6-m )+45.而二面角P-QD-A 的余弦值为37,因此√(6-m )+45=37,解得m=4或m=8(舍去),此时Q (6,4,0).设DP ⃗⃗⃗⃗⃗ =λDD 1⃗⃗⃗⃗⃗⃗⃗⃗ (0<λ≤1),而DD 1⃗⃗⃗⃗⃗⃗⃗⃗ =(0,-3,6),由此得点P (0,6-3λ,6λ),所以PQ ⃗⃗⃗⃗⃗ =(6,3λ-2,-6λ).因为PQ ∥平面ABB 1A 1,且平面ABB 1A 1的一个法向量是n 3=(0,1,0),所以PQ ⃗⃗⃗⃗⃗ ·n 3=0,即3λ-2=0,亦即λ=23,从而P (0,4,4).于是,将四面体ADPQ 视为以△ADQ 为底面的三棱锥P-ADQ ,则其高h=4.故四面体ADPQ 的体积V=13S △ADQ ·h=13×12×6×6×4=24.2.如图,在正三棱柱ABC-A 1B 1C 1中,AB=AA 1=2,点P ,Q 分别为A 1B 1,BC 的中点.(1)求异面直线BP 与AC 1所成角的余弦值; (2)求直线CC 1与平面AQC 1所成角的正弦值.解:如图,在正三棱柱ABC-A 1B 1C 1中,设AC ,A 1C 1的中点分别为O ,O 1,则OB ⊥OC ,OO 1⊥OC ,OO 1⊥OB ,以{OB ⃗⃗⃗⃗⃗ ,OC ⃗⃗⃗⃗⃗ ,OO 1⃗⃗⃗⃗⃗⃗⃗⃗ }为基底,建立空间直角坐标系O-xyz.因为AB=AA 1=2,所以A (0,-1,0),B (√3,0,0),C (0,1,0),A 1(0,-1,2),B 1(√3,0,2),C 1(0,1,2).(1)因为P 为A 1B 1的中点, 所以P (√32,-12,2), 从而BP⃗⃗⃗⃗⃗ =(-√32,-12,2),AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2), 故|cos <BP ⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗⃗ >|=|BP⃗⃗⃗⃗⃗ ·AC 1⃗⃗⃗⃗⃗⃗⃗⃗||BP⃗⃗⃗⃗⃗ ||AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |=√5×2√2=3√1020. 因此,异面直线BP 与AC 1所成角的余弦值为3√1020. (2)因为Q 为BC 的中点,所以Q (√32,12,0),因此AQ ⃗⃗⃗⃗⃗ =(√32,32,0),AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,2),CC 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2).设n =(x ,y ,z )为平面AQC 1的一个法向量,则{AQ ⃗⃗⃗⃗⃗ ·n =0,AC 1⃗⃗⃗⃗⃗⃗⃗ ·n =0,即{√32x +32y =0,2y +2z =0.不妨取n =(√3,-1,1).设直线CC 1与平面AQC 1所成角为θ,则sin θ=|cos <CC 1⃗⃗⃗⃗⃗⃗⃗ ,n >|=|CC 1⃗⃗⃗⃗⃗⃗⃗⃗·n ||CC1⃗⃗⃗⃗⃗⃗⃗⃗ ||n |=√5×2=√55, 所以直线CC 1与平面AQC 1所成角的正弦值为√55.3.已知四棱锥S-ABCD 的底面ABCD 是菱形,∠ABC=π3,SA ⊥底面ABCD ,E 是SC 上的任意一点.(1)求证:平面EBD ⊥平面SAC ;(2)设SA=AB=2,是否存在点E 使平面BED 与平面SAD 所成的锐二面角的大小为30°?如果存在,求出点E 的位置;如果不存在,请说明理由.答案:(1)证明∵SA ⊥平面ABCD ,BD ⊂平面ABCD ,∴SA ⊥BD. ∵四边形ABCD 是菱形,∴AC ⊥BD. ∵AC ∩AS=A , ∴BD ⊥平面SAC. ∵BD ⊂平面EBD ,∴平面EBD ⊥平面SAC.(2)解设AC 与BD 的交点为O ,以OC ,OD 所在直线分别为x 轴、y 轴, 以过O 垂直平面ABCD 的直线为z 轴建立空间直角坐标系(如图). 则点A (-1,0,0),C (1,0,0),S (-1,0,2),B (0,-√3,0),D (0,√3,0).设点E (x ,0,z ),则SE ⃗⃗⃗⃗⃗ =(x+1,0,z-2),EC⃗⃗⃗⃗⃗ =(1-x ,0,-z ),设SE ⃗⃗⃗⃗⃗ =λEC ⃗⃗⃗⃗⃗ ,∴{x =λ-1λ+1,z =2λ+1.∴E (λ-1λ+1,0,2λ+1). ∴DE ⃗⃗⃗⃗⃗ =(λ-1λ+1,-√3,2λ+1),BD⃗⃗⃗⃗⃗⃗ =(0,2√3,0). 设平面BDE 的法向量n =(x 1,y 1,z 1), 可得{n ⊥DE ⃗⃗⃗⃗⃗ ,n ⊥BD ⃗⃗⃗⃗⃗⃗ .∴{n ·DE ⃗⃗⃗⃗⃗ =0,n ·BD ⃗⃗⃗⃗⃗⃗ =0,即{λ-1λ+1x 1-√3y 1+2λ+1z 1=0,2√3y 1=0,令x 1=2,可得z 1=1-λ.故n =(2,0,1-λ)为平面BDE 的一个法向量. 同理可得平面SAD 的一个法向量为m =(√3,-1,0).∵平面BED 与平面SAD 所成的锐二面角的大小为30°,∴cos 30°=|m ·n ||m |·|n |=√3,2√4+(1-λ)=√32,解得λ=1.∴E 为SC 的中点.4.在如图所示的组合体中,ABCD-A 1B 1C 1D 1是一个长方体,P-ABCD 是一个四棱锥.AB=2,BC=3,点P ∈平面CC 1D 1D ,且PD=PC=√2.(1)证明:PD ⊥平面PBC ;(2)求PA 与平面ABCD 所成角的正切值; (3)当AA 1的长为何值时,PC ∥平面AB 1D ? 答案:(1)证明如图,建立空间直角坐标系.设棱长AA 1=a ,则点D (0,0,a ),P (0,1,a+1),B (3,2,a ),C (0,2,a ).于是PD ⃗⃗⃗⃗⃗ =(0,-1,-1),PB ⃗⃗⃗⃗⃗ =(3,1,-1),PC ⃗⃗⃗⃗⃗ =(0,1,-1),所以PD ⃗⃗⃗⃗⃗ ·PB ⃗⃗⃗⃗⃗ =0,PD ⃗⃗⃗⃗⃗ ·PC⃗⃗⃗⃗⃗ =0. 所以PD 垂直于平面PBC 内的两条相交直线PC 和PB ,由线面垂直的判定定理,得PD ⊥平面PBC.(2)解因为点A (3,0,a ),PA⃗⃗⃗⃗⃗ =(3,-1,-1), 而平面ABCD 的一个法向量为n 1=(0,0,1), 所以cos <PA⃗⃗⃗⃗⃗ ,n 1>=√11×1=-√1111.所以PA 与平面ABCD 所成角的正弦值为√1111. 所以PA 与平面ABCD 所成角的正切值为√1010. (3)解因为点D (0,0,a ),B 1(3,2,0),A (3,0,a ), 所以DA ⃗⃗⃗⃗⃗ =(3,0,0),AB 1⃗⃗⃗⃗⃗⃗⃗ =(0,2,-a ).设平面AB 1D 的法向量为n 2=(x ,y ,z ),则有{DA ⃗⃗⃗⃗⃗ ·n 2=3x =0,AB 1⃗⃗⃗⃗⃗⃗⃗ ·n 2=2y -az =0,令z=2,可得平面AB 1D 的一个法向量为n 2=(0,a ,2).若要使得PC ∥平面AB 1D ,则要PC ⃗⃗⃗⃗⃗ ⊥n 2, 即PC⃗⃗⃗⃗⃗ ·n 2=a-2=0,解得a=2. 所以当AA 1=2时,PC ∥平面AB 1D.5.如图,在四棱锥P-ABCD 中,PA ⊥平面ABCD ,AC ⊥AD ,AB ⊥BC ,∠BAC=45°,PA=AD=2,AC=1.(1)证明:PC ⊥AD ;(2)求二面角A-PC-D 的正弦值;(3)设E 为棱PA 上的点,满足异面直线BE 与CD 所成的角为30°,求AE 的长. 解:如图,以点A 为原点建立空间直角坐标系,依题意得点A (0,0,0),D (2,0,0),C (0,1,0),B (-12,12,0),P (0,0,2).(1)证明:易得PC ⃗⃗⃗⃗⃗ =(0,1,-2),AD ⃗⃗⃗⃗⃗ =(2,0,0).于是PC ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ =0,所以PC ⊥AD.(2)PC ⃗⃗⃗⃗⃗ =(0,1,-2),CD ⃗⃗⃗⃗⃗ =(2,-1,0).设平面PCD 的法向量n =(x ,y ,z ). 则{n ·PC⃗⃗⃗⃗⃗ =0,n ·CD ⃗⃗⃗⃗⃗ =0,即{y -2z =0,2x -y =0.不妨令z=1,可得n =(1,2,1).可取平面PAC 的法向量m =(1,0,0). 于是cos <m ,n >=m ·n|m |·|n |=√6=√66, 从而sin <m ,n >=√306. 所以二面角A-PC-D 的正弦值为√306. (3)设点E 的坐标为(0,0,h ),其中h ∈[0,2].由此得BE ⃗⃗⃗⃗⃗ =(12,-12,ℎ).又CD ⃗⃗⃗⃗⃗ =(2,-1,0),故cos <BE ⃗⃗⃗⃗⃗ ,CD ⃗⃗⃗⃗⃗ >=BE⃗⃗⃗⃗⃗ ·CD ⃗⃗⃗⃗⃗ |BE⃗⃗⃗⃗⃗ |·|CD⃗⃗⃗⃗⃗ |=32√12+ℎ2×√5=√10+20ℎ2,所以√10+20ℎ2=cos 30°=√32, 解得h=√1010,即AE=√1010.6.已知四边形ABCD 满足AD ∥BC ,BA=AD=DC=12BC=a ,E 是BC 的中点,将△BAE 沿AE 翻折成△B 1AE ,使平面B 1AE ⊥平面AECD ,F 为B 1D 的中点.(1)求四棱锥B 1-AECD 的体积;(2)证明:B 1E ∥平面ACF ;(3)求平面ADB 1与平面ECB 1所成锐二面角的余弦值.答案:(1)解取AE 的中点M ,连接B 1M.因为BA=AD=DC=12BC=a ,△ABE 为等边三角形,所以B 1M=√32a.又因为平面B 1AE ⊥平面AECD ,所以B 1M ⊥平面AECD ,所以V=13×√32a×a×a×sin π3=a 34.(2)证明连接ED 交AC 于点O ,连接OF ,因为四边形AECD 为菱形,OE=OD ,所以FO ∥B 1E ,所以B 1E ∥平面ACF.(3)解连接MD ,则∠AMD=90°,分别以ME ,MD ,MB 1所在直线为x ,y ,z 轴建立空间直角坐标系,则点E (a2,0,0),C (a ,√32a ,0),A -a2,0,0,D (0,√32a ,0),B 1(0,0,√32a),所以EC⃗⃗⃗⃗⃗ =(a 2,√32a ,0),EB 1⃗⃗⃗⃗⃗⃗⃗ =(-a2,0,√3a2), AD ⃗⃗⃗⃗⃗ =(a 2,√3a 2,0),AB 1⃗⃗⃗⃗⃗⃗⃗ =(a 2,0,√3a2).设平面ECB 1的法向量为u =(x ,y ,z ),则{a2x +√32ay =0,-a2x +√32az =0,令x=1,u =(1,-√33,√33),同理平面ADB 1的法向量为v =(1,-√33,-√33), 所以cos <u ,v >=1+13-13√1+13+13×√1+13+13=35,故平面ADB 1与平面ECB 1所成锐二面角的余弦值为35.。
高考满分数学压轴题14 立体几何的动态问题(可编辑可打印)
一.方法综述立体几何的动态问题是高考的热点,问题中的“不确定性”与“动感性”元素往往成为学生思考与求解问题的思维障碍,使考题的破解更具策略性、挑战性与创新性.一般立体动态问题形成的原因有动点变化、平面图形的翻折、几何体的平移和旋转以及投影与截面问题,由此引发的常见题型为动点轨迹、角度与距离的计算、面积与体积的计算、探索性问题以及有关几何量的最值求解等.动态立体几何题在变化过程中总蕴含着某些不变的因素,因此要认真分析其变化特点,寻找不变的静态因素,从静态因素中,找到解决问题的突破口.求解动态范围的选择、填空题,有时应把这类动态的变化过程充分地展现出来,通过动态思维,观察它的变化规律,找到两个极端位置,即用特殊法求解范围.对于探究存在问题或动态范围(最值)问题,用定性分析比较难或繁时,可以引进参数,把动态问题划归为静态问题.具体地,可通过构建方程、函数或不等式等进行定量计算,以算促证.二.解题策略类型一 立体几何中动态问题中的角度问题例1. 已知平行四边形ABCD 中,1AB =,2AD =,60A ∠=︒,沿对角线BD 将ABD △折起到PBD △的位置,使得平面PBD ⊥平面BCD ,如图,若M ,N 均是线段PD 的三等分点,点Q 是线段MN 上(包含端点)的动点,则二面角Q BC D --的正弦值的取值范围为( )A .12,23⎡⎤⎢⎥⎣⎦B .14192⎡⎢⎣⎦C .24193⎡⎢⎣⎦D .11,32⎡⎤⎢⎥⎣⎦【来源】2021年浙江省新高考测评卷数学(第五模拟) 【答案】B【解析】在ABD △中,1AB =,2AD =,60BAD ∠=︒,所以由余弦定理得3BD =,所以222AB BD AD +=,所以AB BD ⊥,由翻折的性质可知,PB BD ⊥.又平面PBD ⊥平面BCD ,平面PBD 平面BCD BD =,所以PB ⊥平面BCD ,过点Q 作//QQ PB ',交BD 于点Q ',则QQ '⊥平面BCD ,所以QQ BC '⊥,过Q '作Q T BC '⊥,垂足为T ,连接QT ,则BC ⊥平面QQ T ',立体几何的动态问题所以QTQ '∠为二面角Q BC D --的平面角. 设2QD a =(1233a ≤≤),则QQ a '=,3DQ a '=,33BQ a '=-,()113322Q T BQ a ''==-,所以2222211(33)76322QT QQ Q T a a a a ⎡⎤''=+=+-=-+⎢⎥⎣⎦, 所以22222sin 136176373142QQ aQTQ QT a a a aa ''∠====⎛⎫-+-+-+ ⎪⎝⎭. 由二次函数的单调性知,21314y a ⎛⎫=-+ ⎪⎝⎭在12,33⎡⎤⎢⎥⎣⎦上的值域为19,164⎡⎤⎢⎥⎣⎦,所以221419sin ,2191314QTQ a ⎡⎤'∠=∈⎢⎥⎣⎦⎛⎫-+ ⎪⎝⎭,即二面角Q BC D --的正弦的取值范围为1419,219⎡⎤⎢⎥⎣⎦. 故选:B.【举一反三】1.(2020·黑龙江牡丹江一中高三(理))如图,在正方体1111ABCD A B C D -中,O 是AC 中点,点P 在线段11A C 上,若直线OP 与平面11A BC 所成的角为θ,则sin θ的取值范围是( ).A .23⎣⎦B .11,32⎡⎤⎢⎥⎣⎦C .33⎣⎦D .11,43⎡⎤⎢⎥⎣⎦【答案】A【解析】如图,设正方体棱长为1,()11101A PAC λλ=≤≤.以D 为原点,分别以DA ,DC ,1DD 所在直线为x ,y ,z 轴建立空间直角坐标系. 则11,,022O ⎛⎫ ⎪⎝⎭,()1,,1P λλ-,所以11,,122OP λλ⎛⎫=--⎪⎝⎭.在正方体1111ABCD A B C D -中,可证1B D ⊥平面11A BC , 所以()11,1,1B D =---是平面11A BC 的一个法向量.所以122211()()122sin cos ,1113163222OP B D λλθλλλ-----===⎛⎫⎛⎫⎛⎫⨯-+-+-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以当12λ=时,sin θ30λ=或1时,sin θ取得最小值23. 所以23sin 3θ∈⎣⎦.故选A . 2.(2020·广东高考模拟)在正方体1111ABCD A B C D -中,E 是侧面11ADD A 内的动点,且1B E //平面1BDC ,则直线1B E 与直线AB 所成角的正弦值的最小值是( )A .13 B .33 C .12 D .22【答案】B【解析】以D 为原点,DA 为x 轴,DC 为y 轴,1DD 为z 轴,建立空间直角坐标系,设正方体1111ABCD A B C D -中棱长为1, 设E(a,0,c),0a 1≤≤,0c 1≤≤,1B (1,1,1),B(1,1,0), D(0,0,0),1C (0,1,1),()1B E a 1,1,c 1=---,DB (1,=1,0),1DC (0,=1,1),设平面1DBC 的法向量n (x,=y ,z),则1n DB 0n DC 0x y y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,取x 1=,得()n 1,1,1=-,1B E //平面1BDC ,1B E n a 11c 10∴⋅=-++-=,解得a c 1+=,()222a c a c 2ac 12ac ∴+=+-=-,2a c 1ac 24+⎛⎫≤=⎪⎝⎭,设直线1B E 与直线AB 所成角为θ,AB (0,=1,0),()()1221AB B E 1cos θAB B Ea 11c 1⋅∴==⋅-++-2a c 1ac 24+⎛⎫≤= ⎪⎝⎭,322ac 2∴-≥,1222ac 3∴≤-,()()()222211sin θ11a c 2a c 3a 11c 1∴=-=-+-++-++-221123111a c 122ac 33=-=-≥-=++-. ∴直线1B E 与直线AB 所成角的正弦值的最小值是33.3.(2020·浙江台州中学高三)如图,已知正方体ABCD EFGR -的上底面中心为H ,点O 为AH 上的动点,P 为FG 的三等分点(靠近点F ),Q 为EF 的中点,分别记二面角P OQ R --,Q OR P --,R OP Q --的平面角为,,αβγ,则( )A .γαβ<<B .αγβ<<C .αβγ<<D .βαγ<<【答案】D【解析】分析:建立空间直角坐标系,对动点O 选取一个特殊位置,然后求出三个侧面的法向量,根据向量夹角的余弦值求得三个二面角的余弦值,比较后可得二面角的大小.详解:建立如图所示的空间直角坐标系E xyz -.考虑点O 与点A 重合时的情况.设正方体的棱长为1,则()()111,,0,Q ,0,0,R 01,0,O 0,0,132P ⎛⎫⎛⎫⎪⎪⎝⎭⎝⎭. 设平面OPQ 的一个法向量为1(,,)n x y z =,由111(,,)(,0,1)02211(,,)(,,0)02323x n OQ x y z z x y n PQ x y z ⎧⋅=⋅-=-=⎪⎪⎨⎪⋅=⋅--=--=⎪⎩,得322x y x z ⎧=-⎪⎪⎨⎪=⎪⎩,令2x =,得1(2,3,1)n =-.同理可得平面OPR 和平面OQR 的法向量分别为23(2,3,3),(6,3,7)n n ==. 结合图形可得:1323521cos cos ,,cos cos ,7471147n n n n αβ====⨯⨯12cos cos ,711n n γ==⨯∴cos cos cos γαβ<<,又0,,γαβπ<<,∴γαβ>>.故选D . 类型二 立体几何中动态问题中的距离问题【例2】(2020·山西高三)设点M 是棱长为2的正方体ABCD -A 1B 1C 1D 1的棱AD 的中点,点P 在面BCC 1B 1所在的平面内,若平面D 1PM 分别与平面ABCD 和平面BCC 1B 1所成的锐二面角相等,则点P 到点C 1的最短距离是( ) A 25B .22C .1D .63【答案】A【解析】如图,过点P 作1D M 的平行线交BC 于点Q 、交11B C 于点E ,连接MQ ,则PQ 是平面1D PM 与平面11BCC B 的交线,MQ 是平面1D PM 与平面ABCD 的交线.EF 与1BB 平行,交BC 于点F ,过点F 作FG 垂直MQ 于点G ,则有,MQ 与平面EFG 垂直,所以,EG 与MQ 垂直,即角EGF 是平面1D PM 与平面ABCD 的夹角的平面角,且sin EFEGF EG∠=, MN 与CD 平行交BC 于点N ,过点N 作NH 垂直EQ 于点H ,同上有:sin MNMHN MH∠=,且有EGF MHN ∠=∠,又因为EF MN AB ==,故EG MH =, 而2EMQ S EG MQ MH EQ ∆=⨯=⨯,故MQ EQ =,而四边形1EQMD 一定是平行四边形,故它还是菱形,即点E 一定是11B C 的中点, 点P 到点1C 的最短距离是点1C 到直线BE 的距离,以A 为原点,AB 为x 轴,AD 为y 轴,1AA 为z 轴,建立空间直角坐标系,()2,1,2E ,()2,0,0B , ()12,2,2C ,()0,1,2BE =, ()10,2,2BC =,∴点P 到点1C 的最短距离:22111||625||1()221()5||||58BE BC d BC BE BC =-=⨯-=⨯.故选:A .【指点迷津】求两点间的距离或其最值.一种方法,可建立坐标系,设点的坐标,用两点间距离公式写出距离,转化为求函数的最值问题;另一种方法,几何法,根据几何图形的特点,寻找那两点间的距离最大(小),求其值. 【举一反三】1.(2020·四川高三(理))已知三棱锥S ABC -中,1SA SB SC ===,且SA 、SB 、SC 两两垂直,P 是三棱锥S ABC -外接球面上一动点,则P 到平面ABC 的距离的最大值是( )A .33B .3C .233D .433【答案】C 【解析】【分析】,,SA SB SC 是棱长为1的正方体MNQB ADCS -上具有公共顶点S 的三条棱,以B 为原点,,,BM BQ BS 分别为x 轴,y 轴,z 轴,建立空间直角坐标系,三棱锥S ABC -外接球就是正方体MNQB ADCS -的外接球,由正方体及球的几何性质可得点P 与N 重合时,点P 到平面ABC 的距离最大,求出平面ABC 的法向量,由点到直线的距离公式即可得结果. 【详解】三棱锥S ABC -,满足,,SA SB SC 两两垂直,且,,1SA SB SC =,∴如图,,SA SB SC 是棱长为1的正方体MNQB ADCS -上具有公共顶点S 的三条棱,以B 为原点,,,BM BQ BS 分别为x 轴,y 轴,z 轴,建立空间直角坐标系, 则()()()()()0,0,0,1,0,1,0,1,1,0,0,1,1,1,0B A C S N ,()()()1,0,1,0,1,1,1,1,0BA BC BN ===,设平面ABC 的法向量(),,n x y z =,则00n BA x z n BC y z ⎧⋅=+=⎨⋅=+=⎩,取1x =,得()1,1,1n =-,三棱锥S ABC -外接球就是棱长为1的正方体MNQB ADCS -的外接球,P 是三棱锥S ABC -外接球上一动点,∴由正方体与球的几何性质可得,点P 点与N 重合时,点P 到平面ABC 的距离最大,∴点P 到平面ABC 的距离的最大值为1102333BN n d n⋅++===.故选C. 2.已知四边形ABCD 是边长为5的菱形,对角线8BD =(如图1),现以AC 为折痕将菱形折起,使点B 达到点P 的位置.棱AC ,PD 的中点分别为E ,F ,且四面体PACD 的外接球球心落在四面体内部(不含边界,如图2),则线段EF 长度的取值范围为( )A .14,42⎛⎫ ⎪ ⎪⎝⎭B .141,2⎛⎫⎪ ⎪⎝⎭C .14,62⎛⎫⎪ ⎪⎝⎭D .()3,4【来源】江西省鹰潭市2021届高三高考二模数学(文)试题 【答案】A 【解析】由题意可知△APC 的外心1O 在中线PE 上, 设过点1O 的直线1l ⊥平面APC ,可知1l ⊂平面PED , 同理△ADC 的外心2O 在中线DE 上,设过点2O 的直线2l ⊥平面ADC ,则2l ⊂平面PED , 由对称性知直线12,l l 的交点O 在直线EF 上.根据外接球的性质,点O 为四面体PACD 的外接球的球心. 由题意得3,4EA PE ==,而2221111,4O A O E EA O A O E PE =++==所以178O E =. 令PEF θ∠=,显然02πθ<<,所以cos 4cos 4EF PE θθ==<. 因为1cos EF O EPE OEθ==, 所以172OE EF O E PE ⋅=⋅=, 又OE EF <,所以272EF >,即142EF >. 综上可知1442EF <<. 故选:A.3(2020广西柳州市模考)如图,在正方体中,棱长为1,点为线段上的动点(包含线段端点),则下列结论错误的是( )A .当时,平面B .当为中点时,四棱锥的外接球表面为C .的最小值为D .当时,平面【答案】C【解析】对于,连结,,,则,,,设到平面的距离为,则,解得,∴.∴当时,为与平面的交点.∵平面∥平面, ∵平面,∴∥平面,故A 正确. 又由以上分析可得,当时,即为三棱锥的高,∴平面,所以D 正确. 对于B ,当为中点时,四棱锥为正四棱锥, 设平面的中心为,四棱锥的外接球为,所以,解得,故四棱锥的外接球表面积为,所以B 正确.对于C ,连结,,则, ∴,由等面积法得的最小值为,∴的最小值为.所以C 不正确.故选:C.类型三 立体几何中动态问题中的面积、体积问题【例3】(2020·河南高三(理))在棱长为3的正方体1111ABCD A B C D -中,E 是1AA 的中点,P 是底面ABCD 所在平面内一动点,设1PD ,PE 与底面ABCD 所成的角分别为12θθ,(12θθ,均不为0),若12θθ=,则三棱锥11P BB C -体积的最小值是( ) A .92B .52C .32D .54【答案】C【解析】建系如图,正方体的边长为3,则(3E ,0,3)2,1(0D ,0,3),设(P x ,y ,0)(0x ,0)y ,则(3PE x =-,y -,3)2,1(PD x =-,y -,3),12θθ=,(0z =,0,1),12cos cos θθ∴=,即11||||||||||||PD z PE z PE z PD z =,代入数据,得:222233299(3)4x y x y =++-++,整理得:228120x y x +-+=,变形,得:22(4)4(02)x y y -+=, 即动点P 的轨迹为圆的一部分,过点P 作PF BC ⊥,交BC 于点F ,则PF 为三棱锥11P BB C -的高∴点P 到直线AD 的距离的最大值是2.则min 321PF =-=.1111119332212BB C BB B C S ∆=⋅⋅=⨯⨯=,1111193132213P BB C BB C V PF S -∆=⨯⨯⋅⋅=∴=故选:C .【指点迷津】求几何体体积的最值,先观察几何图形三棱锥,其底面的面积为不变的几何量,求点P到平面BCD 的距离的最大值,选择公式,可求最值. 【举一反三】1.(2020·四川高三期末)长方体1111ABCD A B C D -中,2AB =,1BC =,12AA =,P 为该正方体侧面11CC D D 内(含边界)的动点,且满足tan tan 22PAD PBC ∠+∠=.则四棱锥P ABCD -体积的取值范围是( ) A .20,3⎛⎤ ⎥⎝⎦B .22,33⎡⎤⎢⎥⎣⎦ C .40,3⎛⎤ ⎥⎝⎦D .24,33⎡⎤⎢⎥⎣⎦ 【答案】B【解析】如图所示:在RT PAD 中,tan PD PAD PD AD ∠==,在RT PBC 中,tan PCPBC PC BC∠==, 因为tan tan 22PAD PBC ∠+∠=,所以22PD PC +=.因为222PD PC CD +=>=,所以点P 的轨迹是以,C D 为焦点 222a =的椭圆. 如下图所示:2a =1c =,211b =-=,椭圆的标准方程为:2212x y +=.1(0,1)P联立22112x x y =⎧⎪⎨+=⎪⎩,解得:2y =.所以22()P -,32P . 当点P 运动到1P 位置时,此时四棱锥P ABCD -的高最长, 所以max 1112()21333P ABCD ABCD V S PO -=⨯⨯=⨯⨯=. 当点P 运动到2P 或3P 位置时,此时四棱锥P ABCD -的高最短,所以min 21122()23323P ABCD ABCD V S P D -=⨯⨯=⨯⨯=. 综上所述:2233P ABCD V -≤≤. 2.如图,长方形ABCD 中,152AB =,1AD =,点E 在线段AB (端点除外)上,现将ADE 沿DE 折起为A DE '.设ADE α∠=,二面角A DE C '--的大小为β,若π2αβ+=,则四棱锥A BCDE '-体积的最大值为( )A .14 B .23 C 151-D 51- 【答案】A【解析】设过A 与DE 垂直的线段长为a ,则tan AE α=,150tan 2α<<,1cos DE α=,sin a α=,则四棱锥A BCDE '-的高πsin sin sin sin cos 2h a βαααα⎛⎫=⋅=⋅-=⎪⎝⎭, 则111515tan 1sin cos 3222A BCDE V ααα'-⎛=⨯⨯-+⨯⨯ ⎝⎭)115tan sin cos 6ααα=⨯ )2115cos sin 6ααα=- )11152cos 21212αα=+- 115112cos 234412αα⎛⎫=+- ⎪ ⎪⎝⎭()11sin 2312αϕ=+-,15tan 15ϕ⎛⎫= ⎪ ⎪⎝⎭, ∴四棱锥A BCDE '-体积的最大值为1113124-=. 故选:A.3.(2020·重庆市松树桥中学校高三)如图,在单位正方体1111ABCD A B C D -中,点P 在线段1AD 上运动,给出以下四个命题:①异面直线1A P 与1BC 间的距离为定值;②三棱锥1D BPC -的体积为定值;③异面直线1C P 与直线1CB 所成的角为定值; ④二面角1P BC D --的大小为定值.其中真命题有( ) A .1个 B .2个 C .3个 D .4个【答案】D【解析】对于①,异面直线1A P 与1BC 间的距离即为两平行平面11ADD A 和平面11BCC B 间的距离,即为正方体的棱长,为定值.故①正确.对于②,由于11D BPC P DBC V V --=,而1DBC S ∆为定值,又P ∈AD 1,AD 1∥平面BDC 1,所以点P 到该平面的距离即为正方体的棱长,所以三棱锥1D BPC -的体积为定值.故②正确.对于③,由题意得在正方体1111ABCD A B C D -中,B 1C ⊥平面ABC 1D 1,而C 1P ⊂平面ABC 1D 1,所以B 1C ⊥C 1P ,故这两条异面直线所成的角为90︒.故③正确;对于④,因为二面角P −BC 1−D 的大小,即为平面ABC 1D 1与平面BDC 1所成的二面角的大小,而这两个平面位置固定不变,故二面角1P BC D --的大小为定值.故④正确.综上①②③④正确.选D .类型四 立体几何中动态问题中的轨迹问题【例4】(2020南充高考一模)如图,直二面角AB αβ--,P α∈,C β∈,D β∈,且AD AB ⊥,BC AB ⊥,5AD =,10BC =,6AB =,APD CPB ∠=∠,则点P 在平面α内的轨迹是( )A.圆的一部分B.椭圆的一部分C.一条直线D.两条直线【答案】A【解析】以AB 所在直线为x 轴,AB 的中垂线为y 轴,建立平面直角坐标系,设点(),P x y ,()30A -,,()3,0B ,AD AB ⊥,BC AB ⊥,则AD α⊥,BC α⊥,5AD =,10BC =,6AB =,APD CPB ∠=∠,Rt APDRt CPB∴∆∆,()()22223511023x y APAD BPBC x y ++∴====-+ ,即()()2222343x y x y ⎡⎤-+=++⎣⎦,整理得:()22516x y ++=,故点P 的轨迹是圆的一部分,故选A .【指点迷津】空间轨迹问题的求解策略:1.利用侧面展开或展到一个平面上寻求轨迹;2.利用圆锥曲线定义求轨迹;3.这辗转过程中动点的轨迹;4.利用函数观点探求轨迹 【举一反三】1.已知正方体1111ABCD A B C D -的棱长为23M ,N 为体对角线1BD 的三等分点,动点P 在三角形1ACB 内,且三角形PMN 的面积63PMN S =△P 的轨迹长度为( )A .269π B .263π C .469π D .463π 【答案】B【解析】如图所示:连接11BC B C O =,因为四边形11BCC B 是正方形,所以11BC B C ⊥,因为11D C ⊥平面11BCC B ,1B C ⊂平面11BCC B ,所以11D C ⊥1B C , 又11111,BC D C C BC =⊂平面11BC D ,11D C ⊂平面11BC D ,所以1B C ⊥平面11BC D ,所以11B C D B ⊥, 同理可知:11B A D B ⊥,又因为1B C ⊂平面1ACB ,1B A ⊂平面1ACB ,111B C B A B =,所以1D B ⊥平面1ACB ,根据题意可知:11136,26D B AB AB BC AC =====所以1ACB 为正三角形,所以160∠=︒B AC ,所以11326266322ACB S=⨯⨯⨯=,设B 到平面1ACB 的距离为h , 因为11B ACB B ABC V V --=,所以111133ACB ACBSh S BB ⋅⋅=⋅⋅,所以11ACB ACBSh SBB ⋅=⋅,所以()232323262342h ⨯⨯⨯=⨯,所以1123h D B ==,所以h BN =, 所以N 即为1D B 与平面1ACB 的交点,由题意可知:1D B ⊥平面1ACB ,所以MN PN ⊥,所以11262223PMNSMN PN PN PN =⋅=⋅⋅==,再如下图所示:在正三角形1ACB 中,高3sin 6026322AO AC =︒== 所以内切圆的半径16233r AO ==<,且623AN <=,取1B C 的两个三等分点,E F ,连接,EN FN ,所以1//,//NE AB NF AC ,所以NEF 是以PN 长度为边长的正三角形,所以P 的轨迹是以N 为圆心,半径等于263的圆,圆的周46π,在1ACB 内部的轨迹是三段圆弧,每一段圆弧的圆心角为60︒,所以对应的轨迹长度是圆周长的一半为63π,故选:B. 2、(2020贵阳高考模拟)在正方体1111ABCD A B C D -中,已知点P 为平面11AA D D 中的一个动点,且点P 满足:直线1PC 与平面11AA D D 所成的角的大小等于平面PBC 与平面11AA D D 所成锐二面角的大小,则点P 的轨迹为( )A .直线B .椭圆C .圆D .抛物线 【答案】DF E P C 1B 1D 1A 1DCBA z yx3.几何中常用表示L 的测度,当L 为曲线、平面图形和空间几何体时,L 分别对应其长度、面积和体积.在ABC 中,3AB =,4BC =,5AC =,P 为ABC 内部一动点(含边界),在空间中,到点P 的距离为1的点的轨迹为L ,则L 等于( ) A .612π+B .2263π+ C .20123π+ D .22123π+ 【来源】安徽省合肥市2021届高三下学期第三次教学质量检测理科数学试题 【答案】D【解析】空间中,到点P 的距离为1的点的轨迹所构成的空间几何体在垂直于平面ABC 的角度看,如下图所示:其中:BCDF ,ACEI 和ABGH 区域内的几何体为底面半径为1的半圆柱;CDE ,BFG ,AHI 区域内的几何体为被两平面所截得的部分球体,球心分别为,,C B A ;ABC 区域内的几何体是高为2的直三棱柱. 四边形BCDF 和ACEI 为矩形,2DCB ECA π∴∠=∠=,2DCE ACB ACB πππ∴∠=--∠=-∠,同理可得:FBG ABC π∠=-∠,HAI CAB π∠=-∠,()332DCE FBG HAI ACB ABC CAB ππππ∴∠+∠+∠=-∠+∠+∠=-=,∴CDE ,BFG ,AHI 区域内的几何体合成一个完整的,半径为1的球,则CDE ,BFG ,AHI 区域内的几何体的体积之和3144133V ππ=⨯=; 又BCDF ,ACEI 和ABGH 区域内的几何体的体积之和()221134562V ππ=⨯⨯++=;ABC 区域内的直三棱柱体积31342122V =⨯⨯⨯=,4226121233L πππ∴=++=+.故选:D.三.强化训练1.(2020·内蒙古高三期末)如图,棱长为1的正方体1111ABCD A B C D -中,M 是线段1A B 上的动点,则下列结论正确的是( ).①异面直线AD 与1CB 所成的角为45︒②11DC D M ⊥③三棱锥1M DCC -的体积为定值 ④1AM MD +的最小值为2. A .①②③ B .①②④C .③④D .②③④【答案】A【解析】①∵AD ∥BC ,∴异面直线AD 与1CB 所成的角即为BC 与1CB 所成的角, 可得夹角为45︒,故①正确;②连接1CD ,∵1DC ⊥平面A 1BCD 1,1D M ⊂平面A 1BCD 1, ∴11DC D M ⊥,故②正确;③∵1A B ∥平面DCC 1D 1,∴线段A 1B 上的点M 到平面DCC 1D 1的距离都为1, 又△DCC 1的面积为定值12, 因此三棱锥M −DCC 1的体积1111326V =⨯⨯=为定值,故③正确; ④将面AA 1B 与面A 1BCD 1沿A 1B 展成平面图形,线段AD 1即为AP +PD 1的最小值, 在△D 1A 1A 中,∠D 1A 1A =135°, 利用余弦定理解三角形得111211135222AD cos =+-⨯⨯⨯︒=+<,故④不正确.因此只有①②③正确.故选:A .2.(2020河南省焦作市高三)在棱长为4的正方体ABCD ﹣A 1B 1C 1D 1中,点E 、F 分别在棱AA 1和AB 上,且C 1E ⊥EF ,则|AF|的最大值为( )A .B .1C .D .2【答案】B【解析】以AB ,AD ,AA 1所在直线为x ,y ,z 轴,建立空间直角坐标系如图所示,则C 1(4,4,4),设E (0,0,z ),z ∈[0,4],F (x ,0,0),x ∈[0,4],则|AF|=x .=(4,4,4﹣z ),=(x ,0,﹣z ).因为C 1E ⊥EF ,所以,即:z 2+4x ﹣4z =0,x =z ﹣.当z =2时,x 取得最大值为1.|AF|的最大值为1.故选:B .3.(2020·重庆巴蜀中学高三(理))棱长为2的正方体1111ABCD A B C D -中,N 为1CC 的中点,P 在底面ABCD 内运动,1D P 与平面ABCD 所成角为1θ,NP 与平面ABCD 所成角为2θ,若12θθ=,则AP 的最小值为( ) A .2 B .83C .4D .1【答案】A【解析】分析:先证明PD=2PC ,再在底面ABCD 内建立如图所示的直角坐标系,求出211680sin()99PA αϕ=-+,再利用三角函数的图象和性质求出|AP|的最小值. 【详解】设12θθθ==,所以12tan tan DD PD θθ==,1PC tan tan CN θθ==,所以PD=2PC. 在底面ABCD 内建立如图所示的直角坐标系,设点P(x,y),则2222(1)2(+1)x y x y -+=+整理得22516454(),cos ,sin 39333x y x y αα++=∴=-=, 所以2224841168011680(cos )(sin 2)sin()43339999PA αααϕ=-+-=-+≥-=, 即||2AP ≥,所以|AP|的最小值为2.故选:A4.已知三棱锥A BCD -的所有棱长均为2,E 为BD 的中点,空间中的动点P 满足PA PE ⊥,PC AB ⊥,则动点P 的轨迹长度为( ) A .1116πB 3πC 11πD 3π【来源】浙江省五校2021届高三下学期5月联考数学试题 【答案】C【解析】正四面体A BCD -2,建立空间直角坐标系如图所示,()()22,,2,2,2,0,0,2,222E C B ⎛⎫ ⎪ ⎪⎝⎭,设(),,P x y z ,()22,,2,,,22PE x y z AP x y z ⎛⎫=---= ⎪ ⎪⎝⎭,()2,2,PC x y z =---.由于PA PE ⊥,PC AB ⊥,所以00AP PE PC AB ⎧⋅=⎨⋅=⎩,即()()2220222220x x y y z z y z ⎧⎛⎫⎛⎫-+-+-=⎪ ⎪ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎨⎪--=⎪⎩,即22222202220x x y y z z y z ⎧-+-+-=⎪⎨⎪+-=⎩, 即2222223442420x y z y z ⎧⎛⎫⎛⎫⎛⎫⎪-+-+-= ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎨⎝⎭⎝⎭⎝⎭⎪+-=⎪⎩, 22222234424x y z ⎛⎫⎛⎫⎛⎫-+-+-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭表示球心为222,,442⎛⎫ ⎪ ⎪⎝⎭,半径为32R =的球. 20y z +-=表示垂直于yAz 平面的一个平面.所以P 的轨迹是上述平面截球面所得圆.球心222,,442⎛⎫ ⎪ ⎪⎝⎭到平面20y z +-=的距离为22222142411d +-==+, 所以截得的圆的半径2231114164r R d =-=-=, 所以截得的圆,也即P 点的轨迹的长度为11112242r πππ=⨯=. 故选:C5.(2020郑州一中高三期末)在三棱锥中,平面,M是线段上一动点,线段长度最小值为,则三棱锥的外接球的表面积是()A.B.C.D.【答案】C【解析】如图所示:三棱锥中,平面,M是线段上一动点,线段长度最小值为,则:当时,线段达到最小值,由于:平面,所以:,解得:,所以:,则:,由于:,所以:则:为等腰三角形.所以:,在中,设外接圆的直径为,则:,所以:外接球的半径,则:,故选:C.(2020九江高三一模)在长方体中,,,分别是棱6.的中点,是底面内一动点,若直线与平面没有公共点,则三角形面积的最小值为()A.B.C.D.【答案】C【解析】补全截面EFG为截面EFGHQR如图,其中H 、Q 、R 分别为、的中点,易证平面ACD 1∥平面EFGHQR ,∵直线D 1P 与平面EFG 不存在公共点, ∴D 1P∥面ACD 1,∴D 1P 面ACD 1,∴P ∈AC ,∴过P 作AC 的垂线,垂足为K ,则BK=,此时BP 最短,△PBB 1的面积最小, ∴三角形面积的最小值为,故选:C .7.(2020·浙江高三期末)在三棱锥P ABC -中,2,3PA PB PC AB AC BC ======,点Q 为ABC ∆ 所在平面内的动点,若PQ 与PA 所成角为定值θ,π(0,)4θ∈,则动点Q 的轨迹是 A .圆 B .椭圆C .双曲线D .抛物线【答案】B【解析】建立空间直角坐标系,根据题意,求出Q 轨迹方程,可得其轨迹.由题,三棱锥P ABC -为正三棱锥,顶点P 在底面ABC 的射影O 是底面三角形ABC 的中心,则以O 为坐标原点,以OA 为x 轴,以OP 为z 轴,建立如图所示的空间直角坐标系,根据题意可得1OA OP ==,设Q 为平面ABC 内任 一点,则()()()()()1,0,0,0,0,1,,,0,1,0,1,,,1A P Q x y PA PQ x y =-=- ,由题PQ 与PA 所成角为定值θ,π0,4θ⎛⎫∈ ⎪⎝⎭,则,221cos 21PA PQ x PA PQ x y θ⋅+==⋅++则()()22222cos11x y x θ++=+ ,化简得222cos22cos 2cos20x y x θθθ⋅+⋅-+= ,ππ0,,20,,cos 20,42θθθ⎛⎫⎛⎫∈∴∈> ⎪ ⎪⎝⎭⎝⎭故动点Q 的轨迹是椭圆.选B8.(2020·上海格致中学高三月考)在正方体''''ABCD A B C D -中,若点P (异于点B )是棱上一点,则满足BP 与AC '所成的角为45︒的点P 的个数为( )A .0B .3C .4D .6【答案】B 【解析】【分析】建立空间直角坐标系,通过分类讨论利用异面直线的方向向量所成的夹角即可找出所有满足条件的点P 的个数.【详解】建立如图所示的空间直角坐标系,不妨设棱长1AB =,(1B ,0,1),(1C ,1,1). ①在Rt △AA C ''中,||tan 2||A C A AC AA '''∠'=='45A AC '∠'≠︒.同理AB ,AD 与AC '所成的角都为arctan 245≠︒.故当点P 位于(分别与上述棱平行或重合)棱BB ',BA ,BC 上时,与AC '所成的角都为arctan 245≠︒,不满足条件;②当点P 位于棱AD 上时,设(0P ,y ,1),(01)y ,则(1BP =-,y ,0),(1AC '=,1,1)-.若满足BP 与AC '所成的角为45︒,则22|||1||cos ,|2||||13BP AC y BP AC BP AC y '-+=<'>=='+, 化为2410y y ++=,无正数解,舍去; 同理,当点P 位于棱A D ''上时,也不符合条件; ③当点P 位于棱B C ''上时,设(1P ,y ,0),(01)y , 则(0BP =,y ,1)-,(1AC '=,1,1)-.若满足BP 与AC '所成的角为45︒,则22|||1||cos ,|2||||13BP AC y BP AC BP AC y '+=<'>=='+, 化为2410y y -+=,01y ,解得23y =-,满足条件,此时点(1,23,0)P -.④同理可求得棱C D ''上一点(532,1,0)P -,棱C C '上一点(1,1,324)P -. 而其它棱上没有满足条件的点P .综上可知:满足条件的点P 有且只有3个.故选:B 9.(2020上海交通大学附属中学高三)如图,已知三棱锥,平面,是棱上的动点,记与平面所成的角为,与直线所成的角为,则与的大小关系为( )A .B .C .D .不能确定【答案】C【解析】如图所示:∵PA ⊥平面ABC ,∴PD 与平面ABC 所成的角=∠PDA, 过点A 作AE ⊥BC ,垂足为E ,连接PE ,∵PA ⊥平面ABC ,∴PA ⊥BC ,∴BC⊥平面PAE ,∴BC⊥PE,在Rt△AED ,Rt△PAD ,Rt△PED 中:cos ,cos ,cos,∴coscoscos < cos ,又均为锐角, ∴,故选C.10.(2020·湖南长郡中学高三(理))在三棱锥P ABC -中,PA ⊥平面ABC ,23BAC π∠=,3AP =,23AB =,Q 是边BC 上的一动点,且直线PQ 与平面ABC 所成角的最大值为3π,则三棱锥P ABC -的外接球的表面积为( ) A .45π B .57πC .63πD .84π【答案】B【解析】分析:根据题意画出图形,结合图形找出ABC △的外接圆圆心与三棱锥P ABC - 外接球的球心,求出外接球的半径,再计算它的表面积.详解:三棱锥P ABC PA ABC 中,平面,-⊥ 设直线PQ 与平面ABC 所成角为θ ,如图所示;则3PAsinPQ PQ ,θ== 由题意且θ的最大值是3π3PQ=,,解得PQ =即PQ 的最小值为∴AQ ,即点A 到BC ,AQ BC ∴⊥,AB BC ∴== 6BC ;∴= 取ABC △的外接圆圆心为O ',作OO PA ' ,62120r sin ∴=︒,解得r =;O A ∴'=M 为PA 的中点,32OM O A PM ∴='==,由勾股定理得CP R === ∴三棱锥P ABC -的外接球的表面积是224457S R πππ==⨯⨯=.故选B.11.在直三棱柱111ABC A B C -中,底面ABC 是以B 为直角的等腰三角形,且3AB =,1AA =若点D 为棱1AA 的中点,点M 为面BCD 的一动点,则11 B M C M +的最小值为( )A .B .6C . D【来源】江西省赣州市2021届高三二模数学(理)试题 【答案】C【解析】由题意知,BC AB ⊥,111ABC A B C -为直三棱柱,即面ABC ⊥面11ABB A ,面ABC面11ABB A AB =,BC ⊂面ABC ,∴BC ⊥面11ABB A ,又BC ⊂面BCD , ∴面BCD ⊥面11ABB A .∴易得1B 关于平面BCD 对称点E 落在1A A 的延长线上,且AE =1A E =11 B M C M +的最小时,1C 、M 、E 三点共线.∴221111111||992735B M C M EM C M EC AC A E +=+≥=+=++=. 故选:C12.在棱长为2的正四面体ABCD 中,点P 为ABC 所在平面内一动点,且满足433PA PB +=,则PD 的最大值为( ) A .3B .2103C .393D .2【来源】河南省鹤壁市2021届高三一模数学(文)试题 【答案】B【解析】如图所示,在平面ABC 内,4323PA PB +=>, 所以点P 在平面ABC 内的轨迹为椭圆,取AB 的中点为点O ,连接CO ,以直线AB 为x 轴,直线OC 为y 建立如下图所示的空间直角坐标系O xyz -,则椭圆的半焦距1c =,长半轴a =b ==所以,椭圆方程为()2233104x y z +==.点D 在底面的投影设为点E ,则点E 为ABC 的中心,11333OE OC ===, 故点E 正好为椭圆短轴的一个端点,23CE OC ==,则DE ==, 因为222PD DE EP =+,故只需计算EP 的最大值.设(),,0P x y ,则E ⎛⎫⎪ ⎪⎝⎭,则22222241543333EP x y y y y y y ⎛=+=-++=--+ ⎝⎭,当y ⎡=⎢⎣⎦时,2EP 取最大值,即22max516393939EP ⎛⎛=-⨯---+= ⎝⎭⎝⎭,因此可得2241640999PD ≤+=,故PD . 故选:B.13.在棱长为1的正方体1111ABCD A B C D -中,P 是线段1BC 上的点,过1A 的平面α与直线PD 垂直,当P 在线段1BC 上运动时,平面α截正方体1111ABCD A B C D -所得的截面面积的最小值是( )A .1B .54C D【来源】北京市朝阳区2021届高三一模数学试题 【答案】C【解析】以点A 为坐标原点,AB 、AD 、1AA 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则()0,0,0A 、()10,0,1A 、()1,0,0B 、()11,0,1B 、()1,1,0C 、()11,1,1C 、()0,1,0D 、()10,1,1D , 设点()1,,P t t ,其中01t ≤≤.①当0t =时,点P 与点B 重合,()1,1,0BD =-,()1,1,0AC =,()10,0,1AA =, 所以,0BD AC ⋅=,10BD AA ⋅=,则BD AC ⊥,1BD AA ⊥, 1AC AA A ⋂=,BD ∴⊥平面11AAC C ,此时平面α即为平面11AAC C ,截面面积为12S AA AC =⋅= ②当1t =时,同①可知截面面积为2S =③当01t <<时,()1,1,DP t t =-,()11,1,1AC =-, 1110DP AC t t ⋅=+--=,1A C PD ∴⊥,则1A C α⊂, 设平面α交棱1DD 于点()0,1,E z ,()1,0,CE z =-,10DP CE tz ⋅=-+=,可得11z t=>,不合乎题意. 设平面α交棱AB 于点(),0,0M x ,()1,1,0CM x =--,()110DP CM x t ⋅=---=,可得x t =,合乎题意,即(),0,0M t ,同理可知,平面α交棱11C D 于点()1,1,1N t -,()11,1,0A N t MC =-=,且1A N 与MC 不重合,故四边形1A MCN 为平行四边形,()11,1,1AC =-,()11,1,0A N t =-,1112112cos 322AC A N t CA N AC A N t t ⋅-∠==⋅⋅-+,则()()2211221sin 1cos 322t t CA N CA N t t -+∠=-∠=-+,所以,截面面积为()1221111362sin 2122242CA NS S AC A N CA N t t t ⎡⎤⎛⎫==⋅∠=-+=-+=<⎢⎥ ⎪⎝⎭⎢⎥⎣⎦△. 综上所述,截面面积的最小值为62. 故选:C.14.如图,斜线段AB 与平面α所成的角为π4,B 为斜足.平面α上的动点P 满足π6PAB ∠=,则点P 的轨迹为( )A .圆B .椭圆C .双曲线的一部分D .抛物线的一部分【答案】B【解析】建立如图所示的空间直角坐标系,设(0,1,0),(0,0,1),(,,0)(0,1,1),(,,1)B A P x y AB AP x y ⇒=-=-22223cos ,62(2)1121AB AP x y x y ⇒<>=⇒+-=⋅++ 所以点P 的轨迹是椭圆. 故选:B.15.已知正方体ABCD A B C D ''''-的棱长为1,点M ,N 分别为线段AB ',AC 上的动点,点T 在平面BCC B ''内,则MT NT +的最小值是( )A .2B .233C .62D .1【答案】B【解析】A 点关于BC 的对称点为E ,M 关于BB '的对称点为M ', 记d 为直线EB '与AC 之间的距离,则MT NT M T NT M N d ''+=+≥≥, 由//B E D C '',d 为E 到平面ACD '的距离, 因为111111333D ACE ACEV S '-=⨯⨯==⨯⨯=,而()21332346D ACE E ACD V V d d ''--==⨯⨯⨯=,故233d =, 故选:B.16.如图,ABC 是等腰直角三角形,AB AC =,点D 是AB 上靠近A 的三等分点,点E 是AC 上靠近C 的三等分点,沿直线DE 将ADE 翻折成A DE ',所成二面角A DE B '--的平面角为α,则( )A .A DB A EC α∠≥∠'≥' B .A EC A DB α∠≥∠'≥' C .A DB A EC α≥∠'∠≥'D .A EC A DB α≥∠'∠≥'【答案】B【详解】如图,在等腰直角三角形中,过B 作直线//l DE ,作BM ED ⊥交直线DE 于点M ,过C 作直线DE 的垂线,垂足为R ,交直线l 与T ,过A 作DE 的垂线,垂足为O ,且交l 于N ,不妨设3AB =,则1,2AD CE BD AE ====, 在直角三角形ADE 中,255AO ==, 因为BMD AOD ,故12AO AD BM BD ==,故455BM =,同理52522155DM DO ==⨯⨯= 所以45ON =,35BN OM ==,同理5RC OS ==65NT =.在几何体中连接,,A B A S A C ''',如图,因为,,A O DE NO DE '⊥⊥故NOA '∠为二面角A DE B '--的平面角,故NOA α'∠=,而A O NO O '⋂=,故DE ⊥平面AON ',所以TB ⊥平面AON ',而A N '⊂平面AON ',故BN A N '⊥.24162545162cos 4cos 55555A N αα'=+-⨯=-, 故216929164cos cos 5555A B αα'=-+=-,故29165cos 4155cos cos 21255A DB αα-+'∠==-⨯⨯, 同理14cos cos 55A EC α'∠=-,11cos cos cos 055A DB αα'∠-=--<,故cos cos A DB α'∠<,同理cos cos A EC α'∠<,33cos cos cos 055A DB A EC α''∠-∠=+>,故cos cos A DB A EC ''∠>∠,因为(),,0,A DB A EC απ''∠∠∈,故A EC A DB α''∠>∠>, 故选B.17.如图,棱长为2的长方体1111ABCD A B C D -中,P 为线段11B D 上动点(包括端点).则以下结论正确的为( )A .三棱锥1P A BD -中,点P 到面1A BD 2B .过点P 平行于面1A BD 的平面被正方体1111ABCD A BCD -3C .直线1PA 与面1A BD 所成角的正弦值的范围为36⎣⎦D .当点P 和1B 重合时,三棱锥1P A BD -3【来源】广东省普宁市2020-2021学年高三上学期期末数学试题 【答案】C【解析】对于A 中,由111142222323P A BD A PBD V V --==⨯=,1A BD 为等边三角形,面积为11226232A BD =⨯=△S ,设点P 到面1A BD 的距离为h ,由142333h ⨯=,求得23h =所以A不正确;对于B 中,过点P 平行于平面1A BD 的平面被正方体截得的多边形平面11B D C , 此时三角形11B D C 为边长为221226=232⨯B 不正确; 对于C 中,由正方体的结构特征和性质,可得点P 到平面1A BD 23当点P 在线段11B D 上运动时,1max 2PA =(P 为端点时),in 1m 2PA =设直线1PA 与平面1A BD 所成角为θ,则36sin ,33θ∈⎣⎦,所以C 正确;对于D 中,当点P 与1B 重合时,此时三棱锥为11B A BD -,设1B D 的中点为O ,因为11190B BD B A D ∠=∠=︒,可得11OA OB OD OB === 所以三棱锥1P A BD -的外接球的球心为1B D 的中点,其半径为3,所以三棱锥1P A BD -的外接球的体积为34(3)433ππ⨯=,所以D 不正确.故选:C.18.如图,在棱长为33的正方体1111ABCD A B C D -中,点P 是平面11A BC 内一个动点,且满足15213DP PB +=+,则直线1B P 与直线1AD 所成角的取值范围为( )(参考数据:43sin 53,sin 3755==)A .37,143⎡⎤⎣⎦B .37,90⎡⎤⎣⎦C .53,143⎡⎤⎣⎦D .37,127⎡⎤⎣⎦【来源】江西省景德镇一中2020-2021学年高三上学期期末考试数学(理)试题 【答案】B【解析】如图,建立空间直接坐标系,连结1B D ,交平面11A BC 于点O ,()0,0,0D ,()133,33,33B ,()133,0,33A ,()33,33,0B ,()10,33,33C ,()133,33,33DB =,()10,33,33A B =-,()133,0,33BC =-,110DB A B ⋅=,110DB BC ⋅=,111111,DB A B DB BC A B BC B ∴⊥⊥⋂=,,1DB ∴⊥平面11A BC ,根据等体积转化可知111111B A BC B A B C V V --=, 即()()23111311363332232B O ⨯⨯⨯⨯=⨯⨯,解得:13B O =, 13339B D =⨯=,16D O ∴=,11//AD BC ,∴异面直线1AD 与1B P 所成的角,转化为1BC 与1B P 所成的角,如图,将部分几何体分类出来,再建立一个空间直角坐标系,取1BC 的中点E ,过点O 作1//OF BC ,则以点O 为原点,1,,OF OE OB 为,,x y z 轴的正方向,建立空间直角坐标系(),,0P x y ,()10,0,3B ,()0,0,6D -,3326,22B ⎫⎪⎪⎭,13326,22C ⎛⎫ ⎪ ⎪⎝⎭,()1,,3B P x y =-,()136,0,0BC =-, 15213PB PD +=+,22229365213x y x y ++++=+2222936x y x y ++<++,即15PB =22925x y ∴++=,即2216x y +=,[]4,4x ∈-1111113644cos ,,555365B P BC x x B P BC B P BC ⋅-⎡⎤<>===-∈-⎢⎥⨯⎣⎦,因为异面直线所成的角是锐角,并设为θ,则4cos 0,5θ⎛⎤∈ ⎥⎝⎦,4sin 535=,4cos375∴=,37,90θ⎡⎤∴∈⎣⎦ 故选:B19.如图,在三棱锥D ABC -中,,1,1AD BC BC AD ⊥==.且2AB BD AC CD +=+=,则四面体ABCD 的体积的最大值为( )A .14B .212C .36D .524【来源】浙江省衢州市五校联盟2020-2021学年高三上学期期末联考数学试题 【答案】B【解析】作BE ⊥AD 于E ,连接CE ,如图,因为,AD BC ⊥,BE BC 再平面BEC 内相交,所以AD ⊥平面BEC , 因为CE ⊂平面BEC ,所以CE ⊥AD , 因为2AB BD AC CD +=+=,所以B 与C 都是在以A 、D 为焦点的椭球上,且BE 、CE 都垂直于焦距AD , AB +BD = AC +CD =2,显然ABD ACD ≅,所以BE =CE . 取BC 中点F ,,,BC E AD E F F ⊥∴⊥ 要求四面体ABCD 的体积的最大值,因为AD 是定值,只需三角形EBC 的面积最大, 因为BC 是定值,所以只需EF 最大即可,当△ABD 是等腰直角三角形时几何体的体积最大, 因为AB +BD = AC +CD =2,1AB ∴=,22222131121,(1)22222EB EF ⎛⎫⎛⎫⎛⎫∴=-==--= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 所以几何体的体积为11221132212⨯⨯⨯⨯=故选:B20.如图,三棱锥A BCD -的底面BCD 在平面α内,所有棱均相等,E 是棱AC 的中点,若三棱锥A BCD -绕棱CD 旋转,设直线BE 与平面α所成的角为θ,则cos θ的取值范围为( )A .36⎤⎥⎣⎦B .5,16⎡⎤⎢⎥⎣⎦C .110,6⎡⎢⎣⎦D .330,6⎡⎢⎣⎦【来源】浙江省宁波市慈溪市2020-2021学年高三上学期期末数学试题 【答案】A【解析】取AD 的中点F ,连接EF 、BF ,如下图所示:。
2023全国甲卷数学立体几何18题
(1)证明见解析.
(2) 13 13
【基本思路】 (1)根据线面垂直,面面垂直的判定与性质定理可得 A1O 平面 BCC1B1 ,再由勾股定理 求出 O 为中点,即可得证; (2)利用直角三角形求出 AB1 的长及点 A 到面的距离,根据线面角定义直接可得正弦值. 【详细解析】⑴如图,
第 4 页(共 5 页)
由 CM∥A1C1,CM A1C1知四边形 A1CMC1 为平行四边形, C1M∥A1C ,C1M 平面 ABC ,又 AM 平面 ABC ,
C1M AM 则在 Rt△AC1M 中, AM 2AC,C1M A1C , AC1 (2AC)2 A1C2 , 在 Rt△AB1C1 中, AC1 (2AC)2 A1C2 , B1C1 BC 3 ,
(1)证明见解析. (2)1
【基本思路】
(1)由 A1C 平面 ABC 得 A1C BC ,又因为 AC BC ,可证 BC 平面 ACC1A1 ,从而 证得平面 ACC1A1 平面 BCC1B1 ; (2) 过点 A1 作 A1O CC1 ,可证四棱锥的高为 A1O ,由三角形全等可证 A1C AC ,从而证 得 O 为 CC1 中点,设 A1C AC x ,由勾股定理可求出 x ,再由勾股定理即可求 A1O .
AB1 (2 2)2 ( 2)2 ( 3)2 13 , 又 A 到平面 BCC1B1 距离也为 1,
所以 AB1 与平面 BCC1B1 所成角的正弦值为
1 13
13
.
13
第 5 页(共 5 页)
【详细解析】 ⑴证明:因为 A1C 平面 ABC , BC 平面 ABC , 所以 A1C BC , 又因为 ACB 90o,即 AC BC ,
【2022高考必备】2012-2021十年全国高考数学真题分类汇编 立体几何大题(原卷版)
2012-2021十年全国高考数学真题分类汇编 立体几何大题(原卷版)1.(2021年高考全国甲卷理科)已知直三棱柱111ABC A B C -中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 中点,D 为棱11A B 上地点.11BF A B ⊥(1)证明:BF DE ⊥。
(2)当1B D 为何值时,面11BB C C 与面DFE 所成地二面角地正弦值最小?2.(2021年高考全国乙卷理科)如图,四棱锥P ABCD -地底面是矩形,PD ⊥底面ABCD ,1PD DC ==,M 为BC 地中点,且PB AM ⊥.(1)求BC 。
(2)求二面角A PM B --地正弦值.3.(2020年高考数学课标Ⅰ卷理科)如图,D 为圆锥地顶点,O 是圆锥底面地圆心,AE 为底面直径,AE AD =.ABC 是底面地内接正三角形,P 为DO 上一点,PO =.的(1)证明:PA ⊥平面PBC 。
(2)求二面角B PC E --地余弦值.4.(2020年高考数学课标Ⅱ卷理科)如图,已知三棱柱ABC -A 1B 1C 1地底面是正三角形,侧面BB 1C 1C 是矩形,M ,N 分别为BC ,B 1C 1地中点,P 为AM 上一点,过B 1C 1和P 地平面交AB 于E ,交AC 于F .(1)证明:AA 1∥MN ,且平面A 1AMN ⊥EB 1C 1F 。
(2)设O 为△A 1B 1C 1地中心,若AO ∥平面EB 1C 1F ,且AO =AB ,求直线B 1E 与平面A 1AMN 所成角地正弦值.5.(2020年高考数学课标Ⅲ卷理科)如图,在长方体1111ABCD A B C D -中,点,E F 分别在棱11,DD BB 上,且12DE ED =,12BF FB =.(1)证明:点1C 平面AEF 内。
(2)若2AB =,1AD =,13AA =,求二面角1A EF A --地正弦值.6.(2019年高考数学课标Ⅲ卷理科)图1是由矩形ADEB ,Rt △ABC 和菱形BFGC 组成地一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°,将其沿AB ,BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明:图2中地A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何 大题
(17Ι)18.如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠=.
(1)证明:平面PAB ⊥平面PAD ;
(2)若PA =PD =AB =DC ,90APD ∠=,求二面角A -PB -C 的余弦值.
(17П)19.如图,四棱锥P -ABCD 中,侧面PAD 为等比三角形且垂直于底面ABCD ,
o 1,90,2
AB BC AD BAD ABC ==
∠=∠= E 是PD 的中点. (1)证明:直线//CE 平面PAB (2)点M 在棱PC 上,且直线BM 与底面ABCD 所成
锐角为o 45 ,求二面角M -AB -D 的余弦值
(17Ш)19.如图,四面体ABCD 中,△ABC 是正三角形,△ACD 是直角三角形,∠ABD =∠CBD ,AB =BD .
(1)证明:平面ACD ⊥平面ABC ;
(2)过AC 的平面交BD 于点E ,若平面AEC 把四面体ABCD
分成体积相等的两部分,求二面角D –AE –C 的余弦值.
F E A
B C
D (16Ι)(18)如图,在已A ,B ,C ,D ,
E ,
F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,90AFD ∠=,且二面角D -AF -E 与二面角C -BE -F 都是60.
(I )证明;平面ABEF ⊥平面EFDC ;
(II )求二面角E -BC -A 的余弦值.
(16П)(19)如图,菱形ABCD 的对角线AC 与BD 交于点O ,AB =5,AC =6,点E ,F 分别在AD ,CD 上,AE =CF =
,EF 交BD 于点H .将△DEF 沿EF 折到△的位置,.
(I )证明:
平面ABCD ; (II )求二面角的正弦值.
(19)如图,四棱锥P-ABCD 中,PA ⊥地面ABCD ,AD ∥BC ,AB=AD=AC =3,PA=BC =4,M 为线段AD 上一点,AM=2MD ,N 为PC 的中点.
(I )证明MN ∥平面PAB ;
(II )求直线AN 与平面PMN 所成角的正弦值.
(15Ι)(18)如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,
BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC 。
(1)证明:平面AEC ⊥平面AFC
(2)求直线AE 与直线CF 所成角的余弦值
(14Ι)19. 如图三棱锥111ABC A B C -中,侧面11BB C C 为菱形,1AB B C ⊥.
(Ⅰ) 证明:1AC AB =;
(Ⅱ)若1AC AB ⊥,o 160CBB ∠=,AB=Bc ,
求二面角111A A B C --的余弦值.
(14П)18. 如图,四棱锥P-ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点. (Ⅰ)证明:PB ∥平面AEC ;
(Ⅱ)设二面角D-AE-C 为60°,AP=1,AD=3,
求三棱锥E-ACD 的体积.。
