坐标转换计算方式
对数坐标与普通坐标的转换计算

对数坐标与普通坐标的转换计算对数坐标与普通坐标是数学中常见的两种坐标系统。
它们在不同的场景中都有着各自的优势和适用性。
本文将介绍对数坐标与普通坐标的转换计算方法。
普通坐标系统是我们通常使用的坐标系统,也称为直角坐标系统。
在这个坐标系统中,任意点可以表示为一个有序数对(x, y),其中x表示横坐标,y表示纵坐标。
这种表示方法通过两个数值的大小和正负关系来确定点的位置。
而对数坐标系统则是以对数函数为基础的坐标系统。
在对数坐标系统中,数值的大小代表了对数函数的值,而点的位置则通过数值的指数来表示。
对数坐标系统常用于表示非线性关系,可以将数据的广度差异较大的部分更好地展示出来。
在对数坐标系统中,横坐标通常是以对数形式表示的。
常见的对数坐标包括常用对数坐标(以10为底)、自然对数坐标(以e为底)等。
对于对数坐标与普通坐标之间的转换,下面将分别介绍两种情况的计算方法:1.对数坐标转换为普通坐标:对数坐标转换为普通坐标时,我们需要知道坐标轴上的起始点和单位长度。
以常用对数坐标为例,起始点为(0, 0),单位长度为1,指数表示坐标轴上的位置。
假设需要将对数坐标(x, y)转换为普通坐标(X, Y),计算公式如下:X = 10^xY = 10^y例如,对于对数坐标(2, 3):X = 10^2 = 100Y = 10^3 = 1000则对应的普通坐标为(100, 1000)。
2.普通坐标转换为对数坐标:普通坐标转换为对数坐标时,我们需要知道坐标轴上的起始点和单位长度。
以常用对数坐标为例,起始点为(0, 0),单位长度为1,指数表示坐标轴上的位置。
假设需要将普通坐标(X, Y)转换为对数坐标(x, y),计算公式如下:x = log10(X)y = log10(Y)例如,对于普通坐标(100, 1000):x = log10(100) = 2y = log10(1000) = 3则对应的对数坐标为(2, 3)。
以上就是对数坐标与普通坐标之间的转换计算方法。
坐标转换公式详细计算步骤

坐标转换公式详细计算步骤1. 引言嘿,朋友们,今天咱们来聊聊一个听上去有点高深、实际上却超级有趣的话题——坐标转换公式!可能有些小伙伴一听到“坐标”就觉得头大,仿佛在听外星人说话。
其实啊,这就像用不同的语言描述同一个地方,只不过这回我们要把点的位置从一个地方“搬家”到另一个地方,听上去是不是挺简单的?想象一下,你在一个城市里,想把你的小店从市中心搬到郊区。
你会用什么?对了,地图!坐标就是地图上的标记。
现在,我们要的是如何把这些标记从一个地图转换到另一个地图。
是不是挺刺激的?2. 坐标的基本概念2.1 坐标系首先,我们得搞清楚坐标系是个啥。
其实,坐标系就像是一个大舞台,每一个点都是舞台上的演员。
有的坐标系是二维的,比如我们常见的平面图,x轴和y轴就像是舞台的左右两边。
而三维坐标系则多了一条z轴,像是把舞台抬高,给演员多了一点表演的空间。
2.2 坐标的表示好了,了解了坐标系后,咱们得学会如何表示这些坐标。
想象一下,一个点在平面上被表示成(x, y),这就像是这个点的身份证号。
它告诉你这个点在舞台上的确切位置。
对于三维坐标系呢,咱们就加上一个z,比如(x, y, z),这就像是在舞台上多了一个层次感,让表演更丰富。
3. 坐标转换的必要性3.1 为什么要转换你可能会问,为什么我们需要坐标转换呢?哈哈,这就好比你去一个新城市玩,没地图可不行!在不同的坐标系中,我们可能会遇到一些需要转换的情况,比如, GPS 导航中就经常涉及到这个问题。
简单来说,转换可以帮助我们在不同的场合使用不同的坐标系,不管是搞科研,还是逛商场,都是必须的。
3.2 常见的转换公式接下来,咱们进入正题——坐标转换公式。
最常用的两种转换就是从极坐标转到直角坐标,反之亦然。
极坐标呢,就是用角度和距离来描述点的位置,直角坐标则用横纵坐标来描述。
公式如下:从极坐标(r, θ)转换到直角坐标(x, y):。
x = r * cos(θ)y = r * sin(θ)反之,从直角坐标转换到极坐标:r = √(x² + y²)θ = arctan(y/x)哎呀,听上去有点复杂,不过没关系,慢慢来,大家肯定能学会!4. 计算步骤详解4.1 实际示例假设你有一个点的极坐标是(5, 30°),你想把它转换成直角坐标。
直角坐标系坐标变换公式

直角坐标系坐标变换公式在数学中,直角坐标系是描述平面上点位置的一种常用方式。
当需要在不同坐标系之间进行转换时,我们可以利用坐标变换公式来实现。
本文将介绍二维平面上的直角坐标系坐标变换公式。
假设有一个点P在直角坐标系中的坐标为(x, y),现在我们希望将其坐标转换为另一个直角坐标系下的坐标(x’, y’)。
为了实现这一转换,我们需要进行如下的操作:平移首先,我们需要对点P进行平移操作。
设平移向量为(a, b),则点P在新坐标系下的坐标为(x + a, y + b)。
旋转接着,我们可以对点P进行旋转操作。
设旋转角度为θ,旋转中心为原点O(0, 0),则点P在新坐标系下的坐标为:x’ = x * cos(θ) - y * sin(θ) y’ = x * sin(θ) + y * cos(θ)缩放最后,我们可以对点P进行缩放操作。
设缩放比例为(sx, sy),则点P在新坐标系下的坐标为:x’ = x * sx y’ = y * sy综合变换将上述平移、旋转和缩放操作综合起来,我们可以得到点P在新坐标系下的完整变换公式:x’ = (x - xo) * cos(θ) * sx - (y - yo) * sin(θ) * sy + xo y’ = (x - xo) * sin(θ) * sx + (y - yo) * cos(θ) * sy + yo其中(xo, yo)为旋转中心,θ为旋转角度,(sx, sy)为缩放比例。
示例假设在某直角坐标系下,有一个点P(2, 3),希望将其转换到新坐标系下,旋转角度为30度,旋转中心为原点O(0, 0),缩放比例为1.5。
根据上述公式,我们可以计算出点P在新坐标系下的坐标为:x’ = (2 - 0) * cos(30) * 1.5 - (3 - 0) * sin(30) * 1.5 + 0 = 2.366 y’ = (2 - 0) * sin(30) * 1.5 + (3 - 0) * cos(30) * 1.5 + 0 = 3.133因此,点P在新坐标系下的坐标为(2.366, 3.133)。
坐标转换之计算公式+7参+四参模型

坐标转换之计算公式一、参心大地坐标与参心空间直角坐标转换1名词解释:A :参心空间直角坐标系:a) 以参心0为坐标原点;b) Z 轴与参考椭球的短轴(旋转轴)相重合;c) X 轴与起始子午面和赤道的交线重合;d) Y 轴在赤道面上与X 轴垂直,构成右手直角坐标系0-XYZ ;e) 地面点P 的点位用(X ,Y ,Z )表示;B :参心大地坐标系:a) 以参考椭球的中心为坐标原点,椭球的短轴与参考椭球旋转轴重合;b) 大地纬度B :以过地面点的椭球法线与椭球赤道面的夹角为大地纬度B ;c) 大地经度L :以过地面点的椭球子午面与起始子午面之间的夹角为大地经度L ;d) 大地高H :地面点沿椭球法线至椭球面的距离为大地高H ;e) 地面点的点位用(B ,L ,H )表示。
2 参心大地坐标转换为参心空间直角坐标:⎪⎭⎪⎬⎫+-=+=+=B H e N Z L B H N Y L B H N X sin *])1(*[sin *cos *)(cos *cos *)(2公式中,N 为椭球面卯酉圈的曲率半径,e 为椭球的第一偏心率,a 、b 椭球的长短半径,f 椭球扁率,W 为第一辅助系数ab a e 22-= 或 f f e 1*2-= W a N BW e =-=22sin *1(3 参心空间直角坐标转换参心大地坐标[]N BY X H H e N Y X H N Z B XY L -+=+-++==cos ))1(**)()(*arctan()arctan(22222 二 高斯投影及高斯直角坐标系1、高斯投影概述高斯-克吕格投影的条件:1. 是正形投影;2. 中央子午线不变形高斯投影的性质:1. 投影后角度不变;2. 长度比与点位有关,与方向无关;3. 离中央子午线越远变形越大为控制投影后的长度变形,采用分带投影的方法。
常用3度带或6度带分带,城市或工程控制网坐标可采用不按3度带中央子午线的任意带。
2、高斯投影正算公式:522242532236425442232)5814185(cos 120)1(cos 6cos )5861(cos sin 720 495(cos sin 24cos sin 2l t t t B N l t B N Bl N y l t t B B N l t B B N Bl B N X x ηηηηη-++-++-+=+-+++-++=)3、高斯投影反算公式:()()()⎥⎥⎦⎤⎪⎪⎭⎫ ⎝⎛+++⎪⎪⎭⎫ ⎝⎛⎢⎣⎡-++-⎪⎪⎭⎫ ⎝⎛-=⎥⎥⎥⎥⎦⎤⎪⎪⎭⎫ ⎝⎛+++++⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++-⎪⎪⎭⎫ ⎝⎛=442222224222422224590613601 9351211286242851201 )21(611cos 1f f f f f f f f f f f f f f f f f f f f f f f N y t t N y t t N y y M t B B N y t t t N y t N y B l ηηηηη四参数模型:。
平面坐标系之间转换计算
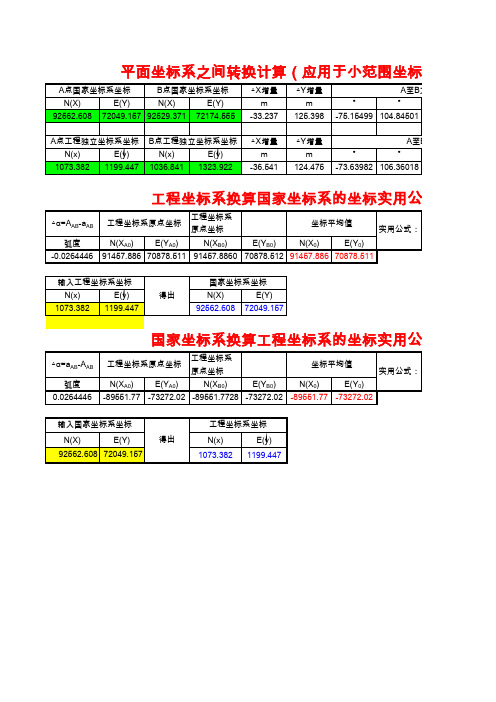
A点国家坐标系坐标 N(X) 92562.608 E(Y) B点国家坐标系坐标 N(X) E(Y) 72174.555 △X增量 m -33.237 △X增量 m -36.541 △Y增量 m 125.398 △Y增量 m 124.475 ° ° ° A至B方位角( ° -75.15499 104.84501 A至B -73.63982 106.36018 72049.157 92529.371
输入工程坐标系坐标 N(x) 1073.382 E(y) 1199.447 得出
国家坐标系坐标 N(X) 92562.608 E(Y) 72049.157
国家坐标系换算工程坐标系的坐标实用公式
△α=aAB-AAB 弧度 0.0264446 工程坐标系原点坐标 N(XA0) E(YA0) 工程坐标系原点坐标 N(XB0) E(YB0) 坐标平均值 N(X0) E(Y0) 实用公式: -89551.77 -73272.02 -89551.7728 -73272.02 -89551.77 -73272.02 工程坐标系坐标 得出 N(x) 1073.382 E(y) 1199.447
标实用公式
xP=Xp*COS(△α)-Y*SIN(△α)+X0 yP=Xp*SIN(△α)+Y*COS(△α)+Y0
A点工程独立坐标系坐标 N(x) 1073.382 E(y) 1199.441 E(y) 1323.922
工程坐标系换算国家坐标系的坐标实用公式
△α=AAB-aAB 弧度 -0.0264446 工程坐标系原点坐标 N(XA0) E(YA0) 工程坐标系原点坐标 N(XB0) E(YB0) 坐标平均值 N(X0) E(Y0) 实用公式: 91457.886 70878.511 91457.8860 70878.512 91457.886 70878.511
坐标系转换问题及转换参数的计算方法

坐标系转换问题及转换参数的计算方法对于坐标系的转换,给很多GPS的使用者造成一些迷惑,尤其是对于刚刚接触的人,搞不明白到底是怎么一回事。
我对坐标系的转换问题,也是一知半解,对于没学过测量专业的人来说,各种参数的搞来搞去实在让人迷糊。
在我有限的理解范围内,我想在这里简单介绍一下,主要是抛砖引玉,希望能引出更多的高手来指点迷津。
我们常见的坐标转换问题,多数为WGS84转换成北京54或西安80坐标系。
其中WGS84坐标系属于大地坐标,就是我们常说的经纬度坐标,而北京54或者西安80属于平面直角坐标。
对于什么是大地坐标,什么是平面直角坐标,以及他们如何建立,我们可以另外讨论。
这里不多罗嗦。
那么,为什么要做这样的坐标转换呢?因为GPS卫星星历是以WGS84坐标系为根据而建立的,我国目前应用的地形图却属于1954年北京坐标系或1980年国家大地坐标系;因为不同坐标系之间存在着平移和旋转关系(WGS84坐标系与我国应用的坐标系之间的误差约为80),所以在我国应用GPS进行绝对定位必须进行坐标转换,转换后的绝对定位精度可由80提高到5-10米。
简单的来说,就一句话,减小误差,提高精度。
下面要说到的,才是我们要讨论的根本问题:如何在WGS84坐标系和北京54坐标系之间进行转换。
说到坐标系转换,还要罗嗦两句,就是上面提到过的椭球模型。
我们都知道,地球是一个近似的椭球体。
因此为了研究方便,科学家们根据各自的理论建立了不同的椭球模型来模拟地球的形状。
而且我们刚才讨论了半天的各种坐标系也是建立在这些椭球基准之上的。
比如北京54坐标系采用的就是克拉索夫斯基椭球模型。
而对应于WGS84坐标系有一个WGS84椭球,其常数采用IUGG第17届大会大地测量常数的推荐值。
WGS84椭球两个最常用的几何常数:长半轴:6378137±2(m);扁率:1:298.257223563之所以说到半长轴和扁率倒数是因为要在不同的坐标系之间转换,就需要转换不同的椭球基准。
坐标转换参数计算

坐标转换参数计算
平移参数:
平移参数是指将一个坐标系中的点平移至另一个坐标系中所需的平移量。
平移参数通常包括x偏移量和y偏移量。
计算平移参数的方法是通过比较两个坐标系中的控制点的坐标值来确定平移量。
通过计算两个坐标系中控制点的x、y坐标值之差,即可得到相应的平移参数。
旋转参数:
旋转参数是指将一个坐标系中的点旋转至另一个坐标系中所需的旋转角度。
旋转参数通常用一个角度或弧度来表示。
计算旋转参数的方法是通过比较两个坐标系中的控制点的坐标值来确定旋转角度。
常用的计算方法包括最小二乘法和最大似然估计法。
缩放参数:
缩放参数是指将一个坐标系中的点缩放至另一个坐标系中所需的缩放比例。
缩放参数通常包括x缩放比例和y缩放比例。
计算缩放参数的方法是通过比较两个坐标系中的控制点的坐标值来确定缩放比例。
通过计算两个坐标系中控制点的x、y坐标值之比,即可得到相应的缩放参数。
其他参数:
除了平移、旋转和缩放参数外,坐标转换还可能涉及其他参数,例如倾斜、挤压等。
这些参数的计算方法与平移、旋转和缩放参数类似,也是通过比较两个坐标系中的控制点的坐标值来确定。
总结:
在进行坐标转换时,常常需要利用一些参数来实现不同坐标系之间的转换。
这些参数包括平移、旋转、缩放以及其他参数。
计算这些参数的方法通常是通过比较两个坐标系中的控制点的坐标值来确定。
通过计算两个坐标系中控制点之间的差异,即可得到相应的转换参数。
不同的坐标转换方法有不同的计算公式和步骤,实际应用时需要根据具体情况选择合适的方法进行计算。
坐标转换计算程序
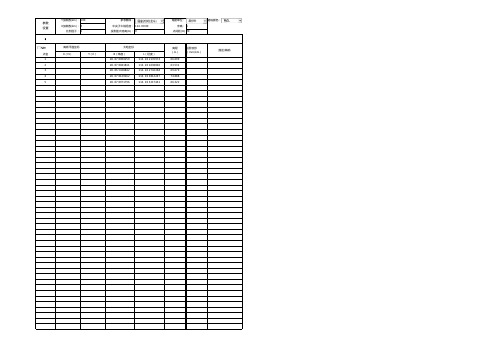
Y加常数(km): 500 X加常数(km): 0
比例因子: 1
高斯平面坐标 X(N)
Y(E)
参考椭球: 中央子午线经度: 114. 00 00 投影面大地高(m): 0
大地坐标 B(纬度)
L(经度)
角度单位: 字高: 5
点间距(m) 20
路线颜色:
高程 (m)
投影变形 (mm/km)
描述/编码
参数 设置
5
点名
Y加常数(km): 500 X加常数(km): 0
比例因子: 1
高斯平面坐标 X(N)
Y(E)
参考椭球: 中央子午线经度: 114. 00 00 投影面大地高(m): 0
大地坐标 B(纬度)
L(经度)
角度单位: 字高: 5
点间距(m) 20
路线颜色:
高程 (m)
投影变形 (mm/km)
描述/编码
参数 设置
5
点名
Y加常数(km): 500 X加常数(km): 0
比例因子: 1
高斯平面坐标 X(N)
Y(E)
参考椭球: 中央子午线经度: 114. 00 00 投影面大地高(m): 0
大地坐标 B(纬度)
L(经度)
角度单位: 字高: 5
点间距(m) 20
路线颜色:
高程 (m)
投影变形 (mm/km)
描述/编码
L(经度) 113. 10 2135974 113. 10 1630002 113. 10 2742368 113. 10 3812247 113. 10 3217441
高程 (m)
66.699 63.531 69.679 74.888 66.322
投影变形 (m点名
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
72绝对坐标转换为相对坐标在直线段施工测量中,可以把绝对坐标转换为相对坐标进行放线测量,此方法比较快捷实用。
如,已知直线段线路中线A点的里程与绝对坐标X1,Y1.和其直线A点至线路前进方向的方位角a。
同样已知附近的控制点Q的绝对坐标QX1,QY1.那么现在为了使用方便,要将其Q点的绝对坐标转换为相对于直线段的相对坐标,计算方法如下:
根据以上所知,根据坐标发算可以得出点A至控制点Q 的距离为L,以及点A至控制点Q方向的方位角简称R。
已知线路中心线前进方向的方位角a,那么由点A至线路前进方向,和点A至控制点Q方向就形成一个夹角r,r=R-a。
现在做控制点到线路中线的垂直线Y,(也就是所谓的Y坐标数据)。
根据直角三角形计算方式得出Y=SIN r×L(L,是点A至点Q的距离)那么相对于线路X的坐标计算方式(X坐标表示里程)。
X=COSr×L+A点里程。
即得出控制点Q相对于直线的相对坐标。
例题:例如,ZDK400至ZDK700为直线段,已知里程400的线路中心线坐标X=22580.40165 Y=27356.42893 里程700的线路中心线坐标X=22558.58105 Y=27655.63522
欲求J2点X=22562.1789 Y=27510.4874相对于400至700的相对坐标,图示如下:
解:根据已知,经过坐标反算可以求得点A至点B的坐标方位角为94 10 16 AB距离为300。
A 至D的坐标方位角为96 44 45.26 距离为155.132 那么可求得角FAD=2 34 29.26
因现已知AD=155.132 角FAD=2 24 29.26
根据三角函数可计算DF=sinfa d×AD=0.045×155.132=6.969 AF=cosfad×AD=0.999×155.132=154.975。
